Dynamical Multimodality in Systems Driven by Ornstein–Uhlenbeck Noise
Abstract
1. Introduction
2. Model and Results
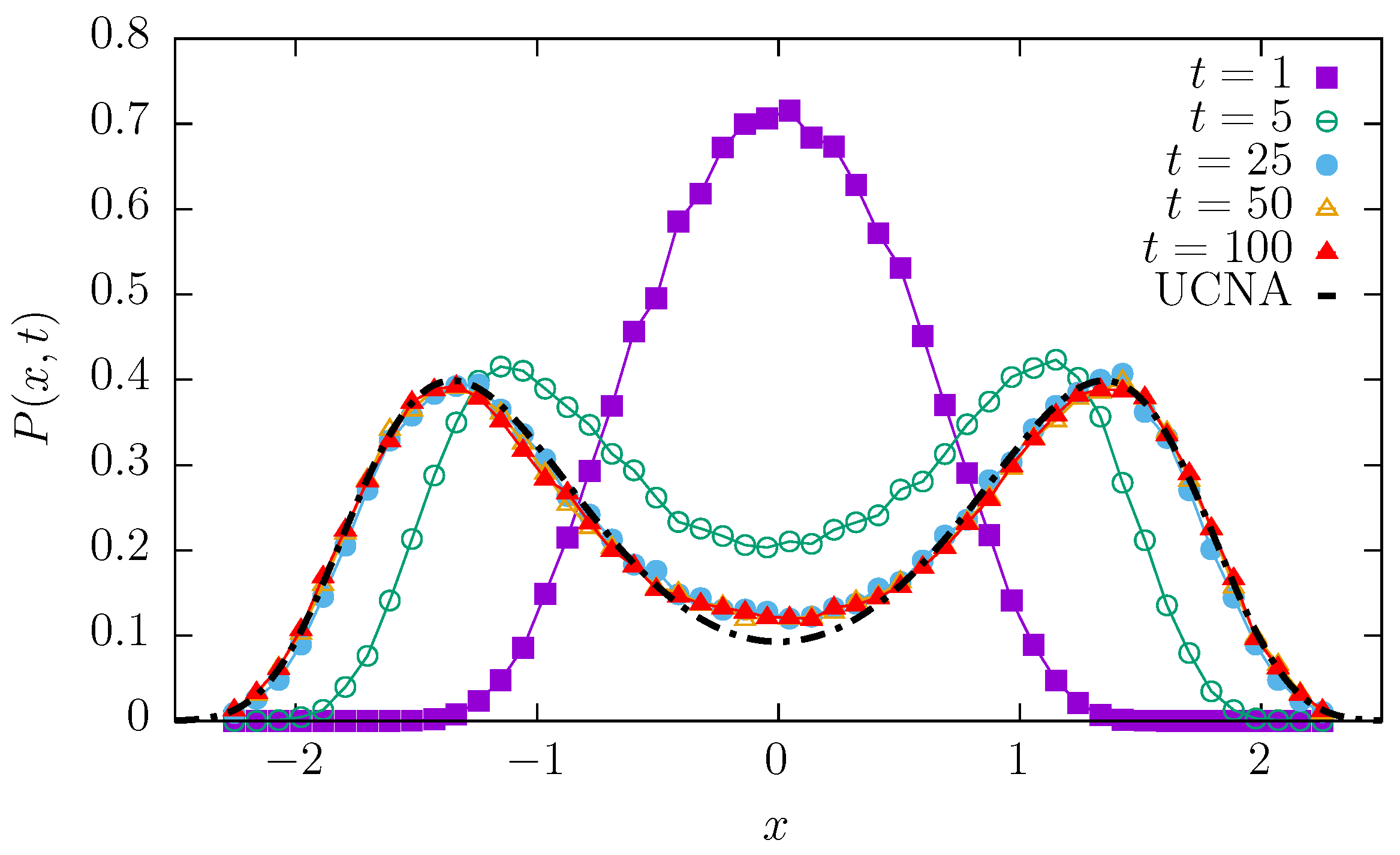
2.1. Test Bench: Static Potentials
2.2. Proper Model: Random Potentials
2.2.1. One-Dimensional Random Potentials
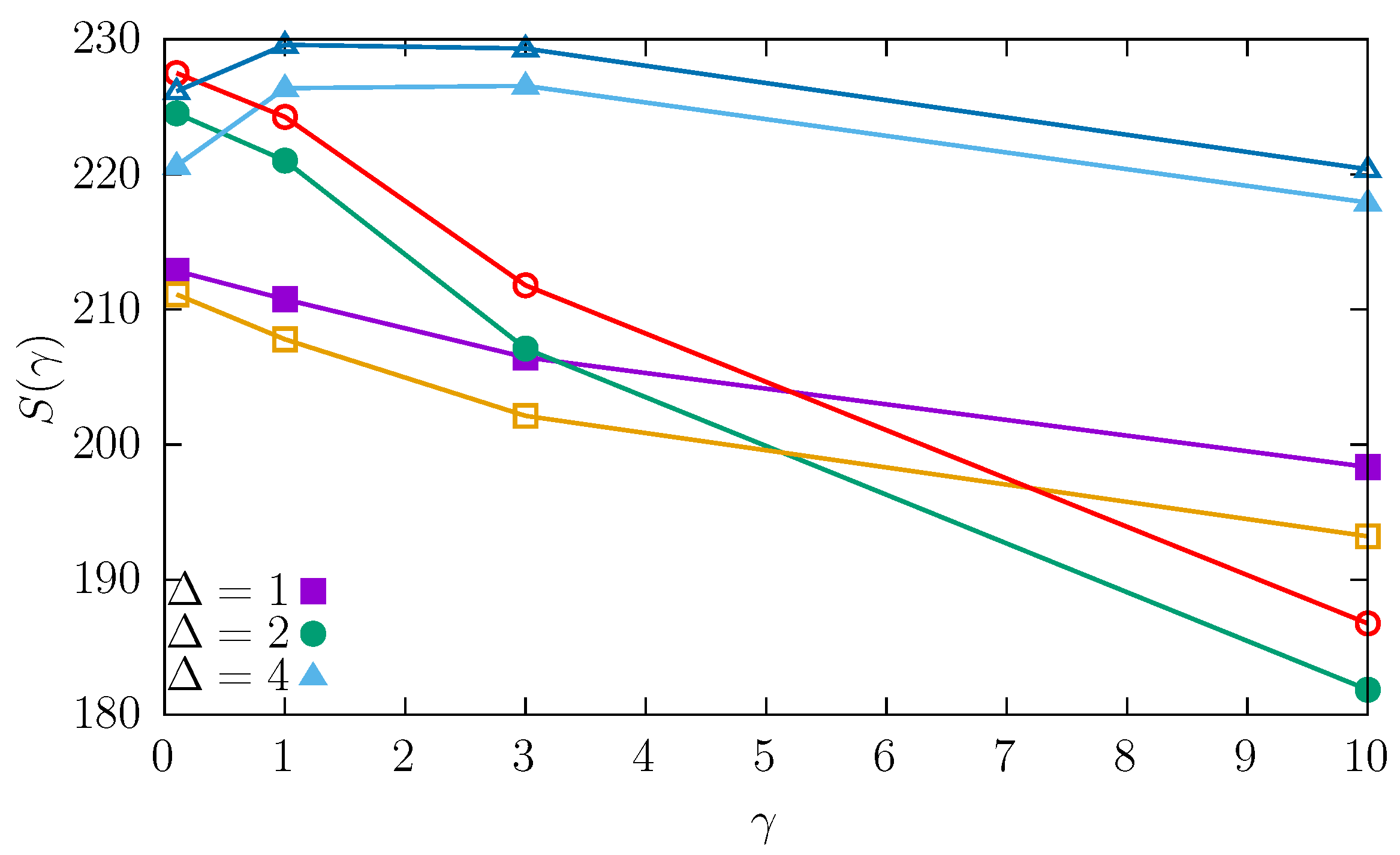
2.2.2. Two-Dimensional Random Potentials
3. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DN | dichotomous noise |
| GWN | Gaussian white noise |
| OU | Ornstein–Uhlenbeck |
| UCNA | unified colored noise approximation |
References
- Horsthemke, W.; Lefever, R. Noise-Inducted Transitions. Theory and Applications in Physics, Chemistry, and Biology; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Dubkov, A.A.; Spagnolo, B.; Uchaikin, V.V. Lévy flight superdiffusion: An introduction. Int. J. Bifurc. Chaos. Appl. Sci. Eng. 2008, 18, 2649–2672. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Risken, H. Fokker-Planck Equation. In The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Łuczka, J. An approximate master equation for systems driven by linear Ornstein-Uhlenbeck noise. Phys. A 1988, 153, 619–635. [Google Scholar] [CrossRef]
- Łuczka, J.; Sadkowski, J. A new approximate stationary probability distribution for processes driven by Ornstein-Uhlenbeck noise. J. Phys. A Math. Gen. 1988, 21, L1169. [Google Scholar] [CrossRef]
- Hanggi, P.; Mroczkowski, T.J.; Moss, F.; McClintock, P. Bistability driven by colored noise: Theory and experiment. Phys. Rev. A 1985, 32, 695. [Google Scholar] [CrossRef]
- Gang, H.; Haken, H. Steepest-descent approximation of stationary probability distribution of systems driven by weak colored noise. Phys. Rev. A 1990, 41, 7078. [Google Scholar] [CrossRef]
- Wilkinson, M. Perturbation theory for a stochastic process with Ornstein-Uhlenbeck noise. J. Stat. Phys. 2010, 139, 345–353. [Google Scholar] [CrossRef]
- Hasegawa, H. A moment approach to non-Gaussian colored noise. Phys. A 2007, 384, 241–258. [Google Scholar] [CrossRef]
- Jung, P.; Hänggi, P. Dynamical systems: A unified colored-noise approximation. Phys. Rev. A 1987, 35, 4464. [Google Scholar] [CrossRef]
- Jacquet, Q.; Kim, E.j.; Hollerbach, R. Time-Dependent Probability Density Functions and Attractor Structure in Self-Organised Shear Flows. Entropy 2018, 20, 613. [Google Scholar] [CrossRef]
- Guggenberger, T.; Chechkin, A.; Metzler, R. Fractional Brownian motion in superharmonic potentials and non-Boltzmann stationary distributions. J. Phys. A Math. Theor. 2021, 54, 29LT01. [Google Scholar] [CrossRef]
- Guggenberger, T.; Chechkin, A.; Metzler, R. Absence of stationary states and non-Boltzmann distributions of fractional Brownian motion in shallow external potentials. New J. Phys. 2022, 24, 073006. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Klafter, J.; Metzler, R. Fundamentals of Lévy flight processes. In Fractals, Diffusion, and Relaxation in Disordered Complex Systems: Advances in Chemical Physics, Part B; Coffey, W.T., Kalmykov, Y.P., Eds.; John Wiley & Sons: New York, NY, USA, 2006; Volume 133, pp. 439–496. [Google Scholar]
- Chechkin, A.V.; Metzler, R.; Klafter, J.; Gonchar, V.Y. Introduction to the theory of Lévy flights. In Anomalous Transport: Foundations and Applications; Klages, R., Radons, G., Sokolov, I.M., Eds.; Wiley-VCH: Weinheim, Germany, 2008; pp. 129–162. [Google Scholar]
- Capała, K.; Dybiec, B. Multimodal stationary states in symmetric single-well potentials driven by Cauchy noise. J. Stat. Mech. 2019, 033206. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E. Lévy stable noise induced transitions: Stochastic resonance, resonant activation and dynamic hysteresis. J. Stat. Mech. 2009, 05004. [Google Scholar] [CrossRef]
- Solomon, T.H.; Weeks, E.R.; Swinney, H.L. Chaotic advection in a two-dimensional flow: Lévy flights and anomalous diffusion. Phys. D 1994, 76, 70–84. [Google Scholar] [CrossRef]
- del Castillo-Negrete, D. Asymmetric transport and non-Gaussian statistics of passive scalars in vortices in shear. Phys. Fluids 1998, 10, 576. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Szydłowski, M. Fractional kinetics for relaxation and superdiffusion in a magnetic field. Phys. Plasmas 2002, 9, 78–88. [Google Scholar] [CrossRef]
- del Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Nondiffusive transport in plasma turbulence: A fractional diffusion approach. Phys. Rev. Lett. 2005, 94, 065003. [Google Scholar] [CrossRef]
- Katori, H.; Schlipf, S.; Walther, H. Anomalous Dynamics of a Single Ion in an Optical Lattice. Phys. Rev. Lett. 1997, 79, 2221–2224. [Google Scholar] [CrossRef]
- Peng, C.K.; Mietus, J.; Hausdorff, J.M.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef] [PubMed]
- Segev, R.; Benveniste, M.; Hulata, E.; Cohen, N.; Palevski, A.; Kapon, E.; Shapira, Y.; Ben-Jacob, E. Long Term Behavior of Lithographically Prepared In Vitro Neuronal Networks. Phys. Rev. Lett. 2002, 88, 118102. [Google Scholar] [CrossRef] [PubMed]
- Lomholt, M.A.; Ambjörnsson, T.; Metzler, R. Optimal target search on a fast-folding polymer chain with volume exchange. Phys. Rev. Lett. 2005, 95, 260603. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Lefebvre, M. Moment generating function of a first hitting place for the integrated Ornstein-Uhlenbeck process. Stoch. Proc. Appl. 1989, 32, 281–287. [Google Scholar] [CrossRef]
- Garbaczewski, P.; Olkiewicz, R. Ornstein-Uhlenbeck-Cauchy Process. J. Math. Phys. 2000, 41, 6843–6860. [Google Scholar] [CrossRef]
- Mallick, K.; Marcq, P. Scaling Behavior of a Nonlinear Oscillator with Additive Noise, White and Colored. Eur. Phys. J. B 2003, 31, 553–561. [Google Scholar] [CrossRef]
- Mallick, K.; Marcq, P. On the Stochastic Pendulum with Ornstein-Uhlenbeck Noise. J. Phys. A Math. Gen. 2004, 37, 4769–4785. [Google Scholar] [CrossRef]
- Mallick, K.; Marcq, P. Anharmonic Oscillator Driven by Additive Ornstein-Uhlenbeck Noise. J. Stat. Phys. 2005, 119, 1–33. [Google Scholar] [CrossRef]
- Mannella, R. A Gentle Introduction to the Integration of Stochastic Differential Equations. In Stochastic Processes in Physics, Chemistry, and Biology; Freund, J.A., Pöschel, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 353–364. [Google Scholar]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Mandrysz, M.; Dybiec, B. Energetics of the undamped stochastic harmonic oscillator. Acta Phys. Pol. B 2018, 49, 871–882. [Google Scholar] [CrossRef]
- Mandrysz, M.; Dybiec, B. Energetics of single-well undamped stochastic oscillators. Phys. Rev. E 2019, 99, 012125. [Google Scholar] [CrossRef]
- Dybiec, B. Multimodality in systems driven by Ornstein–Uhlenbeck noise. Chaos 2024, 34, 113105. [Google Scholar] [CrossRef]
- Kłosek-Dygas, M.M.; Matkowsky, B.J.; Schuss, Z. Uniform asymptotic expansions in dynamical systems driven by colored noise. Phys. Rev. A 1988, 38, 2605–2613. [Google Scholar] [CrossRef]
- Van den Broeck, C. On the Relation between White Shot Noise, Gaussian-white Noise and the Dichotomic Markov Process. J. Stat. Phys. 1983, 31, 467. [Google Scholar] [CrossRef]
- Bena, I.; Van den Broeck, C.; Kawai, R.; Lindenberg, K. Drift by dichotomous Markov noise. Phys. Rev. E 2003, 68, 041111. [Google Scholar] [CrossRef]
- Dybiec, B.; Schimansky-Geier, L. Emergence of bimodality in noisy systems with single-well potential. Eur. Phys. J. B 2007, 57, 313. [Google Scholar] [CrossRef]
- Calisto, H.; Bologna, M.; Chandía, K.J. Forced dichotomic diffusion in a viscous media. Eur. Phys. J. B 2017, 90, 24. [Google Scholar] [CrossRef]
- Dong, Y.; Deng, Y.; Wu, J. Bimodal distribution of path multiplicity in random networks. Chaos Solitons Fractals 2025, 193, 116124. [Google Scholar] [CrossRef]
- Lobo, J.M.; Favila, M.E. Different ways of constructing octaves and their consequences on the prevalence of the bimodal species abundance distribution. Oikos 1999, 87, 321–326. [Google Scholar] [CrossRef]
- Turley, M.C.; Ford, E.D. Detecting bimodality in plant size distributions and its significance for stand development and competition. Oecologia 2011, 167, 991–1003. [Google Scholar] [CrossRef]
- Pawar, S.; Dell, A.I.; Lin, T.; Wieczynski, D.J.; Savage, V.M. Interaction dimensionality scales up to generate bimodal consumer-resource size-ratio distributions in ecological communities. Front. Ecol. Evol. 2019, 7, 202. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandrysz, M.; Dybiec, B. Dynamical Multimodality in Systems Driven by Ornstein–Uhlenbeck Noise. Entropy 2025, 27, 263. https://doi.org/10.3390/e27030263
Mandrysz M, Dybiec B. Dynamical Multimodality in Systems Driven by Ornstein–Uhlenbeck Noise. Entropy. 2025; 27(3):263. https://doi.org/10.3390/e27030263
Chicago/Turabian StyleMandrysz, Michał, and Bartłomiej Dybiec. 2025. "Dynamical Multimodality in Systems Driven by Ornstein–Uhlenbeck Noise" Entropy 27, no. 3: 263. https://doi.org/10.3390/e27030263
APA StyleMandrysz, M., & Dybiec, B. (2025). Dynamical Multimodality in Systems Driven by Ornstein–Uhlenbeck Noise. Entropy, 27(3), 263. https://doi.org/10.3390/e27030263





