Improved Ionization Potential Depression Model Incorporating Dynamical Structure Factors and Electron Degeneracy for Non-Ideal Plasma Composition
Abstract
1. Introduction
2. Methods
2.1. Saha Equation
2.2. IPD Models and Dynamical Structure Factor Approach
2.3. Inclusion of the Electron Degeneracy
2.4. The Algorithm for Solving the Saha Equation
- Initial guess: Start with an initial guess for . Also, find by using another model explicitly expressed in terms of and . For instance,where is the effective charge state of the ion [40].
- Check convergence: Compare the recalculated with the previous value. If the difference exceeds the desired accuracy, use the recalculated as the guess values.
- Converge: Iterate until the difference between the calculated and guess falls below the predefined accuracy.
3. Results and Discussion
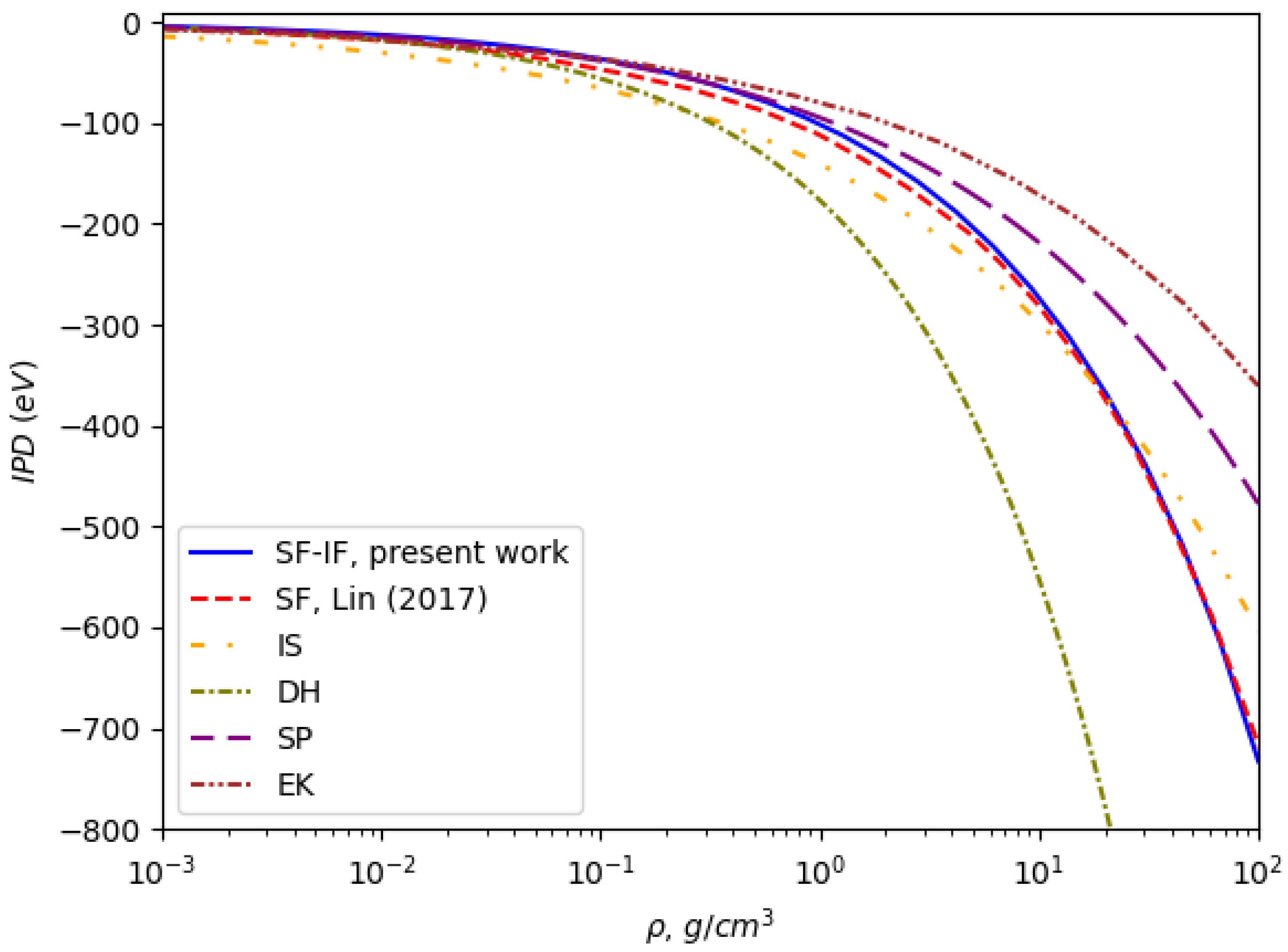
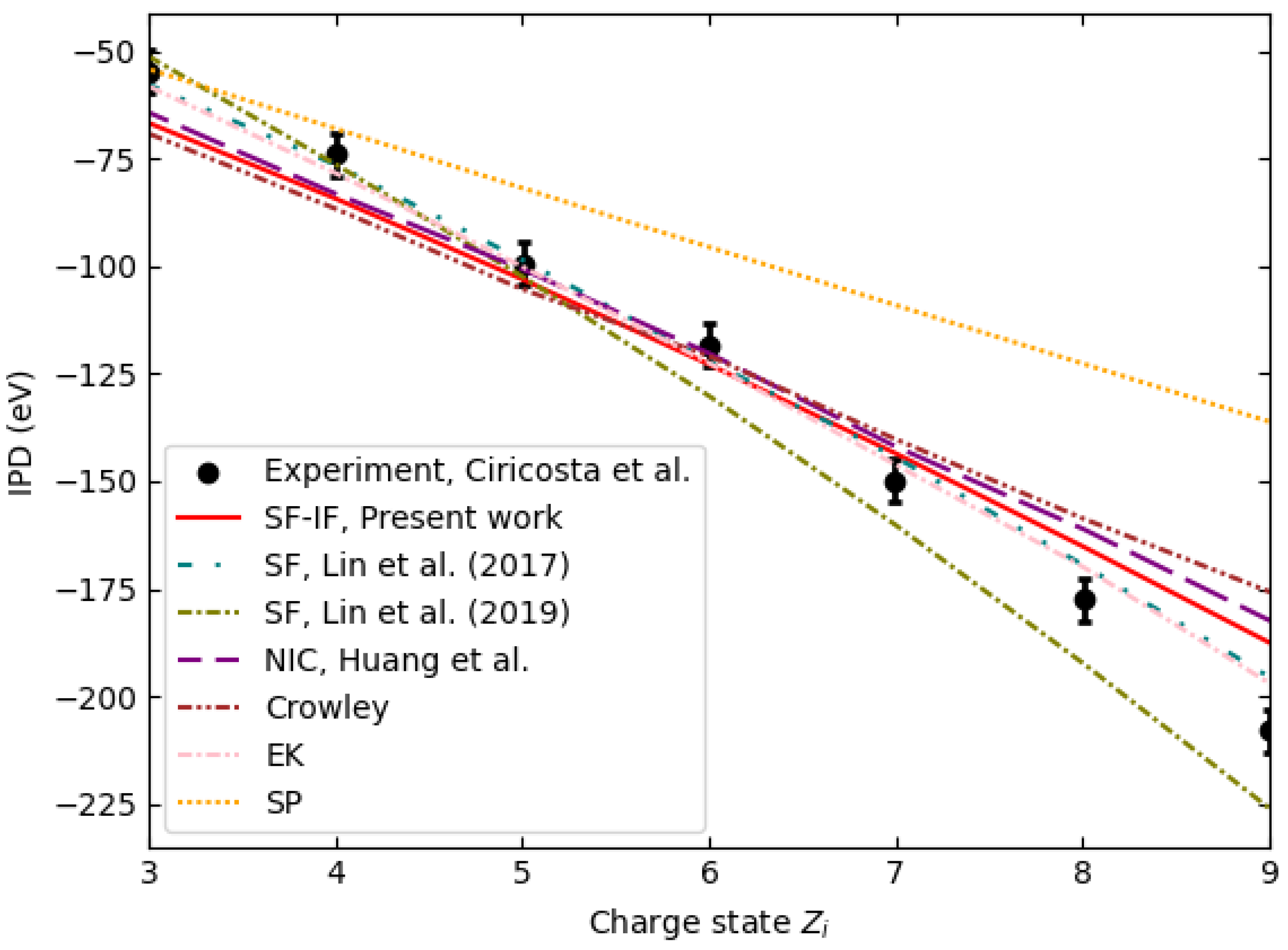
3.1. Ionization Potential Depression
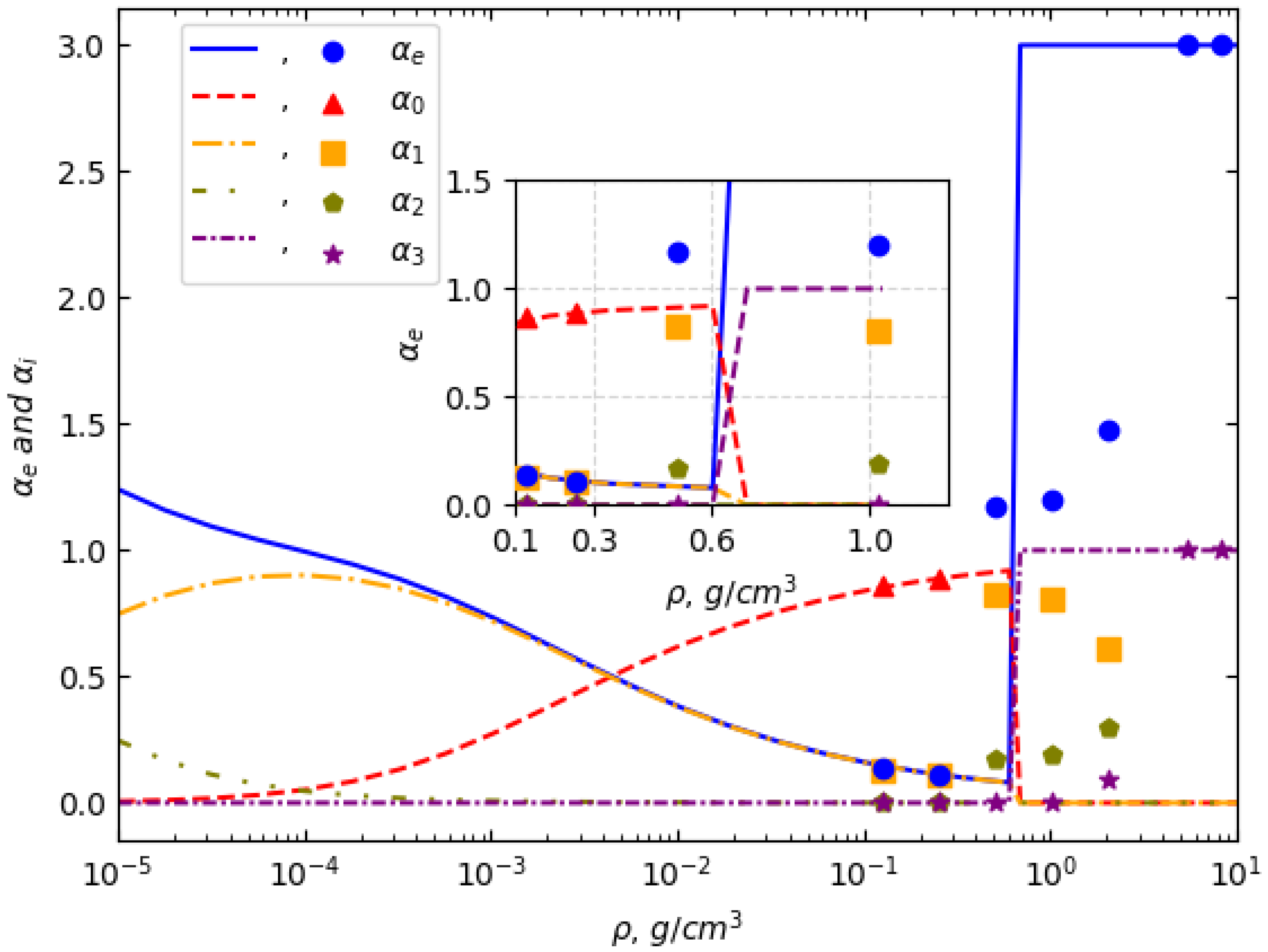
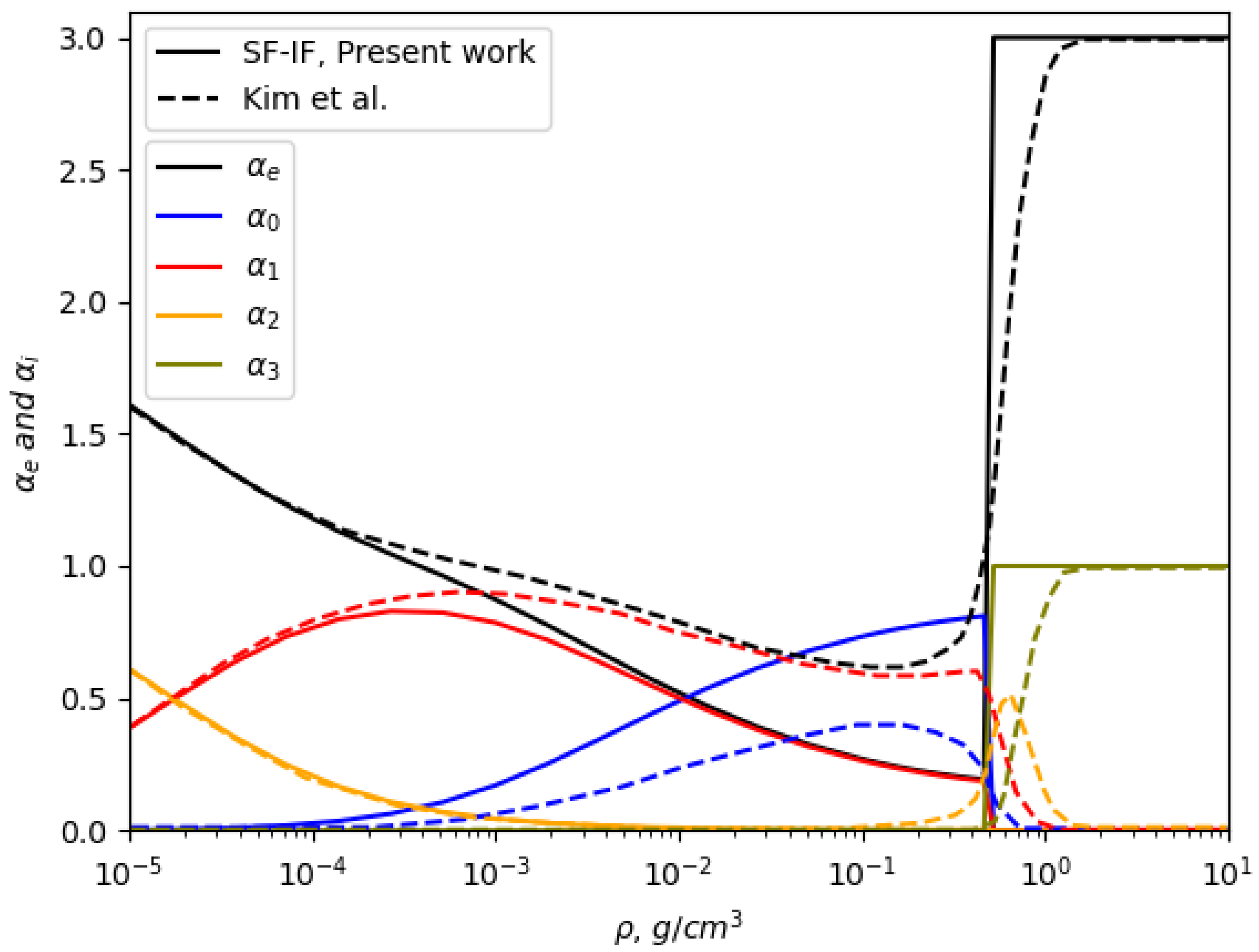
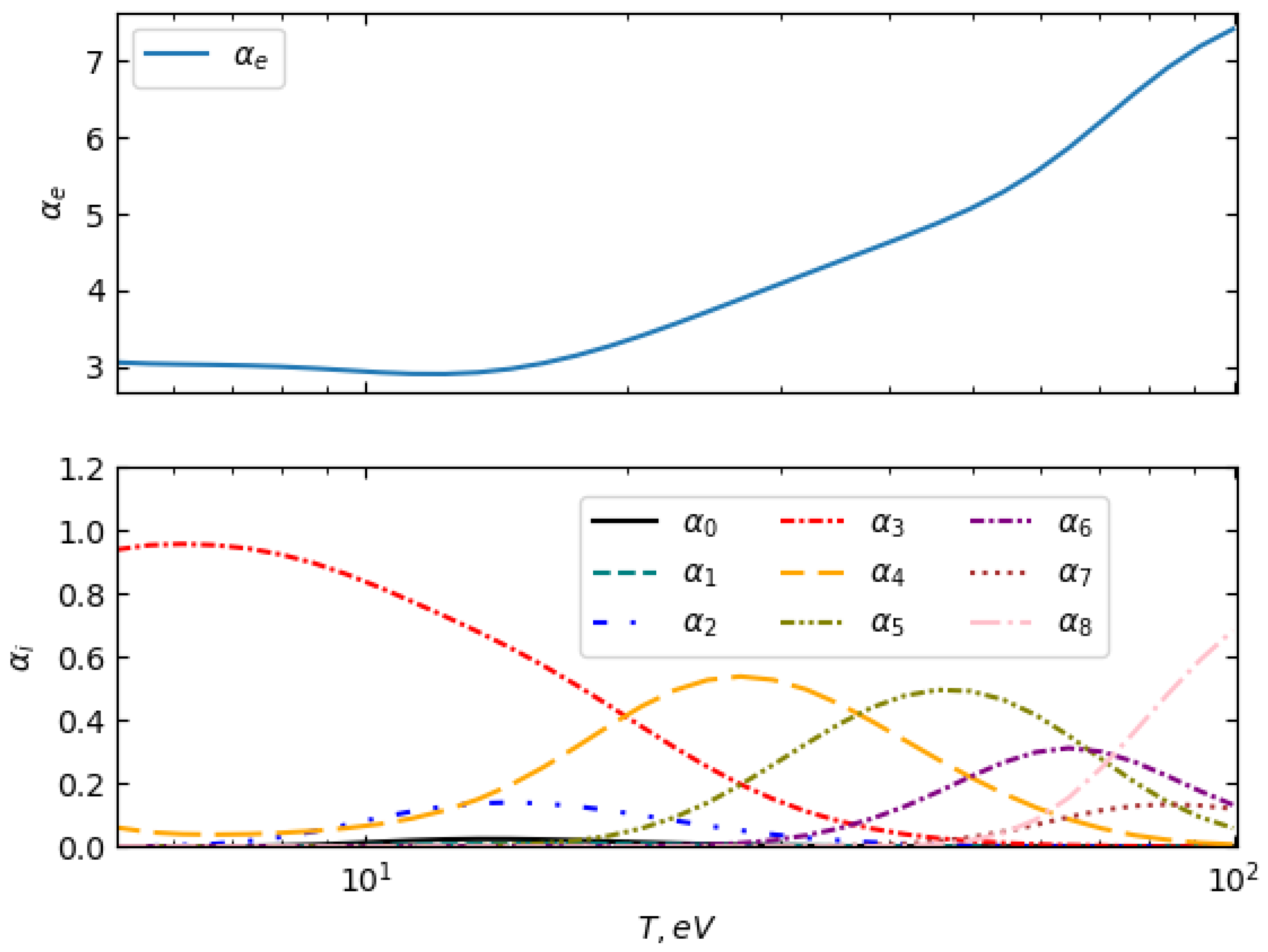
3.2. Plasma Composition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ciricosta, O.; Vinko, S.M.; Chung, H.K.; Cho, B.I.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Engelhorn, K.; Falcone, R.W.; Graves, C.; et al. Direct Measurements of the Ionization Potential Depression in a Dense Plasma. Phys. Rev. Lett. 2012, 109, 065002. [Google Scholar] [CrossRef] [PubMed]
- Ciricosta, O.; Vinko, S.M.; Barbrel, B.; Rackstraw, D.S.; Preston, T.R.; Burian, T.; Chalupský, J.; Cho, B.I.; Chung, H.K.; Dakovski, G.L.; et al. Measurements of continuum lowering in solid-density plasmas created from elements and compounds. Nat. Commun. 2016, 7, 11713. [Google Scholar] [CrossRef]
- Fletcher, L.; Kritcher, A.; Pak, A.; Ma, T.; Döppner, T.; Fortmann, C.; Divol, L.; Jones, O.; Landen, O.; Scott, H.; et al. Observations of Continuum Depression in Warm Dense Matter with X-Ray Thomson Scattering. Phys. Rev. Lett. 2014, 112, 145004. [Google Scholar] [CrossRef]
- Hoarty, D.J.; Allan, P.; James, S.F.; Brown, C.R.D.; Hobbs, L.M.R.; Hill, M.P.; Harris, J.W.O.; Morton, J.; Brookes, M.G.; Shepherd, R.; et al. Observations of the Effect of Ionization-Potential Depression in Hot Dense Plasma. Phys. Rev. Lett. 2013, 110, 265003. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.X.; Bishel, D.T.; Chin, D.A.; Nilson, P.M.; Karasiev, V.V.; Golovkin, I.E.; Gu, M.; Hansen, S.B.; Mihaylov, D.I.; Shaffer, N.R.; et al. Probing atomic physics at ultrahigh pressure using laser-driven implosions. Nat. Commun. 2022, 13, 6780. [Google Scholar] [CrossRef] [PubMed]
- Kraus, D.; Bachmann, B.; Barbrel, B.; Falcone, R.W.; Fletcher, L.B.; Frydrych, S.; Gamboa, E.J.; Gauthier, M.; Gericke, D.O.; Glenzer, S.H.; et al. Characterizing the ionization potential depression in dense carbon plasmas with high-precision spectrally resolved X-ray scattering. Plasma Phys. Control. Fusion 2019, 61, 014015. [Google Scholar] [CrossRef]
- Kraus, D.; Chapman, D.A.; Kritcher, A.L.; Baggott, R.A.; Bachmann, B.; Collins, G.W.; Glenzer, S.H.; Hawreliak, J.A.; Kalantar, D.H.; Landen, O.L.; et al. X-ray scattering measurements on imploding CH spheres at the National Ignition Facility. Phys. Rev. E 2016, 94, 011202. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.M.; Ciricosta, O.; Wark, J.S. Density functional theory calculations of continuum lowering in strongly coupled plasmas. Nat. Commun. 2014, 5, 3533. [Google Scholar] [CrossRef]
- Rogers, F.J. Ionization equilibrium and equation of state in strongly coupled plasmas. Phys. Plasmas 2000, 7, 51–58. [Google Scholar] [CrossRef]
- Calisti, A.; Ferri, S.; Talin, B. Ionization potential depression for non equilibrated aluminum plasmas. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 224003. [Google Scholar] [CrossRef][Green Version]
- Dai, J.; Hou, Y.; Yuan, J. Unified First Principles Description from Warm Dense Matter to Ideal Ionized Gas Plasma: Electron-Ion Collisions Induced Friction. Phys. Rev. Lett. 2010, 104, 245001. [Google Scholar] [CrossRef] [PubMed]
- Perrot, F.; Dharma-wardana, M.W.C. Equation of state and transport properties of an interacting multispecies plasma: Application to a multiply ionized Al plasma. Phys. Rev. E 1995, 52, 5352–5367. [Google Scholar] [CrossRef] [PubMed]
- Magro, W.R.; Ceperley, D.M.; Pierleoni, C.; Bernu, B. Molecular Dissociation in Hot, Dense Hydrogen. Phys. Rev. Lett. 1996, 76, 1240–1243. [Google Scholar] [CrossRef] [PubMed]
- Stransky, M. Monte Carlo simulations of ionization potential depression in dense plasmas. Phys. Plasmas 2016, 23, 012708. [Google Scholar] [CrossRef]
- Lısal, M.; Smith, W.R.; Nezbeda, I. Computer simulation of the thermodynamic properties of high-temperature chemically-reacting plasmas. J. Chem. Phys. 2000, 113, 4885–4895. [Google Scholar] [CrossRef]
- Saha, M.N. Ionization in the solar chromosphere. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1920, 40, 472–488. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D., Jr. Lowering of Ionization Potentials in Plasmas. Astrophys. J. 1966, 144, 1203. [Google Scholar] [CrossRef]
- Ecker, G.; Kröll, W. Lowering of the Ionization Energy for a Plasma in Thermodynamic Equilibrium. Phys. Fluids 1963, 6, 62–69. [Google Scholar] [CrossRef]
- Son, S.K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-Mechanical Calculation of Ionization-Potential Lowering in Dense Plasmas. Phys. Rev. E 2014, 4, 031004. [Google Scholar] [CrossRef]
- Lin, C.; Röpke, G.; Kraeft, W.D.; Reinholz, H. Ionization potential depression and dynamical structure factor in dense plasmas. Phys. Rev. E 2017, 96, 013202. [Google Scholar] [CrossRef] [PubMed]
- Crowley, B. Continuum lowering—A new perspective. High Energy Density Phys. 2014, 13, 84–102. [Google Scholar] [CrossRef]
- Davletov, A.E.; Arkhipov, Y.V.; Mukhametkarimov, Y.S.; Yerimbetova, L.T.; Tkachenko, I.M. Generalized chemical model for plasmas with application to the ionization potential depression. New J. Phys. 2023, 25, 063019. [Google Scholar] [CrossRef]
- Rosmej, F.B. Ionization potential depression in an atomic-solid-plasma picture. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 09LT01. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Y.; Hou, Y.; Gao, C.; Yuan, J. Ionization potential depression and ionization balance in dense carbon plasma under solar and stellar interior conditions. Astron. Astrophys. 2020, 644, A92. [Google Scholar] [CrossRef]
- Colonna, G.; Laricchiuta, A. Thermodynamic and Transport Properties of Equilibrium Debye Plasmas. Entropy 2020, 22, 237. [Google Scholar] [CrossRef] [PubMed]
- Lin, C. Quantum statistical approach for ionization potential depression in multi-component dense plasmas. Phys. Plasmas 2019, 26, 122707. [Google Scholar] [CrossRef]
- Zaghloul, M.R.; Bourham, M.A.; Doster, J.M. A simple formulation and solution strategy of the Saha equation for ideal and nonideal plasmas. J. Phys. D Appl. Phys. 2000, 33, 977–984. [Google Scholar] [CrossRef]
- Zaghloul, M.R. Reduced formulation and efficient algorithm for the determination of equilibrium composition and partition functions of ideal and nonideal complex plasma mixtures. Phys. Rev. E 2004, 69, 026702. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.K.; Kim, I. Calculation of ionization balance and electrical conductivity in nonideal aluminum plasma. Phys. Rev. E 2003, 68, 056410. [Google Scholar] [CrossRef] [PubMed]
- Griem, H.R. High-Density Corrections in Plasma Spectroscopy. Phys. Rev. 1962, 128, 997–1003. [Google Scholar] [CrossRef]
- Zimmerman, G.B.; More, R.M. Pressure ionization in laser-fusion target simulation. J. Quant. Spectrosc. Radiat. Transf. 1980, 23, 517–522. [Google Scholar] [CrossRef]
- Scott, H.A. Cretin—A radiative transfer capability for laboratory plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 689–701. [Google Scholar] [CrossRef]
- Chung, H.K.; Chen, M.; Morgan, W.; Ralchenko, Y.; Lee, R. FLYCHK: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Phys. 2005, 1, 3–12. [Google Scholar] [CrossRef]
- Lee, Y.T. A model for ionization balance and L-shell spectroscopy of non-LTE plasmas. J. Quant. Spectrosc. Radiat. Transf. 1987, 38, 131–145. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Sterne, P.A. Fluctuations and the ionization potential in dense plasmas. High Energy Density Phys. 2013, 9, 103–107. [Google Scholar] [CrossRef]
- Gregori, G.; Ravasio, A.; Höll, A.; Glenzer, S.; Rose, S. Derivation of the static structure factor in strongly coupled non-equilibrium plasmas for X-ray scattering studies. High Energy Density Phys. 2007, 3, 99–108. [Google Scholar] [CrossRef]
- Stanton, L.G.; Murillo, M.S. Unified description of linear screening in dense plasmas. Phys. Rev. E 2015, 91, 033104. [Google Scholar] [CrossRef]
- Moldabekov, Z. Quantum Fluid Description of Dense Plasmas. Ph.D. Thesis, Christian-Albrechts-University of Kiel, Faculty of Mathematics and Natural Sciences, Kiel, Germany, 2018. [Google Scholar]
- Kremp, D.; Schlanges, M.; Kraeft, W.D.; Bornath, T. Quantum Statistics of Nonideal Plasmas; Number 25 in Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Drawin, H.W.; Felenbok, P. Data for Plasmas in Local Thermodynamic Equilibrium; Gauthier-Villars: Paris, France, 1965. [Google Scholar]
- Renner, O.; Rosmej, F.B. Challenges of x-ray spectroscopy in investigations of matter under extreme conditions. Matter Radiat. Extrem. 2019, 4, 024201. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, Z.; Zeng, J.; Yuan, J. Nonideal effects on ionization potential depression and ionization balance in dense Al and Au plasmas. Phys. Rev. E 2024, 109, 045210. [Google Scholar] [CrossRef]
- Sarkisov, G.S.; Rosenthal, S.E.; Cochrane, K.R.; Struve, K.W.; Deeney, C.; McDaniel, D.H. Nanosecond electrical explosion of thin aluminum wires in a vacuum: Experimental and computational investigations. Phys. Rev. E 2005, 71, 046404. [Google Scholar] [CrossRef] [PubMed]
- Redmer, R. Electrical conductivity of dense metal plasmas. Phys. Rev. E 1999, 59, 1073–1081. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Y.; Hou, Y.; Yuan, J. Nonideal effect of free electrons on ionization equilibrium and radiative property in dense plasmas. Phys. Rev. E 2023, 107, L033201. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seitkozhanov, Y.; Dzhumagulova, K.; Shalenov, E. Improved Ionization Potential Depression Model Incorporating Dynamical Structure Factors and Electron Degeneracy for Non-Ideal Plasma Composition. Entropy 2025, 27, 253. https://doi.org/10.3390/e27030253
Seitkozhanov Y, Dzhumagulova K, Shalenov E. Improved Ionization Potential Depression Model Incorporating Dynamical Structure Factors and Electron Degeneracy for Non-Ideal Plasma Composition. Entropy. 2025; 27(3):253. https://doi.org/10.3390/e27030253
Chicago/Turabian StyleSeitkozhanov, Yeldos, Karlygash Dzhumagulova, and Erik Shalenov. 2025. "Improved Ionization Potential Depression Model Incorporating Dynamical Structure Factors and Electron Degeneracy for Non-Ideal Plasma Composition" Entropy 27, no. 3: 253. https://doi.org/10.3390/e27030253
APA StyleSeitkozhanov, Y., Dzhumagulova, K., & Shalenov, E. (2025). Improved Ionization Potential Depression Model Incorporating Dynamical Structure Factors and Electron Degeneracy for Non-Ideal Plasma Composition. Entropy, 27(3), 253. https://doi.org/10.3390/e27030253





