An Improved GAS Algorithm
Abstract
1. Introduction
2. Define CPBO Problem
Penalty Factors and Initial States
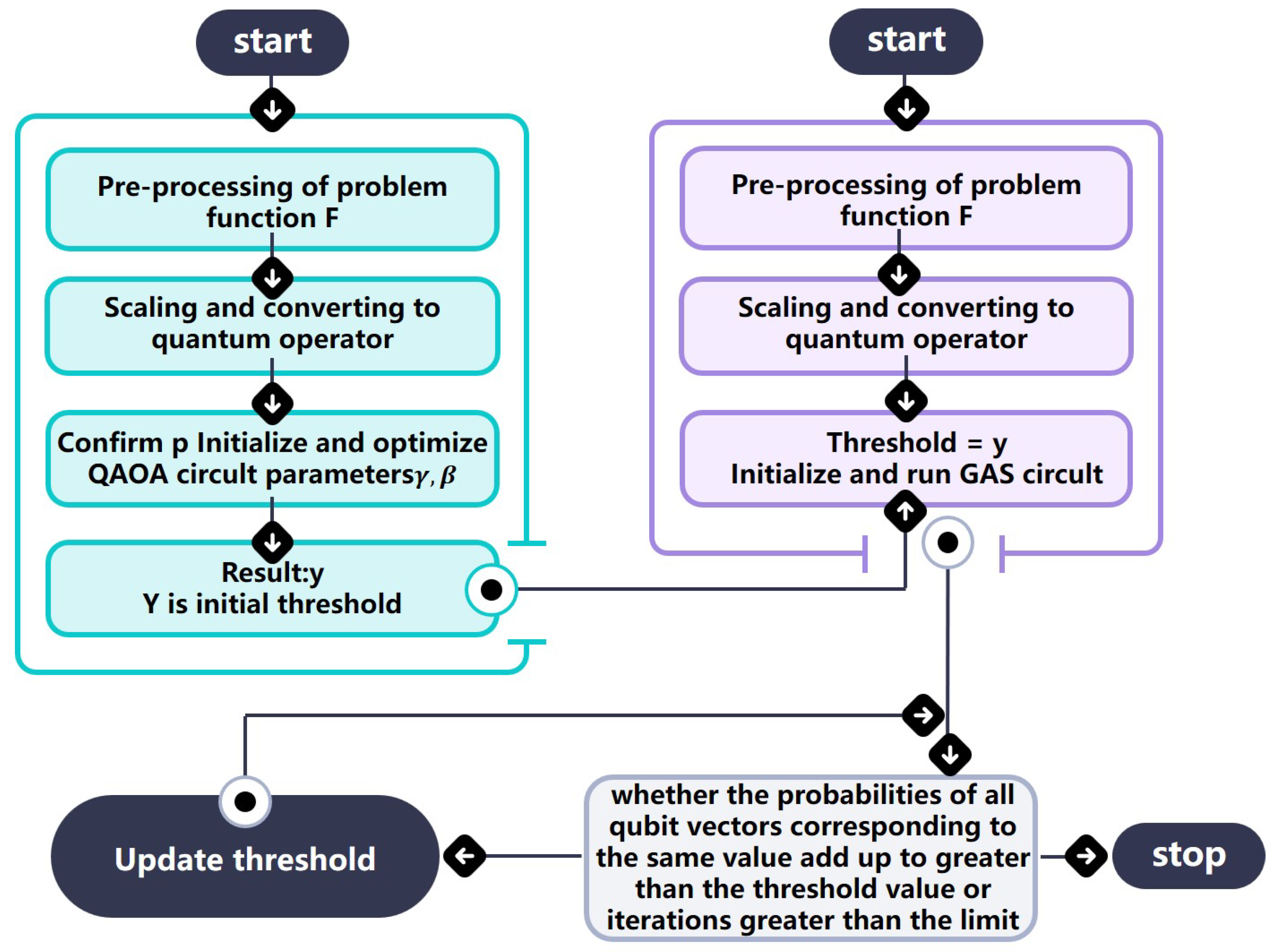
3. The Improved GAS Algorithm
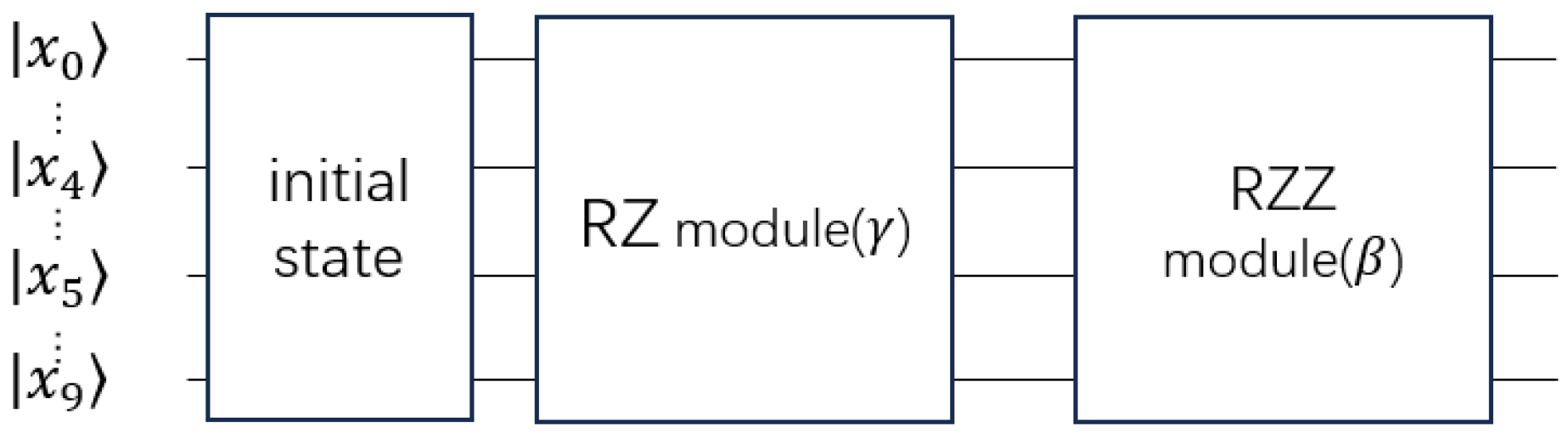
3.1. The QAOA Module
3.2. GAS Module
- 1.
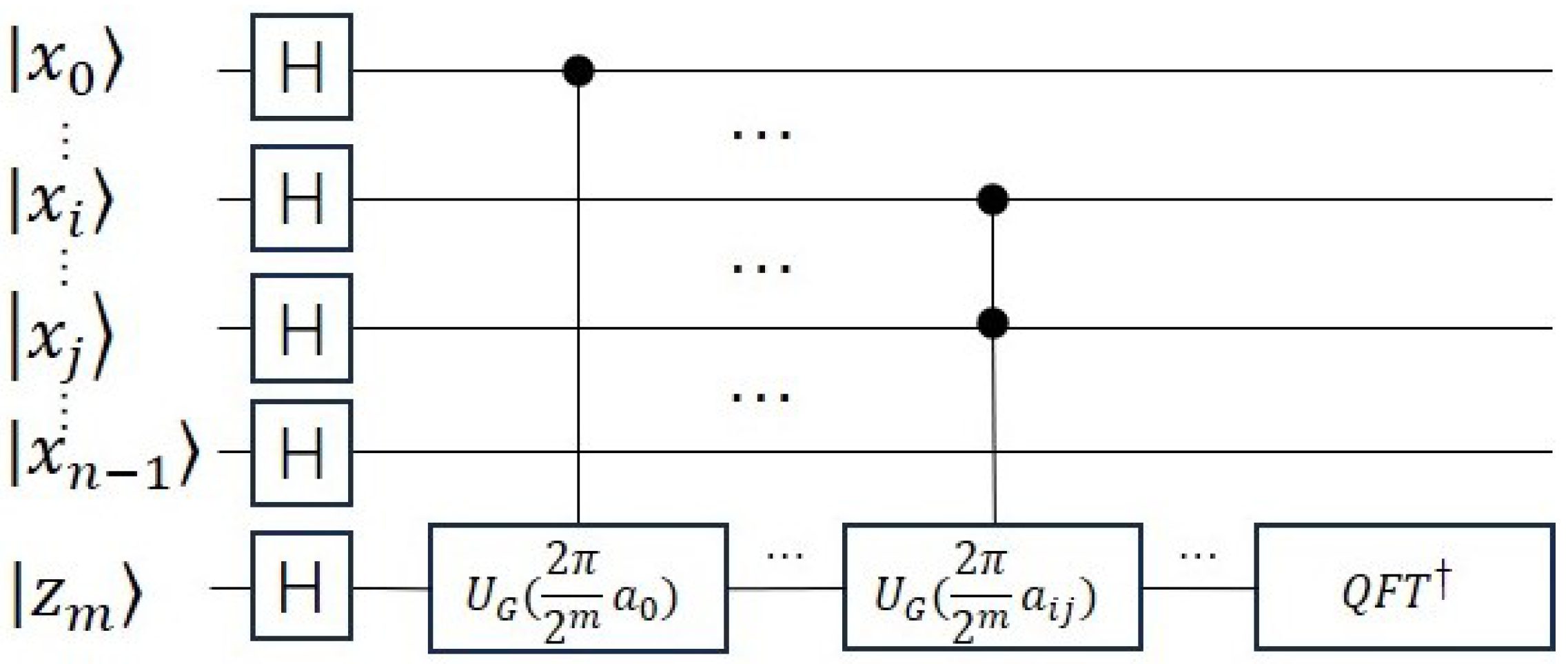
- The prepares an n-qubits input register to represent the equal superposition of all and m-qubits output register to (approximately) represent the corresponding objective function .where is the binary encoding of the integer x.
- 2.
- The oracle O recognizes the states of interest and multiplies their amplitudes by −1.
- 3.
- The Grover diffusion operator D has the effect of flipping all amplitudes in the quantum state according to their mean. This causes all the amplitudes of the states of interest to be magnified, while the amplitudes of all other states are decreased. For more details on building the GAS algorithm, see the Appendix A.
| Algorithm 1: Improved-GAS algorithm | |
| Input: ; | |
| Output: y | |
| 1: | set ; |
| 2: | set ; |
| 3: | set ; |
| 4: | set and ; |
| 5: | set ; |
| 6: | repeat |
| 7: | Run QAOA circuit; |
| 8: | Measure result; |
| 9: | Update ; |
| 10: | until The difference between the updated of the optimizer and the last is less than a certain precision; |
| 11: | |
| 12: | Run QAOA circuit; |
| 13: | Measure result; |
| 14: | |
| 15: | repeat |
| 16: | Select the rotation count from the set randomly; |
| 17: | Run the GAS quantum circuit and apply Grover Search with iterations using oracles and . We denote the outputs y respectively; |
| 18: | if then |
| 19: | y=; |
| 20: | ans = ; |
| 21: | else |
| 22: | ; |
| 23: | ; |
| 24: | end if |
| 25: | until The or y correspond to all of the frequencies greater than the threshold; |
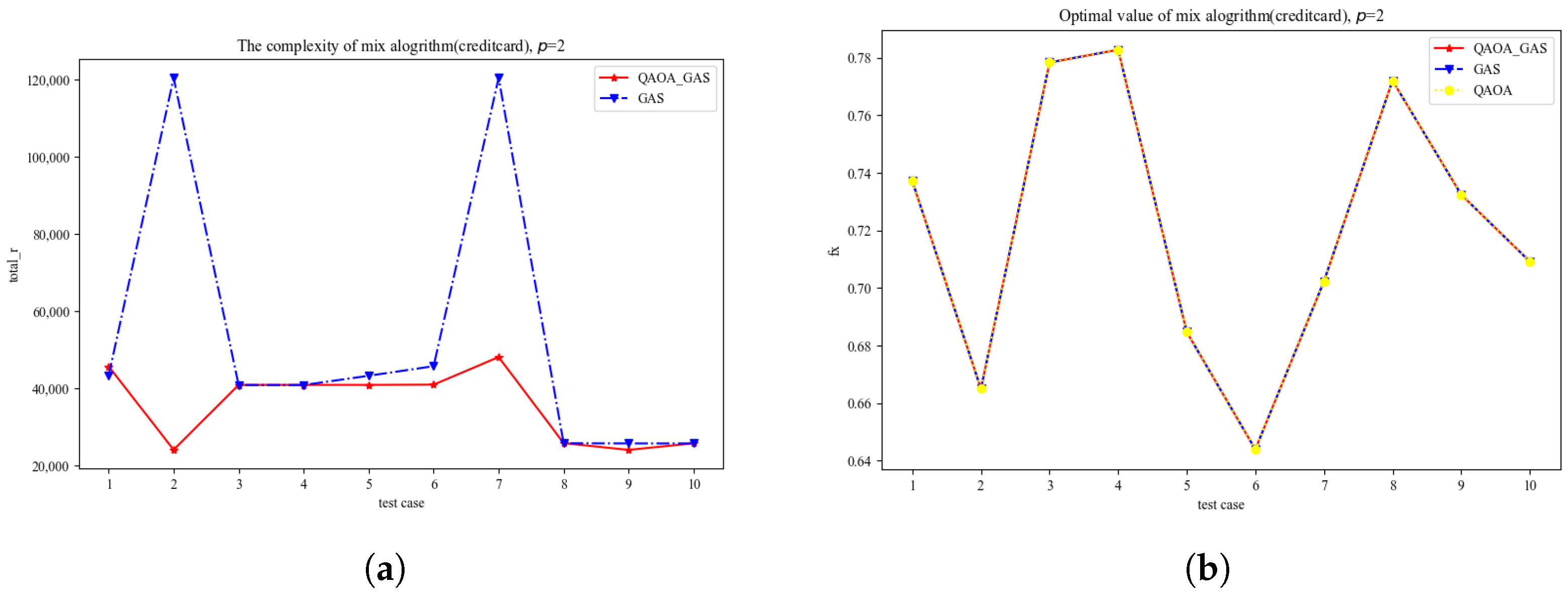
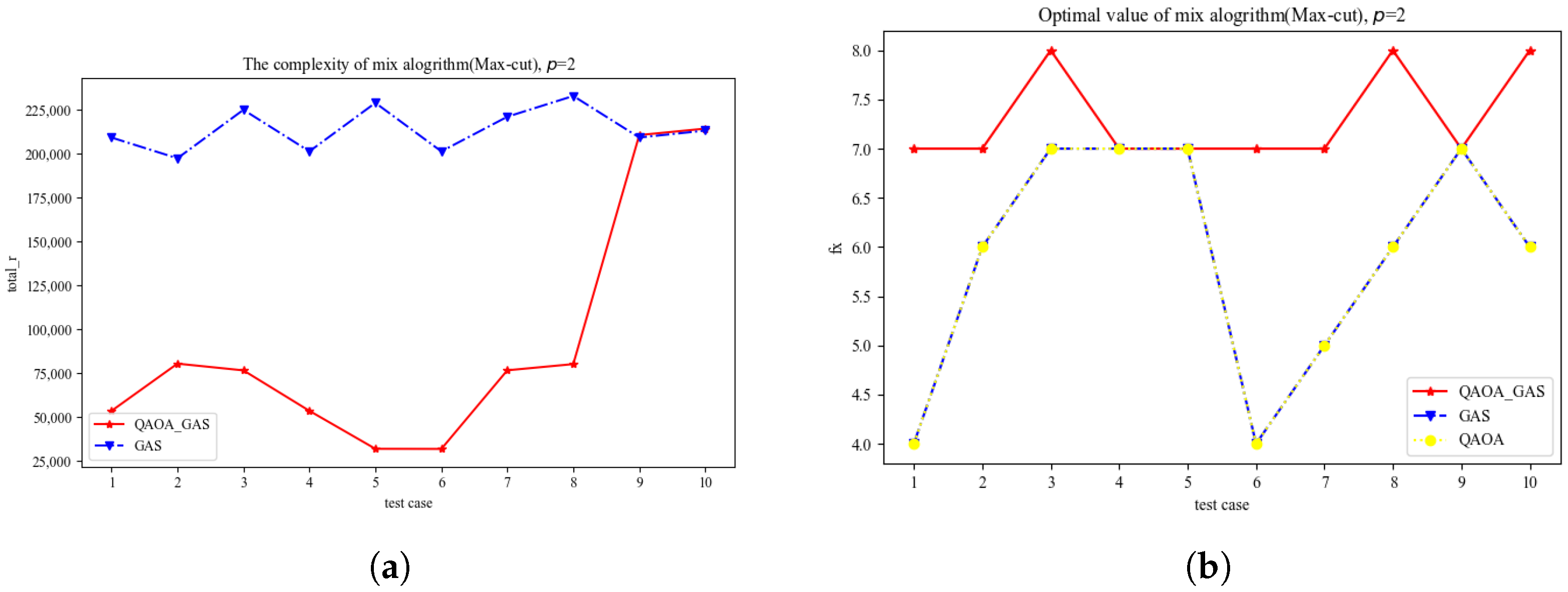
4. Test Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2. Construct Operator A
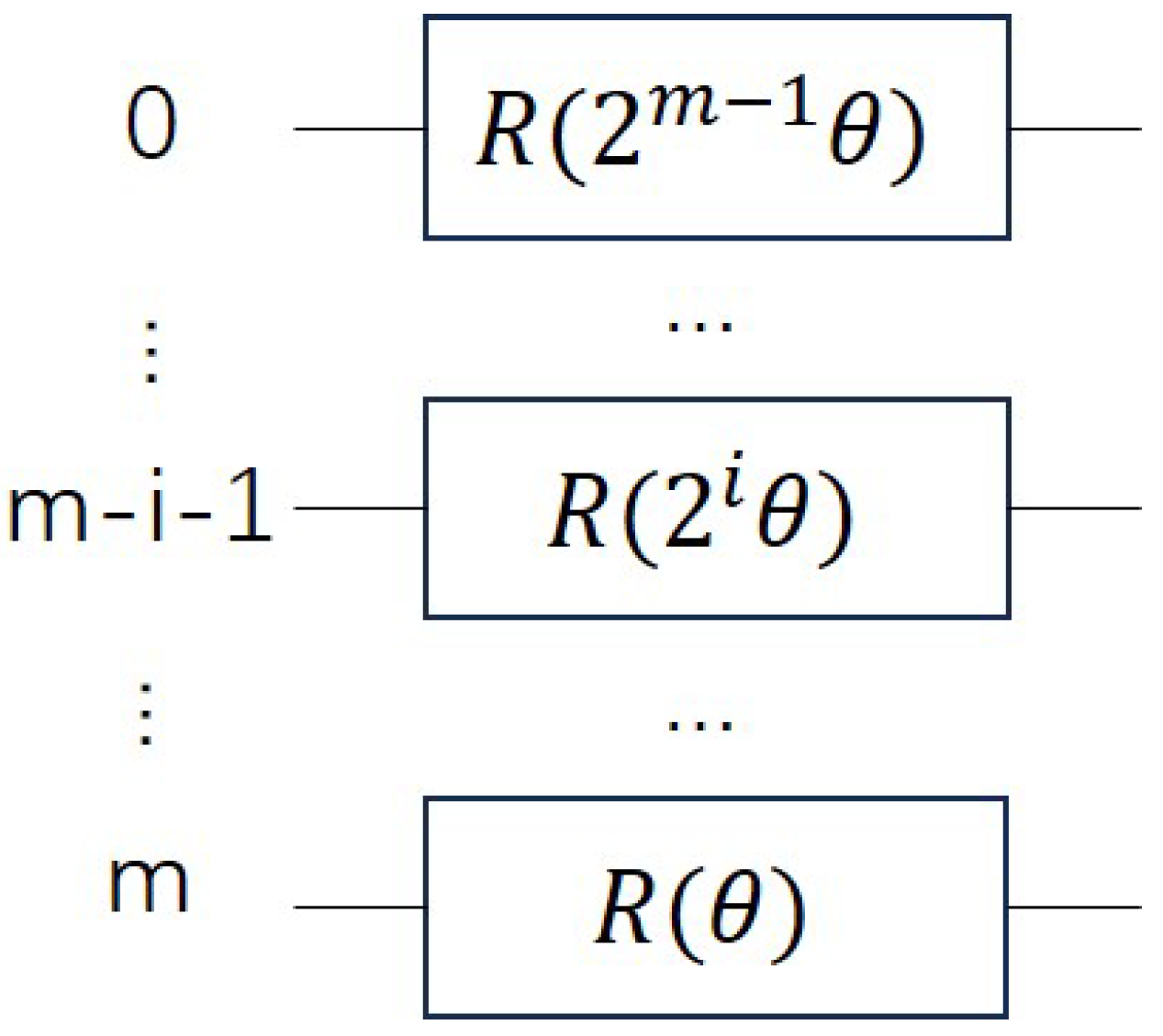
Appendix A.3. Construct Operator O
Appendix A.4. Construct Operator D and Update y

References
- Dunning, I.; Gupta, S.; Silberholz, J. What works best when? A systematic evaluation of heuristics for Max-Cut and QUBO. INFORMS J. Comput. 2018, 30, 608–624. [Google Scholar] [CrossRef]
- Dury, B.; Di Matteo, O. A QUBO formulation for qubit allocation. arXiv 2020, arXiv:2009.00140. [Google Scholar]
- Arora, S. The approximability of NP-hard problems. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; pp. 337–348. [Google Scholar]
- Woeginger, G.J. Exact algorithms for NP-hard problems: A survey. In Proceedings of the Combinatorial Optimization—Eureka, You Shrink! Jack Edmonds 5th International Workshop, Aussois, France, 5–9 March 2001; Revised Papers. Springer: Berlin/Heidelberg, Germany, 2003; pp. 185–207. [Google Scholar]
- Bärtschi, A.; Eidenbenz, S. Grover mixers for QAOA: Shifting complexity from mixer design to state preparation. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 72–82. [Google Scholar]
- Choi, J.; Kim, J. A tutorial on quantum approximate optimization algorithm (QAOA): Fundamentals and applications. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 16–18 October 2019; pp. 138–142. [Google Scholar]
- Guerreschi, G.G.; Matsuura, A.Y. QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci. Rep. 2019, 9, 6903. [Google Scholar] [CrossRef] [PubMed]
- Brandhofer, S.; Braun, D.; Dehn, V.; Hellstern, G.; Hüls, M.; Ji, Y.; Polian, I.; Bhatia, A.S.; Wellens, T. Benchmarking the performance of portfolio optimization with QAOA. Quantum Inf. Process. 2022, 22, 25. [Google Scholar] [CrossRef]
- Gilliam, A.; Woerner, S.; Gonciulea, C. Grover adaptive search for constrained polynomial binary optimization. Quantum 2021, 5, 428. [Google Scholar] [CrossRef]
- Federer, M.; Lenk, S.; Müssig, D.; Wappler, M.; Lässig, J. Constrained Grover Adaptive Search for Optimization of the Bidirectional EV Charging Problem. In Proceedings of the INFORMATIK 2023, Berlin, Germany, 26–28 September 2023. [Google Scholar]
- Long, G.L. Grover algorithm with zero theoretical failure rate. Phys. Rev. A 2001, 64, 022307. [Google Scholar] [CrossRef]
- Jozsa, R. Searching in Grover’s algorithm. arXiv 1999, arXiv:quant-ph/9901021. [Google Scholar]
- Elloumi, S.; Verchère, Z. Efficient linear reformulations for binary polynomial optimization problems. Comput. Oper. Res. 2023, 155, 106240. [Google Scholar] [CrossRef]
- Kapralov, M.; Krachun, D. An optimal space lower bound for approximating MAX-CUT. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Phoenix, AZ, USA, 23–26 June 2019; pp. 277–288. [Google Scholar]
| Notation | Description |
|---|---|
| Payoff function | |
| n | The number of credit card |
| c | Total loan of each card |
| r | Credit card interest rate |
| Card i loan approval rate | |
| Bad debt rate for card i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; He, Y.; Luan, T.; Long, Y. An Improved GAS Algorithm. Entropy 2025, 27, 240. https://doi.org/10.3390/e27030240
Wang Z, He Y, Luan T, Long Y. An Improved GAS Algorithm. Entropy. 2025; 27(3):240. https://doi.org/10.3390/e27030240
Chicago/Turabian StyleWang, Zhijian, Yuchen He, Tian Luan, and Yong Long. 2025. "An Improved GAS Algorithm" Entropy 27, no. 3: 240. https://doi.org/10.3390/e27030240
APA StyleWang, Z., He, Y., Luan, T., & Long, Y. (2025). An Improved GAS Algorithm. Entropy, 27(3), 240. https://doi.org/10.3390/e27030240






