Gradient-Based Multiple Robust Learning Calibration on Data Missing-Not-at-Random via Bi-Level Optimization
Abstract
1. Introduction
- We propose a novel MR calibration method using bi-level optimization via calibrating the ensemble imputation and propensity models and address the non-differentiable issue by adopting differentiable expected calibration errors.
- We further propose a bi-level calibrated multiple robust learning algorithm to update the calibrated imputation models and the prediction model. To the best of our knowledge, this is the first work to perform calibration for the MR estimator.
- We conduct extensive experiments on three real-world datasets, showing the effectiveness of our method compared to the state-of-the-art debiasing methods.
2. Related Works
2.1. Debiased Recommendation
2.2. Model Calibration
3. Preliminary
3.1. Debiased Recommendation
3.2. Calibration
4. Methodology
4.1. Distinctions from Previous Work
4.2. Differentiable Expected Calibration Error
4.3. Calibrated Multiple Robust Learning
Multiple Imputation Calibration
| Algorithm 1: Gradient-Based Bi-level Calibrated Multiple Robust Learning |
 |
5. Experiments
5.1. Datasets
5.2. Baselines
- Naive method [64] naively optimizes the average loss over the observed user-item pairs.
- IPS method [3] reweights the observed ratings with the inverse propensity scores.
- SNIPS method [65] reweights the observed ratings with self-normalized propensity scores to further reduce the variance.
- ASIPS method [22] generates reliable pseudo-ratings to mitigate propensity estimation bias and high variance problem.
- DR method [10] combines error imputation and inverse propensity reweighting to construct a doubly robust estimator, where imputed errors are typically set based on label prior knowledge, such as the mean value of the labels.
- DR-JL method [2] further proposes modeling error imputation with neural networks and jointly learns the prediction model and imputation model.
- MRDR method [66] enhances the DR-JL method by explicitly controlling the variance of the DR estimator through imputation model learning.
- DR-BIAS method [67] enhances the DR-JL method by further reducing the bias of the DR estimator through imputation model learning.
- DR-MSE method [67] further combines MRDR method and DR-BIAS method to achieve bias-variance trade-off and control the generalization error.
- MR method [11] adopts multiple candidate propensity and imputation models to mitigate inaccuracies in single-model propensity scores or error imputation in DR methods.
- TDR and TDR-JL methods [27] correct the imputed errors with targeted learning to reduce the bias and variance simultaneously for existing DR approaches
- StableDR method [26] constructs a stabilized DR estimator that has a weaker dependence on extrapolation and is robust to small propensities by learning constrained propensity scores.
- IPS-V2 and DR-V2 methods [68] learn the propensity model which can balance some manually selected functions such as the first and second moments of the features.
- KBIPS and KBDR methods [32] further propose to conduct causal balancing in the reproducing kernel Hilbert space (RKHS) and randomly select some kernel functions to balance for propensity model learning.
- AKBIPS and AKBDR methods [32] adaptively select the kernel functions which contribute the most to reducing the estimation bias to balance for propensity model learning.
- DCE-DR and DCE-TDR method [12] propose to calibrate the single propensity model and single imputation model in DR and TDR estimators through Mixture-of-Experts technique.
5.3. Experiment Protocols and Details
- AUC [69] is a performance metric for classifiers that measures the probability of a randomly chosen positive example being ranked higher than a randomly chosen negative one. A higher AUC score reflects better ranking performance in differentiating positive instances from negative ones.
- NDCG@T [70] evaluates ranking performance by comparing the Discounted Cumulative Gain (DCG) of the top-T results to the Ideal DCG (IDCG), producing a normalized score between 0 and 1. A higher NDCG@T implies that more relevant items are ranked towards the top.
- F1@T [71] is the harmonic mean of precision and recall computed over the top-T predictions returned by a model. A higher F1@T indicates a better trade-off between precision and recall in the top-T results.
5.4. Performance Analysis
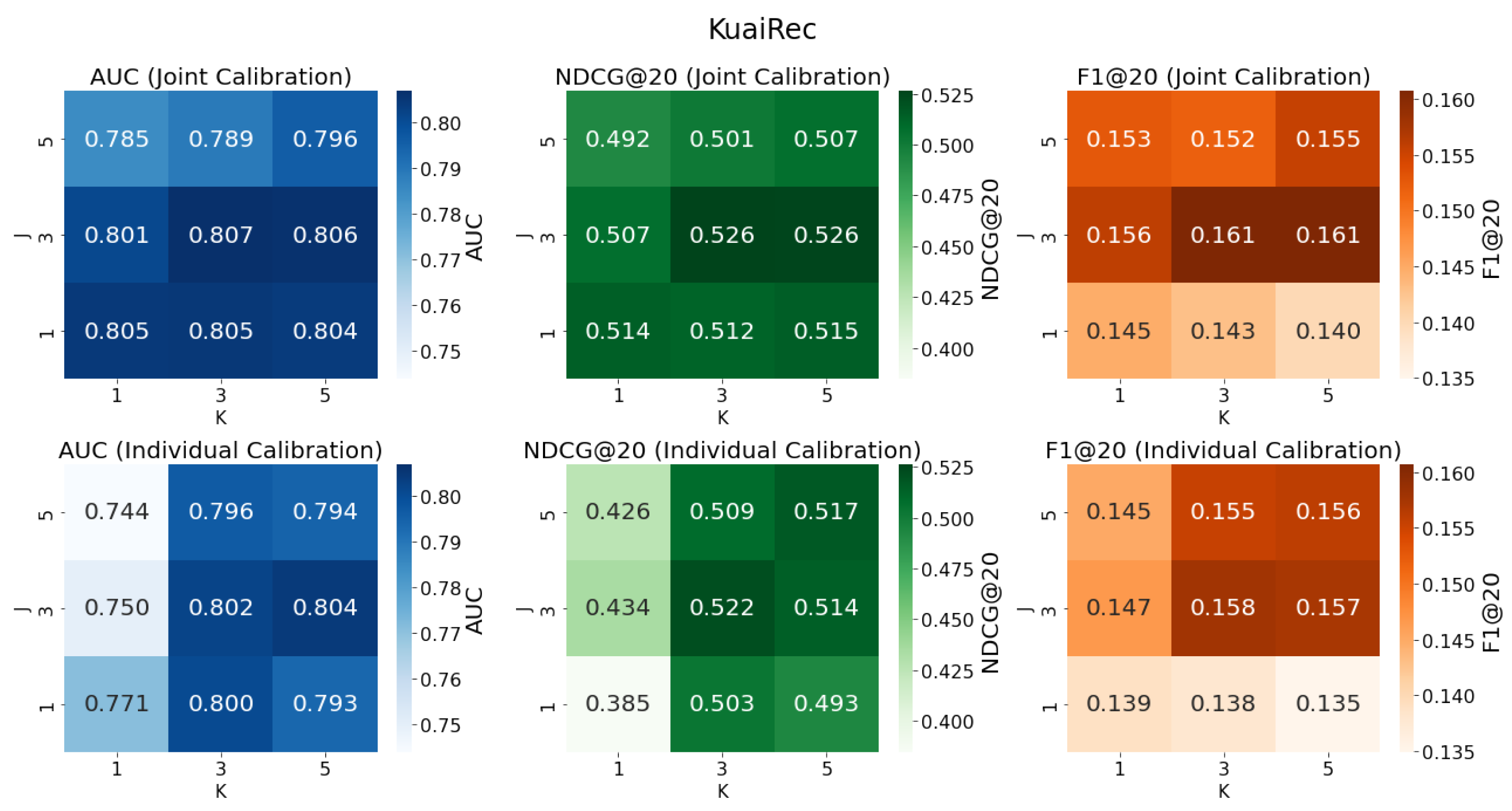
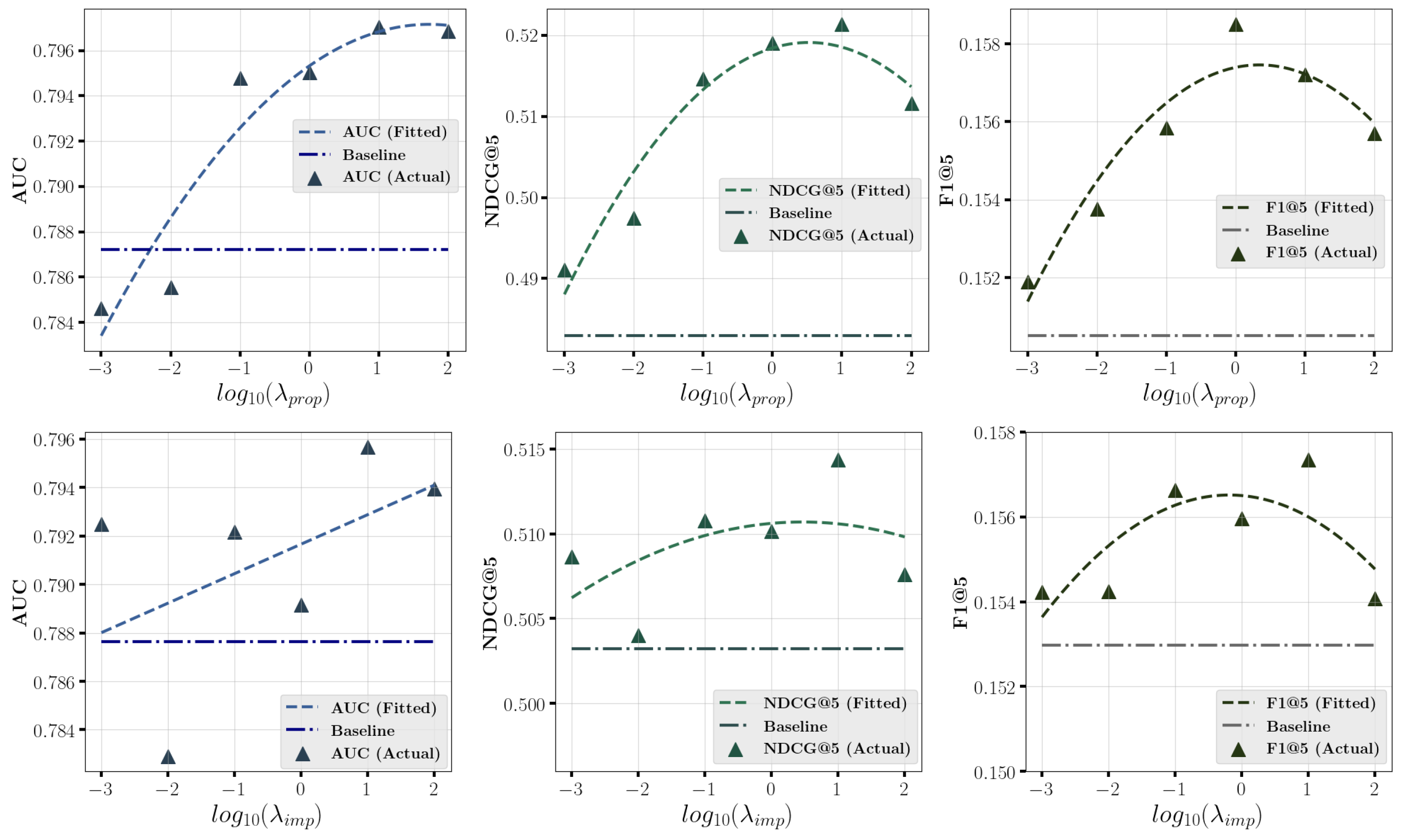
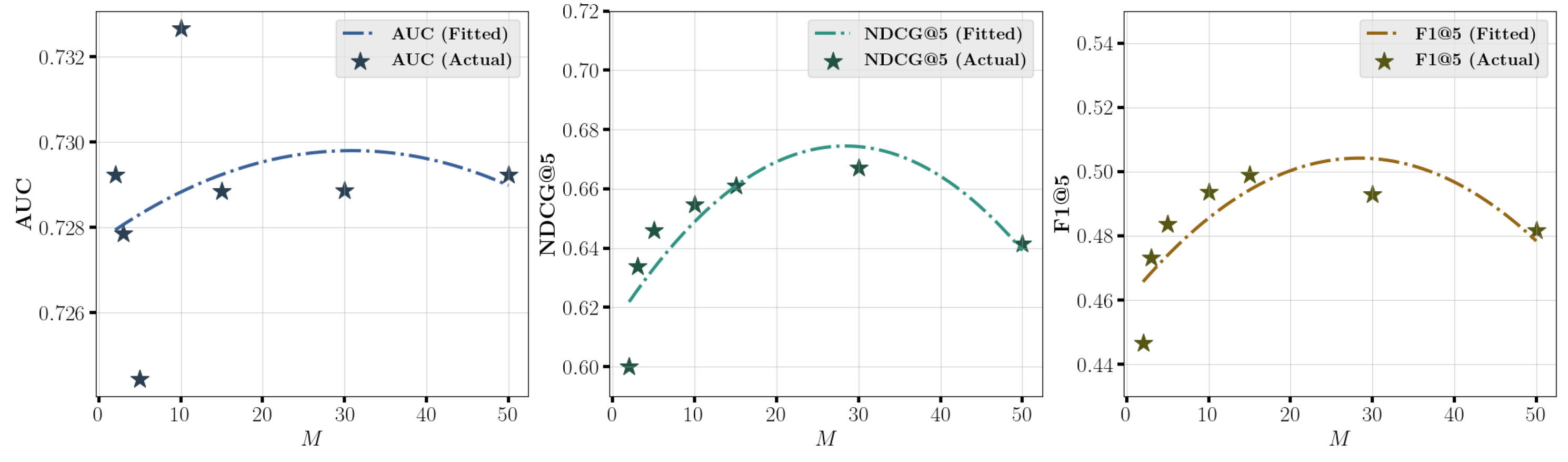
5.5. In-Depth Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Ricci, F.; Rokach, L.; Shapira, B. Introduction to recommender systems handbook. In Recommender Systems Handbook; Springer: Boston, MA, USA, 2010; pp. 1–35. [Google Scholar]
- Wang, X.; Zhang, R.; Sun, Y.; Qi, J. Doubly Robust Joint Learning for Recommendation on Data Missing Not at Random. In Proceedings of the ICML, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Schnabel, T.; Swaminathan, A.; Singh, A.; Chandak, N.; Joachims, T. Recommendations as Treatments: Debiasing Learning and Evaluation. In Proceedings of the ICML, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Chen, J.; Dong, H.; Wang, X.; Feng, F.; Wang, M.; He, X. Bias and Debias in Recommender System: A Survey and Future Directions. Acm Trans. Inf. Syst. 2022, 41, 1–39. [Google Scholar] [CrossRef]
- Wu, P.; Li, H.; Deng, Y.; Hu, W.; Dai, Q.; Dong, Z.; Sun, J.; Zhang, R.; Zhou, X.H. On the Opportunity of Causal Learning in Recommendation Systems: Foundation, Estimation, Prediction and Challenges. In Proceedings of the IJCAI, Vienna, Austria, 23–29 July 2022. [Google Scholar]
- Steck, H. Training and testing of recommender systems on data missing not at random. In Proceedings of the KDD, Washington, DC, USA, 25–28 July 2010. [Google Scholar]
- Chang, Y.W.; Hsieh, C.J.; Chang, K.W.; Ringgaard, M.; Lin, C.J. Training and testing low-degree polynomial data mappings via linear SVM. J. Mach. Learn. Res. 2010, 11, 1471–1490. [Google Scholar]
- Saito, Y.; Yaginuma, S.; Nishino, Y.; Sakata, H.; Nakata, K. Unbiased recommender learning from missing-not-at-random implicit feedback. In Proceedings of the WSDM, Houston, TX, USA, 3–7 February 2020. [Google Scholar]
- Morgan, S.L.; Winship, C. Counterfactuals and Causal Inference: Methods and Principles for Social Research, 2nd ed.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Saito, Y. Doubly robust estimator for ranking metrics with post-click conversions. In Proceedings of the RecSys, Virtual Event, 22–26 September 2020. [Google Scholar]
- Li, H.; Dai, Q.; Li, Y.; Lyu, Y.; Dong, Z.; Zhou, X.H.; Wu, P. Multiple Robust Learning for Recommendation. In Proceedings of the AAAI, Washington, DC, USA, 7–14 February 2023. [Google Scholar]
- Kweon, W.; Yu, H. Doubly Calibrated Estimator for Recommendation on Data Missing Not At Random. In Proceedings of the WWW, Singapore, 13–17 May 2024. [Google Scholar]
- Luo, H.; Zhuang, F.; Xie, R.; Zhu, H.; Wang, D.; An, Z.; Xu, Y. A survey on causal inference for recommendation. Innovation 2024, 5, 100590. [Google Scholar] [CrossRef]
- Li, M.; Sui, H. Causal Recommendation via Machine Unlearning with a Few Unbiased Data. In Proceedings of the AAAI Workshop on Artificial Intelligence with Causal Techniques, Philadelphia, PA, USA, 25 February–4 March 2025. [Google Scholar]
- Wang, W.; Zhang, Y.; Li, H.; Wu, P.; Feng, F.; He, X. Causal Recommendation: Progresses and Future Directions. In Proceedings of the SIGIR, Taipei, Taiwan, 23–27 July 2023. [Google Scholar]
- Saito, Y.; Nomura, M. Towards Resolving Propensity Contradiction in Offline Recommender Learning. In Proceedings of the IJCAI, Vienna, Austria, 23–29 July 2022. [Google Scholar]
- Wang, H.; Yang, W.; Yang, L.; Wu, A.; Xu, L.; Ren, J.; Wu, F.; Kuang, K. Estimating Individualized Causal Effect with Confounded Instruments. In Proceedings of the KDD, Washington, DC, USA, 14–18 August 2022. [Google Scholar]
- Zou, H.; Wang, H.; Xu, R.; Li, B.; Pei, J.; Jian, Y.J.; Cui, P. Factual Observation Based Heterogeneity Learning for Counterfactual Prediction. In Proceedings of the CCLR, Tübingen, Germany, 11–14 April 2023. [Google Scholar]
- Wang, H.; Kuang, K.; Lan, L.; Wang, Z.; Huang, W.; Wu, F.; Yang, W. Out-of-distribution generalization with causal feature separation. IEEE Trans. Knowl. Data Eng. 2024, 36, 1758–1772. [Google Scholar] [CrossRef]
- Wang, H.; Kuang, K.; Chi, H.; Yang, L.; Geng, M.; Huang, W.; Yang, W. Treatment effect estimation with adjustment feature selection. In Proceedings of the KDD, Long Beach, CA, USA, 6–10 August 2023. [Google Scholar]
- Wu, A.; Kuang, K.; Xiong, R.; Li, B.; Wu, F. Stable estimation of heterogeneous treatment effects. In Proceedings of the ICML, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Saito, Y. Asymmetric Tri-training for Debiasing Missing-Not-At-Random Explicit Feedback. In Proceedings of the SIGIR, Xi’an, China, 25–30 July 2020. [Google Scholar]
- Wang, H.; Chang, T.W.; Liu, T.; Huang, J.; Chen, Z.; Yu, C.; Li, R.; Chu, W. Escm2: Entire space counterfactual multi-task model for post-click conversion rate estimation. In Proceedings of the SIGIR, Madrid, Spain, 11–15 July 2022. [Google Scholar]
- Zhang, W.; Bao, W.; Liu, X.Y.; Yang, K.; Lin, Q.; Wen, H.; Ramezani, R. Large-scale Causal Approaches to Debiasing Post-click Conversion Rate Estimation with Multi-task Learning. In Proceedings of the WWW, Taipei, Taiwan, 20–24 April 2020. [Google Scholar]
- Ding, S.; Wu, P.; Feng, F.; He, X.; Wang, Y.; Liao, Y.; Zhang, Y. Addressing Unmeasured Confounder for Recommendation with Sensitivity Analysis. In Proceedings of the KDD, Washington, DC, USA, 14–18 August 2022. [Google Scholar]
- Li, H.; Zheng, C.; Wu, P. StableDR: Stabilized Doubly Robust Learning for Recommendation on Data Missing Not at Random. In Proceedings of the ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Li, H.; Lyu, Y.; Zheng, C.; Wu, P. TDR-CL: Targeted Doubly Robust Collaborative Learning for Debiased Recommendations. In Proceedings of the ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Song, Z.; Chen, J.; Zhou, S.; Shi, Q.; Feng, Y.; Chen, C.; Wang, C. CDR: Conservative Doubly Robust Learning for Debiased Recommendation. In Proceedings of the CIKM, Birmingham, UK, 21–25 October 2023. [Google Scholar]
- Li, H.; Zheng, C.; Ding, S.; Feng, F.; He, X.; Geng, Z.; Wu, P. Be Aware of the Neighborhood Effect: Modeling Selection Bias under Interference for Recommendation. In Proceedings of the ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Zhang, H.; Wang, S.; Li, H.; Zheng, C.; Chen, X.; Liu, L.; Luo, S.; Wu, P. Uncovering the Propensity Identification Problem in Debiased Recommendations. In Proceedings of the ICDE, Utrecht, The Netherlands, 13–17 May 2024. [Google Scholar]
- Li, H.; Zheng, C.; Wang, S.; Wu, K.; Wang, E.; Wu, P.; Geng, Z.; Chen, X.; Zhou, X.H. Relaxing the Accurate Imputation Assumption in Doubly Robust Learning for Debiased Collaborative Filtering. In Proceedings of the ICML, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Li, H.; Zheng, C.; Xiao, Y.; Wu, P.; Geng, Z.; Chen, X.; Cui, P. Debiased collaborative filtering with kernel-based causal balancing. In Proceedings of the ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Liu, D.; Cheng, P.; Zhu, H.; Dong, Z.; He, X.; Pan, W.; Ming, Z. Debiased representation learning in recommendation via information bottleneck. ACM Trans. Recomm. Syst. 2023, 1, 1–27. [Google Scholar] [CrossRef]
- Yang, M.; Dai, Q.; Dong, Z.; Chen, X.; He, X.; Wang, J. Top-n recommendation with counterfactual user preference simulation. In Proceedings of the CIKM, Virtual Event, 1–5 November 2021. [Google Scholar]
- Wang, J.; Li, H.; Zhang, C.; Liang, D.; Yu, E.; Ou, W.; Wang, W. Counterclr: Counterfactual contrastive learning with non-random missing data in recommendation. In Proceedings of the ICDM, Shanghai, China, 1–4 December 2023. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the ICML, Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Kull, M.; Silva Filho, T.; Flach, P. Beta calibration: A well-founded and easily implemented improvement on logistic calibration for binary classifiers. In Proceedings of the AISTATS, Fort Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the KDD, Sydney, NSW, Australia, 10–13 August 2015. [Google Scholar]
- Huang, Y.; Li, W.; Macheret, F.; Gabriel, R.A.; Ohno-Machado, L. A tutorial on calibration measurements and calibration models for clinical prediction models. J. Am. Med. Inform. Assoc. 2020, 27, 621–633. [Google Scholar] [CrossRef]
- Bojarski, M. End to end learning for self-driving cars. arXiv 2016, arXiv:1604.07316. [Google Scholar]
- Chen, Z.; Huang, X. End-to-end learning for lane keeping of self-driving cars. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1856–1860. [Google Scholar]
- Büchel, P.; Kratochwil, M.; Nagl, M.; Rösch, D. Deep calibration of financial models: Turning theory into practice. Rev. Deriv. Res. 2022, 25, 109–136. [Google Scholar] [CrossRef]
- Biagini, F.; Gonon, L.; Walter, N. Approximation rates for deep calibration of (rough) stochastic volatility models. SIAM J. Financ. Math. 2024, 15, 734–784. [Google Scholar] [CrossRef]
- Niculescu-Mizil, A.; Caruana, R. Predicting good probabilities with supervised learning. In Proceedings of the ICML, Bonn, Germany, 7–11 August 2005. [Google Scholar]
- Wang, C. Calibration in deep learning: A survey of the state-of-the-art. arXiv 2023, arXiv:2308.01222. [Google Scholar]
- Zadrozny, B.; Elkan, C. Obtaining calibrated probability estimates from decision trees and naive bayesian classifiers. In Proceedings of the ICML, Williamstown, MA, USA, 28 June–1 July 2001. [Google Scholar]
- Zadrozny, B.; Elkan, C. Transforming classifier scores into accurate multiclass probability estimates. In Proceedings of the KDD, Edmonton, AB, Canada, 23–26 July 2002. [Google Scholar]
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Pereyra, G.; Tucker, G.; Chorowski, J.; Kaiser, Ł.; Hinton, G. Regularizing neural networks by penalizing confident output distributions. arXiv 2017, arXiv:1701.06548. [Google Scholar]
- Liang, G.; Zhang, Y.; Wang, X.; Jacobs, N. Improved trainable calibration method for neural networks on medical imaging classification. arXiv 2020, arXiv:2009.04057. [Google Scholar]
- Kumar, A.; Sarawagi, S.; Jain, U. Trainable calibration measures for neural networks from kernel mean embeddings. In Proceedings of the ICML, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Bohdal, O.; Yang, Y.; Hospedales, T. Meta-Calibration: Learning of Model Calibration Using Differentiable Expected Calibration Error. Trans. Mach. Learn. Res. 2023. Available online: https://openreview.net/forum?id=R2hUure38l (accessed on 15 January 2025).
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural network. In Proceedings of the ICML, Lille, France, 6–11 July 2015. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. In Proceedings of the NeurIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the ICML, New York City, NY, USA, 19–24 June 2016. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical Reparametrization with Gumble-Softmax. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhang, J.; Kailkhura, B.; Han, T.Y.J. Mix-n-match: Ensemble and compositional methods for uncertainty calibration in deep learning. In Proceedings of the ICML, Virtual Event, 13–18 July 2020. [Google Scholar]
- Laves, M.H.; Ihler, S.; Kortmann, K.P.; Ortmaier, T. Well-calibrated model uncertainty with temperature scaling for dropout variational inference. arXiv 2019, arXiv:1909.13550. [Google Scholar]
- Naeini, M.P.; Cooper, G.; Hauskrecht, M. Obtaining well calibrated probabilities using bayesian binning. In Proceedings of the AAAI, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Gao, C.; Li, S.; Lei, W.; Chen, J.; Li, B.; Jiang, P.; He, X.; Mao, J.; Chua, T.S. KuaiRec: A Fully-observed Dataset and Insights for Evaluating Recommender Systems. In Proceedings of the CIKM, Atlanta, GA, USA, 17–21 October 2022. [Google Scholar]
- Chen, J.; Dong, H.; Qiu, Y.; He, X.; Xin, X.; Chen, L.; Lin, G.; Yang, K. AutoDebias: Learning to Debias for Recommendation. In Proceedings of the SIGIR, Online, 11–15 July 2021. [Google Scholar]
- Li, H.; Wu, K.; Zheng, C.; Xiao, Y.; Wang, H.; Geng, Z.; Feng, F.; He, X.; Wu, P. Removing Hidden Confounding in Recommendation: A Unified Multi-Task Learning Approach. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar]
- Li, H.; Xiao, Y.; Zheng, C.; Wu, P. Balancing Unobserved Confounding with a Few Unbiased Ratings in Debiased Recommendations. In Proceedings of the WWW, Austin, TX, USA, 30 April–4 May 2023. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Swaminathan, A.; Joachims, T. The Self-Normalized Estimator for Counterfactual Learning. In Proceedings of the NeurIPS, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Guo, S.; Zou, L.; Liu, Y.; Ye, W.; Cheng, S.; Wang, S.; Chen, H.; Yin, D.; Chang, Y. Enhanced Doubly Robust Learning for Debiasing Post-Click Conversion Rate Estimation. In Proceedings of the SIGIR, Online, 11–15 July 2021. [Google Scholar]
- Dai, Q.; Li, H.; Wu, P.; Dong, Z.; Zhou, X.H.; Zhang, R.; Zhang, R.; Sun, J. A generalized doubly robust learning framework for debiasing post-click conversion rate prediction. In Proceedings of the KDD, Washington, DC, USA, 14–18 August 2022. [Google Scholar]
- Li, H.; Xiao, Y.; Zheng, C.; Wu, P.; Cui, P. Propensity Matters: Measuring and Enhancing Balancing for Recommendation. In Proceedings of the ICML, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Järvelin, K.; Kekäläinen, J. Cumulated gain-based evaluation of IR techniques. ACM Trans. Inf. Syst. (TOIS) 2002, 20, 422–446. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Elkan, C.; Naryanaswamy, B. Optimal thresholding of classifiers to maximize F1 measure. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2014, Nancy, France, 15–19 September 2014; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2014; pp. 225–239. [Google Scholar]



| Coat | Yahoo! R3 | KuaiRec | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | AUC | NDCG@5 | F1@5 | AUC | NDCG@5 | F1@5 | AUC | NDCG@20 | F1@20 |
| Naive | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| IPS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| SNIPS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| ASIPS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| IPS-V2 | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| KBIPS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| AKBIPS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| DR | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| DR-JL | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| MRDR-JL | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| DR-BIAS | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| DR-MSE | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| MR | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| TDR | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| TDR-JL | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| StableDR | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| DR-V2 | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| KBDR | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. | 0. |
| AKBDR | 0. | 0.493±0.007 | 0. | 0. | 0. | 0. | 0. | 0. | |
| DCE-DR | 0. | 0. | 0. | 0. | 0. | 0.333±0.003 | 0. | 0. | 0. |
| DCE-TDR | 0. | 0.651±0.006 | 0. | 0.701±0.002 | 0.672±0.002 | 0. | 0.514±0.006 | 0.155±0.002 | |
| Cali-MR | |||||||||
| Method | Coat | Yahoo! R3 | KuaiRec | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AUC | NDCG@5 | F1@5 | AUC | NDCG@5 | F1@5 | AUC | NDCG@20 | F1@20 | |
| Cali-MR | 0.741 | 0.658 | 0.495 | 0.703 | 0.678 | 0.338 | 0.798 | 0.521 | 0.158 |
| Cali-MR w/o prop | 0.730 | 0.640 | 0.486 | 0.700 | 0.674 | 0.336 | 0.787 | 0.483 | 0.151 |
| Cali-MR w/o imp | 0.736 | 0.639 | 0.483 | 0.703 | 0.674 | 0.336 | 0.793 | 0.509 | 0.155 |
| Cali-MR w/o imp & prop | 0.727 | 0.635 | 0.477 | 0.698 | 0.667 | 0.331 | 0.783 | 0.482 | 0.148 |
| Coat | Yahoo! R3 | KuaiRec | ||||
|---|---|---|---|---|---|---|
| Method | ECE | RD | ECE | RD | ECE | RD |
| DR-JL | 0.1626 | - | 0.0589 | - | 0.0999 | - |
| DCE-DR | 0.1428 | 0.0198 | 0.0554 | 0.0035 | 0.0451 | 0.0548 |
| TDR-JL | 0.1468 | - | 0.0481 | - | 0.0499 | - |
| DCE-TDR | 0.1270 | 0.0198 | 0.0476 | 0.0005 | 0.0488 | 0.0011 |
| MR | 0.1512 | - | 0.1594 | - | 0.2367 | - |
| Cali-MR | 0.1239 | 0.0273 | 0.0349 | 0.1245 | 0.0519 | 0.1848 |
| Method | Coat | Yahoo! R3 | KuaiRec | |||
|---|---|---|---|---|---|---|
| Time | Params | Time | Params | Times | Params | |
| Naive | 4.04 | 1× | 26.07 | 1× | 11.67 | 1× |
| IPS | 6.54 | 2× | 32.84 | 2× | 15.14 | 2× |
| DR | 17.41 | 3× | 43.18 | 3× | 31.20 | 3× |
| DR-JL | 18.81 | 3× | 166.21 | 3× | 110.01 | 3× |
| TDR-JL | 21.13 | 3× | 128.88 | 3× | 101.09 | 3× |
| MR (J = 2, K = 2) | 13.55 | 5× | 127.8 | 5× | 114.78 | 5× |
| Cali-DR (J = 1, K = 1) | 21.03 | 3× | 132.98 | 3× | 128.31 | 3× |
| Cali-MR (J = 2, K = 2) | 23.28 | 5× | 144.56 | 5× | 124.58 | 5× |
| Cali-MR (J = 1, K = 5) | 21.57 | 5× | 139.80 | 5× | 130.34 | 5× |
| Cali-MR (J = 1, K = 5) | 21.43 | 7× | 136.77 | 7× | 141.46 | 7× |
| Cali-MR (J = 3, K = 3) | 19.55 | 5× | 127.80 | 5× | 106.66 | 7× |
| Cali-MR (J = 3, K = 3) | 25.43 | 7× | 151.97 | 7× | 127.47 | 7× |
| Cali-MR (J = 3, K = 5) | 23.59 | 9× | 166.42 | 9× | 163.02 | 9× |
| Cali-MR (J = 5, K = 3) | 23.71 | 9× | 143.76 | 9× | 103.60 | 9× |
| Cali-MR (J = 5, K = 3) | 29.35 | 9× | 132.74 | 9× | 128.03 | 9× |
| Cali-MR (J = 5, K = 5) | 25.65 | 11× | 153.79 | 11× | 166.73 | 11× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, S.; Ma, C. Gradient-Based Multiple Robust Learning Calibration on Data Missing-Not-at-Random via Bi-Level Optimization. Entropy 2025, 27, 196. https://doi.org/10.3390/e27020196
Gong S, Ma C. Gradient-Based Multiple Robust Learning Calibration on Data Missing-Not-at-Random via Bi-Level Optimization. Entropy. 2025; 27(2):196. https://doi.org/10.3390/e27020196
Chicago/Turabian StyleGong, Shuxia, and Chen Ma. 2025. "Gradient-Based Multiple Robust Learning Calibration on Data Missing-Not-at-Random via Bi-Level Optimization" Entropy 27, no. 2: 196. https://doi.org/10.3390/e27020196
APA StyleGong, S., & Ma, C. (2025). Gradient-Based Multiple Robust Learning Calibration on Data Missing-Not-at-Random via Bi-Level Optimization. Entropy, 27(2), 196. https://doi.org/10.3390/e27020196





