Revisiting Endoreversible Carnot Engine: Extending the Yvon Engine
Abstract
1. Introduction
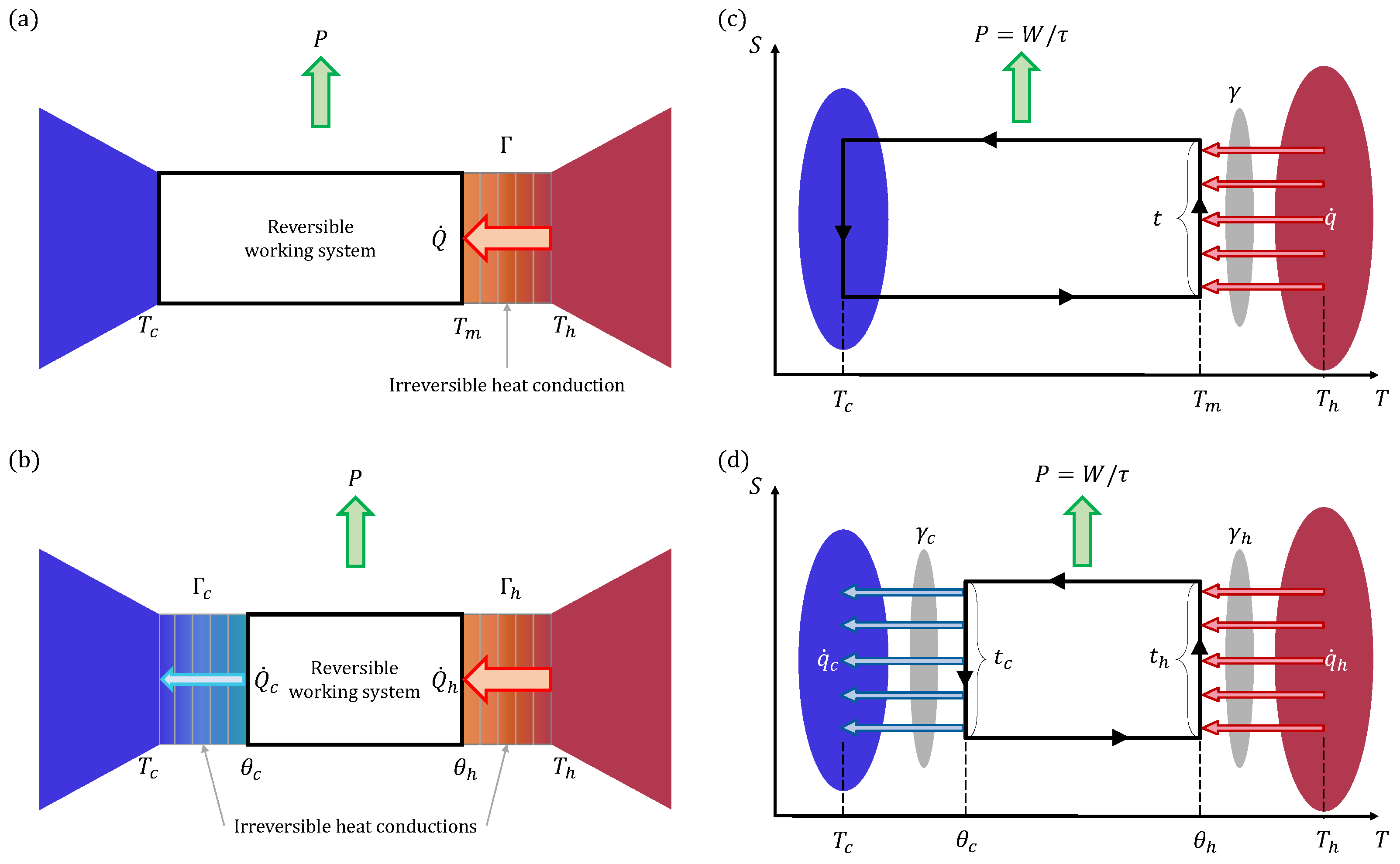
2. Yvon Engine
3. Extended Yvon Engine
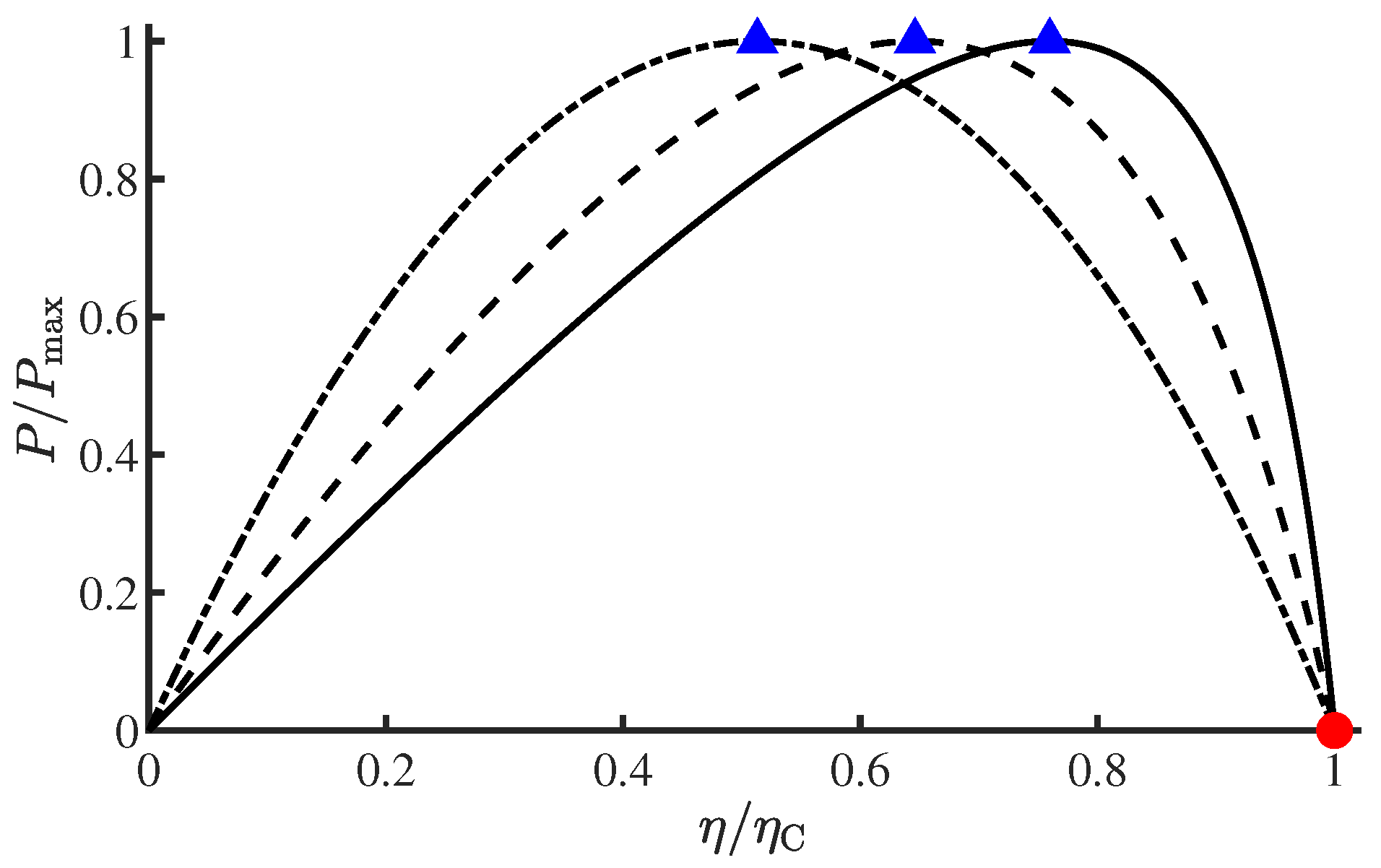
4. Comparison of Curzon–Ahlborn and Extended Yvon Engines
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- Tu, Z.C. Recent advance on the efficiency at maximum power of heat engines. Chin. Phys. B 2012, 21, 020513. [Google Scholar] [CrossRef]
- Leff, H.S. Reversible and Irreversible Heat Engine and Refrigerator Cycles. Am. J. Phys. 2018, 86, 344–353. [Google Scholar] [CrossRef]
- Berry, R.S.; Salamon, P.; Andresen, B. (Eds.) Finite-Time Thermodynamics; MDPI—Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2022. [Google Scholar] [CrossRef]
- Ma, Y.H.; Zhao, X.H. Finite-Time Thermodynamics: A Journey Beginning with Optimizing Heat Engines. arXiv 2024, arXiv:2411.03853. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z.; Lin, G.; Andresen, B. On the Curzon–Ahlborn Efficiency and Its Connection with the Efficiencies of Real Heat Engines. Energ. Convers. Manag. 2001, 42, 173–181. [Google Scholar] [CrossRef]
- Van den Broeck, C. Thermodynamic Efficiency at Maximum Power. Phys. Rev. Lett. 2005, 95, 190602. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. True Nature of the Curzon-Ahlborn Efficiency. Phys. Rev. E 2017, 96, 022119. [Google Scholar] [CrossRef]
- Dechant, A.; Kiesel, N.; Lutz, E. Underdamped stochastic heat engine at maximum efficiency. Europhys. Lett. 2017, 119, 50003. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chen, J.F.; Fei, Z.; Quan, H.T. Microscopic Theory of the Curzon–Ahlborn Heat Engine Based on a Brownian Particle. Phys. Rev. E 2022, 106, 024105. [Google Scholar] [CrossRef] [PubMed]
- Salamon, P.; Nitzan, A. Finite Time Optimizations of a Newton’s Law Carnot Cycle. J. Chem. Phys. 1981, 74, 3546–3560. [Google Scholar] [CrossRef]
- Chen, L.; Yan, Z. The Effect of Heat-transfer Law on Performance of a Two-heat-source Endoreversible Cycle. J. Chem. Phys. 1989, 90, 3740–3743. [Google Scholar] [CrossRef]
- Feldmann, T.; Geva, E.; Kosloff, R.; Salamon, P. Heat Engines in Finite Time Governed by Master Equations. Am. J. Phys. 1996, 64, 485–492. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Kumar, S. Finite Time Thermodynamic Analysis of Endoreversible Stirling Heat Engine with Regenerative Losses. Energy 2000, 25, 989–1003. [Google Scholar] [CrossRef]
- Kosloff, R. A Quantum Mechanical Open System as a Model of a Heat Engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Efficiency at Maximum Power: An Analytically Solvable Model for Stochastic Heat Engines. Europhys. Lett. 2007, 81, 20003. [Google Scholar] [CrossRef]
- Tu, Z.C. Efficiency at Maximum Power of Feynman’s Ratchet as a Heat Engine. J. Phys. A Math. Theor. 2008, 41, 312003. [Google Scholar] [CrossRef]
- Esposito, M.; Kawai, R.; Lindenberg, K.; Van den Broeck, C. Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Efficiency at Maximum Power of Minimally Nonlinear Irreversible Heat Engines. Europhys. Lett. 2012, 97, 10004. [Google Scholar] [CrossRef]
- Ryabov, A.; Holubec, V. Maximum Efficiency of Steady-State Heat Engines at Arbitrary Power. Phys. Rev. E 2016, 93, 050101. [Google Scholar] [CrossRef]
- Shiraishi, N.; Saito, K.; Tasaki, H. Universal trade-off relation between power and efficiency for heat engines. Phys. Rev. Lett. 2016, 117, 190601. [Google Scholar] [CrossRef]
- Ma, Y.H.; Xu, D.; Dong, H.; Sun, C.P. Universal Constraint for Efficiency and Power of a Low-Dissipation Heat Engine. Phys. Rev. E 2018, 98, 042112. [Google Scholar] [CrossRef]
- Pietzonka, P.; Seifert, U. Universal Trade-Off between Power, Efficiency, and Constancy in Steady-State Heat Engines. Phys. Rev. Lett. 2018, 120, 190602. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.F.; Sun, C.P.; Dong, H. Achieve higher efficiency at maximum power with finite-time quantum Otto cycle. Phys. Rev. E 2019, 100, 062140. [Google Scholar] [CrossRef]
- Sheng, S.; Tu, Z.C. Constitutive Relation for Nonlinear Response and Universality of Efficiency at Maximum Power for Tight-Coupling Heat Engines. Phys. Rev. E 2015, 91, 022136. [Google Scholar] [CrossRef]
- Johal, R.S. Heat Engines at Optimal Power: Low-Dissipation versus Endoreversible Model. Phys. Rev. E 2017, 96, 012151. [Google Scholar] [CrossRef]
- Ma, Y.H.; Fu, C. Unified Approach to Power-Efficiency Trade-Off of Generic Thermal Machines. arXiv 2024, arXiv:2411.03849. [Google Scholar] [CrossRef]
- Bejan, A. Models of Power Plants That Generate Minimum Entropy While Operating at Maximum Power. Am. J. Phys. 1996, 64, 1054–1059. [Google Scholar] [CrossRef]
- Vaudrey, A.; Lanzetta, F.; Feidt, M.H.B. Reitlinger and the Origins of the Efficiency at Maximum Power Formula for Heat Engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Moreau, M.; Pomeau, Y. Carnot Principle and Its Generalizations: A Very Short Story of a Long Journey. Eur. Phys. J. Spec. Top. 2015, 224, 769–780. [Google Scholar] [CrossRef]
- Ouerdane, H.; Apertet, Y.; Goupil, C.; Lecoeur, P. Continuity and Boundary Conditions in Thermodynamics: From Carnot’s Efficiency to Efficiencies at Maximum Power. Eur. Phys. J. Spec. Top. 2015, 224, 839–864. [Google Scholar] [CrossRef]
- Yvon, J. Saclay Reactor: Acquired Knowledge by Two Years Experience in Heat Transfer Using Compressed Gas. In Proceedings of the 1955 United Nations Conference on the Peaceful Uses of Atomic Energy Geneva Conference, Geneva, Switzerland, August 1955. [Google Scholar]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. [Google Scholar]
- Novikov, I.I. Efficiency of an Atomic Power Generating Installation. Sov. J. At. Energy 1957, 3, 1269–1272. [Google Scholar] [CrossRef]
- Tu, Z.C. Abstract Models for Heat Engines. Front. Phys. 2021, 16, 33202. [Google Scholar] [CrossRef]
- Vollmer, M. Newton’s Law of Cooling Revisited. Eur. J. Phys. 2009, 30, 1063. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Onsager Coefficients of a Finite-Time Carnot Cycle. Phys. Rev. E 2009, 80, 021121. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.H.; Zhai, R.X.; Chen, J.; Sun, C.P.; Dong, H. Experimental Test of the 1/τ-Scaling Entropy Generation in Finite-Time Thermodynamics. Phys. Rev. Lett. 2020, 125, 210601. [Google Scholar] [CrossRef]
- Rubin, M.H. Optimal Configuration of a Class of Irreversible Heat Engines. I. Phys. Rev. A 1979, 19, 1272–1276. [Google Scholar] [CrossRef]
- Demirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Yuan, H.; Ma, Y.H.; Sun, C.P. Optimizing Thermodynamic Cycles with Two Finite-Sized Reservoirs. Phys. Rev. E 2022, 105, L022101. [Google Scholar] [CrossRef] [PubMed]
- Zhai, R.X.; Cui, F.M.; Ma, Y.H.; Sun, C.P.; Dong, H. Experimental Test of Power-Efficiency Trade-off in a Finite-Time Carnot Cycle. Phys. Rev. E 2023, 107, L042101. [Google Scholar] [CrossRef]
- Reyes-Ramírez, I.; Barranco-Jiménez, M.A.; Rojas-Pacheco, A.; Guzmán-Vargas, L. Global Stability Analysis of a Curzon–Ahlborn Heat Engine under Different Regimes of Performance. Entropy 2014, 16, 5796–5809. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Hernández, A.C.; Medina, A.; Roco, J.M.M.; White, J.A.; Velasco, S. Unified Optimization Criterion for Energy Converters. Phys. Rev. E 2001, 63, 037102. [Google Scholar] [CrossRef]
- Sieniutycz, S. Analysis of Power and Entropy Generation in a Chemical Engine. Int. J. Heat Mass Transf. 2008, 51, 5859–5871. [Google Scholar] [CrossRef]
- De Parga-Regalado, A.M.A. Optimal Efficiencies of an Isothermal Endoreversible Chemical Engine. Eur. J. Phys. 2023, 44, 035101. [Google Scholar] [CrossRef]
- Kaur, J.; Johal, R.S.; Feidt, M. Thermoelectric Generator in Endoreversible Approximation: The Effect of Heat-Transfer Law under Finite Physical Dimensions Constraint. Phys. Rev. E 2022, 105, 034122. [Google Scholar] [CrossRef]
- Juárez-Huerta, V.H.; Sánchez-Salas, N.; Chimal-Eguía, J.C. Optimization Criteria and Efficiency of a Thermoelectric Generator. Entropy 2022, 24, 1812. [Google Scholar] [CrossRef] [PubMed]
- Salamon, P.; Berry, R.S. Thermodynamic Length and Dissipated Availability. Phys. Rev. Lett. 1983, 51, 1127–1130. [Google Scholar] [CrossRef]
- Chen, J.F. Optimizing Brownian Heat Engine with Shortcut Strategy. Phys. Rev. E 2022, 106, 054108. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.H.; Gong, Z.N.; Tu, Z.C. Low-Dissipation Engines: Microscopic Construction via Shortcuts to Adiabaticity and Isothermality, the Optimal Relation between Power and Efficiency. Phys. Rev. E 2022, 106, 064117. [Google Scholar] [CrossRef]
- Ondrechen, M.J.; Andresen, B.; Mozurkewich, M.; Berry, R.S. Maximum Work from a Finite Reservoir by Sequential Carnot Cycles. Am. J. Phys. 1981, 49, 681–685. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Work Output and Efficiency at Maximum Power of Linear Irreversible Heat Engines Operating with a Finite-Sized Heat Source. Phys. Rev. Lett. 2014, 112, 180603. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.H. Effect of Finite-Size Heat Source’s Heat Capacity on the Efficiency of Heat Engine. Entropy 2020, 22, 1002. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.H. Simple realization of the polytropic process with a finite-sized reservoir. Am. J. Phys. 2023, 91, 555. [Google Scholar] [CrossRef]
- Martínez, I.A.; Roldán, É.; Dinis, L.; Petrov, D.; Parrondo, J.M.R.; Rica, R.A. Brownian Carnot Engine. Nat. Phys. 2016, 12, 67–70. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in Finite Time: Extremals for Imperfect Heat Engines. J. Chem. Phys. 1977, 66, 1571–1577. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.-H.; Ma, Y.-H. Revisiting Endoreversible Carnot Engine: Extending the Yvon Engine. Entropy 2025, 27, 195. https://doi.org/10.3390/e27020195
Zhao X-H, Ma Y-H. Revisiting Endoreversible Carnot Engine: Extending the Yvon Engine. Entropy. 2025; 27(2):195. https://doi.org/10.3390/e27020195
Chicago/Turabian StyleZhao, Xiu-Hua, and Yu-Han Ma. 2025. "Revisiting Endoreversible Carnot Engine: Extending the Yvon Engine" Entropy 27, no. 2: 195. https://doi.org/10.3390/e27020195
APA StyleZhao, X.-H., & Ma, Y.-H. (2025). Revisiting Endoreversible Carnot Engine: Extending the Yvon Engine. Entropy, 27(2), 195. https://doi.org/10.3390/e27020195






