Solving Flexible Job-Shop Scheduling Problems Based on Quantum Computing
Abstract
1. Introduction
- Processing constraint: Operations must be assigned to eligible machines based on their performance capabilities. It is important to note that not all machines are capable of processing each operation.
- Operation constraint: Once assignment decisions are made for each machine, the next step involves optimizing the sequence of operations allocated to that machine. During the scheduling process, it is essential to ensure that the processing sequence of each pair of operations of the same job remains orderly and non-chaotic.
- Overlapping constraint: We optimize the starting time of each operation on each machine. That is, we ascertain that there are no temporal conflicts among operations assigned to the same machine, as well as between operations of the same job allocated to different machines.
- We introduce quantum computing as a method for solving FJSPs and propose a quadratic unconstrained binary optimization (QUBO) model with the objective of minimizing the system’s maximum completion time (makespan). The variable pruning approach, which minimizes the predecessors and successors, effectively reduces the number of qubits required for quantum computing.
- We conducted numerical experiments using a traditional computer and a coherent Ising machine (CIM) to evaluate the proposed mixed-integer programming (MIP) model and the QUBO model, respectively. The experimental results indicate that the computation speed of a CIM significantly exceeds that of traditional computers, highlighting the substantial potential of CIMs in solving FJSPs and other combinatorial optimization challenges.
2. Problem Definition and Modelling
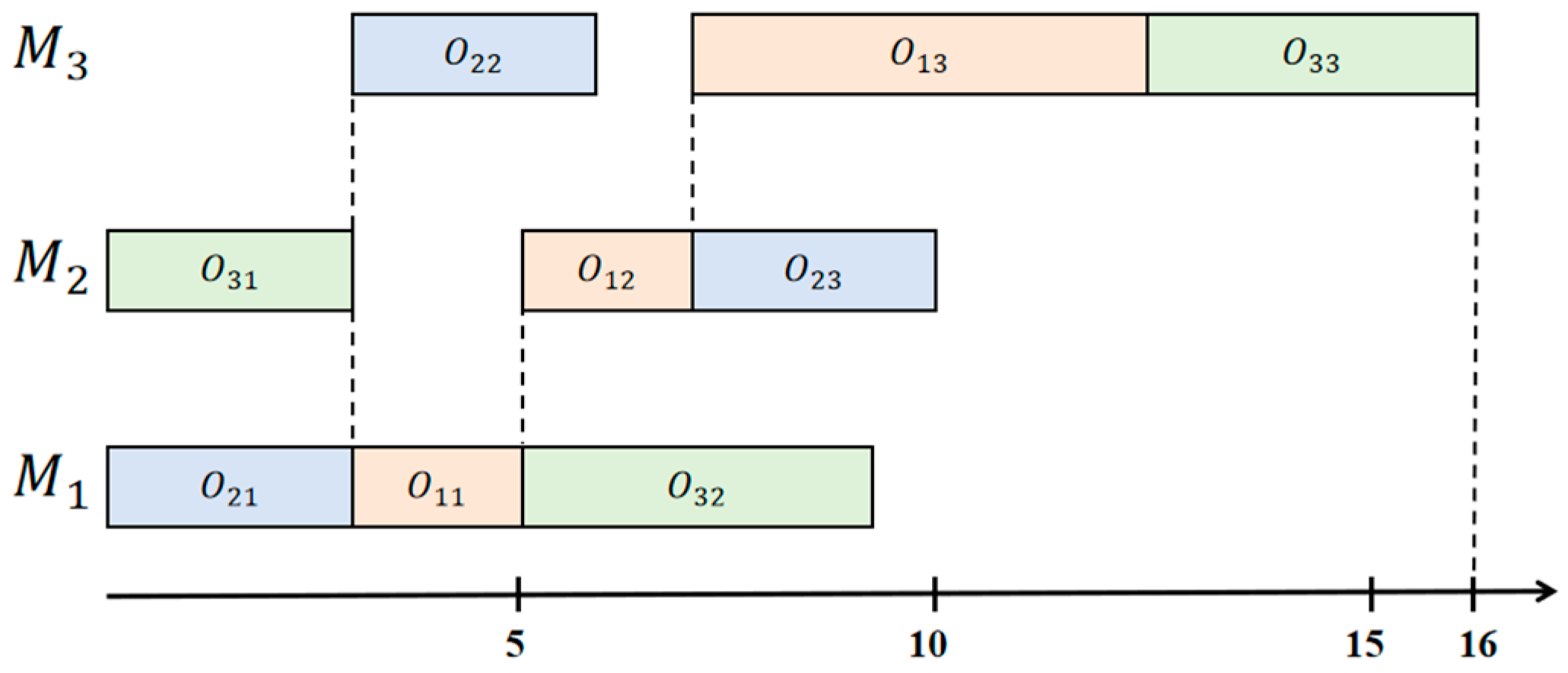
2.1. Problem Description
2.2. Mixed-Integer Programming Model
2.3. Quadratic Unconstrained Binary Optimization Model
- Not every operation can be assigned to every machine, so we set for all .
- To consider the characteristics of an FJSP, every operation can only be assigned at the time of its minimum predecessor and minimum successor operations, so for all , , we set for all times with and , where,
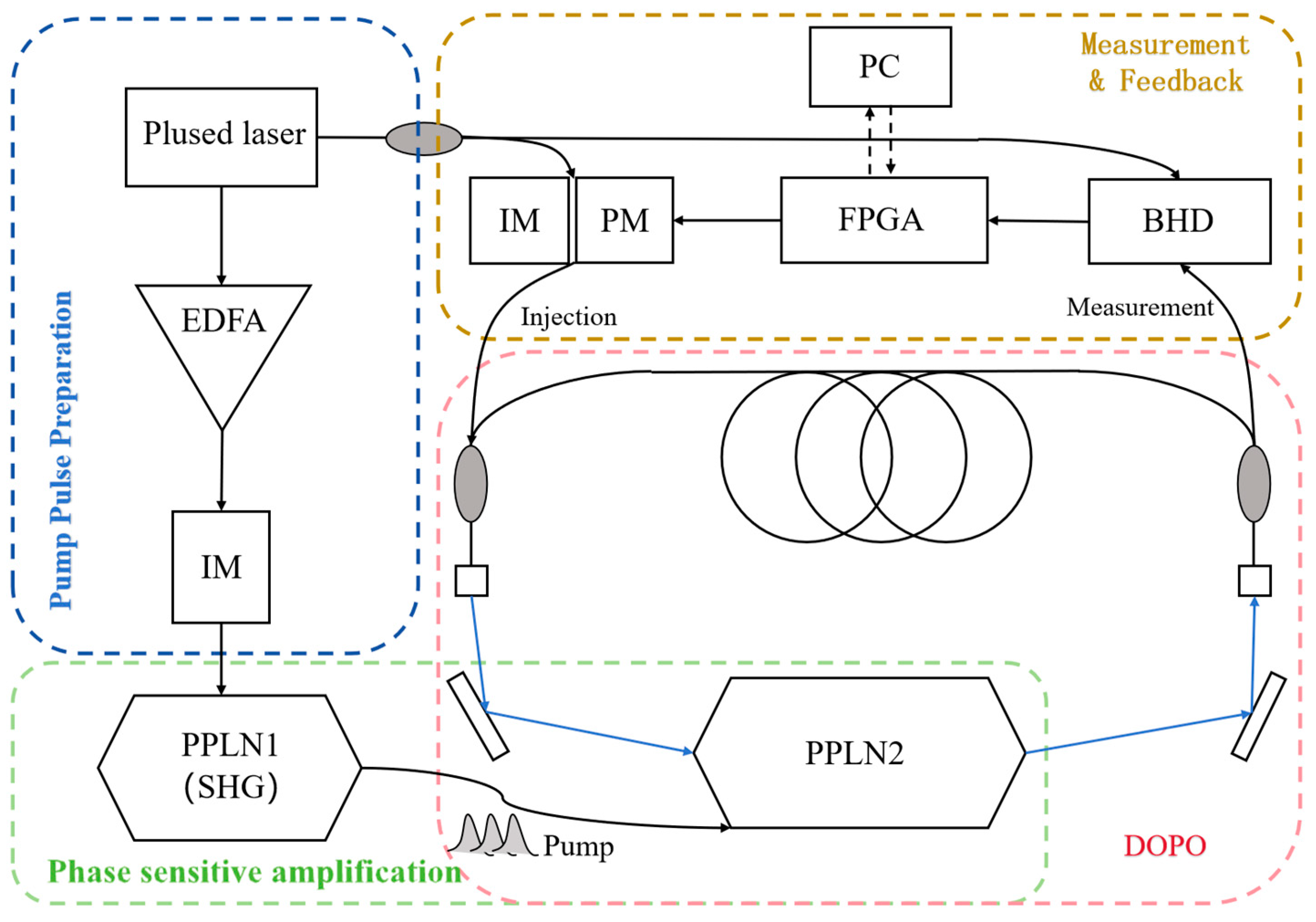
3. Solving FJSPs via a Coherent Ising Machine
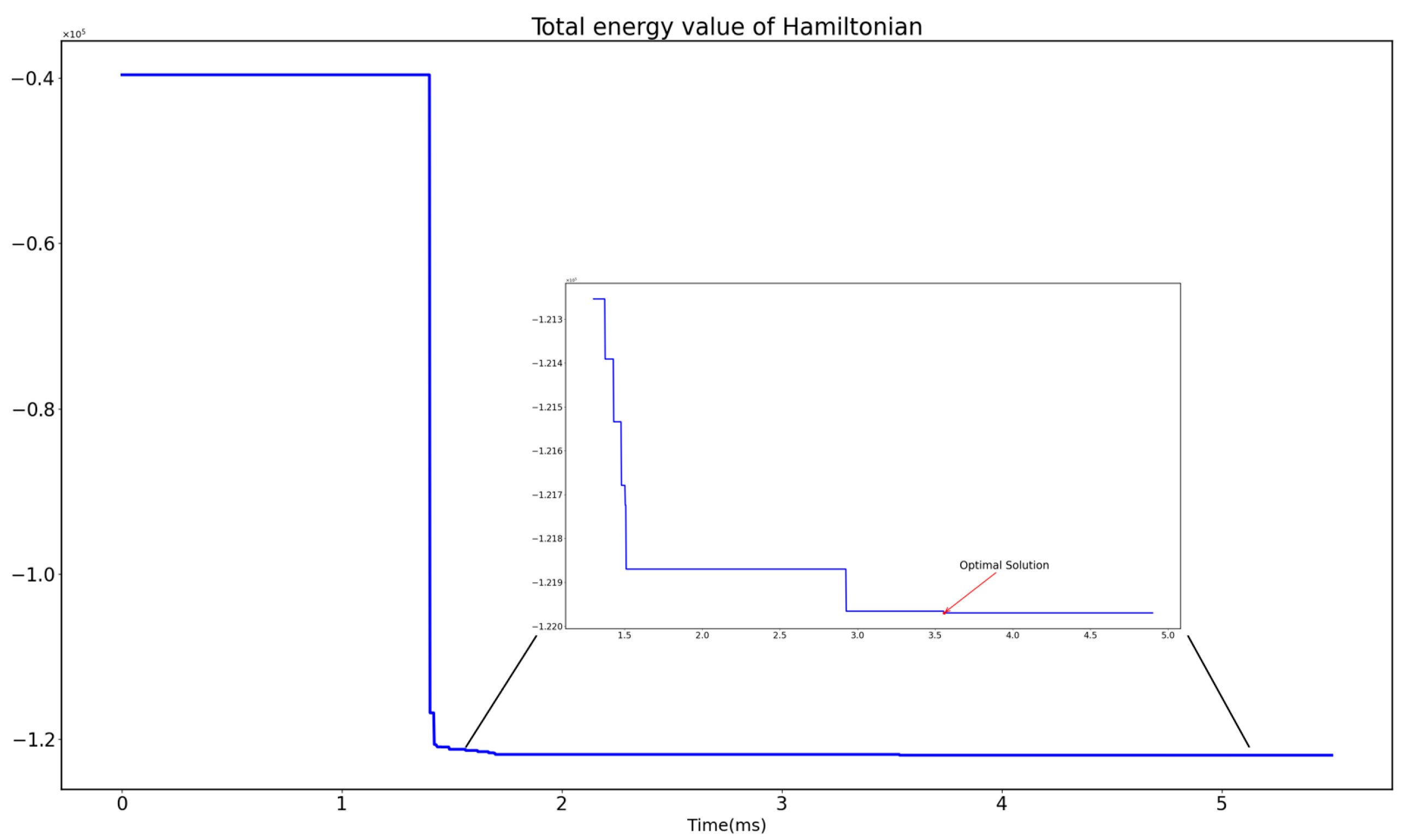
4. Experiment and Discussion
5. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Naderi, B.; Roshanaei, V. Critical-path-search logic-based benders decomposition approaches for flexible job shop scheduling. INFORMS J. Optim. 2022, 4, 1–28. [Google Scholar] [CrossRef]
- Kesen, S.; Güngör, Z. Job scheduling in virtual manufacturing cells with lot-streaming strategy: A new mathematical model formulation and a genetic algorithm approach. J. Oper. Res. Soc. 2012, 64, 683–695. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Alvarez-Valdés, R.; Fuertes, A.; Tamarit, J.M.; Giménez, G.; Ramos, R. A heuristic to schedule flexible job-shop in a glass factory. Eur. J. Oper. Res. 2005, 165, 525–534. [Google Scholar] [CrossRef]
- Pezzella, F.; Morganti, G.; Ciaschetti, G. A genetic algorithm for the flexible job-shop scheduling problem. Comput. Oper. Res. 2008, 3, 3202–3212. [Google Scholar] [CrossRef]
- Bagheri, A.; Zandieh, M.; Mahdavi, I.; Yazdani, M. An artificial immune algorithm for the flexible job-shop scheduling problem. Future Gener. Comput. Syst. 2010, 26, 533–541. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Shen, L.; Dauzère-Pérès, S.; Neufeld, J.S. Solving the flexible job shop scheduling problem with sequence-dependent setup times. Eur. J. Oper. Res. 2018, 265, 503–516. [Google Scholar] [CrossRef]
- Juvin, C.; Houssin, L.; Lopez, P. Logic-based Benders decomposition for the preemptive flexible job-shop scheduling problem. Comput. Oper. Res. 2023, 152, 106156. [Google Scholar] [CrossRef]
- Chaudhry, I.A.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Fattahi, P.; Saidi Mehrabad, M.; Jolai, F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. J. Intell. Manuf. 2007, 18, 331–342. [Google Scholar] [CrossRef]
- Demir, Y.; İşleyen, S.K. Evaluation of mathematical models for flexible job-shop scheduling problems. Appl. Math. Model. 2013, 37, 977–988. [Google Scholar] [CrossRef]
- Thomalla, C.S. Job shop scheduling with alternative process plans. Int. J. Prod. Econ. 2001, 74, 125–134. [Google Scholar] [CrossRef]
- Özgüven, C.; Yavuz, Y.; Özbakır, L. Mixed integer goal programming models for the flexible job-shop scheduling problems with separable and non-separable sequence dependent setup times. Appl. Math. Model. 2012, 36, 856–858. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Ren, Y.; Zhang, B.; Lv, C. Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem. Comput. Ind. Eng. 2020, 142, 106347. [Google Scholar] [CrossRef]
- Ajagekar, A.; Humble, T.; You, F. Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems. Comput. Chem. Eng. 2020, 132, 106630. [Google Scholar] [CrossRef]
- Inagaki, T.; Haribara, Y.; Igarashi, K.; Sonobe, T.; Tamate, S.; Honjo, T.; Marandi, A.; McMahon, P.L.; Umeki, T.; Enbutsu, K.; et al. A coherent Ising machine for 2000-node optimization problems. Science 2016, 354, 603–606. [Google Scholar] [CrossRef]
- Honjo, T.; Sonobe, T.; Inaba, K.; Inagaki, T.; Ikuta, T.; Yamada, Y.; Kazama, T.; Enbutsu, K.; Umeki, T.; Kasahara, R.; et al. 100,000-spin coherent Ising machine. Sci. Adv. 2021, 70, eabh09521. [Google Scholar]
- Lu, B.; Fan, C.R.; Liu, L.; Wen, K.; Wang, C. Speed-up coherent Ising machine with a spiking neural network. Opt. Express 2023, 31, 3676–3684. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Liu, L.; Song, J.Y.; Wen, K.; Wang, C. Recent progress on coherent computation based on quantum squeezing. AAPPS Bull. 2023, 33, 7. [Google Scholar] [CrossRef]
- Venturelli, D.; Marchand, D.J.J.; Rojo, G. Quantum annealing based factory layout planning. Manuf. Lett. 2022, 32, 59–62. [Google Scholar]
- Zielewski, M.R.; Agung, M.; Egawa, R.; Takizawa, H. Improving Quantum Annealing Performance on Embedded Problems. Supercomput. Front. Innov. 2020, 7, 32–48. [Google Scholar]
- Amaro, D.; Rosenkranz, M.; Fitzpatrick, N.; Hirano, K.; Fiorentini, M. A case study of variational quantum algorithms for a job shop scheduling problem. EPJ Quantum Technol. 2022, 9, 5. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, J.; Ma, Y.; Tresp, V. Differentiable Quantum Architecture Search for Job Shop Scheduling Problem. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 236–240. [Google Scholar]
- Denkena, B.; Schinkel, F.; Pirnay, J.; Wilmsmeier, S. Quantum algorithms for process parallel flexible job shop scheduling. CIRPJ Manuf. Sci. Technol. 2021, 33, 100–114. [Google Scholar] [CrossRef]
- Schworm, P.; Wu, X.; Glatt, M.; Aurich, J.C. Solving flexible job shop scheduling problems in manufacturing with Quantum Annealing. Prod. Manag. 2022, 17, 105–115. [Google Scholar] [CrossRef]
- Zhengfeng, L.I.; Xiaozhong, Y.U.; Guohui, Z.H.; Lujun, C.U. Optimization for the Flexible Job Shop Scheduling Problems with Production Process Time. Ind. Eng. J. 2020, 23, 26. [Google Scholar]
- Wu, X.L.; Xiao, X.; Zhao, N. Flexible job shop dual resource scheduling problem considering loading and unloading. Control Decis. 2020, 35, 2475–2485. [Google Scholar] [CrossRef]
- Zhu, G.; Xu, W. Multi-objective flexible job shop scheduling method for machine tool component production line considering energy consumption and quality. Control Decis. 2019, 34, 252–260. [Google Scholar]
- Wang, Z.; Marandi, A.; Wen, K. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 2013, 88, 063853. [Google Scholar] [CrossRef]
| Job | Operation | |||
|---|---|---|---|---|
| 2 | 7 | - | ||
| - | 3 | 6 | ||
| 7 | - | 5 | ||
| 3 | 8 | - | ||
| - | 9 | 3 | ||
| 7 | 3 | - | ||
| - | 3 | 8 | ||
| 4 | 8 | - | ||
| - | 8 | 3 |
| Instances | Qubits (Before Pruning) | Qubits (After Pruning) |
|---|---|---|
| SSFJS01 | 48 | 16 |
| SSFJS02 | 252 | 84 |
| SSFJS03 | 864 | 159 |
| SSFJS04 | 1755 | 192 |
| SSFJS05 | 1200 | 126 |
| Instances | Machines | Jobs | Operations | QUBO Matrix | Ising Matrix | |
|---|---|---|---|---|---|---|
| SSFJS01 | 2 | 2 | 4 | 6 | 16 × 16 | 17 × 17 |
| SSFJS02 | 2 | 3 | 6 | 21 | 84 × 84 | 85 × 85 |
| SSFJS03 | 3 | 3 | 9 | 32 | 159 × 159 | 160 × 160 |
| SSFJS04 | 5 | 3 | 9 | 39 | 192 × 192 | 193 × 193 |
| SSFJS05 | 4 | 3 | 12 | 25 | 126 × 126 | 127 × 127 |
| Penalty Coefficient | Value |
|---|---|
| 150 | |
| 100 | |
| 100 |
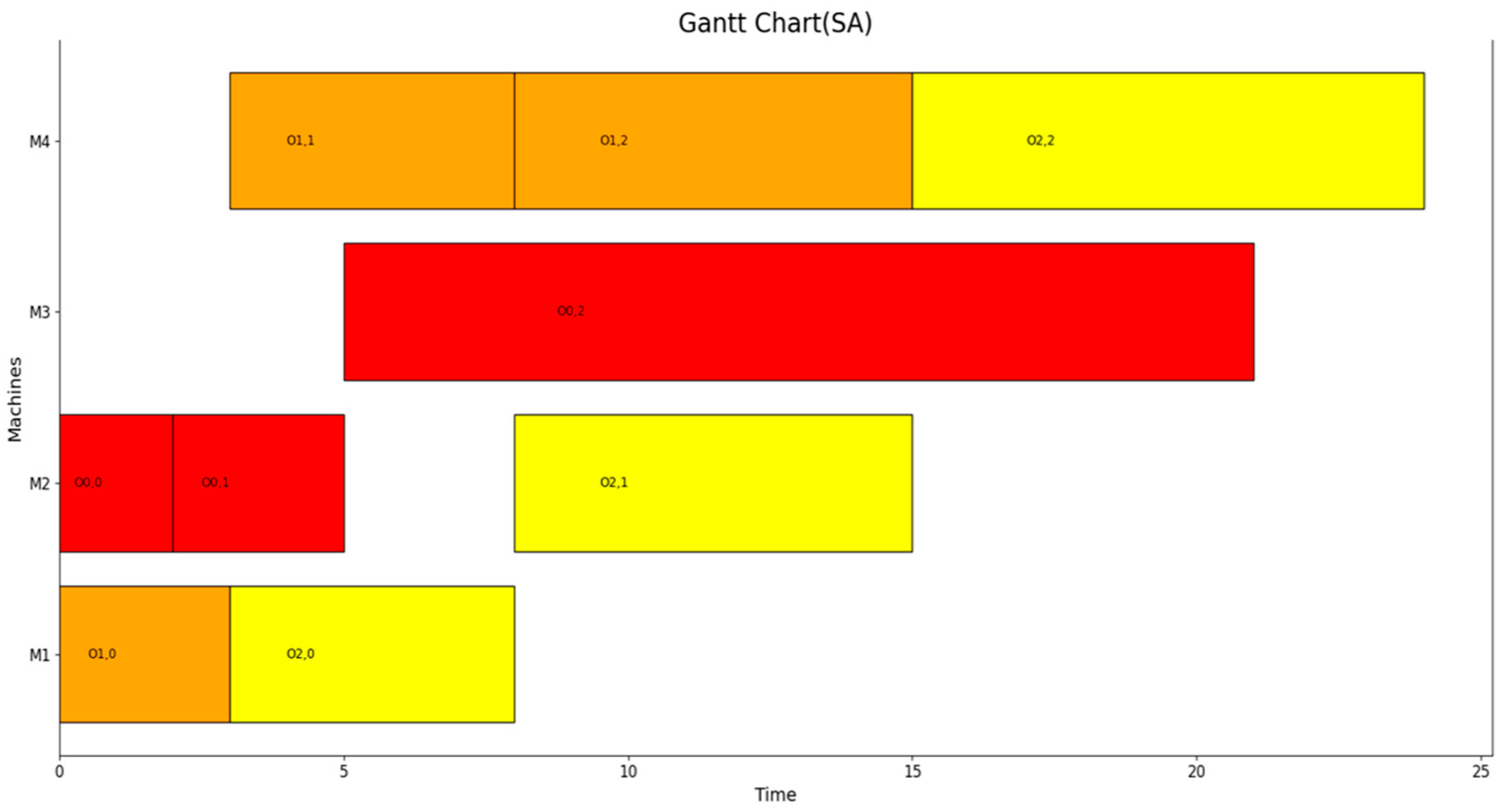
| Instances | CIM | Gurobi | SA | Tabu |
|---|---|---|---|---|
| SSFJS01 | 6/3.38 | 6/8.15 | 6/14,325.77 | 6/71,828.07 |
| SSFJS02 | 21/3.96 | 21/15.74 | 21/19,818.04 | 21/9973.27 |
| SSFJS03 | 32/3.46 | 32/40.85 | 32/55,791.76 | 41/9983.57 |
| SSFJS04 | 39/3.48 | 39/78.27 | 39/88,914.52 | 45/17,255.84 |
| SSFJS05 | 25/3.51 | 25/25.31 | 25/47,121.93 | 25/9918.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, K.; Liu, J.; Chen, M.; Zhang, H. Solving Flexible Job-Shop Scheduling Problems Based on Quantum Computing. Entropy 2025, 27, 189. https://doi.org/10.3390/e27020189
Fu K, Liu J, Chen M, Zhang H. Solving Flexible Job-Shop Scheduling Problems Based on Quantum Computing. Entropy. 2025; 27(2):189. https://doi.org/10.3390/e27020189
Chicago/Turabian StyleFu, Kaihan, Jianjun Liu, Miao Chen, and Huiying Zhang. 2025. "Solving Flexible Job-Shop Scheduling Problems Based on Quantum Computing" Entropy 27, no. 2: 189. https://doi.org/10.3390/e27020189
APA StyleFu, K., Liu, J., Chen, M., & Zhang, H. (2025). Solving Flexible Job-Shop Scheduling Problems Based on Quantum Computing. Entropy, 27(2), 189. https://doi.org/10.3390/e27020189







