Fiducial Inference in Linear Mixed-Effects Models
Abstract
1. Introduction
2. Fiducial Distribution in LME
2.1. Conditional Fiducial Distribution
2.2. Gibbs Sampler and the Final Fiducial Distribution
| Algorithm 1: Gibbs sampling for |
3. Fiducial Inference for LME
3.1. Interval Estimation
| Algorithm 2: Interval estimation for |
|
3.2. Fiducial p-Value
| Algorithm 3: Fiducial p-value for : |
|
4. Simulation
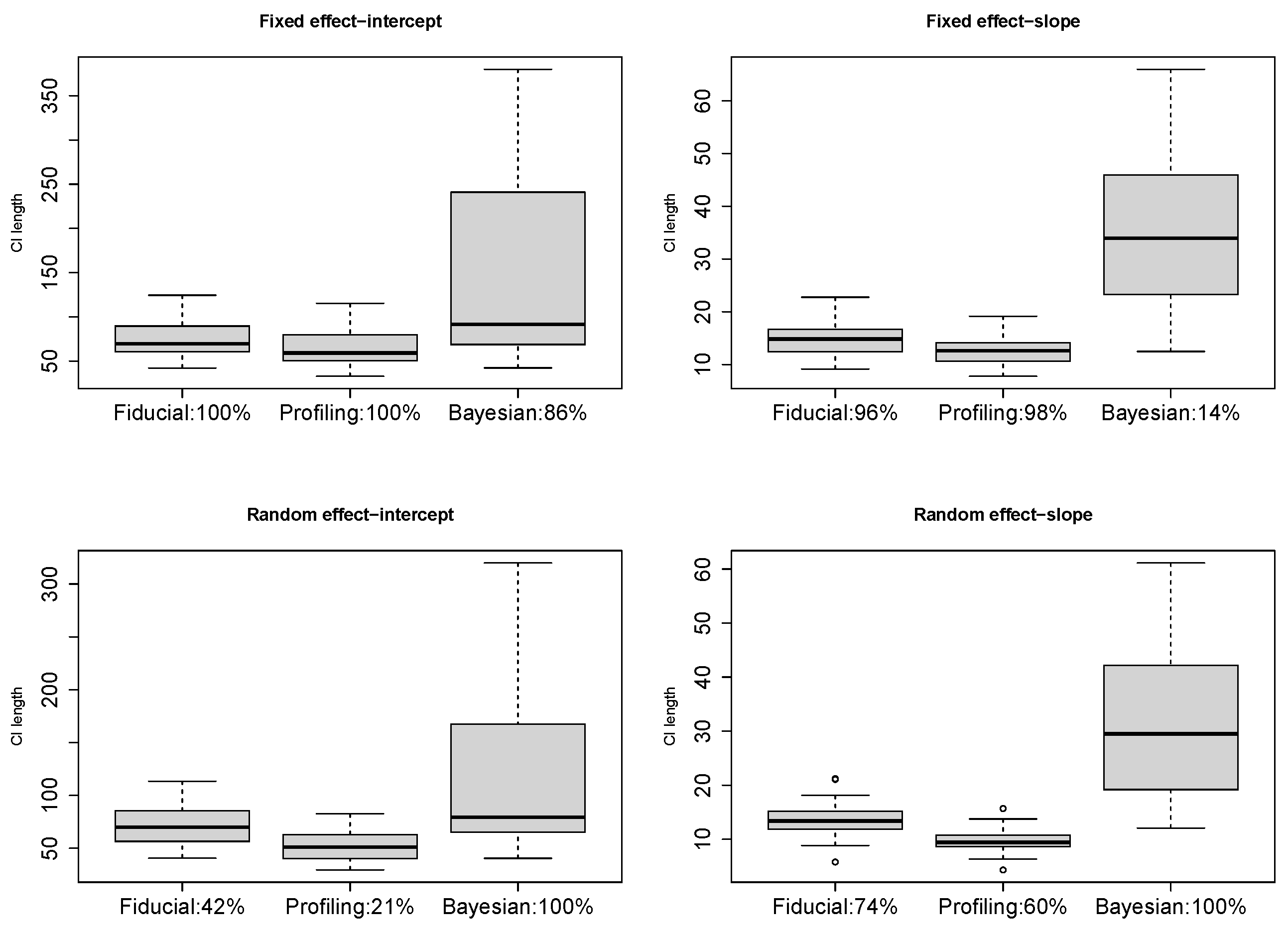
4.1. Confidence Intervals
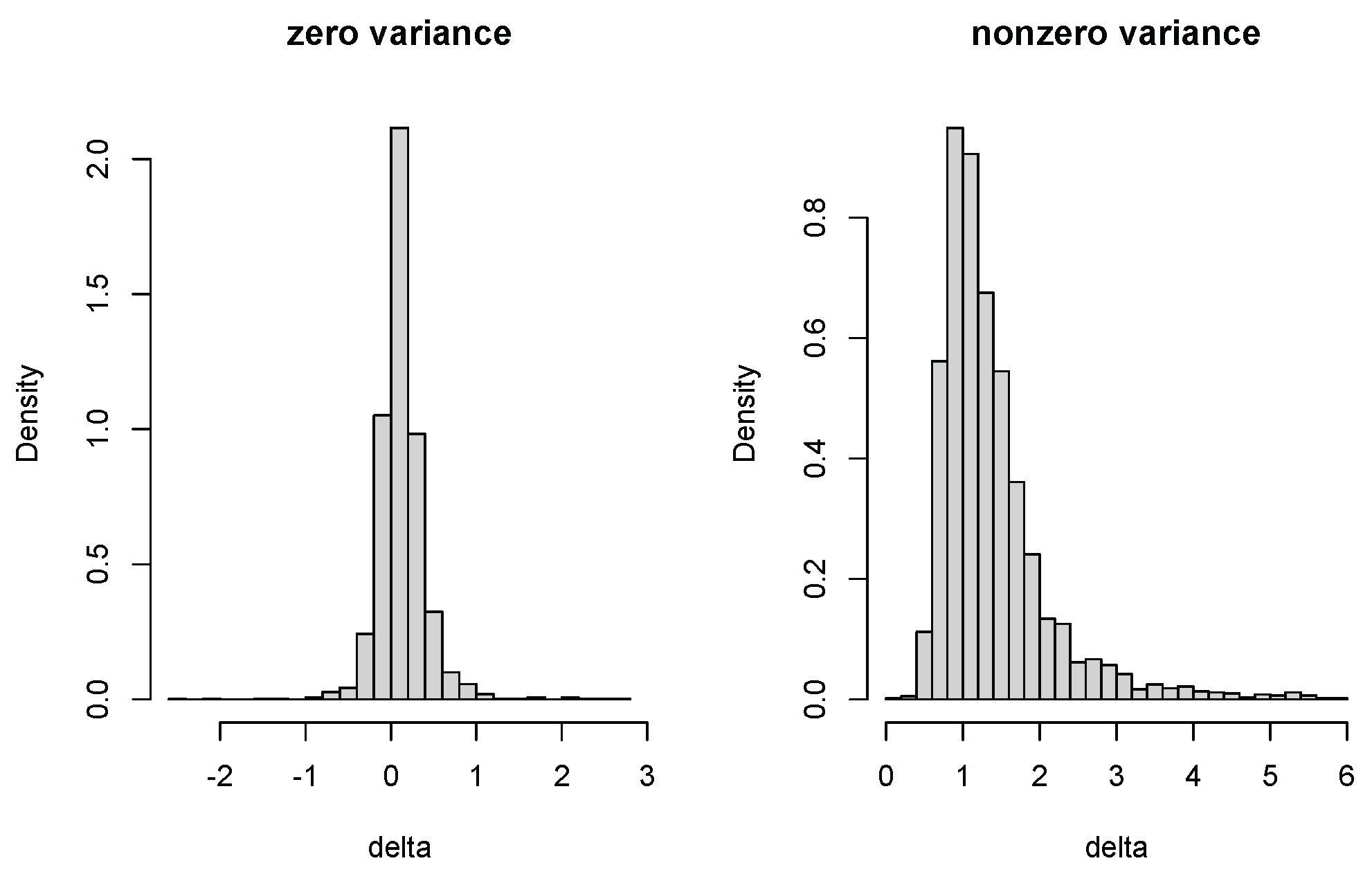
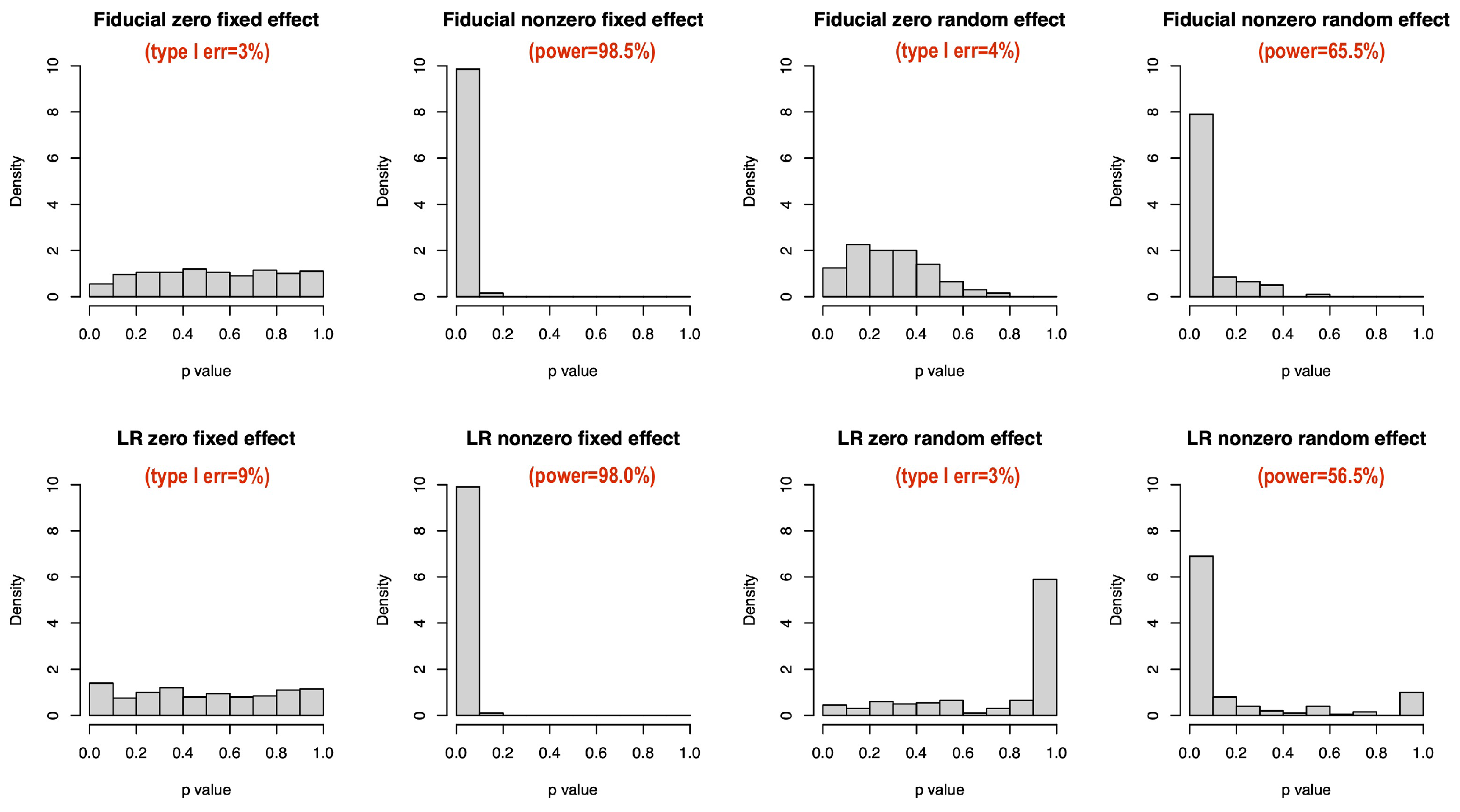
4.2. Zero-Variance Test for Random Effects
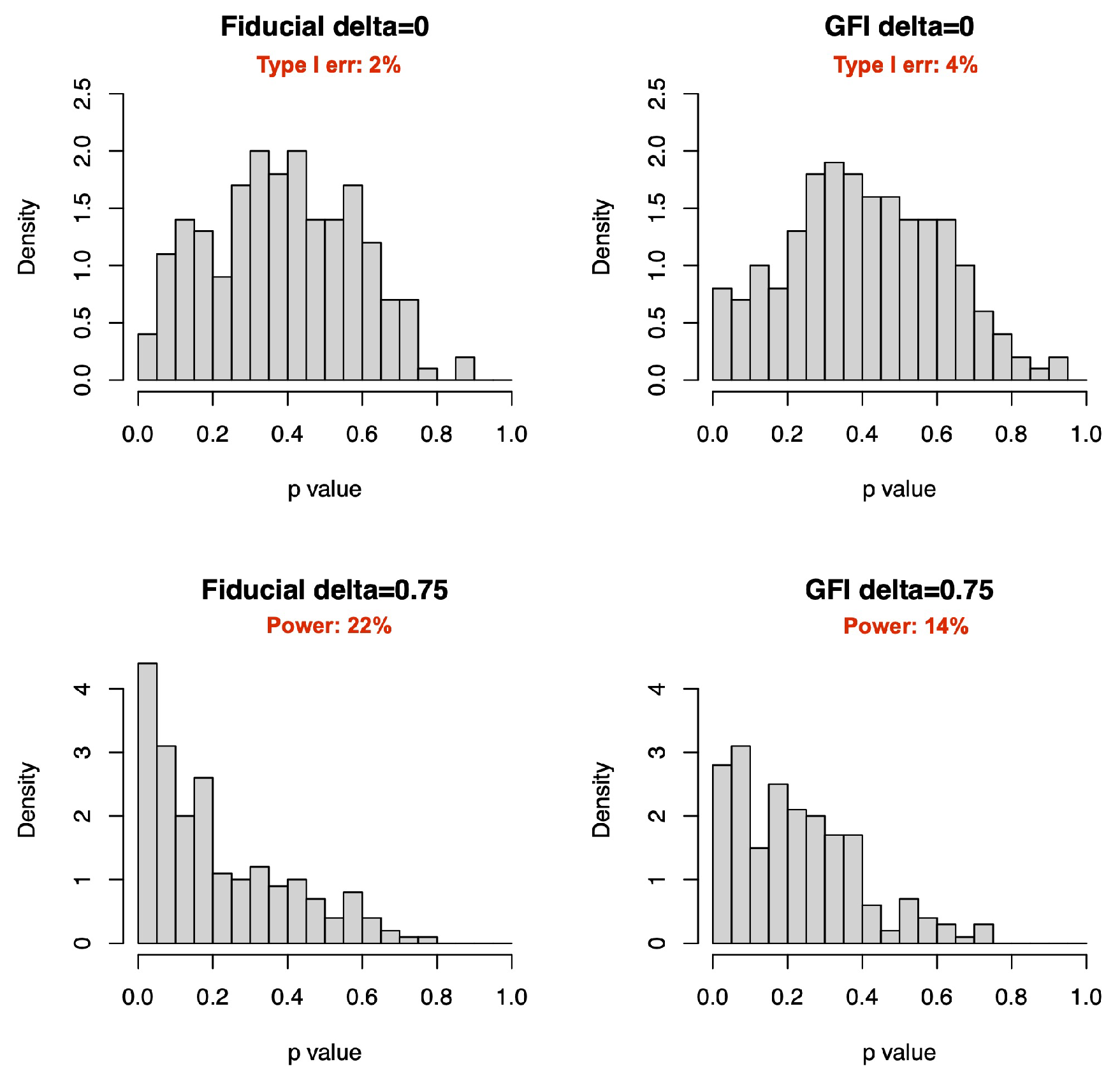
4.3. Comparison with GFIlmm
5. Empirical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, J. Linear and Generalized Linear Mixed Models and Their Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Buscemi, S.; Plaia, A. Model selection in linear mixed-effect models. Asta-Adv. Stat. Anal. 2019, 104, 1–47. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, G.; Liang, H. Model averaging and weight choice in linear mixed-effects models. Biometrika 2014, 101, 205–218. [Google Scholar] [CrossRef]
- Waterman, M.J.; Birch, J.B.; Abdel-Salam, A.-S.G. Several nonparametric and semiparametric approaches to linear mixed model regression. J. Stat. Comput. Simul. 2015, 85, 956–977. [Google Scholar] [CrossRef]
- Dion, C. New adaptive strategies for nonparametric estimation in linear mixed models. J. Stat. Plan. Inference 2014, 150, 30–48. [Google Scholar] [CrossRef]
- Jiang, J. Asymptotic Analysis of Mixed Effects Models: Theory, Applications, and Open Problems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Breslow, N.E.; Clayton, D.G. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993, 88, 9–25. [Google Scholar] [CrossRef]
- Chung, Y.; Rabe-Hesketh, S.; Dorie, V.; Gelman, A.; Liu, J. A non-degenerate estimator for variance parameters in multilevel models via penalized likelihood estimation. Psychometrika 2013, 78, 685–709. [Google Scholar] [CrossRef] [PubMed]
- Bates, D. Fitting linear mixed-effects models using lme4. arXiv 2014, arXiv:1406.5823. [Google Scholar]
- Burkner, P.-C. brms: An r package for bayesian multilevel models using stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef]
- Das, S.; Krishen, A. Some bootstrap methods in nonlinear mixed-effect models. J. Stat. Plan. Inference 1999, 75, 237–245. [Google Scholar] [CrossRef]
- Flores-Agreda, D.; Cantoni, E. Bootstrap estimation of uncertainty in prediction for generalized linear mixed models. Comput. Stat. Data Anal. 2019, 130, 1–17. [Google Scholar] [CrossRef]
- Thai, H.-T.; Mentre, F.; Holford, N.; Veyrat-Follet, C.; Comets, E. A comparison of bootstrap approaches for estimating uncertainty of parameters in linear mixed-effects models. Pharm. Stat. 2013, 12, 129–140. [Google Scholar] [CrossRef]
- Fisher, R.A. On a point raised by m. s. bartlett on fiducial probability. Ann. Hum. Genet. 1937, 7, 370–375. [Google Scholar] [CrossRef]
- Hannig, J.; Iyer, H.; Lai, R.C.S.; Lee, T.C.M. Generalized fiducial inference: A review and new results. J. Am. Stat. Assoc. 2016, 111, 1346–1361. [Google Scholar] [CrossRef]
- Martin, R.; Liu, C. Inferential models: A framework for prior-free posterior probabilistic inference. J. Am. Stat. Assoc. 2013, 108, 301–313. [Google Scholar] [CrossRef]
- Li, X.; Su, H.; Liang, H. Fiducial generalized p-values for testing zero-variance components in linear mixed-effects models. Sci. China Math. 2018, 61, 1–16. [Google Scholar] [CrossRef]
- Lidong, E.; Hannig, J.; Iyer, H.K. Fiducial intervals for variance components in an unbalanced two-component normal mixed linear model. J. Am. Stat. Assoc. 2008, 103, 854–865. [Google Scholar]
- Cisewski, J.; Hannig, J. Generalized fiducial inference for normal linear mixed models. Ann. Stat. 2012, 40, 2102–2127. [Google Scholar] [CrossRef]
- Grimmett, G.R.; Stirzaker, D.R. Probability and Random Processes; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Betancourt, M. A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar] [CrossRef]
- Shi, W.J.; Hannig, J.; Lai, R.C.S.; Lee, T.C.M. Covariance estimation via fiducial inference. Stat. Theory Relat. Fields 2021, 5, 316–331. [Google Scholar] [PubMed]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest package: Tests in linear mixed effects models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Belenky, G.; Wesensten, N.; Thorne, D.; Thomas, M.; Sing, H.; Redmond, D.; Russo, M.; Balkin, T. Patterns of performance degradation and restoration during sleep restriction and subsequent recovery: A sleep dose-response study. J. Sleep Res. 2003, 12, 1–12. [Google Scholar] [CrossRef] [PubMed]
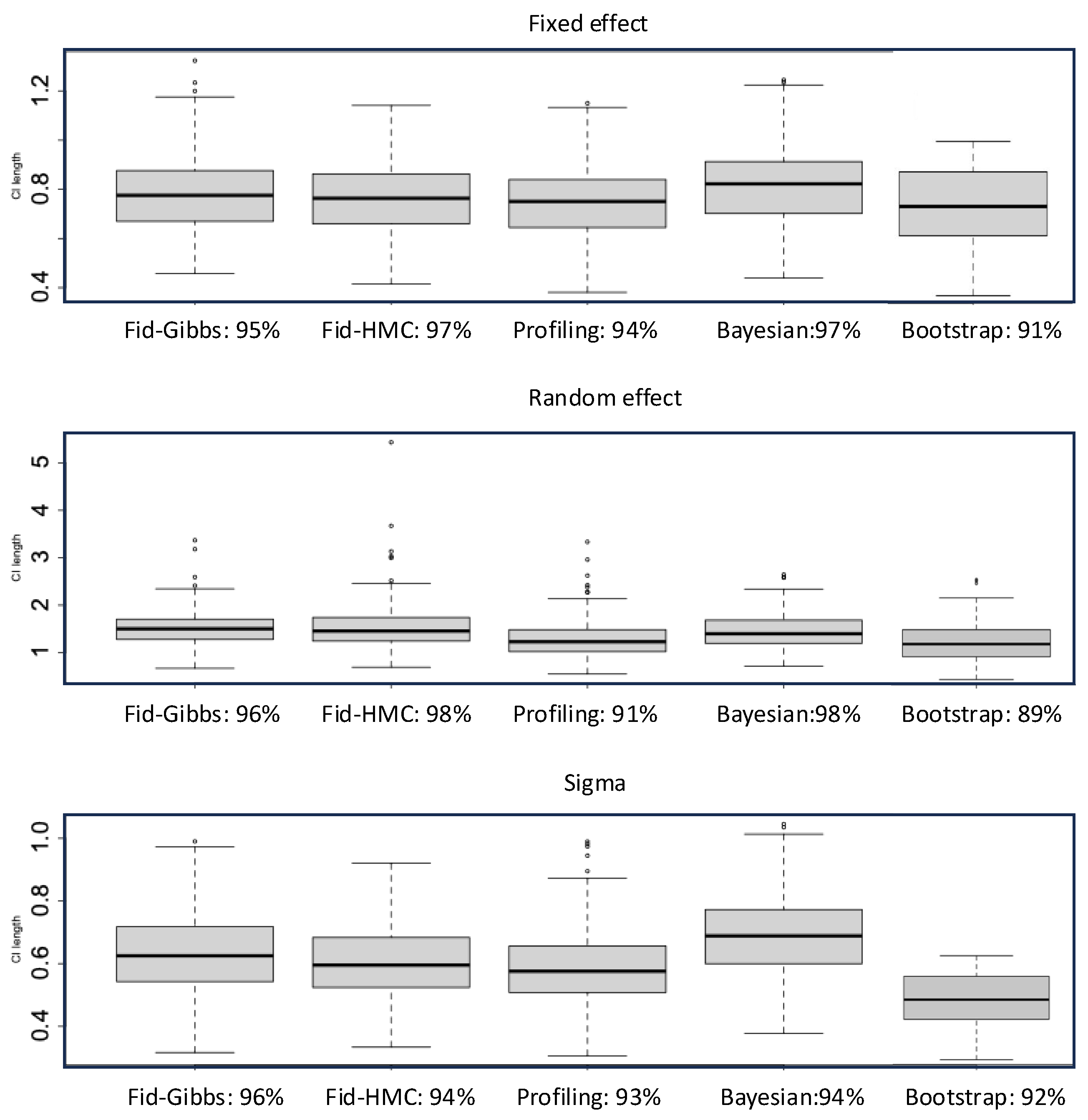
| Fiducial | 0.99 (0.99) | 0.95 (1.01) | 0.97 (1.63) | 0.95 (0.71) |
| Profiling | 0.93 (0.80) | 0.97 (0.70) | 0.89 (1.38) | 0.87 (0.64) |
| Bayesian | 0.97 (1.03) | 0.00 (0.98) | 0.97 (1.49) | 0.96 (0.77) |
| Fiducial | 1.00 (1.30) | 0.98 (1.50) | 0.96 (2.21) | 0.95 (0.60) |
| Profiling | 0.95 (0.86) | 0.99 (0.65) | 0.93 (1.78) | 0.92 (0.54) |
| Bayesian | 1.00 (1.15) | 0.00 (1.38) | 0.97 (1.99) | 0.95 (0.67) |
| , | |||||
|---|---|---|---|---|---|
| Fiducial | 0.99 (16.31) | 0.98 (3.36) | 1.00 (9.89) | 0.98 (2.06) | 1.00 (6.26) |
| Profiling | NA | NA | NA | NA | NA |
| Baysian | 0.97 (20.87) | 0.94 (4.36) | 0.97 (9.01) | 0.96 (2.79) | 0.77 (8.58) |
| Parameter | ||||
| Fiducial | 0.97 (1.56) | 0.94 (0.83) | 0.98 (1.55) | 0.96 (0.82) |
| Profling | 0.94 (1.43) | 0.92 (0.82) | 0.94 (1.25) | 0.96 (0.79) |
| GFI | 0.96 (1.60) | 96 (0.93) | 1.0 (1.45) | 0.95 (0.93) |
| Parameter | ||||
| Fiducial | 0.98 (1.23) | 0.95 (1.00) | 0.98 (1.21) | 0.95 (0.78) |
| Profling | 0.93 (0.96) | 0.93 (0.75) | 0.96 (0.88) | 0.91 (0.66) |
| GFI | 0.97 (1.15) | 0.94 (0.82) | 0.98 (1.09) | 0.96 (0.77) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, X.; Gao, H.; Zou, C. Fiducial Inference in Linear Mixed-Effects Models. Entropy 2025, 27, 161. https://doi.org/10.3390/e27020161
Yang J, Li X, Gao H, Zou C. Fiducial Inference in Linear Mixed-Effects Models. Entropy. 2025; 27(2):161. https://doi.org/10.3390/e27020161
Chicago/Turabian StyleYang, Jie, Xinmin Li, Hongwei Gao, and Chenchen Zou. 2025. "Fiducial Inference in Linear Mixed-Effects Models" Entropy 27, no. 2: 161. https://doi.org/10.3390/e27020161
APA StyleYang, J., Li, X., Gao, H., & Zou, C. (2025). Fiducial Inference in Linear Mixed-Effects Models. Entropy, 27(2), 161. https://doi.org/10.3390/e27020161









