Causal Discovery and Reasoning for Continuous Variables with an Improved Bayesian Network Constructed by Locality Sensitive Hashing and Kernel Density Estimation
Abstract
1. Introduction
- This paper offers new mutual information and conditional mutual information based on KDE for CI testing. The mathematical formula is derived based on the Gaussian kernel. By using such information formulas, a new conditional entropy is calculated, which can be used as a scoring function. The index is used for evaluating the uncertainty degree of a node by providing a set of parent nodes. The index can be used as an effective tool for deciding the parent nodes of a given node. This method can more accurately handle continuous variables without making assumptions about the data distribution, avoiding information loss and erroneous dependencies caused by discretization, thereby improving the accuracy of network structure learning.
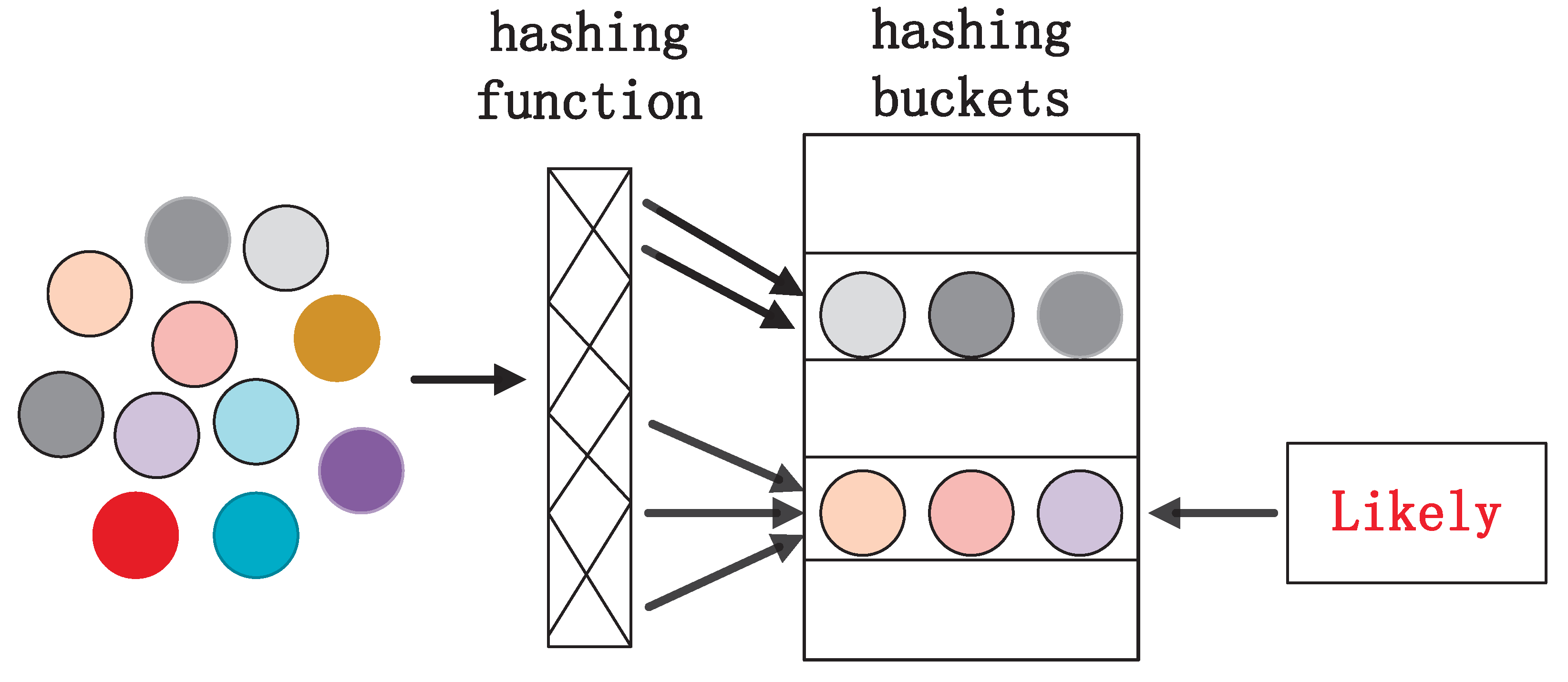
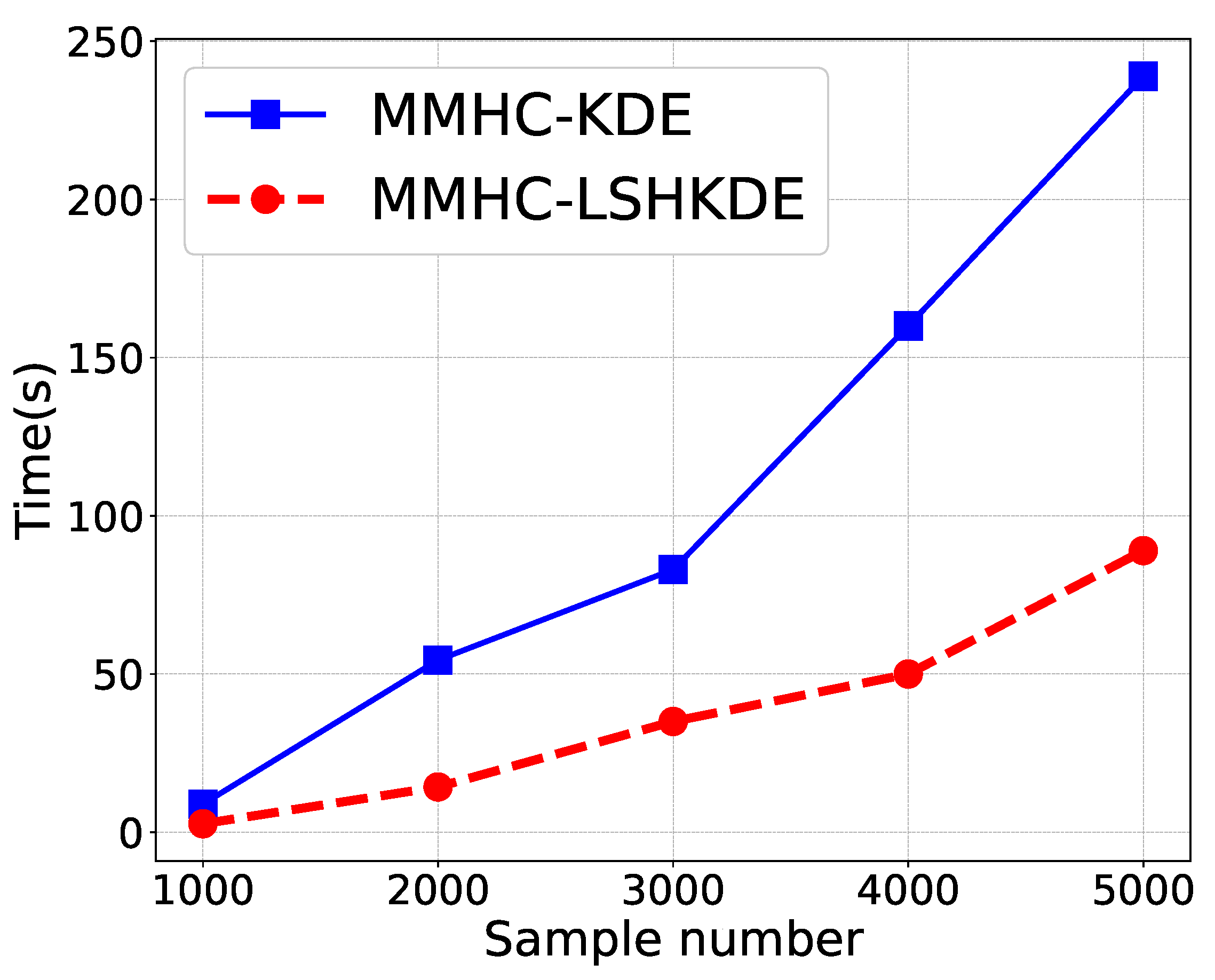
- This paper lowers the computational complexity of KDE. The new KDE introduces LSH functions to accelerate the computational speed of the Gaussian KDE. Without sacrificing estimation accuracy, it reduces the computational cost from to where n is the number of samples and L is the number of hashing functions. This improvement significantly enhances computational efficiency, providing a more practical and operable method for datasets in real-world applications.
- By treating the class attribute as parents of all non-class attributes, this paper provides a new method for BNC, which considers the dependency of variables. In the application, our BN classification model has a higher performance in classifying actual data compared to classic classifiers. Due to the graph structure, it can effectively describe the correlation between attributes, which greatly improves the interpretability of the model. The advantage improves its usability in application scenarios, particularly for the medical disease data.
2. Related Work
2.1. BN Structure Learning Methods for Discrete Variables
2.2. BN Structure Learning Methods for Continuous Variables
3. Bayesian Network Learning
3.1. Bayesian Network
3.2. Hybrid BN Structure Learning Algorithm
4. Hybrid BN Structure Learning Based on LSHKDE
4.1. Gaussian KDE
4.2. Mutual Information and Conditional Mutual Information Based on KDE
4.3. Conditional Entropy Based on KDE
4.4. Gaussian KDE Based on LSH
- If , and then
- If , and then
| Algorithm 1: LSHKDE algorithm |
| Input: Dataset , ; Query data ; Kernel ; LSH family ; Integer ; Bandwidth h. Output: The estimation probability density 1: Preprocessing phase: 2: Initialize L hash functions 3: for i 1 to n do 4: for j 1 to L do 5: Randomly hash according to the hash function from and save it to 6: end for 7: end for 8: Query phase: 9: for k 1 to L do 10: Sample a uniformly random point from the bin set 11: and calculate the by using Equation (19) 12: end for 13: Return |
4.5. Mutual Information and Conditional Entropy Based on LSHKDE
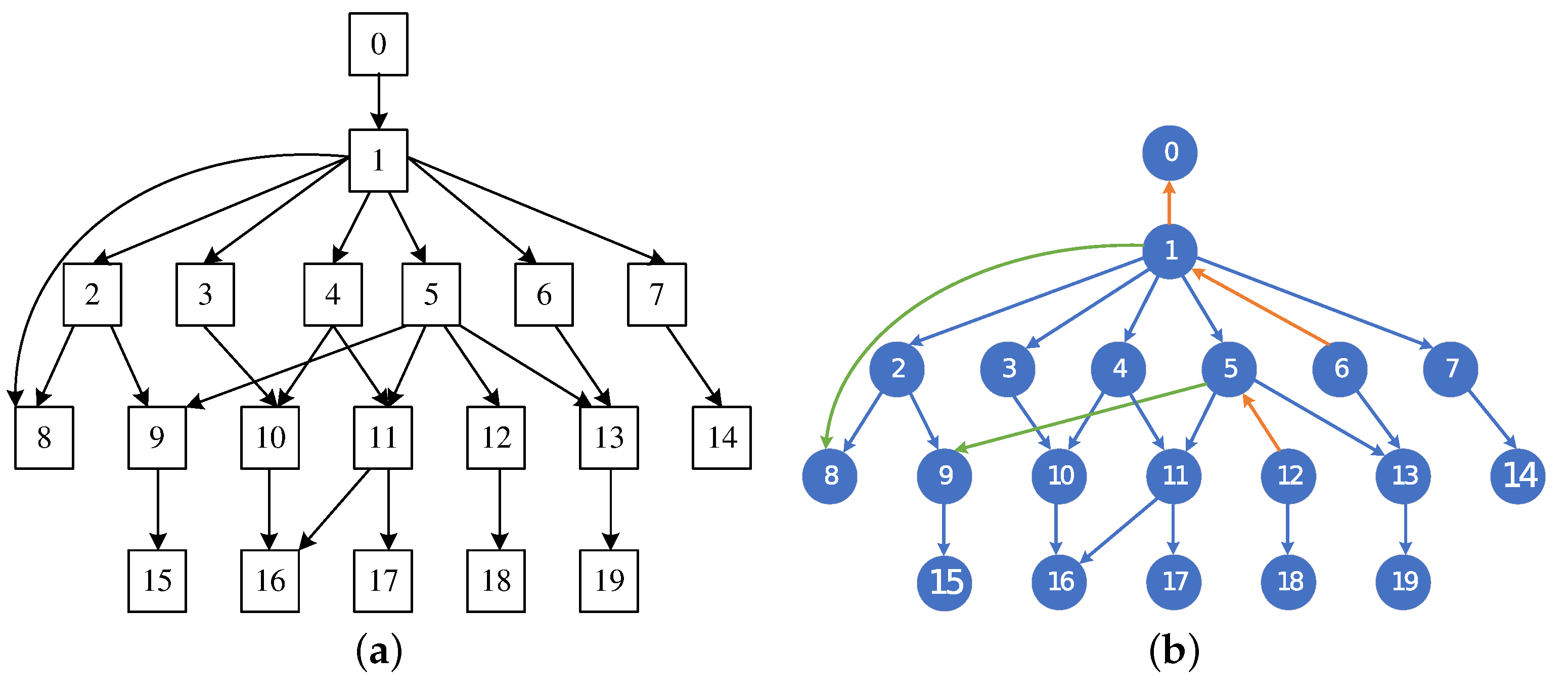
4.6. MMHC-LSHKDE Algorithm
| Algorithm 2: MMHC-LSHKDE algorithm |
| Input: Dataset D; Variable set ; Threshold value Output: DAG 1: Constraint phase: 2: for do 3: using Algorithm 3 4: for do 5: if then 6: 7: else 8: 9: end if 10: end for 11: end for 12: Search phase: 13: Initialize network structure G 14: using Equations (24)–(26) 15: 16: for do 17: using Equations (24)–(26) 18: if then 19: 20: 21: 22: else 23: break 24: end if 25: end for |
| Algorithm 3: MMPC-LSHKDE algorithm |
| Input: Dataset D; Variable set ; Threshold value Output: 1: 2: repeat 3: Calculation using Equations (22) and (23) 4: Calculation using Equations (22) and (23) 5: if then 6: 7: else 8: 9: end if 10: until has not changed 11: for do 12: if and then 13: 14: else 15: 16: end if 17: end for |
5. Hybrid BNC Based on LSHKDE
| Algorithm 4: MMHC-LSHKDE-based BNC algorithm |
| Input: Training dataset D, Output: BNC 1: Invoke the Algorithm 2 to perform network structure learning 2: Calculate the mutual information in the Algorithm 2 using Equation (29) 3: Calculate the conditional mutual information in the Algorithm 2 using Equation (30) 4: Add C as a parent node of each 5: Perform parameter learning and compute posterior probabilities for each category using Equation (28) 6: Select the category with the maximum posteriori probability as the classification result output |
6. Experiment Results
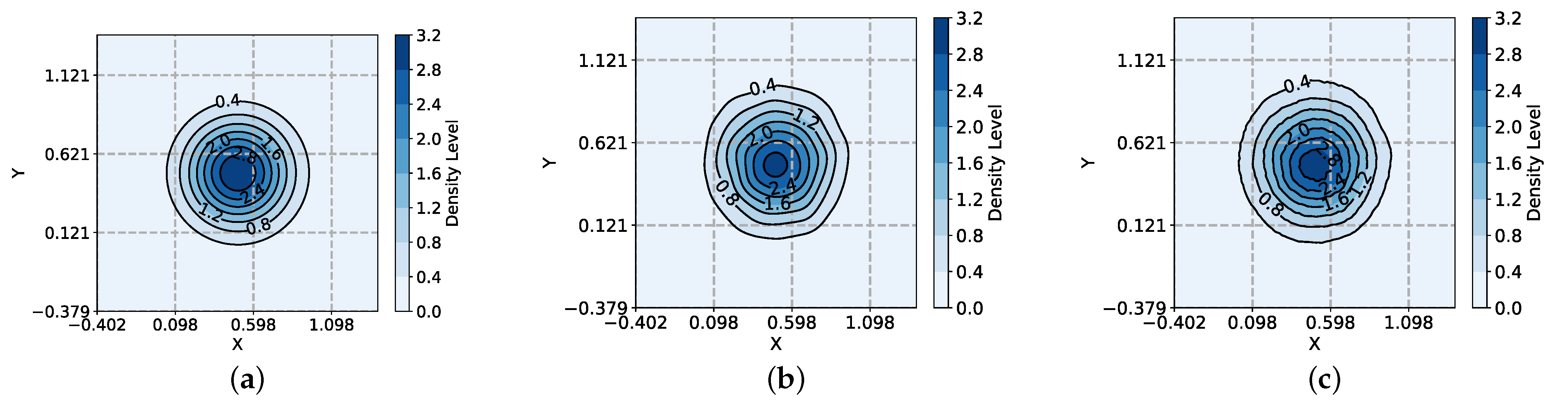
6.1. Compare LSHKDE with KDE in Curve Fitting Performance
6.2. Comparison of BN Structure Learning Algorithms
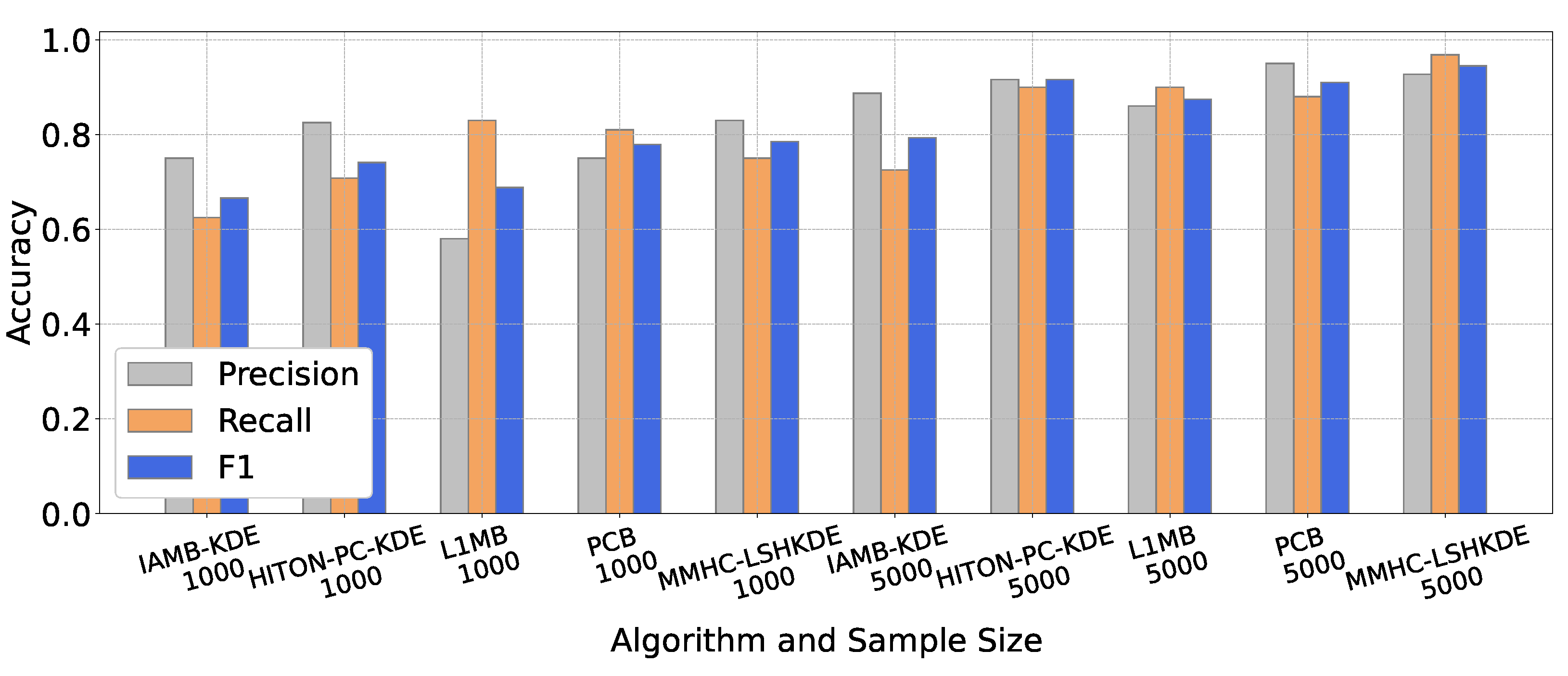
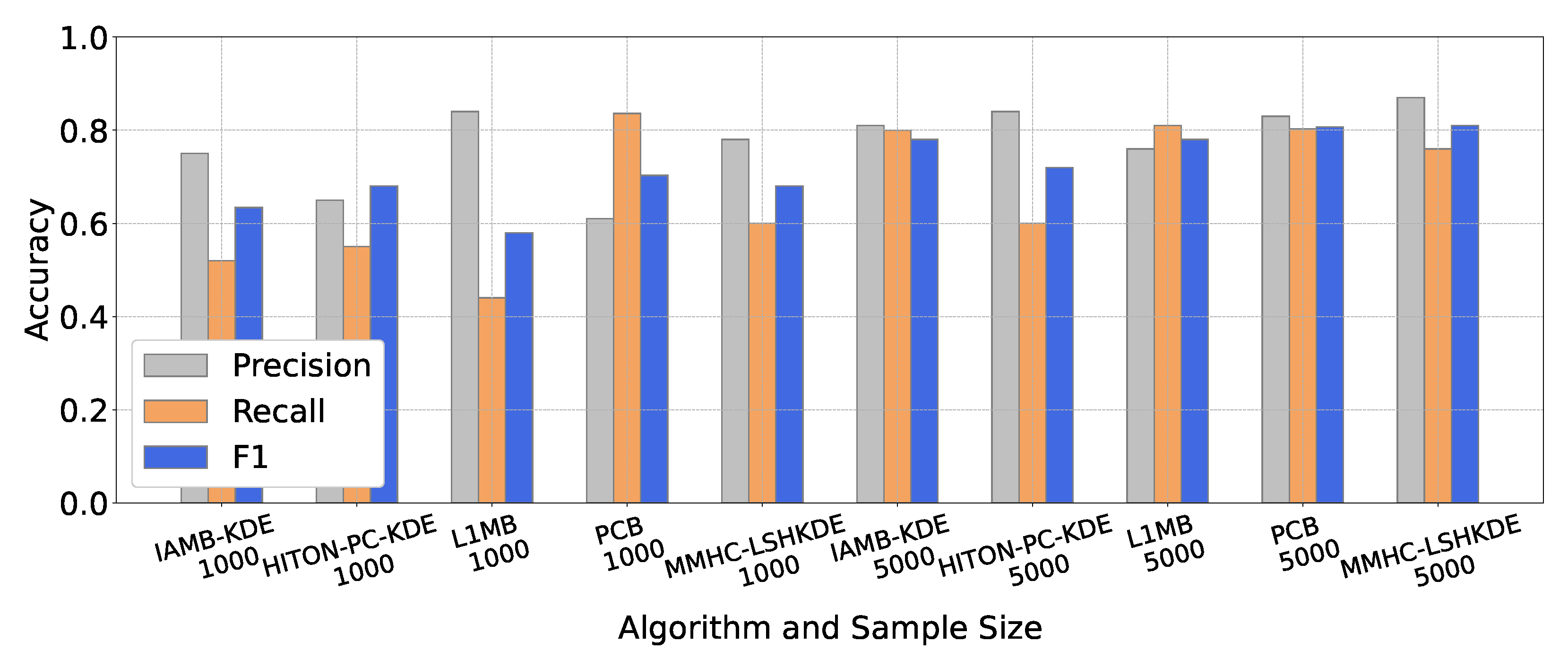
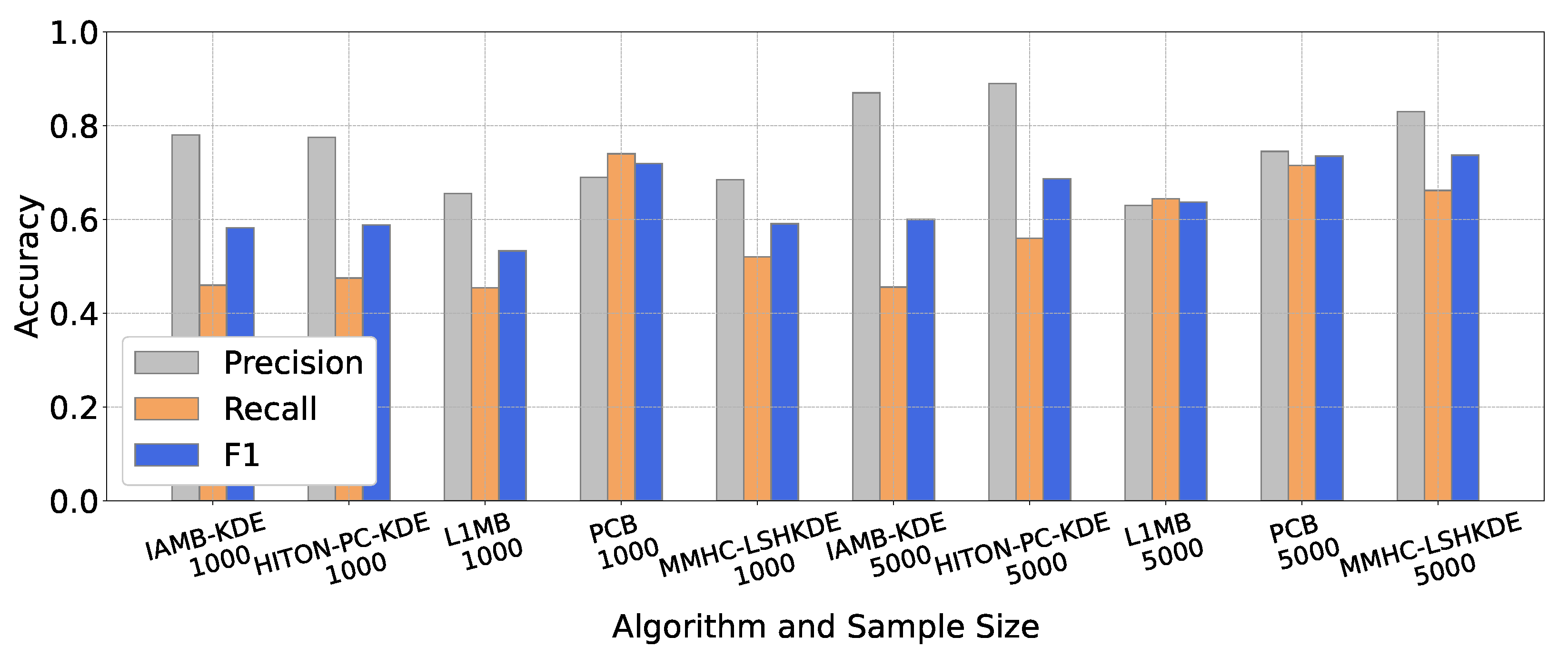
6.2.1. Datasets and Assessment Indicators
6.2.2. Performance Comparison
6.3. Classification Performance Comparison
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, M.; Lang, X.; You, Q.; Jing, Y.; Huang, D.; Dai, H.; Kang, J. Dynamic risk evaluation of hydrogen station leakage based on fuzzy dynamic Bayesian network. Int. J. Hydrogen Energy 2024, 50, 1131–1145. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, M.; Wan, C.; Dong, Z.; Wu, X. A Bayesian network-based model for risk modeling and scenario deduction of collision accidents of inland intelligent ships. Reliab. Eng. Syst. Saf. 2024, 243, 109816. [Google Scholar] [CrossRef]
- Ahsan, M.; Khan, A.; Khan, K.R.; Sinha, B.B.; Sharma, A. Advancements in medical diagnosis and treatment through machine learning: A review. Expert Syst. J. Knowl. Eng. 2024, 41, 13499. [Google Scholar] [CrossRef]
- Glymour, C.; Zhang, K.; Spirtes, P. Review of causal discovery methods based on graphical models. Front. Genet. 2019, 10, 524. [Google Scholar] [CrossRef]
- Wang, X.; Ren, H.; Guo, X. A novel discrete firefly algorithm for Bayesian network structure learning. Knowl. Based Syst. 2022, 242, 108426. [Google Scholar] [CrossRef]
- Gao, W.; Zhi, M.; Ke, Y.; Wang, X.; Zhuo, Y.; Liu, A.; Yang, Y. Bayesian network structure learning based on HC-PSO algorithm. J. Intell. Fuzzy Syst. 2024, 41, 4347–4359. [Google Scholar] [CrossRef]
- Bouchaala, L.; Masmoudi, A.; Gargouri, F.; Rebai, A. Improving algorithms for structure learning in Bayesian Networks using a new implicit score. Expert Syst. Appl. 2010, 37, 5470–5475. [Google Scholar] [CrossRef]
- DeCampos, C.P.; Zeng, Z.; Ji, Q. Structure learning of Bayesian networks using constraints. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 113–120. [Google Scholar]
- Li, H.; Cabeli, V.; Sella, N.; Isambert, H. Constraint-based causal structure learning with consistent separating sets. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 14257–14266. [Google Scholar]
- Martins, M.S.; Yafrani, M.E.; Delgado, M.; Lüders, R.; Santana, R.; Siqueira, H.V.; Akcay, H.G.; Ahiod, B. Analysis of Bayesian network learning techniques for a hybrid multi-objective Bayesian estimation of distribution algorithm: A case study on MNK landscape. J. Heuristics 2021, 27, 549–573. [Google Scholar] [CrossRef]
- Jose, S.; Liu, S.; Louis, S.; Dascalu, S. Towards a hybrid approach for evolving Bayesian networks using genetic algorithms. In Proceedings of the IEEE International Conference on Tools with Artificial Intelligence, Portland, UT, USA, 4–6 November 2019; pp. 705–712. [Google Scholar]
- Wang, N.; Liu, H.; Zhang, L.; Cai, Y.; Shi, Q. An efficient skeleton learning approach-based hybrid algorithm for identifying Bayesian network structure. Eng. Appl. Artif. Intell. 2024, 133, 108105. [Google Scholar] [CrossRef]
- He, C.; Wang, P.; Tian, L.; Di, R.; Wang, Z.; Yang, Y. A novel structure learning method of Bayesian networks based on the neighboring complete node ordering search. Neurocomputing 2024, 585, 127620. [Google Scholar] [CrossRef]
- Mabrouk, A.; Gonzales, C.; Jabet-Chevalier, K.; Chojnaki, E. Multivariate cluster-based discretization for Bayesian network structure learning. In Scalable Uncertainty Management—SUM 2015; Beierle, C., Dekhtyar, A., Eds.; Springer International Publishing: Cham, Swizerland, 2015; pp. 155–169. [Google Scholar]
- Dimitris, M. Distribution-Free Learning of Bayesian Network Structure in Continuous Domains. In Proceedings of the National Conference on Artificial Intelligence and the Innovative Applications of Artificial Intelligence Conference, Pittsburgh, PA, USA, 9–13 July 2005; pp. 825–830. [Google Scholar]
- Hao, Z.; Zhou, S.G.; Guan, J.H. Measuring conditional independence by independent residuals: Theoretical results and application in causal discovery. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 2029–2036. [Google Scholar]
- Bach, F.; Jordan, M. Learning Graphical Models with Mercer Kernels. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 1009–1016. [Google Scholar]
- Schmidt, M.; Niculescu-Mizil, A.; Murphy, K. Learning graphical model structure using L1-regularization paths. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; pp. 1278–1283. [Google Scholar]
- Hyvarinen, A.; Zhang, K.; Shimizu, S.; Hoyer, P.O. Estimation of a structural vector autoregression model using non-gaussianity. J. Mach. Learn. Res. 2010, 11, 1709–1731. [Google Scholar]
- Chen, J.; He, Y.; Cheng, Y.; Fournier-Viger, P.; Huang, J.Z. A multiple kernel-based kernel density estimator for multimodal probability density functions. Eng. Appl. Artif. Intell. 2024, 132, 107979. [Google Scholar] [CrossRef]
- Jiang, Y.; Liang, Z.; Gao, H.; Guo, Y.; Zhong, Z.; Yang, C.; Liu, J. An improved constraint-based Bayesian network learning method using Gaussian kernel probability density estimator. Expert Syst. Appl. 2018, 113, 544–554. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A.R.; Statnikov, E. Algorithms for large scale Markov blanket discovery. In Proceedings of the International Florida Artificial Intelligence Research Society Conference, St. Augustine, FL, USA, 12–14 May 2003; pp. 376–381. [Google Scholar]
- Aliferis, C.F.; Tsamardinos, I.; Statnikov, A. HITON: A novel Markov Blanket algorithm for optimal variable selection. In Proceedings of the American Medical Informatics Association Annual Symposium, Washington, DC, USA, 8–12 November 2003; pp. 21–25. [Google Scholar]
- Marella, D.; Vicard, P. Bayesian network structural learning from complex survey data: A resampling based approach. Stat. Method. Appl. 2022, 31, 981–1013. [Google Scholar] [CrossRef]
- Cooper, G.F.; Herskovits, E. A Bayesian method for the induction of probabilistic networks from data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
- Behjati, S.; Beigy, H. Improved K2 algorithm for Bayesian network structure learning. Eng. Appl. Artif. Intell. 2020, 91, 103617–103629. [Google Scholar] [CrossRef]
- Singh, M.; Valtorta, M. An algorithm for the construction of Bayesian network structures from data. In Proceedings of the Annual Conference on Uncertainty in Artificial Intelligence, Washington, DC, USA, 9–11 July 1993; pp. 259–265. [Google Scholar]
- Spirtes, P.; Glymour, C. An algorithm for fast recovery of sparse causal graphs. Sol. Sci. Comput. Rev. 1991, 9, 62–72. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A. Time and sample efficient discovery of Markov blankets and direct causal relations. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 673–678. [Google Scholar]
- Song, W.; Gong, H.; Wang, Q.; Zhang, L.; Qiu, L.; Hu, X.; Han, H.; Li, Y.; Li, R.; Li, Y. Using Bayesian networks with Max-Min Hill-Climbing algorithm to detect factors related to multimorbidity. Front. Cardiovasc. Med. 2022, 9, 984883. [Google Scholar] [CrossRef]
- Chen, Y.; Wheeler, T.A.; Kochenderfer, M.J. Learning discrete Bayesian networks from continuous data. Front. Cardiovasc. Med. 2017, 59, 103–132. [Google Scholar] [CrossRef]
- Wang, Z.X.; Chan, L.W. A heuristic partial-correlation-based algorithm for causal relationship discovery on continuous data. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Burgos, Spain, 23–26 September 2009; pp. 234–241. [Google Scholar]
- Wang, Z.X.; Chan, L.W. An efficient causal discovery algorithm for linear models. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1109–1118. [Google Scholar]
- Huegle, J.; Hagedorn, C.; Schlosser, R. A KNN-Based Non-Parametric Conditional Independence Test for Mixed Data and Application in Causal Discovery. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: Research Track-European Conference, Turin, Italy, 18–22 September 2023; pp. 541–558. [Google Scholar]
- Pál, D.; Póczos, B.; Szepesvári, C. Estimation of Rényi entropy and mutual information based on generalized nearest-neighbor graphs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 1849–1857. [Google Scholar]
- Nguyen, H.B.; Xue, B.; Andreae, P. Mutual information for feature selection: Estimation or counting? Evol. Intell. 2016, 9, 95–110. [Google Scholar] [CrossRef]
- Charikar, M.; Siminelakis, P. Hashing-based-estimators for kernel density in high dimensions. In Proceedings of the IEEE Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 15–17 October 2017; pp. 1032–1043. [Google Scholar]
- Geiger, D.; Heckerman, D. Learning gaussian networks. In Proceedings of the Annual Conference on Uncertainty in Artificial Intelligence, Seattle, Washington, DC, USA, 29–31 July 1994; pp. 235–243. [Google Scholar]
- Andrews, B.; Ramsey, J.; Cooper, G.F. Scoring Bayesian networks of mixed variables. Int. J. Data Sci. Anal. 2018, 6, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Li, L.; Wang, A. A partial correlation-based Bayesian network structure learning algorithm under linear SEM. Knowl. Based Syst. 2011, 24, 963–976. [Google Scholar] [CrossRef]
- Laborda, J.D.; Torrijos, P.; Puerta, J.M.; Gámez, J.A. Parallel structural learning of Bayesian networks: Iterative divide and conquer algorithm based on structural fusion. Knowl. Based Syst. 2024, 296, 111840. [Google Scholar] [CrossRef]
- Neuberg, L.G. Causality: Models, reasoning, and inference, by judea pearl, cambridge university press, 2000. Econom. Theory 2003, 19, 675–685. [Google Scholar] [CrossRef]
- Kitson, N.K.; Constantinou, A.C. The impact of variable ordering on Bayesian Network Structure Learning. Data Min. Knowl. Discov. 2024, 38, 2545–2569. [Google Scholar] [CrossRef]
- Han, Q.; Ma, S.; Wang, T.; Chu, F. Kernel density estimation model for wind speed probability distribution with applicability to wind energy assessment in China. Renew. Sustain. Energy Rev. 2019, 115, 109387. [Google Scholar] [CrossRef]
- Węglarczyk, S. Kernel density estimation and its application. In Proceedings of the ITM Web Conference, Kraków, Poland, 8 November 2018; p. 00037. [Google Scholar]
- Kala, Z. Global sensitivity analysis based on entropy: From differential entropy to alternative measures. Entropy 2021, 23, 778. [Google Scholar] [CrossRef]
- Segal, G.; Parkinson, D.; Bartlett, S. Planetary Complexity Revealed by the Joint Differential Entropy of Eigencolors. Astorn. J. 2024, 167, 114. [Google Scholar] [CrossRef]
- Álvarez Chaves, M.; Gupta, H.V.; Ehret, U.; Guthke, A. On the Accurate Estimation of Information-Theoretic Quantities from Multi-Dimensional Sample Data. Entropy 2024, 26, 387. [Google Scholar] [CrossRef] [PubMed]
- Fischer, I. The conditional entropy bottleneck. Entropy 2020, 22, 999. [Google Scholar] [CrossRef] [PubMed]
- Coleman, B.; Shrivastava, A. Sub-linear race sketches for approximate kernel density estimation on streaming data. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 1739–1749. [Google Scholar]
- Backurs, A.; Indyk, P.; Wagner, T. Space and time efficient kernel density estimation in high dimensions. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 15773–15782. [Google Scholar]
- Ou, G.; He, Y.; Fournier-Viger, P.; Huang, J.Z. A Novel Mixed-Attribute Fusion-Based Naive Bayesian Classifier. Appl. Sci. 2022, 12, 10443. [Google Scholar] [CrossRef]
- Bielza, C.; Larranaga, P. Discrete Bayesian network classifiers: A survey. ACM Comput. Surv. 2014, 47, 4–23. [Google Scholar] [CrossRef]
- Dai, J.; Liu, Y.; Chen, J. Feature selection via max-independent ratio and min-redundant ratio based on adaptive weighted kernel density estimation. Inf. Sci. 2021, 568, 86–112. [Google Scholar] [CrossRef]
- Perez, A.; Larranaga, P.; Inza, I. Bayesian classifiers based on kernel density estimation: Flexible classifiers. Int. J. Approx. Reason 2009, 50, 341–362. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.F.; Xie, K.; Chen, Q.; Wang, A.G. Causal structure learning algorithm based on partial rank correlation under additive noise model. Appl. Artif. Intell. 2022, 36, 2023390. [Google Scholar] [CrossRef]
- Ma, D.L.; Zhou, T.; Li, Y.; Chen, J.; Huang, Y.P. Bayesian network analysis of heat transfer deterioration in supercritical water. Nucl. Eng. Des. 2022, 391, 111733. [Google Scholar] [CrossRef]



| Distribution | Gaussian | T-Distribution | Cauchy | Laplace |
|---|---|---|---|---|
| d dimension | =[, …, ]; ==0; = ; = =1; | ; ; ; ; | ; ; ; ; | ; ; = ; = |
| Distribution Function | Model | d = 10 | d = 30 | d = 50 |
|---|---|---|---|---|
| Gaussian Distribution | KDE | 2.12 × 10−7 | 3.21 × 10−18 | 1.03 × 10−28 |
| LSHKDE | 1.98 × 10−7 | 3.20 × 10−18 | 1.03 × 10−28 | |
| T-distribution | KDE | 1.27 × 10−6 | 5.55 × 10−14 | 1.56 × 10−20 |
| LSHKDE | 1.24 × 10−6 | 5.55 × 10−14 | 1.56 × 10−20 | |
| Cauchy distribution | KDE | 4.55 × 10−6 | 1.00 × 10−14 | 4.22 × 10−32 |
| LSHKDE | 4.54 × 10−6 | 1.00 × 10−14 | 4.21 × 10−32 | |
| Laplace distribution | KDE | 1.19 × 10−7 | 6.18 × 10−19 | 2.41 × 10−31 |
| LSHKDE | 1.09 × 10−7 | 6.18 × 10−19 | 2.40 × 10−31 |
| NO. | Dataset | Instances | Attributes | Class |
|---|---|---|---|---|
| 1 | Abalone | 4177 | 8 | 3 |
| 2 | Cmc | 1473 | 6 | 3 |
| 3 | Ecoli | 292 | 5 | 4 |
| 4 | Fires | 244 | 11 | 2 |
| 5 | Glass | 214 | 9 | 6 |
| 6 | Haberman | 306 | 3 | 2 |
| 7 | Ilpd | 583 | 9 | 2 |
| 8 | Ionosphere | 351 | 34 | 2 |
| 9 | Iris | 150 | 4 | 3 |
| 10 | Maternal | 1013 | 6 | 3 |
| 11 | Parkinsons | 195 | 22 | 2 |
| 12 | Pima | 768 | 8 | 2 |
| 13 | Raisin | 900 | 7 | 2 |
| 14 | Red wine | 1599 | 11 | 5 |
| 15 | Transfusion | 748 | 4 | 2 |
| 16 | Wdbc | 569 | 30 | 2 |
| 17 | Wholesale | 440 | 6 | 3 |
| 18 | Wine | 178 | 13 | 3 |
| 19 | Wpbc | 198 | 33 | 2 |
| 20 | Yeast | 1484 | 6 | 4 |
| Dataset Name | NBC | TAN | FBC | KNN | C4.5 | NN | SVM | BNC |
|---|---|---|---|---|---|---|---|---|
| Abalone | 0.518 ± 0.066 | 0.498 ± 0.056 | 0.502 ± 0.064 | 0.520 ± 0.062 | 0.488 ±0.055 | 0.516 ±0.065 | 0.543 ± 0.069 | 0.644± 0.068 |
| Cmc | 0.470 ± 0.029 | 0.491 ± 0.032 | 0.485 ± 0.023 | 0.484 ± 0.029 | 0.475 ±0.044 | 0.508 ± 0.038 | 0.511 ± 0.036 | 0.517± 0.032 |
| Ecoli | 0.910 ± 0.040 | 0.900 ± 0.036 | 0.905 ± 0.042 | 0.913± 0.040 | 0.862 ± 0.049 | 0.909 ± 0.032 | 0.875 ± 0.034 | 0.875 ± 0.041 |
| Fire | 0.942 ± 0.044 | 0.916 ± 0.042 | 0.902 ± 0.042 | 0.922 ± 0.034 | 0.976± 0.028 | 0.934 ± 0.046 | 0.946 ±0.038 | 0.920 ± 0.036 |
| Glass | 0.636 ± 0.116 | 0.698 ± 0.096 | 0.474 ± 0.099 | 0.520 ± 0.105 | 0.641 ± 0.112 | 0.547 ± 0.095 | 0.690 ± 0.121 | 0.717± 0.093 |
| Haberman | 0.745 ± 0.079 | 0.755 ± 0.072 | 0.745 ± 0.065 | 0.722 ± 0.083 | 0.644 ±0.077 | 0.755 ± 0.086 | 0.735 ± 0.090 | 0.767± 0.082 |
| Ilpd | 0.554 ± 0.086 | 0.678 ± 0.079 | 0.648 ± 0.072 | 0.663 ± 0.084 | 0.649 ± 0.083 | 0.703 ± 0.067 | 0.715 ±0.062 | 0.844± 0.070 |
| Ionosphere | 0.751 ± 0.079 | 0.712 ± 0.066 | 0.682 ± 0.056 | 0.740 ± 0.062 | 0.761 ± 0.061 | 0.765 ± 0.075 | 0.781± 0.065 | 0.705 ± 0.068 |
| Iris | 0.946 ± 0.061 | 0.926 ± 0.067 | 0.951 ± 0.068 | 0.933 ± 0.063 | 0.941 ± 0.073 | 0.931 ± 0.062 | 0.960± 0.064 | 0.920 ± 0.065 |
| Maternal | 0.583 ± 0.076 | 0.663 ± 0.088 | 0.623 ± 0.092 | 0.682 ± 0.072 | 0.674 ± 0.095 | 0.587 ± 0.083 | 0.591 ± 0.090 | 0.686± 0.075 |
| Parkinsons | 0.669 ± 0.056 | 0.875± 0.054 | 0.798 ± 0.060 | 0.772 ± 0.041 | 0.778 ± 0.064 | 0.797 ± 0.062 | 0.833 ± 0.049 | 0.754 ± 0.059 |
| Pima | 0.755 ± 0.054 | 0.765 ± 0.043 | 0.755 ± 0.043 | 0.744 ± 0.056 | 0.718 ± 0.049 | 0.766 ± 0.050 | 0.768 ± 0.054 | 0.792± 0.049 |
| Raisin | 0.827 ± 0.029 | 0.835 ± 0.023 | 0.805 ± 0.020 | 0.830 ± 0.039 | 0.793± 0.035 | 0.865 ± 0.026 | 0.833 ± 0.025 | 0.867± 0.024 |
| Red wine | 0.541 ± 0.046 | 0.530 ± 0.045 | 0.560 ± 0.052 | 0.526 ± 0.062 | 0.487 ± 0.048 | 0.587 ± 0.059 | 0.575 ± 0.064 | 0.588± 0.050 |
| Transfusion | 0.751 ± 0.152 | 0.784± 0.142 | 0.760 ± 0.112 | 0.763 ± 0.140 | 0.731 ± 0.138 | 0.774 ± 0.121 | 0.762 ± 0.155 | 0.768 ± 0.132 |
| Wdbc | 0.926 ± 0.039 | 0.962 ± 0.017 | 0.934 ± 0.021 | 0.963 ± 0.025 | 0.940 ± 0.030 | 0.970 ± 0.011 | 0.977± 0.016 | 0.946 ± 0.020 |
| Wholesale | 0.500 ± 0.197 | 0.718 ± 0.156 | 0.715 ± 0.201 | 0.609 ± 0.122 | 0.534 ± 0.110 | 0.715 ± 0.103 | 0.718 ± 0.099 | 0.718± 0.102 |
| Wine | 0.964± 0.029 | 0.880 ± 0.023 | 0.943 ± 0.037 | 0.938 ± 0.044 | 0.904 ±0.045 | 0.961 ±0.027 | 0.944 ±0.038 | 0.905 ± 0.039 |
| Wpbc | 0.681 ± 0.079 | 0.645 ± 0.073 | 0.750 ± 0.068 | 0.747 ± 0.075 | 0.655 ± 0.068 | 0.758 ± 0.072 | 0.759 ± 0.070 | 0.764± 0.069 |
| Yeast | 0.512 ± 0.048 | 0.582 ± 0.050 | 0.497 ± 0.039 | 0.576 ± 0.053 | 0.531 ± 0.046 | 0.589± 0.052 | 0.588 ± 0.045 | 0.568 ± 0.042 |
| Average | 0.706 ± 0.070 | 0.741 ± 0.063 | 0.721 ±0.063 | 0.728 ± 0.064 | 0.709 ± 0.065 | 0.748 ± 0.061 | 0.754 ± 0.064 | 0.764± 0.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Li, C.; Liu, Y.; Chen, S.; Zuo, Z.; Wang, P.; Ye, Z. Causal Discovery and Reasoning for Continuous Variables with an Improved Bayesian Network Constructed by Locality Sensitive Hashing and Kernel Density Estimation. Entropy 2025, 27, 123. https://doi.org/10.3390/e27020123
Wei C, Li C, Liu Y, Chen S, Zuo Z, Wang P, Ye Z. Causal Discovery and Reasoning for Continuous Variables with an Improved Bayesian Network Constructed by Locality Sensitive Hashing and Kernel Density Estimation. Entropy. 2025; 27(2):123. https://doi.org/10.3390/e27020123
Chicago/Turabian StyleWei, Chenghao, Chen Li, Yingying Liu, Song Chen, Zhiqiang Zuo, Pukai Wang, and Zhiwei Ye. 2025. "Causal Discovery and Reasoning for Continuous Variables with an Improved Bayesian Network Constructed by Locality Sensitive Hashing and Kernel Density Estimation" Entropy 27, no. 2: 123. https://doi.org/10.3390/e27020123
APA StyleWei, C., Li, C., Liu, Y., Chen, S., Zuo, Z., Wang, P., & Ye, Z. (2025). Causal Discovery and Reasoning for Continuous Variables with an Improved Bayesian Network Constructed by Locality Sensitive Hashing and Kernel Density Estimation. Entropy, 27(2), 123. https://doi.org/10.3390/e27020123






