Entropy, Periodicity and the Probability of Primality
Abstract
1. Introduction
2. Periodicity and Compositeness in Binary Numbers
2.1. Definition of Periodic Numbers
2.2. Periodic Numbers Are Composite
2.3. n-Periodic Binary Numbers Are Composite
- Let
2.4. z-Periodic Numbers Are Composite
2.5. Periodic Numbers Are Composite by Construction
2.6. Periodicity and Shannon Entropy
3. The Binary Derivative and Its Entropic Properties
3.1. Definition of the Binary Derivative
3.2. Periodicity and the Zero Derivative
3.3. Statistical Independence of the Binary Derivatives
3.4. Independence of Successive Derivatives
3.5. Binary Integrands, Complements and Derivatives
3.6. Termination of the Derivative Chain
3.7. The Primes Are Equidistributed Across the Binary Derivatives
4. The Entropic Probability of Primality
4.1. Definition of the Entropic Probability of Primality
4.2. Connection to the Prime Number Theorem
4.3. Entropic Interpretation
4.4. Bounded Stochastic Variance of the Prime Distribution in p(s′) Space
5. Empirical Results
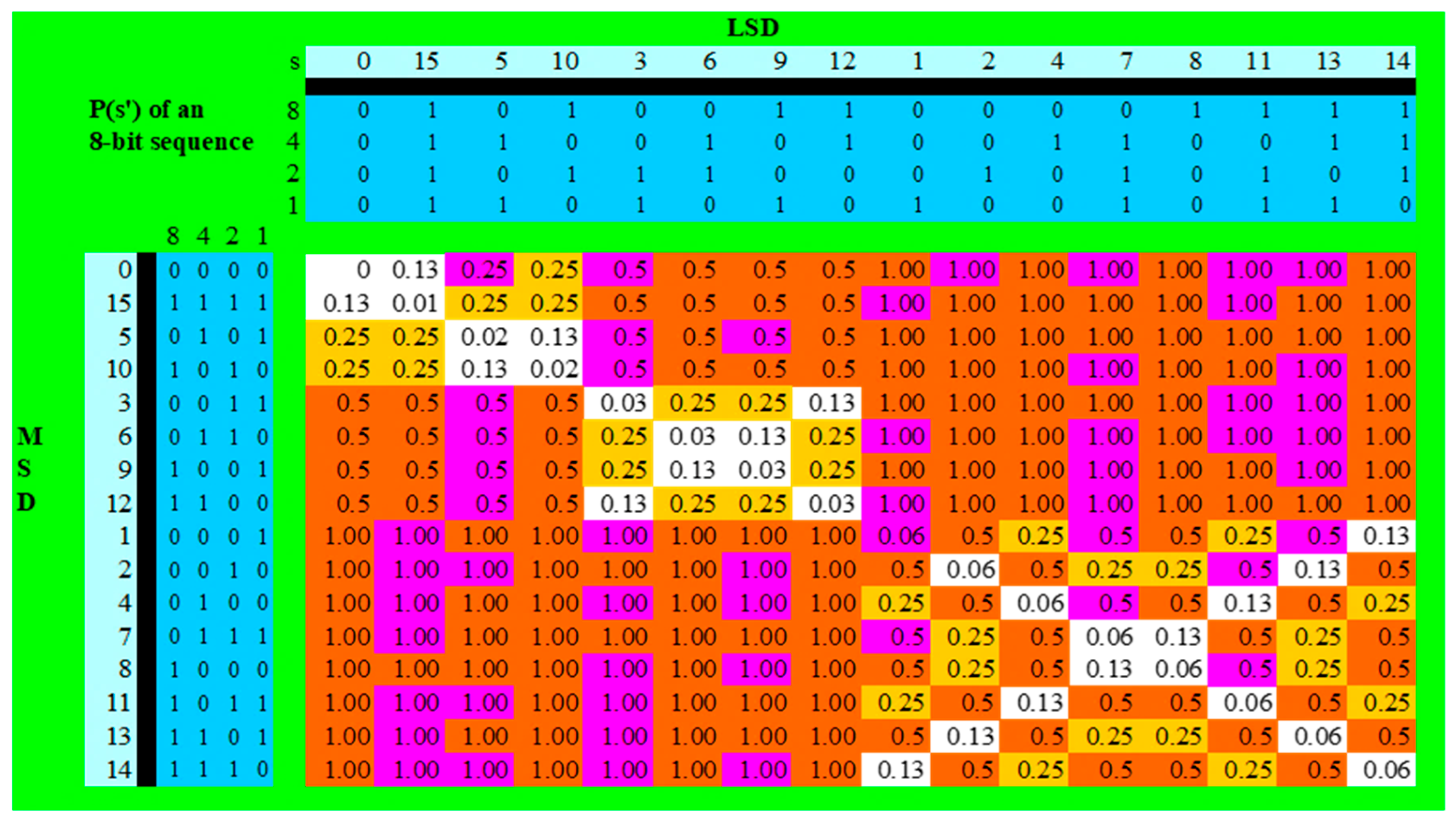
5.1. Numerical Evaluation of p(s′)
5.2. Primes Below 256
5.3. Extension to s < 65,536
5.3.1. Scale Invariance
5.3.2. Balanced Stochastic Asymmetry
5.3.3. Diminishing Imbalance
5.4. Large-Scale Sampling (s < 232)
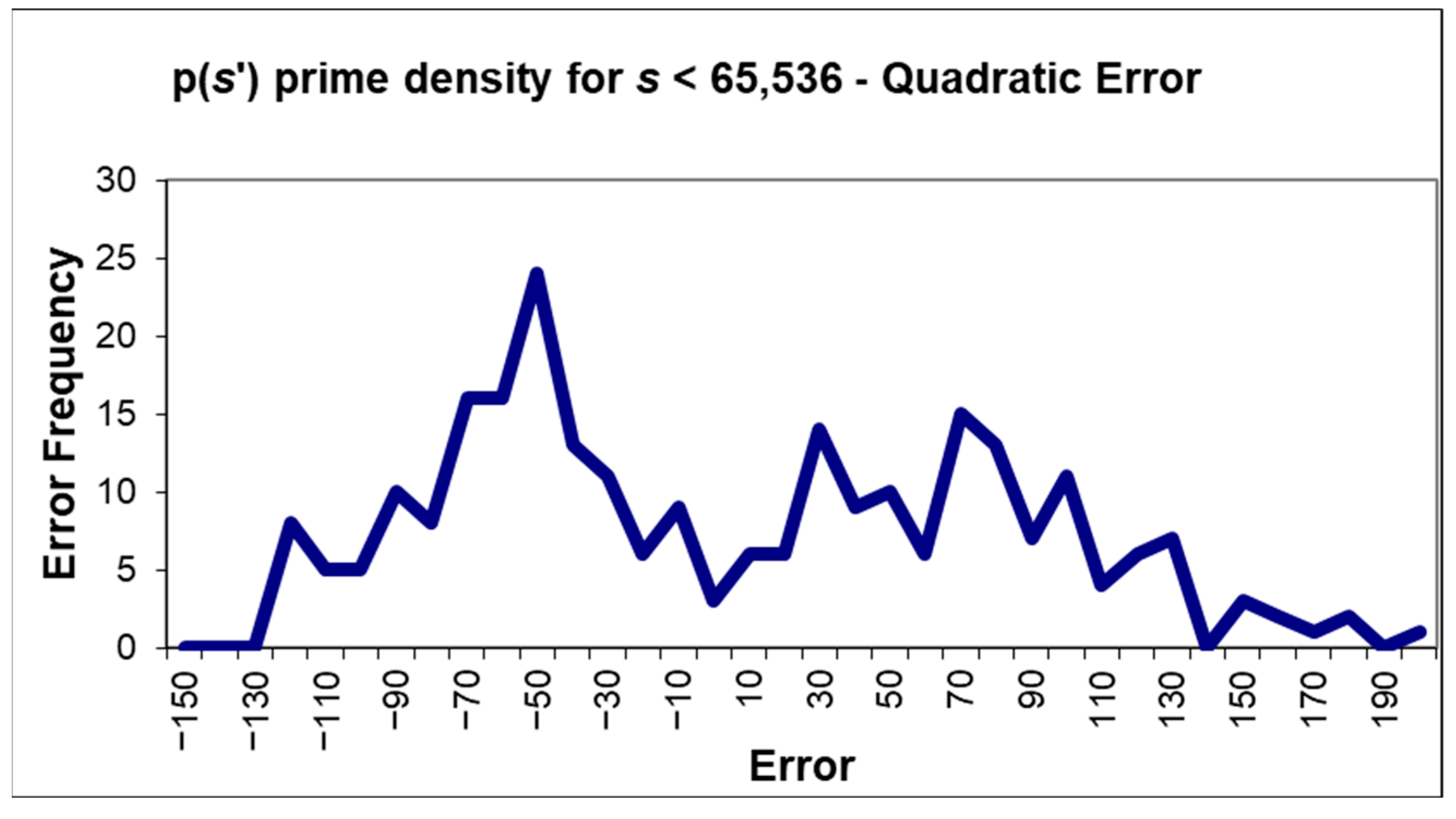
5.5. Prime Density for p(s′)
6. Discussion
6.1. Entropy, Periodicity and Primality
6.2. Entropic Structure of Number Space
6.3. Statistical Structure of Number Space
6.4. Computational and Cryptographic Implications
6.5. Comparison Between p(s′) and BiEntropy
6.6. Comparison with Rabin–Miller and AKS Primality Tests
6.7. Twin, Fermat, and Mersenne Primes
6.8. The Riemann Hypothesis and Skewes’ Number
6.9. Limitations and Future Work
7. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kontoyiannis, I. Counting the primes using entropy. In Proceedings of the 2008 IEEE Information Theory Workshop (ITW), Porto, Portugal, 5–9 May 2008; IEEE: Piscataway, NJ, USA, 2008; p. 268. [Google Scholar] [CrossRef]
- Billingsley, P. Prime numbers and Brownian motion. Am. Math. Mon. 1973, 80, 1099–1115. [Google Scholar] [CrossRef]
- Wolf, M. 1/f noise in the distribution of prime numbers. Phys. A Stat. Mech. Its Appl. 1997, 241, 493–499. [Google Scholar] [CrossRef]
- Szpiro, G.G. The gaps between the gaps: Some patterns in the prime number sequence. Phys. A Stat. Mech. Its Appl. 2004, 341, 607–617. [Google Scholar] [CrossRef]
- Southier, A.L.M.; Santos, L.F.; Ribeiro, P.H.S.; Ribeiro, A.D. Identifying primes from entanglement dynamics. Phys. Rev. A 2023, 108, 042404. [Google Scholar] [CrossRef]
- Croll, G.J. BiEntropy—The Approximate Entropy of a Finite Binary String. arXiv 2013, arXiv:1305.0954. [Google Scholar] [CrossRef]
- Croll, G.J. BiEntropy, TriEntropy and Primality. Entropy 2020, 22, 311. [Google Scholar] [CrossRef]
- Croll, G.J. BiEntropy of Knots on the Simple Cubic Lattice. In Unified Field Mechanics II: Formulations and Empirical Tests, Proceedings of the Xth Symposium Honoring Noted French Mathematical Physicist Jean-Pierre Vigier, Porto Novo, Italy, 25–28 July 2016; World Scientific: Singapore, 2018; p. 447. [Google Scholar] [CrossRef]
- Saini, A.; Tsokanos, A.; Kirner, R. CryptoQNRG: A new framework for evaluation of cryptographic strength in quantum and pseudorandom number generation for key-scheduling algorithms. J. Supercomput. 2023, 79, 12219–12237. [Google Scholar] [CrossRef]
- Goyal, R. Genealogy Interceded Phenotypic Analysis (GIPA) of ECA Rules. In Proceedings of the Second Asian Symposium on Cellular Automata Technology, West Bengal, India, 2–4 March 2023; Springer Nature: Singapore, 2023; pp. 177–191. [Google Scholar] [CrossRef]
- Calvet, E.; Rouat, J.; Reulet, B. Excitatory/inhibitory balance emerges as a key factor for RBN performance, overriding attractor dynamics. Front. Comput. Neurosci. 2023, 17, 1223258. [Google Scholar] [CrossRef]
- Calvet, E.; Reulet, B.; Rouat, J. The connectivity degree controls the difficulty in reservoir design of random boolean networks. Front. Comput. Neurosci. 2024, 18, 1348138. [Google Scholar] [CrossRef]
- Aguiar, C.; Camps, M.; Dattani, N.; Camps, I. Functionalized boron–nitride nanotubes: First-principles calculations. Appl. Surf. Sci. 2023, 611, 155358. [Google Scholar] [CrossRef]
- Kauffman, L.H. Iterant Algebra. Entropy 2017, 19, 347. [Google Scholar] [CrossRef]
- Kauffman, L.H. Iterants, Majorana Fermions and the Majorana-Dirac Equation. Symmetry 2021, 13, 1373. [Google Scholar] [CrossRef]
- Wagstaff, S.S. Prime numbers with a fixed number of one bits or zero bits in their binary representation. Exp. Math. 2001, 10, 267–273. [Google Scholar] [CrossRef]
- Nathanson, M.B. Derivatives of binary sequences. SIAM J. Appl. Math. 1971, 21, 407–412. [Google Scholar] [CrossRef]
- Davies, N.; Dawson, E.; Gustafson, H.; Pettitt, A.N. Testing for randomness in stream ciphers using the binary derivative. Stat. Comput. 1995, 5, 307–310. [Google Scholar] [CrossRef]
- Nathanson, M.B. Integrals of binary sequences. SIAM J. Appl. Math. 1972, 23, 84–86. [Google Scholar] [CrossRef]
- von Koch, H. Ueber die Riemann’sche Primzahlfunction. Math. Ann. 1901, 55, 441–464. [Google Scholar] [CrossRef]
- OEIS Foundation Inc. Entry A333409 in the On-Line Encyclopedia of Integer Sequences. 2023. Available online: https://oeis.org/A333409 (accessed on 23 November 2025).
- Rabin, M.O. Probabilistic algorithm for testing primality. J. Number Theory 1980, 12, 128–138. [Google Scholar] [CrossRef]
- Agrawal, M.; Kayal, N.; Saxena, N. PRIMES is in P. Ann. Math. 2004, 160, 781–793. [Google Scholar] [CrossRef]
- Littlewood, J.E. Sur la distribution des nombres premiers. Comptes Rendus. Acad. Sci. 1914, 158, 1869–1872. [Google Scholar]
- Skewes, S. On the difference π (x) − Li (x). J. Lond. Math. Soc. 1933, 8, 277–283. [Google Scholar] [CrossRef]
- Chao, K.F.; Plymen, R. A new bound for the smallest x with π (x) > Li (x). Int. J. Number Theory 2010, 6, 681–690. [Google Scholar] [CrossRef]
- Csernoch, M.; Biró, P.; Máth, J.; Abari, K. Testing algorithmic skills in traditional and non-traditional programming environments. Inform. Educ. 2015, 14, 175–197. [Google Scholar] [CrossRef]
| s | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | 1’s | n | z | k | 28−k | z/28−k |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 4 | 8 | 1 | 0 | 256 | 0.0039 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 3 | 7 | 1 | 1 | 128 | 0.0078 | ||
| 0 | 1 | 0 | 0 | 1 | 0 | 2 | 6 | 1 | 2 | 64 | 0.0156 | |||
| 1 | 1 | 0 | 1 | 1 | 4 | 5 | 1 | 3 | 32 | 0.0313 | ||||
| 0 | 1 | 1 | 0 | 2 | 4 | 1 | 4 | 16 | 0.0625 | |||||
| 1 | 0 | 1 | 2 | 3 | 1 | 5 | 8 | 0.1250 | ||||||
| 1 | 1 | 2 | 2 | 1 | 6 | 4 | 0.2500 | |||||||
| 0 | 0 | 1 | 0 | 7 | 2 | 0.0000 | ||||||||
| ∑ | 0.4961 | |||||||||||||
| Mersenne | 0.0039 | |||||||||||||
| p(s′) | 0.5000 |
| Fraction | p(s′) | Expected | Actual | PNT (Li(x)) |
|---|---|---|---|---|
| 256 | 0.0078 | 0.21 | 0 | 0.24 |
| 128 | 0.0156 | 0.42 | 0 | 0.47 |
| 64 | 0.0313 | 0.84 | 0 | 0.95 |
| 32 | 0.0625 | 1.89 | 1 | 1.89 |
| 16 | 0.1250 | 3.38 | 0 | 3.78 |
| 8 | 0.2500 | 6.75 | 1 | 7.56 |
| 4 | 0.5000 | 13.50 | 14 | 15.13 |
| 2 | 1.0000 | 27.00 | 38 | 30.26 |
| Total | 54.00 | 54 | 60.51 |
| p(s′) | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 | 32,768 | 65,536 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ≤0.001953 | |||||||||||||
| 0.003906 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 0.007813 | |||||||||||||
| 0.015625 | 2 | 3 | 5 | 9 | 11 | 23 | 51 | ||||||
| 0.031250 | 0 | 2 | 2 | 5 | 8 | 14 | 28 | 53 | 95 | ||||
| 0.062500 | 1 | 1 | 1 | 1 | 1 | 3 | 5 | 9 | 16 | 31 | 56 | 102 | |
| 0.125000 | 3 | 8 | 17 | 30 | 62 | 108 | 211 | 403 | |||||
| 0.250000 | 1 | 1 | 1 | 1 | 1 | 4 | 9 | 18 | 26 | 79 | 149 | 287 | 494 |
| 0.500000 | 1 | 3 | 5 | 10 | 14 | 28 | 41 | 79 | 144 | 264 | 484 | 958 | 1712 |
| 1.000000 | 4 | 6 | 11 | 19 | 36 | 58 | 106 | 181 | 341 | 583 | 1088 | 1923 | 3684 |
| ∑ =π(s) | 6 | 11 | 18 | 31 | 54 | 97 | 172 | 309 | 564 | 1028 | 1900 | 3512 | 6542 |
| Note: Li(s) | 9 | 14 | 22 | 36 | 61 | 104 | 181 | 321 | 577 | 1048 | 1920 | 3544 | 6584 |
| p(s′) | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 | 32,768 | 65,536 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ≤0.000244 | 1 | ||||||||||||
| 0.000488 | 1 | 2 | |||||||||||
| 0.000977 | 1 | 1 | 2 | 3 | |||||||||
| 0.001953 | 1 | 1 | 2 | 3 | 6 | ||||||||
| 0.003906 | 1 | 1 | 2 | 4 | 7 | 13 | |||||||
| 0.007813 | 1 | 1 | 2 | 4 | 7 | 14 | 26 | ||||||
| 0.015625 | 1 | 1 | 2 | 4 | 8 | 15 | 27 | 51 | |||||
| 0.031250 | 1 | 2 | 3 | 5 | 9 | 16 | 30 | 55 | 102 | ||||
| 0.062500 | 1 | 1 | 2 | 3 | 5 | 10 | 18 | 32 | 59 | 110 | 204 | ||
| 0.125000 | 1 | 1 | 2 | 3 | 6 | 11 | 19 | 35 | 64 | 119 | 220 | 409 | |
| 0.250000 | 1 | 1 | 2 | 4 | 7 | 12 | 22 | 39 | 71 | 129 | 238 | 439 | 818 |
| 0.500000 | 2 | 3 | 5 | 8 | 14 | 24 | 43 | 77 | 141 | 257 | 475 | 878 | 1636 |
| 1.000000 | 3 | 6 | 9 | 16 | 27 | 49 | 86 | 155 | 282 | 514 | 950 | 1756 | 3271 |
| ∑ =π(s) | 6 | 11 | 18 | 31 | 54 | 97 | 172 | 309 | 564 | 1028 | 1900 | 3512 | 6542 |
| Note: Li(s) | 9 | 14 | 22 | 36 | 61 | 104 | 181 | 321 | 577 | 1048 | 1920 | 3544 | 6584 |
| p(s′) | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16,384 | 32,768 | 65,536 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ≤0.000244 | −1 | ||||||||||||
| 0.000488 | −1 | −2 | |||||||||||
| 0.000977 | −1 | −1 | −2 | −3 | |||||||||
| 0.001953 | −1 | −1 | −2 | −3 | −6 | ||||||||
| 0.003906 | 1 | 1 | −1 | −3 | −6 | −12 | |||||||
| 0.007813 | −1 | −1 | −2 | −4 | −7 | −14 | −26 | ||||||
| 0.015625 | −1 | 1 | 1 | 1 | 1 | −4 | −4 | 0 | |||||
| 0.031250 | −1 | −1 | −1 | −2 | −2 | −2 | −7 | ||||||
| 0.062500 | 1 | −1 | −2 | −2 | −5 | −9 | −16 | −28 | −54 | −102 | |||
| 0.125000 | −1 | −1 | −2 | −3 | −3 | −3 | −2 | −5 | −2 | −11 | −9 | −6 | |
| 0.250000 | −1 | −3 | −6 | −8 | −13 | −21 | −45 | −50 | −89 | −152 | −324 | ||
| 0.500000 | −1 | 1 | 2 | 1 | 4 | −2 | 2 | 3 | 7 | 9 | 80 | 77 | |
| 1.000000 | 1 | 1 | 2 | 4 | 11 | 10 | 20 | 27 | 59 | 69 | 136 | 167 | 413 |
| ∑p(s′) < 0.5 | 0 | −1 | −2 | −6 | −11 | −13 | −18 | −28 | −62 | −76 | −147 | −247 | −489 |
| ∑p(s′) ≥ 0.5 | 1 | 1 | 3 | 6 | 12 | 13 | 18 | 28 | 62 | 76 | 147 | 247 | 490 |
| Set | Entropic Interpretation | Observation |
|---|---|---|
| S (Periodic Numbers) | Zero entropy p(s′) ≈ 0 | Composite (*) |
| S′ (Non-PeriodicNumbers) | Non-Zero entropy p(s′) > 0 | Potentially Prime |
| P (Primes) | All Entropies | Prime |
| C (Composites) | All Entropies | Not Prime |
| P ∩ S | ∅ | Empty Set (*) |
| S ∪ S′ | Union of all Entropies | Natural Numbers |
| S ⊆ C | Lower Entropy | Composite |
| P ⊆ S′ | Higher Entropy | Prime |
| X | High Entropy p(s′) = 1 | Potentially prime |
| Y | Low Entropy p(s′) < 1 | Probably composite |
| |X| = |Y| | High and Low Entropy | Equality of set size |
| X ⊆ S′ | High Entropy | Potentially prime |
| S ⊆ Y | Low Entropy | Composite (*) |
| |P|⊆ X ≈ |P|⊆ Y | High and Low Entropy | Equality of set size |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croll, G.J. Entropy, Periodicity and the Probability of Primality. Entropy 2025, 27, 1204. https://doi.org/10.3390/e27121204
Croll GJ. Entropy, Periodicity and the Probability of Primality. Entropy. 2025; 27(12):1204. https://doi.org/10.3390/e27121204
Chicago/Turabian StyleCroll, Grenville J. 2025. "Entropy, Periodicity and the Probability of Primality" Entropy 27, no. 12: 1204. https://doi.org/10.3390/e27121204
APA StyleCroll, G. J. (2025). Entropy, Periodicity and the Probability of Primality. Entropy, 27(12), 1204. https://doi.org/10.3390/e27121204






