Figure 1.
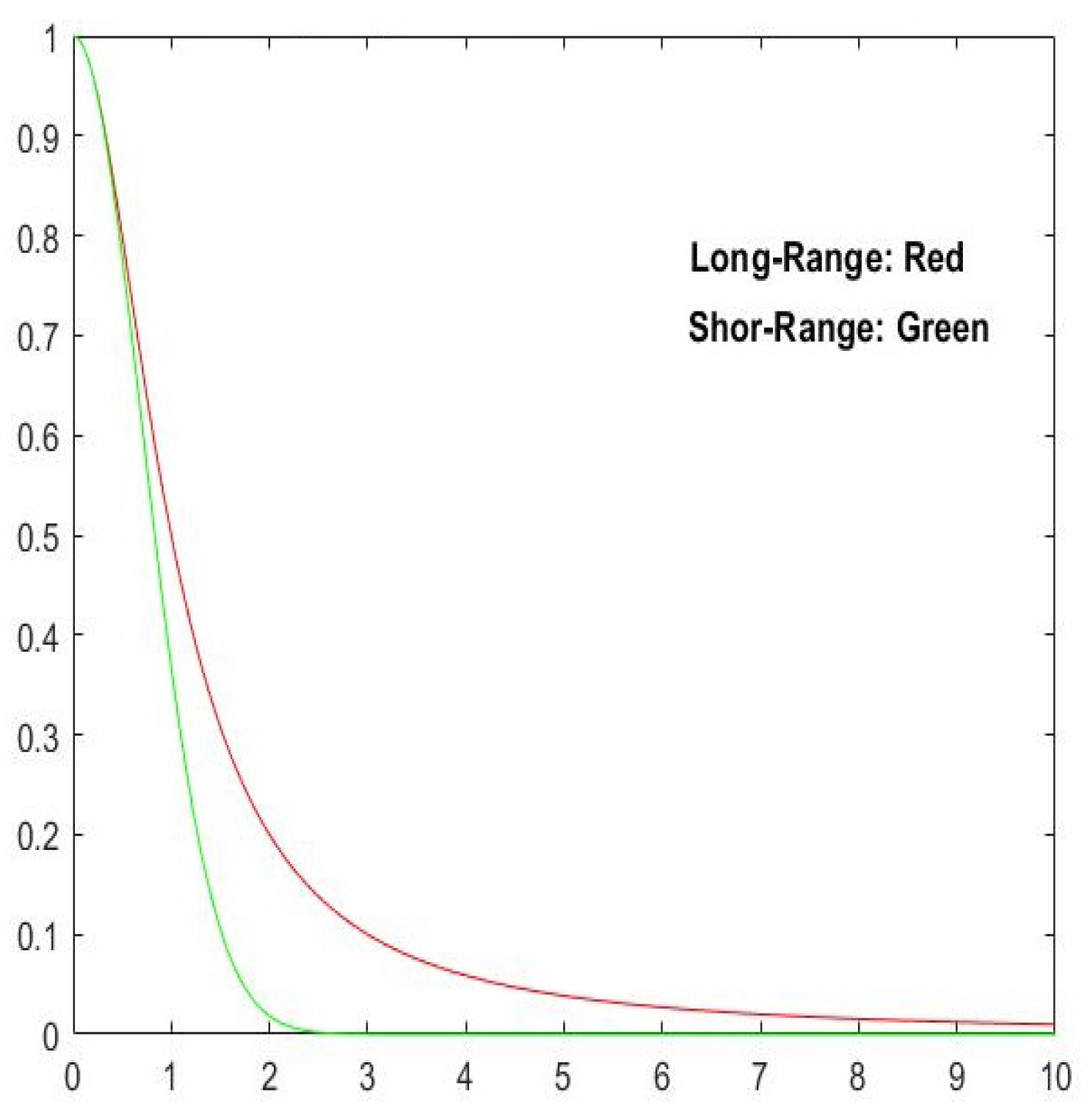
Plots of functions (
22) and (
23) showing short-range correlation in green and long-range correlation in red, respectively (Source [
38]).
Figure 1.
Plots of functions (
22) and (
23) showing short-range correlation in green and long-range correlation in red, respectively (Source [
38]).
Figure 2.
Some images of BSDS500-50 dataset with ground truth.
Figure 2.
Some images of BSDS500-50 dataset with ground truth.
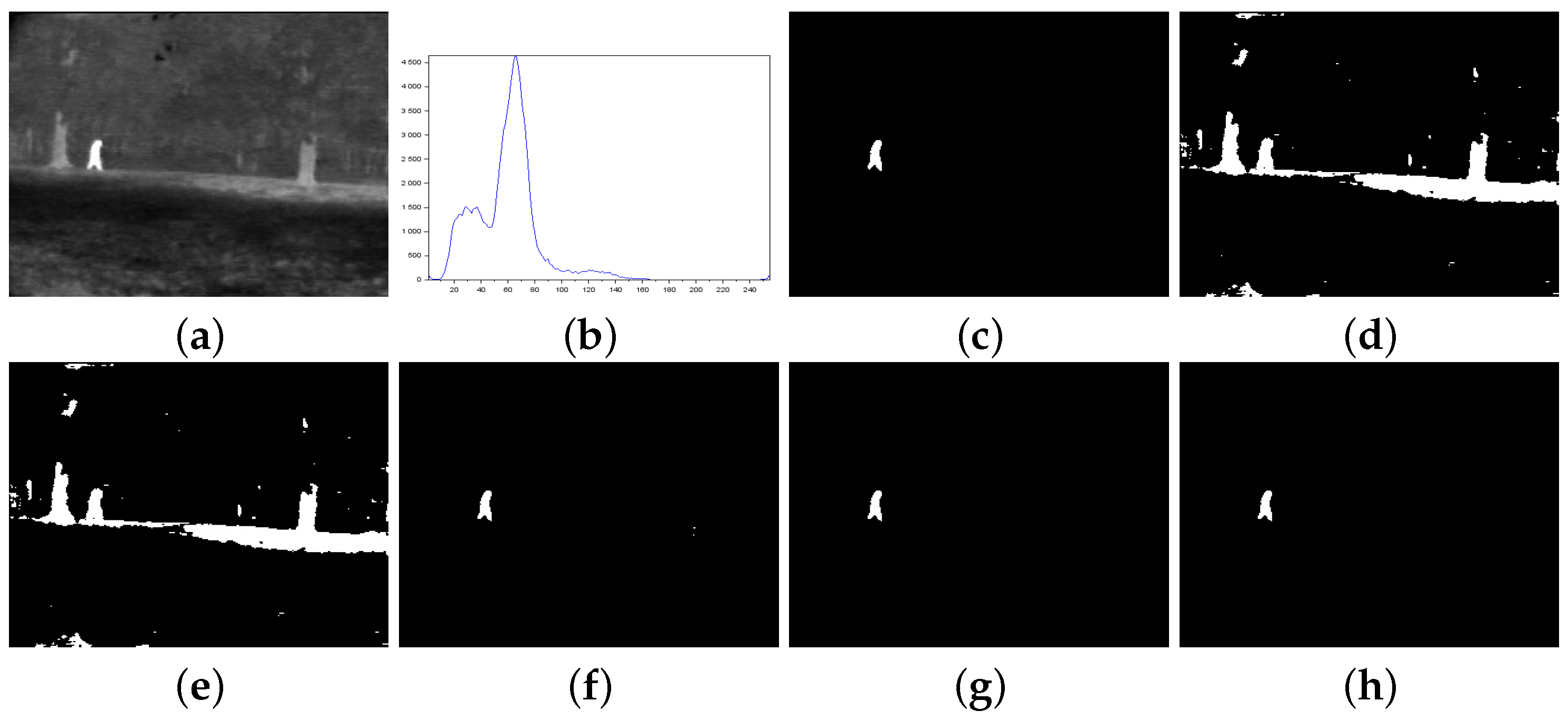
Figure 3.
Thresholding results of 000280 image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and threshold threshold ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and threshold ).
Figure 3.
Thresholding results of 000280 image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and threshold threshold ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and threshold ).
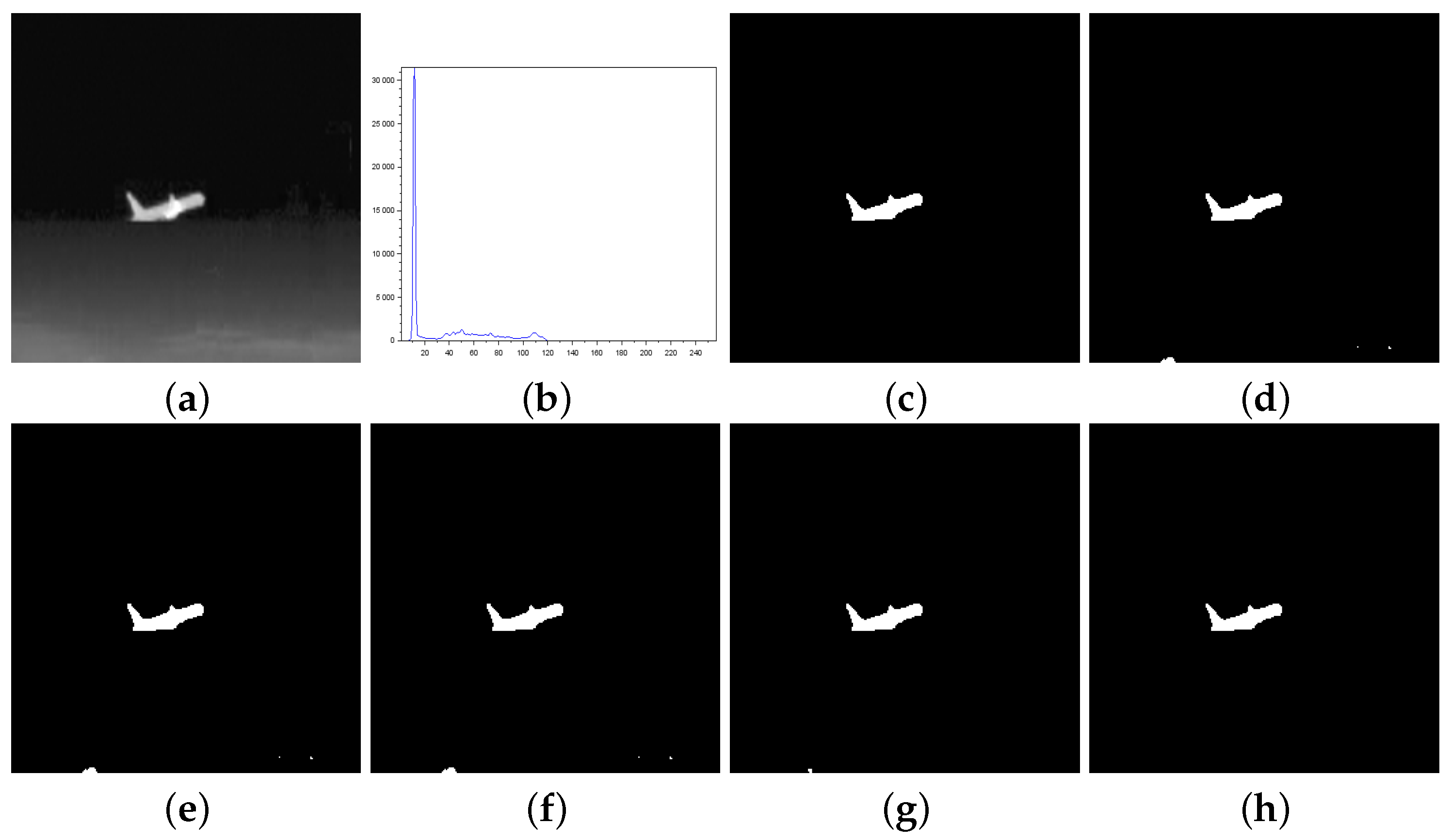
Figure 4.
Thresholding results of Airplane image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al. method (entropic parameter and threshold value ), and (h) the proposed method ( and ).
Figure 4.
Thresholding results of Airplane image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al. method (entropic parameter and threshold value ), and (h) the proposed method ( and ).
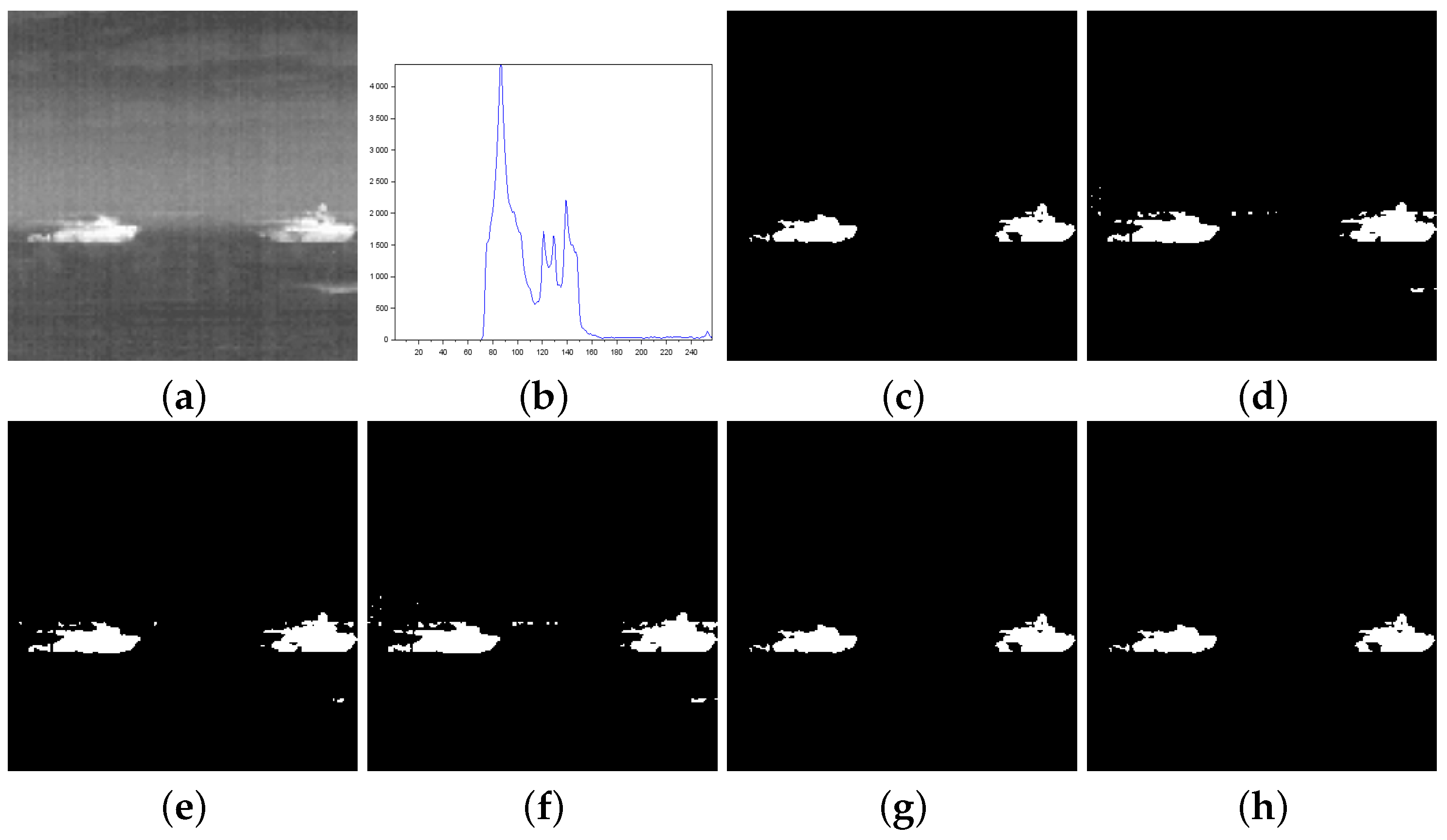
Figure 5.
Thresholding results of Tank image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 5.
Thresholding results of Tank image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
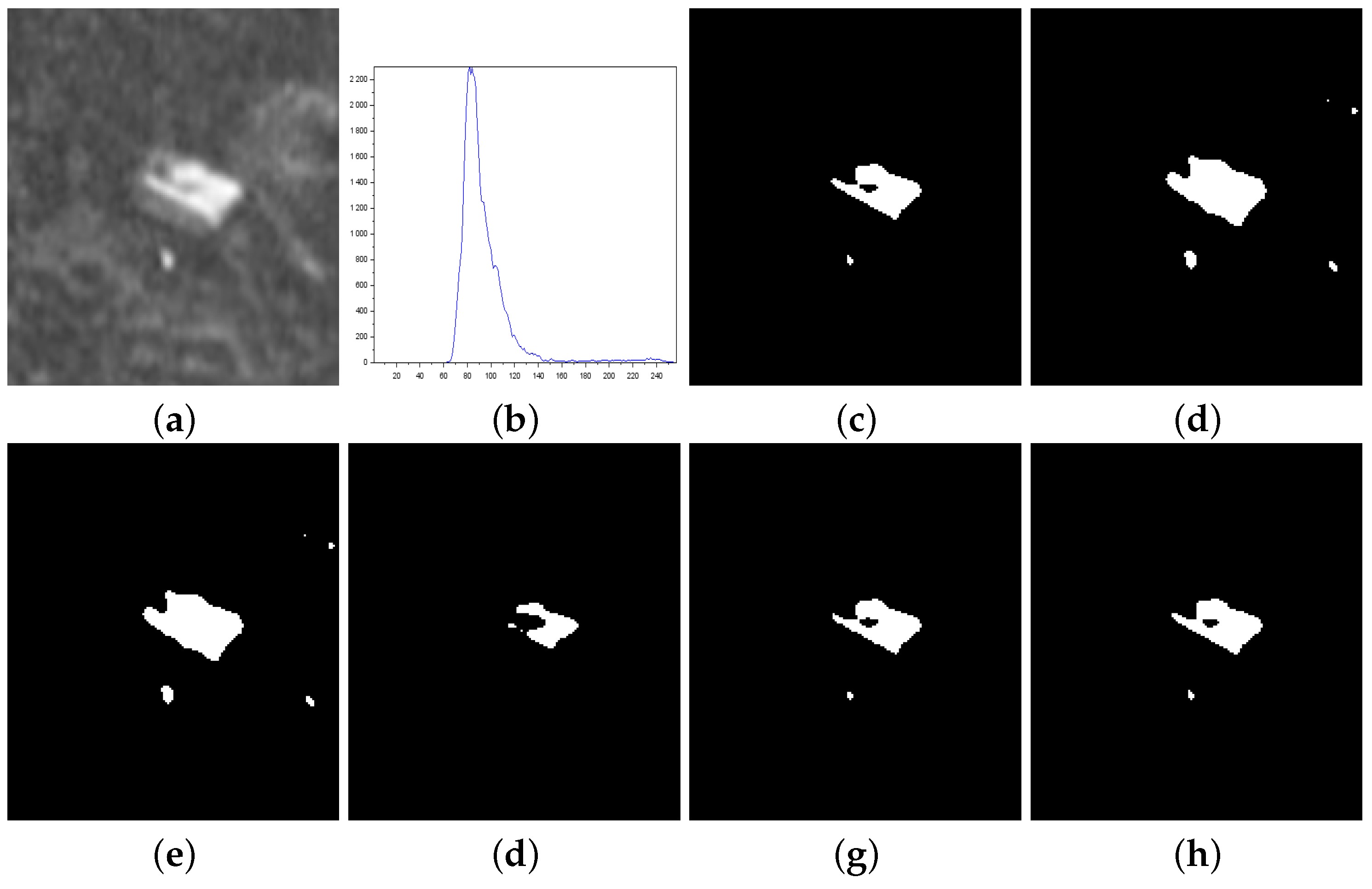
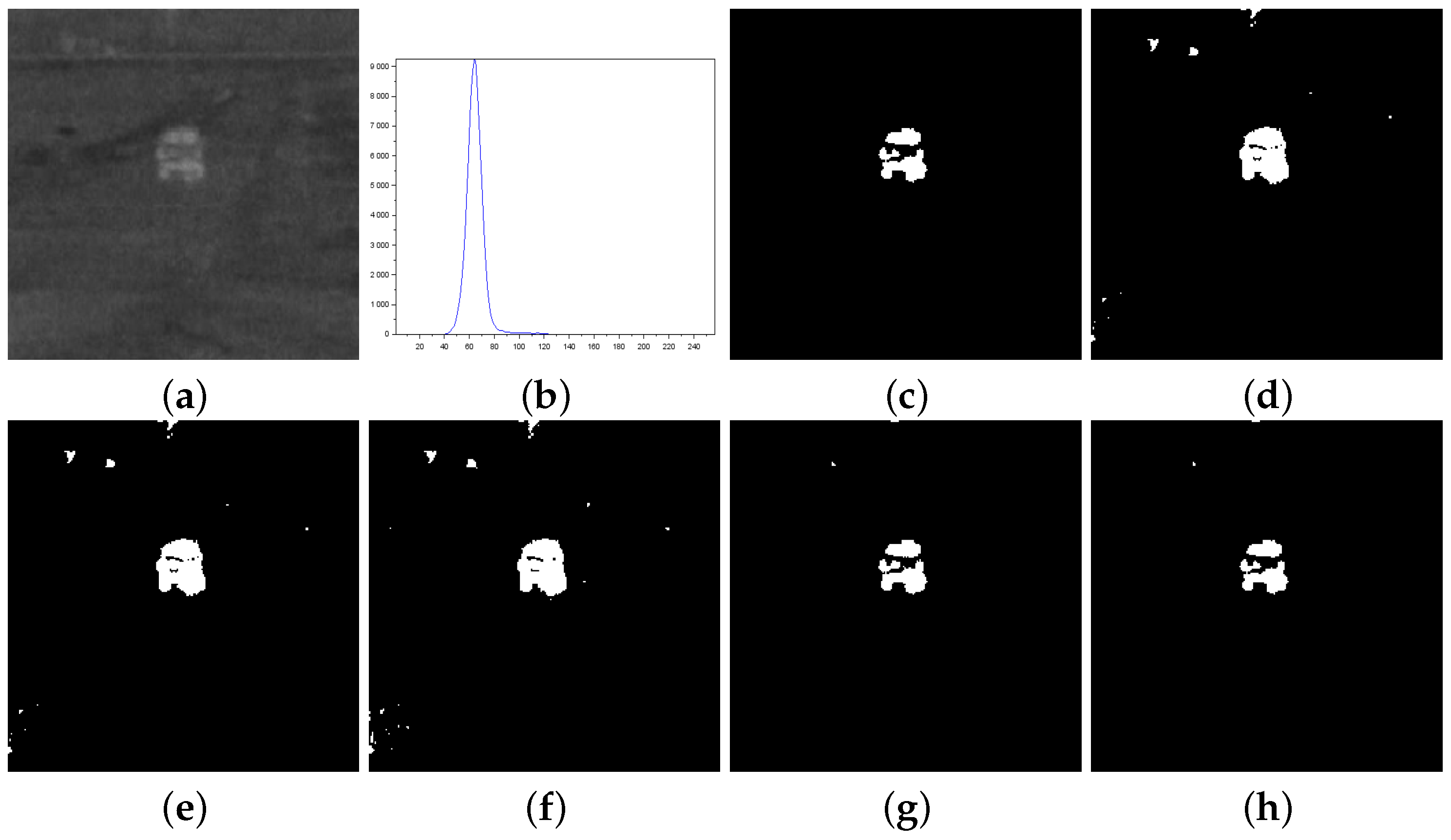
Figure 6.
Thresholding results of Panzer image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 6.
Thresholding results of Panzer image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 7.
Thresholding results of Car image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 7.
Thresholding results of Car image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (), (e) Albuquerque’s method (entropic parameter and threshold value ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
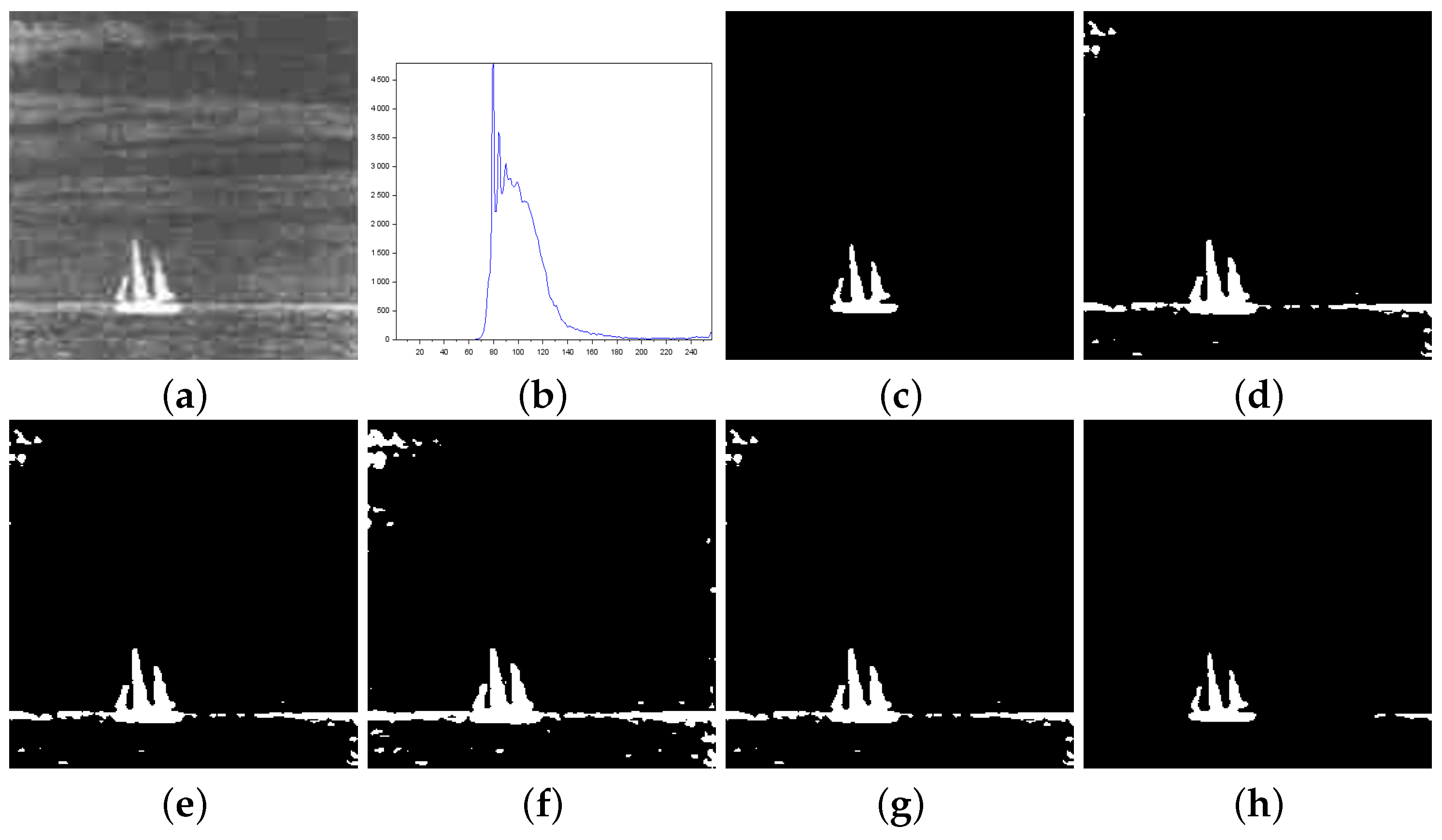
Figure 8.
Thresholding results of Sailboat image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method ( threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 8.
Thresholding results of Sailboat image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method ( threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
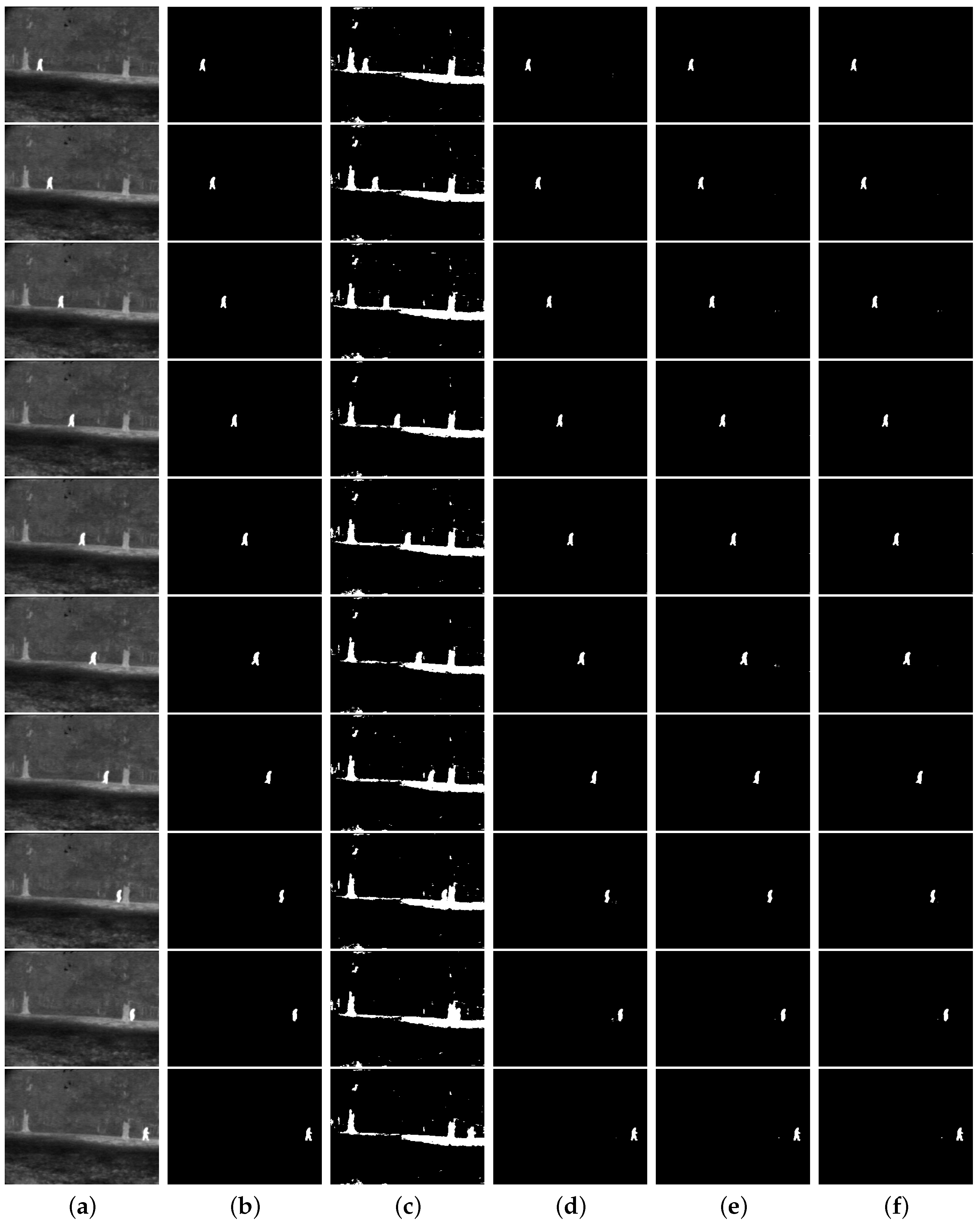
Figure 9.
Infrared image sequence and their thresholding results: (a) original, (b) ground-truth image, (c) Albuquerque’s method (entropic parameter ), the thresholds from top to bottom: 91, 93, 91, 97, 90, 98, 93, 96, 94, 96, (d) Lin & Ou’s method (entropic parameter ), the thresholds from top to bottom: 169, 178, 185, 177, 179, 178, 179, 173, 175, 192, (e) Nie et al.’s method, the parameters r and thresholds from the top to bottom: , , , , , , , , , , (f) the proposed method, the parameters r and thresholds from top to bottom: , , , , , , , , , .
Figure 9.
Infrared image sequence and their thresholding results: (a) original, (b) ground-truth image, (c) Albuquerque’s method (entropic parameter ), the thresholds from top to bottom: 91, 93, 91, 97, 90, 98, 93, 96, 94, 96, (d) Lin & Ou’s method (entropic parameter ), the thresholds from top to bottom: 169, 178, 185, 177, 179, 178, 179, 173, 175, 192, (e) Nie et al.’s method, the parameters r and thresholds from the top to bottom: , , , , , , , , , , (f) the proposed method, the parameters r and thresholds from top to bottom: , , , , , , , , , .
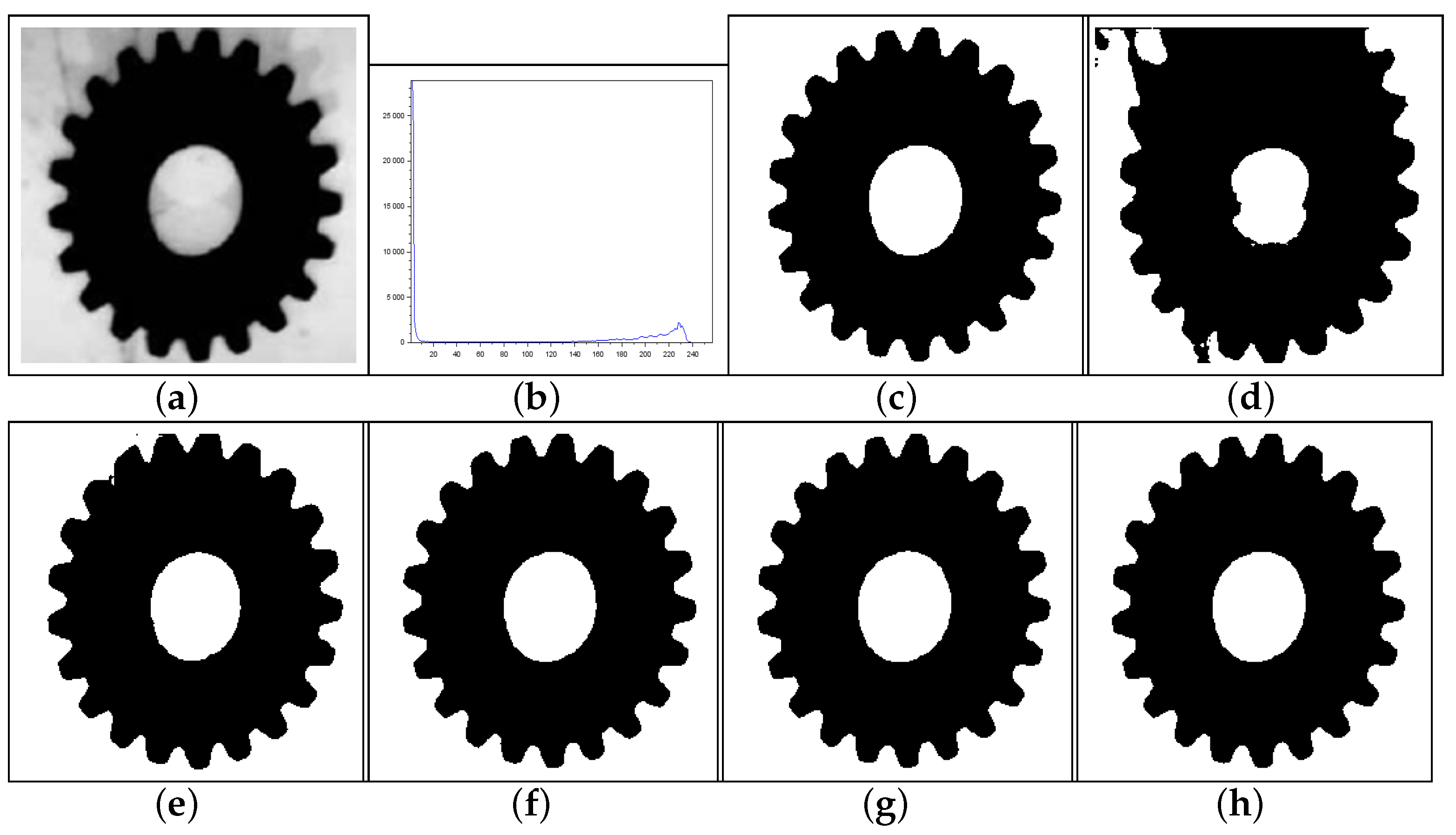
Figure 10.
Thresholding results of Gear image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 10.
Thresholding results of Gear image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
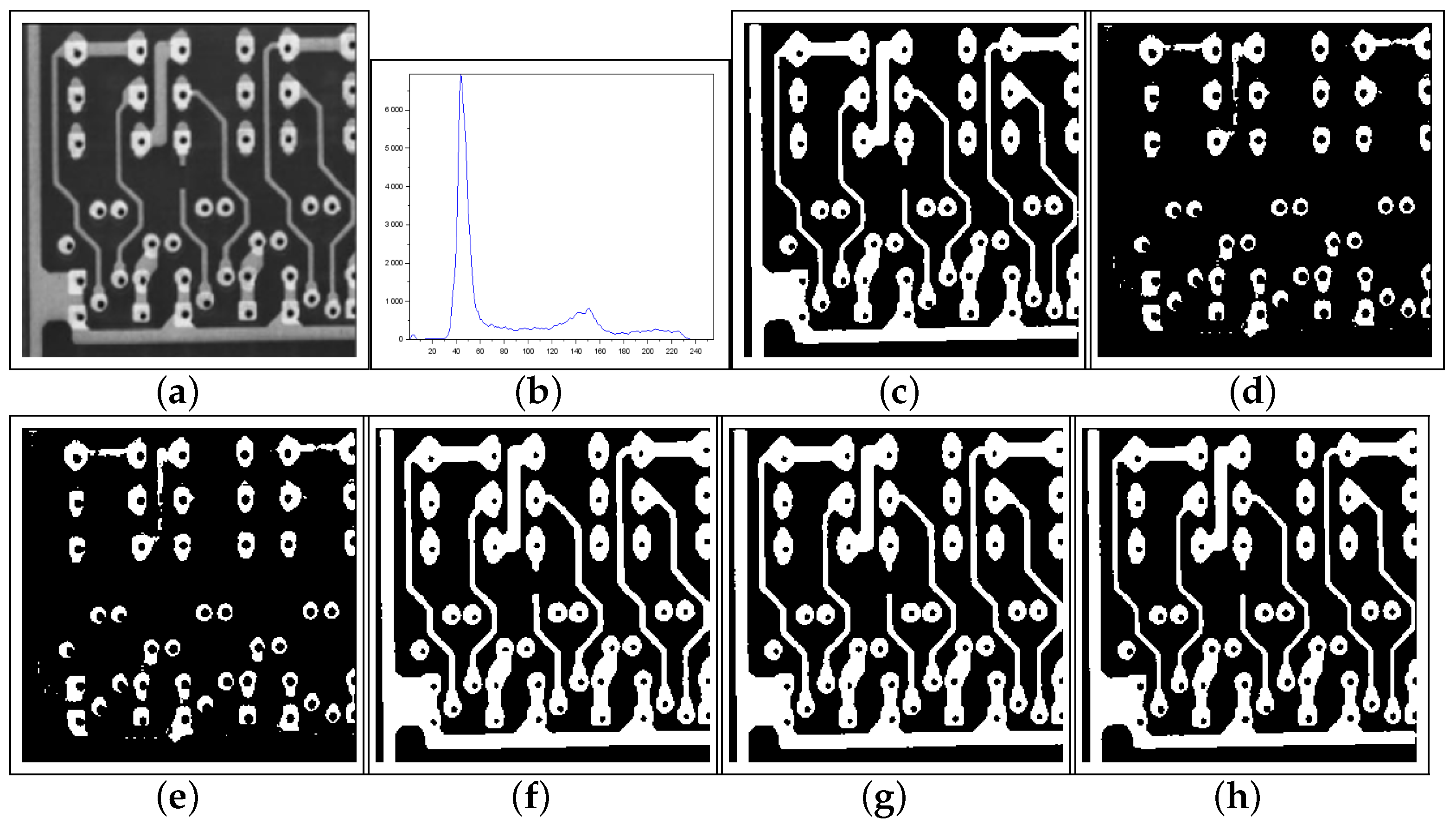
Figure 11.
Thresholding results of Pcb image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 11.
Thresholding results of Pcb image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
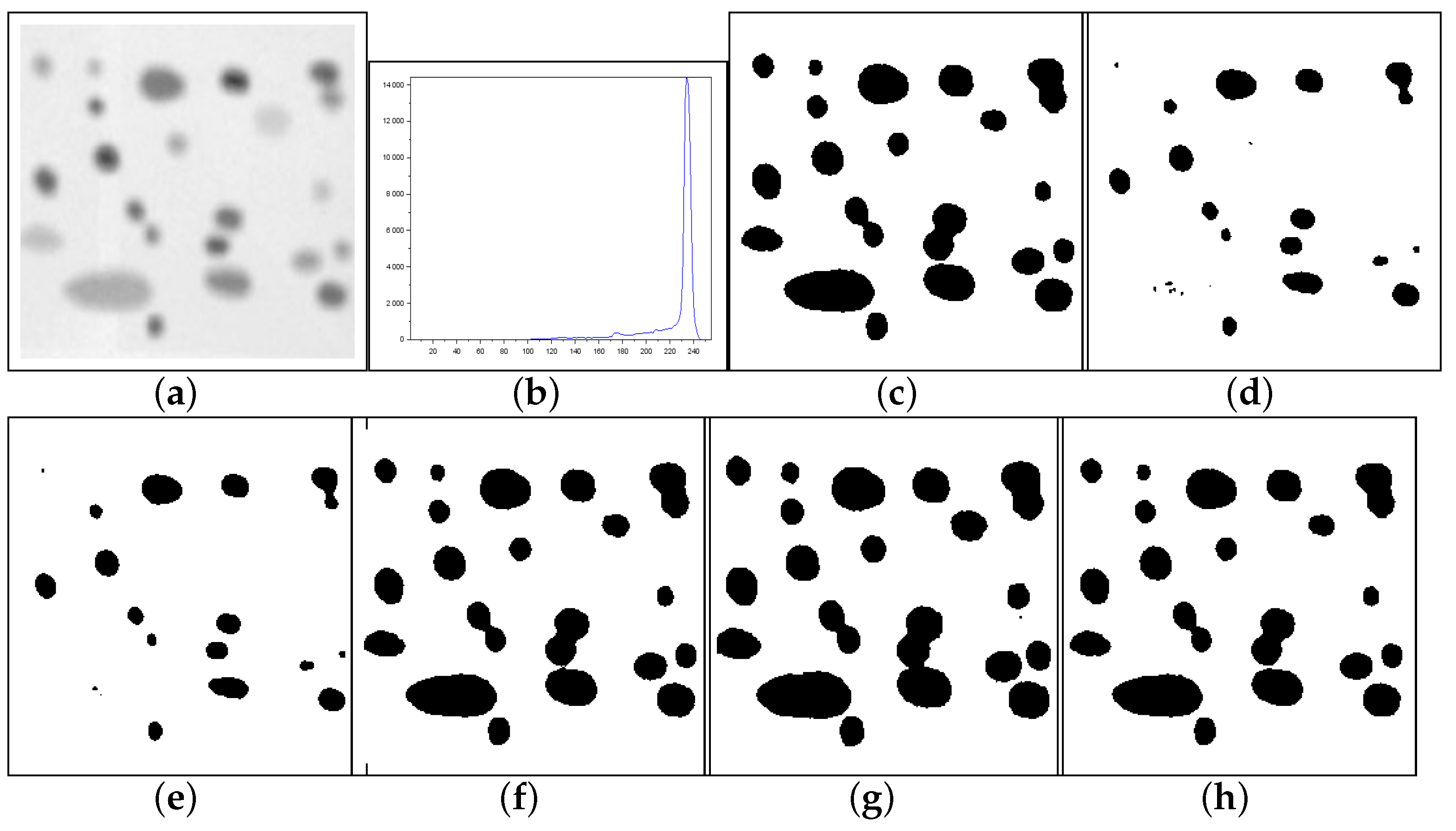
Figure 12.
Thresholding results of Cell image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
Figure 12.
Thresholding results of Cell image: (a) original, (b) Histogram, (c) ground-truth image, (d) Shannon method (threshold value ), (e) Albuquerque’s method (entropic parameter and ), (f) Lin & Ou’s method ( and ), (g) Nie et al.’s method (entropic parameter and ), and (h) the proposed method ( and ).
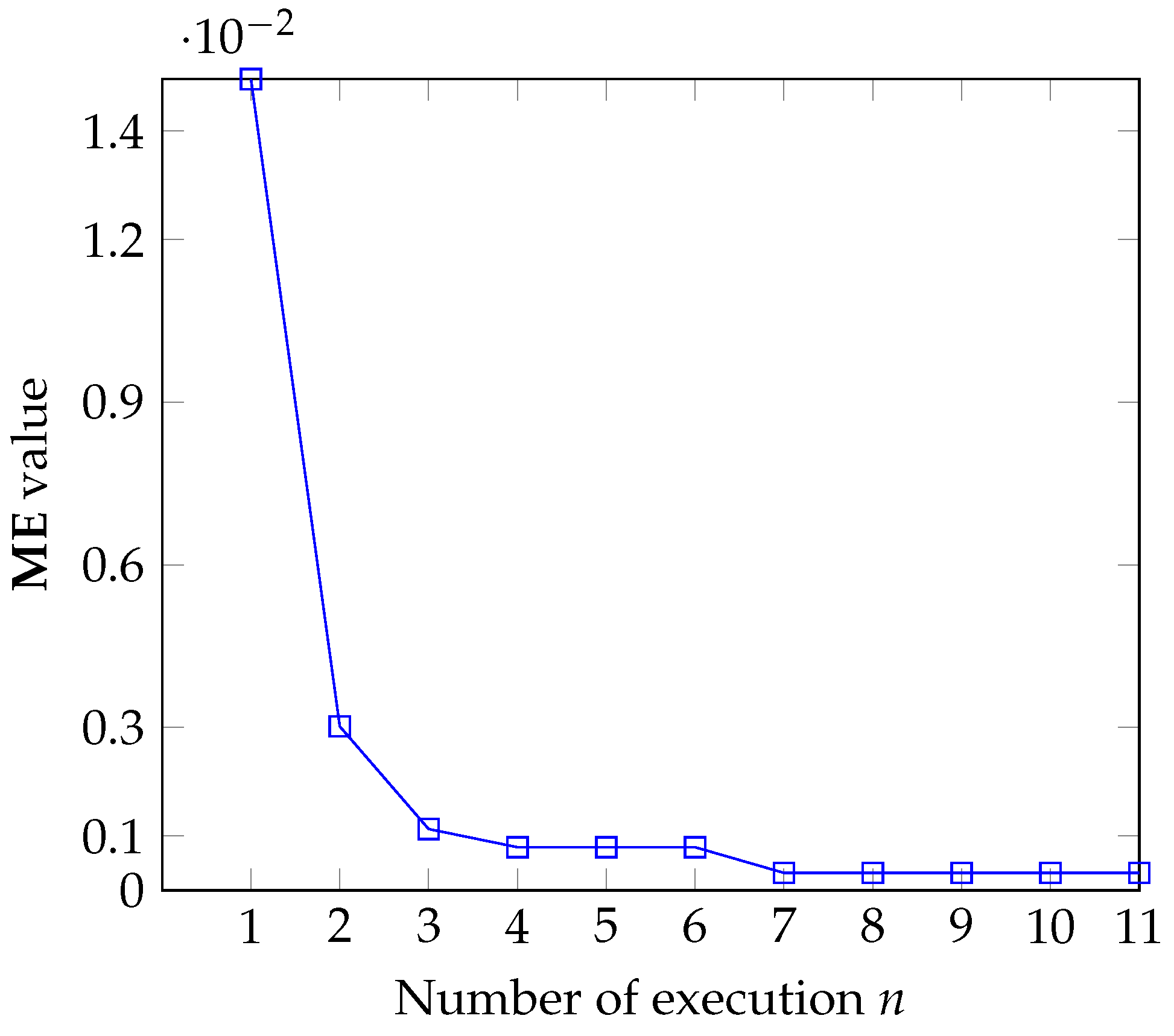
Figure 13.
Results of convergence test: ME versus number of executions.
Figure 13.
Results of convergence test: ME versus number of executions.
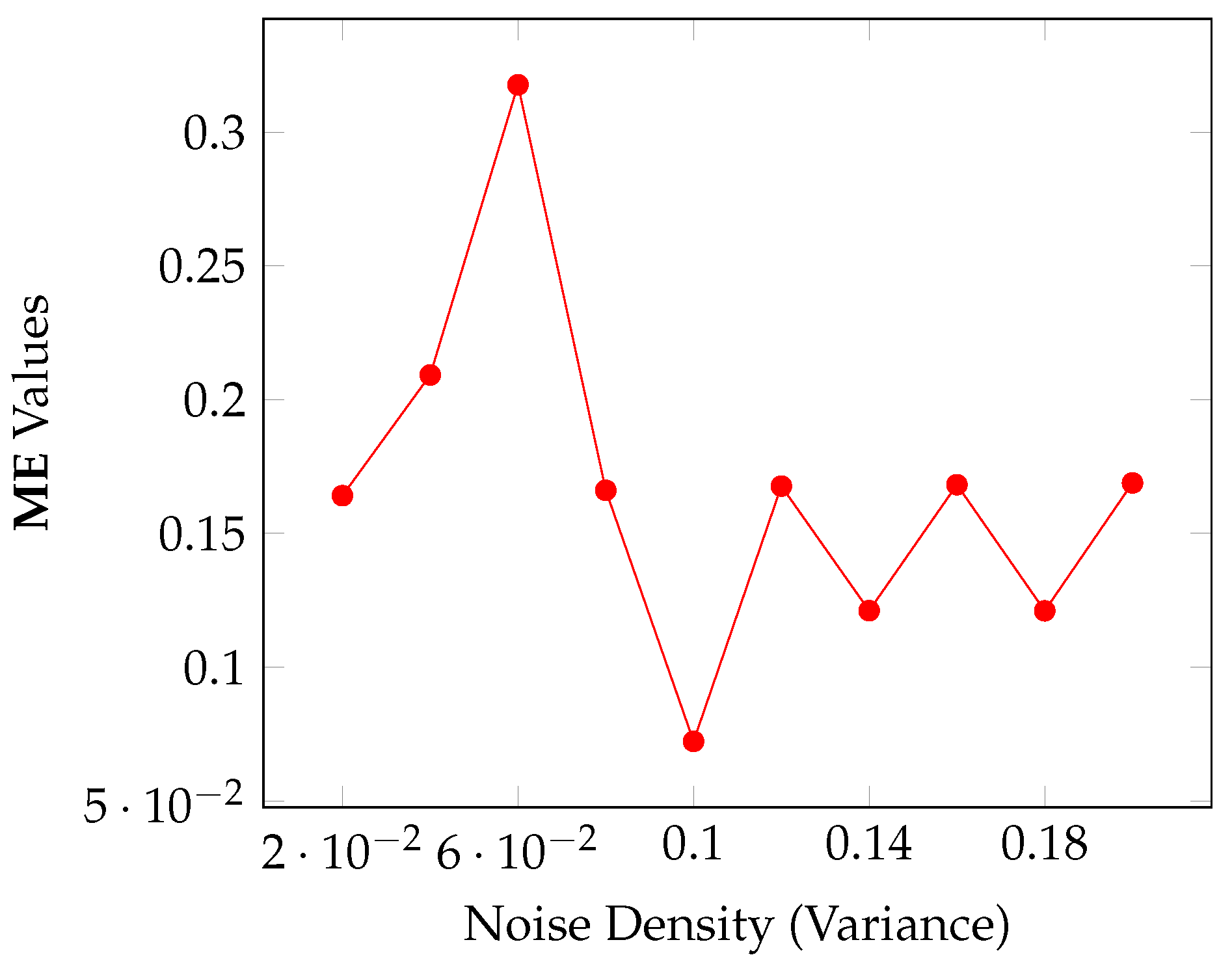
Figure 14.
ME behavior against variance in noisy images for Algorithm 1.
Figure 14.
ME behavior against variance in noisy images for Algorithm 1.
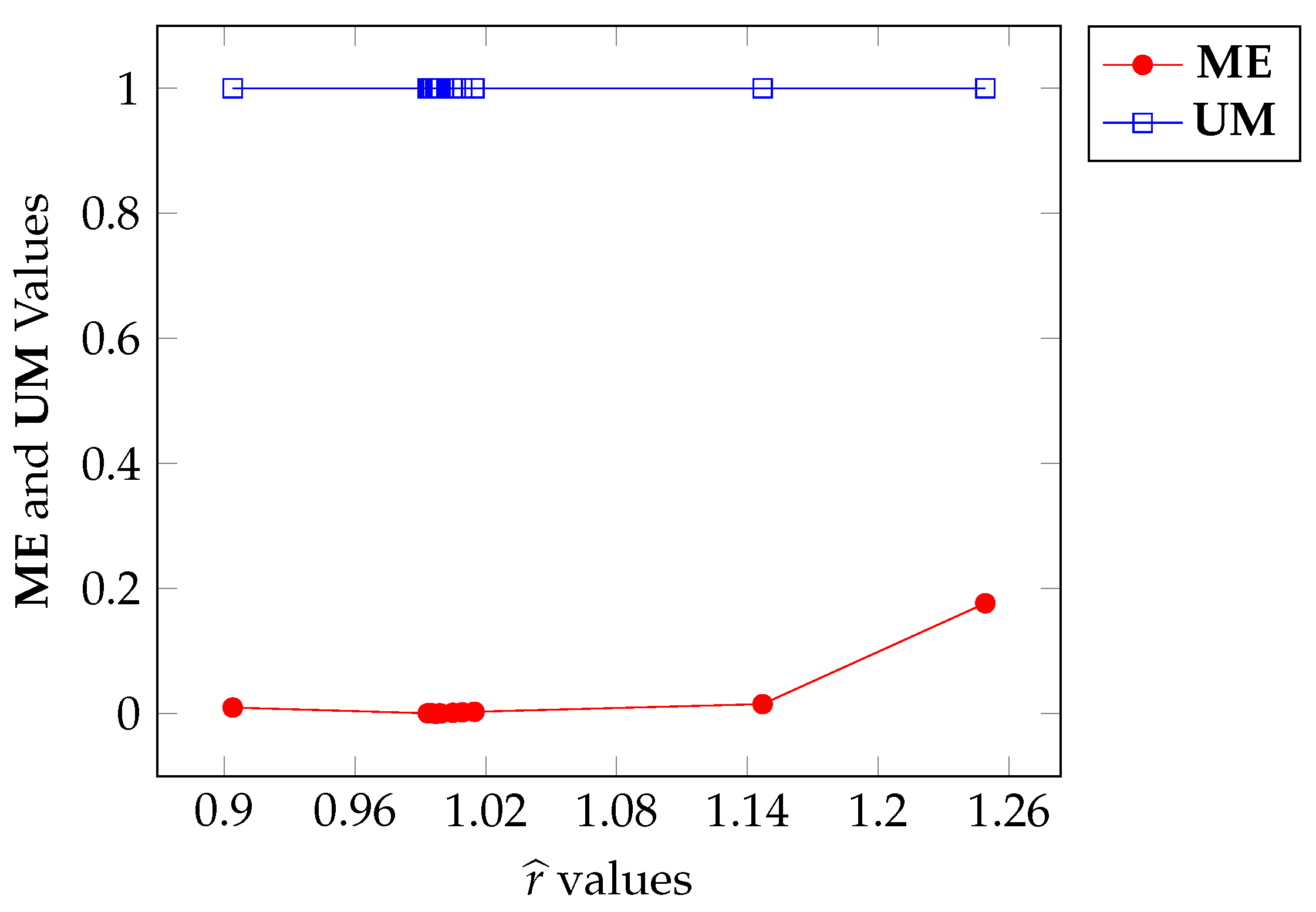
Figure 15.
ME and UM variation with respect to calculated through Algorithm 1.
Figure 15.
ME and UM variation with respect to calculated through Algorithm 1.
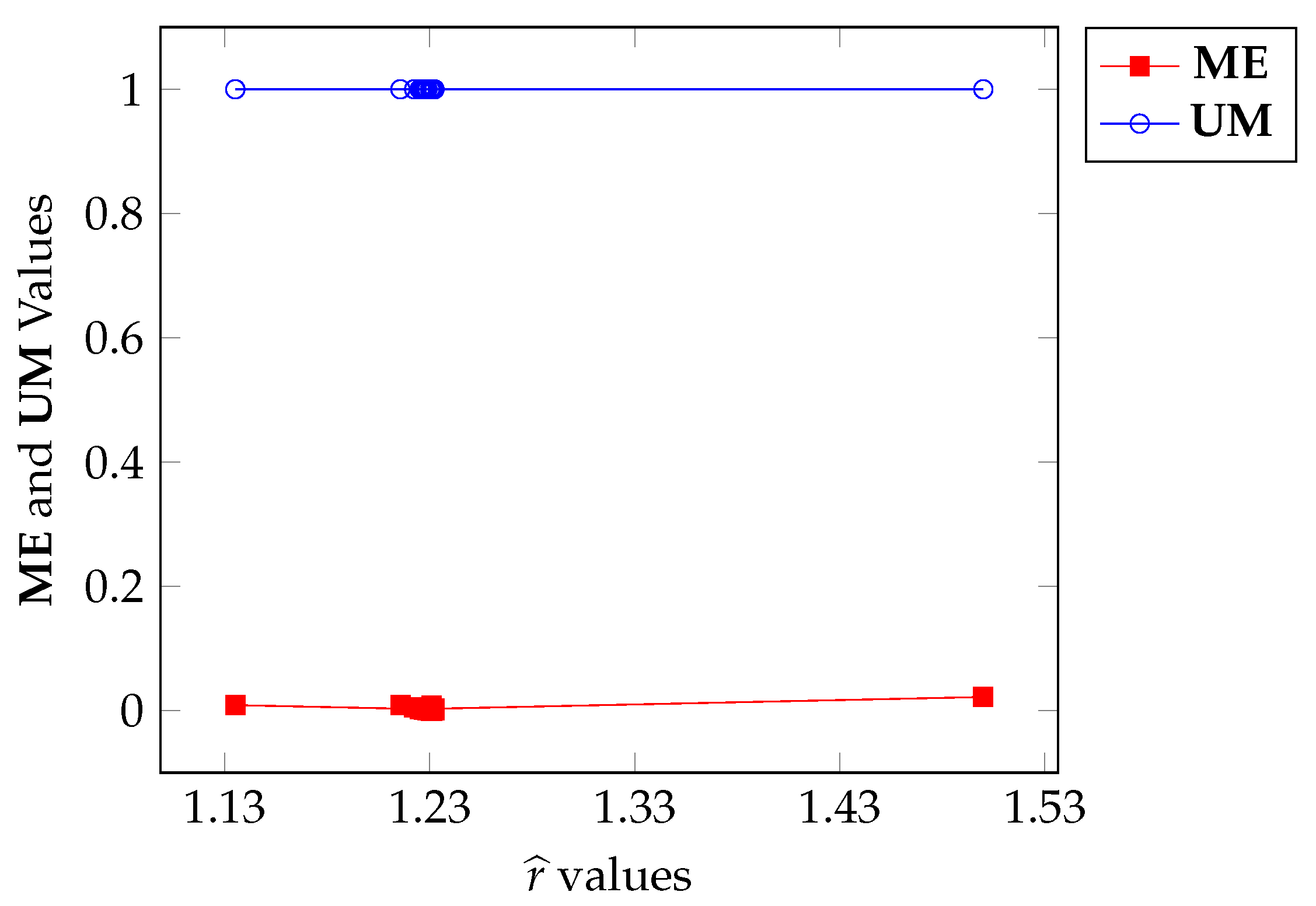
Figure 16.
ME and UM variation with respect to calculated through Algorithm A1.
Figure 16.
ME and UM variation with respect to calculated through Algorithm A1.
Figure 17.
Images used for SVM training (black rectangle) and inference (red rectangle).
Figure 17.
Images used for SVM training (black rectangle) and inference (red rectangle).
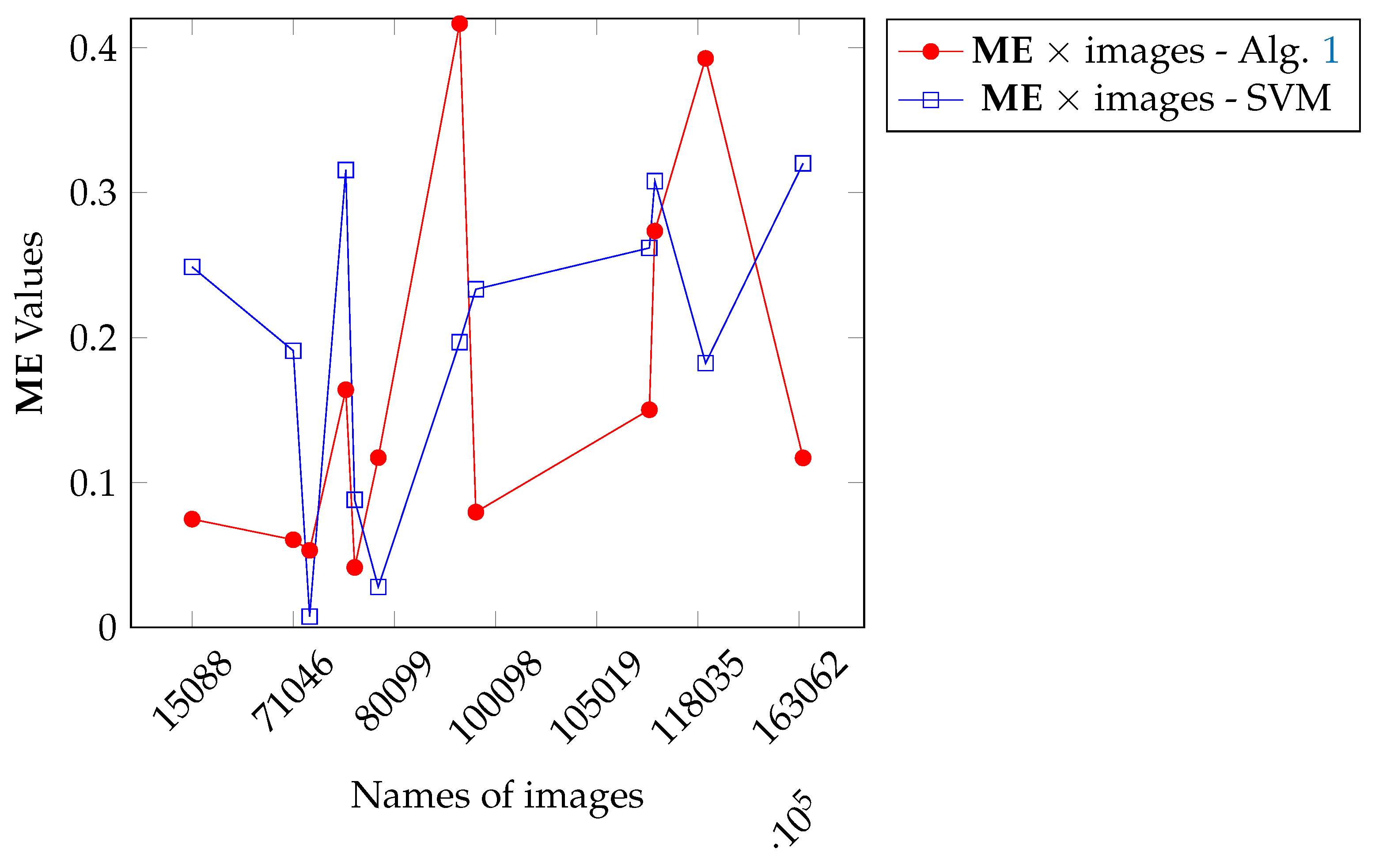
Figure 18.
Comparison between Algorithm 1 and SVM results.
Figure 18.
Comparison between Algorithm 1 and SVM results.
Table 1.
Comparison between the techniques. Ideal values: , , , . In black, the best results are highlighted.
Table 1.
Comparison between the techniques. Ideal values: , , , . In black, the best results are highlighted.
| Images | Thresholding Methods |
|---|
|
Shannon
|
Albuquerque
|
Lin & Ou
|
Nie et al.
|
Our Method
|
|---|
| 000280 | Threshold | 91 | 91 | 169 | 173 | |
| | Misclassified pixels | 4900 | 4900 | 6 | 6 | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | 0 | | |
| | | | | | | |
| Airplane | Threshold | 117 | 117 | 117 | 121 | |
| | Misclassified pixels | 44 | 44 | 44 | 8 | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | | | |
| | | | | | | |
| Tank | Threshold | 140 | 140 | 220 | 194 | |
| | Misclassified pixels | 390 | 390 | 255 | 21 | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | | | |
| | | | | | | |
| Panzer | Threshold | 154 | 157 | 153 | | |
| | Misclassified pixels | 574 | 426 | 642 | | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | | | |
| | | | | | | |
| Car | Threshold | 81 | 81 | 80 | 89 | |
| | Misclassified pixels | 492 | 492 | 581 | 55 | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | | | |
| | | | | | | |
| Sailboat | Threshold | 155 | 155 | 141 | 155 | |
| | Misclassified pixels | 1295 | 1295 | 2447 | 1295 | |
| | ME | | | | | |
| | JS (%) | | | | | |
| | RAE | | | | | |
| | | | | | | |
Table 2.
The thresholding accuracy (JS, Equation (
12)) of methods. Ideal value: JS = 100%. In
black, the best results are highlighted.
Table 2.
The thresholding accuracy (JS, Equation (
12)) of methods. Ideal value: JS = 100%. In
black, the best results are highlighted.
| Images | Albuquerque | Lin & Ou | Nie et al. | Our |
|---|
|
(%)
|
(%)
|
(%)
|
(%)
|
|---|
| 000280 | 3.94 | 97.06 | 96.02 | 97.51 |
| 000300 | 4.25 | 94.47 | 94.04 | 95.87 |
| 000320 | 3.75 | 90.05 | 94.91 | 94.93 |
| 000340 | 4.85 | 95.02 | 94.59 | 95.02 |
| 000360 | 4.26 | 91.21 | 92.08 | 92.08 |
| 000380 | 5.98 | 89.78 | 90.38 | 92.36 |
| 000400 | 4.23 | 98.20 | 100.00 | 100.00 |
| 000420 | 3.96 | 97.51 | 98.98 | 99.49 |
| 000440 | 3.87 | 93.67 | 97.61 | 97.61 |
| 000460 | 5.12 | 94.05 | 96.86 | 98.05 |
| Average | | | | |
Table 3.
Comparison between the techniques concerning misclassified pixels and ME. Ideal value: . In black, the best results are highlighted.
Table 3.
Comparison between the techniques concerning misclassified pixels and ME. Ideal value: . In black, the best results are highlighted.
| Images | Thresholding Methods |
|---|
|
Albuquerque
|
Lin & Ou
|
Nie et al.
|
Our Method
|
|---|
| 000280 | Threshold | 91 | 169 | 173 | |
| | Misclassified pixels | 4900 | 6 | 6 | |
| | ME | | | | |
| 000300 | Threshold | 93 | 178 | 177 | |
| | Misclassified pixels | 4895 | 12 | 13 | |
| | ME | | | | |
| 000320 | Threshold | 91 | 185 | 171 | |
| | Misclassified pixels | 5413 | 21 | | |
| | ME | | | | |
| 000340 | Threshold | 97 | | 176 | |
| | Misclassified pixels | 4339 | | 12 | |
| | ME | | | | |
| 000360 | Threshold | 90 | 179 | | |
| | Misclassified pixels | 5355 | 21 | | |
| | ME | | | | |
| 000380 | Threshold | 98 | 178 | 170 | |
| | Misclassified pixels | 4309 | 28 | 28 | |
| | ME | | | | |
| 000400 | Threshold | 98 | 179 | | |
| | Misclassified pixels | 5033 | 4 | | |
| | ME | | | | |
| 000420 | Threshold | 96 | 173 | 176 | |
| | Misclassified pixels | 4756 | 5 | 2 | |
| | ME | | | | |
| 000440 | Threshold | 94 | 175 | | |
| | Misclassified pixels | 5142 | 14 | | |
| | ME | | | | |
| 000460 | Threshold | 96 | 192 | 182 | |
| | Misclassified pixels | 4654 | 15 | 8 | |
| | ME | | | | |
Table 4.
Comparison between the—NDT images. Ideal values: , , , . In black, the best results are highlighted.
Table 4.
Comparison between the—NDT images. Ideal values: , , , . In black, the best results are highlighted.
| Images | Thresholding Methods |
|---|
|
Shannon
|
Albuquerque
|
Lin & Ou
|
Nie et al.
|
Our Method
|
|---|
| Gear | Threshold | 185 | 128 | 87 | 75 | 80 |
| | Misclassified pixels | 8200 | 1553 | 188 | 139 | 0 |
| | ME | | | | | 0 |
| | JS (%) | | | | | 100.00 |
| | RAE | | | | | 0 |
| | | | | | | 1 |
| Pcb | Threshold | 158 | 158 | 78 | 82 | 99 |
| | Misclassified pixels | 13852 | 13852 | 2808 | 2166 | 145 |
| | ME | | | | | 0.00221252 |
| | JS (%) | | | | | 99.33 |
| | RAE | | | | | 0.00669839 |
| | | | | | | 0.997757 |
| Cell | Threshold | 172 | 171 | 214 | 222 | 213 |
| | Misclassified pixels | 7276 | 7375 | 271 | 2634 | 0 |
| | ME | | | | | 0 |
| | JS (%) | | | | | 100.00 |
| | RAE | | | | | 0 |
| | | | | | | 1 |
Table 5.
Input parameters used in the executions of Algorithm 1.
Table 5.
Input parameters used in the executions of Algorithm 1.
| Parameter | Value |
|---|
| |
| d | |
| L | 255 |
| |
| |
| |
| 20 |
| 100 |
| |
| |
| 0 or 1 |
Table 6.
Sensitivity test of the r parameter—panzer image.
Table 6.
Sensitivity test of the r parameter—panzer image.
| k | ME Values | Sensitivity (S) |
|---|
| | |
| | |
| | |
| 0 | | 0 |
| 1 | | |
| 2 | | |
| 3 | | |
Table 7.
Mean of ME values and standard deviations (Adapted from [
38]).
Table 7.
Mean of ME values and standard deviations (Adapted from [
38]).
| Thresholding Methods | ME Mean: | Std Deviat.: | [, ] |
|---|
| Albuquerque [3] | 0.32 | 0.24 | [0.08, 0.56] |
| Nie et al. [6] | 0.31 | 0.25 | [0.06, 0.56] |
| Lin & Ou [5] | 0.38 | 0.25 | [0.13, 0.63] |
| Deng [37] | 0.49 | 0.26 | [0.23, 0.75] |
| Manda & Hyun [36] | 0.48 | 0.25 | [0.23, 0.73] |
| Elaraby & Moratal [35] | 0.27 | 0.19 | [0.08, 0.46] |
| Proposal 1 of [38] | 0.31 | 0.22 | [0.09, 0.53] |
| Proposal 2 of [38] | 0.44 | 0.26 | [0.18, 0.70] |
| Our Algorithm 1 | | | [−0.0232, 0.0332] |