Quantum AI in Speech Emotion Recognition
Abstract
1. Introduction
2. Literature Review
2.1. Quantum Computing in Artificial Intelligence
2.2. Speech Emotion Recognition
2.3. Quantum AI in Speech Emotion Recognition
2.4. Training Data
2.5. Evaluation
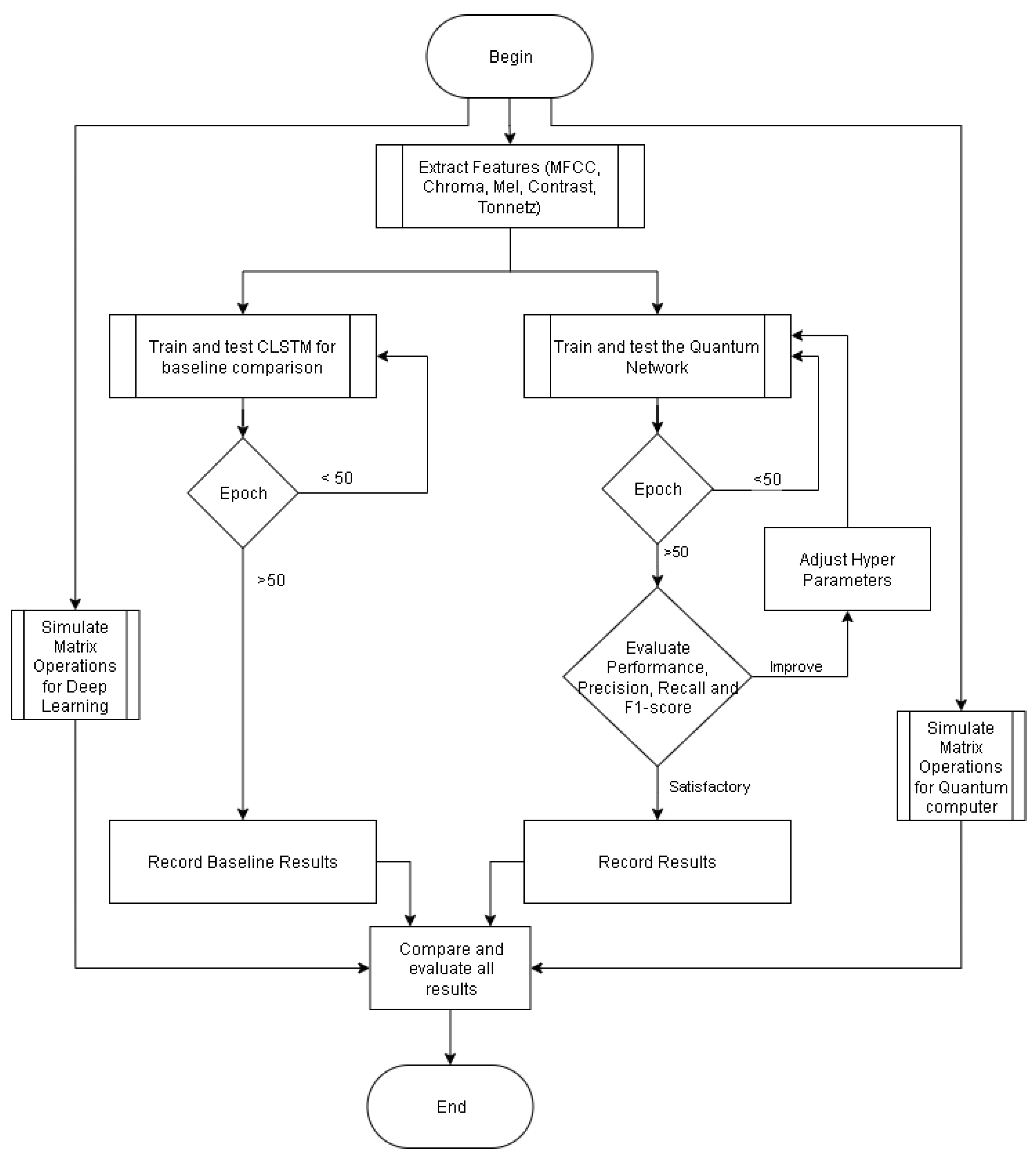
3. Materials and Methods
3.1. Current Challenges
3.2. Proposed System
3.3. Dataset Preparation
3.4. Training Procedure
3.5. Model Specifications (Architectures, Hyperparameters, Training)
3.6. CLSTM
3.7. Quantum Models Evaluated
- A variational quantum classifier (VQC) trained end-to-end with angle embedding;
- A quantum support vector machine (QSVM) using an angle-embedded fidelity kernel;
- A QAOA-based classifier (depth ).
3.8. DataEncoding (Classical → Quantum)
3.9. Measurement and Noise Regimes
3.10. ClassicalVersus Quantum-Inspired Matrix Multiplication
4. Results
4.1. Test Data
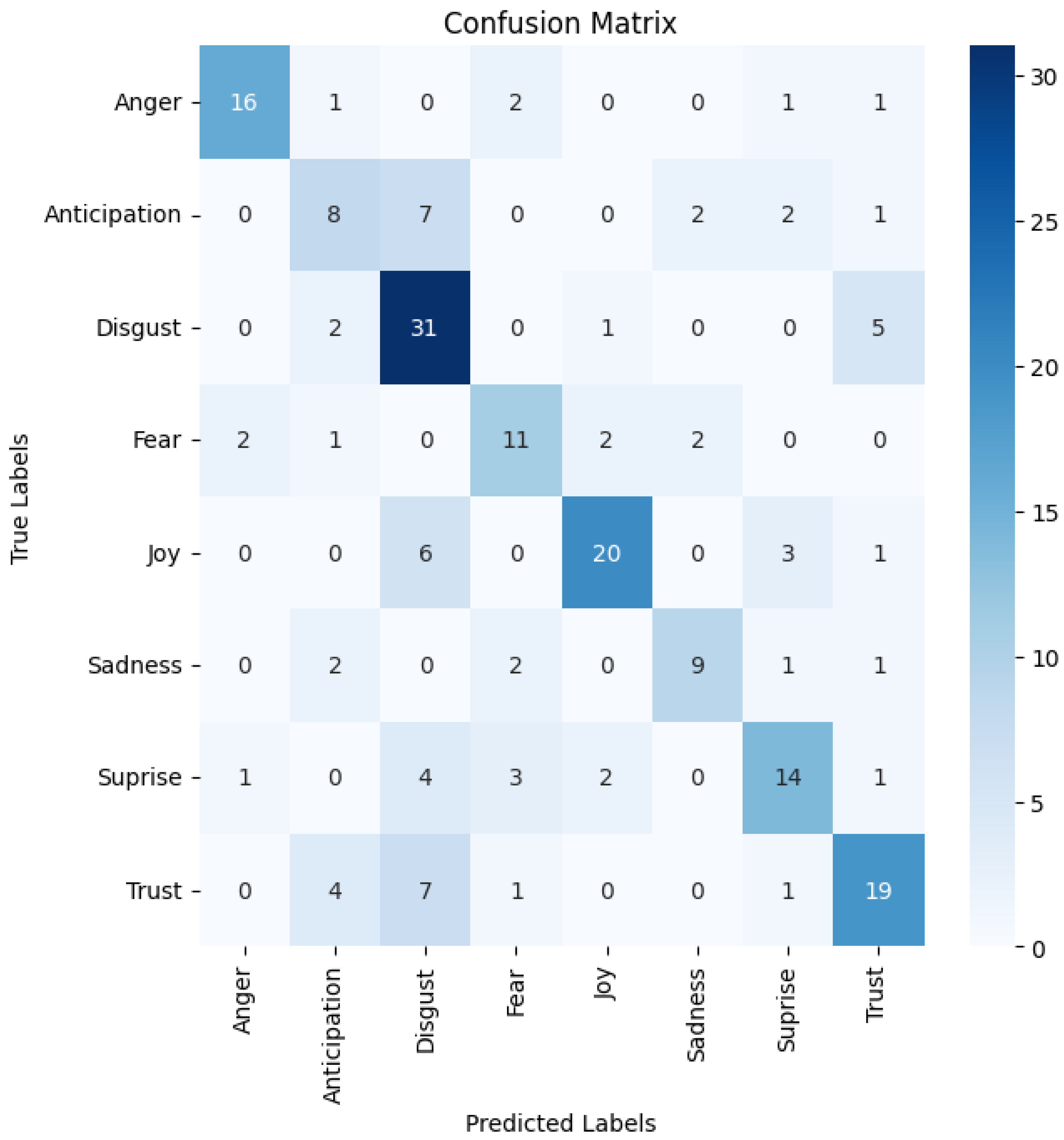
4.2. CLSTM
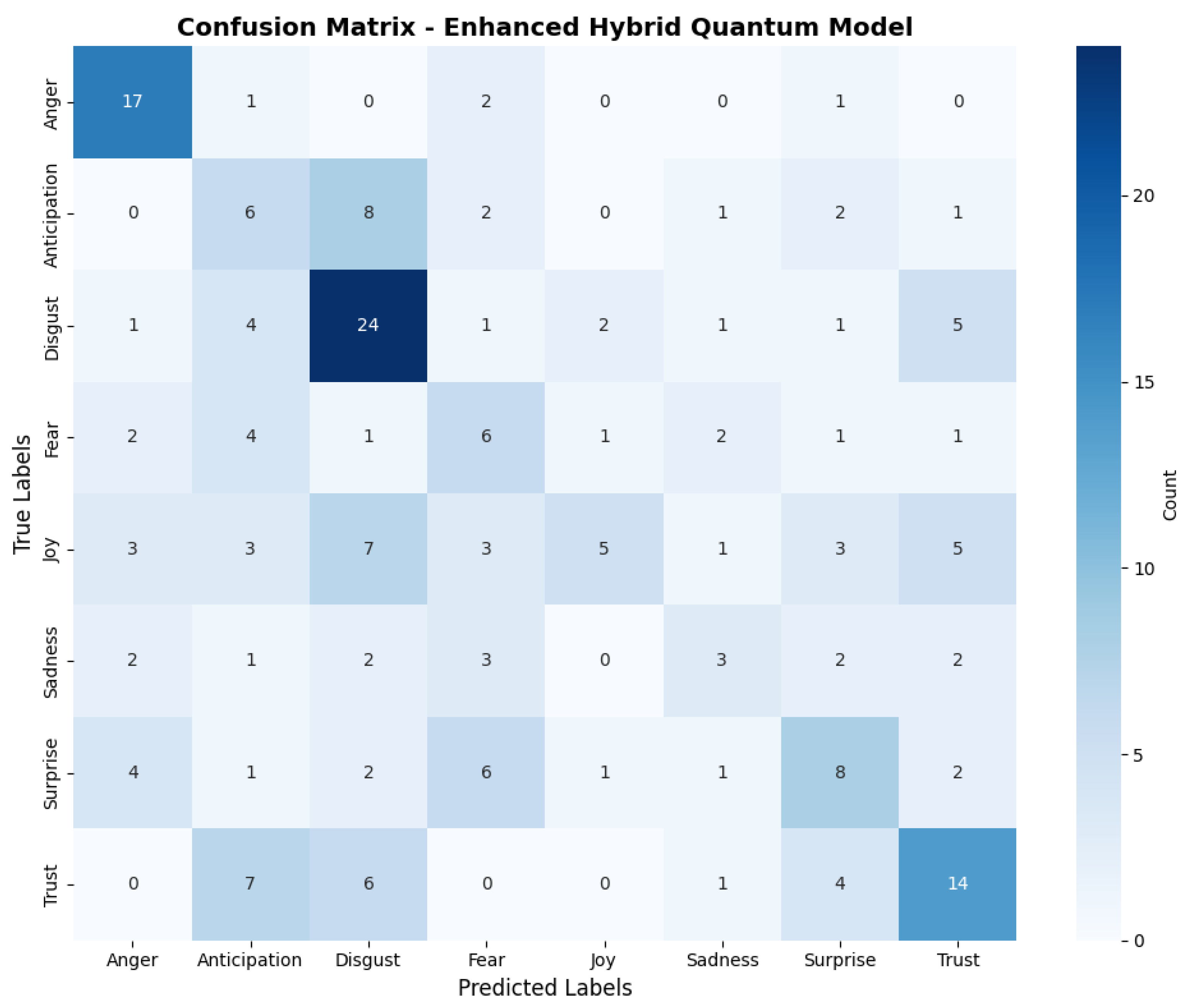
4.3. Performance of the Three Quantum Classifiers
- VQC (Variational Quantum Classifier): The best run reaches 41.5% accuracy (Table 4, mean across four runs 35.75 ± 3.44%).
- QSVM (Quantum Support Vector Machine): With an angle-embedded fidelity kernel and increasing shot budget, accuracy climbs to a maximum of 42.0% at 1000 shots (Table 5).
- QAOA-based classifier: The deepest tested ansatz (, ideal simulation) yields the highest quantum accuracy of 43.0% (Table 6).
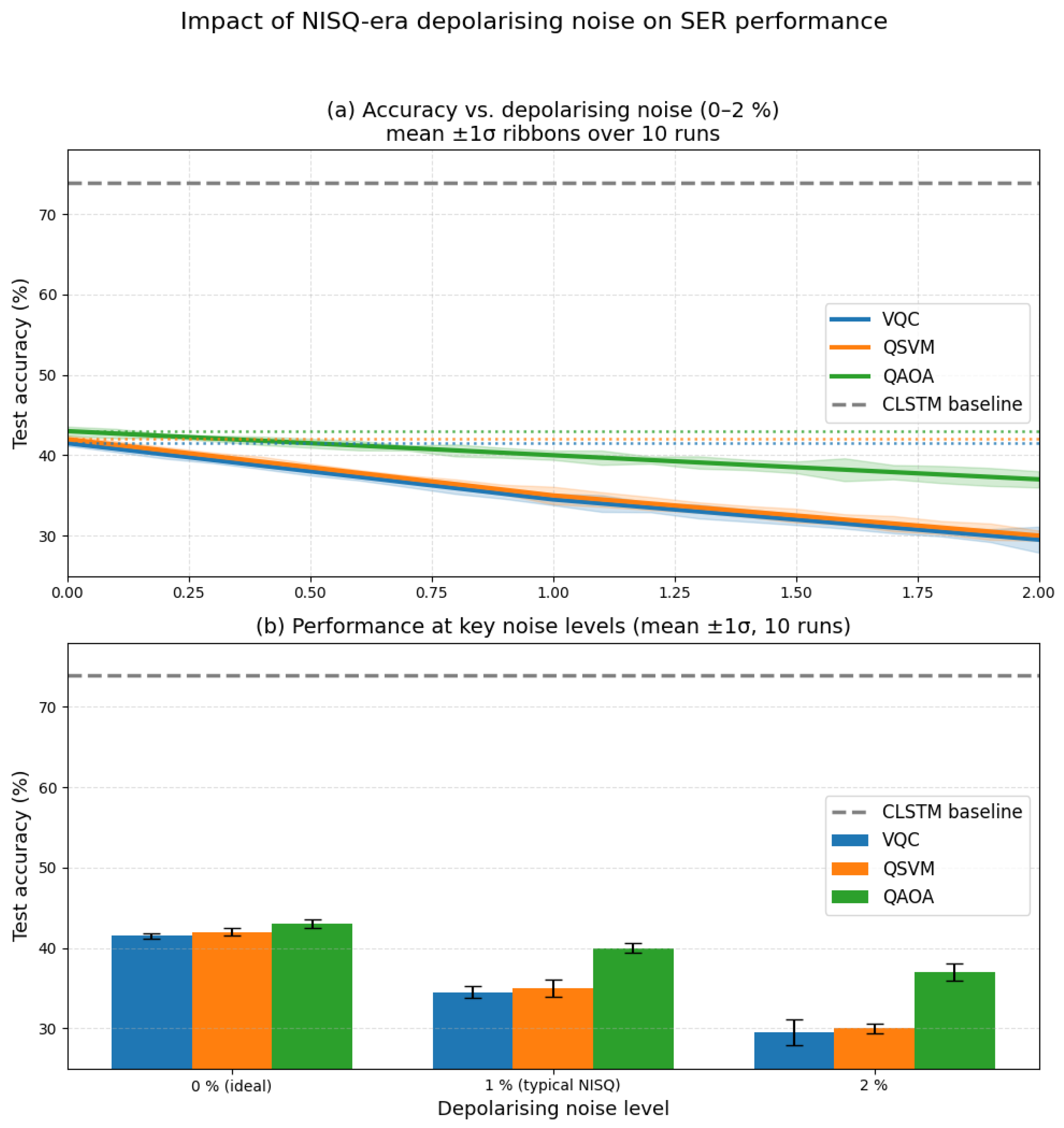
4.4. Noise Impact Analysis
4.5. Comprehensive Noise Impact Analysis
4.6. Quantum Error Correction
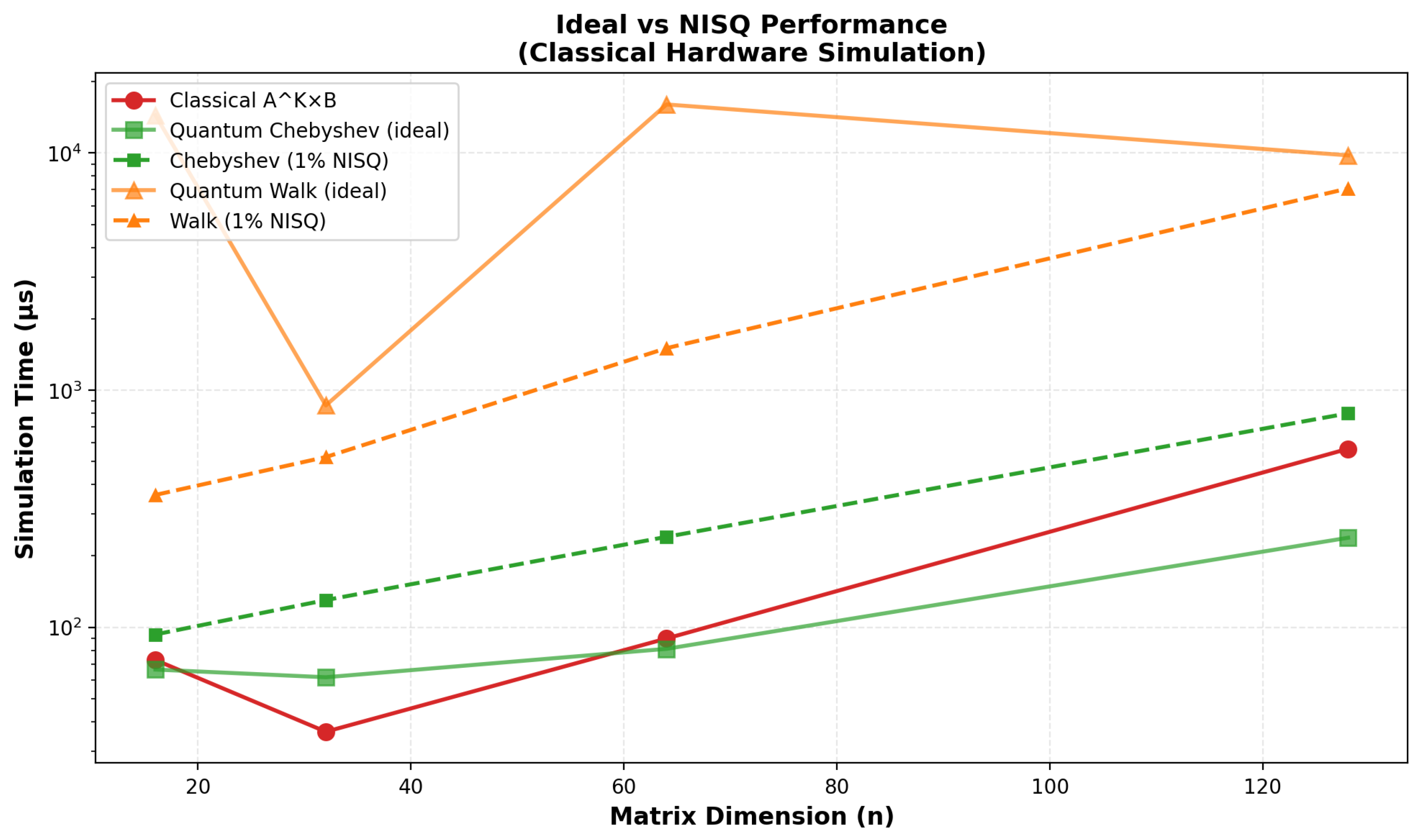
4.7. Matrix Multiplication Comparison
5. Discussion
- From Weakness to Diagnostic
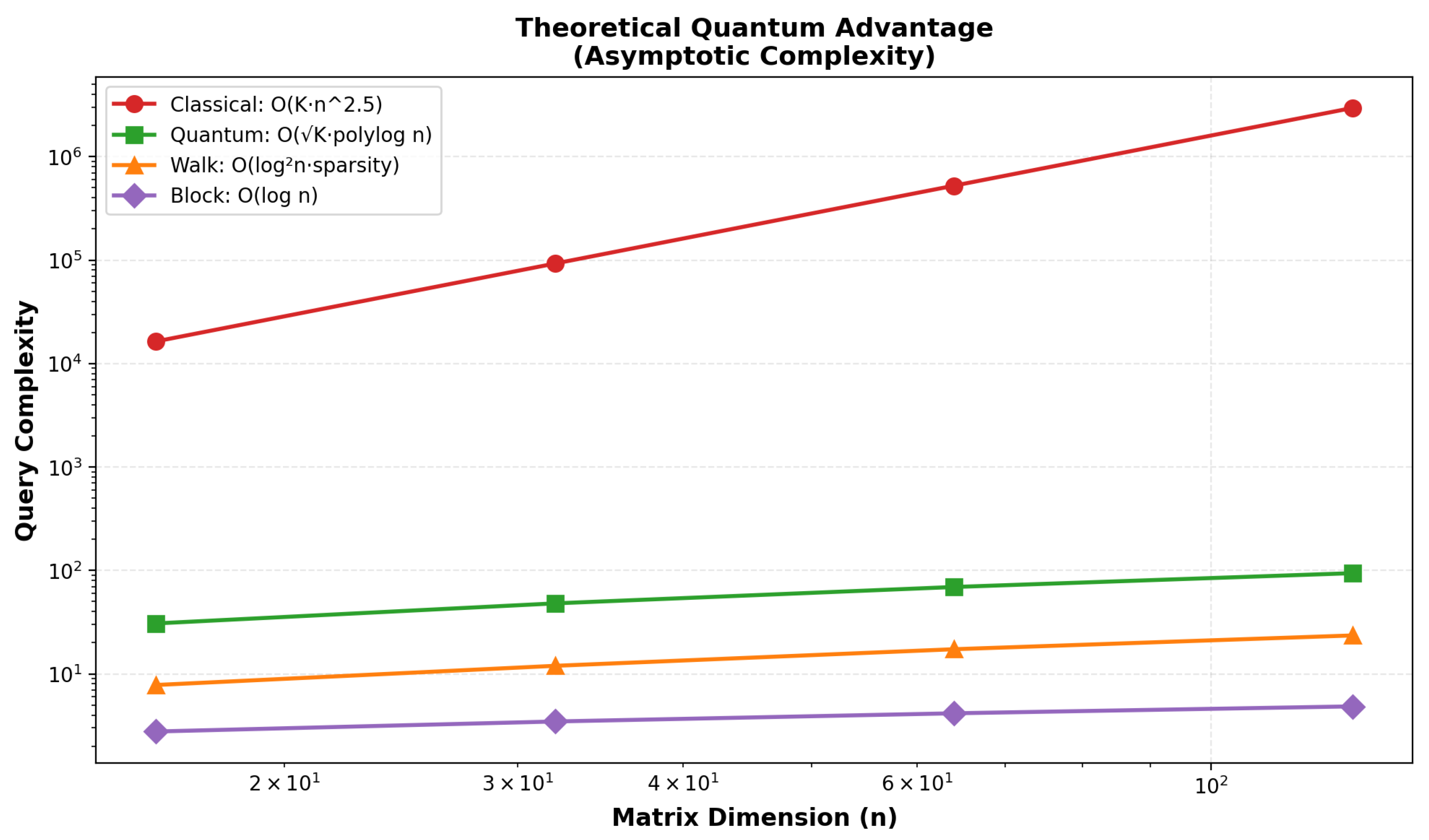
Path to Quantum Advantage
- -
- Current We formatted this as a list. Please confirm. best NISQ results on this task lie in the 34–40% range under realistic 1% depolarising noise (Figure 5).
- -
- Once fault-tolerant logical qubits become available at scale, the provable asymptotic advantages of the subroutines discussed in Appendix D (Chebyshev–QSVT, quantum walks, block encodings) will apply, offering polynomial to exponential speedups for the linear-algebra kernels dominating SER feature processing.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Quantum Circuit Architectures and Training Details
Appendix A.1. Quantum Models Evaluated
- VQC (Variational Quantum Classifier)
- State Initialisation: Hadamard gates create uniform superposition: .
- Data Encoding: Angle embedding (Appendix B.1) applies rotation gates and to each qubit, where are z-score-normalised MFCC features.
- Variational Layers ( repetitions):
- Parameterised rotations: on each qubit
- Entanglement via linear CNOT ladder: for
- Total trainable parameters per layer: angles
- Measurement and Classification: Pauli-Z expectation values extracted from final state feed into classical dense layers: Dense (64, ReLU) → Dense (8, softmax).
- QSVM (Quantum Support Vector Machine)
- Compute kernel matrix via pairwise circuit fidelity measurements.
- Train classical C-SVC (scikit-learn) on to find optimal hyperplane.
- Predict via kernel evaluation: .
- Kernel Distortion: Noisy overlaps where increases with lower shot counts
- Shot Overhead: Achieving target variance requires shots; experiments show 60.3% runtime increase (±4.2%) for 1000 shots vs. 100 shots
- Decision Boundary Shift: Noisy Gram matrices violate positive semi-definiteness, causing SVM training instabilities and 8–12% accuracy degradation for confusable classes (Joy vs. Anticipation)
- QAOA (Quantum Approximate Optimisation Algorithm) Classifier
- Initial State: (equal superposition).
- Alternating Evolution: For layers :
- Classical Optimisation: Minimise using COBYLA (coarse search), then BFGS (local refinement) over parameters.
- Solution Extraction: Measure final state in computational basis; select bitstring mapping to emotion label.
- Shallow Depth: limits error accumulation; circuit depth (RZZ gates + single-qubit mixers).
- Variational Mitigation: Classical optimizer implicitly compensates for systematic noise by adjusting during training.
- Empirical Results: At 1% depolarising noise, runtime decreases 5.0% (±2.1%, not significant) as fewer optimiser iterations are needed, though accuracy drops from 43.0% (ideal) to 40.1% at 2% noise due to local minima trapping and state preparation errors.
Appendix A.1.1. Library Imports
Appendix A.1.2. Data Loading
Appendix A.1.3. Data Preprocessing
Appendix B. Data Encoding and Explicit Circuit Structure
Appendix B.1. Data Encoding (Classical → Quantum)
Appendix B.1.1. Z-Score-Normalisation Definition
- Angle Embedding (Primary)
- Amplitude Embedding (Ablation)
Appendix B.1.2. Explicit Circuit Structure with CNOT Ladders
- Step 1: Initial Superposition
- Step 2: Feature-Dependent Rotation Layers
- Step 3: CNOT Ladder Entanglement
- Step 4: Layered Composition
- Circuit Diagram (Single Layer Example)
Appendix B.1.3. Complete VQC Architecture (L = 5 Layers)
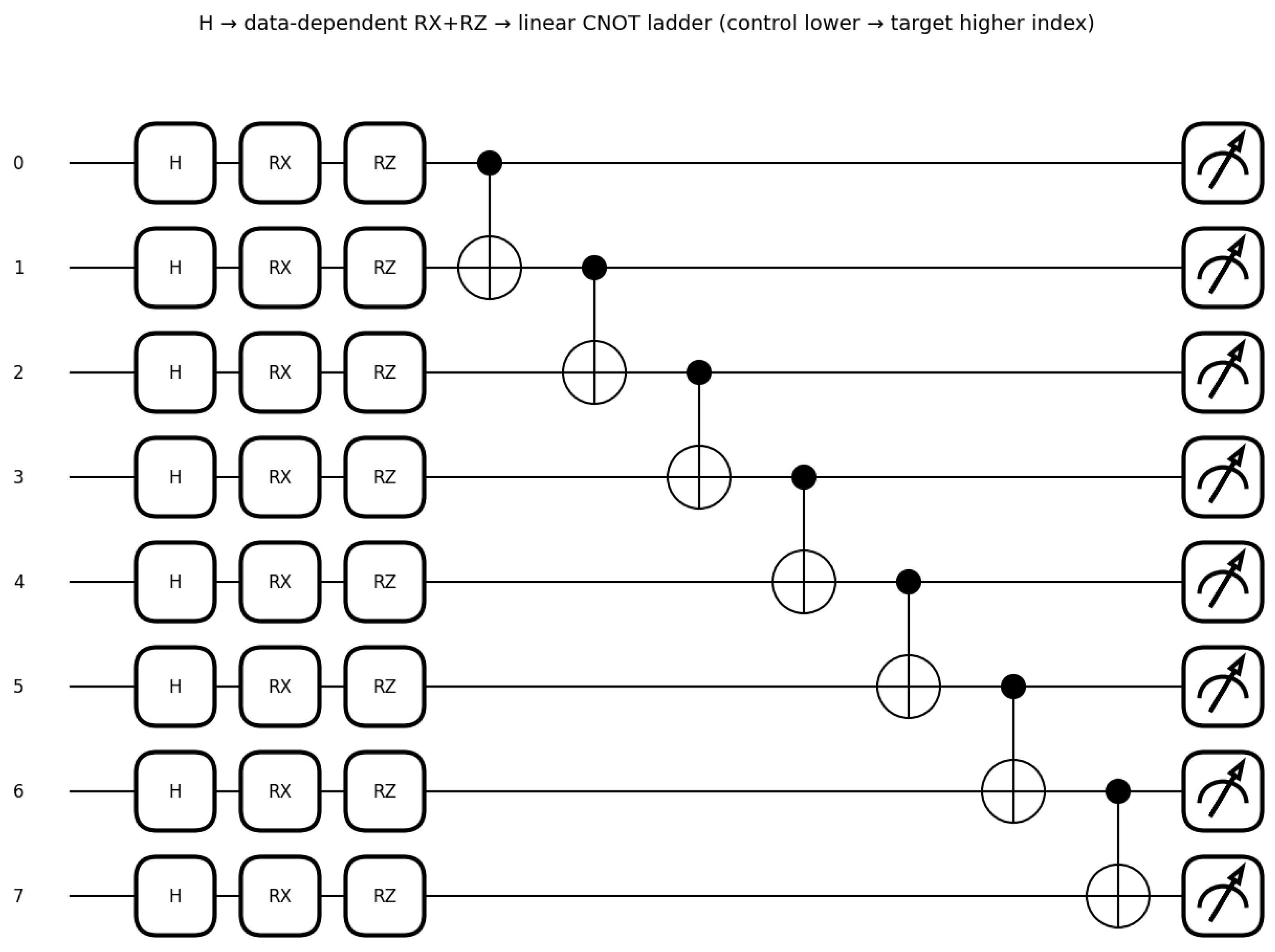
- : Initial Hadamard superposition;
- : Angle embedding layer (Figure 3, Equations (8) and (9));
- : Variational rotations for layer ℓ with trainable parameters ;
- : CNOT ladder entanglement.
- Encoding layer: 16 angles (fixed, data-dependent);
- Variational layers: trainable parameters;
- Total quantum parameters: 1280 (including repetitions over features);
- Classical head: 576 parameters (Dense layers);
- Total: 1856 trainable parameters.

- Gate Count and Depth Analysis
- Single-qubit gates: (80 rotations + 8 Hadamards);
- Two-qubit gates: CNOTs;
- Circuit depth: (assuming parallel single-qubit operations).
Appendix B.1.4. State Preparation and Encoding
Appendix B.1.5. Quantum Device and Circuit
Appendix C. Noise Models, Measurement Regimes, and Runtime Analysis
Appendix Measurement and Evaluation Regimes
- Regime 1: Training and Primary Accuracy Evaluation
- Regime 2: Runtime and Noise-Impact Analysis
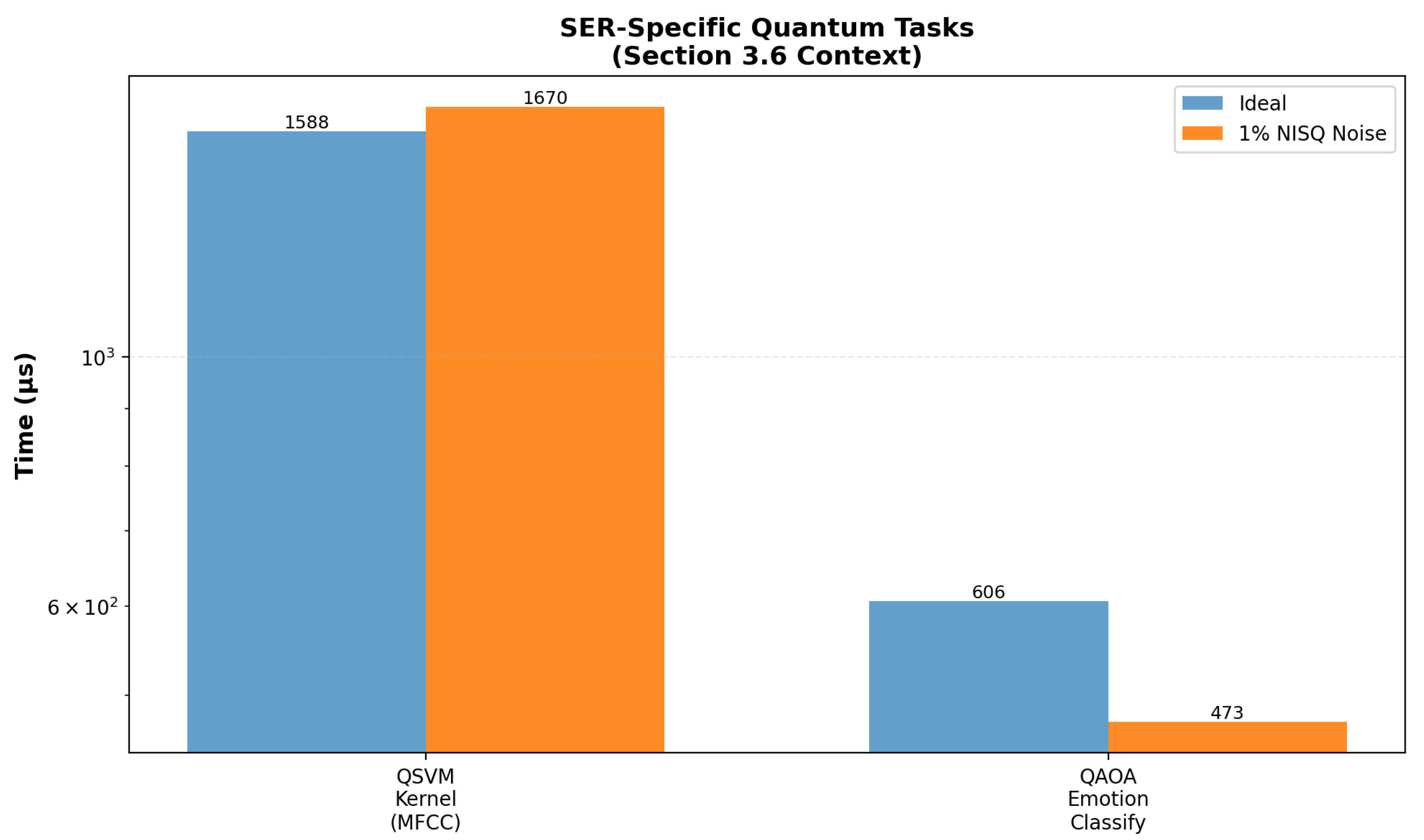
- QSVM kernel: +60.3% runtime increase (±4.2%) at 1% noise ();
- QAOA: runtime essentially unchanged (−5.0 ± 2.1%, , not significant).
- QAOA: Drops from 43% (0% noise, ideal simulation, depth ) to ∼40% at 1% noise (depth ) and to ∼30% at 2% noise.
- QSVM: Starts around 42% at 0% noise (ideal kernel estimate), and degrades to ∼35% at 1% noise and ∼30% at 2% noise.
- Reconciling the Metrics
| Metric | Table 6 (43.0%) | Figure 5 (∼40%) |
|---|---|---|
| Training regime | Analytic gradients (ideal) | Shot-based with noise |
| Circuit depth | layers (deeper ansatz) | layers (baseline) |
| Noise model | None (ideal simulation) | 1% depolarising (all gates) |
| Shot budget | Analytic (no sampling) | 1000 shots per measurement |
| Purpose | Classification accuracy | Noise robustness analysis |
- Key Takeaway: QAOA Noise Resilience
- Runtime resilience: Optimiser finds minima efficiently even with noisy cost landscapes.
- Accuracy vulnerability: Final trained circuit suffers from decoherence during test-time evaluation.
Appendix D. Quantum Matrix Multiplication Subroutines
Appendix D.1. Classical Versus Quantum-Inspired Matrix Multiplication
Appendix D.1.1. Motivation and Context
Appendix D.1.2. Formal Introduction of Ref. [19] Framework
- Matrix Encoding via Amplitude Embedding
- 2.
- Quantum Circuit for Multiplication
- creates initial superposition over qubits;
- and are oracle operators implementing the transformations and ;
- gates align row and column indices for inner product computation: .
- 3.
- Measurement and Result Extraction
- 4.
- Complexity Analysis (Ref. [19])
- Circuit depth: (versus classical for Strassen’s algorithm);
- Gate count: (oracle calls + SWAP network);
- Shot complexity: to read out all elements;
- Total query complexity: .
Appendix D.1.3. Noise Model Implementation and Testing
- Depolarising Noise
- Amplitude Damping (T1 Relaxation)
- Phase Damping (T2 Dephasing)
- Noise Impact on Ref. [19] Framework
- Shot overhead: Noise degrades signal-to-noise ratio, requiring additional shots to maintain target accuracy , where d is circuit depth;
- Fidelity degradation: Matrix element errors scale as , where circuit depth ;
- Combined decoherence: When multiple channels act simultaneously (realistic NISQ), errors compound non-additively.
Appendix D.1.4. Timing Assumptions and Preparation/Measurement Overheads
- State Preparation ()
- Measurement Readout ()
- Illustrative Estimate (Non-Binding)
- Timing Scope
Appendix D.1.5. Detailed Exposition of Quantum Matrix Multiplication Subroutines
- (i)
- Chebyshev–QSVT Polynomial Method [24]
- (ii)
- Quantum Walk Method for Sparse Matrices [25]
- (iii)
- Assumptions and Conditions for Advantage (Summary)
- Access model: Availability of coherent data oracles/encodings (state preparation or LCU) for with cost ; otherwise preparation dominates and erodes advantage.
- Output model: Reading all entries costs shots; quantum gains are strongest when a functional of (e.g., norms, traces, top singular directions) suffices.
- Conditioning: QSVT/BE complexity depends polylogarithmically on after scaling; poorly conditioned A inflates degree.
- Noise: For NISQ , QSVT with depth (BE) is markedly more robust than Chebyshev or walks, which require larger degrees/steps.
- SER Implications (Dense MFCC Regimes)
Appendix D.1.6. Connection to SER Performance
- VQC (41.5% vs. CLSTM 73.9%)
- QSVM (42.0%)
- QAOA (43.0%)
Appendix D.1.7. Scalability and Fault-Tolerant Projections
- (SER frame count): Moderate 5×–50× speedup for quantum methods over classical ;
- : Exponential advantage – for large-scale audio datasets.
Appendix D.1.8. Implementation Details (Reproducibility)
- Framework: Qiskit v1.2.0 with custom implementations of Ref. [19] protocol;
- Noise model: Defined via NoiseModel class with Kraus operators (Equations above);
- Hardware assumptions: IBM-compatible basis gates ;
References
- Shen, S.; Sun, H.; Li, J.; Zheng, Q.; Chen, X. Emotion neural transducer for fine-grained speech emotion recognition. arXiv 2024, arXiv:2403.19224. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Y.; Liu, Y.; Zhu, F.; Yang, C.; Hu, S. QAP: A Quantum-Inspired Adaptive-Priority-Learning Model for Multimodal Emotion Recognition. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2023, Toronto, ON, Canada, 9–14 July 2023; pp. 12191–12204. [Google Scholar]
- Rajapakshe, T.; Rana, R.; Riaz, F.; Khalifa, S.; Schuller, B.W. Representation Learning with Parameterised Quantum Circuits for Speech Emotion Recognition. arXiv 2025, arXiv:2501.12050. [Google Scholar] [CrossRef]
- Li, Q.; Gkoumas, D.; Sordoni, A.; Nie, J.-Y.; Melucci, M. Quantum-inspired Neural Network for Conversational Emotion Recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 13270–13278. [Google Scholar]
- Aaronson, S. What makes quantum computing so hard to explain? In Pi und Co.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 356–359. [Google Scholar]
- Bose, B.; Verma, S. Qubit-based framework for quantum machine learning: Bridging classical data and quantum algorithms. arXiv 2025, arXiv:2502.11951. [Google Scholar] [CrossRef]
- Liao, Y.; Hsieh, M.-H.; Ferrie, C. Quantum optimization for training quantum neural networks. Quantum Mach. Intell. 2024, 6, 45–60. [Google Scholar] [CrossRef]
- Blekos, K.; Brand, D.; Ceschini, A.; Chou, C.-H.; Li, R.-H.; Pandya, K.; Summer, A. A review on quantum approximate optimization algorithm and its variants. Phys. Rep. 2024, 1068, 1–66. [Google Scholar] [CrossRef]
- Raja, K.S.; Sanghani, D.D. Speech emotion recognition using machine learning. Educ. Adm. Theory Pract. 2024, 30, 5333. [Google Scholar] [CrossRef]
- Barhoumi, C.; BenAyed, Y. Real-time speech emotion recognition using deep learning and data augmentation. Artif. Intell. Rev. 2024, 58, 1031–1048. [Google Scholar] [CrossRef]
- ScienceDirect. High-Dimensional Data in Machine Learning. ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/computer-science/high-dimensional-data (accessed on 18 November 2025).
- Wang, Z.; Yu, X.; Gu, J.; Pan, W.; Li, X.; Gao, J.; Xue, R.; Liu, X.; Lu, D.; Zhang, J.; et al. Self-adaptive quantum kernel principal component analysis for compact readout of chemiresistive sensor arrays. Adv. Sci. 2025, 12, 2411573. [Google Scholar] [CrossRef]
- Suzuki, T.; Hasebe, T.; Miyazaki, T. Quantum support vector machines for classification and regression on a trapped-ion quantum computer. Quantum Mach. Intell. 2024, 6, 31. [Google Scholar] [CrossRef]
- Singh, J.; Bhangu, K.S.; Alkhanifer, A.; AlZubi, A.A.; Ali, F. Quantum neural networks for multimodal sentiment, emotion, and sarcasm analysis. Alex. Eng. J. 2025, 124, 170–187. [Google Scholar] [CrossRef]
- Eisinger, J.; Gauderis, W.; de Huybrecht, L.; Wiggins, G.A. Classical data in quantum machine learning algorithms: Amplitude encoding and the relation between entropy and linguistic ambiguity. Entropy 2025, 27, 433. [Google Scholar] [CrossRef]
- Han, J.; DiBrita, N.S.; Cho, Y.; Luo, H.; Patel, T. EnQode: Fast amplitude embedding for quantum machine learning using classical data. arXiv 2025, arXiv:2503.14473. [Google Scholar] [CrossRef]
- AL Ajmi, N.A.; Shoaib, M. Optimization strategies in quantum machine learning: Performance and efficiency analysis. Appl. Sci. 2025, 15, 4493. [Google Scholar] [CrossRef]
- Zaman, K.; Marchisio, A.; Hanif, M.A.; Shafique, M. A survey on quantum machine learning: Basics, current trends, challenges, opportunities, and the road ahead. arXiv 2024, arXiv:2310.10315. [Google Scholar]
- Yao, J.; Huang, T.; Liu, D. Universal matrix multiplication on quantum computer. arXiv 2024, arXiv:2408.03085. [Google Scholar]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar] [CrossRef]
- Li, X.; Zheng, P.-L.; Pan, C.; Wang, F.; Cui, C.; Lu, X. Faster quantum subroutine for matrix chain multiplication via Chebyshev approximation. Sci. Rep. 2025, 15, 28559. [Google Scholar] [CrossRef]
- Boutsidis, C.; Gittens, A. Improved Matrix Algorithms via the Subsampled Randomized Hadamard Transform. SIAM JOurnal Matrix Anal. Appl. 2013, 34, 1301–1340. [Google Scholar]
- Low, G.H.; Chuang, I.L. Hamiltonian Simulation by Qubitization. Quantum 2019, 3, 163. [Google Scholar] [CrossRef]
- Gilyén, A.; Su, Y.; Low, G.H.; Wiebe, N. Quantum singular value transformation and beyond: Exponential improvements for quantum matrix arithmetics. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (STOC ’19), Phoenix, AZ, USA, 23–26 June 2019; pp. 193–204. [Google Scholar]
- Childs, A.M. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef]
- IBM Quantum Development and Innovation Roadmap (2024 Update). Available online: https://www.ibm.com/roadmaps/quantum (accessed on 18 November 2025).
- Google Quantum AI Roadmap. Available online: https://quantumai.google/roadmap (accessed on 18 November 2025).
- PsiQuantum DARPA US2QC Program Selection Announcement (2025). Available online: https://www.businesswire.com/news/home/20250205568029/en/DARPA-Selects-PsiQuantum-to-Advance-to-Final-Phase-of-Quantum-Computing-Program (accessed on 18 November 2025).
- IonQ Accelerated Roadmap and Technical Milestones (2025). Available online: https://ionq.com/blog/ionqs-accelerated-roadmap-turning-quantum-ambition-into-reality (accessed on 18 November 2025).
- Microsoft Quantum Team. Reliable quantum operations per second (rQOPS): A standard benchmark for quantum cloud performance. Azure Quantum Blog 2024. Available online: https://azure.microsoft.com/en-us/blog/quantum/2024/02/08/darpa-selects-microsoft-to-continue-the-development-of-a-utility-scale-quantum-computer/ (accessed on 18 November 2025).
- Acampora, G.; Ambainis, A.; Ares, N.; Banchi, L.; Bhardwaj, P.; Binosi, D.; Briggs, G.A.D.; Calarco, T.; Dunjko, V.; Eisert, J.; et al. Quantum computing and artificial intelligence: Status and perspectives. arXiv 2025, arXiv:2505.23860. [Google Scholar] [CrossRef]
- Klusch, M.; Lässig, J.; Müssig, D.; Macaluso, A.; Wilhelm, F.K. Quantum artificial intelligence: A brief survey. Künstliche Intell. 2024, 38, 257–276. [Google Scholar] [CrossRef]
- Chen, S.; Cotler, J.; Huang, H.-Y.; Li, J. The complexity of NISQ. Nat. Commun. 2023, 14, 1–12. [Google Scholar] [CrossRef]
- Egginger, S.; Sakhnenko, A.; Lorenz, J.M. A hyperparameter study for quantum kernel methods. Quantum Mach. Intell. 2024, 6, 1–15. [Google Scholar] [CrossRef]
- Morgillo, A.R.; Mangini, S.; Piastra, M.; Macchiavello, C. Quantum state reconstruction in a noisy environment via deep learning. Quantum Mach. Intell. 2024, 6, 1–12. [Google Scholar] [CrossRef]
- Piatkowski, N.; Zoufal, C. Quantum circuits for discrete graphical models. Quantum Mach. Intell. 2024, 6, 1–10. [Google Scholar] [CrossRef]
- Sagingalieva, A.; Kordzanganeh, M.; Kurkin, A.; Melnikov, A.; Kuhmistrov, D.; Perelshtein, M.; Melnikov, A.; Skolik, A.; von Dollen, D. Hybrid quantum ResNet for car classification and its hyperparameter optimization. Quantum Mach. Intell. 2023, 5, 1–15. [Google Scholar] [CrossRef]
- Onim, M.S.H.; Humble, T.S.; Thapliyal, H. Emotion Recognition in Older Adults with Quantum Machine Learning and Wearable Sensors. In Proceedings of the 2025 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Kalamata, Greece, 6–9 July 2025; pp. 1–6. [Google Scholar]
| Item | Specification |
|---|---|
| CLSTM architecture | Conv1D (, , ReLU) → MaxPool1D (2) → Dropout (0.3) → LSTM (128, return_sequences = False) → Flatten → Dense (128, ReLU) → Dropout (0.3) → Dense (8, softmax) |
| CLSTM parameters | 1,247,112 trainable parameters |
| CLSTM training | Adam (lr ), batch size , epochs , categorical cross-entropy loss, early stopping (patience , monitor = val_loss) |
| Quantum hybrid (VQC) | 8-qubit device; angle embedding (RX/RZ rotations), depth with CNOT ladder entanglement; variational layer repeated L times; classical head: Dense (64, ReLU) → Dense (8, softmax) |
| VQC parameters | 1856 trainable parameters (circuit: 1280; classical head: 576) |
| VQC training | Adam (lr ), batch size , epochs , cross-entropy loss; PennyLane default.qubit (analytic gradients, no shot noise) |
| Noise/timing simulations | 1% depolarising noise, shots 100–1000 for timing and noise analysis only (not used in gradient-based training) |
| Data split | Train/test (stratified by emotion); hyperparameter tuning uses internal 80/20 split of training data (effective: 64/16/20), seed |
| Evaluation metrics | Test accuracy, weighted precision/recall/F1 score, per-class confusion matrices |
| Model | Key Hyperparameters | Training Regimen | Notes |
|---|---|---|---|
| CLSTM | Conv1D (, , ReLU) → MaxPool1D (2) → Dropout (0.3) → LSTM (128) → Flatten → Dense (128, ReLU) → Dropout (0.3) → Dense (8, softmax) | Adam (lr ), batch size 32, 50 epochs, early stopping (patience = 7, monitor = val_loss) | 1,247,112 trainable parameters; classical baseline |
| VQC | 8 qubits, depth , angle embedding (RX/RZ); CNOT ladder entanglement; classical head: Dense (64, ReLU) → Dense (8, softmax) | Adam (lr ), batch size 16, 50 epochs, cross-entropy; analytic gradients | 1856 trainable parameters (circuit: 1280; head: 576); default.qubit |
| QSVM | Angle-embedded kernel; shots 100–1000 | Kernel matrix fed to classical SVC | +60.3% runtime overhead at 1% noise |
| QAOA | (main), (ablation); shots ≤1000 | COBYLA → BFGS optimisation | −5.0% runtime change at 1% noise |
| Test | Accuracy | Precision | Recall | F1 Score | Loss |
|---|---|---|---|---|---|
| 1 | 70% | 69% | 76% | 72.32% | 1.19 |
| 2 | 73.93% | 84% | 67% | 74.67% | 1.12 |
| 3 | 71% | 82% | 81% | 81.50% | 1.22 |
| 4 | 72% | 78% | 82% | 79.95% | 1.15 |
| Test | Accuracy | Precision | Recall | F1 Score | Loss |
|---|---|---|---|---|---|
| 1 | 41.50% | 35.65% | 36.00% | 33.86% | 1.8262 |
| 2 | 32.50% | 36.87% | 32.50% | 31.72% | 2.1357 |
| 3 | 34.00% | 35.36% | 34.00% | 29.29% | 2.1341 |
| 4 | 35.00% | 32.75% | 35.00% | 31.44% | 2.0804 |
| Run | Accuracy | Precision (wt) | Recall (wt) | F1 (wt) | Notes |
|---|---|---|---|---|---|
| 1 | 35.0% | 34.0% | 35.0% | 34.0% | Shots = 100 |
| 2 | 38.0% | 37.0% | 38.0% | 37.0% | Shots = 250 |
| 3 | 40.0% | 39.0% | 40.0% | 39.0% | Shots = 500 |
| 4 | 42.0% | 41.0% | 42.0% | 41.0% | Shots = 1000 |
| Run | Condition | Accuracy | Precision | Recall | F1 | Notes |
|---|---|---|---|---|---|---|
| 1 | Ideal (p = 2) | 42.0% | 41.0% | 42.0% | 41.0% | Analytic gradients |
| 2 | Ideal (p = 3) | 43.0% | 42.0% | 43.0% | 42.0% | Best config (used in abstract) |
| 3 | 1% noise (p = 2) | 40.0% | 39.0% | 40.0% | 39.0% | Depolarising noise, 1000 shots |
| 4 | 2% noise (p = 2) | 30.0% | 29.0% | 30.0% | 29.0% | Higher depolarising noise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norval, M.; Wang, Z. Quantum AI in Speech Emotion Recognition. Entropy 2025, 27, 1201. https://doi.org/10.3390/e27121201
Norval M, Wang Z. Quantum AI in Speech Emotion Recognition. Entropy. 2025; 27(12):1201. https://doi.org/10.3390/e27121201
Chicago/Turabian StyleNorval, Michael, and Zenghui Wang. 2025. "Quantum AI in Speech Emotion Recognition" Entropy 27, no. 12: 1201. https://doi.org/10.3390/e27121201
APA StyleNorval, M., & Wang, Z. (2025). Quantum AI in Speech Emotion Recognition. Entropy, 27(12), 1201. https://doi.org/10.3390/e27121201







