Unveiling Self-Organization and Emergent Phenomena in Urban Transportation Systems via Multilayer Network Analysis
Abstract
1. Introduction
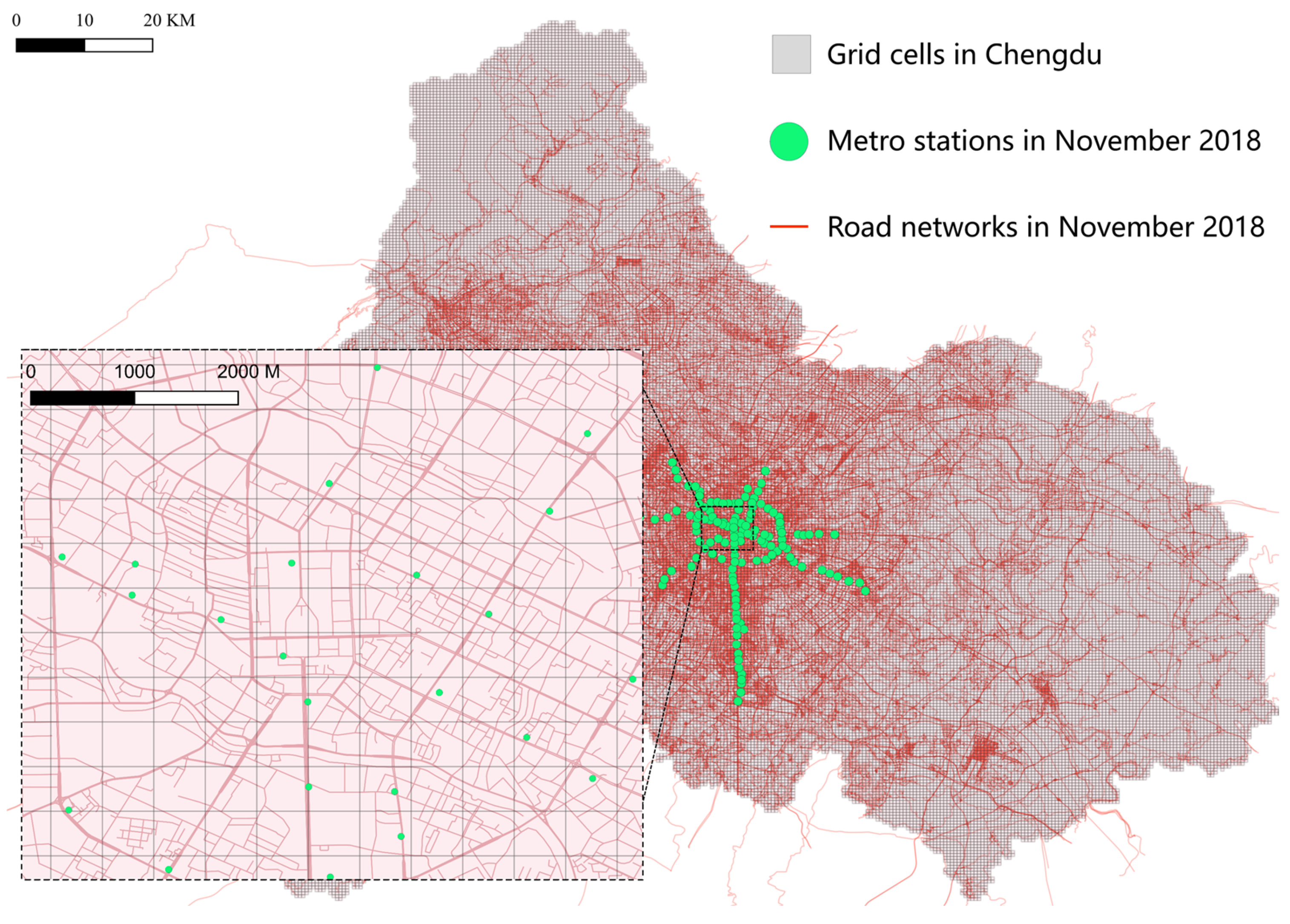
2. Data Preparation and Multilayer Network
2.1. Data Description and Preprocessing
- (1)
- Identifying a single ride: a change in the vehicle status identifier codes of the same vehicle (0 → 1 or 1 → 0) is marked as the start (O) and end (D) of an independent trip event.
- (2)
- Standardization of OD trip units: all passengers within a single ride share the same origin and destination and are considered as a single OD trip unit, where each ride corresponds to one standardized OD trip unit.
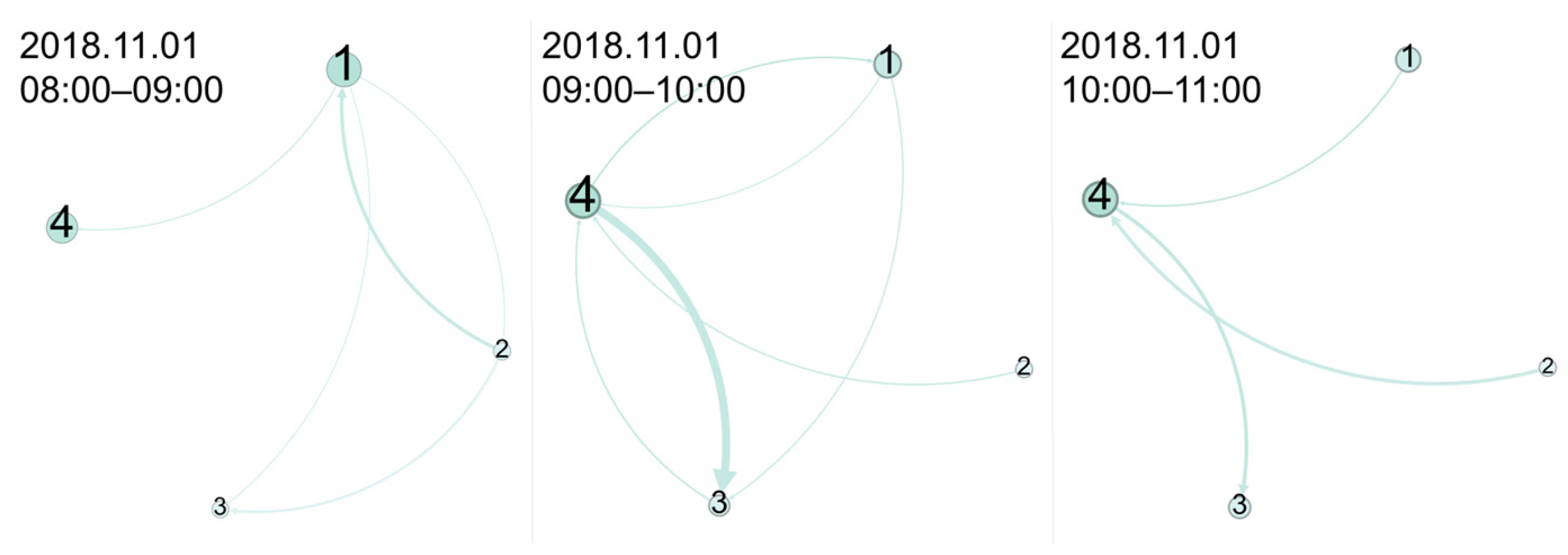
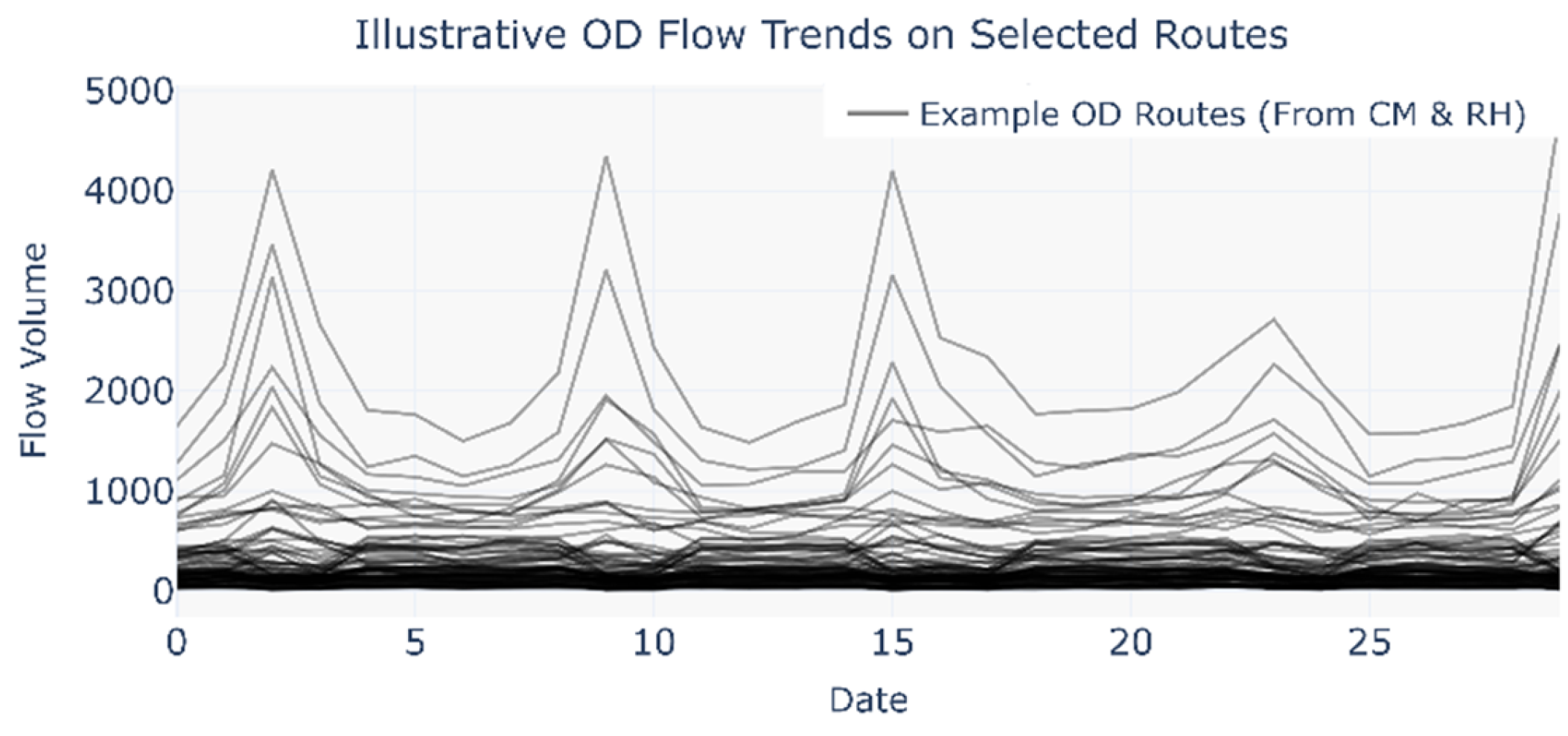
2.2. Temporal Urban Mobility Network
2.2.1. Temporal Chengdu Metro Network (CM)
2.2.2. Temporal Ride-Hailing Network (RH)
- (1)
- Single-station constraint: no road network unit can contain more than one metro station;
- (2)
- Service radius constraint: the side length of each unit should match the service radius (walking accessibility area) of the metro station.
2.2.3. CM&RH Network (O)
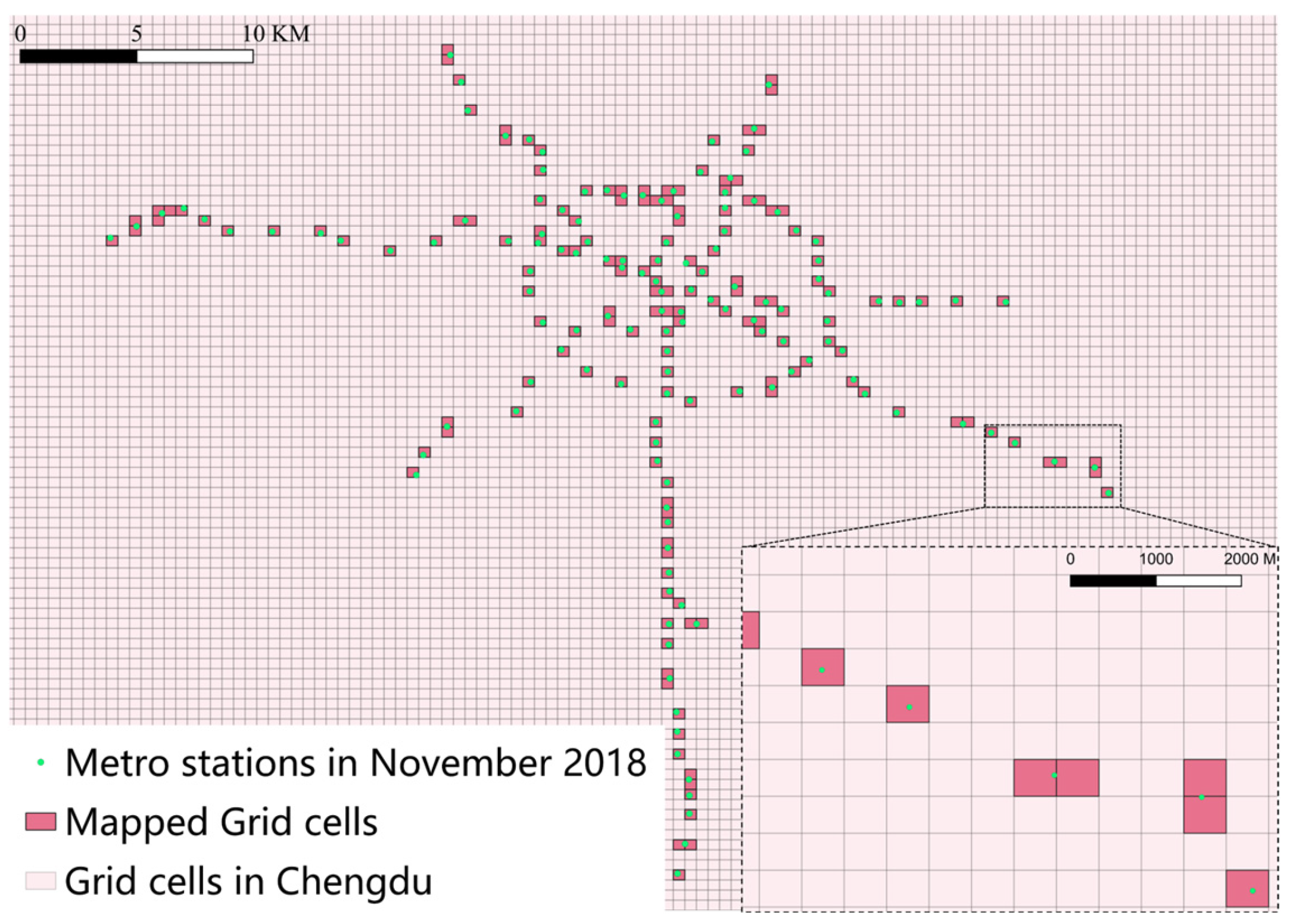
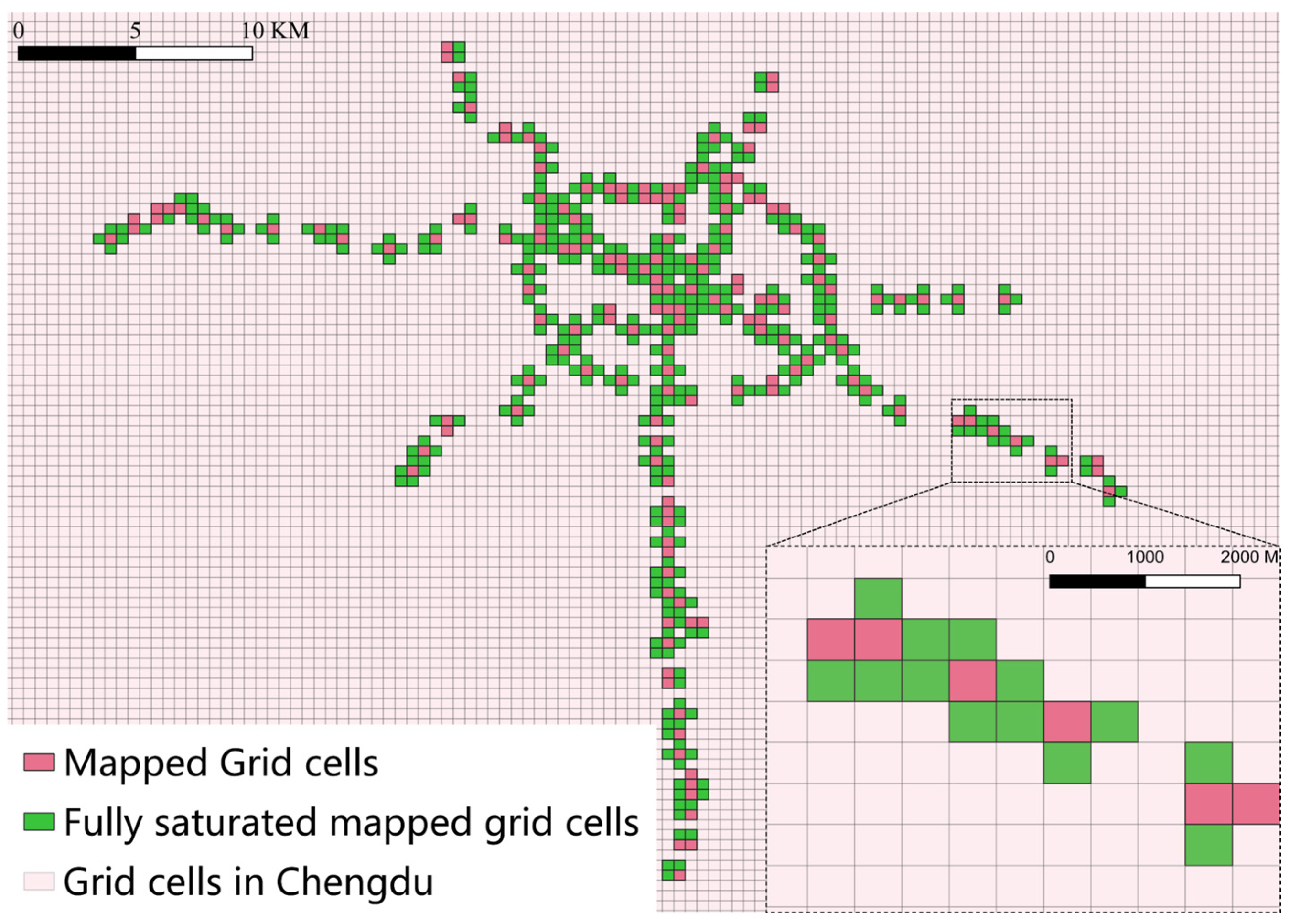
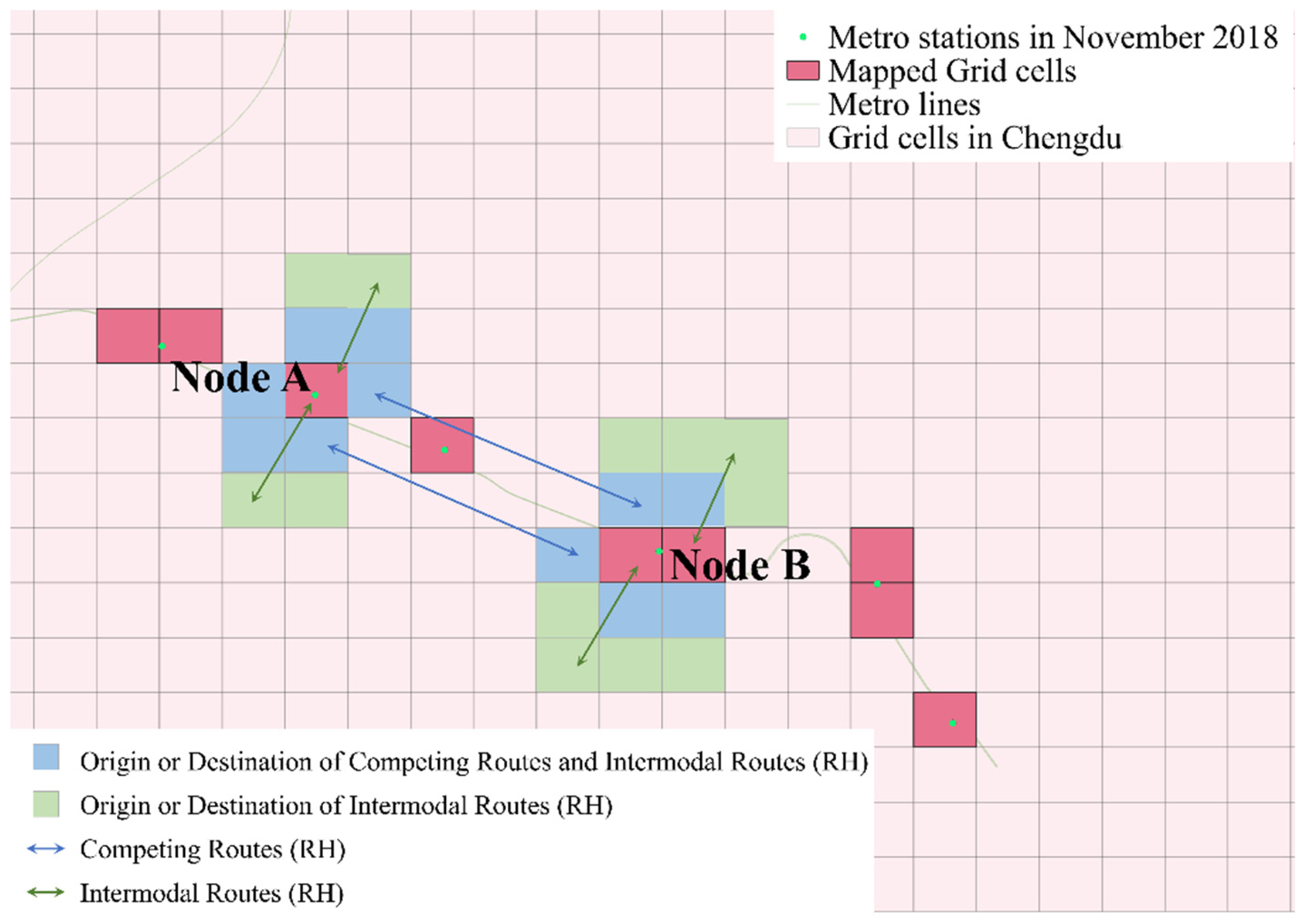
2.3. Mapping Between CM and RH
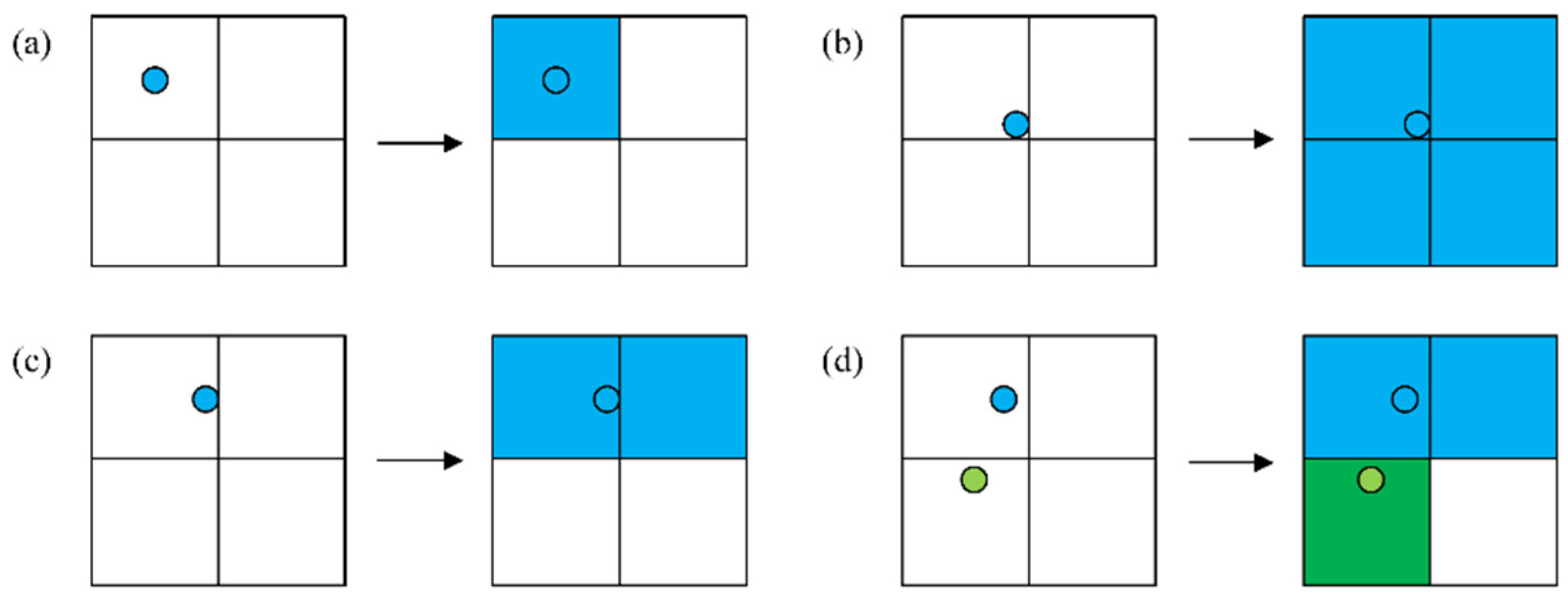
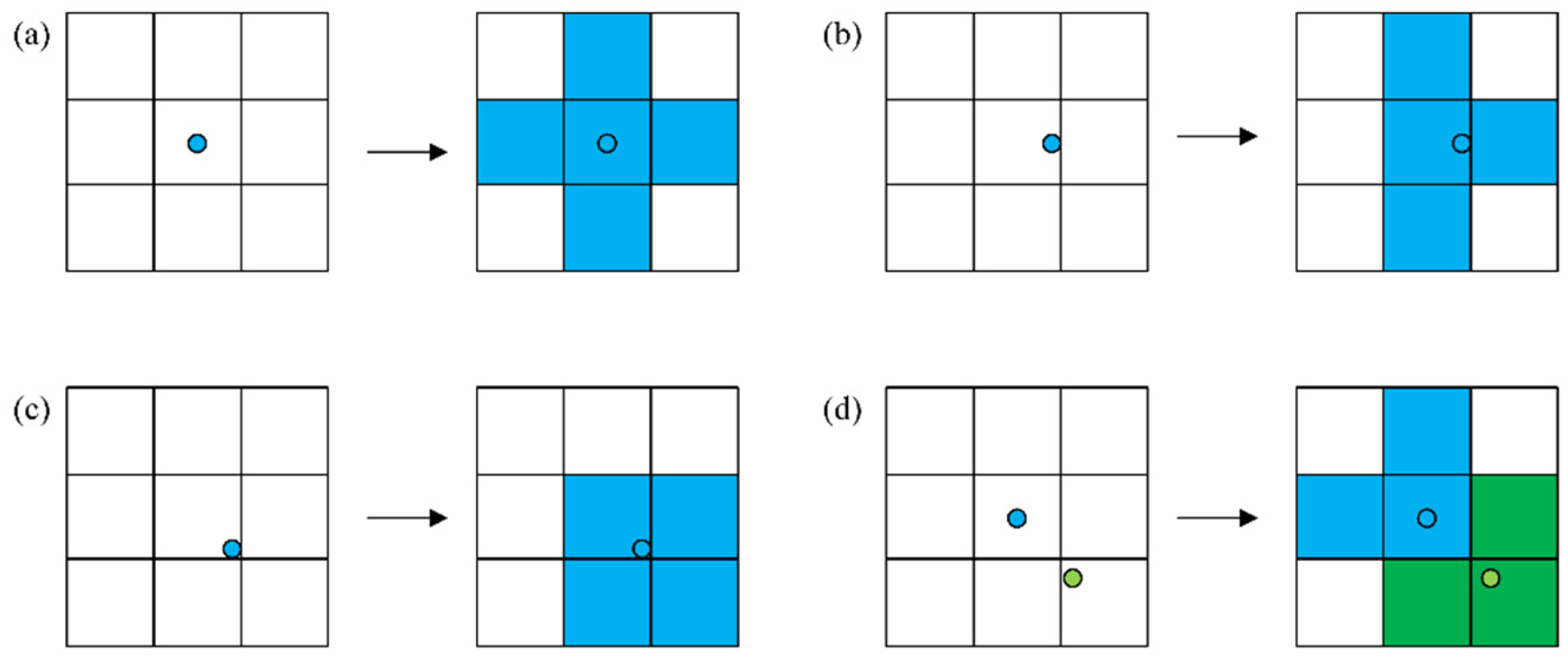
2.3.1. Network Mapping
- (1)
- The central area mapping rule means that when a metro station is situated in the central region (greater than 50 m from the boundary), the station establishes bidirectional topological associations exclusively with its located unit (Figure 3a).
- (2)
2.3.2. Network Mapping Control Group
- (1)
- The central area mapping rule is when a metro station is situated in the central region (greater than 200 m from the boundary); Figure 5a shows the mapping rule.
- (2)
2.4. Potential Intermodal Network (PI)
3. Research Methods
3.1. Uncover Self-Organized Intermodality
3.1.1. Strength Distribution
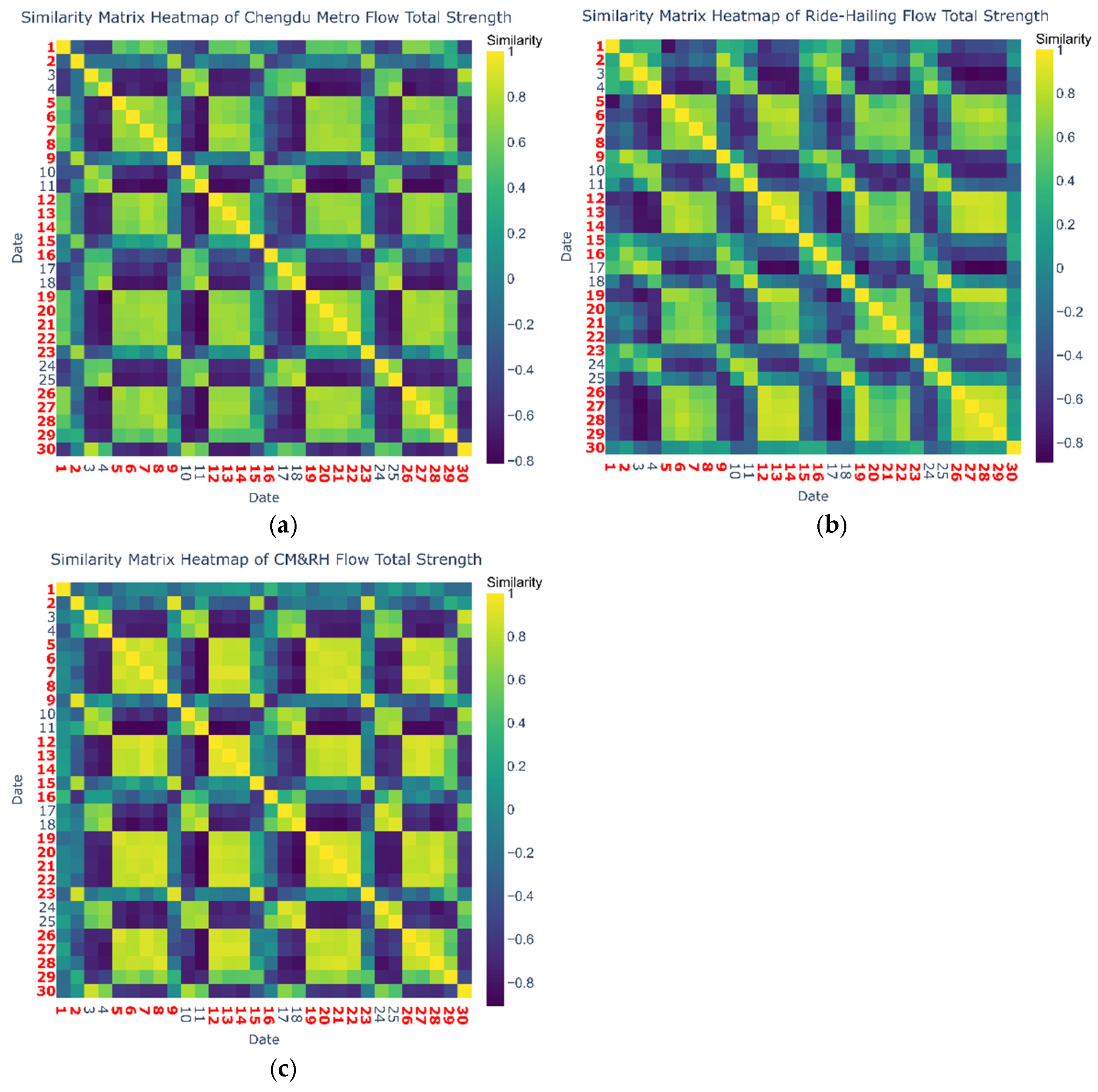
3.1.2. Cosine Similarity
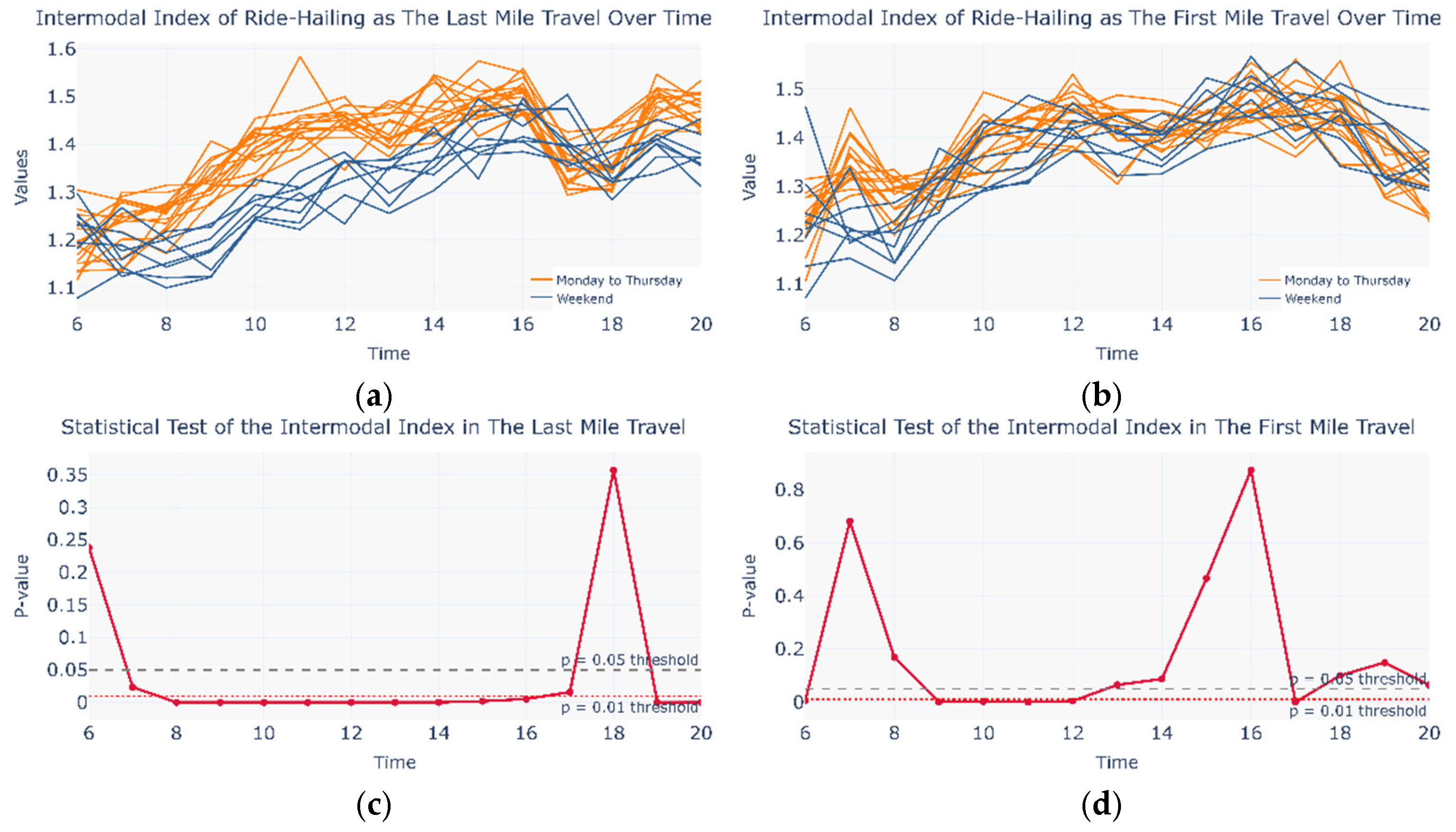
3.1.3. Intermodal Index
3.2. Identify the Key Intermodal Node
3.2.1. Rich-Club Coefficient
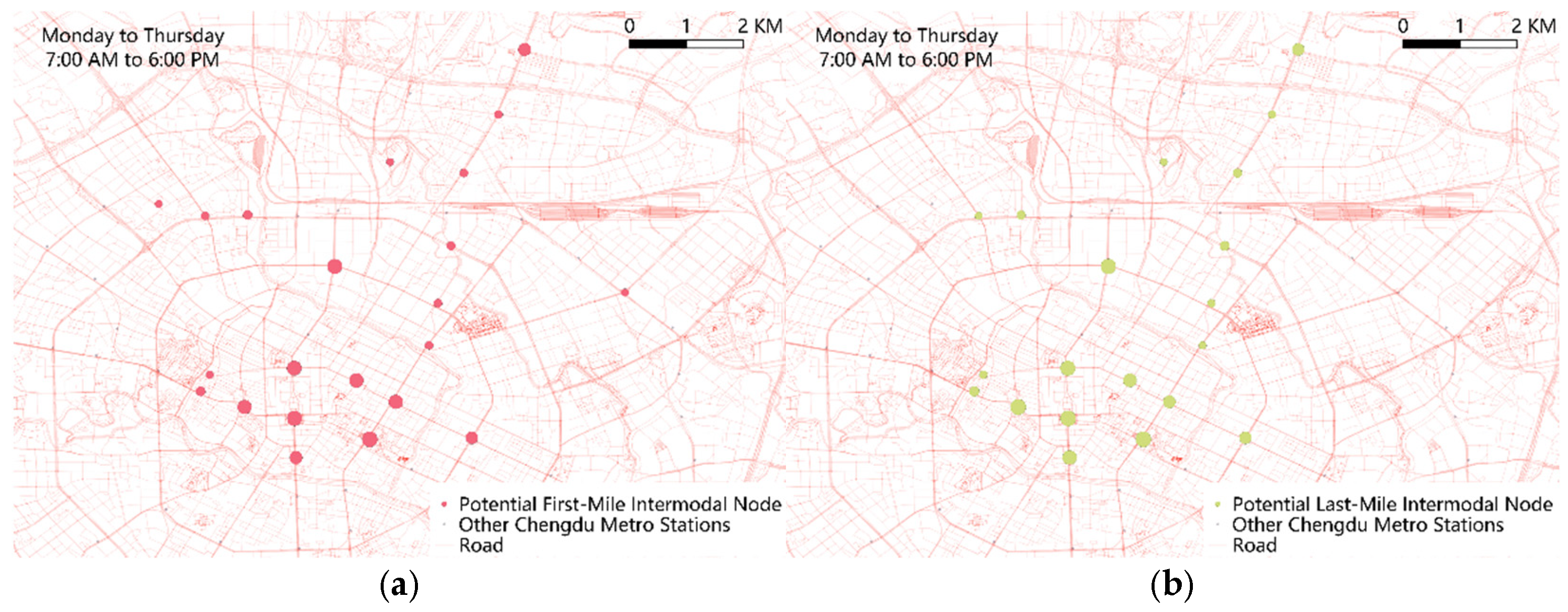
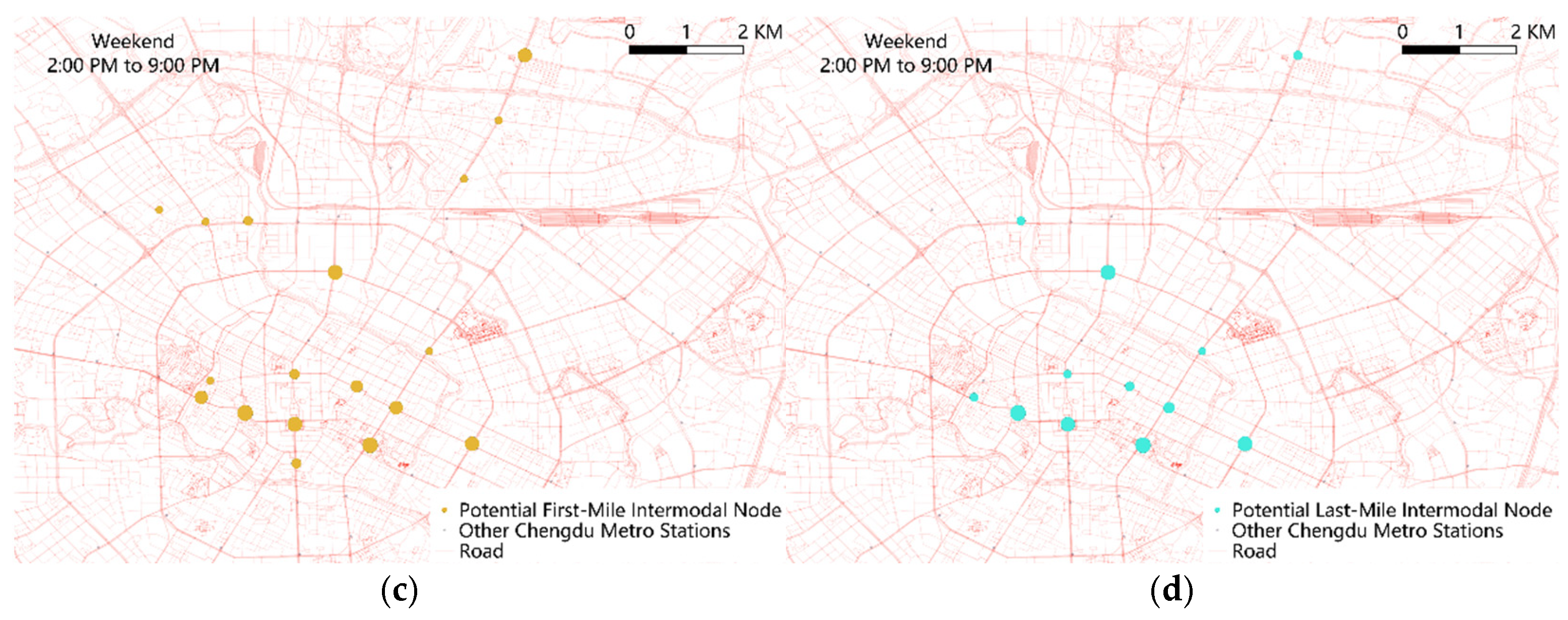
3.2.2. Potential Intermodal Node
3.2.3. Node Importance Coefficient
- (1)
- IC of nodes serving first-mile tasks during commuting periods;
- (2)
- IC of nodes serving first-mile tasks during leisure periods;
- (3)
- IC of nodes serving last-mile tasks during commuting periods;
- (4)
- IC of nodes serving last-mile tasks during leisure periods.
4. Results and Discussion
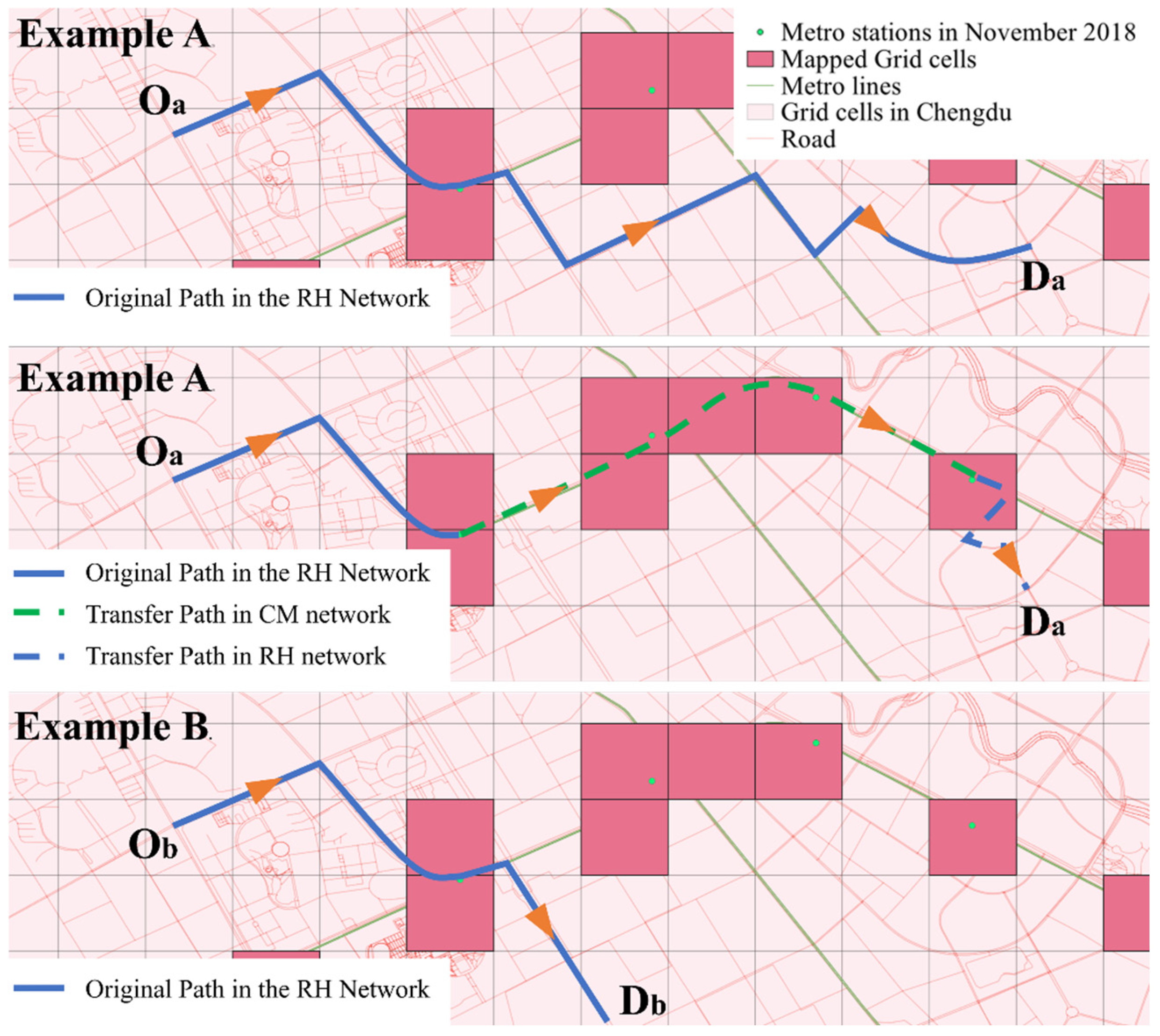
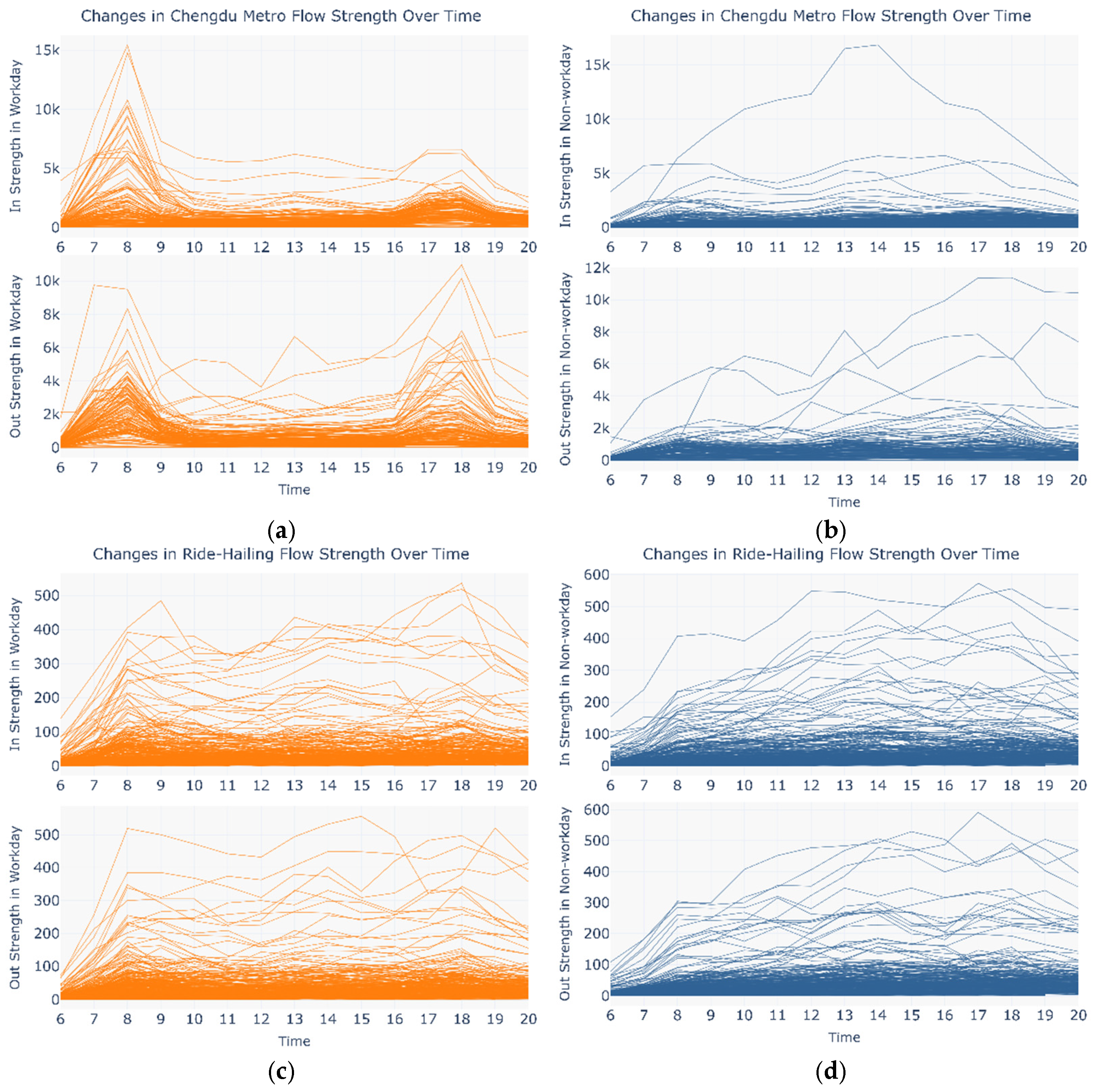
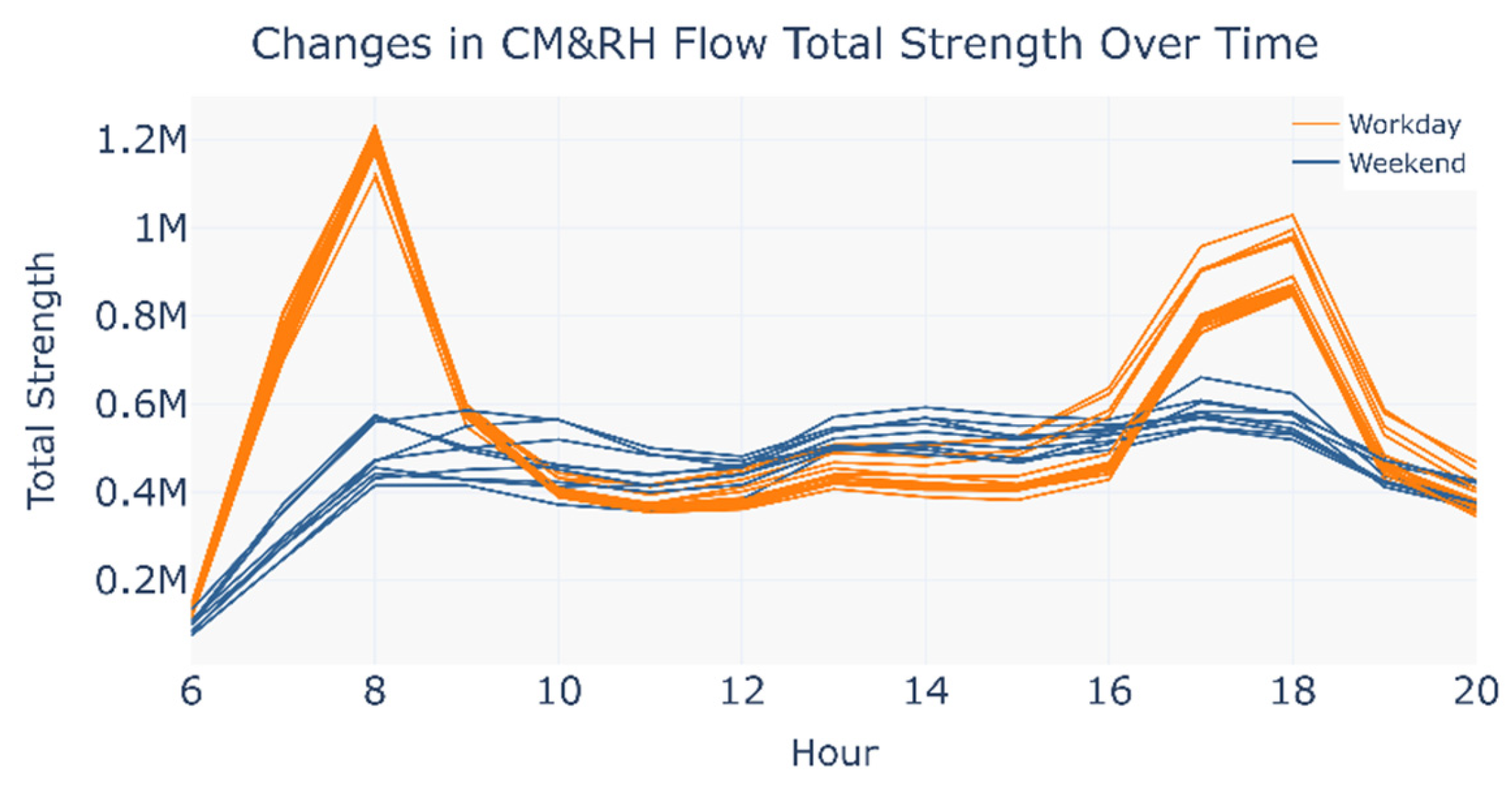
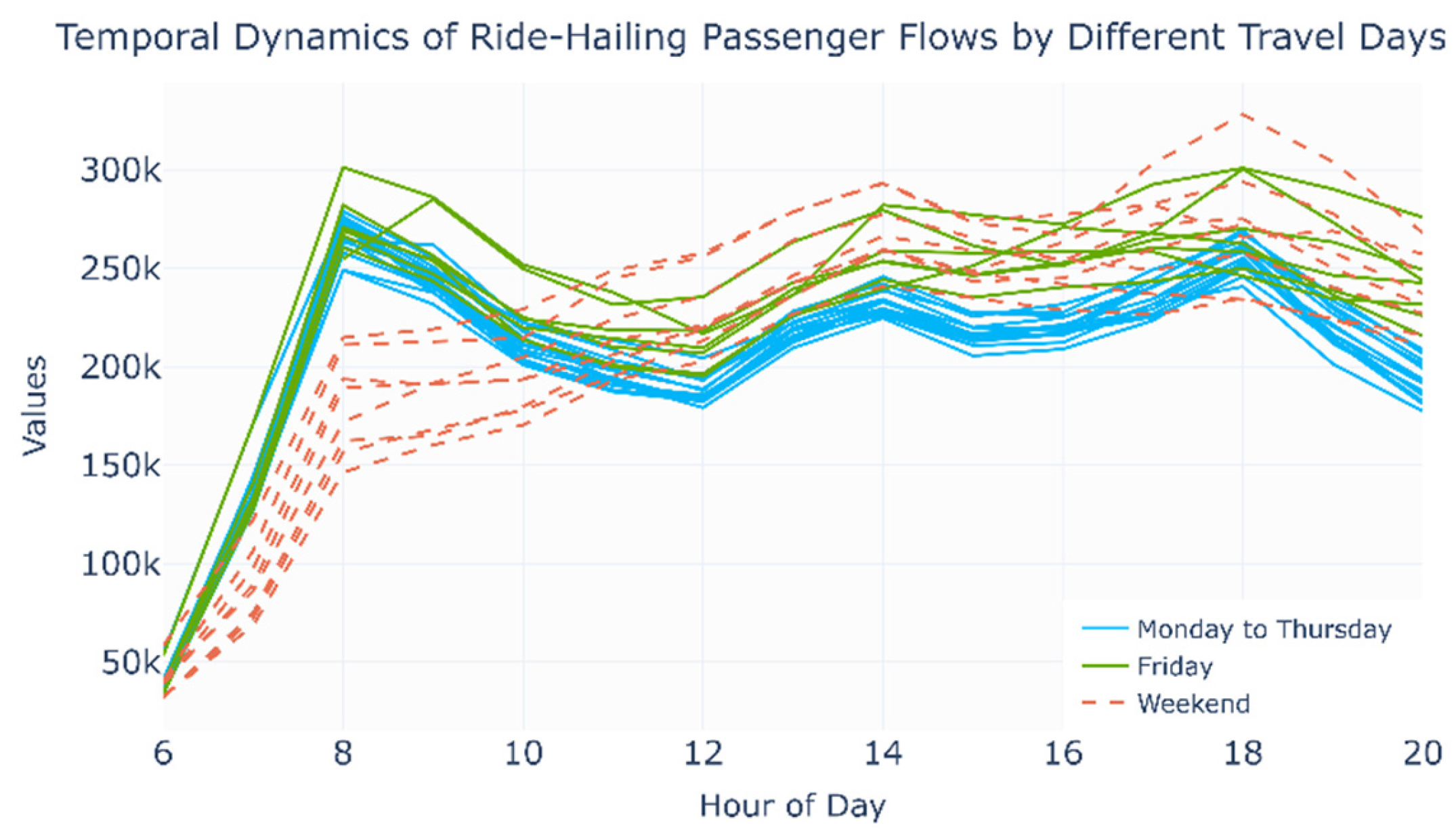
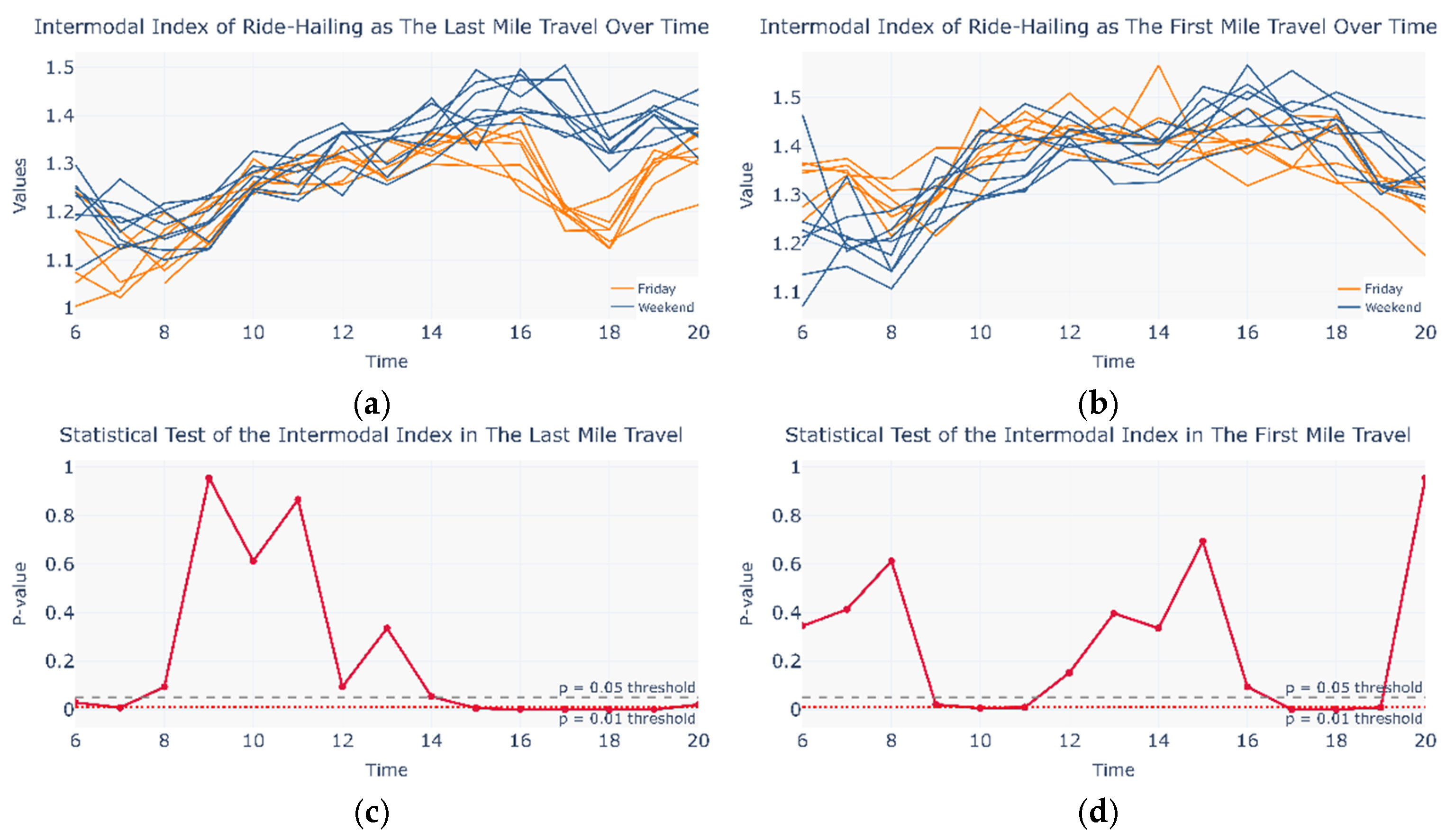
4.1. Emergence of Modal Substitution and the Intermodal Network
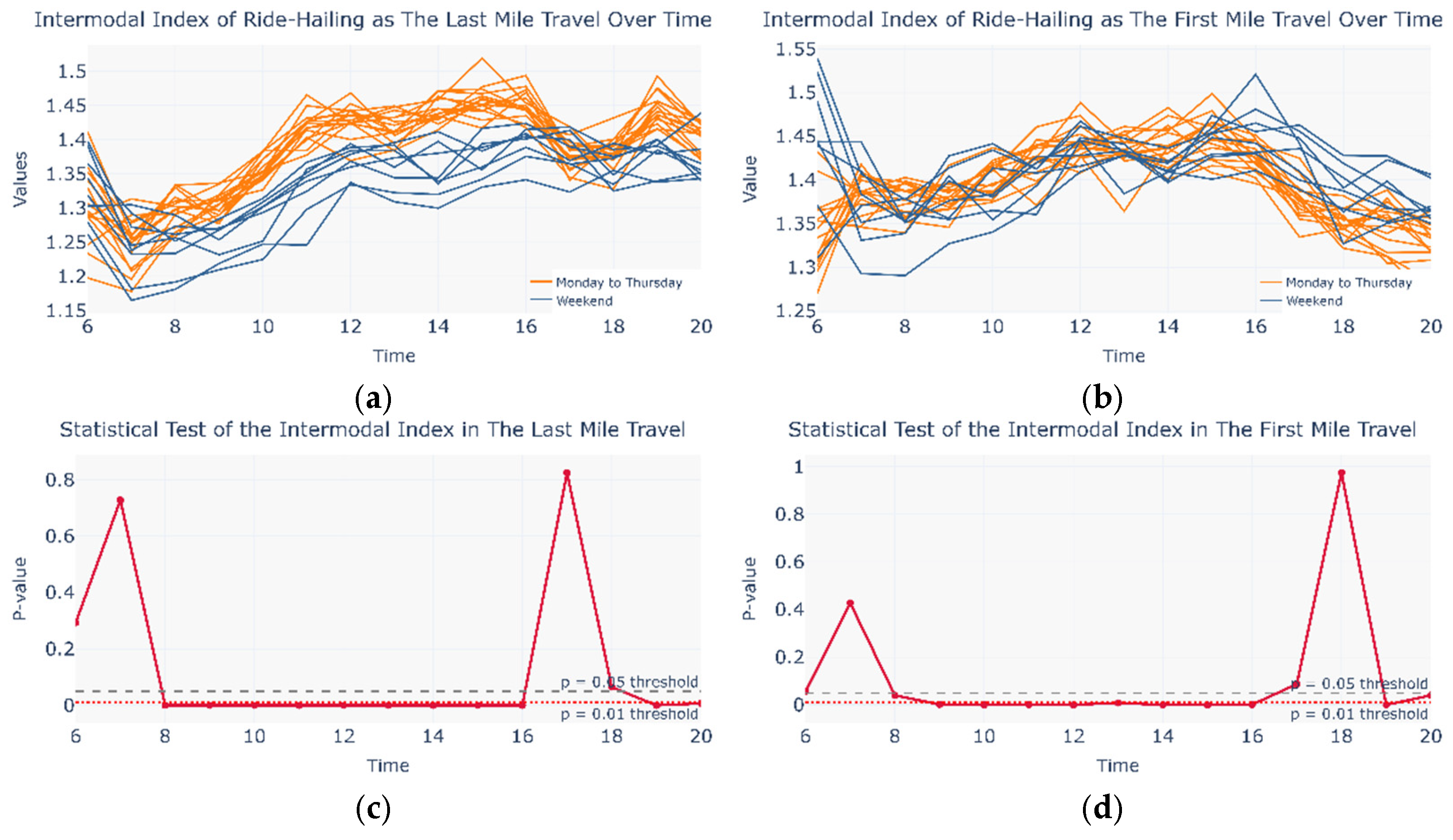
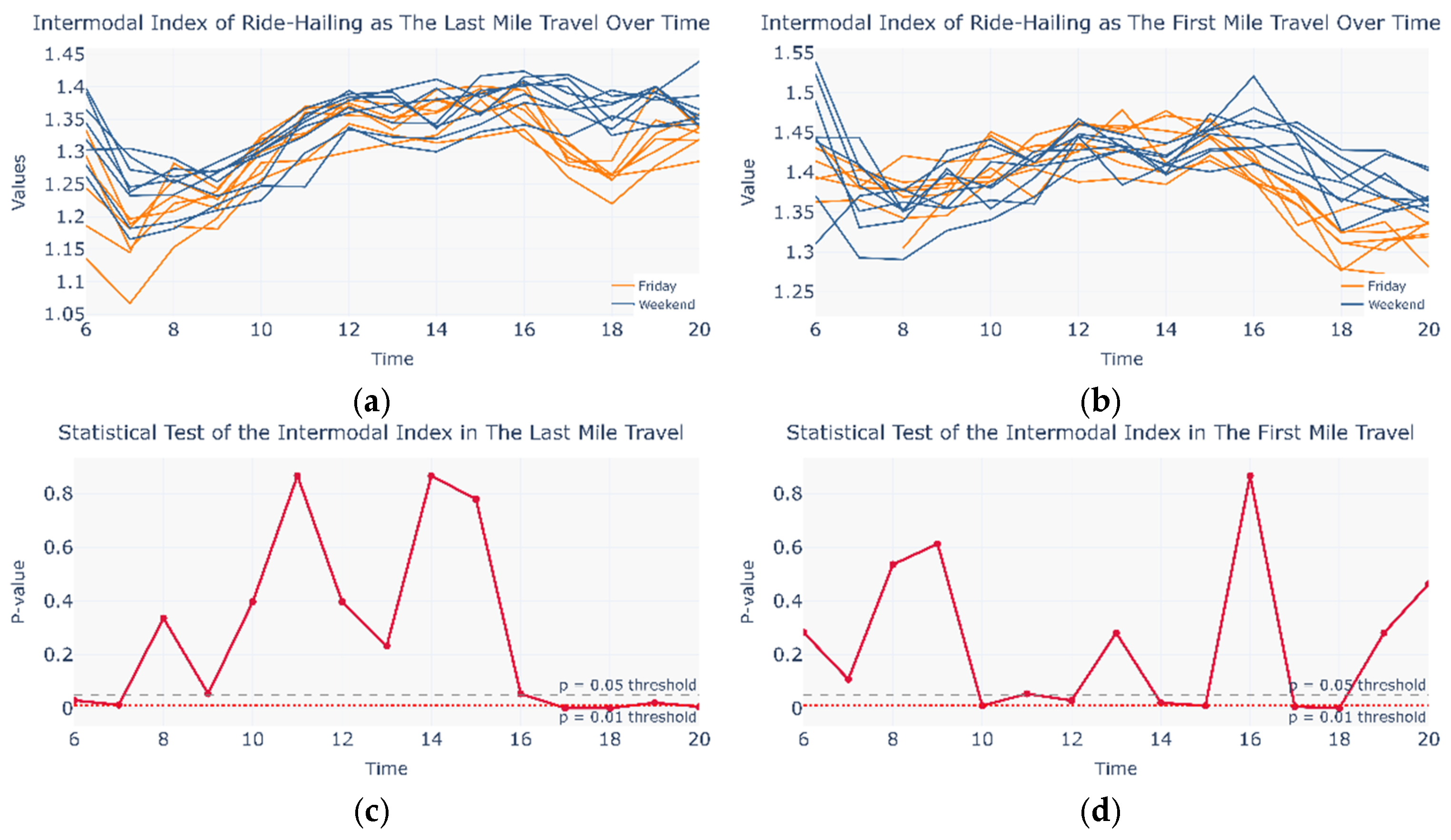
4.2. Sensitivity of the Intermodal Index to Network Mapping Methods
4.3. Identify the Potential Intermodal Node
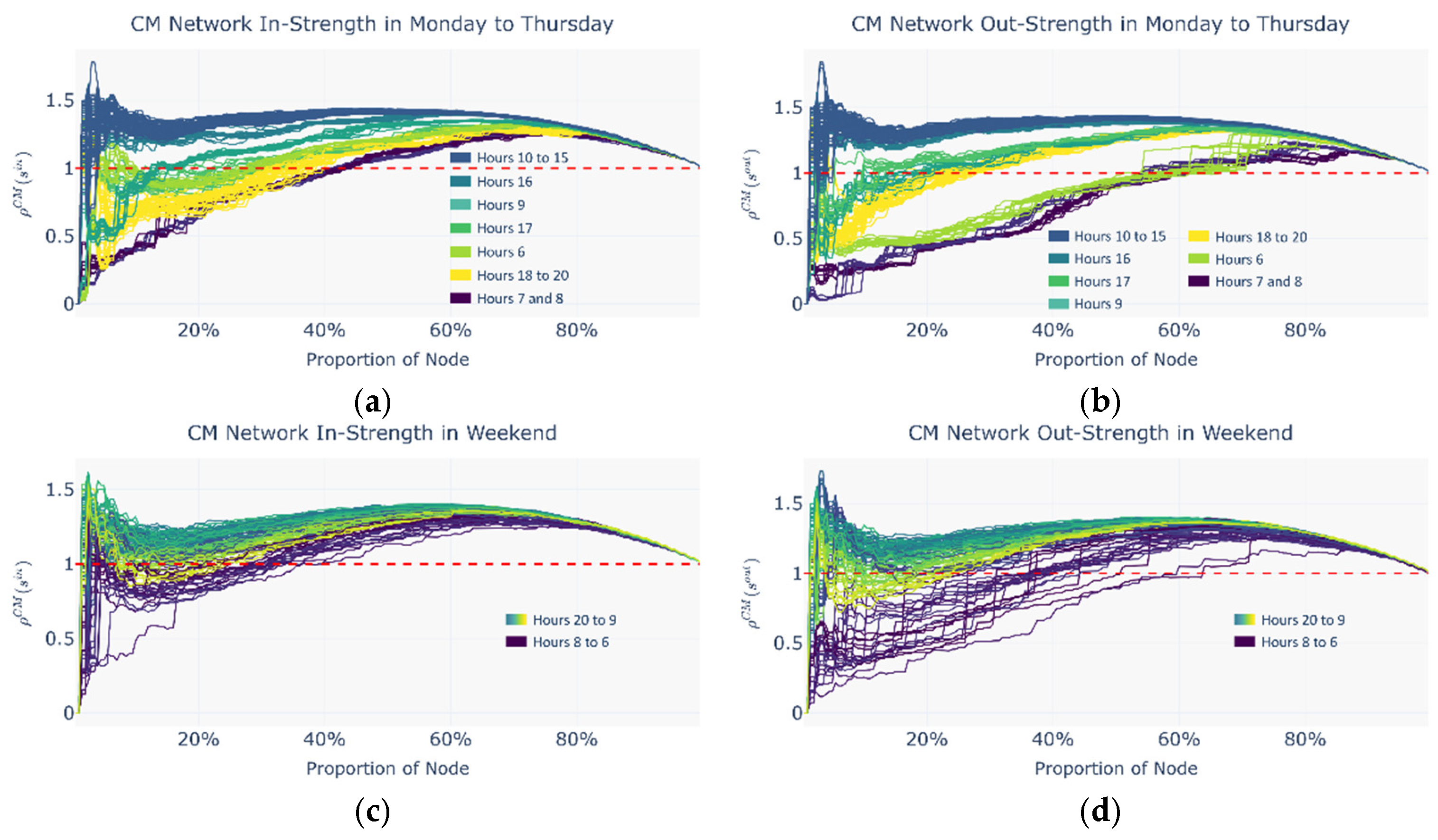
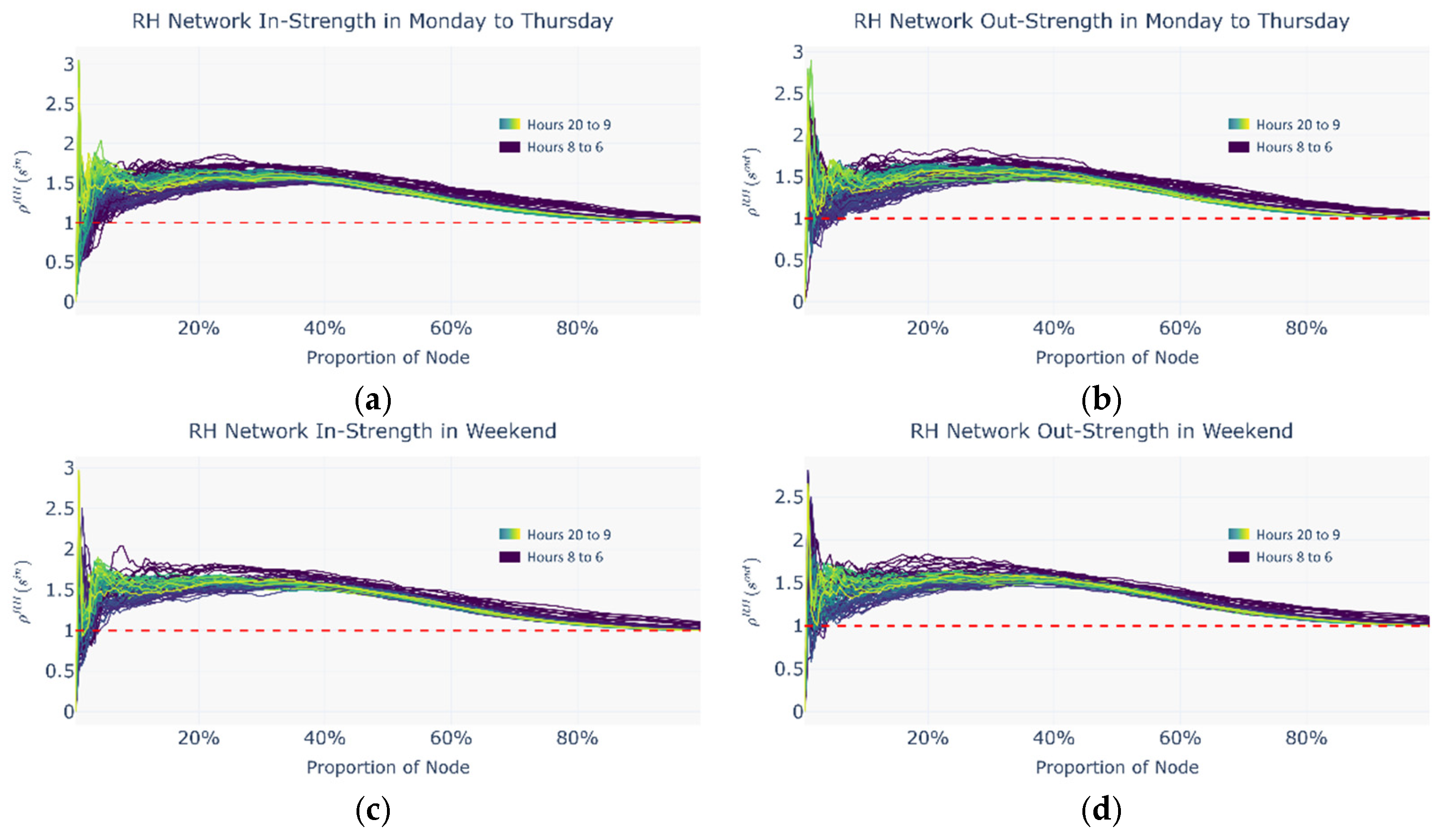
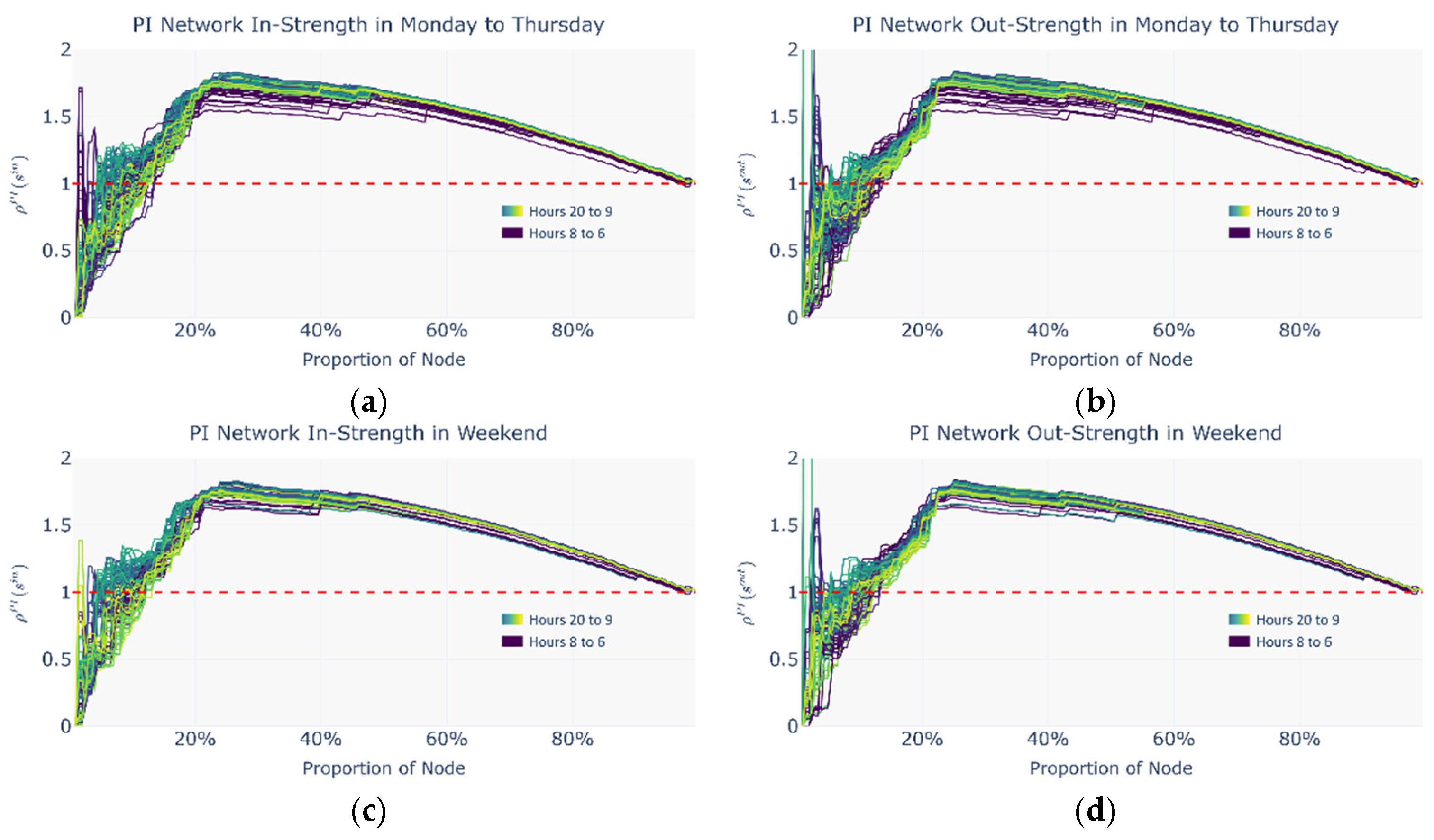
4.3.1. Positive Rich-Club Phenomenon and Secondary Rich Nodes
- (1)
- In the low node-proportion range, the curve rises sharply to the first local maximum and then rapidly falls to a local minimum;
- (2)
- In the medium-to-high node-proportion range, the curve gradually rises again to a secondary peak before eventually declining towards 1.
- (1)
- In the low node-proportion range, a core rich-club consisting of the richest nodes forms, characterized by highly dense internal connectivity;
- (2)
- In the medium-to-high range, a secondary rich-club group emerges, incorporating both core and near-core nodes, revealing the network’s multi-scale hierarchical structure.
- (1)
- Normalized rich-club coefficients in the CM
- (2)
- Normalized rich-club coefficients in the RH
- (3)
- Normalized rich-club coefficients in the PI
4.3.2. Potential Intermodal Node and Importance Coefficient
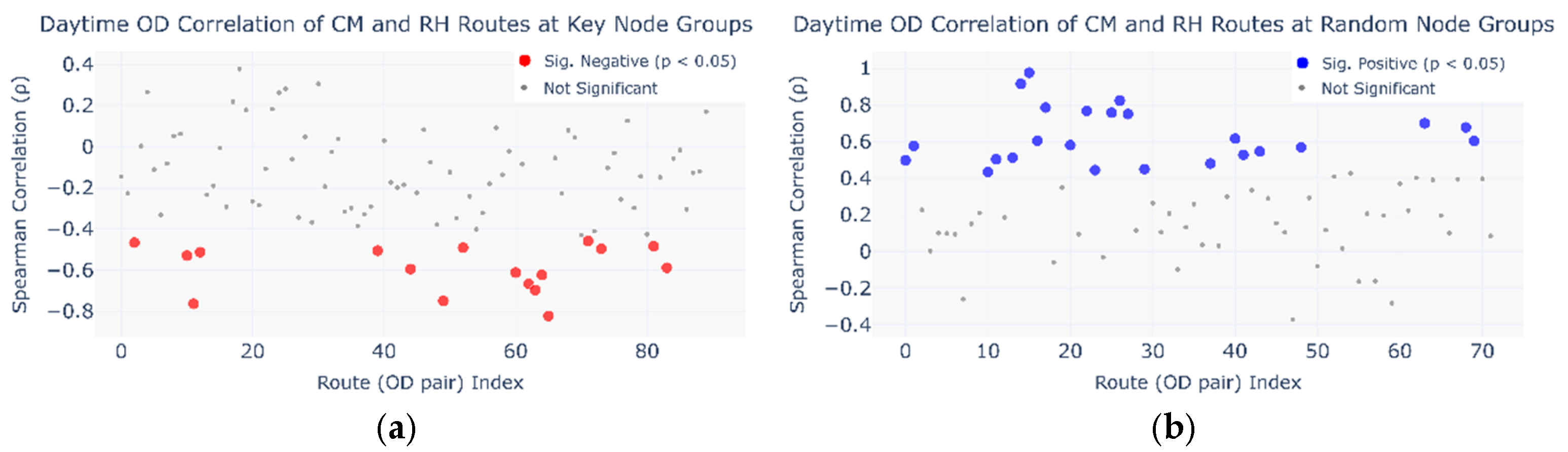
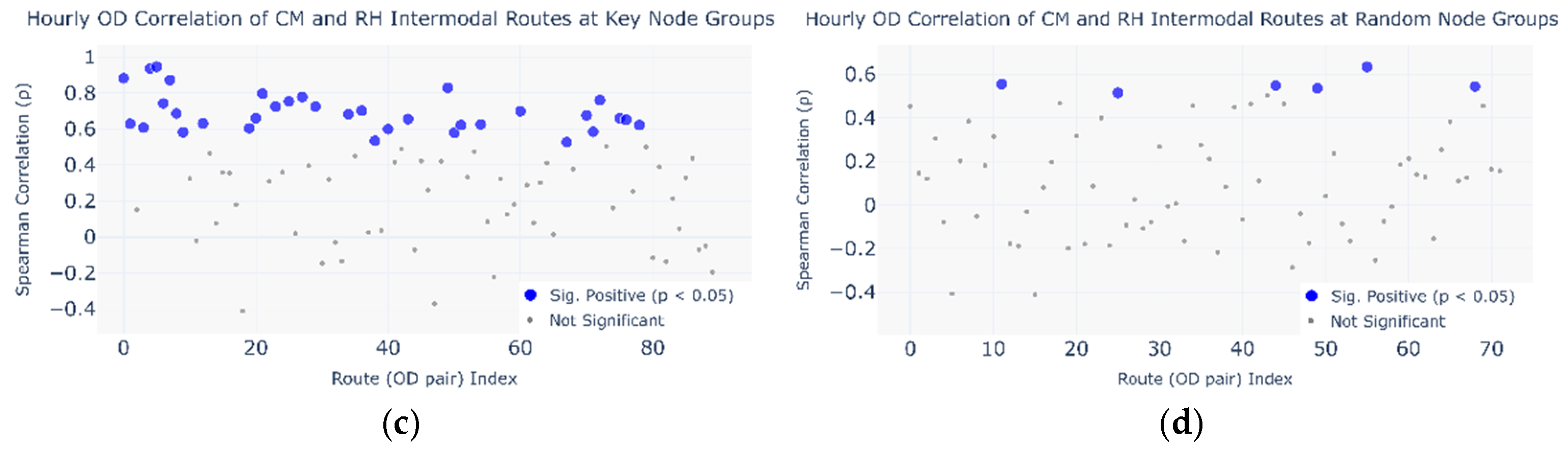
4.4. Testing for Self-Organizing Phenomena
- (1)
- The top ten key transfer subway nodes, ranked by the node importance coefficient;
- (2)
- Ten randomly selected non-key subway nodes.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Stead, D. Mid-term review of the European Commission’s 2001 Transport White Paper. Eur. J. Transp. Infrastruct. Res. 2006, 6, 365–370. [Google Scholar] [CrossRef]
- Nobis, C. Multimodality: Facets and Causes of Sustainable Mobility Behavior. Transp. Res. Rec. 2010, 2010, 35–44. [Google Scholar] [CrossRef]
- Timmer, S.; Bösehans, G.; Henkel, S. Behavioural norms or personal gains?—An empirical analysis of commuters‘ intention to switch to multimodal mobility behaviour. Transp. Res. Part A Policy Pract. 2023, 170, 103620. [Google Scholar] [CrossRef]
- Heinen, E.; Mattioli, G. Does a high level of multimodality mean less car use? An exploration of multimodality trends in England. Transportation 2019, 46, 1093–1126. [Google Scholar] [CrossRef]
- Fu, X.; van Lierop, D.; Ettema, D. Travel contexts for different forms of multimodality in the new urban mobility landscape: A latent class analysis. Transportation 2025. [Google Scholar] [CrossRef]
- Iogansen, X.; Lee, Y.; Young, M.; Compostella, J.; Circella, G.; Jenn, A. Ridehailing use, travel patterns and multimodality: A latent-class cluster analysis of one-week GPS-based travel diaries in California. Travel Behav. Soc. 2025, 38, 100855. [Google Scholar] [CrossRef]
- Auad-Perez, R.; Van Hentenryck, P. Ridesharing and fleet sizing for On-Demand Multimodal Transit Systems. Transp. Res. Part C Emerg. Technol. 2022, 138, 103594. [Google Scholar] [CrossRef]
- Lu, J.; Riley, C.; Gurumurthy, K.M.; Van Hentenryck, P. Revitalizing Public Transit in Low Ridership Areas: An Exploration of On-Demand Multimodal Transit Systems. arXiv 2023. [Google Scholar] [CrossRef]
- Van Hentenryck, P.; Riley, C.; Trasatti, A.; Guan, H.; Santanam, T.; Huertas, J.A.; Dalmeijer, K.; Watkins, K.; Drake, J.; Baskin, S. MARTA Reach: Piloting an On-Demand Multimodal Transit System in Atlanta. arXiv 2023, 1–31. [Google Scholar] [CrossRef]
- Wang, R.; Chen, F.; Liu, X.; Liu, X.; Li, Z.; Zhu, Y. A matching model for door-to-door multimodal transit by integrating taxi-sharing and subways. ISPRS Int. J. Geo-Inf. 2021, 10, 469. [Google Scholar] [CrossRef]
- Yonah, A.; Nassir, N.; Zhao, J. Multimodal Relationships: Shared and Autonomous Vehicles and High-Capacity Public Transit. In Shared Mobility and Automated Vehicles; Khan, A., Shaheen, S., Eds.; IET Books: London, UK, 2021; pp. 119–144. [Google Scholar] [CrossRef]
- Etsibah, S.A. Intermodal and multimodal passenger transport systems integration: A contribution towards better understanding. IOSR J. Humanit. Soc. Sci. (IOSR-JHSS) 2024, 29, 35–48. Available online: https://www.iosrjournals.org/iosr-jhss/papers/Vol.29-Issue2/Ser-3/F2902033548.pdf (accessed on 16 November 2025).
- Rayle, L.; Dai, D.; Chan, N.; Cervero, R.; Shaheen, S. Just a better taxi? A survey-based comparison of taxis, transit, and ridesourcing services in San Francisco. Transp. Policy 2016, 45, 168–178. [Google Scholar] [CrossRef]
- Young, M.; Allen, J.; Farber, S. Measuring when Uber behaves as a substitute or supplement to transit: An examination of travel-time differences in Toronto. J. Transp. Geogr. 2020, 82, 102629. [Google Scholar] [CrossRef]
- Cats, O.; Kucharski, R.; Danda, S.R.; Yap, M. Beyond the dichotomy: How ride-hailing competes with and complements public transport. PLoS ONE 2022, 17, e0262496. [Google Scholar] [CrossRef]
- Qiao, S.; Yeh, A.G.-O. Is ride-hailing competing or complementing public transport? A perspective from affordability. Transp. Res. Part D Transp. Environ. 2023, 114, 103533. [Google Scholar] [CrossRef]
- Korecki, M. Deep Reinforcement Meta-Learning and Self-Organization in Complex Systems: Applications to Traffic Signal Control. Entropy 2023, 25, 982. [Google Scholar] [CrossRef]
- Hall, J.D.; Palsson, C.; Price, J. Is Uber a substitute or complement for public transit? J. Urban Econ. 2018, 108, 36–50. [Google Scholar] [CrossRef]
- Sikder, S. Who Uses Ride-Hailing Services in the United States? Transp. Res. Rec. 2019, 2673, 40–54. [Google Scholar] [CrossRef]
- Conway, M.W.; Salon, D.; King, D.A. Trends in Taxi Use and the Advent of Ridehailing, 1995–2017: Evidence from the US National Household Travel Survey. Urban Sci. 2018, 2, 79. [Google Scholar] [CrossRef]
- Shaheen, S.; Chan, N. Mobility and the sharing economy: Potential to facilitate the first-and last-mile public transit connections. Built Environ. 2016, 42, 573–588. [Google Scholar] [CrossRef]
- Tang, B.J.; Li, X.Y.; Yu, B.; Wei, Y.M. How app-based ride-hailing services influence travel behavior: An empirical study from China. Int. J. Sustain. Transp. 2020, 14, 554–568. [Google Scholar] [CrossRef]
- Scholl, L.; Lleras, G.; Oviedo, D.; Castro, J.; Sabogal-Cardona, O. The Potential for Integration of Ride-Hailing with Mass Transit Systems: A Choice Experiment in Latin America. 2024. Available online: https://publications.iadb.org/en/potential-ride-hailing-integration-mass-transit-systems-choice-experiment-latin-america (accessed on 16 November 2025).
- Kurant, M.; Thiran, P. Layered complex networks. Phys. Rev. Lett. 2006, 96, 138701. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; del Genio, C.I.; Gómez-Gardeñes, J.; Romance, M.; Sendiña-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Alessandretti, L.; Natera Orozco, L.G.; Saberi, M.; Szell, M.; Battiston, F. Multimodal urban mobility and multilayer transport networks. Environ. Plan. B Urban Anal. City Sci. 2023, 50, 2038–2070. [Google Scholar] [CrossRef]
- Kurant, M.; Thiran, P. Extraction and analysis of traffic and topologies of transportation networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 036114. [Google Scholar] [CrossRef]
- Cardillo, A.; Gomez-Gardeñes, J.; Zanin, M.; Romance, M.; Papo, D.; Del Pozo, F.; Boccaletti, S. Emergence of network features from multiplexity. Sci. Rep. 2013, 3, 1344. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, S.; Wang, Y.; Wang, L. Identification of critical nodes in multimodal transportation network. Phys. A Stat. Mech. Appl. 2021, 580, 126170. [Google Scholar] [CrossRef]
- Kopsidas, A.; Kepaptsoglou, K. Identification of critical stations in a Metro System: A substitute complex network analysis. Phys. A Stat. Mech. Appl. 2022, 596, 127123. [Google Scholar] [CrossRef]
- Shen, J.; Zong, H. Identification of critical transportation cities in the multimodal transportation network of China. Phys. A Stat. Mech. Appl. 2023, 628, 129174. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, K.; Massobrio, R.; Bombelli, A.; Cats, O. Quantification and comparison of hierarchy in Public Transport Networks. Phys. A Stat. Mech. Appl. 2024, 634, 129479. [Google Scholar] [CrossRef]
- Wang, B.; Su, Q.; Chin, K.S. Vulnerability assessment of China–Europe Railway Express multimodal transport network under cascading failures. Phys. A Stat. Mech. Appl. 2021, 584, 126359. [Google Scholar] [CrossRef]
- Guo, J.; Xu, J.; He, Z.; Liao, W. Research on risk propagation method of multimodal transport network under uncertainty. Phys. A Stat. Mech. Appl. 2021, 563, 125494. [Google Scholar] [CrossRef]
- Yu, P.D.; Tan, C.W.; Fu, H.L. Averting Cascading Failures in Networked Infrastructures: Poset-Constrained Graph Algorithms. IEEE J. Sel. Top. Signal Process. 2018, 12, 733–748. [Google Scholar] [CrossRef]
- Tang, H.; Zhou, D. Understanding the Competition and Cooperation between Dockless Bike-Sharing and Metro Systems in View of Mobility. Sustainability 2024, 16, 5780. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, Y. Understanding multimodal travel mobilities of dockless bike-sharing and metro: A multilayer network analysis. Phys. A Stat. Mech. Appl. 2024, 648, 129962. [Google Scholar] [CrossRef]
- Ma, J.; Zheng, C.; Yu, M.; Shen, J.; Zhang, H.; Wang, Y. The analysis of spatio-temporal characteristics and determinants of dockless bike-sharing and metro integration. Transp. Lett. 2024, 16, 182–195. [Google Scholar] [CrossRef]
- Wolf, T.D.; Holvoet, T. Emergence Versus Self Organisation: Different Concepts but Promising When Combined. Eng. Self-Organising Syst. 2005, 3464, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Ng, S.T. Unveiling the rich-club phenomenon in urban mobility networks through the spatiotemporal characteristics of passenger flow. Phys. A Stat. Mech. Appl. 2021, 584, 126377. [Google Scholar] [CrossRef]
- Tan, C.W.; Yu, P.-D. Contagion Source Detection in Epidemic and Infodemic Outbreaks: Mathematical Analysis and Network Algorithms. Found. Trends Netw. 2023, 13, 107–251. [Google Scholar] [CrossRef]
- Xia, F.; Wang, J.; Kong, X.; Zhang, D.; Wang, Z. Ranking Station Importance with Human Mobility Patterns Using Subway Network Datasets. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2840–2852. [Google Scholar] [CrossRef]
- Li, Z.T.; Nie, W.P.; Cai, S.M.; Zhao, Z.D.; Zhou, T. Exploring the topological characteristics of urban trip networks based on taxi trajectory data. Phys. A Stat. Mech. Appl. 2023, 609, 128391. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the Web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Hamers, L.; Hemeryck, Y.; Herweyers, G.; Janssen, M.; Keters, H.; Rousseau, R.; Vanhoutte, A. Similarity measures in scientometric research: The Jaccard index versus Salton’s cosine formula. Inf. Process. Manag. 1989, 25, 315–318. [Google Scholar] [CrossRef]
- Zhou, Q.; Leydesdorff, L. The normalization of occurrence and Co-occurrence matrices in bibliometrics using Cosine similarities and Ochiai coefficients. J. Assoc. Inf. Sci. Technol. 2016, 67, 2805–2814. [Google Scholar] [CrossRef]
- Zhang, R.J.; Ye, F.Y. Measuring similarity for clarifying layer difference in multiplex ad hoc duplex information networks. J. Inf. 2020, 14, 100987. [Google Scholar] [CrossRef]
- Huang, C.; Xiao, C.; Rong, L. Integrating Point-of-Interest Density and Spatial Heterogeneity to Identify Urban Functional Areas. Remote Sens. 2022, 14, 4201. [Google Scholar] [CrossRef]
- Cinelli, M.; Ferraro, G.; Iovanella, A. Rich-club ordering and the dyadic effect: Two interrelated phenomena. Phys. A Stat. Mech. Appl. 2018, 490, 808–818. [Google Scholar] [CrossRef]
- Wei, Y.; Song, W.; Xiu, C.; Zhao, Z. The rich-club phenomenon of China’s population flow network during the country’s spring festival. Appl. Geogr. 2018, 96, 77–85. [Google Scholar] [CrossRef]
- Zeng, Z.; Sun, Y.; Zhang, X. Entropy-Based Node Importance Identification Method for Public Transportation Infrastructure Coupled Networks: A Case Study of Chengdu. Entropy 2024, 26, 159. [Google Scholar] [CrossRef]
- Opsahl, T.; Colizza, V.; Panzarasa, P.; Ramasco, J.J. Prominence and control: The weighted rich-club effect. Phys. Rev. Lett. 2008, 101, 168702. [Google Scholar] [CrossRef]
- Colizza, V.; Flammini, A.; Serrano, M.A.; Vespignani, A. Detecting rich-club ordering in complex networks. Nat. Phys. 2006, 2, 110–115. [Google Scholar] [CrossRef]
- Chen, E.; Stathopoulos, A.; Nie, Y. (Marco) Transfer station choice in a multimodal transit system: An empirical study. Transp. Res. Part A Policy Pract. 2022, 165, 337–355. [Google Scholar] [CrossRef]
- Ye, J.; Jiang, Y.; Chen, J.; Liu, Z.; Guo, R. Joint optimisation of transfer location and capacity for a capacitated multimodal transport network with elastic demand: A bi-level programming model and paradoxes. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102540. [Google Scholar] [CrossRef]
- Wu, X.; Liao, J.; Zhang, X. Employment-residence Space Characters and Their Influencing Factors Based on Multi-sourced Data Integration, Chengdu. Planners 2023, 39, 120–127. [Google Scholar] [CrossRef]
- Koza, J.R. Hidden Order: How Adaptation Builds Complexity. Artif. Life 1995, 2, 333–335. [Google Scholar] [CrossRef]
- Holland, J.H. Emergence: From Chaos to Order. Oxford, 1998; Online Ed.; Oxford Academic, 31 October 2023. Available online: https://www.researchgate.net/publication/375270833_Emergence_From_Chaos_to_Order (accessed on 16 November 2025).
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution. 1993. Available online: https://academic.oup.com/book/53153 (accessed on 16 November 2025).
- Braithwaite, J.; Churruca, K.; Long, J.C.; Ellis, L.A.; Herkes, J. When complexity science meets implementation science: A theoretical and empirical analysis of systems change. BMC Med. 2018, 16, 63. [Google Scholar] [CrossRef]
- Zheng, B.; Rao, B.; Zhu, T.; Tan, C.W.; Duan, J.; Zhou, Z.; Chen, X.; Zhang, X. Online Location Planning for AI-Defined Vehicles: Optimizing Joint Tasks of Order Serving and Spatio-Temporal Heterogeneous Model Fine-Tuning. IEEE Trans. Mob. Comput. 2025, 1–18. [Google Scholar] [CrossRef]
| Data |
|---|
| [[104.0689, 30.66593, 1,541,143,701.0, 1], [104.0689, 30.66593, 1,541,143,704.0, 1], …] |
| [[104.06285, 30.69422, 1,541,200,108.0, 1], [104.06285, 30.69422, 1,541,200,111.0, 0], …] |
| [[104.07084, 30.67528, 1,541,138,954.0, 0], [104.07082, 30.67532, 1,541,138,957.0, 0], …] |
| Operational Metro Line | Number of Stations | Number of Transfer Stations |
|---|---|---|
| Chengdu Metro Line 1 | 35 | 5 |
| Chengdu Metro Line 2 | 32 | 5 |
| Chengdu Metro Line 3 | 17 | 5 |
| Chengdu Metro Line 4 | 30 | 5 |
| Chengdu Metro Line 7 | 31 | 8 |
| Chengdu Metro Line 10 | 6 | 1 |
| Card ID | Card Type | EntS Name (ID) | Entry Time | ExiS Name (ID) | Exit Time |
|---|---|---|---|---|---|
| / | One-way | Zoo (323) | 8 November 2018 17:04 | Moziqiao (332) | 8 November 2018 17:28 |
| / | Tianfutong | ChunxiRoad (330) | 8 November 2018 17:07 | Hi-TechZone (133) | 8 November 2018 17:27 |
| / | Tianfutong | ChunxiRoad (330) | 8 November 2018 17:05 | Hi-TechZone (133) | 8 November 2018 17:25 |
| Cosine Similarity | Monday to Thursday | Friday | Weekend |
|---|---|---|---|
| Chengdu Metro | 0.70 | 0.71 | 0.58 |
| Ride-Hailing | 0.68 | 0.41 | 0.49 |
| CM&RH | 0.82 | 0.48 | 0.72 |
| Station | Commute First Mile | Commute Last Mile | Leisure First Mile | Leisure Last Mile |
|---|---|---|---|---|
| Chunxi Road | 1 | 1 | 1 | 1 |
| Tianfu Square | 0.93 | 0.99 | 0.89 | 0.86 |
| Renmin North Road | 0.92 | 0.96 | 0.91 | 0.93 |
| Luomashi | 0.88 | 0.91 | 0.32 | 0.14 |
| Taisheng South Road | 0.84 | 0.75 | 0.59 | 0.25 |
| Chengdu Second People’s Hospital | 0.82 | 0.63 | 0.75 | 0.46 |
| People’s Park | 0.81 | 0.99 | 1 | 1 |
| Panda Avenue | 0.66 | 0.59 | 0.82 | 0.21 |
| Jinjiang Hotel | 0.66 | 0.84 | 0.32 | 0 |
| Yushuang Road | 0.61 | 0.59 | 0.84 | 0.91 |
| Tonghuimen | 0.25 | 0.30 | 0.71 | 0.16 |
| Jiulidi | 0.24 | 0.17 | 0.25 | 0.16 |
| Lijiatuo | 0.16 | 0.26 | 0 | 0 |
| Qianfeng Road | 0.13 | 0.07 | 0 | 0 |
| Zoo | 0.11 | 0.04 | 0.05 | 0 |
| Southwest Jiaotong University | 0.10 | 0.02 | 0.05 | 0 |
| Hongxing Bridge | 0.10 | 0.03 | 0.04 | 0.02 |
| Zhaojuesi South Road | 0.10 | 0.19 | 0.05 | 0 |
| Kuanzhaixiangzi Alley | 0.04 | 0.09 | 0.05 | 0 |
| Erxianqiao | 0.02 | 0 | 0 | 0 |
| Shengxian Lake | 0.02 | 0.01 | 0 | 0 |
| Huazhaobi | 0.02 | 0 | 0.04 | 0 |
| Other Chengdu Metro stations | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, H.; Luo, X.; Li, X.; Zhao, Y. Unveiling Self-Organization and Emergent Phenomena in Urban Transportation Systems via Multilayer Network Analysis. Entropy 2025, 27, 1169. https://doi.org/10.3390/e27111169
Bao H, Luo X, Li X, Zhao Y. Unveiling Self-Organization and Emergent Phenomena in Urban Transportation Systems via Multilayer Network Analysis. Entropy. 2025; 27(11):1169. https://doi.org/10.3390/e27111169
Chicago/Turabian StyleBao, Hongqing, Xia Luo, Xuan Li, and Yiyang Zhao. 2025. "Unveiling Self-Organization and Emergent Phenomena in Urban Transportation Systems via Multilayer Network Analysis" Entropy 27, no. 11: 1169. https://doi.org/10.3390/e27111169
APA StyleBao, H., Luo, X., Li, X., & Zhao, Y. (2025). Unveiling Self-Organization and Emergent Phenomena in Urban Transportation Systems via Multilayer Network Analysis. Entropy, 27(11), 1169. https://doi.org/10.3390/e27111169







