Information-Theoretic ESG Index Direction Forecasting: A Complexity-Aware Framework
Abstract
1. Introduction
2. Literature
2.1. Key Determinants of Financial Sustainability in ESG Markets: A Multi-Scale Perspective
2.2. Traditional and Emerging Approaches to ESG/Sustainability Index Forecasting
2.3. Information-Theoretic and Entropy-Based Approaches in Financial Time Series Modeling
2.4. Synthesizing the Literature: The Case for a Complexity-Aware Forecasting Framework
3. Data and Methodology
3.1. Data
3.1.1. ESG Index Data
3.1.2. Complementary Market Variables
3.1.3. Technical Indicators
3.2. Feature Engineering
3.2.1. Optimization of Technical Indicator Parameters
3.2.2. Information-Theoretic Feature Extraction
3.3. Modeling Framework
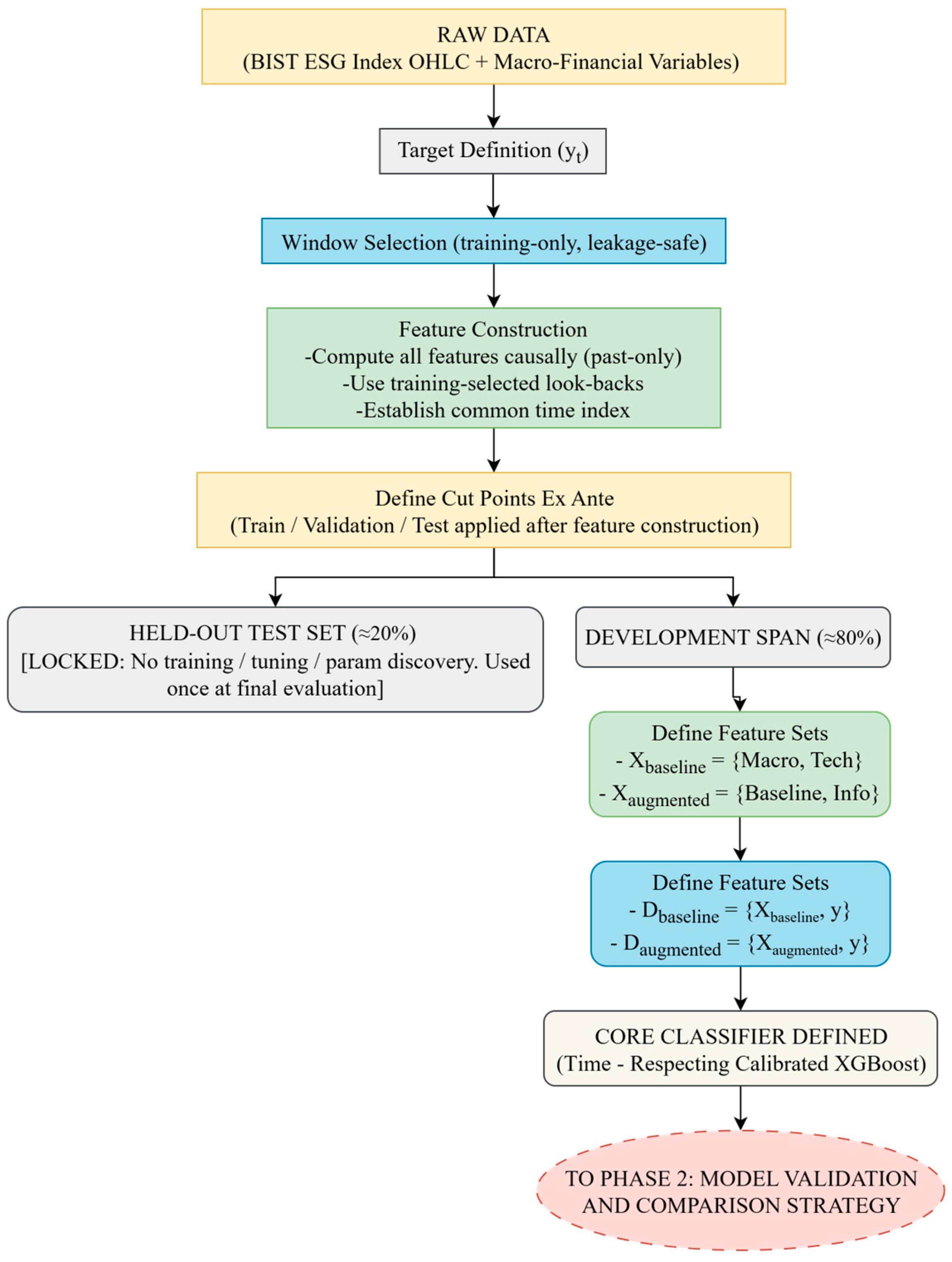
3.3.1. Phase 1: Model and Data Preparation
- (i)
- The block of external macroeconomic variables;
- (ii)
- The block of empirically optimized technical indicators and the fixed-parameter PSAR. No information-theoretic measures are included.
- (i)
- The block of market state indicators (SE and PE);
- (ii)
- The market transition measure (KL divergence).
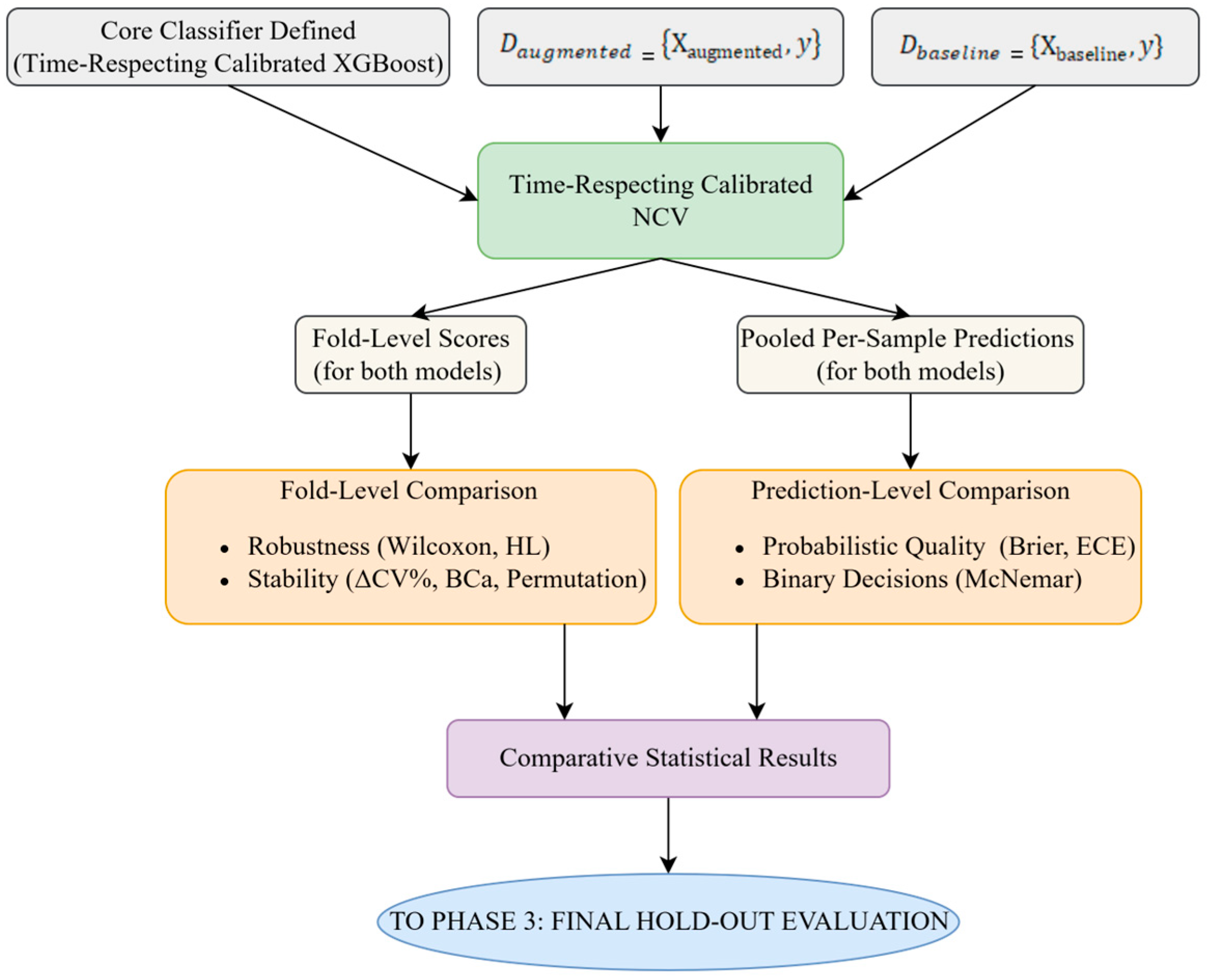
3.3.2. Phase 2: Model Validation and Comparison Strategy
- Fold StructureA TimeSeriesSplit scheme was employed, which preserved chronological order (no shuffling) with 3 inner folds (for hyperparameter tuning via RandomizedSearchCV) and 5 outer folds (for performance estimation). The choice of a 3 × 5-fold structure aimed to balance the bias–variance trade-off, consistent with established recommendations for time-series tasks of this scale [111,112].
- Inner Loop (Hyperparameter Tuning)Given the broad hyperparameter space of the XGBoost + calibration wrapper (see Supplementary Table S1), the inner loop used RandomizedSearchCV rather than an exhaustive grid due to the wide parameter ranges and the diminishing returns of exhaustive enumeration. Within this loop, the search treated the choice of calibration method (Platt vs. isotonic) as a tunable hyperparameter, which was optimized jointly with the standard XGBoost hyperparameters and a calibration-holdout fraction drawn from the range [0.15, 0.30), ensuring a minimum of 100 observations in the calibration slice. With a budget of n_iter = 200 per inner loop and a 3-fold TimeSeriesSplit, each outer fold evaluates approximately 600 candidate model fits; across 5 outer folds this totals approximately 3000 inner-loop fits per specification (200 × 3 × 5), plus 5 refits of the selected configurations.
- Outer Loop (Performance Estimation)For each outer split, the model was trained on the outer-train slice, calibrated on its past-only calibration slice, and evaluated on the outer-validation slice. The resulting outer-fold scores were then aggregated to obtain an unbiased estimate of generalization performance.
- Protocol Application and Bias Prevention
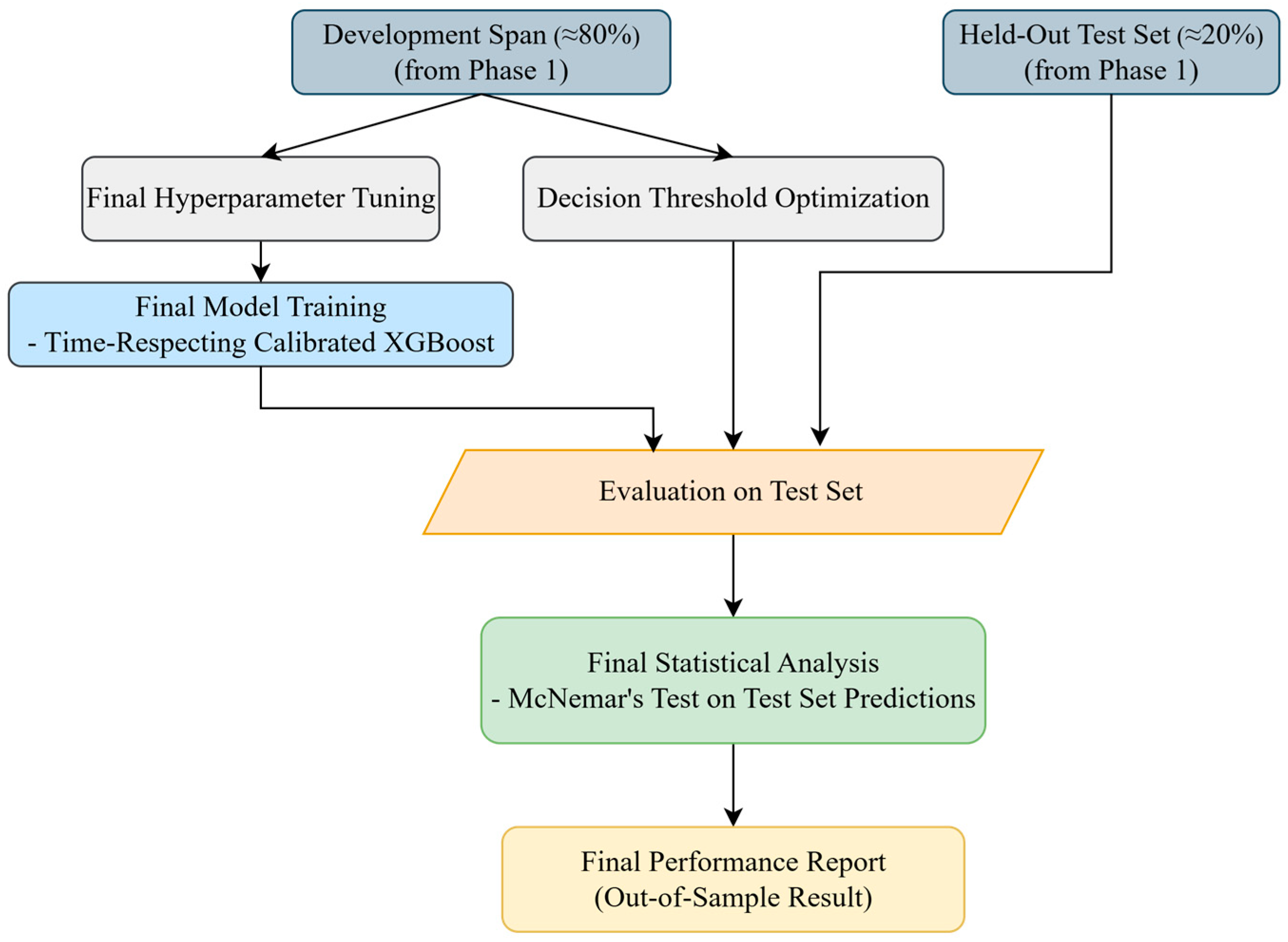
3.3.3. Phase 3: Final Model Training and Hold-Out Evaluation
4. Results
4.1. Experimental Setup and Data Overview
- Panel A shows a weakly stationary yet volatility-clustered return process, consistent with the ADF and Ljung–Box test results discussed in Section 4.1.
- Panel B presents the volatility, where shaded regions denote persistent high-volatility regimes, most prominently during the 2020 COVID-19 shock and the 2022–2023 turbulence period. The dashed line marks the high-volatility threshold, defined as the 75th percentile of the rolling volatility distribution.
- Panel C reveals that SE tends to decline during and immediately after sharp market drawdowns (e.g., 2020), suggesting a temporary compression of informational diversity and a transition toward more consensus-driven, one-sided trading.
- Panel D shows that PE tends to decline in parallel with SE during high-stress episodes, illustrating its sensitivity to synchronized trading activity. As market stress (Panel B) intensifies, price dynamics appear to simplify and lose ordinal complexity, indicating the emergence of coordinated market movements and herd-driven behavior, conditions that are typically associated with diminished informational diversity and reduced market efficiency.
- Panel E shows that KL values often rise sharply during and immediately after major shocks (e.g., 2020, 2022), indicating its usefulness as a sensitive indicator of market regime transitions. The measure appears to capture both the intensity of structural breaks and the lingering distributional instability that can remain once the market’s underlying return-generating structure has been affected by external forces
4.2. Comparative Performance in Nested Cross-Validation
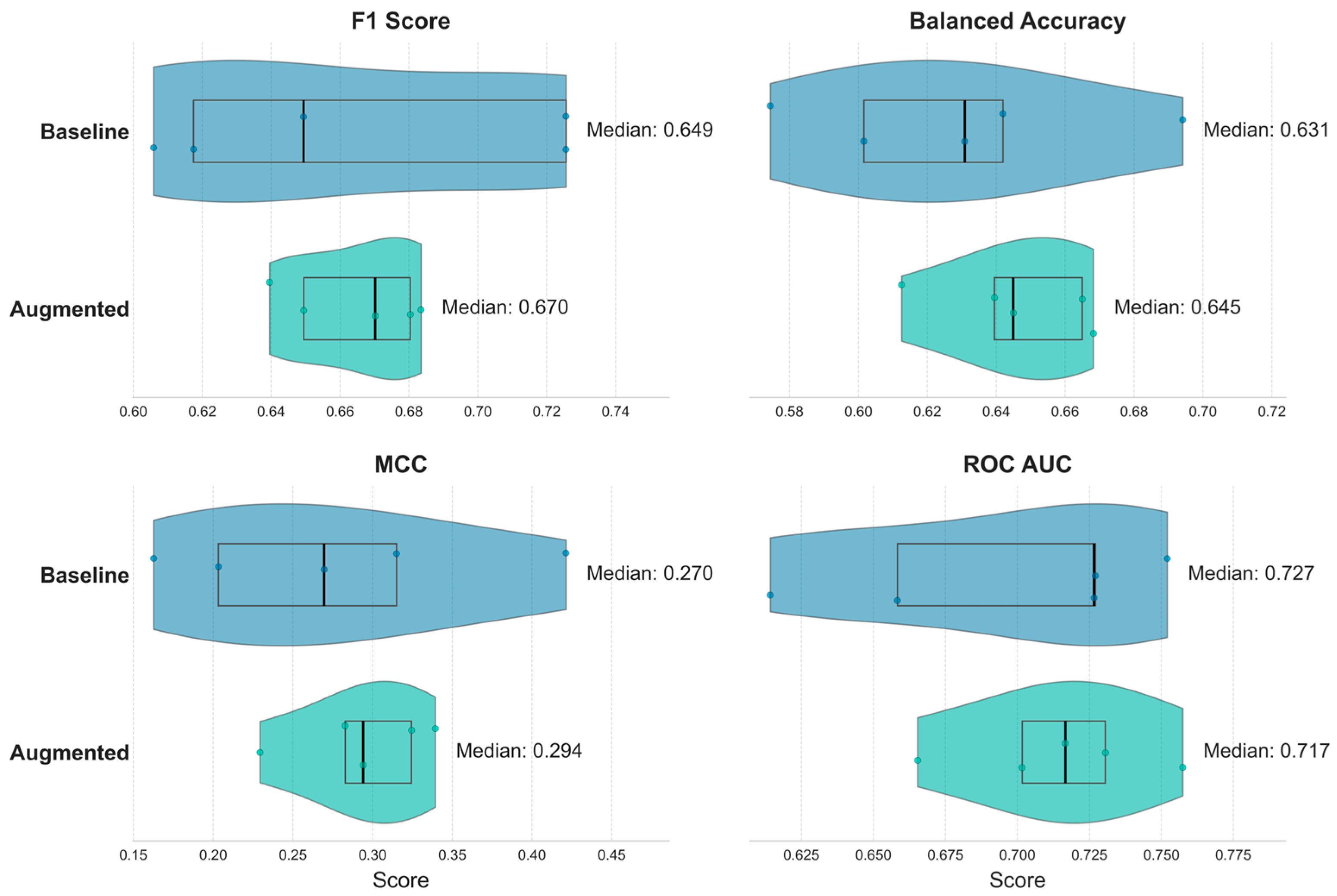
4.2.1. Overall Performance Summary
4.2.2. Statistical Significance of NCV Results
4.3. Definitive Performance on the Held-Out Test Set
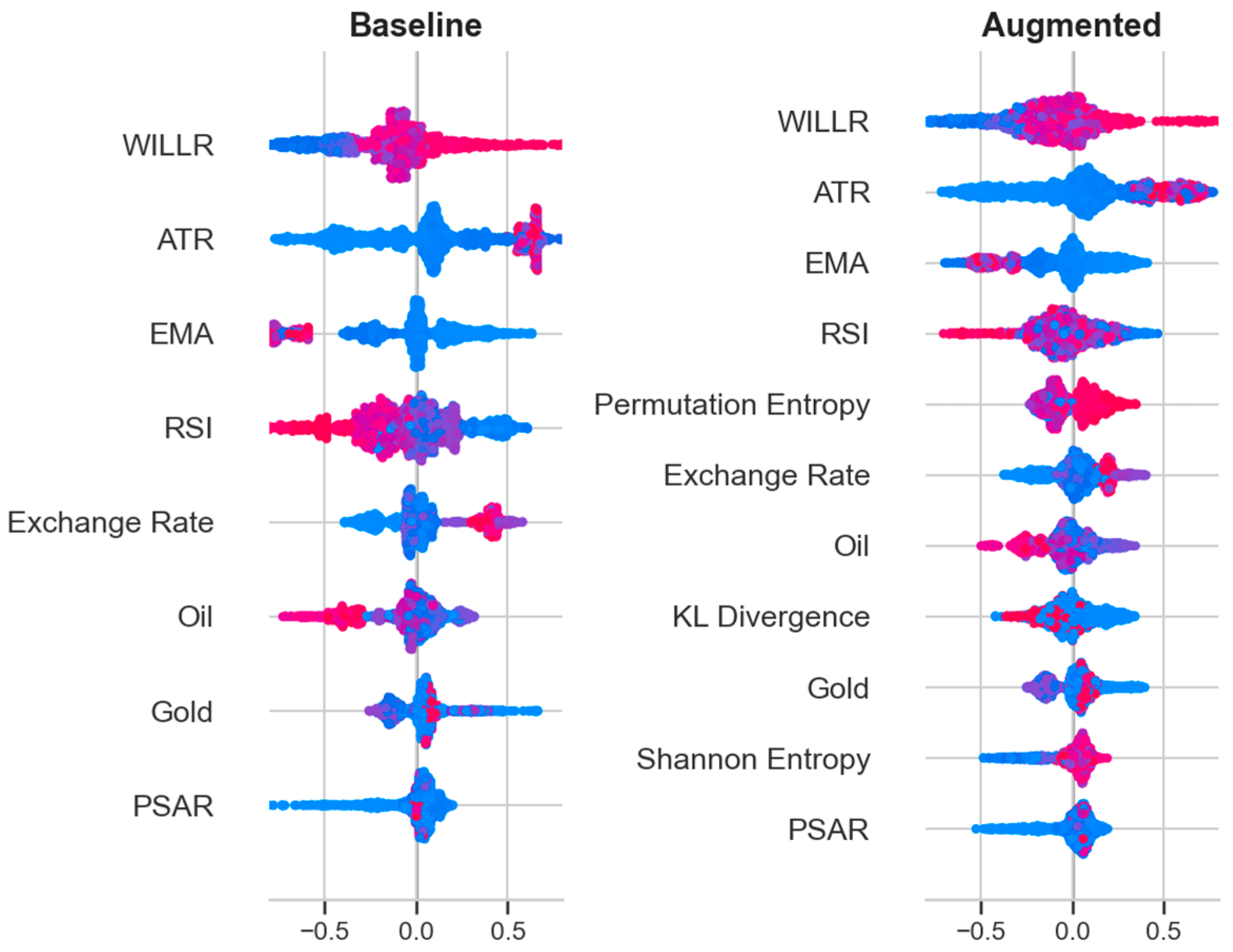
4.4. Model Interpretability (SHAP Analysis)
4.5. Model Sensitivity (Entropy Window Parameter)
5. Discussion
5.1. Interpretation of Findings
5.2. Theoretical Implications
5.3. Practical Implications
5.4. Limitations and Future Research
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Information-Theoretic Feature Definitions
- Shannon Entropy (SE):
- Number of bins
- Numerical offset (for stability);
- Embedding dimension ;
Appendix B. Time-Respecting Calibration Protocol
- Fit the base XGBoost .
- Score the later, disjoint calibration holdout (uncalibrated margins/probabilities as implemented).
- Fit a mapping g on and apply it forward, yielding calibrated probabilities .
Appendix C. Evaluation Metrics
- Directional-accuracy metrics:
References
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T.P. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Hamilton, J.D. A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Cont, R. Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
- Global Sustainable Investment Alliance (GSIA). Global Sustainable Investment Review 2022; GSIA: London, UK, 2023; Available online: https://www.gsi-alliance.org/members-resources/gsir2022/ (accessed on 12 September 2025).
- Tucker, J.J., III; Jones, S. Environmental, Social, and Governance Investing: Investor Demand, the Great Wealth Transfer, and Strategies for ESG Investing. J. Financ. Serv. Prof. 2020, 74, 56. [Google Scholar]
- Morningstar. Global Sustainable Fund Flows Quarterly Data; Morningstar: Chicago, IL, USA, 2025; Available online: https://www.morningstar.com/business/insights/blog/funds/global-sustainable-fund-flows-quarterly-data (accessed on 12 September 2025).
- MSCI. Sustainability and Climate Trends to Watch for 2025; MSCI ESG Research LLC: New York, NY, USA, 2025; Available online: https://www.msci.com/documents/1296102/51277550/2025%2BSustainability%2Band%2BClimate%2BTrends%2BPaper.pdf (accessed on 12 September 2025).
- Vo, N.N.; He, X.; Liu, S.; Xu, G. Deep Learning for Decision Making and the Optimization of Socially Responsible Investments and Portfolio. Decis. Support Syst. 2019, 124, 113097. [Google Scholar] [CrossRef]
- Xidonas, P.; Essner, E. On ESG Portfolio Construction: A Multi-Objective Optimization Approach. Comput. Econ. 2024, 63, 21–45. [Google Scholar] [CrossRef] [PubMed]
- De Lucia, C.; Pazienza, P.; Bartlett, M. Does Good ESG Lead to Better Financial Performances by Firms? Machine Learning and Logistic Regression Models of Public Enterprises in Europe. Sustainability 2020, 12, 5317. [Google Scholar] [CrossRef]
- Sorathiya, A.; Saval, P.; Sorathiya, M. Data-Driven Sustainable Investment Strategies: Integrating ESG, Financial Data Science, and Time Series Analysis for Alpha Generation. Int. J. Financ. Stud. 2024, 12, 36. [Google Scholar] [CrossRef]
- Sabbaghi, O. The Impact of News on the Volatility of ESG Firms. Glob. Financ. J. 2022, 51, 100570. [Google Scholar] [CrossRef]
- Suprihadi, E.; Danila, N. Forecasting ESG Stock Indices Using a Machine Learning Approach. Glob. Bus. Rev. 2024, 09721509241234033. [Google Scholar] [CrossRef]
- Bhandari, H.N.; Pokhrel, N.R.; Rimal, R.; Dahal, K.R.; Rimal, B. Implementation of Deep Learning Models in Predicting ESG Index Volatility. Financ. Innov. 2024, 10, 75. [Google Scholar] [CrossRef]
- Gunduz, H.; Cataltepe, Z. Borsa Istanbul (BIST) Daily Prediction Using Financial News and Balanced Feature Selection. Expert Syst. Appl. 2015, 42, 9001–9011. [Google Scholar] [CrossRef]
- Sadorsky, P. Modeling Volatility and Conditional Correlations between Socially Responsible Investments, Gold and Oil. Econ. Model. 2014, 38, 609–618. [Google Scholar] [CrossRef]
- De Oliveira, E.M.; Cunha, F.A.F.S.; Cyrino Oliveira, F.L.; Samanez, C.P. Dynamic Relationships between Crude Oil Prices and Socially Responsible Investing in Brazil: Evidence for Linear and Non-Linear Causality. Appl. Econ. 2017, 49, 2125–2140. [Google Scholar] [CrossRef]
- Maraqa, B.; Bein, M. Dynamic Interrelationship and Volatility Spillover among Sustainability Stock Markets, Major European Conventional Indices, and International Crude Oil. Sustainability 2020, 12, 3908. [Google Scholar] [CrossRef]
- Guo, T.; Jamet, N.; Betrix, V.; Piquet, L.A.; Hauptmann, E. ESG2Risk: A Deep Learning Framework from ESG News to Stock Volatility Prediction. arXiv 2020, arXiv:2005.02527. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden Patterns, Permutation Entropy and Stock Market Inefficiency. Physica A 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Bariviera, A.F.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. A Permutation Information Theory Tour through Different Interest Rate Maturities: The Libor Case. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20150119. [Google Scholar] [CrossRef]
- World Commission on Environment and Development. Our Common Future: Report of the World Commission on Environment and Development; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Cassen, R.H. Our Common Future: Report of the World Commission on Environment and Development. Int. Aff. 1987, 64, 126. [Google Scholar] [CrossRef]
- Harris, J.M. Sustainability and Sustainable Development. Int. Soc. Ecol. Econ. 2003, 1, 1–12. Available online: https://isecoeco.org/pdf/susdev.pdf (accessed on 15 July 2025).
- S&P Dow Jones Indices. S&P ESG Indices Methodology; S&P Global: New York, NY, USA, 2024; Available online: https://www.spglobal.com/spdji/en/documents/methodologies/methodology-sp-esg%2B-indices.pdf (accessed on 14 September 2025).
- Robiyanto, R.; Nugroho, B.A.; Huruta, A.D.; Frensidy, B.; Suyanto, S. Identifying the Role of Gold on Sustainable Investment in Indonesia: The DCC-GARCH Approach. Economies 2021, 9, 119. [Google Scholar] [CrossRef]
- Sahoo, S. Harmony in Diversity: Exploring Connectedness and Portfolio Strategies among Crude Oil, Gold, Traditional and Sustainable Index. Resour. Policy 2024, 97, 103222. [Google Scholar] [CrossRef]
- Shaikh, I. On the Relationship between Policy Uncertainty and Sustainable Investing. J. Model. Manag. 2022, 17, 1504–1523. [Google Scholar] [CrossRef]
- Özçim, H. BİST Sürdürülebilirlik Endeksi ve Makroekonomik Veriler Arasındaki İlişkinin GARCH Modelleri Çerçevesinde İncelenmesi. Pamukkale Univ. J. Soc. Sci. Inst. 2022, 49, 115–126. [Google Scholar]
- Kaya, M. BİST Sürdürülebilirlik Endeksi ile Fosil Yakıt Fiyatları Arasındaki İlişkinin Analizi. Abant Soc. Sci. J. 2023, 23, 1475–1495. [Google Scholar]
- Umar, Z.; Abrar, A.; Zaremba, A.; Teplova, T.; Vo, X.V. Network connectedness of environmental attention—Green and dirty assets. Financ. Res. Lett. 2022, 50, 103209. [Google Scholar] [CrossRef]
- Umar, Z.; Gubareva, M. The relationship between the COVID-19 media coverage and the environmental, social and governance leaders equity volatility: A time–frequency wavelet analysis. Appl. Econ. 2021, 53, 3193–3206. [Google Scholar] [CrossRef]
- Akhtaruzzaman, M.; Boubaker, S.; Umar, Z. COVID-19 media coverage and ESG leader indices. Financ. Res. Lett. 2022, 45, 102170. [Google Scholar] [CrossRef]
- Pina, V.; Bachiller, P.; Ripoll, L. Testing the reliability of financial sustainability: The case of Spanish local governments. Sustainability 2020, 12, 6880. [Google Scholar] [CrossRef]
- Rodríguez Bolívar, M.P.; López Subires, M.D.; Alcaide Muñoz, L.; Navarro Galera, A. The financial sustainability of local authorities in England and Spain: A comparative empirical study. Int. Rev. Adm. Sci. 2021, 87, 97–114. [Google Scholar] [CrossRef]
- Santis, S. The demographic and economic determinants of financial sustainability: An analysis of Italian local governments. Sustainability 2020, 12, 7599. [Google Scholar] [CrossRef]
- Benito, B.; Guillamón, M.D.; Ríos, A.M. The sustainable development goals: How does their implementation affect the financial sustainability of the largest Spanish municipalities? Sustain. Dev. 2023, 31, 2836–2850. [Google Scholar] [CrossRef]
- Alshubiri, F.N. Analysis of financial sustainability indicators of higher education institutions on foreign direct investment: Empirical evidence in OECD countries. Int. J. Sustain. High. Educ. 2021, 22, 77–99. [Google Scholar] [CrossRef]
- Bui, T.D.; Nguyen, T.P.T.; Sethanan, K.; Chiu, A.S.; Tseng, M.L. Natural resource management in Vietnam: Merging circular economy practices and financial sustainability approach. J. Clean. Prod. 2024, 480, 144094. [Google Scholar] [CrossRef]
- Yi, H.; Kim, K.N. Transforming aid-funded renewable energy systems: A case study of policy-driven financial sustainability in rural Bangladesh. Renew. Energy 2025, 246, 122752. [Google Scholar] [CrossRef]
- Maeenuddin, M.K.; Hamid, S.A.; Nassir, A.M.; Fahlevi, M.; Aljuaid, M.; Jermsittiparsert, K. Measuring the financial sustainability and its influential factors in microfinance sector of Pakistan. SAGE Open 2024, 14, 21582440241259288. [Google Scholar] [CrossRef]
- Awaworyi Churchill, S. Microfinance financial sustainability and outreach: Is there a trade-off? Empir. Econ. 2020, 59, 1329–1350. [Google Scholar] [CrossRef]
- Atichasari, A.S.; Ratnasari, A.; Kulsum, U.; Kahpi, H.S.; Wulandari, S.S.; Marfu, A. Examining non-performing loans on corporate financial sustainability: Evidence from Indonesia. Sustain. Futures 2023, 6, 100137. [Google Scholar] [CrossRef]
- Zabolotnyy, S.; Wasilewski, M. The concept of financial sustainability measurement: A case of food companies from Northern Europe. Sustainability 2019, 11, 5139. [Google Scholar] [CrossRef]
- Githaiga, P.N. Revenue diversification and financial sustainability of microfinance institutions. Asian J. Account. Res. 2022, 7, 31–43. [Google Scholar] [CrossRef]
- Najam, H.; Abbas, J.; Alvarez-Otero, S.; Dogan, E.; Sial, M.S. Towards green recovery: Can banks achieve financial sustainability through income diversification in ASEAN countries? Econ. Anal. Policy 2022, 76, 522–533. [Google Scholar] [CrossRef]
- Kong, Y.; Donkor, M.; Musah, M.; Nkyi, J.A.; Ampong, G.O.A. Capital structure and corporates financial sustainability: Evidence from listed non-financial entities in Ghana. Sustainability 2023, 15, 4211. [Google Scholar] [CrossRef]
- Githaiga, P.N.; Soi, N.; Buigut, K.K. Does Intellectual Capital Matter to MFIs’ Financial Sustainability? Asian J. Account. Res. 2023, 8, 41–52. [Google Scholar] [CrossRef]
- Gleißner, W.; Günther, T.; Walkshäusl, C. Financial Sustainability: Measurement and Empirical Evidence. J. Bus. Econ. 2022, 92, 467–516. [Google Scholar] [CrossRef]
- Berg, F.; Lo, A.W.; Rigobon, R.; Singh, M.; Zhang, R. Quantifying the returns of ESG investing: An empirical analysis with six ESG metrics. MIT Sloan Research Paper No. 6930-23. SSRN 2023. [Google Scholar] [CrossRef]
- Tao, J.; Shan, P.; Liang, J.; Zhang, L. Influence Mechanism between Corporate Social Responsibility and Financial Sustainability: Empirical Evidence from China. Sustainability 2024, 16, 2406. [Google Scholar] [CrossRef]
- Wong, S.M.H.; Chan, R.Y.K.; Wong, P.; Wong, T. Promoting Corporate Financial Sustainability through ESG Practices: An Employee-Centric Perspective and the Moderating Role of Asian Values. Res. Int. Bus. Financ. 2025, 75, 102733. [Google Scholar] [CrossRef]
- Ur Rahman, R.; Ali Shah, S.M.; El-Gohary, H.; Abbas, M.; Haider Khalil, S.; Al Altheeb, S.; Sultan, F. Social Media Adoption and Financial Sustainability: Learned Lessons from Developing Countries. Sustainability 2020, 12, 10616. [Google Scholar] [CrossRef]
- Muneer, S.; Singh, A.; Choudhary, M.H.; Alshammari, A.S.; Butt, N.A. Does Environmental Disclosure and Corporate Governance Ensure the Financial Sustainability of Islamic Banks? Adm. Sci. 2025, 15, 54. [Google Scholar] [CrossRef]
- Nabipour, M.; Nayyeri, P.; Jabani, H.; Shahab, S.; Mosavi, A. Predicting stock market trends using machine learning and deep learning algorithms via continuous and binary data: A comparative analysis. IEEE Access 2020, 8, 150199–150212. [Google Scholar] [CrossRef]
- Bonello, J.; Brédart, X.; Vella, V. Machine learning models for predicting financial distress. J. Res. Econ. 2018, 2, 174–185. [Google Scholar] [CrossRef]
- Molina-Gómez, N.I.; Rodriguez-Rojas, K.; Calderón-Rivera, D.; Díaz-Arévalo, J.L.; López-Jiménez, P.A. Using machine learning tools to classify sustainability levels in the development of urban ecosystems. Sustainability 2020, 12, 3326. [Google Scholar] [CrossRef]
- Ting, T.; Mia, M.A.; Hossain, M.I.; Wah, K.K. Predicting the financial performance of microfinance institutions with machine learning techniques. J. Model. Manag. 2025, 20, 322–347. [Google Scholar] [CrossRef]
- Shi, Y.; Charles, V.; Zhu, J. Bank financial sustainability evaluation: Data envelopment analysis with random forest and Shapley additive explanations. Eur. J. Oper. Res. 2025, 321, 614–630. [Google Scholar] [CrossRef]
- Lee, O.; Joo, H.; Choi, H.; Cheon, M. Proposing an integrated approach to analyzing ESG data via machine learning and deep learning algorithms. Sustainability 2022, 14, 8745. [Google Scholar] [CrossRef]
- Raman, N.; Bang, G.; Nourbakhsh, A. Mapping ESG trends by distant supervision of neural language models. Mach. Learn. Knowl. Extract. 2020, 2, 453–468. [Google Scholar] [CrossRef]
- Lin, S.-L.; Jin, X. Does ESG predict systemic banking crises? A computational economics model of early warning systems with interpretable multi-variable LSTM based on mixture attention. Mathematics 2023, 11, 410. [Google Scholar] [CrossRef]
- Maasoumi, E. A compendium to information theory in economics and econometrics. Econom. Rev. 1993, 12, 137–181. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Zhou, R.; Cai, R.; Tong, G. Applications of entropy in finance: A review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Shternshis, A.; Mazzarisi, P.; Marmi, S. Measuring Market Efficiency: The Shannon Entropy of High-Frequency Financial Time Series. Chaos Solitons Fractals 2022, 162, 112403. [Google Scholar] [CrossRef]
- Scrucca, L. Entropy-Based Volatility Analysis of Financial Log-Returns Using Gaussian Mixture Models. Entropy 2024, 26, 907. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Huang, X.; Shang, H.L.; Pitt, D. Permutation Entropy and Its Variants for Measuring Temporal Dependence. Aust. N. Z. J. Stat. 2022, 64, 442–477. [Google Scholar] [CrossRef]
- Olbryś, J. Entropy of Volatility Changes: Novel Method for Assessment of Regularity in Volatility Time Series. Entropy 2025, 27, 318. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Henry, M.; Judge, G. Permutation Entropy and Information Recovery in Nonlinear Dynamic Economic Time Series. Econometrics 2019, 7, 10. [Google Scholar] [CrossRef]
- Siokis, F. High Short Interest Stocks Performance during the COVID-19 Crisis: An Informational Efficacy Measure Based on Permutation-Entropy Approach. J. Econ. Stud. 2023, 50, 1570–1584. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, Y.; Wang, Z.; Gao, M. Instability of Financial Time Series Revealed by Irreversibility Analysis. Entropy 2025, 27, 402. [Google Scholar] [CrossRef]
- Maasoumi, E.; Racine, J. Entropy and predictability of stock market returns. J. Econom. 2002, 107, 291–312. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Li, J.; Shang, P. Time Irreversibility of Financial Time Series Based on Higher Moments and Multiscale Kullback–Leibler Divergence. Physica A 2018, 502, 248–255. [Google Scholar] [CrossRef]
- Ishizaki, R.; Inoue, M. Short-Term Kullback–Leibler Divergence Analysis to Extract Unstable Periods in Financial Time Series. Evol. Inst. Econ. Rev. 2024, 21, 227–236. [Google Scholar] [CrossRef]
- Ponta, L.; Carbone, A. Kullback–Leibler Cluster Entropy to Quantify Volatility Correlation and Risk Diversity. Phys. Rev. E 2025, 111, 014311. [Google Scholar] [CrossRef]
- Zunino, L.; Tabak, B.M.; Pérez, D.G.; Garavaglia, M.; Rosso, O.A. Inefficiency in Latin-American market indices. Europhys. Lett. 2007, 84, 60008. [Google Scholar] [CrossRef]
- Fernández Bariviera, A.; Zunino, L.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. Revisiting the European sovereign bonds with a permutation-information-theory approach. Eur. Phys. J. B 2013, 86, 509. [Google Scholar] [CrossRef]
- Eichengreen, B.; Rose, A.K.; Wyplosz, C. Exchange market mayhem: The antecedents and aftermath of speculative attacks. Econ. Policy 1995, 10, 249–312. [Google Scholar] [CrossRef]
- Baur, D.G.; McDermott, T.K. Is gold a safe haven? International evidence. J. Bank. Financ. 2010, 34, 1886–1898. [Google Scholar] [CrossRef]
- Hamilton, J.D. Causes and consequences of the oil shock of 2007–08. Natl. Bur. Econ. Res. 2009, 40, 215–283. [Google Scholar]
- Yin, L.; Yang, Q. Predicting the oil prices: Do technical indicators help? Energy Econ. 2016, 56, 338–350. [Google Scholar] [CrossRef]
- Dai, Z.; Zhu, H.; Kang, J. New technical indicators and stock returns predictability. Int. Rev. Econ. Financ. 2021, 71, 127–142. [Google Scholar] [CrossRef]
- Huang, J.Z.; Huang, W.; Ni, J. Predicting bitcoin returns using high-dimensional technical indicators. J. Financ. Data Sci. 2019, 5, 140–155. [Google Scholar] [CrossRef]
- Padhi, D.K.; Padhy, N.; Bhoi, A.K.; Shafi, J.; Ijaz, M.F. A fusion framework for forecasting financial market direction using enhanced ensemble models and technical indicators. Mathematics 2021, 9, 2646. [Google Scholar] [CrossRef]
- Ayala, J.; García-Torres, M.; Noguera, J.L.V.; Gómez-Vela, F.; Divina, F. Technical analysis strategy optimization using a machine learning approach in stock market indices. Knowl. Based Syst. 2021, 225, 107–116. [Google Scholar] [CrossRef]
- McHugh, C.; Coleman, S.; Kerr, D. Technical indicators for energy market trading. Mach. Learn. Appl. 2021, 6, 100–110. [Google Scholar] [CrossRef]
- Das, A.K.; Mishra, D.; Das, K.; Mishra, K.C. A feature ensemble framework for stock market forecasting using technical analysis and Aquila optimizer. IEEE Access 2024, 12, 187899–187918. [Google Scholar] [CrossRef]
- Anggono, A.H. Investment strategy based on exponential moving average and count back line. Rev. Integr. Bus. Econ. Res. 2019, 8, 153–161. [Google Scholar]
- Murphy, J.J. Technical Analysis of the Financial Markets: A Comprehensive Guide to Trading Methods and Applications; Penguin: New York, NY, USA, 1999. [Google Scholar]
- Panchal, M.; Gor, R.; Hemrajani, J. A hybrid strategy using mean reverting indicator PSAR and EMA. IOSR J. Math. 2020, 16, 11–22. [Google Scholar]
- Yazdi, S.H.M.; Lashkari, Z.H. Technical analysis of forex by Parabolic SAR indicator. In Proceedings of the International Islamic Accounting and Finance Conference, Kuala Lumpur, Malaysia, 19–21 November 2012. [Google Scholar]
- Jiang, Z.; Ji, R.; Chang, K.-C. A Machine Learning Integrated Portfolio Rebalance Framework with Risk-Aversion Adjustment. J. Risk Financ. Manag. 2020, 13, 155. [Google Scholar] [CrossRef]
- Panigrahi, A.K.; Vachhani, K.; Chaudhury, S.K. Trend identification with the relative strength index (RSI) technical indicator—A conceptual study. J. Manag. Res. Anal. 2021, 8, 159–169. [Google Scholar] [CrossRef]
- Naved, M.; Srivastava, P. Profitability of oscillators used in technical analysis for financial market. Adv. Econ. Bus. Manag. 2015, 2, 925–931. [Google Scholar] [CrossRef]
- Yamanaka, S. Average true range. Stock. Commod. 2002, 20, 76–79. [Google Scholar]
- Wilder, J.W., Jr. New Concepts in Technical Trading Systems; Trend Research: Greensboro, NC, USA, 1978. [Google Scholar]
- Cohen, G. Trading cryptocurrencies using algorithmic average true range systems. J. Forecast. 2023, 42, 212–222. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy: A tutorial review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Öz, E.; Aşkın, Ö.E. Classification of hepatitis viruses from sequencing chromatograms using multiscale permutation entropy and support vector machines. Entropy 2019, 21, 1149. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Niculescu-Mizil, A.; Caruana, R. Predicting good probabilities with supervised learning. In Proceedings of the 22nd International Conference on MACHINE Learning, Bonn, Germany, 7–11 August 2025; ACM: New York, NY, USA, 2005; pp. 625–632. [Google Scholar]
- Platt, J.C. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. In Advances in Large Margin Classifiers; Smola, A.J., Bartlett, P., Schölkopf, B., Schuurmans, D., Eds.; MIT Press: Cambridge, MA, USA, 1999; pp. 61–74. [Google Scholar]
- Zadrozny, B.; Elkan, C. Transforming classifier scores into accurate multiclass probability estimates. In Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; ACM: New York, NY, USA, 2002; pp. 694–699. [Google Scholar]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Naeini, M.P.; Cooper, G.; Hauskrecht, M. Obtaining well calibrated probabilities using Bayesian binning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29, pp. 2901–2907. [Google Scholar]
- Hodges, J.L.; Lehmann, E.L. Estimates of location based on rank tests. Ann. Math. Stat. 1963, 34, 598–611. [Google Scholar] [CrossRef]
- Efron, B. Better bootstrap confidence intervals. J. Am. Stat. Assoc. 1987, 82, 171–185. [Google Scholar] [CrossRef]
- Stouffer, S.A.; Suchman, E.A.; DeVinney, L.C.; Star, S.A.; Williams, R.M., Jr. The American Soldier, Vol. 1: Adjustment During Army Life; Princeton University Press: Princeton, NJ, USA, 1949. [Google Scholar]
- Hedges, L.V.; Olkin, I. Statistical Methods for Meta-Analysis; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Gneiting, T.; Balabdaoui, F.; Raftery, A.E. Probabilistic forecasts, calibration and sharpness. J. R. Stat. Soc. Ser. B 2007, 69, 243–268. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, Australia, 6–11 August 2017; Volume 3. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular Data: Deep Learning Is Not All You Need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why Do Tree-Based Models Still Outperform Deep Learning on Typical Tabular Data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]

| Determinant Category | Key Variables/Examples | Representative Literature |
|---|---|---|
| Macro-Financial & Market | Commodity and energy prices (oil, gold), exchange and interest rates, economic policy uncertainty, systemic shocks (e.g., pandemics, crypto spillovers). | [17,18,19,27,28,29,30,31,32,33,34] |
| Institutional & Structural | Economic growth, institutional quality, SDG alignment, demographic and public finance indicators, higher education, circular economy, renewable energy systems. | [35,36,37,38,39,40,41,42,43] |
| Corporate & Firm-Level | Financial structure (debt, liquidity), income diversification, intellectual capital efficiency, profitability, capital structure, firm performance. | [44,45,46,47,48,49,50,51] |
| Social, Environmental & Behavioral | Corporate social responsibility, employee engagement, social media activity, environmental disclosure, governance transparency. | [52,53,54,55] |
| Source | Determinant Type | Key Variables/Drivers | ESG Forecasting Models |
|---|---|---|---|
| [9] | ESG-focused Portfolios | Stock Returns, ESG Ratings, Portfolio Weights | DRIP with Multivariate Bidirectional LSTM |
| [15] | Fundamental, Technical, and Macroeconomic Drivers of ESG Index Volatility | Cboe Volatility Index, Interest Rate, Civilian Unemployment Rate, Consumer Sentiment Index, US Dollar Index, Technical Indicators | LSTM, GRU, CNN |
| [20] | ESG Newsflow–Driven Volatility Determinants | ESG-Related Financial News, Textual Features Extracted from Newsflow, Transformer-Based Language Representations | ESG2Risk Deep Learning Pipeline |
| [56] | Technical Indicators-Based Market Drivers | Technical Indicators | Decision Tree, Random Forest, AdaBoost, XGBoost, SVC, Naïve Bayes, KNN, Logistic Regression, ANN, RNN, LSTM |
| [57] | Financial Ratios & Industry-Specific Drivers | Profitability Ratios, Liquidity Ratios, Leverage Ratios, Management Efficiency Ratios, Fraud Checks, İndustry Code, Company Size (96 Financial And Industry-Related Indicators) | Decision Tree, Naïve Bayes, ANN |
| [58] | Urban Sustainability Indicators | Environmental, Social, and Economic Indicators | Decision Tree, ANN, SVM |
| [59] | Financial Sustainability of Microfinance Institutions | Operational, Financial, and Institutional Variables Of Microfinance Institutions | Random Forest, Quantile Random Forest, Linear Regression, Partial Least Squares, Stepwise Linear Regression, Elastic Net, Bayesian Ridge Regression, KNN, SVR |
| [60] | Financial Sustainability of Banks | Loans and Leases, Interest Income, Total Liabilities, Total Assets, Market Capitalization, Revenue To Assets, Revenue Per Share | Random Forest Classification, SHAP-based Feature Analysis, Three-Stage Network DEA |
| [61] | ESG Performance and Investment Decisions | ESG Variables | Light Gradient Boosting Machine, Local Outlier Factors, LSTM, GRU |
| [62] | Corporate ESG Disclosure and Communication | ESG-Related Sentences in Earnings Calls | Neural Language Modeling |
| [63] | Systemic Banking Risk & ESG Factors | ESG Risk Score, Inflation Rate, Unemployment Rate, House Prices, Current Account Balance/GDP Ratio | Interpretable Multivariate LSTM with Focal Loss |
| Definition | Formula |
|---|---|
| Trend-Based Technical Indicators | |
| EMA is a trend-following indicator that applies exponentially decaying weights to past observations [93,94]. Unlike SMA (equal weights), EMA emphasizes recent data, enhancing responsiveness while smoothing noise. It captures short- to intermediate-term directional momentum. | where Pt denotes the closing price and α = 2/(n + 1) is the smoothing coefficient with n lookback window. |
| PSAR captures trend direction and potential reversals; dots below price → uptrend, above → downtrend. Also used as a trailing stop [95,96,97]. | Uptrend: Downtrend: where EP is the extreme point and α is the acceleration factor. |
| Momentum-Based Technical Indicators | |
| RSI is a momentum oscillator, bounded between 0 and 100, that measures the speed and change of price movements. It is used to identify overbought (>70) and oversold (<30) conditions movements [98]. | where RS is the ratio of average gains to average losses over the lookback period [99]. |
| Williams %R is bounded between 0 and −100, that measures the current closing price in relation to the high/low range over a past period n. It is used to identify overbought (>−20) and oversold (<−80) level [94]. | where Pt is the closing price at time t, Hn is the highest price over the lookback period n, and Ln is the lowest price over the same period. |
| Volatility-Based Technical Indicators | |
| ATR is a measure of market volatility that incorporates price gaps. It quantifies the degree of price movement or variability, rather than the direction. High values indicate high volatility [94,100,101,102]. | where Ht is the current high, Lt the current low, Pt-1 the previous close, TRt the true range at time t, and n the lookback period. |
| Category | Features | Preprocessing Notes |
|---|---|---|
| Macroeconomic | exchangerate, gold, oil | Raw levels |
| Technical | EMA, RSI, ATR, WILLR | Optimized lookback windows |
| Technical indicator (fixed) | PSAR | Standard configuration |
| Information-theoretic | SE, PE, KL divergence | Computed on daily returns |
| Test | Statistic/Setting | p-Value | Conclusion (α = 0.05) |
|---|---|---|---|
| ADF | ADF = −50.87 | <0.001 | Stationary; unit root rejected |
| Kendall-Tau | tau = 0.029 | 0.024 | Upward trend (significant) |
| Ljung–Box | Lag 10 | 0.593 | No autocorrelation (≤lag 10) |
| Ljung–Box | Lag 20 | 0.017 | Serial dependence (lag 20) |
| Ljung–Box | Lag 50 | 0.022 | Serial dependence (lag 50) |
| Metric | Baseline Model | Augmented Model |
|---|---|---|
| F1 Score | 0.6648 ± 0.0578 | 0.6646 ± 0.0193 |
| BAcc | 0.6286 ± 0.0451 | 0.6461 ± 0.0225 |
| MCC | 0.2744 ± 0.1010 | 0.2940 ± 0.0427 |
| ROC AUC | 0.6957 ± 0.0574 | 0.7143 ± 0.0342 |
| Metric | HL Median Δ (Aug − Base) | 90%BCa CI (HL) | Wilcoxon p |
|---|---|---|---|
| Brier | −0.01098 | [−0.02784, −0.00610] | 0.0625 |
| ECE | −0.02797 | [−0.06678, −0.01868] | 0.0625 |
| Metric | CV% (Baseline) | CV% (Augmented) | ΔCV% | 90%BCa CI | Interpretation |
|---|---|---|---|---|---|
| F1 Score | 8.69 | 2.91 | −5.78 | [−8.22, −4.15] | Aug more stable |
| BAcc | 7.18 | 3.48 | −3.70 | [−5.46, −0.73] | Aug more stable |
| MCC | 36.81 | 14.51 | −22.29 | [−31.48, −11.04] | Aug more stable |
| ROC AUC | 8.24 | 4.79 | −3.45 | [−5.00, −2.22] | Aug more stable |
| Metric | R (Baseline) [BCa CI] | R (Augmented) 90% [BCa CI] | % Improvement |
|---|---|---|---|
| F1 Score | 11.51 [9.97, 12.76] | 34.35 [27.26, 40.97] | +198.4% |
| BAcc | 13.93 [9.49, 21.61] | 28.72 [21.17, 52.03] | +106.2% |
| MCC | 2.72 [1.88, 3.67] | 6.89 [4.80, 13.27] | +153.6% |
| ROC AUC | 12.13 [8.86, 16.27] | 20.89 [13.93, 29.64] | +72.2% |
| Metric | Mean Δ (Aug − Base) | 90%BCa CI | Wilcoxon p | Perm p | Interpretation |
|---|---|---|---|---|---|
| Brier | −0.0140 | [−0.0199, −0.0084] | 0.0037 | 0.0001 | Aug better |
| ECE | −0.0287 | [−0.0440, −0.0117] | † | † | Aug better |
| Model | F1 | BAcc | ROC-AUC | MCC |
|---|---|---|---|---|
| XGB-Calib (Baseline) | 0.7060 | 0.5480 | 0.7210 | 0.2080 |
| XGB-Calib (Augmented) | 0.7190 | 0.6180 | 0.7230 | 0.2880 |
| Δ% (Aug − Base) | (+1.8%) | (+12.8%) | (+0.3%) | (+38.5%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Öztürk, K.N.; Yiğit, Ö.E. Information-Theoretic ESG Index Direction Forecasting: A Complexity-Aware Framework. Entropy 2025, 27, 1164. https://doi.org/10.3390/e27111164
Öztürk KN, Yiğit ÖE. Information-Theoretic ESG Index Direction Forecasting: A Complexity-Aware Framework. Entropy. 2025; 27(11):1164. https://doi.org/10.3390/e27111164
Chicago/Turabian StyleÖztürk, Kadriye Nurdanay, and Öyküm Esra Yiğit. 2025. "Information-Theoretic ESG Index Direction Forecasting: A Complexity-Aware Framework" Entropy 27, no. 11: 1164. https://doi.org/10.3390/e27111164
APA StyleÖztürk, K. N., & Yiğit, Ö. E. (2025). Information-Theoretic ESG Index Direction Forecasting: A Complexity-Aware Framework. Entropy, 27(11), 1164. https://doi.org/10.3390/e27111164






