An Outlier Suppression and Adversarial Learning Model for Anomaly Detection in Multivariate Time Series
Abstract
1. Introduction
- We introduce AOST, a novel multivariate time series anomaly detection model that fuses adversarial learning with outlier suppression attention within a Transformer architecture.
- We develop OSA to amplify the distinctions between normal and anomalous samples and introduce a new anomaly scoring technique based on longitudinal differences, thereby enhancing detection capabilities.
- We implement adversarial training to mitigate overfitting, ultimately improving the model’s robustness and generalization.
- Comprehensive experiments conducted on three public datasets (SWaT, SMAP, and PSM) demonstrate that our model achieves an average F1 score of 90.74%, surpassing the best-performing method by 1.89% and showcasing advanced performance in the field.
2. Related Work
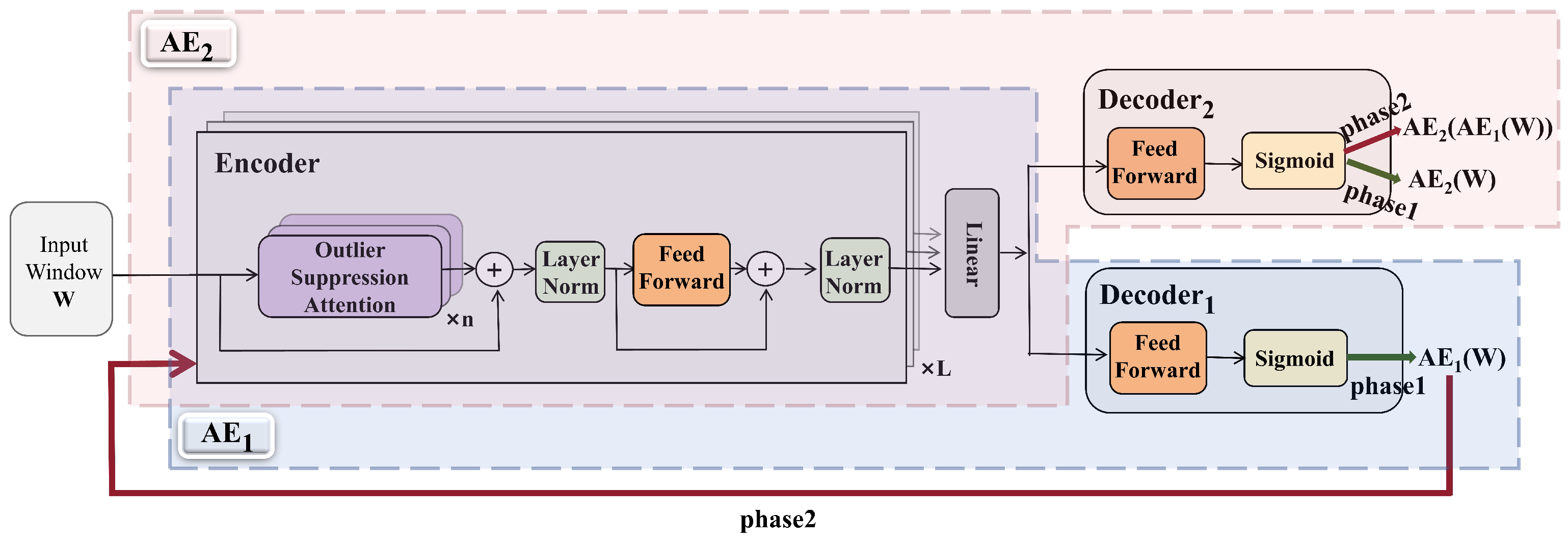
3. Method Overview
3.1. Problem Statement
3.2. Model Architecture
3.2.1. Encoder
3.2.2. ,
3.3. Outlier Suppression Attention
3.4. Model Training
3.4.1. Outlier Suppression Training
3.4.2. Adversarial Training
3.4.3. Total Training Loss
| Algorithm 1: The AOST training algorithm |
 |
3.5. Anomaly Detection
| Algorithm 2: The AOST test algorithm |
 |
4. Experiments
4.1. Datasets
4.2. Evaluation Metric
4.3. Experimental Details
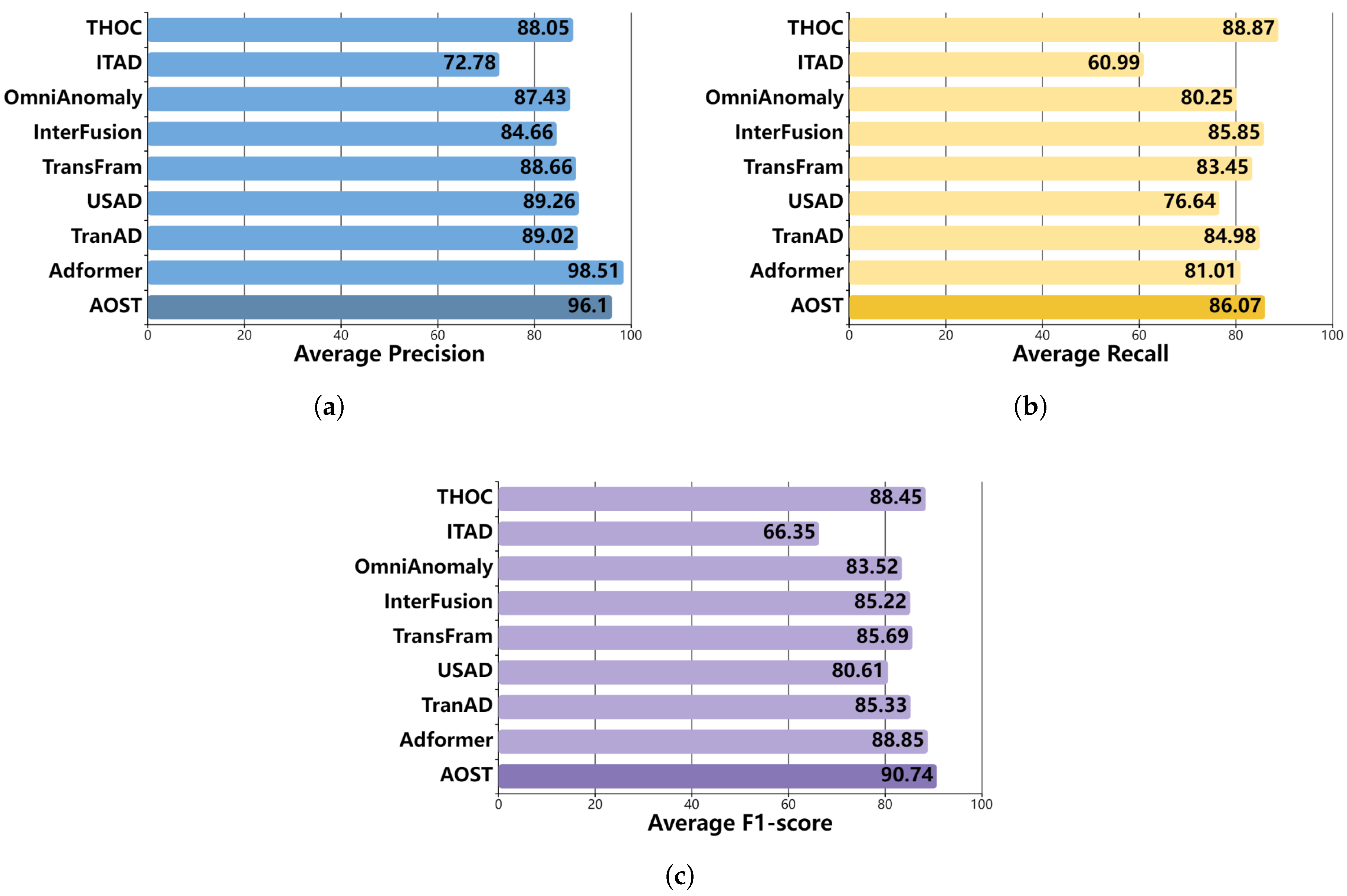
4.4. Experimental Results and Comparative Analysis
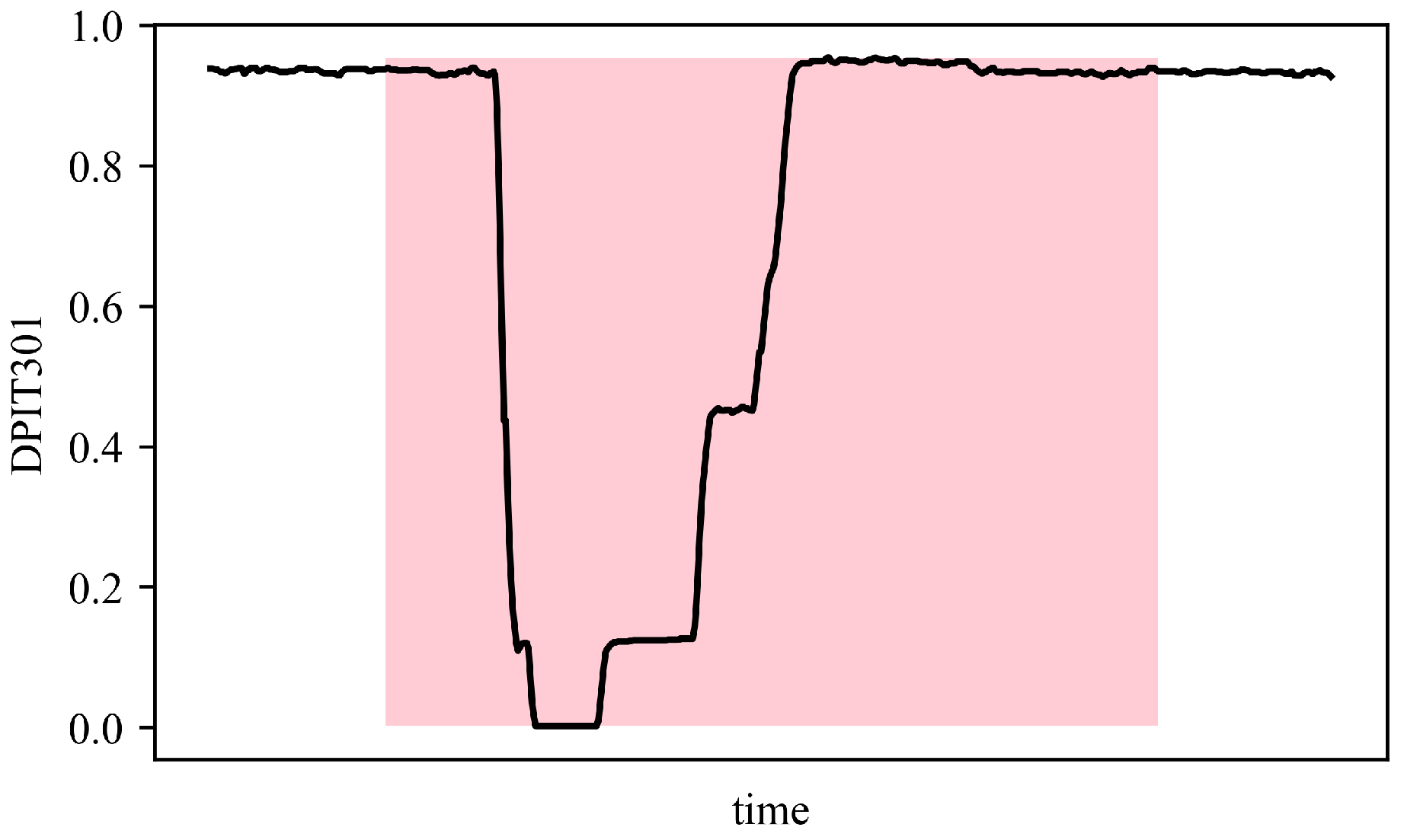
4.5. Anomaly Detection Visualization
4.6. Ablation Study
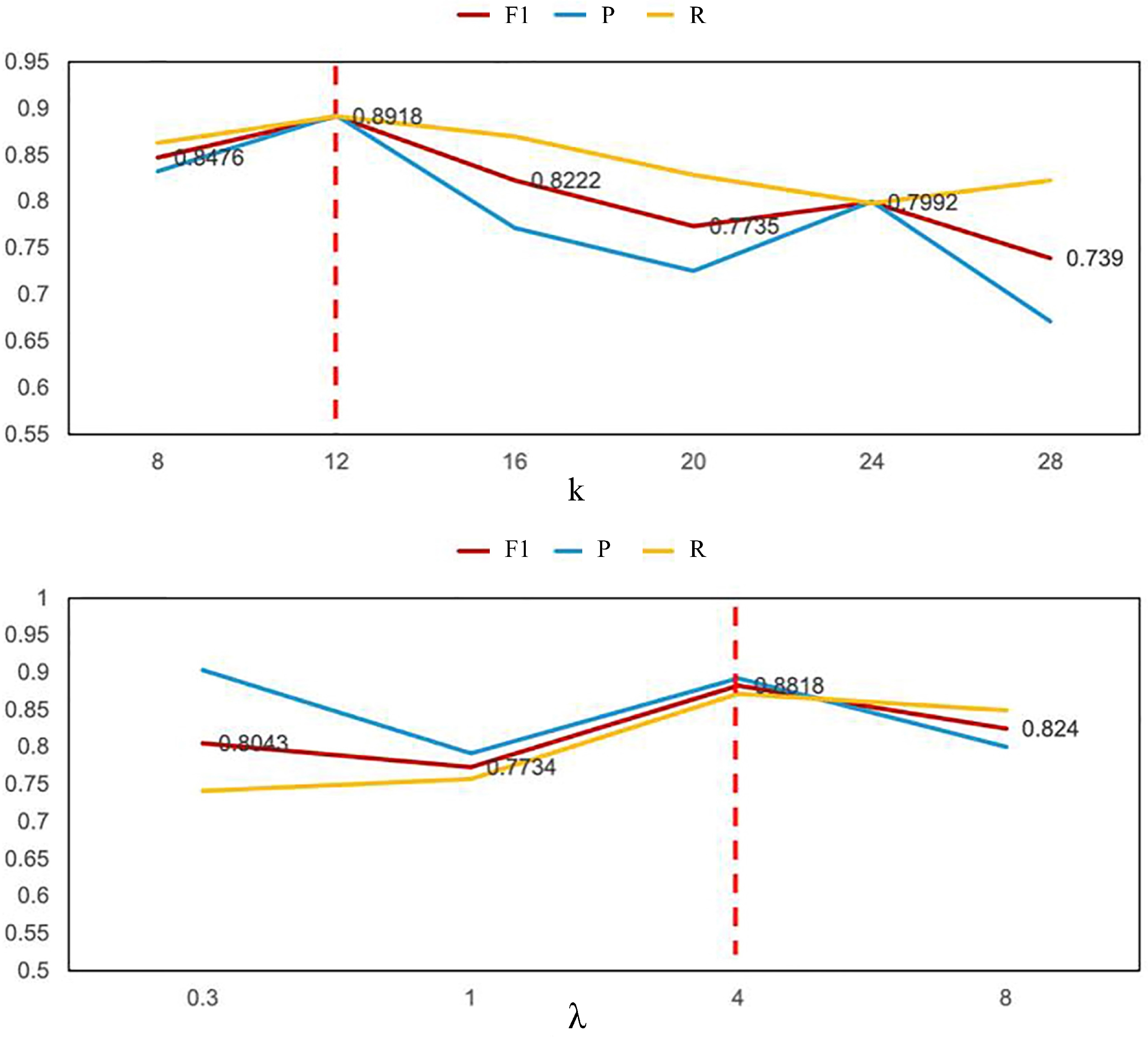
4.7. Parameter Analysis
4.7.1. Encoder Layers Analysis
4.7.2. Window Lengths Parameter and ALD Parameter Analysis
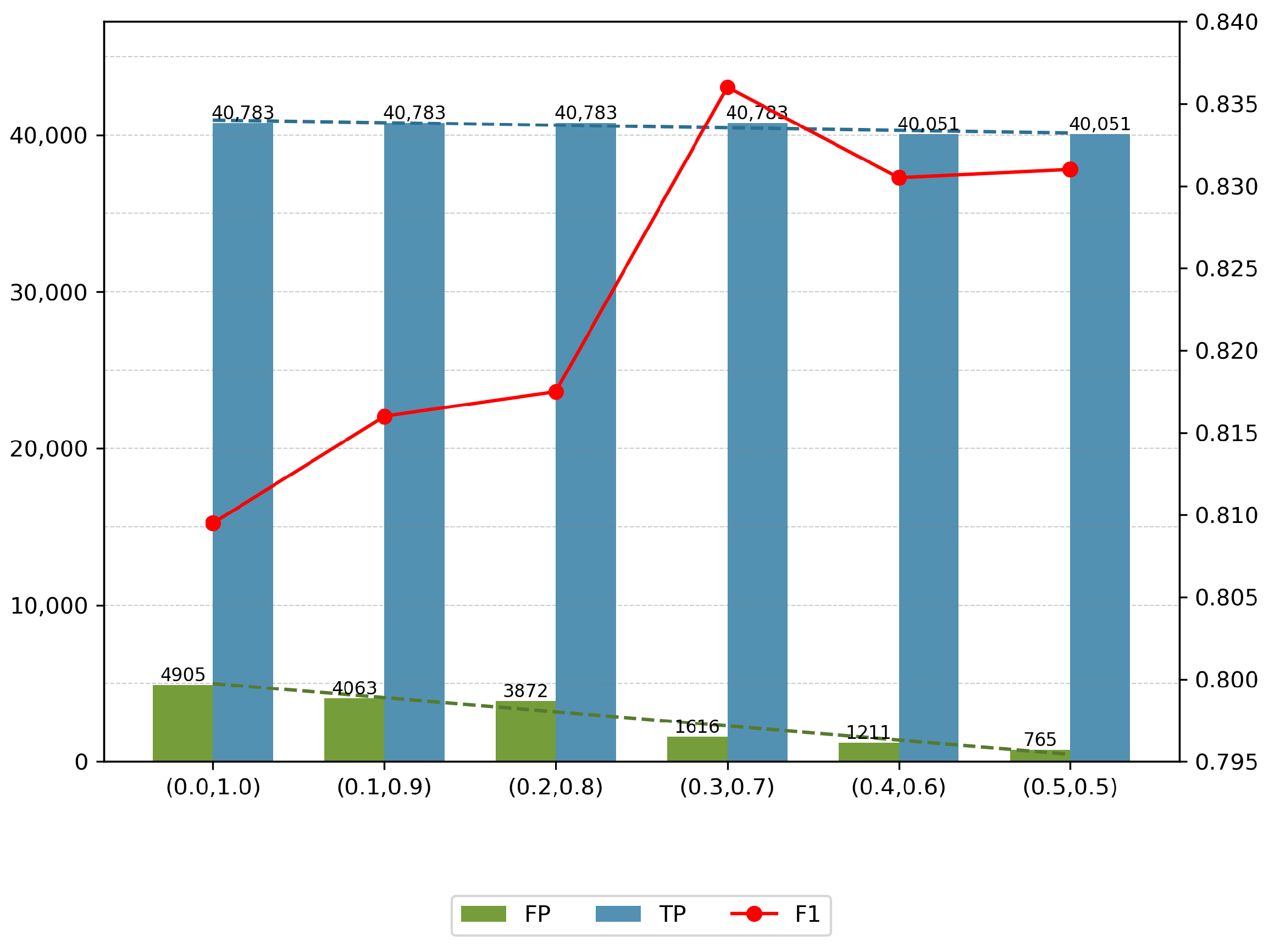
4.7.3. Abnormal Scoring Parameter Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Jung, J.J. Deep learning for anomaly detection in multivariate time series: Approaches, applications, and challenges. Inf. Fusion 2023, 91, 93–102. [Google Scholar] [CrossRef]
- Kim, B.; Alawami, M.A.; Kim, E.; Oh, S.; Park, J.; Kim, H. A comparative study of time series anomaly detection models for industrial control systems. Sensors 2023, 23, 1310. [Google Scholar] [CrossRef] [PubMed]
- Nizam, H.; Zafar, S.; Lv, Z.; Wang, F.; Hu, X. Real-time deep anomaly detection framework for multivariate time-series data in industrial iot. IEEE Sens. J. 2022, 22, 22836–22849. [Google Scholar] [CrossRef]
- Audibert, J.; Michiardi, P.; Guyard, F.; Marti, S.; Zuluaga, M.A. Usad: Unsupervised anomaly detection on multivariate time series. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 3395–3404. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, Y.; Zhong, Q.; Xie, D.; Pu, S.; Zhou, H. Divide-and-assemble: Learning block-wise memory for unsupervised anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 8791–8800. [Google Scholar]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep learning for anomaly detection in time-series data: Review, analysis, and guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, QLD, Australia, 2 December 2014; pp. 4–11. [Google Scholar] [CrossRef]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data. Proc. Aaai Conf. Artif. Intell. 2019, 33, 1409–1416. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar] [CrossRef]
- Qin, S.; Zhu, J.; Wang, D.; Ou, L.; Gui, H.; Tao, G. Decomposed Transformer with Frequency Attention for Multivariate Time Series Anomaly Detection. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–20 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1090–1098. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, K.; Wu, X. LSTM-based VAE-GAN for time-series anomaly detection. Sensors 2020, 20, 3738. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 1–11. [Google Scholar]
- Cai, L.; Janowicz, K.; Mai, G.; Yan, B.; Zhu, R. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Trans. GIS 2020, 24, 736–755. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Chen, Y.; Yu, H.; Qin, T. Adaptive memory networks with self-supervised learning for unsupervised anomaly detection. IEEE Trans. Knowl. Data Eng. 2022, 35, 12068–12080. [Google Scholar] [CrossRef]
- Shen, L.; Li, Z.; Kwok, J. Timeseries anomaly detection using temporal hierarchical one-class network. Adv. Neural Inf. Process. Syst. 2020, 33, 13016–13026. [Google Scholar]
- Shin, Y.; Lee, S.; Tariq, S.; Lee, M.S.; Jung, O.; Chung, D.; Woo, S.S. Itad: Integrative tensor-based anomaly detection system for reducing false positives of satellite systems. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual Event, 19–23 October 2020; pp. 2733–2740. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Han, J.; Su, Y.; Jiao, R.; Wen, X.; Pei, D. Multivariate time series anomaly detection and interpretation using hierarchical inter-metric and temporal embedding. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 3220–3230. [Google Scholar] [CrossRef]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A transformer-based framework for multivariate time series representation learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
- Tuli, S.; Casale, G.; Jennings, N.R. Tranad: Deep transformer networks for anomaly detection in multivariate time series data. arXiv 2022, arXiv:2201.07284. [Google Scholar] [CrossRef]
- Zhao, T.; Jin, L.; Zhou, X.; Li, S.; Liu, S.; Zhu, J. Unsupervised Anomaly Detection Approach Based on Adversarial Memory Autoencoders for Multivariate Time Series. Comput. Mater. Contin. 2023, 76, 329–346. [Google Scholar] [CrossRef]
- Zeng, F.; Chen, M.; Qian, C.; Wang, Y.; Zhou, Y.; Tang, W. Multivariate time series anomaly detection with adversarial transformer architecture in the Internet of Things. Future Gener. Comput. Syst. 2023, 144, 244–255. [Google Scholar] [CrossRef]
- Xu, J.; Wu, H.; Wang, J.; Long, M. Anomaly transformer: Time series anomaly detection with association discrepancy. arXiv 2021, arXiv:2110.02642. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mathur, A.P.; Tippenhauer, N.O. SWaT: A water treatment testbed for research and training on ICS security. In Proceedings of the 2016 International Workshop on Cyber-physical Systems for Smart Water Networks (CySWater), Vienna, Austria, 11 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 31–36. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate time-series anomaly detection via graph attention network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 841–850. [Google Scholar] [CrossRef]
- Garg, A.; Zhang, W.; Samaran, J.; Savitha, R.; Foo, C.S. An evaluation of anomaly detection and diagnosis in multivariate time series. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2508–2517. [Google Scholar] [CrossRef] [PubMed]
- Abdulaal, A.; Liu, Z.; Lancewicki, T. Practical approach to asynchronous multivariate time series anomaly detection and localization. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 2485–2494. [Google Scholar] [CrossRef]
- Xu, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; Liu, Y.; Zhao, Y.; Pei, D.; Feng, Y.; et al. Unsupervised anomaly detection via variational auto-encoder for seasonal kpis in web applications. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 187–196. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]




| Dataset | Training Samples | Testing Samples | Dimensions | Anomaly Rate (%) |
|---|---|---|---|---|
| SWaT | 496,800 | 449,919 | 51 | 11.98 |
| WADI | 1,048,571 | 172,801 | 123 | 5.99 |
| SMAP | 135,183 | 427,617 | 25 | 13.11 |
| PSM | 132,481 | 87,841 | 25 | 27.8 |
| Method | SWaT (%) | SMAP (%) | PSM (%) | WADI (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | P | R | F1 | P | R | F1 | |
| THOC | 83.94 | 86.36 | 85.13 | 92.06 | 89.34 | 90.68 | 88.14 | 90.99 | 89.54 | 68.13 | 74.26 | 71.06 |
| ITAD | 63.13 | 52.08 | 57.08 | 82.42 | 66.89 | 73.85 | 72.80 | 64.02 | 68.13 | 56.62 | 48.38 | 52.18 |
| OmniAnomaly | 81.42 | 84.30 | 82.83 | 92.49 | 81.99 | 86.92 | 88.39 | 74.46 | 80.83 | 75.94 | 62.80 | 68.75 |
| InterFusion | 80.59 | 85.58 | 83.01 | 98.77 | 88.52 | 89.14 | 83.61 | 83.45 | 83.52 | 83.44 | 86.53 | 84.96 |
| TransFram | 92.47 | 75.88 | 83.36 | 85.36 | 87.48 | 86.41 | 88.14 | 86.99 | 87.56 | 81.16 | 83.69 | 82.41 |
| USAD | 98.70 | 74.02 | 84.60 | 76.97 | 98.31 | 86.34 | 92.10 | 57.60 | 70.90 | 72.88 | 80.58 | 76.54 |
| TranAD | 97.60 | 69.97 | 81.51 | 80.43 | 99.99 | 89.15 | 96.44 | 87.37 | 91.68 | 84.89 | 82.96 | 83.91 |
| Adformer | 98.90 | 76.18 | 86.07 | 97.30 | 80.37 | 88.03 | 99.34 | 86.47 | 92.46 | 90.25 | 81.24 | 85.51 |
| AOST | 96.92 | 80.63 | 88.02 | 94.86 | 88.93 | 91.80 | 96.53 | 88.64 | 92.41 | 90.81 | 83.01 | 86.73 |
| Outlier Suppression | Adversarial Learning | P (%) | R (%) | F1 (%) |
|---|---|---|---|---|
| × | ✓ | 99.44 | 68.58 | 81.17 |
| ✓ | × | 64.12 | 81.58 | 71.78 |
| ✓ | ✓ | 96.92 | 80.63 | 88.02 |
| Encoder Layers | SWaT | SMAP | PSM | |||
|---|---|---|---|---|---|---|
| Time (min) | F1 (%) | Time (min) | F1 (%) | Time (min) | F1 (%) | |
| 1 | 10 | 64.9 | 11 | 78.8 | 9 | 81.0 |
| 2 | 12 | 88.0 | 13 | 91.8 | 10 | 92.4 |
| 3 | 20 | 88.2 | 19 | 92.0 | 15 | 92.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, T.; He, P.; Yang, Y.; Wang, S. An Outlier Suppression and Adversarial Learning Model for Anomaly Detection in Multivariate Time Series. Entropy 2025, 27, 1151. https://doi.org/10.3390/e27111151
Zhang W, Li T, He P, Yang Y, Wang S. An Outlier Suppression and Adversarial Learning Model for Anomaly Detection in Multivariate Time Series. Entropy. 2025; 27(11):1151. https://doi.org/10.3390/e27111151
Chicago/Turabian StyleZhang, Wei, Ting Li, Ping He, Yuqing Yang, and Shengrui Wang. 2025. "An Outlier Suppression and Adversarial Learning Model for Anomaly Detection in Multivariate Time Series" Entropy 27, no. 11: 1151. https://doi.org/10.3390/e27111151
APA StyleZhang, W., Li, T., He, P., Yang, Y., & Wang, S. (2025). An Outlier Suppression and Adversarial Learning Model for Anomaly Detection in Multivariate Time Series. Entropy, 27(11), 1151. https://doi.org/10.3390/e27111151





