Higher-Order Correlations Between Thermodynamic Fluctuations in Compressible Aerodynamic Turbulence
Abstract
1. Introduction
2. Fluctuating Equation-of-State
2.1. Definitions
2.2. Favre- and Reynolds-Averaging
2.3. Dilute-Gas Equation-of-State
2.4. A Conceptual Joint -pdf Approach
3. Thermodynamic Turbulence Structure in Compressible Plane Channel Flow
4. Exact and Approximate Relations Between Moments of the Thermodynamic Fluctuations
4.1. Correlation Coefficients of Order n (n)
4.2. Central Moments of
4.3. Unscrambling the Exact Relations
4.4. Linearization of the Equations Between
4.5. Linearized Relations Between
5. Statistical Identities and Bounds
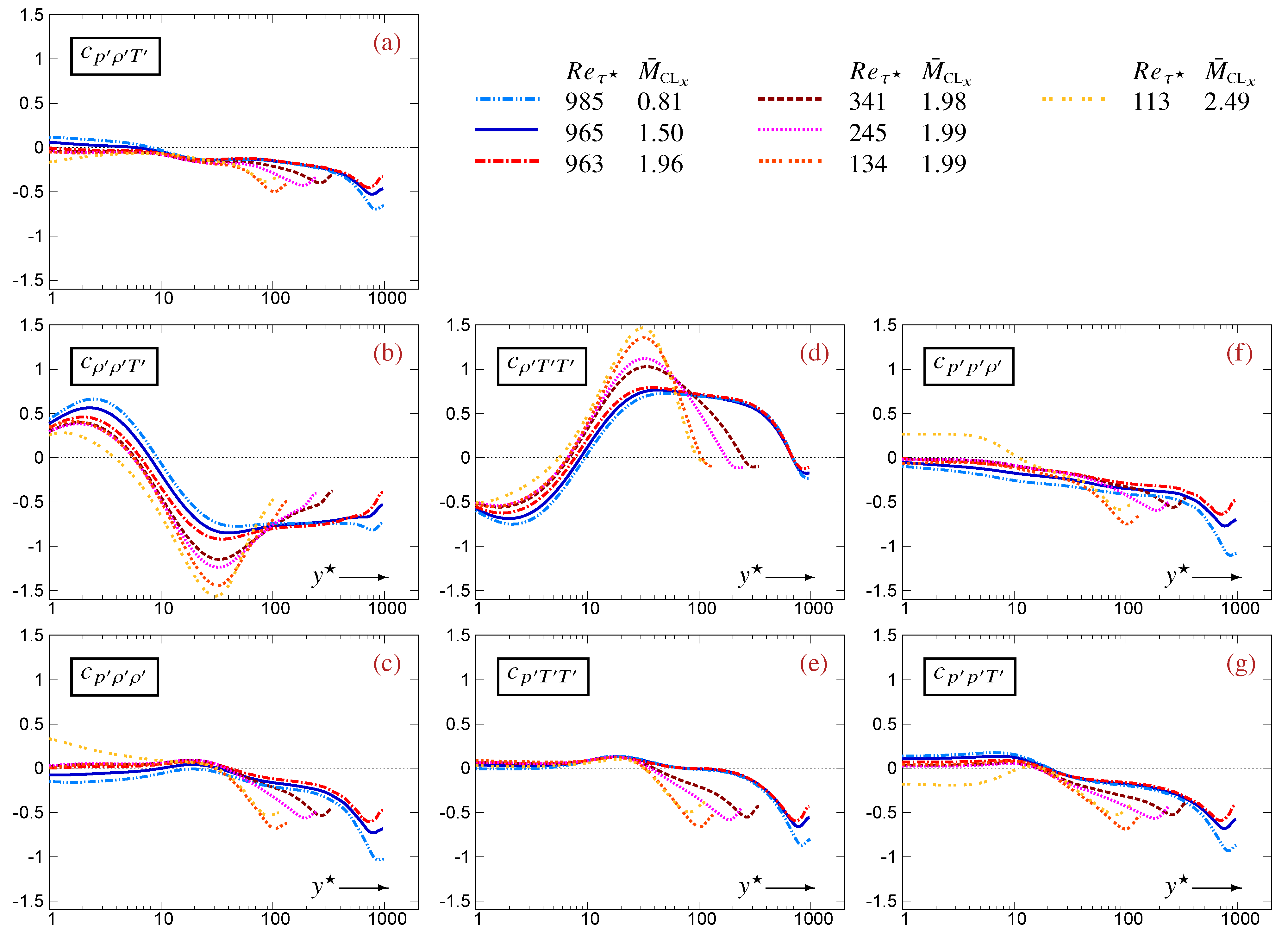
6. Implications for -Correlations
6.1. Profiles of
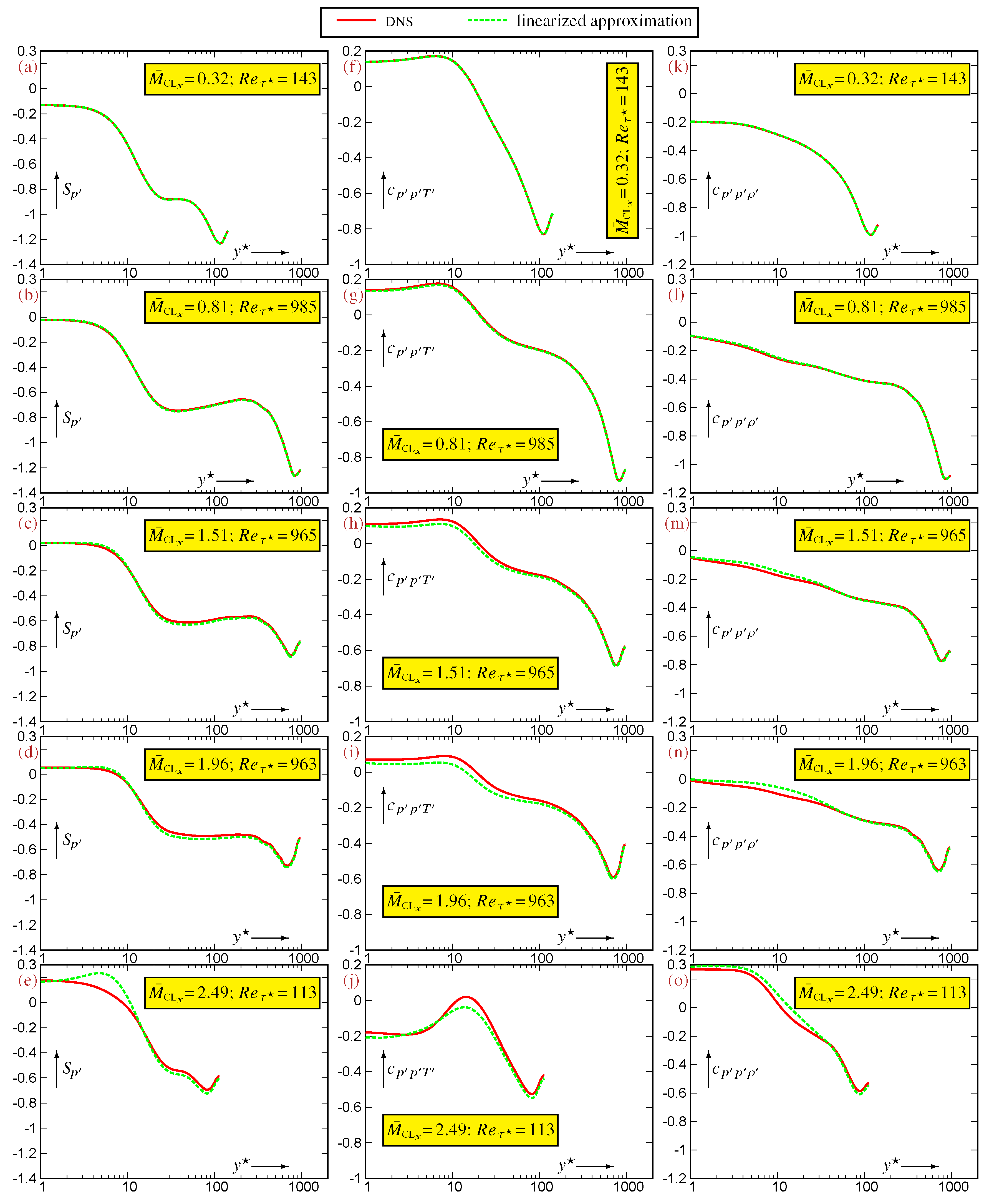
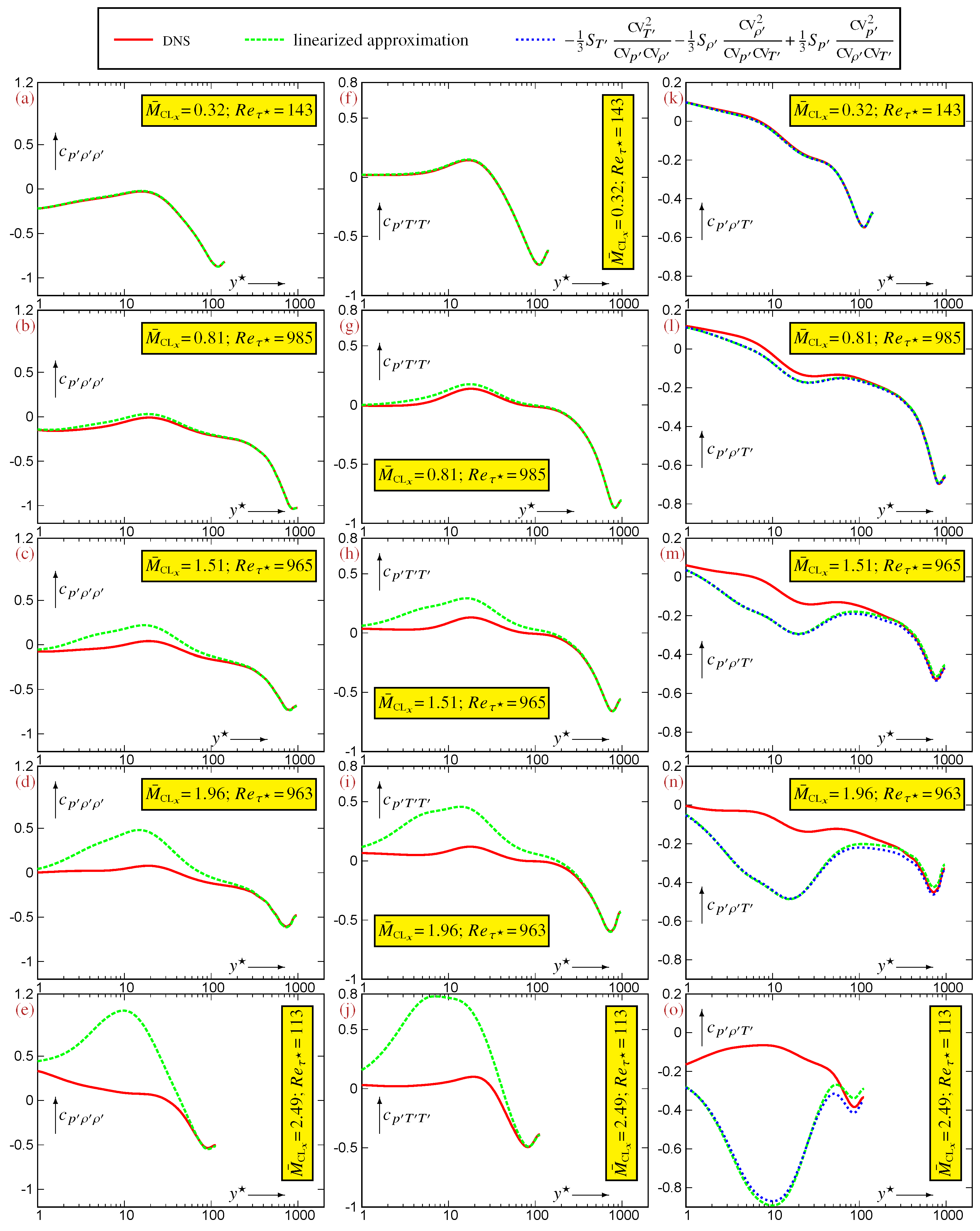
6.2. Linearization Error in Relations Between
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| , | correlation coefficients |
| n, , , | n-order, 2-order, 3-order, 4-order |
| , | coefficient(s) of variation |
| direct numerical simulation | |
| Huang–Coleman–Bradshaw [17] | |
| , n | higher-order terms, n-order terms |
| probability density function | |
| rms | root-mean-square |
| turbulent plane channel |
Appendix A. Does Favre-Averaging Simplify the Equations?
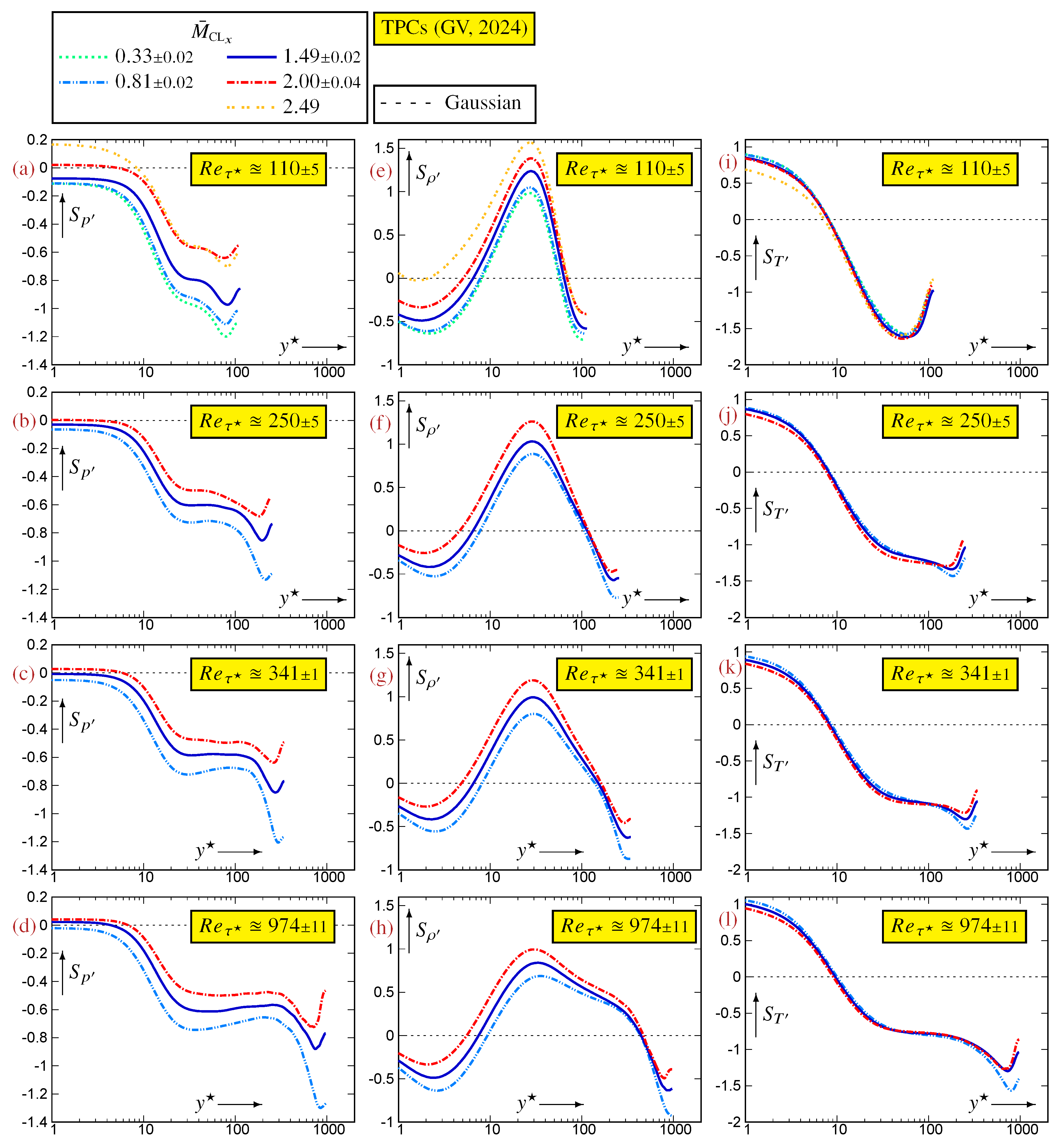
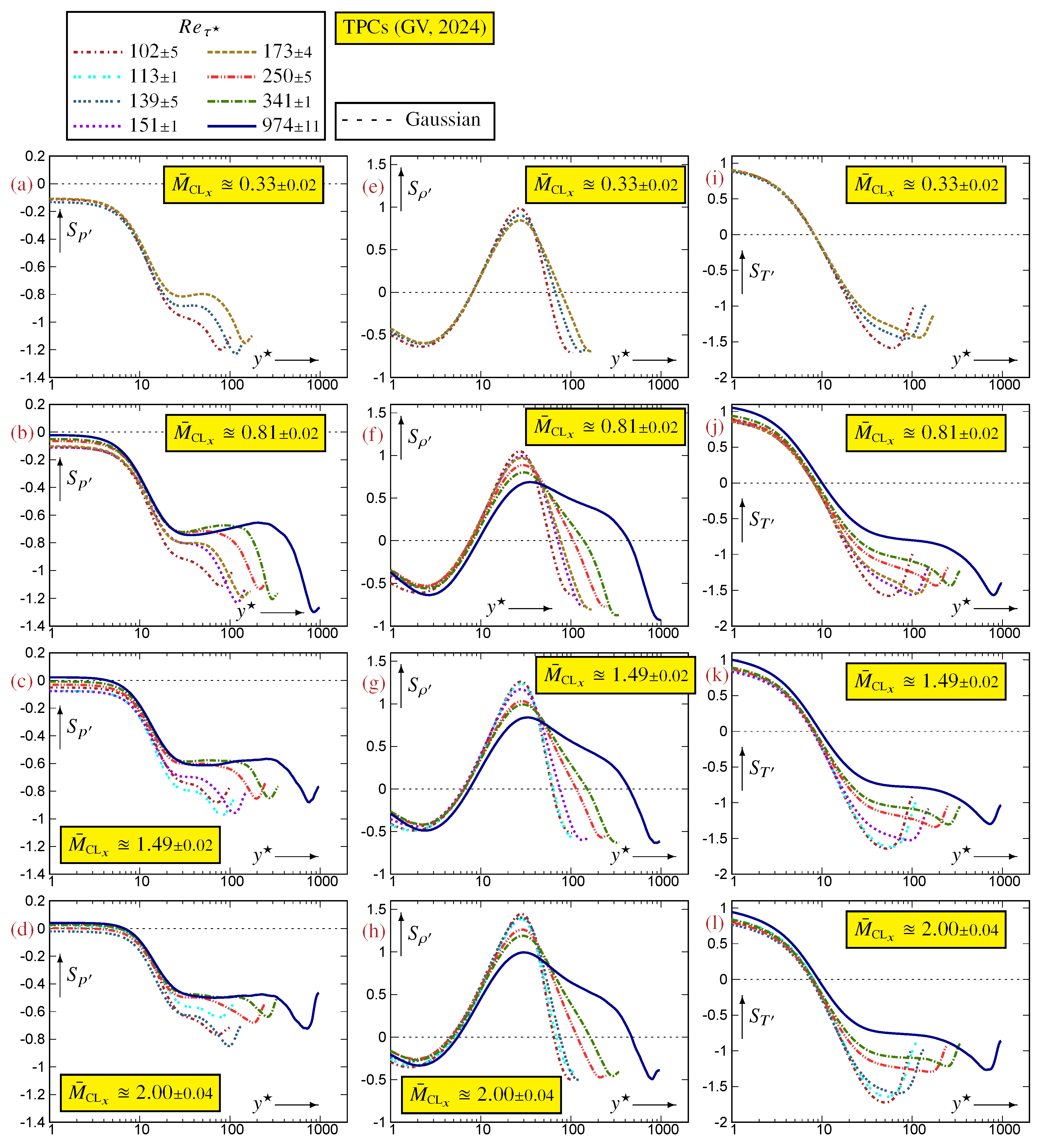
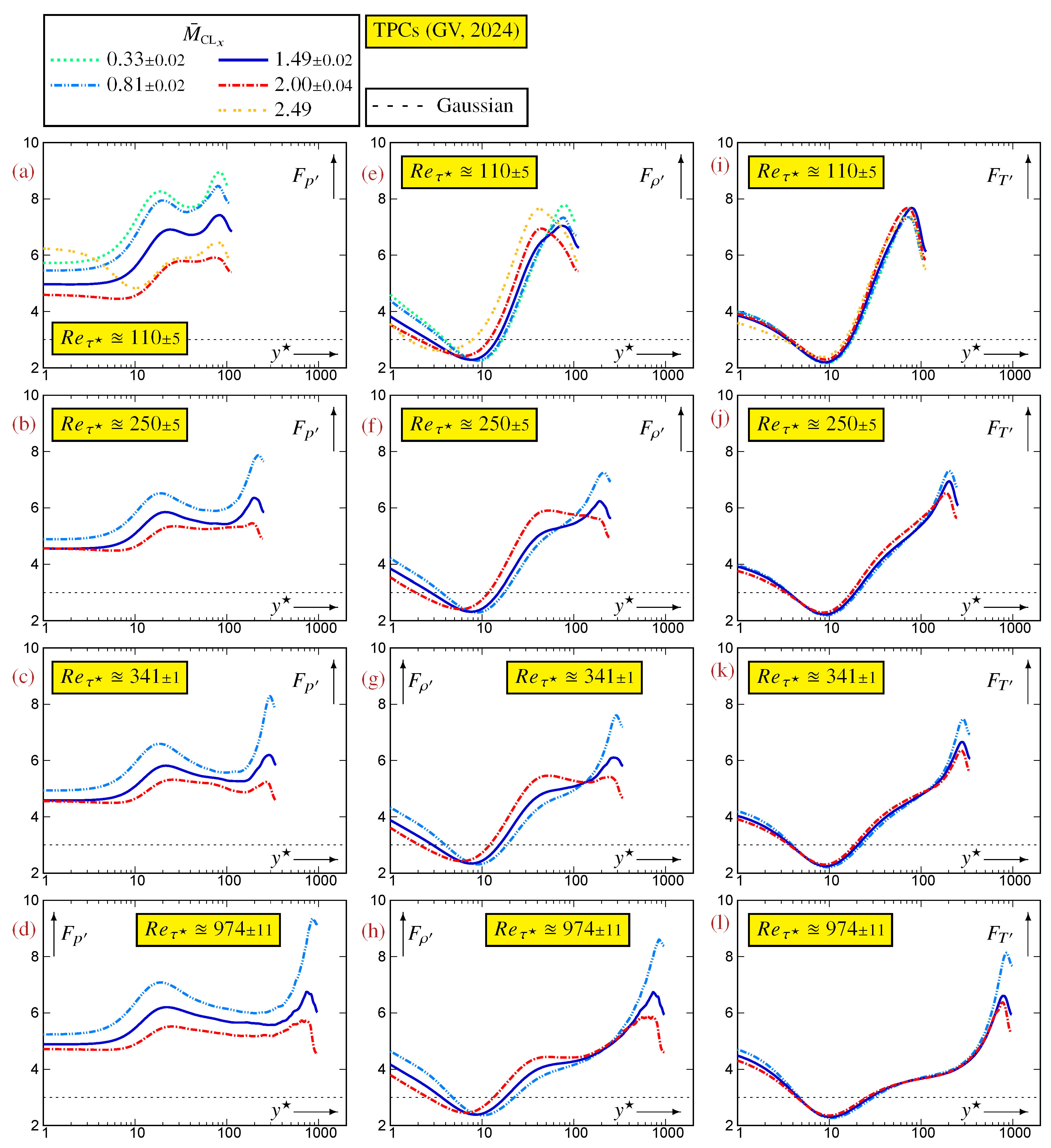
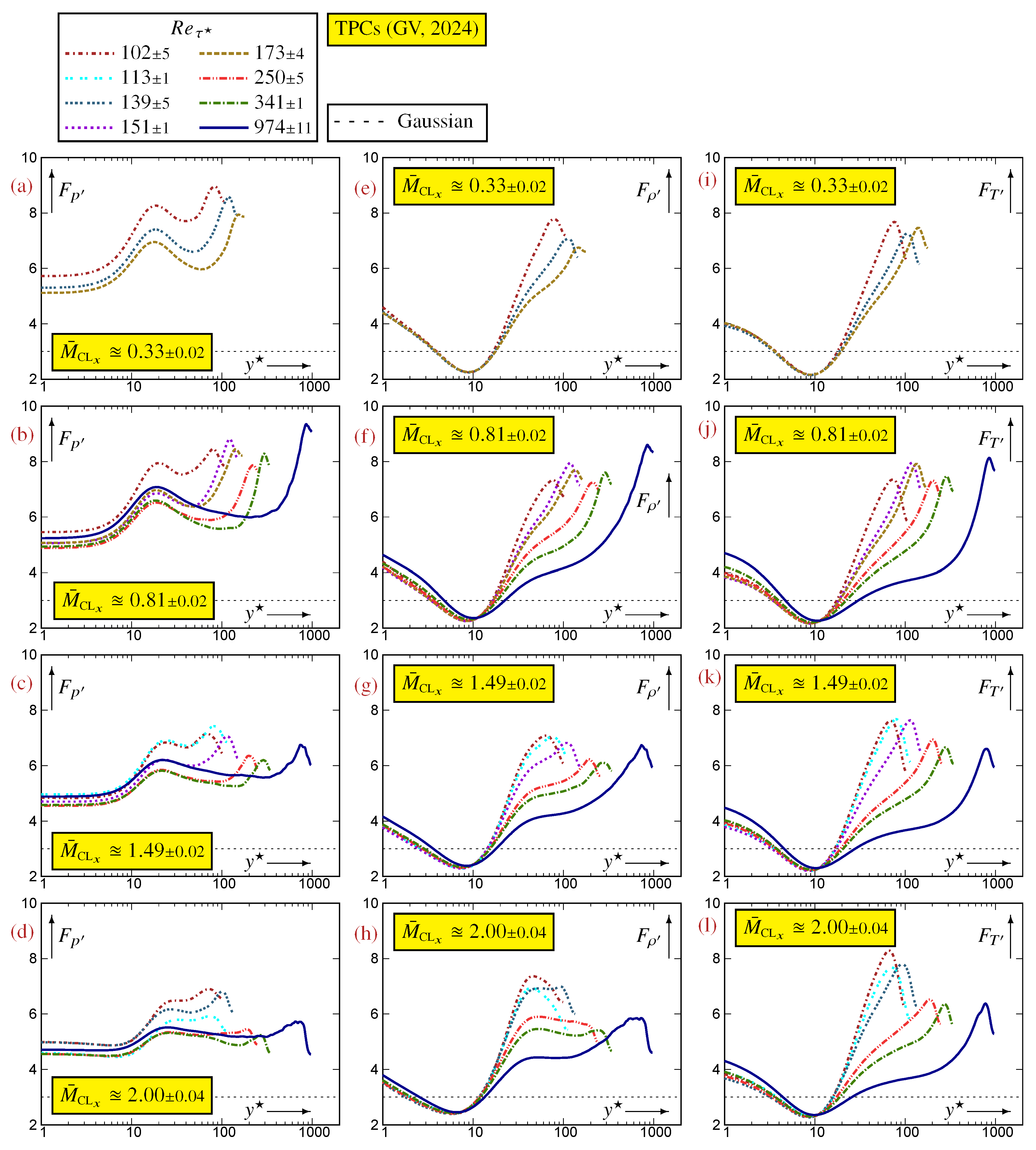
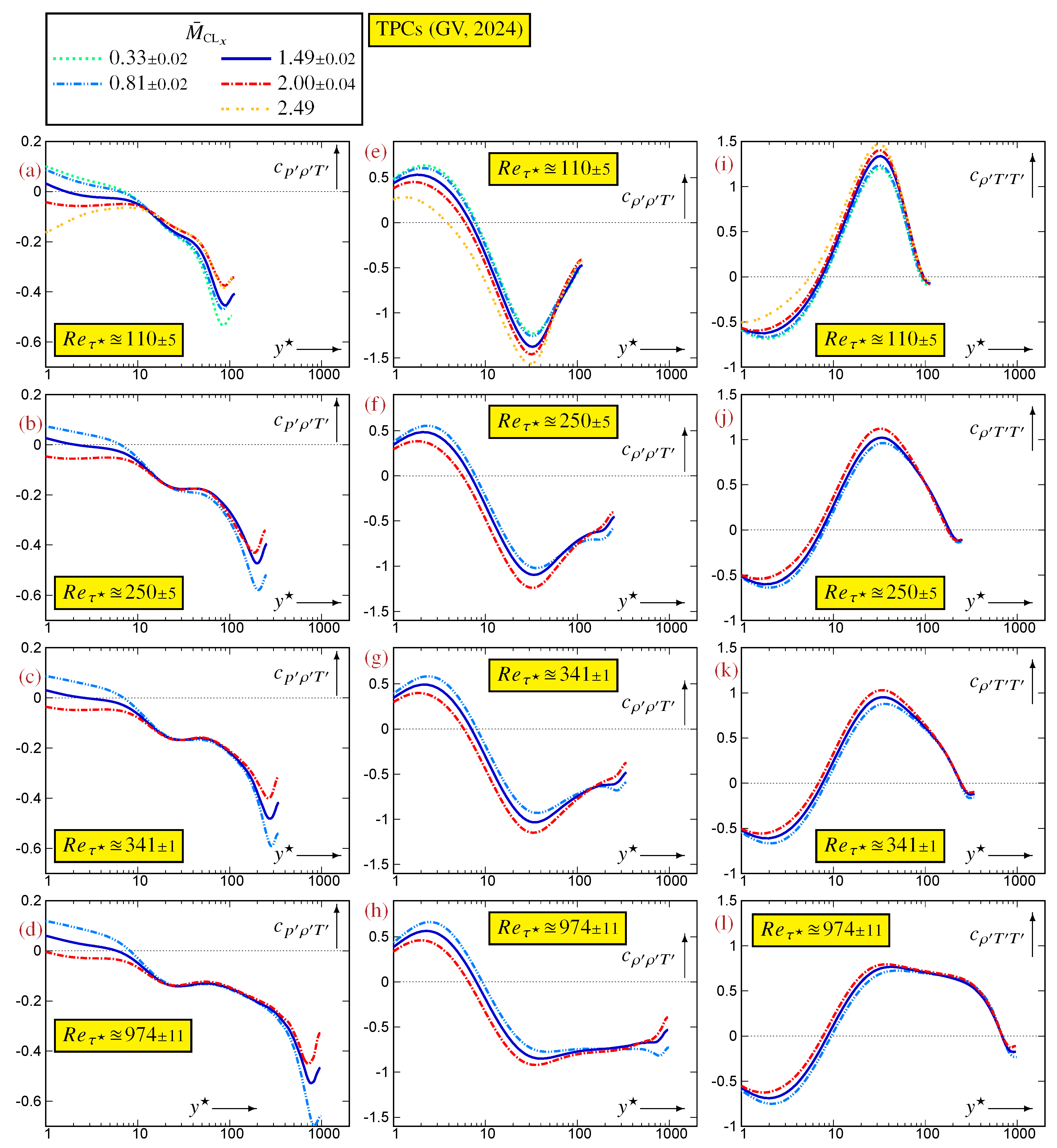
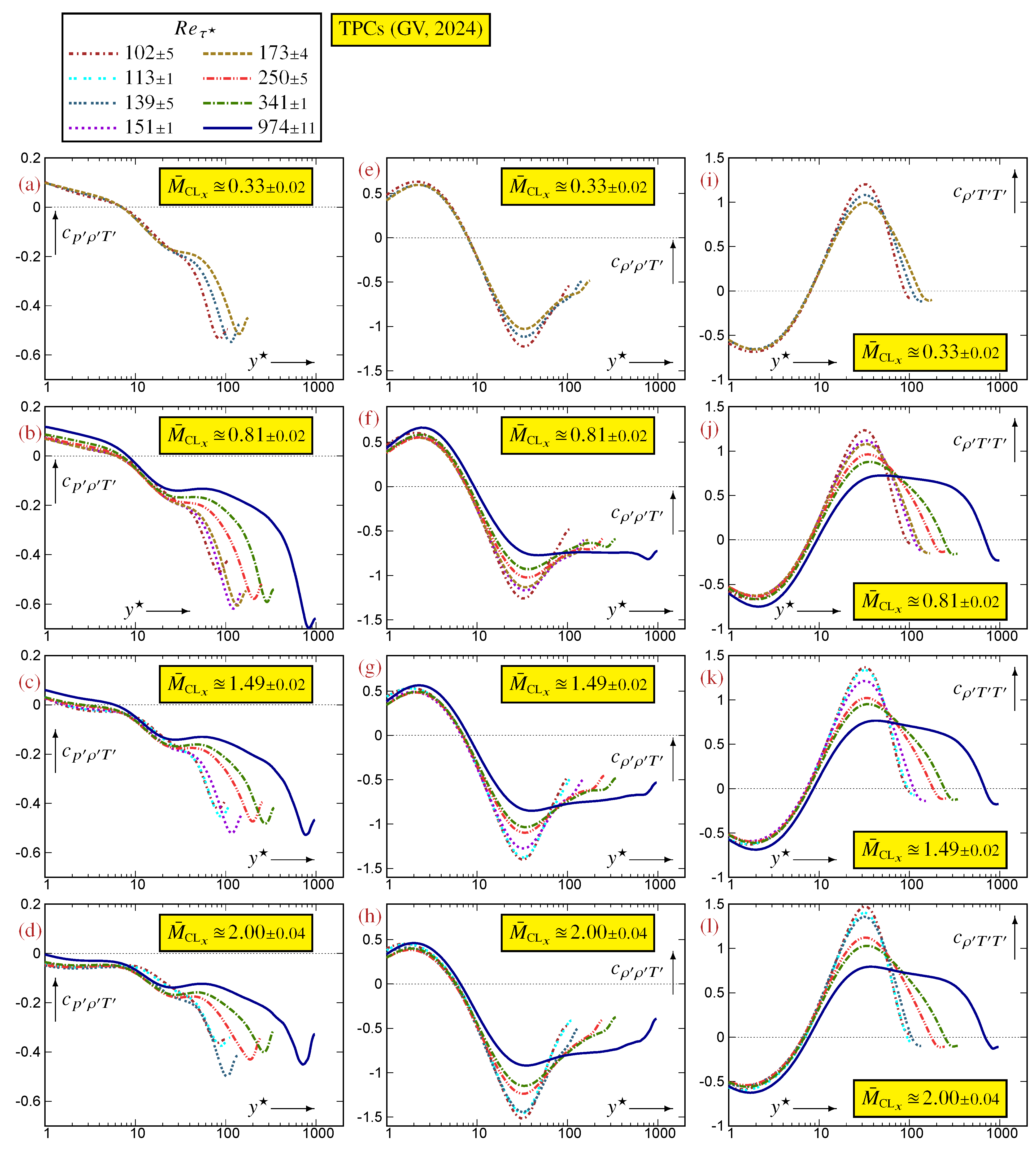
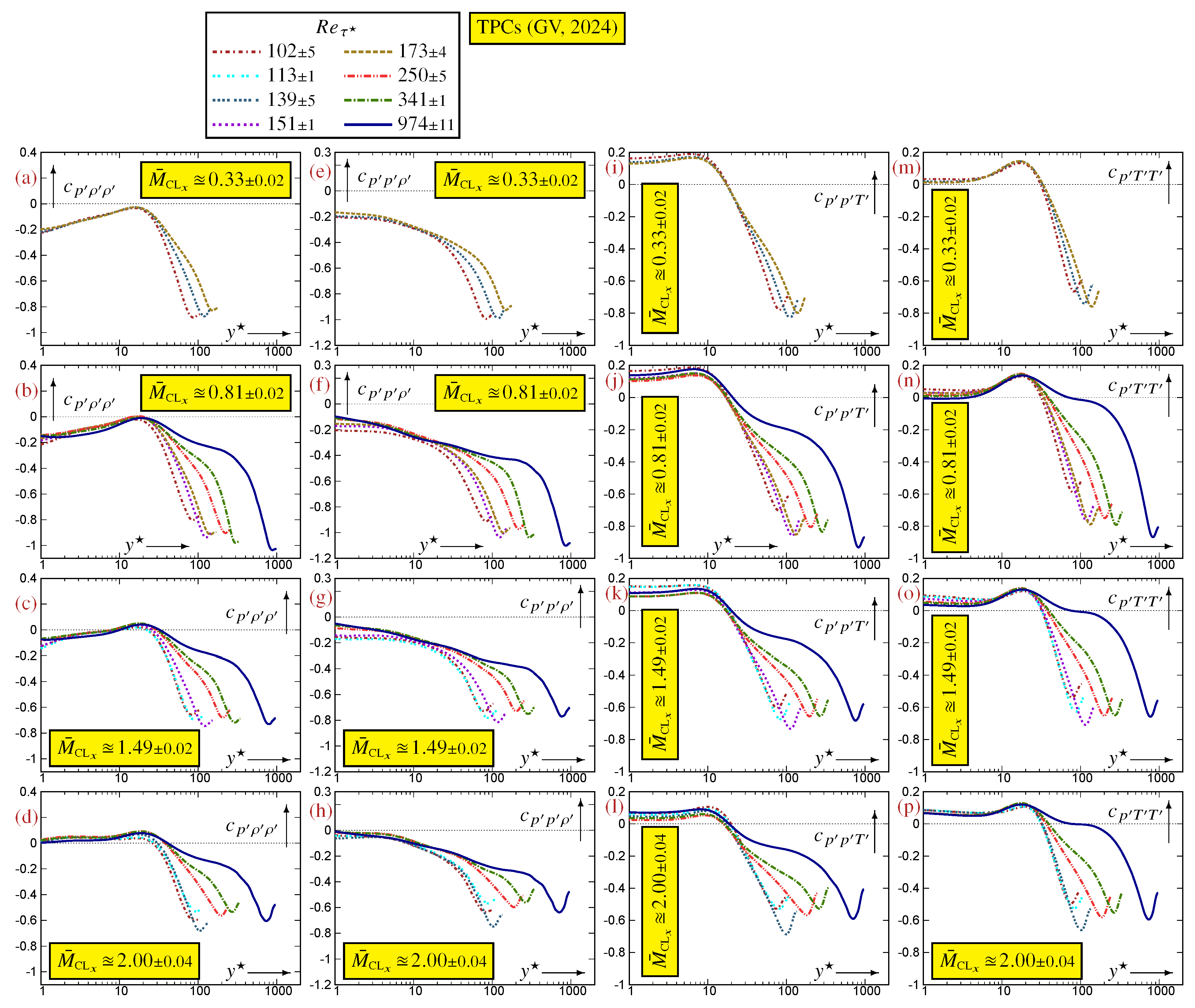
Appendix B. Reynolds and Mach Number Effects in a Turbulent Plane Channel Flow

Appendix C. Power Series and Amplitude Effects
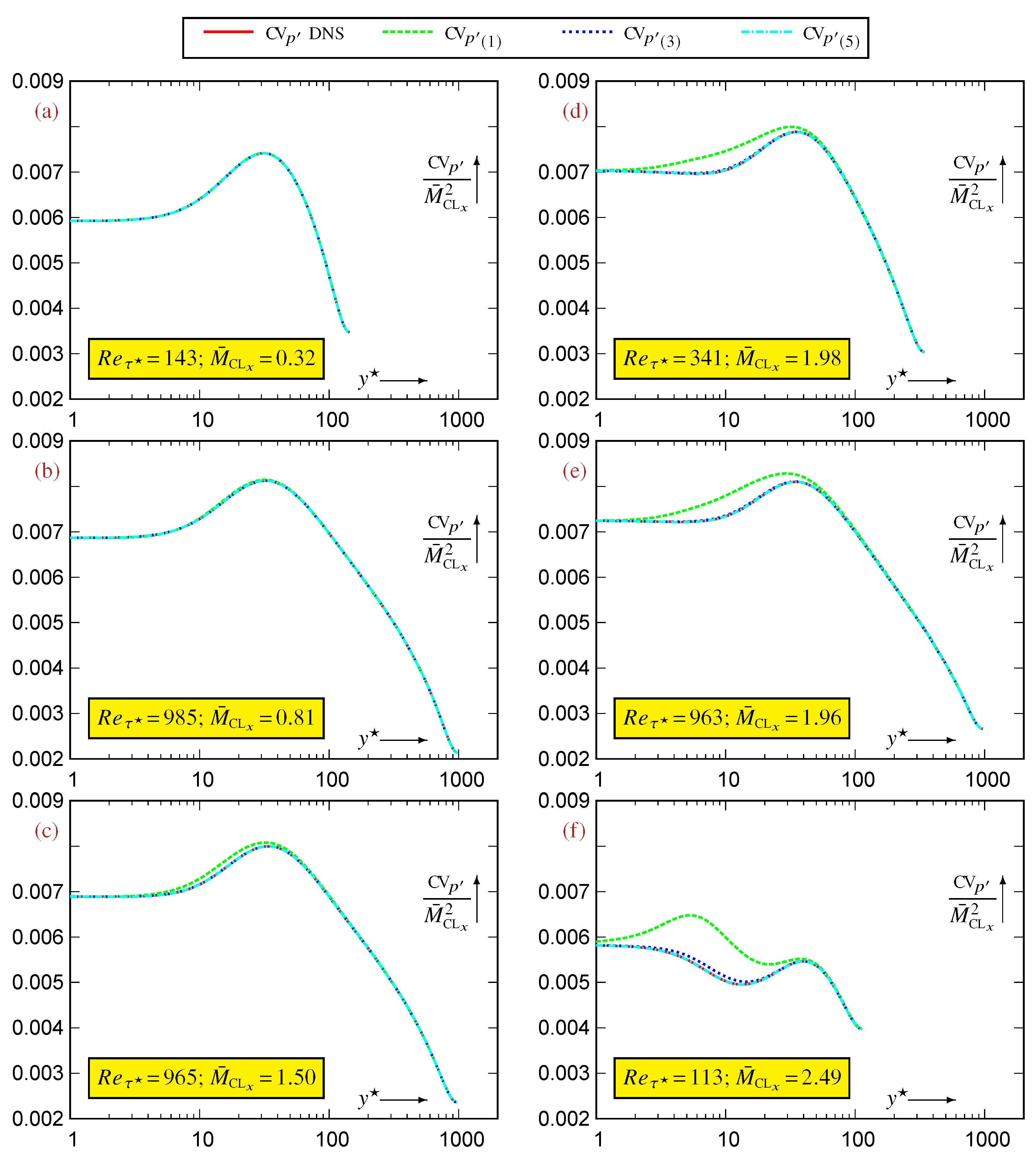
References
- Donzis, D.A.; Jagannathan, S. Fluctuation of thermodynamic variables in stationary compressible turbulence. J. Fluid Mech. 2013, 733, 221–244. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Vallet, I. Pressure, density, temperature and entropy fluctuations in compressible turbulent plane channel flow. J. Fluid Mech. 2014, 757, 701–746. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Bi, W.T.; Hussain, F.; She, Z.S. A generalized Reynolds analogy for compressible wall-bounded turbulent flows. J. Fluid Mech. 2014, 739, 392–420. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Vallet, I. Correlation coefficients of thermodynamic fluctuations in compressible aerodynamic turbulence. J. Fluid Mech. 2018, 851, 447–478. [Google Scholar] [CrossRef]
- Coleman, G.N.; Kim, J.; Moser, R.D. A Numerical Study of Turbulent Supersonic Isothermal-Wall Channel Flow. J. Fluid Mech. 1995, 305, 159–183. [Google Scholar] [CrossRef]
- Bernardini, M.; Pirozzoli, S. Turbulence in supersonic boundary-layers at moderate Reynolds numbers. J. Fluid Mech. 2011, 688, 120–168. [Google Scholar] [CrossRef]
- Modesti, D.; Pirozzoli, S. Reynolds and Mach number effects in compressible turbulent channel. Int. J. Heat Fluid Flow 2016, 59, 33–49. [Google Scholar] [CrossRef]
- Zhang, C.; Duan, L.; Choudhari, M.M. Direct numerical simulation database for supersonic and hypersonic turbulent boundary-layers. AIAA J. 2018, 56, 4297–4311. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Hussain, F. Turbulence statistics ans coherent structures in compressible turbulent channel flow. Phys. Rev. Fluids 2020, 5, 084603. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Vallet, I. Scalings of pressure fluctuations in compressible turbulent plane channel flow. J. Fluid Mech. 2023, 958, A19. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Vallet, I. Total and static temperature statistics in compressible turbulent plane channel flow. J. Fluid Mech. 2024, 978, A25. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Vallet, I. Compressible turbulent plane channel DNS datasets. Data Brief 2024, 55, 110737. [Google Scholar] [CrossRef]
- Liepmann, H.W.; Roshko, A. Elements of Gasdynamics; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
- Gerolymos, G.A.; Vallet, I. Entropy fluctuations and correlations in compressible turbulent plane channel flow. Entropy 2024, 26, 530. [Google Scholar] [CrossRef] [PubMed]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; MIT Press: Cambridge, MA, USA, 1971; Volume 1. [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; MIT Press: Cambridge, MA, USA, 1975; Volume 2. [Google Scholar]
- Huang, P.G.; Coleman, G.N.; Bradshaw, P. Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 1995, 305, 185–218. [Google Scholar] [CrossRef]
- Hou, X.; Xu, D.; Wang, J.; Chen, S. Correlations between thermodynamic fluctuations in shock-wave/turbulent-boundary-layer interaction. Phys. Rev. Fluids 2024, 9, 073401. [Google Scholar] [CrossRef]
- Frenkiel, F.N.; Klebanoff, P.S. Higher-order correlations in a turbulent field. Phys. Fluids 1967, 10, 507–520. [Google Scholar] [CrossRef]
- Lumley, J.L. On 3-order mixed moments. Phys. Fluids 1974, 17, 1127–1129. [Google Scholar] [CrossRef]
- Klaassen, C.A.J.; Mokveld, P.J.; van Es, B. Squared skewness minus kurtosis bounded by 186/125 for unimodal distributions. Stat. Prob. Lett. 2000, 50, 131–135. [Google Scholar] [CrossRef]
- Ogasawara, H. Extension of Pierson’s inequality between skewness and kurtosis to multivariate case. Stat. Prob. Lett. 2017, 130, 12–16. [Google Scholar] [CrossRef]
- Pham, H. (Ed.) Handbook of Engineering Statistics; Springer: London, UK, 2006. [Google Scholar]
- Keener, R.W. Theoretical Statistics; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Sarkar, S.; Erlebacher, G.; Hussaini, M.Y.; Kreiss, H.O. The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 1991, 227, 473–493. [Google Scholar] [CrossRef]
- Canuto, V.M. Compressible Turbulence. Astrophys. J. 1997, 482, 827–851. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Jacobsen, R.T.; Penoncello, S.G.; Friend, D.G. Thermodynamic properties of air and mixtures of nitrogen, argon, and oxygen from 60 to 2000 K at pressures to 2000 MPa. J. Phys. Chem. Data 2000, 29, 331–385. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Foundations of the Theory of Probability, 2nd English ed.; Chelsea Publishing Co.: New York, NY, USA, 1956. [Google Scholar]
- Kestin, J. A Course in Thermodynamics, 1st ed.; Volume 1, Hemisphere; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Gerolymos, G.A. Approximation error of the Lagrange reconstructing polynomial. J. Approx. Theory 2011, 163, 267–305. [Google Scholar] [CrossRef]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Muehlig, H. Handbook of Mathematics; Springer: Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Bóna, M. Handbook of Enumerative Combinatorics, 1st ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Knuth, D.E. 2 notes on notation. Am. Math. Mon. 1992, 99, 403–422. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics, 2nd ed.; Addison–Wesley: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Pearson, K. Mathematical contributions to the theory of evolution. XIX. Second supplement to a memoir on skew variation. Phil. Trans. Roy. Soc. London A 1916, 216, 429–457. [Google Scholar] [CrossRef]
- André, J.C.; de Moor, G.; Lacarrère, P.; du Vachat, R. Turbulence approximation in inhomogeneous flows–I–The clipping approximation. J. Atmos. Sci. 1976, 33, 476–481. [Google Scholar] [CrossRef]
- Dharmadhikari, S.W.; Jogdeo, K. Multivariate unimodality. Ann. Stat. 1976, 4, 607–613. [Google Scholar] [CrossRef]
- Ben Nasr, N.; Gerolymos, G.A.; Vallet, I. Low-diffusion approximate Riemann solvers for Reynolds-stress transport. J. Comput. Phys. 2014, 268, 186–235. [Google Scholar] [CrossRef]
- Favre, A. Equations des gaz turbulents compressibles–I–Formes générales. J. Méc. 1965, 4, 361–390. [Google Scholar]
- Favre, A. Equations des gaz turbulents compressibles–II–Méthode des vitesses moyennes; Méthode des vitesses moyennes pondérées par la masse volumique. J. Méc. 1965, 4, 391–421. [Google Scholar]
- Österlund, J.M.; Johansson, A.V.; Nagib, H.M.; Hites, M.H. A note on the overlap region in turbulent boundary-layers. Phys. Fluids 2000, 12, 1–4. [Google Scholar] [CrossRef]
- Riley, K.F.; Hobson, M.P.; Bence, S.J. Mathematical Methods for Physics and Engineering, 3rd ed.; Canbridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Lele, S.K. Compressibility effects on turbulence. Ann. Rev. Fluid Mech. 1994, 26, 211–254. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerolymos, G.A.; Vallet, I. Higher-Order Correlations Between Thermodynamic Fluctuations in Compressible Aerodynamic Turbulence. Entropy 2025, 27, 1103. https://doi.org/10.3390/e27111103
Gerolymos GA, Vallet I. Higher-Order Correlations Between Thermodynamic Fluctuations in Compressible Aerodynamic Turbulence. Entropy. 2025; 27(11):1103. https://doi.org/10.3390/e27111103
Chicago/Turabian StyleGerolymos, Georges A., and Isabelle Vallet. 2025. "Higher-Order Correlations Between Thermodynamic Fluctuations in Compressible Aerodynamic Turbulence" Entropy 27, no. 11: 1103. https://doi.org/10.3390/e27111103
APA StyleGerolymos, G. A., & Vallet, I. (2025). Higher-Order Correlations Between Thermodynamic Fluctuations in Compressible Aerodynamic Turbulence. Entropy, 27(11), 1103. https://doi.org/10.3390/e27111103






