Compatibility of a Competition Model for Explaining Eye Fixation Durations During Free Viewing
Abstract
1. Introduction
1.1. Short Description of Neural Control of Saccadic Eye Movement and Eye Fixations
1.2. Visual Position Selection
1.3. Eye Fixation Durations (EFDs)
1.4. Competition Model (C Model)
2. Methods
2.1. Database
2.2. Models
2.3. Statistical Analysis
2.4. Shannon Entropy
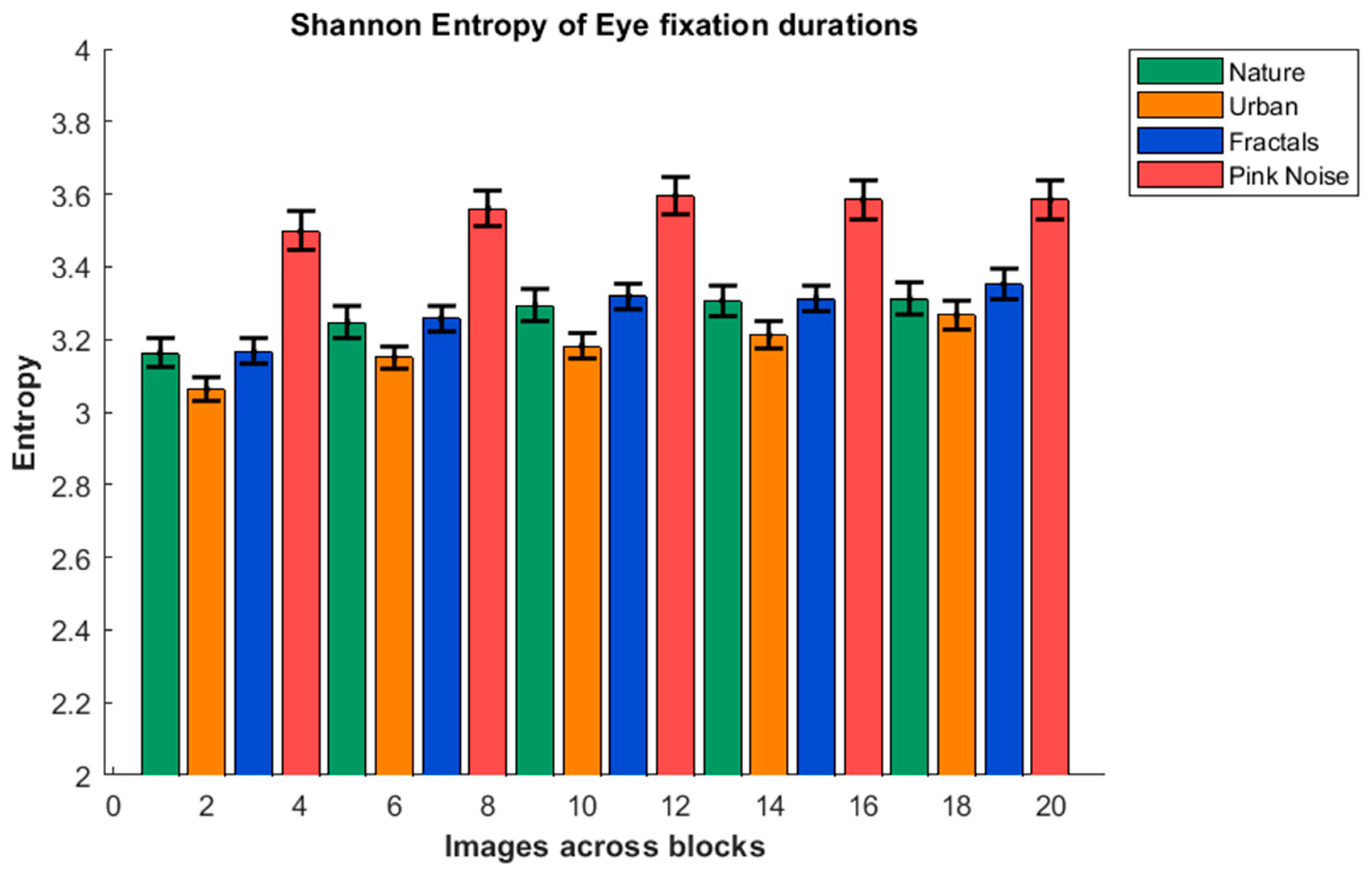
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dodge, R.; Cline, T.S. The angle velocity of eye movements. Psychol. Rev. 1901, 8, 145–157. [Google Scholar] [CrossRef]
- Hyde, J.E. Some Characteristics of voluntary human ocular eye movements in the horizontal plane. Am. J. Ophtalmol. 1959, 48, 85–94. [Google Scholar] [CrossRef]
- Robinson, D.A. The Mechanics of Human Saccadic Eye Movements. J. Physiol. 1964, 174, 245–264. [Google Scholar] [CrossRef]
- Bahill, A.T.; Stark, L. The Trajectories of Saccadic Eye Movements. Sci. Am. 1979, 240, 108–117. [Google Scholar] [CrossRef]
- Van Gisbergen, J.A.; Van Opstal, A.J.; Tax, A.A. Collicular ensemble coding of saccades based on vector summation. Neuroscience 1987, 21, 541–555. [Google Scholar] [CrossRef]
- Carpenter, R.H.S. Movements of the Eyes; Pion: London, UK, 1988. [Google Scholar]
- Luschei, E.S.; Fuchs, A.F. Activity of brain stem neurons during eye movements of alert monkeys. J. Neurophysiol. 1972, 35, 445–461. [Google Scholar] [CrossRef]
- Robinson, D.A. Oculomotor behavior in the monkey. J. Neurophysiol. 1970, 33, 393–404. [Google Scholar] [CrossRef]
- Schiller, P.H. The discharge characteristics of single units in the oculomotor and abducens nuclei of the unanesthetized monkey. Exp. Brain Res. 1970, 10, 347–362. [Google Scholar] [CrossRef]
- Goebel, H.H.; Komatsuzaki, A.; Bender, M.B.; Cohen, B. Lesions of the pontine tegmentum and conjugate gaze paralysis. Arch. Neurol. 1971, 24, 431–440. [Google Scholar] [CrossRef]
- Van Gisbergen, J.; Robinson. Generation of micro and microsaccades by bursts neurons in the monkey. In Control of Gaze by Brain Stem Neurons; Berthoz, A., Baker, R.G., Eds.; Elsevier/North Holland’ Biomedical Press: Amsterdam, The Netherlands, 1977; pp. 301–308. [Google Scholar]
- Van Gisbergen, J.A.; Robinson, D.A.; Gielen, S. A quantitative analysis of generation of saccadic eye movements by burst neurons. J. Neurophysiol. 1981, 45, 417–442. [Google Scholar] [CrossRef]
- Robinson, D.A. The use of control systems analysis in the neurophysiology of eye movements. Annu. Rev. Neurosci. 1981, 4, 463–503. [Google Scholar] [CrossRef] [PubMed]
- Zee, D.S.; Optican, L.M.; Cook, J.D.; Robinson, D.A.; Engel, W.K. Slow saccades in spinocerebellar degeneration. Arch. Neurol. 1976, 33, 243–251. [Google Scholar] [CrossRef]
- Smith, M.A.; Crawford, J.D. Distributed population mechanism for the 3-D oculomotor reference frame transformation. J. Neurophysiol. 2005, 93, 1742–1761. [Google Scholar] [CrossRef]
- Evinger, C.; Kaneko, C.R.; Fuchs, A.F. Activity of omnipause neurons in alert cats during saccadic eye movements and visual stimuli. J. Neurophysiol. 1982, 47, 827–844. [Google Scholar] [CrossRef] [PubMed]
- Nakao, S.; Curthoys, I.S.; Markham, C.H. Direct inhibitory projection of pause neurons to nystagmus-related pontomedullary reticular burst neurons in the cat. Exp. Brain Res. 1980, 40, 283–293. [Google Scholar] [CrossRef] [PubMed]
- Evinger, C.; Kaneko, C.R.S.; Johansen, G.W.; Fuchs, A.F. Omnipause cells in the cat. In Control of Gaze by Brain Stem Neurons; Berthoz, A., Baker, R.G., Eds.; Elsevier/North Holland’ Biomedical Press: Amsterdam, The Netherlands, 1977; pp. 337–348. [Google Scholar]
- Kaneko, C.R.; Fuchs, A.F. Connections of cat omnipause neurons. Brain Res. 1982, 241, 166–170. [Google Scholar] [CrossRef]
- Takahashi, M.; Shinoda, Y. Brain Stem Neural Circuits of Horizontal and Vertical Saccade Systems and their Frame of Reference. Neuroscience 2018, 392, 281–328. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, M.; Sugiuchi, Y.; Na, J.; Shinoda, Y. Brainstem Circuits Triggering Saccades and Fixation. J. Neurosci. 2022, 42, 789–803. [Google Scholar] [CrossRef] [PubMed]
- Rucker, J.C.; Ying, S.H.; Moore, W.; Optican, L.M.; Büttner-Ennever, J.; Keller, E.L.; Shapiro, B.E.; Leigh, R.J. Do brainstem omnipause neurons terminate saccades? Ann. N. Y. Acad. Sci. 2011, 1233, 48–57. [Google Scholar] [CrossRef]
- Delgado-García, J.M.; Vidal, P.P.; Gómez, C.; Berthoz, A. A neurophysiological study of prepositus hypoglossi neurons projecting to oculomotor and preoculomotor nuclei in the alert cat. Neuroscience 1989, 29, 291–307. [Google Scholar] [CrossRef]
- Baker, R.; Berthoz, A.; Delgado-García, J. Monosynaptic excitation of trochlear motoneurons following electrical stimulation of the prepositus hypoglossi nucleus. Brain Res. 1977, 121, 157–161. [Google Scholar] [CrossRef]
- Hikosaka, O.; Kawakami, T. Inhibitory reticular neurons related to the quick phase of vestibular nystagmus: Their location and projection. Exp. Brain Res. 1977, 27, 377–386. [Google Scholar] [CrossRef]
- López-Barneo, J.; Darlot, C.; Berthoz, A.; Baker, R. Neuronal activity in prepositus nucleus correlated with eye movement in the alert cat. J. Neurpphysiol. 1982, 47, 329–352. [Google Scholar] [CrossRef]
- Fukushima, K.; Kaneko, C.R. Vestibular integrators in the oculomotor system. Neurosci. Res. 1995, 22, 249–258. [Google Scholar] [CrossRef]
- Robinson, D.A. Oculomotor control signals. In Basic Mechanisms of Ocular Motility and Their Clinical Implications; Pergamon Press: Oxford, UK; Elmsford, NY, USA, 1975; pp. 337–374. [Google Scholar]
- Izawa, Y.; Suzuki, H.; Shinoda, Y. Suppression of visually and memory-guided saccades induced by electrical stimulation of the monkey frontal eye field. I. Suppression of ipsilateral saccades. J. Neurophysiol. 2004, 92, 2248–2260. [Google Scholar] [CrossRef] [PubMed]
- Adamück, E. Über die Innervation der Augenbewegungen. Zentralbl. Med. Wiss. 1870, 8, 65–67. [Google Scholar]
- Crommelink, M.; Guitton, D.; Roucoux, A. Retinotopic versus spatial coding saccades: Clues obtained by stimulating a deep layer of cat’s superior colliculus. In Control of Gaze by Brain Stem Neurons; Baker, R.G., Berthoz, A., Eds.; Elsevier North-Holland: Amsterdam, The Netherlands, 1977; pp. 425–435. [Google Scholar]
- Mchaffie, J.G.; Stein, B.E. Eye movement evoked by electrical stimulation in the superior colliculus of rats and hamsters. Brain Res. 1982, 247, 243–253. [Google Scholar] [CrossRef]
- McIlwain, J.T. Lateral spread of neural excitation during microstimulation in intermediate gray lager of cat’s superior colliculus. J. Neurophysiol. 1982, 47, 167–178. [Google Scholar] [CrossRef]
- Roucoux, A.; Guitton, D.; Crommelinck, M. Stimulation of the superior colliculus in the alert cat. Exp. Brain Res. 1980, 39, 78–85. [Google Scholar] [CrossRef]
- Grantyn, A.A.; Grantyn, R. Synaptic actions of tectofugal pathways on abducens motoneurons in the cat. Brain Res. 1976, 105, 269–285. [Google Scholar] [CrossRef]
- Grantyn, A.; Grantyn, R.; Robiné, K.P.; Berthoz, A. Electroanatomy of tectal efferent connections related to eye movements in the horizontal plane. Exp. Brain Res. 1979, 37, 149–172. [Google Scholar] [CrossRef]
- Takahashi, M. Neural Circuits of Saccadic Eye Movements: Insights into Active Vision. Brain Nerve 2025, 77, 897–905. [Google Scholar]
- Grantyn, A.; Brandi, A.M.; Dubayle, D.; Graf, W.; Ugolini, G.; Hadjidimitrakis, K.; Moschovakis, A. Density gradients of trans-synaptically labeled collicular neurons after injections of rabies virus in the lateral rectus muscle of the rhesus monkey. J. Comp. Neurol. 2002, 451, 346–361. [Google Scholar] [CrossRef] [PubMed]
- Moschovakis, A.K.; Kitama, T.; Dalezios, Y.; Petit, J.; Brandi, A.M.; Grantyn, A.A. An anatomical substrate for the spatiotemporal transformation. J. Neurosci. 1998, 18, 10219–10229. [Google Scholar] [CrossRef]
- Veale, R.; Takahashi, M. Pathways for Naturalistic Looking Behavior in Primate II. Superior Colliculus Integrates Parallel Top-down and Bottom-up Inputs. Neuroscience 2024, 545, 86–110. [Google Scholar] [CrossRef]
- Takahashi, M.; Veale, R. Pathways for Naturalistic Looking Behavior in Primate I: Behavioral Characteristics and Brainstem Circuits. Neuroscience 2023, 532, 133–163. [Google Scholar] [CrossRef]
- Rutishauser, U.; Koch, C. Probabilistic modeling of eye movement data during conjunction search via feature-based attention. J. Vis. 2007, 7, 5. [Google Scholar] [CrossRef]
- Yantis, S.; Jonides, J. Abrupt visual onsets and selective attention: Evidence from visual search. J. Exp. Psychol. Hum. Percept. Perform. 1984, 10, 601–621. [Google Scholar] [CrossRef] [PubMed]
- Treisman, A.M.; Gelade, G. A feature-integration theory of attention. Cogn. Psychol. 1980, 12, 97–136. [Google Scholar] [CrossRef]
- Mannan, S.K.; Ruddock, K.H.; Wooding, D.S. Fixation patterns made during brief examination of two-dimensional images. Perception 1997, 26, 1059–1072. [Google Scholar] [CrossRef]
- Reinagel, P.; Zador, A.M. Natural scene statistics at the center of gaze. Network 1999, 10, 341–350. [Google Scholar] [CrossRef]
- Krieger, G.; Rentschler, I.; Hauske, G.; Schill, K.; Zetzsche, C. Object and scene analysis by saccadic eye-movements: An investigation with higher-order statistics. Spat. Vis. 2000, 13, 201–214. [Google Scholar] [CrossRef]
- Baddeley, R.J.; Tatler, B.W. High frequency edges (but not contrast) predict where we fixate: A Bayesian system identification analysis. Vis. Res. 2006, 46, 2824–2833. [Google Scholar] [CrossRef]
- Frey, H.P.; König, P.; Einhäuser, W. The role of first- and second-order stimulus features for human overt attention. Percept. Psychophys. 2007, 69, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Itti, L.; Koch, C. A saliency-based search mechanism for overt and covert shifts of visual attention. Vis. Res. 2000, 40, 1489–1506. [Google Scholar] [CrossRef]
- Einhäuser, W.; Rutishauser, U.; Koch, C. Task-demands can immediately reverse the effects of sensory-driven saliency in complex visual stimuli. J. Vis. 2008, 8, 2. [Google Scholar] [CrossRef]
- Nyström, M.; Holmqvist, K. Semantic Override of Low-Level Features in Image Viewing–Both Initially and Overall. J. Eye Mov. Res. 2008, 2, 1–11. [Google Scholar] [CrossRef]
- Otero-Millan, J.; Troncoso, X.G.; Macknik, S.L.; Serrano-Pedraza, I.; Martinez-Conde, S. Saccades and microsaccades during visual fixation, exploration, and search: Foundations for a common saccadic generator. J. Vis. 2008, 8, 21. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.Y.; Matrov, D.; Veale, R.; Onoe, H.; Yoshida, M.; Miura, K.; Isa, T. Properties of visually guided saccadic behavior and bottom-up attention in marmoset, macaque, and human. J. Neurophysiol. 2021, 125, 437–457. [Google Scholar] [CrossRef]
- Henderson, J.M.; Nuthmann, A.; Luke, S.G. Eye movement control during scene viewing: Immediate effects of scene luminance on fixation durations. J. Exp. Psychol. Hum. Percept. Perform. 2013, 39, 318–322. [Google Scholar] [CrossRef]
- Kaspar, K.; König, P. Overt attention and context factors: The impact of repeated presentations, image type, and individual motivation. PLoS ONE 2011, 6, e21719. [Google Scholar] [CrossRef]
- Unema, P.J.; Pannasch, S.; Joos, M.; Velichkovsky, B.M. Time course of information processing during scene perception: The relationship between saccade amplitude and fixation duration. Vis. Cogn. 2005, 12, 473–494. [Google Scholar] [CrossRef]
- Nuthmann, A. Fixation durations in scene viewing: Modeling the effects of local image features, oculomotor parameters, and task. Psychon. Bull. Rev. 2017, 24, 370–392. [Google Scholar] [CrossRef]
- Schwedes, C.; Wentura, D. Through the eyes to memory: Fixation durations as an early indirect index of concealed knowledge. Mem. Cogn. 2016, 44, 1244–1258. [Google Scholar] [CrossRef]
- Guy, N.; Lancry-Dayan, O.C.; Pertzov, Y. Not all fixations are created equal: The benefits of using ex-Gaussian modeling of fixation durations. J. Vis. 2020, 20, 9. [Google Scholar] [CrossRef]
- Gómez, C.; Argandoña, E.D.; Solier, R.G.; Angulo, J.C.; Vázquez, M. Timing and competition in networks representing ambiguous figures. Brain Cogn. 1995, 29, 103–114. [Google Scholar] [CrossRef]
- Gómez, C. A Competition Model of IRT Distributions During the First Training Stages of Variable-Interval Schedule. Psychol. Rec. 1992, 42, 285–293. [Google Scholar] [CrossRef]
- Gómez, C.M.; Rodríguez-Martínez, E.I.; Altahona-Medina, M.A. Unavoidability and Functionality of Nervous System and Behavioral Randomness. Appl. Sci. 2024, 14, 4056. [Google Scholar] [CrossRef]
- Feldman, J.; Ballard, D. Connectionist models and their properties. Cogn. Sci. 1982, 6, 205–254. [Google Scholar] [CrossRef]
- Nuthmann, A.; Smith, T.J.; Engbert, R.; Henderson, J.M. CRISP: A computational model of fixation durations in scene viewing. Psychol. Rev. 2010, 117, 382–405. [Google Scholar] [CrossRef]
- Findlay, J.M.; Walker, R. A model of saccade generation based on parallel processing and competitive inhibition. Behav. Brain Sci. 1999, 22, 661–721. [Google Scholar] [CrossRef]
- Tatler, B.W.; Brockmole, J.R.; Carpenter, R.H. LATEST: A model of saccadic decisions in space and time. Psychol. Rev. 2017, 124, 267–300. [Google Scholar] [CrossRef]
- Marr, D. Vision: A Computational Approach; Freeman & Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Wilming, N.; Onat, S.; Ossandón, J.P.; Açık, A.; Kietzmann, T.C.; Kaspar, K.; Gameiro, R.R.; Vormberg, A.; König, P. An extensive dataset of eye movements during viewing of complex images. Sci. Data 2017, 4, 160126. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Introduction to Biostatistics; Freeman: New York, NY, USA, 1987. [Google Scholar]
- Johansson, T. Exgfit-Fit ExGaussian Distribution to Data. MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/70225-exgfit-fit-exgaussian-distribution-to-data (accessed on 13 October 2025).
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Second International Symposium on Information Theory; Petrov, B.N., Csaki, B.F., Eds.; Academiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- JASP Team. JASP, Version 0.19.3; JASP Team: Amsterdam, The Netherlands, 2024.
- Guy, N.; Azulay, H.; Kardosh, R.; Weiss, Y.; Hassin, R.R.; Israel, S.; Pertzov, Y. A novel perceptual trait: Gaze predilection for faces during visual exploration. Sci. Rep. 2019, 9, 10714. [Google Scholar] [CrossRef]
- Glaholt, M.G.; Rayner, K.; Reingold, E.M. Spatial frequency filtering and the direct control of fixation durations during scene viewing. Atten. Percept. Psychophys. 2013, 75, 1761–1773. [Google Scholar] [CrossRef]
- Luke, S.G.; Smith, T.J.; Schmidt, J.; Henderson, J.M. Dissociating temporal inhibition of return and saccadic momentum across multiple eye-movement tasks. J. Vis. 2014, 14, 9. [Google Scholar] [CrossRef]
- Kieffaber, P.D.; Kappenman, E.S.; Bodkins, M.; Shekhar, A.; O’Donnell, B.F.; Hetrick, W.P. Switch and maintenance of task set in schizophrenia. Schizophr. Res. 2006, 84, 345–358. [Google Scholar] [CrossRef]
- Lintz, M.J.; Essig, J.; Zylberberg, J.; Felsen, G. Spatial representations in the superior colliculus are modulated by competition among targets. Neuroscience 2019, 408, 191–203. [Google Scholar] [CrossRef]
- Hikosaka, O.; Wurtz, R.H. The basal ganglia. Rev. Oculomot. Res. 1989, 3, 257–281. [Google Scholar] [PubMed]
- White, B.J.; Berg, D.J.; Kan, J.Y.; Marino, R.A.; Itti, L.; Munoz, D.P. Superior colliculus neurons encode a visual saliency map during free viewing of natural dynamic video. Nat. Commun. 2017, 8, 14263. [Google Scholar] [CrossRef]
- Harris, C.M.; Hainline, L.; Abramov, I.; Lemerise, E.; Camenzuli, C. The distribution of fixation durations in infants and naive adults. Vis. Res. 1988, 28, 419–432. [Google Scholar] [CrossRef]
- Amit, R.; Abeles, D.; Bar-Gad, I.; Yuval-Greenberg, S. Temporal dynamics of saccades explained by a self-paced process. Sci. Rep. 2017, 7, 886. [Google Scholar] [CrossRef]
- Liu, G.; Zheng, Y.; Tsang, M.H.L.; Zhao, Y.; Hsiao, J.H. Understanding the role of eye movement pattern and consistency during face recognition through EEG decoding. npj Sci. Learn. 2025, 10, 28. [Google Scholar] [CrossRef]
- Abadi, R.V.; Gowen, E. Characteristics of saccadic intrusions. Vis. Res. 2004, 44, 2675–2690. [Google Scholar] [CrossRef]
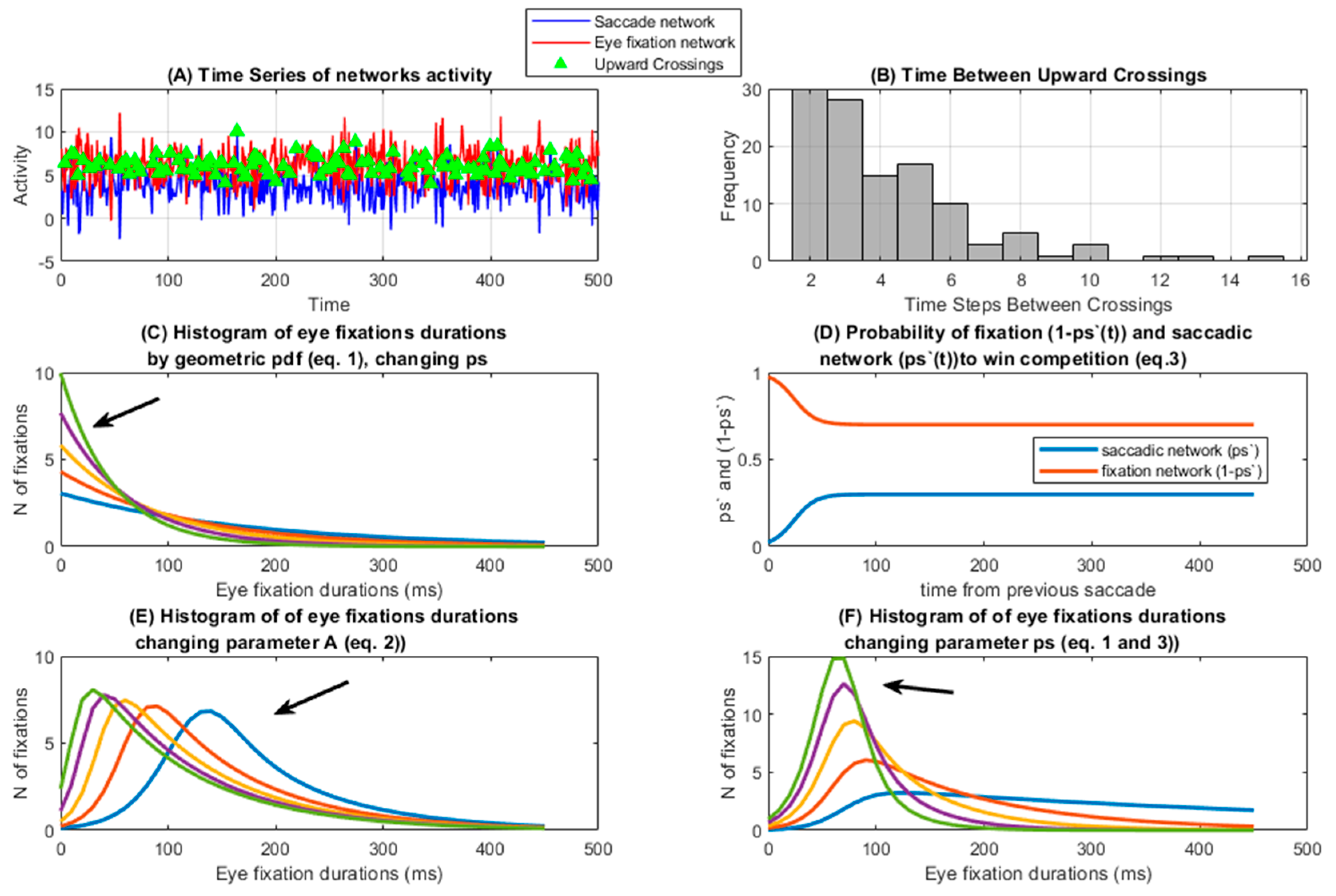

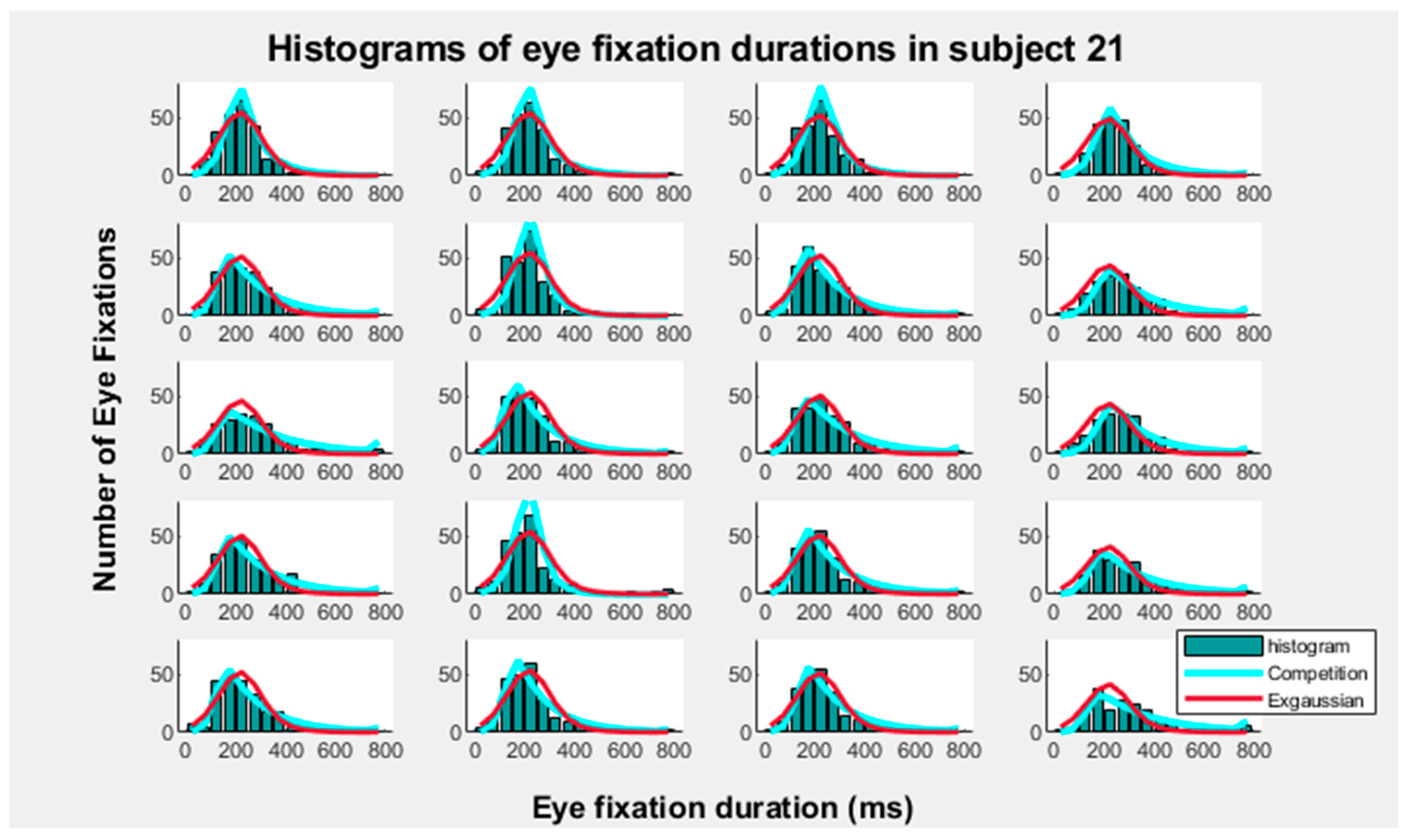
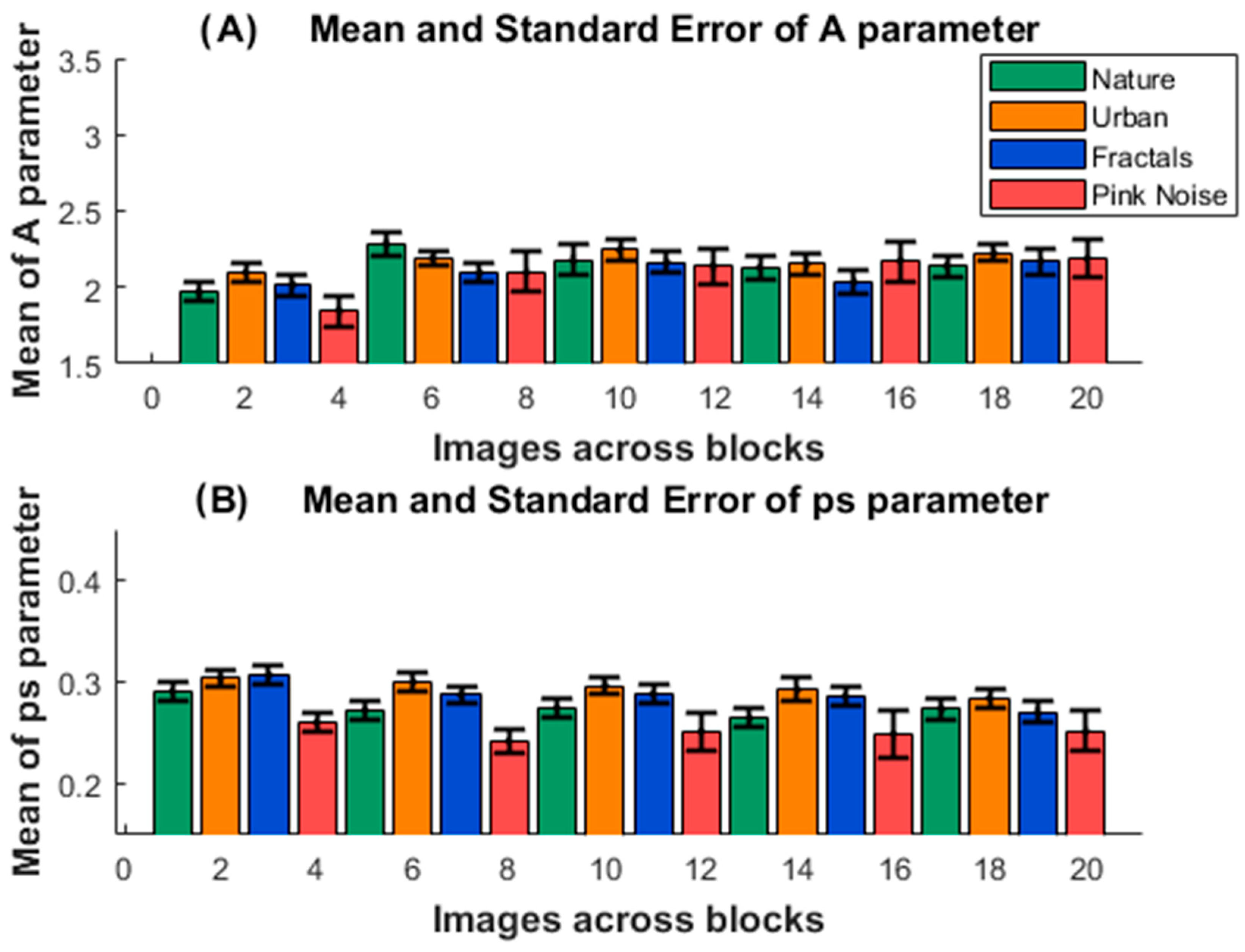
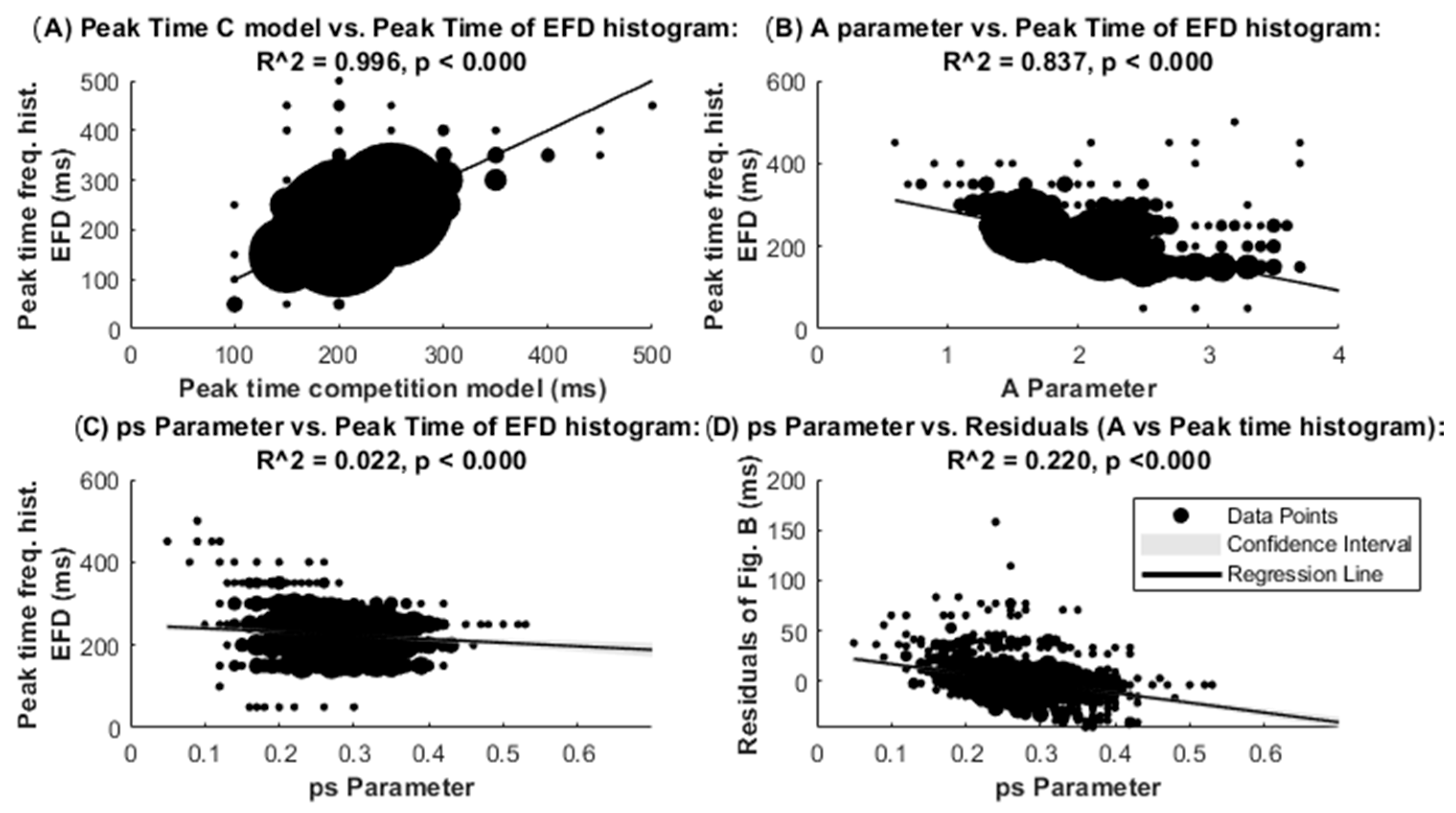

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, C.M.; Altahona-Medina, M.A.; Barrera, G.; Rodriguez-Martínez, E.I. Compatibility of a Competition Model for Explaining Eye Fixation Durations During Free Viewing. Entropy 2025, 27, 1079. https://doi.org/10.3390/e27101079
Gómez CM, Altahona-Medina MA, Barrera G, Rodriguez-Martínez EI. Compatibility of a Competition Model for Explaining Eye Fixation Durations During Free Viewing. Entropy. 2025; 27(10):1079. https://doi.org/10.3390/e27101079
Chicago/Turabian StyleGómez, Carlos M., María A. Altahona-Medina, Gabriela Barrera, and Elena I. Rodriguez-Martínez. 2025. "Compatibility of a Competition Model for Explaining Eye Fixation Durations During Free Viewing" Entropy 27, no. 10: 1079. https://doi.org/10.3390/e27101079
APA StyleGómez, C. M., Altahona-Medina, M. A., Barrera, G., & Rodriguez-Martínez, E. I. (2025). Compatibility of a Competition Model for Explaining Eye Fixation Durations During Free Viewing. Entropy, 27(10), 1079. https://doi.org/10.3390/e27101079





