MAJATNet: A Lightweight Multi-Scale Attention Joint Adaptive Adversarial Transfer Network for Bearing Unsupervised Cross-Domain Fault Diagnosis
Abstract
1. Introduction
- (1)
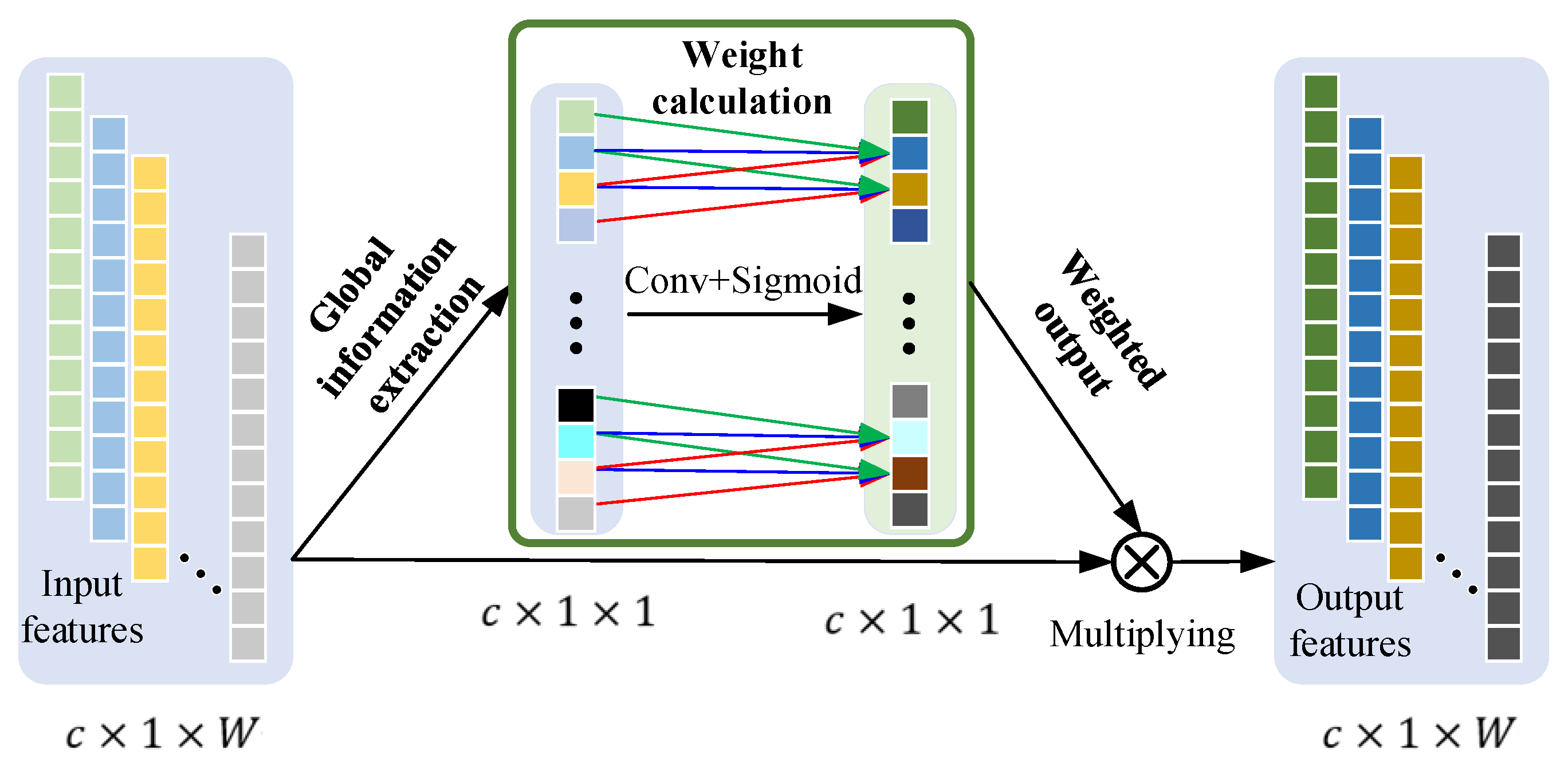
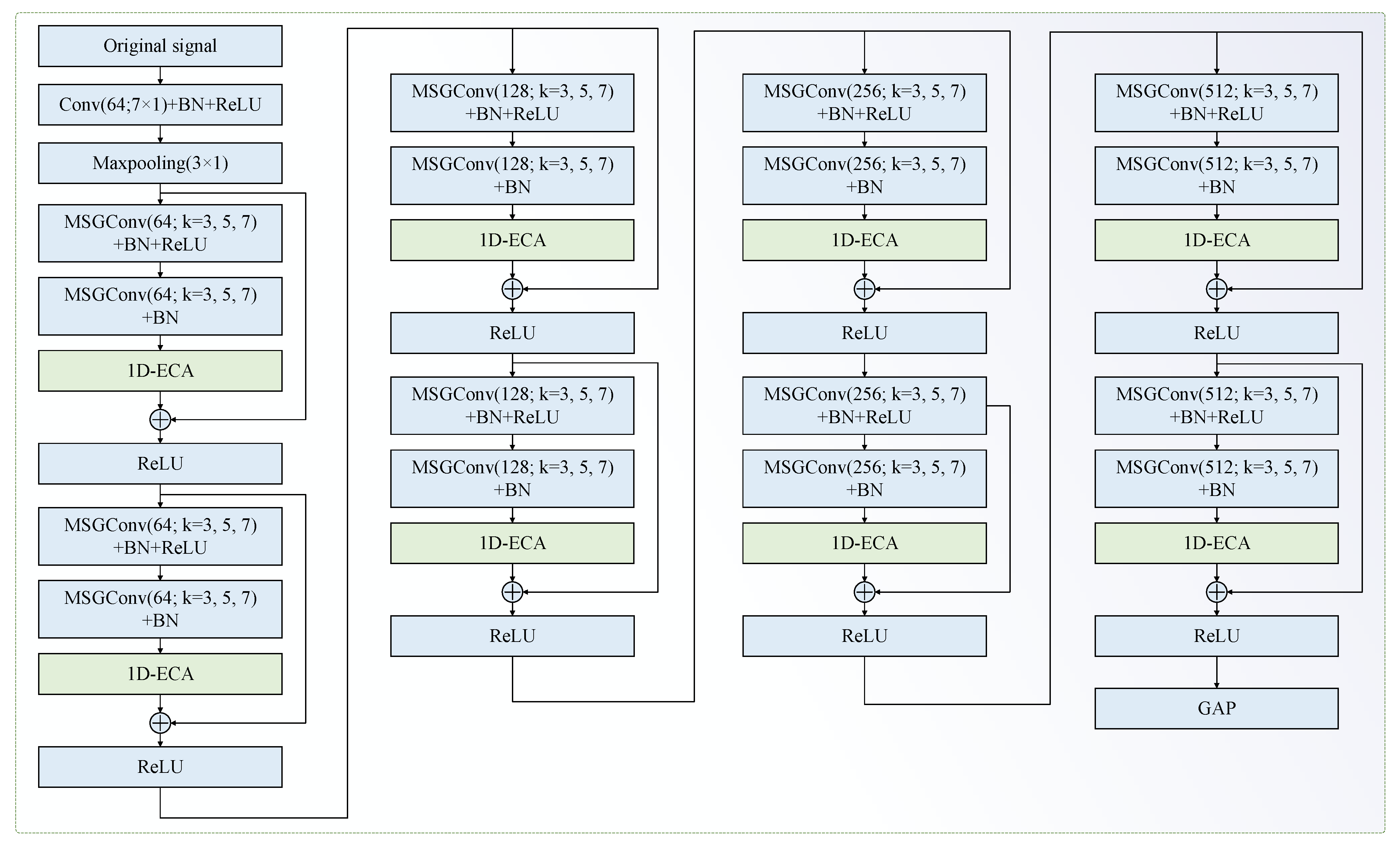
- A novel lightweight multi-scale attention residual network (MAResNet) is proposed, which utilizes multi-scale group convolution (MSGConv) to extract features at different scales and incorporates a one-dimensional efficient channel attention (1D-ECA) mechanism to dynamically recalibrate the importance of channel-wise features. This enhances the ability to capture discriminative fault-related features while significantly reducing model parameters and computational complexity.
- (2)
- A novel loss function, namely IJA loss, is developed, which integrates JMMD and adversarial learning loss. The IJA loss function effectively measures the joint distribution discrepancy of high-dimensional features and labels between the source and target domains, facilitating the extraction of domain-invariant features and improving cross-domain fault diagnosis performance.
- (3)
- MAResNet featurefeatures an extraction backbone and the IJA loss function areis integrated into a unified end-to-end adversarial transfer learning framework. This holistic approach jointly optimizes feature extraction, domain adaptation, and classification.
2. Related Works
2.1. UCFD Problem Definition
- (1)
- The source domain is defined as follows:
- (2)
- The target domain is defined as
- (3)
- The marginal distribution and joint distribution do not coincide in the following:
2.2. Max Mean Discrepancy
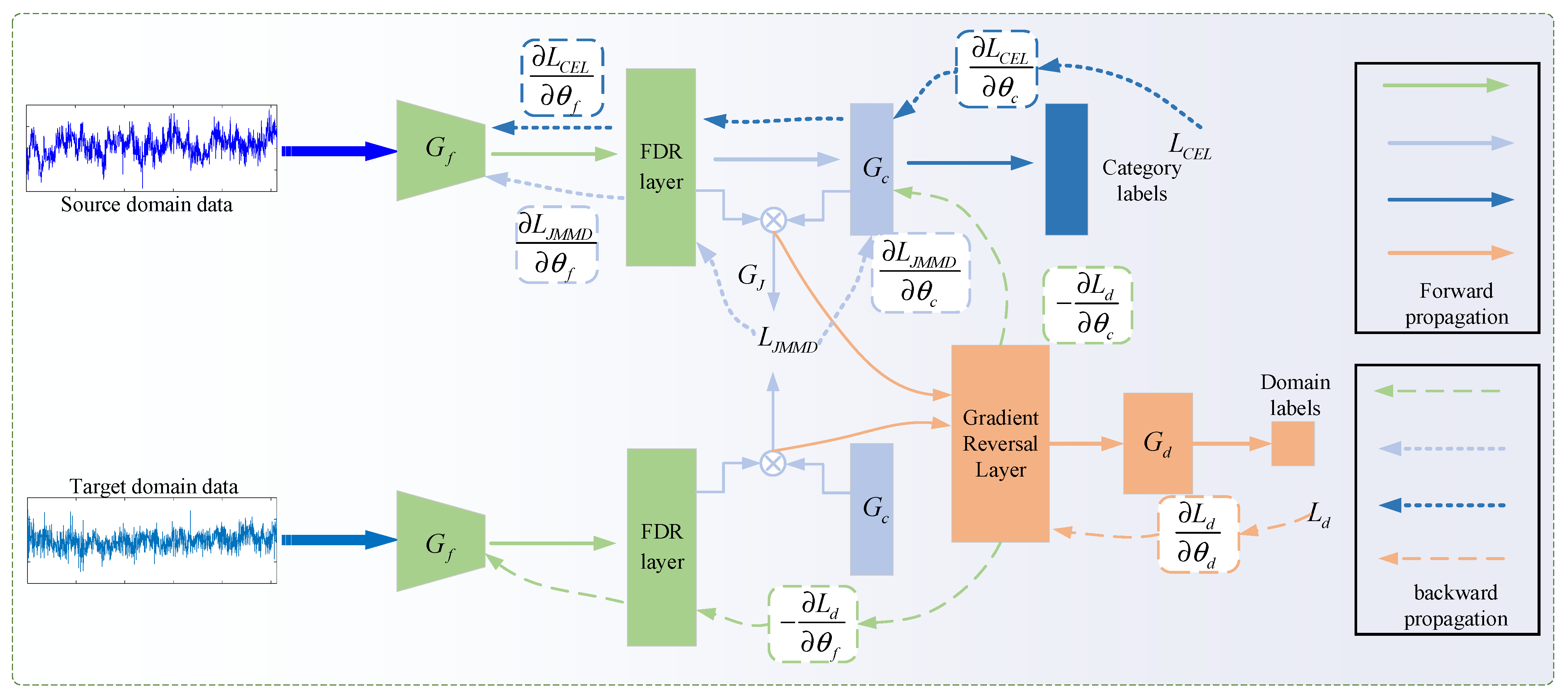
3. Proposed MAJATNet Method
3.1. Multi-Scale Group Convolutional
3.2. Multi-Scale Attention Residual Network
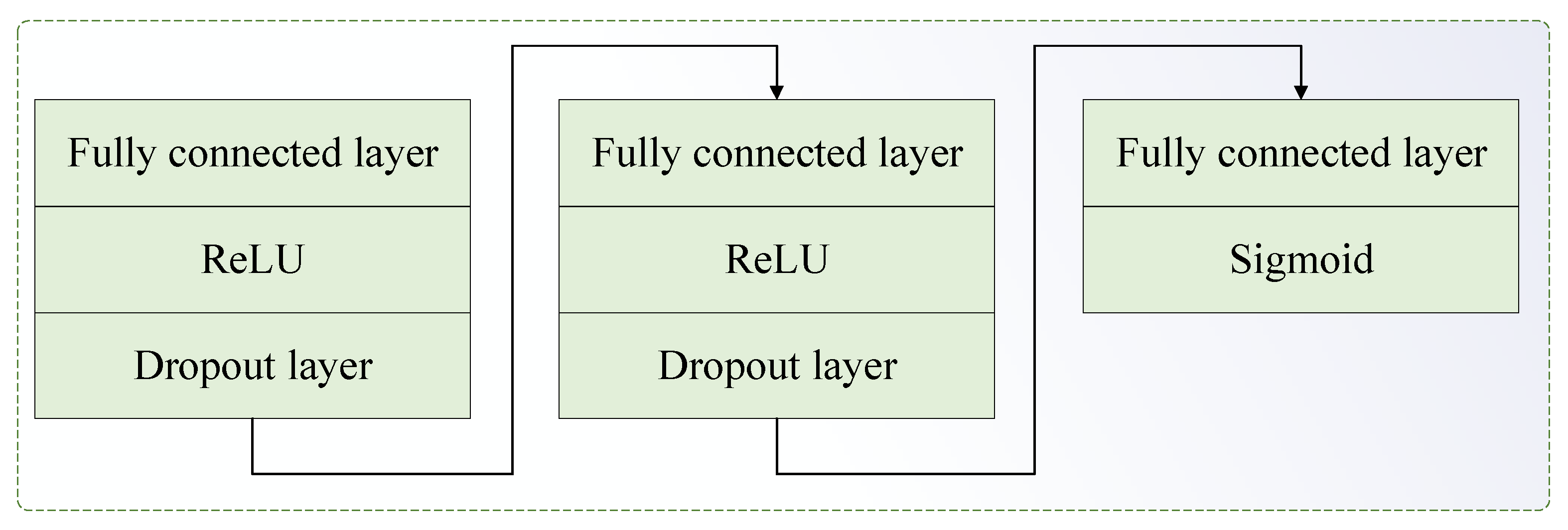
3.3. IJA Loss Function of MAJATNet
- (1)
- JMMD loss
- (2)
- Domain adversarial loss
- (3)
- Classification loss
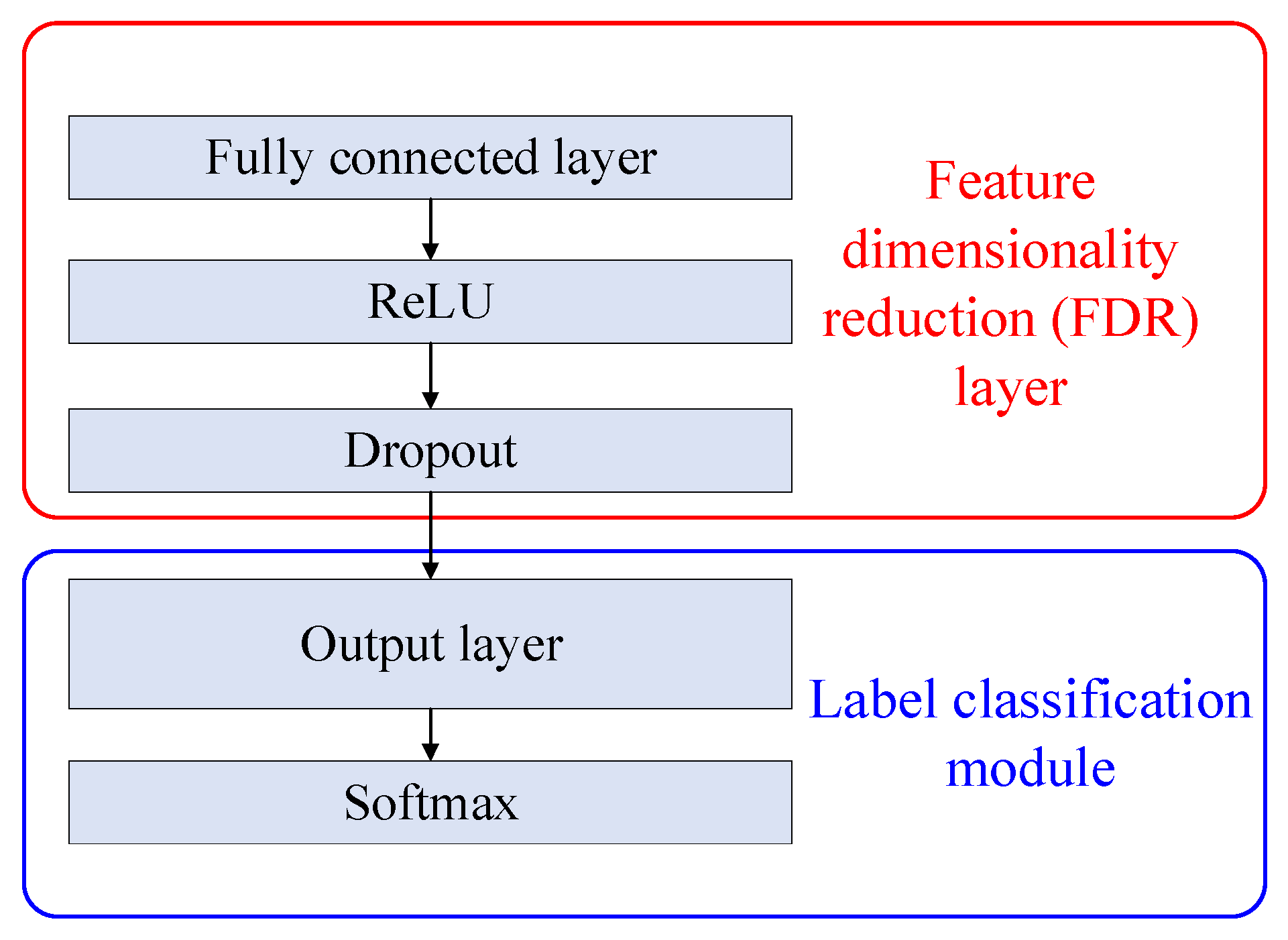
- (4)
- Overall objective functions
3.4. Training the MAJATNet Model
| Algorithm 1: Training the MAJATNet model |
| Input: source domain data ; target domain data ; maximum epoch number and pre-training epoch number . 1: Initialize the parameters of the MAJATNet model 2: for do 3: if do 4: // Source domain data for pre-training 5: // Forward propagation 6: Compute the output of the feature extractor and the output of the classifier 7: Calculate the cross-entropy loss by Equation (23) 8: // Backward propagation 9: Updating the model parameters and by and 10: end if 11: if do 12: // Source and target domain data training 13: // Forward propagation 14: Compute the output of the feature extractor , the output of the classifier and the output of the discriminator 15: Calculate the cross-entropy loss by Equation (23), the JMMD loss by Equation (19), and the adversarial learning loss by Equation (21) 16: Calculate the overall objective loss by Equation (24) 17: // Backward propagation 18: Update the parameter by Equation (27), the parameter by Equation (28), and the parameter by Equation (29) 19: end if 20: end for Output: |
4. Experimental Verification
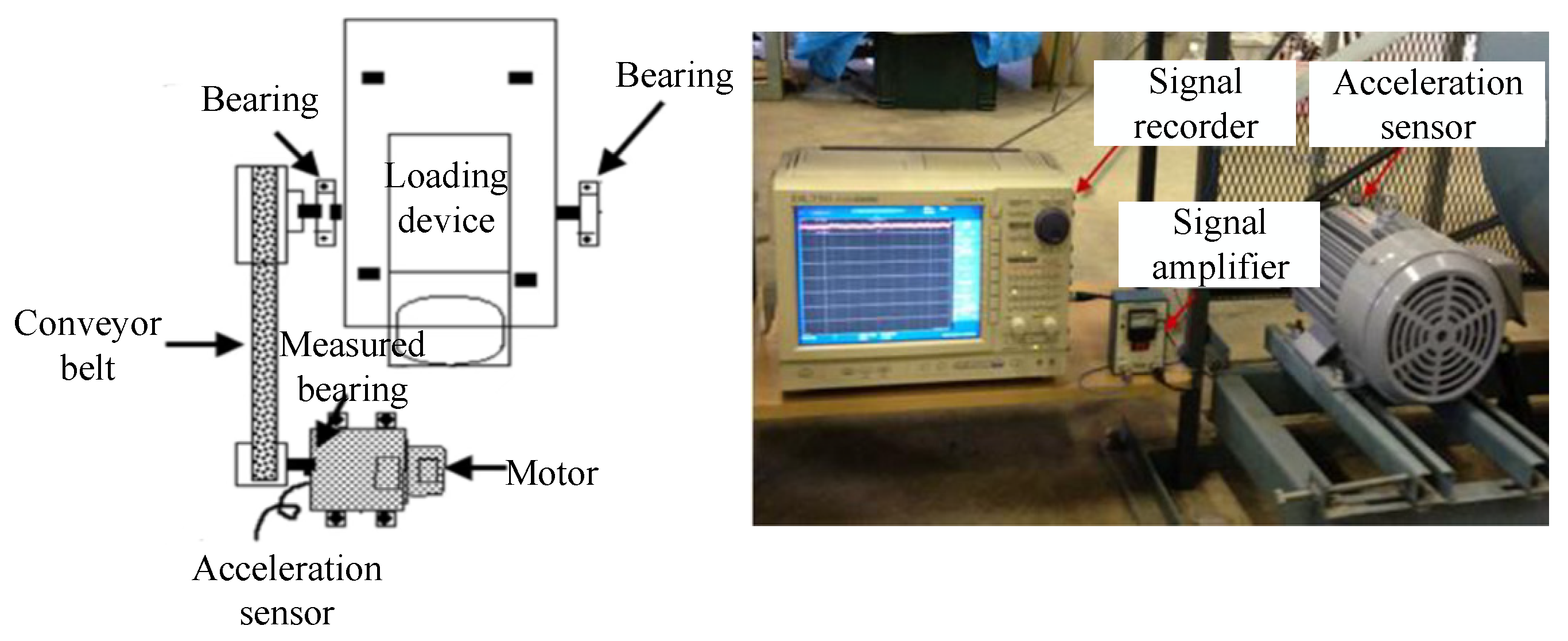
4.1. JNU Dataset Experimental
- (1)
- Experimental platform and data processing
- (2)
- Comparison methods and parameter settings
- (3)
- Comparative experimental results
- (4)
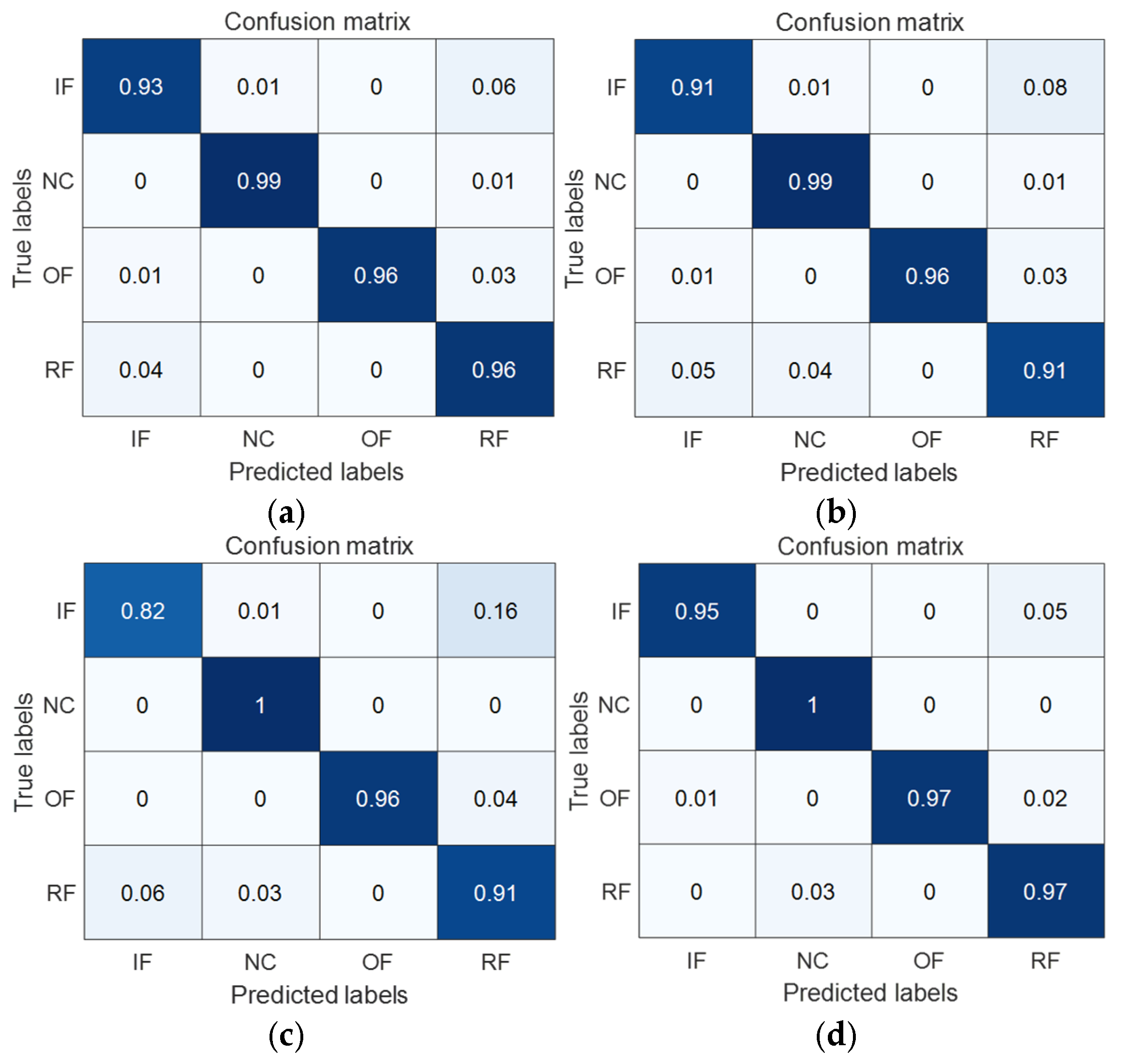
- Confusion matrix
- (5)
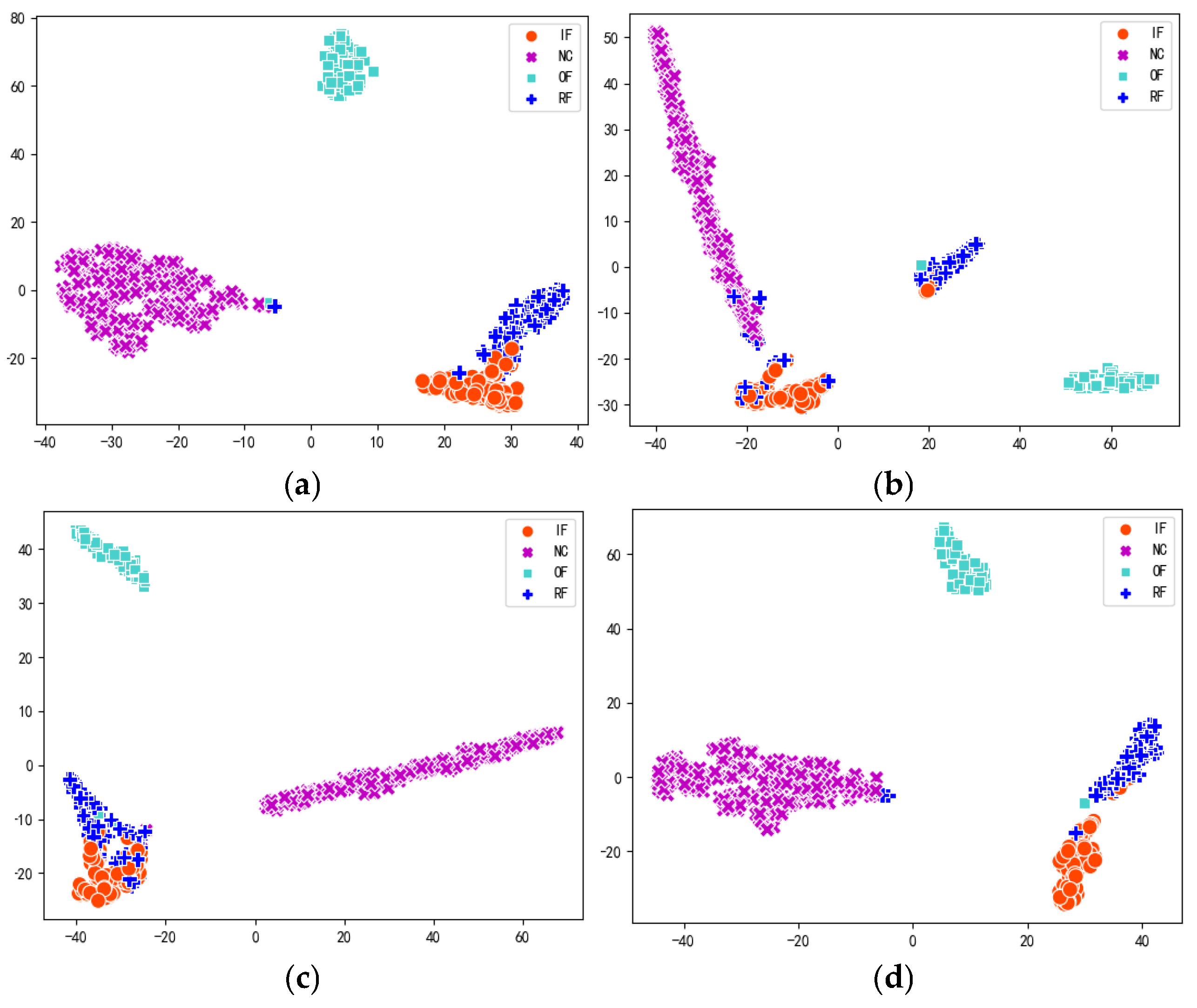
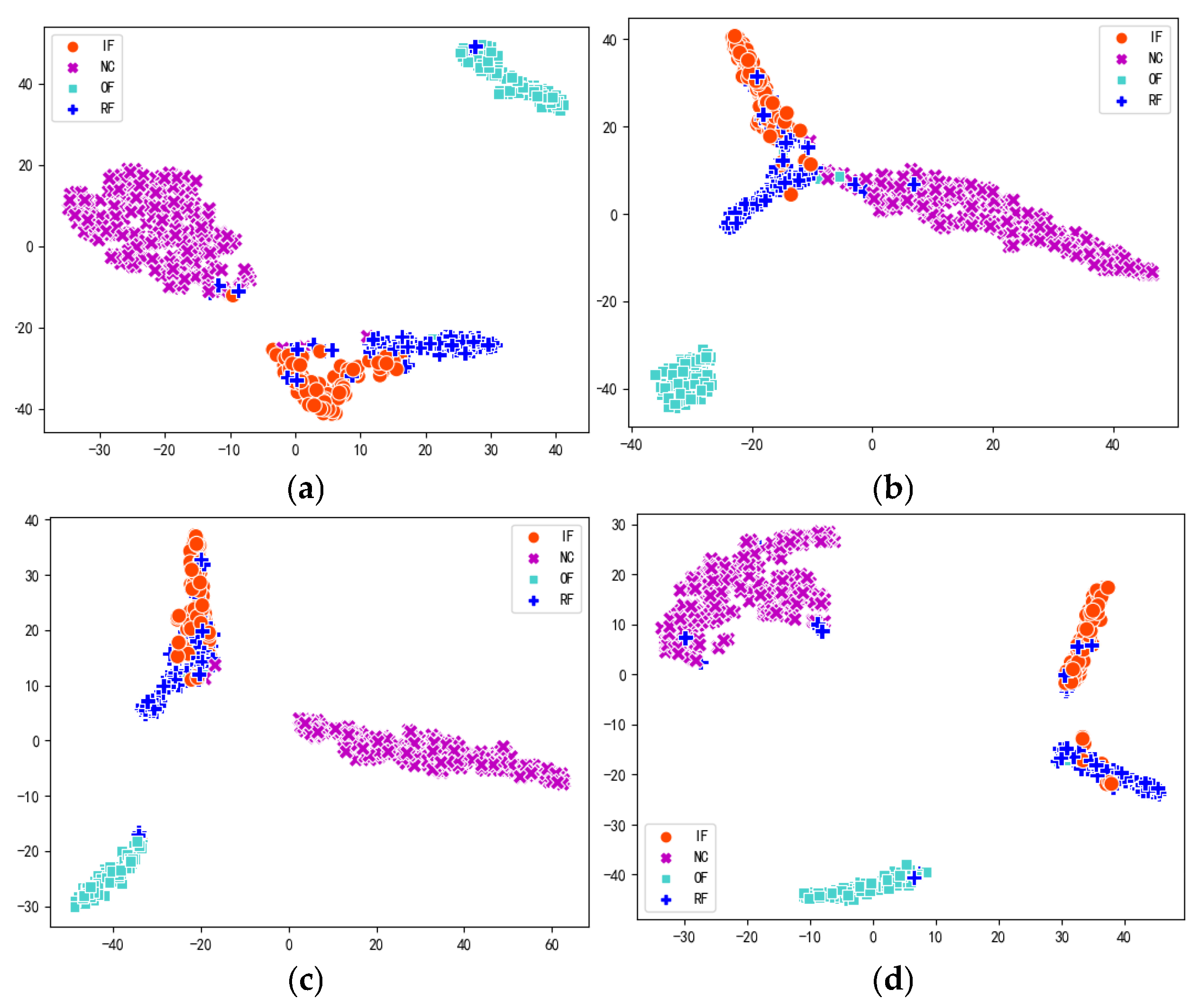
- Feature visualization
- (6)
- Visualization of attention weights
- (7)
- Ablation experiments
4.2. CWRU Dataset Experimental
- (1)
- Experimental platform and data processing
- (2)
- Anti-noise experiment results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Zhang, Z.; Gao, H.; Qi, Y. Rolling bearing fault diagnosis based on multi-source domain adaptive residual network. J. Vib. Shock 2024, 43, 290–299. [Google Scholar]
- Han, K.; Zhan, H.; Yu, J.; Wang, R. Rolling bearing fault diagnosis based on dilated convolution and enhanced multi-scale feature adaptive fusion. J. Zhejiang Univ. (Eng. Sci.) 2024, 58, 1285–1295. [Google Scholar]
- Jia, F.; Lei, Y.; Guo, L.; Lin, J.; Xing, S. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Zhao, J. Bearing fault diagnosis of a permanent magnet synchronous motor via a fast and online order analysis method in an embedded system. Mech. Syst. Signal Process. 2018, 113, 36–49. [Google Scholar] [CrossRef]
- Group, I.M.R.W. Report of large motor reliability survey of industrial and commercial installations, Part I. IEEE Trans. Ind. App. 1985, 21, 853–864. [Google Scholar]
- Fu, G.; Wei, Q.; Yang, Y.; Li, C. Bearing fault diagnosis based on CNN-BiLSTM and residual module. Meas. Sci. Technol. 2023, 34, 125050. [Google Scholar] [CrossRef]
- Song, L.; Wu, J.; Wang, L.; Chen, G.; Shi, Y.; Liu, Z. Remaining useful life prediction of rolling bearings based on multi-scale attention residual network. Entropy 2023, 25, 798. [Google Scholar] [CrossRef]
- Qiao, Z.; Zhang, C.; Zhang, C.; Ma, X.; Zhu, R.; Lai, Z.; Zhou, S. Stochastic resonance array for designing noise-boosted filter banks to enhance weak multi-harmonic fault characteristics of machinery. Appl. Acoust. 2025, 236, 110710. [Google Scholar] [CrossRef]
- Qiao, Z.; He, Y.; Liao, C.; Zhu, R. Noise-boosted weak signal detection in fractional nonlinear systems enhanced by increasing potential-well width and its application to mechanical fault diagnosis. Chaos Solitons Fractals 2023, 175, 113960. [Google Scholar] [CrossRef]
- Qin, N.; You, Y.; Huang, D.; Jia, X.; Zhang, Y.; Du, J.; Wang, T. AttGAN-DPCNN: An Extremely Imbalanced Fault Diagnosis Method for Complex Signals from Multiple Sensors. IEEE Sens. J. 2024, 24, 38270–38285. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Y.; Zhang, Z.; Wu, J. Multi-information fusion fault diagnosis based on KNN and improved evidence theory. J. Vib. Eng. Technol. 2022, 10, 841–852. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Yu, Y.; Yang, J.; Wang, B.; Liu, Z.; Shao, X.; Yang, C. Intelligent diagnosis method for early faults of electric-hydraulic control system based on residual analysis. Reliab. Eng. Syst. Saf. 2025, 261, 111142. [Google Scholar] [CrossRef]
- Cai, B.; Sun, X.; Wang, J.; Yang, C.; Wang, Z.; Kong, X.; Liu, Z.; Liu, Y. Fault detection and diagnostic method of diesel engine by combining rule-based algorithm and BNs/BPNNs. J. Manuf. Syst. 2020, 57, 148–157. [Google Scholar] [CrossRef]
- Cai, B.; Wang, Z.; Zhu, H.; Liu, Y.; Hao, K.; Yang, Z.; Ren, Y.; Feng, Q.; Liu, Z. Artificial intelligence enhanced two-stage hybrid fault prognosis methodology of PMSM. IEEE Trans. Ind. Inform. 2021, 18, 7262–7273. [Google Scholar] [CrossRef]
- Li, X.; Yuan, P.; Su, K.; Li, D.; Xie, Z.; Kong, X. Innovative integration of multi-scale residual networks and MK-MMD for enhanced feature representation in fault diagnosis. Meas. Sci. Technol. 2024, 35, 86108. [Google Scholar] [CrossRef]
- Li, X.; Ma, Z.; Yuan, Z.; Mu, T.; Du, G.; Liang, Y.; Liu, J. A review on convolutional neural network in rolling bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 072002. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Wang, D.; Dong, Y.; Wang, H.; Tang, G. Limited fault data augmentation with compressed sensing for bearing fault diagnosis. IEEE Sens. J. 2023, 23, 14499–14511. [Google Scholar] [CrossRef]
- Shi, L.; Liu, W.; You, D.; Yang, S. Rolling Bearing Fault Diagnosis Based on CEEMDAN and CNN-SVM. Appl. Sci. 2024, 14, 5847. [Google Scholar] [CrossRef]
- Zhou, K.; Diehl, E.; Tang, J. Deep convolutional generative adversarial network with semi-supervised learning enabled physics elucidation for extended gear fault diagnosis under data limitations. Mech. Syst. Signal Process. 2023, 185, 109772. [Google Scholar] [CrossRef]
- Jin, Y.; Hou, L.; Chen, Y. A time series transformer based method for the rotating machinery fault diagnosis. Neurocomputing 2022, 494, 379–395. [Google Scholar] [CrossRef]
- Dong, J.; Su, D.; Jiang, H.; Gao, Y.; Chen, T. A novel algorithm for complex transfer conditions in bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 56118. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, W.; Chen, Y.; Jiang, Y.; Peng, G. Multisource cross-domain fault diagnosis of rolling bearing based on subdomain adaptation network. Meas. Sci. Technol. 2022, 33, 105109. [Google Scholar] [CrossRef]
- Shi, Y.; Deng, A.; Deng, M.; Xu, M.; Liu, Y.; Ding, X. A novel multiscale feature adversarial fusion network for unsupervised cross-domain fault diagnosis. Measurement 2022, 200, 111616. [Google Scholar] [CrossRef]
- Zhao, Z.B.; Zhang, Q.Y.; Yu, X.L.; Sun, C.; Wang, S.B.; Yan, R.Q.; Chen, X.F. Applications of unsupervised deep transfer learning to intelligent fault diagnosis: A survey and comparative study. IEEE Trans. Instrum. Meas. 2021, 70, 3525828. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J. Unsupervised adversarial adaptation network for intelligent fault diagnosis. IEEE Trans. Ind. Electron. 2019, 67, 9904–9913. [Google Scholar] [CrossRef]
- Sun, H.; Zeng, J.; Wang, Y.; Ruan, H.; Meng, L. Step-by-step gradual domain adaptation for rotating machinery fault diagnosis. Meas. Sci. Technol. 2022, 33, 75004. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, J.; He, Z.; Zhou, H.; Zhu, H. Deep transfer learning with metric structure for fault diagnosis. Knowl.-Based Syst. 2022, 256, 109826. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, L.; Zheng, Y.; Xie, J.; Wang, T. Bearing fault diagnostic framework under unknown working conditions based on condition-guided diffusion model. Measurement 2025, 242, 115951. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Wang, J.; Xin, Y.; Xu, K. Generalization of deep neural network for bearing fault diagnosis under different working conditions using multiple kernel method. Neurocomputing 2019, 352, 42–53. [Google Scholar] [CrossRef]
- Che, C.; Wang, H.; Ni, X.; Fu, Q. Domain adaptive deep belief network for rolling bearing fault diagnosis. Comput. Ind. Eng. 2020, 143, 106427. [Google Scholar] [CrossRef]
- Shao, X.; Kim, C. Unsupervised domain adaptive 1D-CNN for fault diagnosis of bearing. Sensors 2022, 22, 4156. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowl.-Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, B.; Wei, H.; Chen, L.; Li, X.; Rätsch, M. Deep adversarial domain adaptation model for bearing fault diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4217–4226. [Google Scholar] [CrossRef]
- Chen, Z.; He, G.; Li, J.; Liao, Y.; Gryllias, K.; Li, W. Domain adversarial transfer network for cross-domain fault diagnosis of rotary machinery. IEEE Trans. Instrum. Meas. 2020, 69, 8702–8712. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Li, X.; Zhou, X.; Wu, D. MPNet: A lightweight fault diagnosis network for rotating machinery. Measurement 2025, 239, 115498. [Google Scholar] [CrossRef]
- Fang, H.; Deng, J.; Zhao, B.; Shi, Y.; Zhou, J.; Shao, S. LEFE-Net: A lightweight efficient feature extraction network with strong robustness for bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 3513311. [Google Scholar] [CrossRef]
- Zhong, H.; Lv, Y.; Yuan, R.; Yang, D. Bearing fault diagnosis using transfer learning and self-attention ensemble lightweight convolutional neural network. Neurocomputing 2022, 501, 765–777. [Google Scholar] [CrossRef]
- Jiang, W.; Qi, Z.; Jiang, A.; Chang, S.; Xia, X. Lightweight network bearing intelligent fault diagnosis based on VMD-FK-ShuffleNetV2. Machines 2024, 12, 608. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, S.; Cui, T.; Mu, X.; Luo, T.; Wang, S.; Wu, G. Edge computing and fault diagnosis of rotating machinery based on MobileNet in wireless sensor networks for mechanical vibration. Sensors 2024, 24, 5156. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Shao, H.; Wang, J.; Zheng, X.; Liu, B. LiConvFormer: A lightweight fault diagnosis framework using separable multiscale convolution and broadcast self-attention. Expert Syst. Appl. 2024, 237, 121338. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, N.; Liang, X.; Gui, W.; Yang, C.; Liu, Y. TCAC-transformer: A fast convolutional transformer with temporal-channel attention for efficient industrial fault diagnosis. Expert Syst. Appl. 2025, 297, 129473. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, D.; Lu, W.; Yang, J.; Li, Z.; Liang, B. A deep transfer model with wasserstein distance guided multi-adversarial networks for bearing fault diagnosis under different working conditions. IEEE Access 2019, 7, 65303–65318. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. Residual joint adaptation adversarial network for intelligent transfer fault diagnosis. Mech. Syst. Signal Process. 2020, 145, 106962. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K.; Ding, C. A mixed adversarial adaptation network for intelligent fault diagnosis. J. Intell. Manuf. 2022, 33, 2207–2222. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, H.; Wang, K.; Pei, Z. Joint distribution adaptation network with adversarial learning for rolling bearing fault diagnosis. Knowl.-Based Syst. 2021, 222, 106974. [Google Scholar] [CrossRef]
- Qian, Q.; Pu, H.; Tu, T.; Qin, Y. Variance discrepancy representation: A vibration characteristic-guided distribution alignment metric for fault transfer diagnosis. Mech. Syst. Signal Process. 2024, 217, 111544. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, J.; Ma, X.; Zhang, X.; Zhang, Q. An unsupervised transfer learning method based on SOCNN and FBNN and its application on bearing fault diagnosis. Mech. Syst. Signal Process. 2024, 208, 111047. [Google Scholar] [CrossRef]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE CVPR, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Long, M.; Cao, Z.; Wang, J.; Jordan, M.I. Conditional adversarial domain adaptation. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; p. 31. [Google Scholar]
- Li, K.; Ping, X.; Wang, H.; Chen, P.; Cao, Y. Sequential fuzzy diagnosis method for motor roller bearing in variable operating conditions based on vibration analysis. Sensors 2013, 13, 8013–8041. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhai, X.; Qiao, F.; Ma, Y.; Lu, H. A novel fault diagnosis method under dynamic working conditions based on a CNN with an adaptive learning rate. IEEE Trans. Instrum. Meas. 2022, 71, 5013212. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Zhang, L.; Li, H.; Cui, J.; Li, W.; Wang, X. Class subdomain adaptation network for bearing fault diagnosis under variable working conditions. IEEE Trans. Instrum. Meas. 2022, 72, 3501417. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhuang, F.; Wang, J.; Ke, G.; Chen, J.; Bian, J.; Xiong, H.; He, Q. Deep subdomain adaptation network for image classification. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1713–1722. [Google Scholar]
- Lu, Y.; Li, M.; Gao, Q.; Zhu, D.; Zhao, D.; Li, T. A novel joint class subdomain adaptive fault diagnosis algorithm for bearing faults under variable operating conditions. IEEE Sens. J. 2024, 24, 35221–35230. [Google Scholar] [CrossRef]







| Hyperparameters | Parameters Information |
|---|---|
| Batch size | 64 |
| Optimization algorithm | Adam |
| Momentum | 0.9 |
| Epoch | 300 |
| Learning rate | 0.001 |
| Learning rate strategy | Step |
| Learning rate decay coefficient | 0.1 |
| Learning rate decay epoch | 150, 250 |
| Weight decay coefficient of the L2 | 0.00001 |
| Method | Complexity | Parameters | Inference Time | 0 → 1 | 0 → 2 | 1 → 0 | 1 → 2 | 2 → 0 | 2 → 1 |
|---|---|---|---|---|---|---|---|---|---|
| CNN | 18.23 MMac | 181.25 K | 0.04 s | 98.33 ± 0.52 | 96.21 ± 0.60 | 82.97 ± 1.52 | 98.87 ± 0.31 | 90.34 ± 0.95 | 98.39 ± 0.26 |
| ResNet | 986 MMac | 3.84 M | 0.32 s | 98.60 ± 0.53 | 96.56 ± 0.25 | 83.93 ± 3.85 | 99.01 ± 0.08 | 87.95 ± 1.58 | 99.39 ± 0.33 |
| AdaBN | 986 MMac | 3.98 M | 14.6 s | 94.62 ± 0.45 | 93.04 ± 0.95 | 88.47 ± 1.17 | 94.61 ± 0.30 | 90.30 ± 0.89 | 95.77 ± 0.58 |
| MK-MMD | 986 MMac | 3.84 M | 0.28 s | 99.18 ± 0.25 | 98.53 ± 0.23 | 96.93 ± 0.12 | 99.80 ± 0.08 | 93.59 ± 0.31 | 99.63 ± 0.30 |
| DA | 986 MMac | 3.84 M | 0.28 s | 99.05 ± 0.49 | 98.02 ± 0.50 | 95.46 ± 0.35 | 99.59 ± 0.15 | 93.31 ± 0.76 | 99.42 ± 0.09 |
| CDA | 986 MMac | 3.84 M | 0.28 s | 99.22 ± 0.19 | 98.76 ± 0.32 | 94.71 ± 0.47 | 99.66 ± 0.12 | 93.07 ± 0.41 | 99.56 ± 0.09 |
| ShuffeResNet | 51 MMac | 1.1 M | 0.08 s | 99.69 ± 0.22 | 99.22 ± 0.26 | 96.18 ± 0.60 | 99.83 ± 0.00 | 93.86 ± 0.17 | 99.90 ± 0.09 |
| SqueezeNet | 94 MMac | 359 K | 0.10 s | 98.67 ± 0.44 | 98.50 ± 0.33 | 93.31 ± 0.28 | 99.56 ± 0.26 | 92.35 ± 0.46 | 99.73 ± 0.15 |
| LiConvFormer | 14 MMac | 320 K | 0.06 s | 98.16 ± 0.48 | 97.30 ± 0.69 | 93.79 ± 0.77 | 98.33 ± 0.56 | 92.69 ± 0.57 | 98.09 ± 0.48 |
| MobileNetV2 | 96 MMac | 2.18 M | 0.11 s | 98.50 ± 0.48 | 97.27 ± 1.05 | 93.28 ± 0.46 | 99.32 ± 0.12 | 92.52 ± 0.35 | 99.35 ± 0.19 |
| CSAN | - | - | - | 94.34 | 92.59 | 91.45 | 90.55 | 87.53 | 93.78 |
| LMMD | - | - | - | 98.12 | 94.17 | 93.80 | 95.94 | 88.54 | 97.50 |
| JCSDAN | - | - | - | 98.54 | 95.00 | 94.69 | 97.08 | 89.12 | 97.95 |
| MAJATNet | 569 MMac | 2.21 M | 0.28 s | 99.90 ± 0.09 | 99.52 ± 0.22 | 97.95 ± 0.42 | 99.86 ± 0.08 | 94.98 ± 0.26 | 99.90 ± 0.09 |
| Transfer Task | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| 0 → 1 | 98.60 ± 0.53 | 99.08 ± 0.26 (↑) | 99.39 ± 0.26 (↑) | 99.86 ± 0.22 (↑) | 99.90 ± 0.09 (↑) |
| 0 → 2 | 96.56 ± 0.25 | 98.57 ± 0.36 (↑) | 99.01 ± 0.52 (↑) | 99.59 ± 0.23 (↑) | 99.52 ± 0.22 (↓) |
| 1 → 0 | 83.93 ± 3.85 | 96.76 ± 0.56 (↑) | 95.56 ± 0.49 (↓) | 96.55 ± 0.74 (↑) | 97.95 ± 0.42 (↑) |
| 1 → 2 | 99.01 ± 0.08 | 99.73 ± 0.09 (↑) | 99.80 ± 0.08 (↑) | 99.80 ± 0.08 (-) | 99.86 ± 0.08 (↑) |
| 2 → 0 | 87.95 ± 1.58 | 93.72 ± 0.28 (↑) | 93.65 ± 0.39 (↓) | 94.23 ± 0.56 (↑) | 94.98 ± 0.26 (↑) |
| 2 → 1 | 99.39 ± 0.33 | 99.66 ± 0.12 (↑) | 99.80 ± 0.08 (↑) | 99.80 ± 0.14 (-) | 99.90 ± 0.09 (↑) |
| Transfer Task | Source Domain | Target Domain | Number of Samples in Source Domain | Number of Samples in Target Domain |
|---|---|---|---|---|
| 2 → 0 | 2 HP | 0 HP | 1539 | 1305 |
| 3 → 0 | 3 HP | 0 HP | 1544 | 1305 |
| Transfer Task | 2 → 0 | 3 → 0 | 2 → 0 | 3 → 0 | 2 → 0 | 3 → 0 |
|---|---|---|---|---|---|---|
| SNR | 2 dB | 2 dB | 0 dB | 0 dB | −2 dB | −2 dB |
| CNN | 94.18 ± 1.22 | 89.13 ± 4.31 | 92.64 ± 0.84 | 85.75 ± 2.48 | 88.04 ± 0.83 | 84.14 ± 3.21 |
| ResNet | 95.02 ± 1.43 | 88.97 ± 2.48 | 92.87 ± 1.55 | 87.20 ± 1.45 | 90.27 ± 2.11 | 83.93 ± 2.16 |
| AdaBN | 91.72 ± 0.49 | 89.15 ± 1.43 | 91.02 ± 1.32 | 88.84 ± 1.30 | 86.82 ± 1.18 | 81.98 ± 2.52 |
| MK-MMD | 94.56 ± 0.50 | 93.18 ± 2.07 | 93.10 ± 1.24 | 91.72 ± 2.31 | 90.65 ± 1.64 | 89.89 ± 2.15 |
| DA | 94.87 ± 0.92 | 95.56 ± 0.84 | 94.64 ± 1.09 | 94.48 ± 0.96 | 91.42 ± 1.68 | 88.04 ± 2.86 |
| CDA | 95.25 ± 0.93 | 93.18 ± 2.29 | 94.33 ± 1.37 | 90.42 ± 2.53 | 91.19 ± 1.35 | 89.04 ± 2.81 |
| ShuffeResNet | 97.09 ± 1.17 | 97.39 ± 0.78 | 95.40 ± 0.90 | 95.63 ± 0.96 | 92.72 ± 1.21 | 90.73 ± 0.95 |
| SqueezeNet | 96.09 ± 0.42 | 94.33 ± 1.52 | 93.49 ± 1.97 | 91.34 ± 2.34 | 81.07 ± 6.33 | 77.04 ± 3.89 |
| LiConvFormer | 88.35 ± 1.11 | 84.37 ± 4.84 | 84.52 ± 2.24 | 80.23 ± 3.03 | 78.24 ± 4.43 | 72.03 ± 3.76 |
| MobileNetV2 | 96.17 ± 1.08 | 94.87 ± 2.73 | 88.97 ± 2.95 | 88.28 ± 4.70 | 88.20 ± 1.44 | 83.91 ± 6.27 |
| MAJATNet | 97.93 ± 0.88 | 98.54 ± 0.42 | 98.08 ± 0.61 | 97.16 ± 0.64 | 94.95 ± 0.74 | 95.02 ± 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; Zhao, Y.; He, J.; Wang, S.; Zhong, B.; Wang, F. MAJATNet: A Lightweight Multi-Scale Attention Joint Adaptive Adversarial Transfer Network for Bearing Unsupervised Cross-Domain Fault Diagnosis. Entropy 2025, 27, 1011. https://doi.org/10.3390/e27101011
Song L, Zhao Y, He J, Wang S, Zhong B, Wang F. MAJATNet: A Lightweight Multi-Scale Attention Joint Adaptive Adversarial Transfer Network for Bearing Unsupervised Cross-Domain Fault Diagnosis. Entropy. 2025; 27(10):1011. https://doi.org/10.3390/e27101011
Chicago/Turabian StyleSong, Lin, Yanlin Zhao, Junjie He, Simin Wang, Boyang Zhong, and Fei Wang. 2025. "MAJATNet: A Lightweight Multi-Scale Attention Joint Adaptive Adversarial Transfer Network for Bearing Unsupervised Cross-Domain Fault Diagnosis" Entropy 27, no. 10: 1011. https://doi.org/10.3390/e27101011
APA StyleSong, L., Zhao, Y., He, J., Wang, S., Zhong, B., & Wang, F. (2025). MAJATNet: A Lightweight Multi-Scale Attention Joint Adaptive Adversarial Transfer Network for Bearing Unsupervised Cross-Domain Fault Diagnosis. Entropy, 27(10), 1011. https://doi.org/10.3390/e27101011






