Abstract
Quantum interference can strongly enhance thermoelectric response, with higher-order “supernodes” predicted to yield scalable gains in thermopower and efficiency. A central question, however, is whether such features are intrinsically more fragile to dephasing. Using Büttiker voltage–temperature probes, we establish an order-selection rule: the effective near-node order is set by the lowest among coherent and probe-assisted channels. Supernodes are therefore fragile in an absolute sense because their transmission is parametrically suppressed with order. However, once an incoherent floor dominates, the fractional suppression of thermopower, efficiency, and figure of merit becomes universal and order-independent. Illustrating these principles with benzene- and biphenyl-based junction calculations, we show that the geometry of environmental coupling—through a single orbital or across many—dictates whether coherence is lost by order reduction or by floor building. These results yield general scaling rules for the thermoelectric response of interference nodes under dephasing.
1. Introduction
Quantum interference (QI) is among the most striking hallmarks of phase-coherent transport at the nanoscale. Owing to the dual wave- and particle-like nature of quantum excitations, electronic conduction need not follow any classical path: coherent amplitudes can superpose destructively, completely suppressing current flow and producing transmission zeros (nodes) in the electronic transmission function . Such nodes strongly influence both charge transport and the thermoelectric response [1,2,3,4,5,6,7,8,9,10,11,12,13]. Their positions and lineshapes are dictated by the symmetries of the full Hamiltonian, including geometric, topological, and many-body aspects, so nodes serve not only as fingerprints of microscopic symmetry but also as potential resources for quantum-enhanced functionality [1,2,6,14].
Thermoelectric performance is particularly sensitive to QI, with a dependence that can generally be related to how rapidly varies with energy. Near a node, charge and entropy currents are suppressed in different ways, and their ratio, the thermopower, is predicted to exhibit strong enhancement [11,15]. Related mechanisms have also been demonstrated in superconducting nanostructures, where spin-splitting, phase coherence, and order–parameter symmetry yield unusually large thermoelectric responses and motivate novel device concepts [16,17,18,19,20,21,22]. The order of a node, defined by the local scaling near , controls the magnitude and scaling of this enhancement [10,11,23]. Large violations of the Wiedemann–Franz law are expected in these regimes, reflecting a breakdown of the free-electron picture and offering opportunities for quantum-engineered thermoelectricity [11,15,24,25,26,27,28].
In systems composed of N node-bearing subunits, destructive interference can combine to produce a higher-order supernode, in which coincident quadratic nodes yield a -th order suppression of transport [11,29]. Such supernodes are predicted within single-determinant, effective single-particle theories, e.g., extended Hückel, Hartree–Fock, or standard Kohn–Sham DFT, where the response function factorizes across connected subunits and local zeros combine in a “series-propagation” manner [5]. By contrast, a full many-body treatment reveals a different structure [5,29,30]. Because the interaction self-energy is intrinsically nonlocal, this simple factorization generally fails. As a result, pure supernodes are likely difficult to realize experimentally: unless protected by exact symmetries, they tend to fragment into multiple quadratic nodes or be lifted altogether [29,30]. Even so, sharp interference features with effective order are neither rare nor irrelevant, e.g., arising as Fano antiresonances, quasi-bound states adjacent to a node, or clusters of nearby zeros that can mimic higher-order behavior over experimentally relevant windows [3,5,11]. Because thermoelectric and thermodynamic responses scale sensitively with effective node order, understanding how dephasing reshapes such higher-order structures is essential.
Decoherence and dephasing occur when coherent electron flow couples to external degrees of freedom, e.g., vibrations, solvent, fluctuating charges, or other environmental baths. Such couplings are unavoidable, and their influence on interference features is therefore central to any realistic description of device performance. We model dephasing using the probe concept introduced by Büttiker [31,32], in which fictitious terminals absorb and re-emit carriers stochastically, randomizing their phase while conserving macroscopic currents [33,34,35]. Two variants are commonly employed: a voltage probe (VP), which enforces local charge conservation (), and a voltage–temperature probe (VTP), which enforces both charge and heat conservation () [36,37,38,39,40]. Although sometimes treated as interchangeable, the two impose distinct thermodynamic conditions [41]. At finite temperature the distinction is crucial: a VP does not enforce local equilibrium and can act as an entropy source or sink, whereas a VTP imposes full local thermodynamic equilibrium. In this work, we therefore focus on VTPs, reverting to VPs only in cases where their predictions coincide.
Here we investigate how dephasing modifies the thermoelectric and thermodynamic response of systems with transmission supernodes. Using single and multiple VTPs to model decoherence, and exploiting the near-node universality of the transmission [42], we establish a simple order-selection rule to determine the effective node order in the presence of dephasing. Supernodes are therefore more fragile in an absolute sense, since their transmission is parametrically weaker with increasing order. However, once an incoherent floor develops, the fractional suppression of thermopower, efficiency, and figure of merit becomes universal and effectively order-independent. We further show that the scaling of the response depends not only on node order but also on the geometry of probe–orbital coupling, suggesting strategies to either mitigate or exploit dephasing in practical applications.
2. Quantum Transport Theory
We investigate how node order and dephasing shape charge and heat transport in interacting open quantum systems, modeled as a nanosystem coupled to M macroscopic electrodes treated as ideal Fermi gases. Transport is analyzed within the non-equilibrium Green’s function (NEGF) formalism, which provides a rigorous framework for such systems [43,44,45]. Our focus is on systems whose transport is predominantly elastic and phase-coherent.
In the linear-response regime, the steady-state current of order flowing into electrode is
where corresponds to particle current and to heat current. The Onsager coefficients are
with being the equilibrium Fermi–Dirac distribution at chemical potential and temperature . In coherent transport, the transmission function between leads and is
where is the junction Green’s function and is the tunneling-width matrix for lead , defined as
with as molecular orbital indices, and the coupling between orbital n and electrode state k of energy . In the wide-band limit considered here, is energy-independent.
Within molecular Dyson equation (MDE) theory [9], the junction Green’s function can be written exactly as
where is the Green’s function of the isolated molecule, is the total tunneling self-energy, and is the Coulomb self-energy correction due to resonance broadening. In the elastic cotunneling regime considered here, and inelastic contributions are negligible [9]. Finally, the molecular Green’s function admits the Lehmann representation [9]
where () creates (annihilates) an electron of spin on orbital n, is an eigenstate of the molecular Hamiltonian with energy , and is its grand-canonical occupation probability at .
Model Hamiltonian and Parameters
To illustrate our results, we consider two representative single-molecule junctions (SMJs) whose -conjugated backbones capture the essential physics of interference nodes: Au-1,3-benzenedithiol-Au (BDT) in the meta configuration, which exhibits a quadratic node, and Au-3,3′-biphenyldithiol-Au (BPDT), where connectivity and torsion-controlled inter-ring coupling give rise to effective higher-order interference features [46,47,48]. We focus on these junctions because they are chemically stable, experimentally benchmarked molecules that exhibit canonical interference features, providing minimal yet physically realistic models for analyzing how dephasing reshapes transport in the vicinity of supernodes.
The effective Hamiltonian for the -system can be derived from first principles by integrating out off-resonant degrees of freedom (e.g., the -system, image-charge effects, and substrate polarization), which are absorbed into renormalized site energies and couplings [49]. In a localized orbital basis, the resulting one-body Hamiltonian is
where is the effective on-site potential, is the effective hopping matrix element, is the local charge density, and denotes nearest-neighbor pairs with . In this notation, denotes the inter-ring hopping in biphenyl and is simply one of the values connecting the two phenyl subunits. Equation (7) is formally equivalent to an extended Hückel Hamiltonian in which electron–electron interactions are neglected. The influence of interactions on thermoelectric transport has been analyzed in detail elsewhere [49,50]. Couplings to electrodes and probes are included through their self-energies within the NEGF formalism.
For the BDT junction we take the electrode couplings to be symmetric, , with nearest-neighbor hopping , values obtained from fits to experiment [9,49]. For the BPDT junction, comparison with measured thermopower and conductance yields [51,52]. The intra-phenyl nearest-neighbor hopping is taken to be the same as in BDT, while the inter-phenyl coupling is modeled as , where is the dihedral angle between adjacent rings. Using the gas-phase torsion angle gives [53,54]. Although we employ experimentally motivated parameters, our conclusions do not depend sensitively on their precise values.
3. Inclusion of Dephasing
Quantum interference effects in molecular conductors can persist even under ambient conditions [48,55,56,57,58,59,60,61,62], but remain intrinsically sensitive to decoherence from coupling to vibrational, photonic, or other environmental degrees of freedom. To model such processes we employ the Büttiker probe approach [31,32], in which fictitious terminals absorb and re-emit carriers stochastically, randomizing phase while preserving global conservation laws.
Two probe types are considered. A voltage probe enforces charge conservation () but permits finite heat currents, and thus does not enforce local thermal equilibrium. A voltage–temperature probe enforces both charge and heat balance (), thereby representing a thermodynamically consistent environment [36,37,38,39,40]. The two models coincide in certain symmetric limits but diverge under finite thermal bias or in systems with appreciable thermoelectric response [41]. Physically, the probes act as local measurements on molecular orbitals, effectively introducing incoherent mixing at the attachment site. This mechanism directly reduces supernode order without invoking additional degrees of freedom.
As emphasized previously [12,37,41], the choice of probe model carries thermodynamic significance. A VP fixes the probe temperature externally and enforces only charge conservation, so at finite temperature or in systems with appreciable thermoelectric response it provides, at best, an incomplete description of dephasing. By contrast, the VTP enforces full local equilibrium and remains physically consistent across operating conditions. In this work we therefore use the VTP throughout our calculations. Nevertheless, we retain the VP as an analytic surrogate: its simplicity affords closed-form results for effective Onsager functions in three-terminal circuits, and it reproduces the correct low-energy exponents of the Onsager moments, providing a transparent view of how probe coupling modifies node order.
4. Thermoelectric Observables
For a two-terminal circuit with leads L and R, the electrical conductance, thermopower, and electronic thermal conductance are conveniently expressed in terms of the Onsager functions as
where . Here G is the electrical conductance, S is the thermopower (Seebeck coefficient), and is the electronic thermal conductance in open-circuit conditions.
In circuits with more than two electrodes we define the thermal conductance by considering a pure thermal circuit: a temperature bias is applied while imposing open-circuit conditions on the charge currents, . Hence the operational thermal conductance is
For a VP, and depends on the probe heat shunt; for a VTP, and , which we report throughout.
Device Performance
A widely used benchmark for thermoelectric performance is the dimensionless figure of merit [25,26]
where is only the electronic contribution to the thermal conductance. In realistic junctions, phonons and other channels provide parallel heat paths that reduce the effective [11]. For small organic molecules, however, phonon transmission across a metal–molecule interface is typically suppressed due to limited spectral overlap between lead Debye frequencies and molecular vibrational modes. Accordingly, our focus here is on the electronic part, with environmental scattering incorporated through voltage–temperature probes.
While is a useful rule of thumb, a more fundamental thermodynamic measure is the thermodynamic efficiency. With a small thermal bias, , applied across the junction, the charge current in linear response is , where is fixed by the load resistance (or, equivalently, the load ratio ). At this operating point the power delivered to the load is simply
For a VTP, which enforces both charge and heat balance, the hot-side heat input retains the two-terminal form but with probe-renormalized coefficients,
where K is the total electronic thermal conductance consistent with . The efficiency at finite load then follows as
When reporting efficiencies we normalize to the Carnot value for the same bias, so that isolates the influence of dephasing and connectivity from temperature scaling. All results below correspond to operating-point efficiencies at fixed finite m; no optimization over load is performed.
5. Effective Node-Order Reduction by Dephasing
We first investigate the -system transport in the vicinity of an interference node (or supernode) for two archetypal junctions: meta-configured Au-1,3-benzenedithiol-Au (BDT) and Au-3,3’-biphenyldithiol-Au (BPDT), each with a single locally coupled probe (shown schematically in the insets of Figure 1). The NEGF + Hückel transmission spectra between all three electrodes are shown in the top and bottom panels of Figure 1 for BDT and BPDT, respectively. For visual comparison, all spectra are shifted so that the node energy is . As expected [9,11,15], the coherent left–right channel displays a quadratic node in BDT () and a quartic supernode in BPDT (). The additional probe transmissions, and , depend on connectivity: in BDT the probe is para to the left electrode and ortho to the right, so neither path exhibits a node and both spectra are smooth (i.e., ). In BPDT, by contrast, the L-P path is para-configured and flat (), while the R-P path exhibits a quadratic () node, as indicated by the black fits in Figure 1.
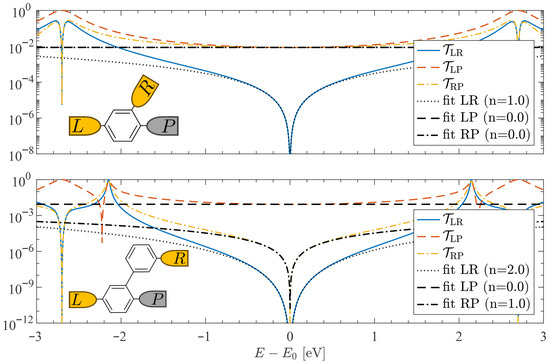
Figure 1.
Transmission functions with a single probe. The -system transmissions for benzene-dithiol (BDT, top) and biphenyl-dithiol (BPDT, bottom) junctions are shown. Solid, dashed, and dash-dotted curves correspond to the , , and channels, respectively. Fits of the form are overlaid, with the extracted exponents indicated in the legend. In the BDT junction, the nodal scaling is quadratic (). In the BPDT junction, higher-order behavior emerges: quartic scaling (), characteristic of a transmission supernode, together with nearly flat background contributions from probe-mediated incoherent transport. Because the thermopower is proportional to the energy derivative of the transmission, higher-order nodes (larger n) produce correspondingly sharper features and enhanced thermopower responses. Insets show the molecular junction geometries and probe coupling sites. Exponents were extracted over the range eV. Calculations used the parameters discussed in Section 2 and assume room temperature .
Transport coefficients inherit their scaling from the order of the node. The effective exponent therefore provides a direct diagnostic of how dephasing reshapes quantum interference. Close to the nodal energy , which is detuned from any molecular resonances, each two-terminal transmission channel admits the expansion [42]
so that the corresponding lowest-order Onsager moments may be expressed as
with , a universal, dimensionless function set solely by the Fermi window.
Eliminating the probe degrees of freedom from the Onsager matrix yields the Schur complement
where bold symbols denote 2 × 2 Onsager blocks over . For a VP, reduces to the scalar , giving the convenient analytic form
in which the effective transmission is a sum of a coherent channel and an incoherent probe-mediated term.
For a VTP, a single energy-local reproducing both charge and heat currents does not generally exist, since the simultaneous constraints mix energy moments. Special cases (e.g., proportional couplings or the narrow-window limit) admit such a representation, but in general one must work directly with Onsager blocks. Either way, Equation (18) shows that is built from rational combinations of primitive moments, each inheriting a power law . Block inversion cannot increase this power, so the effective near-node exponent is
where
A probe, and by extension any environment faithfully represented by one, can only reduce the sharpness of an interference node; it can never sharpen it. Intuitively, phase randomization can destroy interference, but it cannot create new cancellations. Formally, this follows from the Schur-complement structure: dephasing mixes existing channels but does not generate new destructive interference pathways. The effective exponent is therefore fixed by the order-selection rule: a single local probe reduces to the order of the strongest bypass, while distributing probes across all orbitals introduces additional incoherent channels that eventually wash out the node entirely. Small detunings of the nodal energies (see Appendix D), alternate probe placements, asymmetric broadenings, or transmission spectra shift numerical prefactors, but in all cases the effective exponent is determined by the lowest available order among the coherent and probe-assisted paths.
The practical importance of lies in its direct control of thermoelectric response. As Equation (17) shows, all Onsager blocks inherit the near-node exponent, so transport coefficients such as G, S, , , and scale parametrically with . In particular, the peak thermopower grows nearly linearly with , while and the efficiency are strongly enhanced by higher-order nodes [11]. Consequently, changes in under dephasing directly translate into the suppression or survival of QI-induced enhancements.
Figure 2 illustrates these principles for BDT and BPDT junctions with a single local VTP. In BDT, the coherent transmission has order ; probe-assisted channels contribute , so and a constant background, or floor, appears at the node. In BPDT, the coherent order collapses to without producing a floor, yielding a rapid but continuous crossover in the thermopower and figure of merit. In both cases, increasing suppresses coherence and diminishes interference-induced enhancements of S and . Supernodes appear more fragile because their coherent signal is smaller near , so the incoherent bypass overtakes them at weaker coupling.
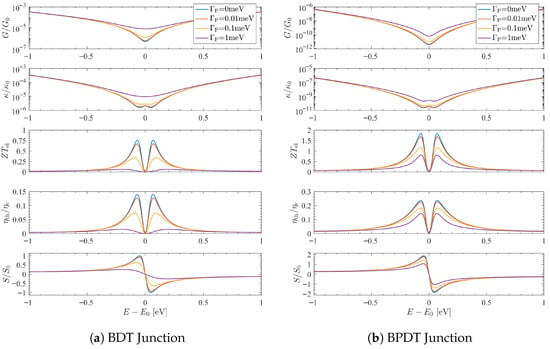
Figure 2.
Order selection under single-probe VTP dephasing. Thermoelectric response of (a) BDT (quadratic node, ) and (b) BPDT (quartic supernode, ) junctions at K. Curves show , , , , and as functions of energy for several probe couplings . Here V/K, and is the Carnot efficiency defined by the applied ( K). In BDT, a probe at the para site generates an incoherent floor (), while in BPDT the quartic supernode collapses to quadratic order (). The loss of higher-order scaling suppresses the interference-enhanced thermopower and figure of merit. These trends exemplify the order-selection principle: quadratic nodes persist by saturating to a floor, whereas supernodes collapse to quadratic response under dephasing.
6. Probe Connectivity: Single vs. N-Probe Effects at Fixed Total Coupling
Building on the selection rule above, we now examine how different probe connectivities govern the onset of incoherent floor behavior. Dephasing probes provide a convenient coarse-grained representation of environmental degrees of freedom. A molecular junction embedded in a fluctuating medium, for example with electrochemical noise, local vibrational baths, or solvent fluctuations, may exchange particles and heat with many modes that do not couple uniquely to a single orbital. To clarify the consequences, we compare two limiting connectivity scenarios. In the single-probe case, one VTP couples locally to a designated orbital with strength . In the N-probe case, each orbital couples to its own independent VTP of strength , so that and every orbital relaxes to a separate local voltage and temperature.
As discussed, a locally coupled probe alters the near-node transmission order according to the selection rule of Equation (20). By contrast, when probes are distributed over all sites, the Schur complement necessarily generates an energy-independent contribution, producing an incoherent floor of the form
with in the weak-coupling limit. Here is a geometry-dependent prefactor reflecting how efficiently the probed orbitals overlap both contacts (see Appendix B).
Once a probe-induced floor is present, the low-energy response is governed entirely by the constant background rather than the coherent order. Generally, the thermopower follows the Mott relation, being proportional to the logarithmic derivative of the transmission near the Fermi level. Here this derivative scales with the thermal window, while the average transmission is set by B, yielding . Because both G and scale with the same B, their ratio cancels in , leaving . Since in the weak-coupling limit, this produces the universal scalings
These relations hold regardless of whether the underlying node is quadratic or quartic; geometry only enters through the prefactor .
The physical origin of the floor is intuitive: once every orbital is equilibrated by its own probe, probe-mediated paths exist with finite spectral weight even at . Although the order-selection rule still dictates the asymptotic exponent, these probe-mediated bypasses, together with higher-order asymmetries or detuned near–zeros, generate a finite incoherent background. In the N-probe configuration this background is unavoidable and dominates once exceeds the coherent contribution within the thermal window.
Small-: A Single Probe Maximally Dephases
At weak coupling, probes act independently and their contributions to the effective block are additive. Denoting by the Onsager blocks over , one finds for a probe on site i,
with positive definite and independent of at leading order. Inserting into Equation (18) yields the first correction to the effective block,
The consequence for thermopower can be written as the initial slope
with weights (). Because this expression is affine in the , the steepest suppression of at fixed occurs when all coupling is placed on a single orbital. The probe opens a direct incoherent pathway through that orbital, whose strength is governed by molecular symmetry and the local spectral weight at site i. Concentrating the coupling on the orbital that maximizes the probe-mediated transmission therefore produces the strongest dephasing effect, directly reducing the effective node order. By contrast, probes attached to symmetry-dark orbitals, i.e., those which carry vanishing spectral weight at , contribute negligibly and are far less disruptive [6].
This behavior is evident in Figure 3. For the BDT node, shown in panel (a), a single local probe depresses the normalized thermopower and efficiency more strongly, across nearly the entire range, than N smaller probes of the same total strength. For BPDT, shown in panel (b), a single probe immediately collapses the supernode () without creating a floor, again producing a steeper normalized suppression. Absolute peak values can nevertheless remain large, depending on prefactors, but the trend is clear: concentrating on a single orbital with significant transport maximizes the dephasing effect.
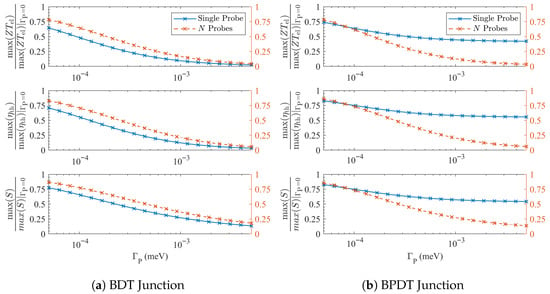
Figure 3.
Reduction of node enhancements versus total probe coupling. Maxima (over E) of , , and S at K, normalized to their coherent peaks, are plotted against the total probe strength . Blue curves show a single local probe of strength ; orange curves show N independent local probes (one per site), each of strength . At small the single-probe traces fall at least as rapidly, consistent with order selection in which a supernode collapses to quadratic order without creating a floor. At larger the all-site traces cross below, reflecting the emergence of a genuine incoherent floor and the ensuing , scaling. The crossover scale follows the same temperature trend as the order-selection scale but is observable- and geometry-dependent.
At larger , however, the balance shifts. When probes are distributed over all orbitals, the cumulative floor grows linearly with the number of available bypasses. Once this floor overtakes the dispersive contribution, many-probe geometries suppress S, , and more efficiently than a single probe, leading to the crossings seen in Figure 3. In other words, single-site coupling dominates in the weak-dephasing regime, whereas N-probe coupling dominates once the incoherent background becomes appreciable.
The resulting contrast is summarized in Figure 4. With one probe per site, each coupled at strength so that the total coupling is fixed, the normalized suppression of S, , and becomes nearly identical for BDT (quadratic node) and BPDT (quartic supernode). This reflects the fact that, once a probe-induced floor is present, the fractional reduction of the thermoelectric response is governed primarily by rather than by the underlying coherent order. Absolute values can still differ substantially—supernodes retain their larger coherent-limit enhancements until the floor dominates—but the shape of the decay becomes order-independent eventually. The modest residual curvature differences between the two molecules reflect only geometry-dependent prefactors in , not a distinct order-selection mechanism. Thus, while single-site probes reveal the fragility of supernodes through immediate order reduction, all-site dephasing renders the fractional suppression effectively order-agnostic.
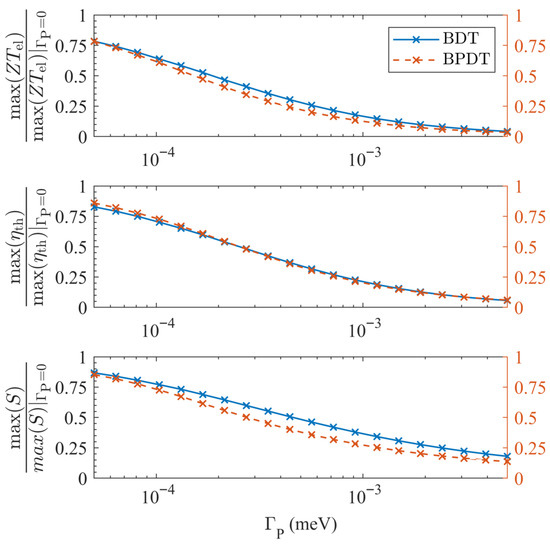
Figure 4.
All-site dephasing renders fractional suppression order-agnostic. With one probe per site (each coupled with , so the total is ), the normalized decays of , , and S versus are nearly indistinguishable for BDT (quadratic node; left vertical axis) and BPDT (quartic supernode; right vertical axis) at K. This demonstrates that once a probe-induced floor is present, the fractional reduction of the response is governed primarily by and is largely insensitive to the coherent order. Absolute values can still remain larger for supernodes, reflecting their higher coherent-limit enhancements, but the shape of the decay is universal. The modest residual curvature differences reflect geometry-dependent prefactors rather than a distinct order-selection mechanism.
7. Order-Dependent Sensitivity to Dephasing
A central question in this work is whether higher-order interference supernodes are intrinsically more fragile to dephasing than ordinary quadratic nodes. Because both the conductance and thermal conductance inherit the near-node exponent, their temperature scaling provides a direct window into how coherence is degraded. Formally, the Onsager relation of Equation (17) implies
so the log–log slopes of G and at give a direct measure of the effective node order . We therefore investigate supernode fragility by tracking how the effective nodal order, extracted from the slopes of G and , evolves as a function of probe coupling strength.
The conductance and electronic thermal conductance are shown in Figure 5 as functions of for several single probe couplings . Each trace is normalized by its geometric mean over the fit window (dotted vertical lines), so that offsets are removed and the slopes directly reveal the effective order . Values extracted independently from G and agree within uncertainty, confirming the robustness of this diagnostic.
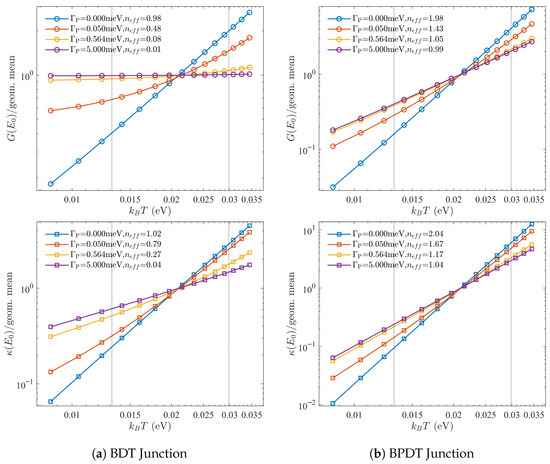
Figure 5.
Node scaling identifies the effective order under dephasing. Log–log plots of conductance and electronic thermal conductance versus for several single probe coupling strengths . Each trace is normalized by its geometric mean over the fit window (dotted vertical lines), so that vertical offsets are removed and slopes directly yield the effective order . Values extracted from G and agree within uncertainty. In panel (a), the BDT (benzene) junction has , giving in the coherent limit. Any introduces an energy-independent floor, driving with and . In panel (b), the BPDT (biphenyl) junction has , yielding (, ) in the coherent limit. As is increased this quartic supernode collapses to quadratic order, , with and . In both cases the probe coupling is weak compared to , so the coherent spectrum is otherwise unaltered; the probe acts only to select the effective order. The single probe junction configurations are indicated in Figure 1.
Panel (a) illustrates the BDT junction . In the coherent limit the slope corresponds to , as expected for a quadratic node. Any finite , however, introduces an energy-independent bypass that drives , yielding and . Panel (b) shows the BPDT supernode , which in the coherent limit yields . Here even an infinitesimal collapses the quartic scaling to quadratic () without generating a floor, reflecting the immediate fragility of the supernode. An analogous analysis applies to N-probe geometries (Appendix A). In this case, distributing probes across all orbitals produces an incoherent floor that enforces as increases, rendering the suppression effectively order-agnostic once the floor dominates.
To quantify these crossovers, we fit the extracted slopes to the interpolation
where and denote the coherent and dephased asymptotes, respectively (see Appendix C). From the single-probe spectra we obtain
The fitted exponents remain close to , as expected for probe-induced incoherent channels that scale linearly with . The crucial difference lies in the crossover scales . Because the coherent transmission of a supernode is parametrically suppressed near , even a weak bypass rapidly overwhelms it. The biphenyl supernode therefore collapses at a probe strength roughly smaller than that required to quench the benzene node. This is the precise sense in which supernodes are “more fragile’’: not that their collapse is sharper, but that it occurs at parametrically smaller . In other words, their enhanced sensitivity is rooted in spectral weight, not in the nature of the dephasing itself.
Extending the same analysis to N-probe geometries gives
indicating that once probes are distributed across all orbitals, both junctions develop a nearly indistinguishable incoherent floor. With this floor, the fractional suppression of , , and is essentially order-agnostic (cf. Figure 4), although geometry sets the prefactors.
We can now return to the central question of this work. Supernodes are indeed more sensitive to local dephasing. However, once the environment acts collectively, as modeled by N-probe configurations, the distinction between quadratic nodes and supernodes effectively disappears. The lesson is twofold. First, although higher-order supernodes provide enhanced thermoelectric response, that enhancement is eroded by weaker coupling than a quadratic node. Second, the way the environment couples, through a single dominant orbital or through many, dictates whether this erosion is abrupt (order reduction) or gradual (floor building). Thus, it is not merely the presence of dephasing, but the geometry of its coupling, that determines whether supernode-based thermoelectric enhancement survives.
8. Conclusions
We have shown that dephasing always reduces, but never sharpens, quantum interference nodes. A probe either leaves the node order unchanged or collapses a supernode to lower order. This asymmetry reflects the Schur-complement structure of the probe formalism: effective Onsager blocks inherit the lowest available power law, so incoherent mixing can only reduce, not enhance, destructive interference. In other words, probes encode incoherent pathways but do not generate new interference routes.
This behavior is summarized by a simple order-selection principle: the effective near-node order is given by the minimum of the coherent exponent and the largest exponent accessible through probe-mediated transport. In practice, a quartic supernode collapses quickly to quadratic order under even weak local perturbations, while a quadratic node preserves its form until incoherent bypass channels introduce a true floor. The associated crossover is characterized by two fitted parameters: , the probe strength at which incoherent processes overtake the coherent node, and , which controls the sharpness of the collapse. We find in both single-probe and N-probe connectivities, consistent with probe-induced channels that scale linearly with , while captures the enhanced sensitivity of supernodes under local coupling.
The reduction of a node’s effective order is continuous: within the thermal window the coherent contribution scales as while probe-mediated terms grow with , so decreases smoothly rather than discontinuously. Both quadratic and quartic nodes degrade at comparable rates with increasing ; the distinction is that supernodes cross over at weaker probe strengths, reflecting their greater fragility in the order-selection sense rather than a faster decay rate.
Probe connectivity plays an equally important role. For fixed total coupling, a single local probe reduces the order but does not produce a floor, whereas distributing the same strength across multiple sites inevitably builds one. Once present, this floor enforces the scaling, and , independent of the initial coherent order. In this regime the degradation of thermopower, efficiency, and figure of merit becomes order-agnostic, governed primarily by the prefactor of the incoherent floor.
The stability of supernodes, and the QI-driven enhancements they support, therefore depends not only on the overall coupling strength but also on how the environment connects to molecular orbitals. Probes make this dependence explicit, revealing when supernodes retain their advantage and when interference collapses to universal scaling laws. In this sense, dephasing becomes a design principle: robustness can be maximized by engineering environmental couplings or by exploiting molecular symmetries that preserve nodal pathways, suggesting practical strategies for realizing quantum-enhanced thermoelectric materials.
Funding
This research was graciously supported by the National Science Foundation under award number QIS-2412920.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Order Selection with N Local Probes
To confirm that the node order-selection rule of Equation (20) is not an artifact of single-probe coupling, we repeated the log–log scaling analysis with N independent VTPs, one attached to each molecular orbital. Each probe enforces local equilibration () with coupling , so that the total strength remains fixed at . This configuration represents the strongest form of dephasing, since every orbital exchanges particles and heat with its own bath.
Figure A1 shows the resulting scaling of and with for BDT and BPDT. In both molecules the effective order is again determined by the lowest available exponent among the coherent and probe-assisted channels, exactly as predicted by the selection rule. No evidence is found for sharpening or enhancement of interference nodes under many-site coupling: the incoherent probe pathways always reduce the effective order.
The principal difference from the single-probe case is quantitative rather than qualitative. Because all orbitals are equilibrated, additional two-step paths () are available, generating an incoherent background that appears as a finite floor at the node [cf. Equation (22)]. This background dominates more rapidly as increases, but the near-node scaling exponents extracted from Figure A1 follow the same order-selection principle already discussed in the main text. Thus, the N-probe geometry confirms that the order-selection rule is general: dephasing can only lower the effective order of a node or introduce a floor, never sharpen it.
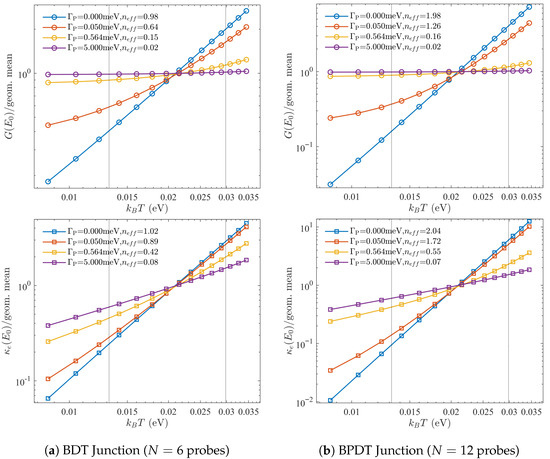
Figure A1.
Effect of probe connectivity on node scaling. Same analysis as in Figure 5, but with N independent VTPs locally coupled and equilibrated to every molecular site. Each probe is allowed to relax locally to its own chemical potential and temperature, thereby providing the strongest form of dephasing. Panel (a) shows the BDT junction and panel (b) the BPDT junction. The qualitative order-selection behavior is unchanged in this case, however.
Appendix B. Distributed Probes and the Linear Floor
Consider an N-probe VTP configuration in the wide-band, weak-coupling limit with local probe couplings at orbitals and total . Let denote the retarded/advanced Green’s functions of the unprobed junction. Then at the nodal energy , the effective two-terminal transmission, after eliminating the probes by the Schur complement, acquires an energy-independent term,
with nonnegative coefficients
and , the usual lead broadenings. In particular, for equal splitting ,
where
is the geometry-dependent prefactor that converts the total probe coupling into an effective incoherent background.
In linear response, eliminating the probes with the VTP constraints () yields the effective Onsager block [41]
for any (we choose for conductance), where P indexes the probe set. To leading order in ,
where transmissions between probes are and can be neglected at this order. Substituting these scalings into (A5) gives the probe contribution
At a node the functions are smooth; over the thermal window they may be replaced by their values at up to corrections, yielding (A1) and (A2).
Equation (A3) shows that the incoherent background generated by N-probe connectivity is linear in the total probe strength. This scaling follows directly from the D’Amato–Pastawski two-step formula, : the numerator scales as while the denominator scales as , leaving a net dependence for each site. The geometry factor in Equation (A2) encodes how efficiently orbital i connects both leads; if a site is symmetry-dark to L or R (for example, due to a wavefunction node or another destructive symmetry), its vanishes and that probe does not contribute. The resulting floor is therefore not universal but determined by geometry and the underlying quantum interference: distributed probes always open energy-independent bypasses, but the magnitude of the background depends sensitively on which orbitals overlap both contacts. Beyond the wide-band approximation, the prefactor may develop curvature with , yet the linear law remains the leading contribution so long as the unprobed Green’s functions are smooth at . Importantly, this linear floor sets the scale at which thermopower, figure of merit, and efficiency saturate: once exceeds the coherent transmission within the thermal window, the probe-induced background dominates the response and erases distinctions between different nodal orders.
Appendix C. Effective Order Under Weak Dephasing
Near a nodal energy the coherent transmission has
so all Onsager blocks inherit the power . Attaching a weak probe opens additional channels of lower near-node order , with amplitudes that scale with the total probe strength:
Two cases capture the probe effects used in the main text: (i) a dispersive lower-order bypass (single-site probe), where ; (ii) an energy-independent floor (all-site probes), where and
To leading order in ,
We define the instantaneous effective order by the log–log slope,
Inserting (A12) gives
Thus, the probe selects the dephased asymptote , while the coherent channel sets the clean asymptote .
In practice we report a window-averaged slope (either over a fixed log- range or weighted by the Fermi window). This average is well captured by the empirical Hill form used in the main text,
with
Here but also reflects details of the averaging window.
The selection rule fixes the lower asymptote . The crossover scale decreases with the order gap , so higher-order supernodes () collapse at smaller than quadratic nodes. The fitted exponent carries no universal meaning, but provides a robust sensitivity measure: it is the value of at which the effective order has decayed halfway between its coherent and dephased limits.
Appendix D. The Influence of Node Detuning
The order-selection rule described in the main text assumes that all relevant channels vanish at the same nodal energy. In practice, this condition need not hold. If the channels are detuned —for example, vanishes at , while and vanish at and with —then near the probe-mediated pathway generically contributes finite weight.
For a VP this follows directly from
so that a finite background
emerges whenever the probe channels do not vanish at . An analogous conclusion holds for a VTP at the level of Onsager moments: detuning injects a zeroth-order term into .
The consequences are straightforward. At asymptotically low T, transport is governed by :
while the thermopower vanishes with temperature. If the intrinsic left–right channel scales as , then (up to prefactors)
Thus, detuning does not protect supernode-enhanced thermopower; instead it erodes it by introducing a floor that dominates in the low-T limit.
Practically, apparent supernode scaling can still be observed over finite experimental ranges, provided the detuning-induced background is small on the thermal scale, i.e.,
with A the prefactor of the coherent channel. But asymptotically the background wins, collapsing the enhancement. The suppression of electronic thermal conductance illustrates this point most clearly. At the nodal energy,
so that the BPDT junction with yields values many orders of magnitude below benzene (). At room temperature ( eV), the factor eV2 already enforces a dramatic reduction. Residual offsets arise from nodal amplitudes and from the constraint, which further restricts probe heat flow. Together with the dephasing analysis of the main text, these results confirm that temperature exposes the intrinsic exponent while dephasing renormalizes it.
References
- Evers, F.; Korytár, R.; Tewari, S.; van Ruitenbeek, J.M. Advances and challenges in single-molecule electron transport. Rev. Mod. Phys. 2020, 92, 035001. [Google Scholar] [CrossRef]
- Dubi, Y.; Di Ventra, M. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 2011, 83, 131. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257. [Google Scholar] [CrossRef]
- Solomon, G.C.; Andrews, D.Q.; Goldsmith, R.H.; Hansen, T.; Wasielewski, M.R.; Van Duyne, R.P.; Ratner, M.A. Quantum interference in acyclic systems: Conductance of cross-conjugated molecules. J. Am. Chem. Soc. 2008, 130, 17301–17308. [Google Scholar] [CrossRef]
- Solomon, G.C.; Bergfield, J.P.; Stafford, C.A.; Ratner, M.A. When “small” terms matter: Coupled interference features in the transport properties of cross-conjugated molecules. Beilstein J. Nanotechnol. 2011, 2, 862–871. [Google Scholar] [CrossRef]
- Cardamone, D.M.; Stafford, C.A.; Mazumdar, S. Controlling quantum transport through a single molecule. Nano Lett. 2006, 6, 2422–2426. [Google Scholar] [CrossRef]
- Stafford, C.A.; Cardamone, D.M.; Mazumdar, S. The quantum interference effect transistor. Nanotech. 2007, 18, 424014. [Google Scholar] [CrossRef]
- Lambert, C. Basic concepts of quantum interference and electron transport in single-molecule electronics. Chem. Soc. Rev. 2015, 44, 875–888. [Google Scholar] [CrossRef] [PubMed]
- Bergfield, J.P.; Stafford, C.A. Many-body theory of electronic transport in single-molecule heterojunctions. Phys. Rev. B 2009, 79, 245125. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Jacquod, P.; Stafford, C.A. Coherent destruction of Coulomb blockade peaks in molecular junctions. Phys. Rev. B 2010, 82, 205405. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Solis, M.A.; Stafford, C.A. Giant thermoelectric effect from transmission supernodes. ACS Nano 2010, 4, 5314–5320. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Stafford, C.A. Thermoelectric corrections to quantum voltage measurement. Phys. Rev. B 2014, 90, 235438. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Solomon, G.C.; Stafford, C.A.; Ratner, M.A. Novel quantum interference effects in transport through molecular radicals. Nano Lett. 2011, 11, 2759–2764. [Google Scholar] [CrossRef]
- Basov, D.; Averitt, R.; Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 2017, 16, 1077–1088. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Stafford, C.A. Thermoelectric Signatures of Coherent Transport in Single-Molecule Heterojunctions. Nano Lett. 2009, 9, 3072–3076. [Google Scholar] [CrossRef] [PubMed]
- Ozaeta, A.; Virtanen, P.; Bergeret, F.; Heikkilä, T. Predicted very large thermoelectric effect in ferromagnet-superconductor junctions in the presence of a spin-splitting magnetic field. Phys. Rev. Lett. 2014, 112, 057001. [Google Scholar] [CrossRef]
- Kolenda, S.; Wolf, M.J.; Beckmann, D. Observation of thermoelectric currents in high-field superconductor-ferromagnet tunnel junctions. Phys. Rev. Lett. 2016, 116, 097001. [Google Scholar] [CrossRef]
- Kalenkov, M.S.; Zaikin, A.D. Large thermoelectric effect in ballistic Andreev interferometers. Phys. Rev. B 2017, 95, 024518. [Google Scholar] [CrossRef]
- Marchegiani, G.; Braggio, A.; Giazotto, F. Nonlinear thermoelectricity with electron-hole symmetric systems. Phys. Rev. Lett. 2020, 124, 106801. [Google Scholar] [CrossRef] [PubMed]
- Guarcello, C.; Braggio, A.; Giazotto, F.; Citro, R. Thermoelectric signatures of order-parameter symmetries in iron-based superconducting tunnel junctions. Phys. Rev. B 2023, 108, L100511. [Google Scholar] [CrossRef]
- Guarcello, C.; Citro, R.; Giazotto, F.; Braggio, A. Bipolar thermoelectrical SQUIPT (BTSQUIPT). Appl. Phys. Lett. 2023, 123. [Google Scholar] [CrossRef]
- Germanese, G.; Paolucci, F.; Marchegiani, G.; Braggio, A.; Giazotto, F. Bipolar thermoelectric Josephson engine. Nat. Nanotechnol. 2022, 17, 1084–1090. [Google Scholar] [CrossRef]
- Wierzbicki, M.; Swirkowicz, R. Influence of interference effects on thermoelectric properties of double quantum dots. Phys. Rev. B 2011, 84, 075410. [Google Scholar] [CrossRef]
- Majidi, D.; Bergfield, J.P.; Maisi, V.; Höfer, J.; Courtois, H.; Winkelmann, C.B. Heat transport at the nanoscale and ultralow temperatures—Implications for quantum technologies. Appl. Phys. Lett. 2024, 124. [Google Scholar] [CrossRef]
- Bell, L.E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef]
- DiSalvo, F.J. Thermoelectric cooling and power generation. Science 1999, 285, 703–706. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.L.; Zou, J.; Chen, Z.G. Advanced thermoelectric design: From materials and structures to devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef] [PubMed]
- Rincón-García, L.; Evangeli, C.; Rubio-Bollinger, G.; Agraït, N. Thermopower measurements in molecular junctions. Chem. Soc. Rev. 2016, 45, 4285–4306. [Google Scholar] [CrossRef]
- Barr, J.D.; Stafford, C.A. On Transmission Node Structure in Interacting Systems. arXiv 2013, arXiv:1303.3618. [Google Scholar] [CrossRef]
- Pedersen, K.G.; Strange, M.; Leijnse, M.; Hedegård, P.; Solomon, G.C.; Paaske, J. Quantum interference in off-resonant transport through single molecules. Phys. Rev. B 2014, 90, 125413. [Google Scholar] [CrossRef]
- Büttiker, M. Four-terminal phase-coherent conductance. Phys. Rev. Lett. 1986, 57, 1761. [Google Scholar] [CrossRef] [PubMed]
- Büttiker, M. Coherent and sequential tunneling in series barriers. IBM J. Res. Dev 1988, 32, 63–75. [Google Scholar] [CrossRef]
- Kilgour, M.; Segal, D. Inelastic effects in molecular transport junctions: The probe technique at high bias. J. Chem. Phys. 2016, 144, 124107. [Google Scholar] [CrossRef] [PubMed]
- Kilgour, M.; Segal, D. Charge transport in molecular junctions: From tunneling to hopping with the probe technique. J. Chem. Phys. 2015, 143, 024111. [Google Scholar] [CrossRef]
- Golizadeh-Mojarad, R.; Datta, S. Nonequilibrium Green’s function based models for dephasing in quantum transport. Phys. Rev. B 2007, 75, 081301. [Google Scholar] [CrossRef]
- Engquist, H.L.; Anderson, P. Definition and measurement of the electrical and thermal resistances. Phys. Rev. B 1981, 24, 1151. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Story, S.M.; Stafford, R.C.; Stafford, C.A. Probing Maxwell’s demon with a nanoscale thermometer. ACS Nano 2013, 7, 4429–4440. [Google Scholar] [CrossRef]
- Meair, J.; Bergfield, J.P.; Stafford, C.A.; Jacquod, P. Local temperature of out-of-equilibrium quantum electron systems. Phys. Rev. B 2014, 90, 035407. [Google Scholar] [CrossRef]
- Stafford, C.A. Local temperature of an interacting quantum system far from equilibrium. Phys. Rev. B 2016, 93, 245403. [Google Scholar] [CrossRef]
- Shastry, A.; Stafford, C.A. Cold Spots in Quantum Systems Far From Equilibrium: Local Entropies and Temperatures Near Absolute Zero. Phys. Rev. B 2015, 92, 245417. [Google Scholar] [CrossRef]
- Erdogan, E.; Bergfield, J.P. When Dephasing Fails: Thermodynamic Consequences of Decoherence Models in Quantum Transport. arXiv 2025, arXiv:2508.20343. [Google Scholar] [CrossRef]
- Bennett, R.X.; Hendrickson, J.R.; Bergfield, J.P. Quantum Interference Enhancement of the Spin-Dependent Thermoelectric Response. ACS Nano 2024, 18, 11876–11885. [Google Scholar] [CrossRef] [PubMed]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors. In Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1996; Volume 123. [Google Scholar]
- Stefanucci, G.; Van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Cuevas, J.C.; Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment; World Scientific Publishing Company: Singapore, 2010; Volume 1. [Google Scholar]
- Markussen, T.; Stadler, R.; Thygesen, K.S. The relation between structure and quantum interference in single molecule junctions. Nano Lett. 2010, 10, 4260–4265. [Google Scholar] [CrossRef]
- Solomon, G.C.; Andrews, D.Q.; Hansen, T.; Goldsmith, R.H.; Wasielewski, M.R.; Van Duyne, R.P.; Ratner, M.A. Understanding quantum interference in coherent molecular conduction. J. Chem. Phys. 2008, 129, 054701. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Wang, F.; Hong, W. Quantum interference effects in charge transport through single-molecule junctions: Detection, manipulation, and application. Acc. Chem. Res. 2018, 52, 151–160. [Google Scholar] [CrossRef]
- Barr, J.D.; Stafford, C.A.; Bergfield, J.P. Effective field theory of interacting π electrons. Phys. Rev. B 2012, 86, 115403. [Google Scholar] [CrossRef]
- Barr, J.D. Transport in Interacting Nanostructures. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 2013. [Google Scholar]
- Mishchenko, A.; Vonlanthen, D.; Meded, V.; Burkle, M.; Li, C.; Pobelov, I.V.; Bagrets, A.; Viljas, J.K.; Pauly, F.; Evers, F.; et al. Influence of conformation on conductance of biphenyl-dithiol single-molecule contacts. Nano Lett. 2009, 10, 156–163. [Google Scholar] [CrossRef]
- Ramasesha, S.; Albert, I.; Sinha, B. Optical and magnetic properties of the exact PPP states of biphenyl. Mol. Phys. 1991, 72, 537–547. [Google Scholar] [CrossRef]
- Bürkle, M.; Viljas, J.K.; Vonlanthen, D.; Mishchenko, A.; Schön, G.; Mayor, M.; Wandlowski, T.; Pauly, F. Conduction mechanisms in biphenyl dithiol single-molecule junctions. Phys. Rev. B 2012, 85, 075417. [Google Scholar] [CrossRef]
- Johansson, M.P.; Olsen, J. Torsional barriers and equilibrium angle of biphenyl: Reconciling theory with experiment. J. Chem. Theory Comput. 2008, 4, 1460–1471. [Google Scholar] [CrossRef] [PubMed]
- Aradhya, S.V.; Meisner, J.S.; Krikorian, M.; Ahn, S.; Parameswaran, R.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Dissecting contact mechanics from quantum interference in single-molecule junctions of stilbene derivatives. Nano Lett. 2012, 12, 1643–1647. [Google Scholar] [CrossRef]
- Arroyo, C.R.; Tarkuc, S.; Frisenda, R.; Seldenthuis, J.S.; Woerde, C.H.; Eelkema, R.; Grozema, F.C.; van der Zant, H.S. Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring. Angew. Chem. 2013, 125, 3234–3237. [Google Scholar] [CrossRef]
- Guédon, C.M.; Valkenier, H.; Markussen, T.; Thygesen, K.S.; Hummelen, J.C.; van der Molen, S.J. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 2012, 7, 305–309. [Google Scholar] [CrossRef]
- Markussen, T.; Thygesen, K.S. Temperature effects on quantum interference in molecular junctions. Phys. Rev. B 2014, 89, 085420. [Google Scholar] [CrossRef]
- Yang, G.; Wu, H.; Wei, J.; Zheng, J.; Chen, Z.; Liu, J.; Shi, J.; Yang, Y.; Hong, W. Quantum interference effect in the charge transport through single-molecule benzene dithiol junction at room temperature: An experimental investigation. Chin. Chem. Lett. 2018, 29, 147–150. [Google Scholar] [CrossRef]
- Bergfield, J.P. Identifying Quantum Interference Effects from Joint Conductance–Thermopower Statistics. Nano Lett. 2024, 24, 15110–15117. [Google Scholar] [CrossRef]
- Tang, C.; Huang, L.; Sangtarash, S.; Noori, M.; Sadeghi, H.; Xia, H.; Hong, W. Reversible switching between destructive and constructive quantum interference using atomically precise chemical gating of single-molecule junctions. J. Am. Chem. Soc. 2021, 143, 9385–9392. [Google Scholar] [CrossRef]
- Greenwald, J.E.; Cameron, J.; Findlay, N.J.; Fu, T.; Gunasekaran, S.; Skabara, P.J.; Venkataraman, L. Highly nonlinear transport across single-molecule junctions via destructive quantum interference. Nat. Nanotechnol. 2021, 16, 313–317. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).