Optimizing Hydrogen Production in the Co-Gasification Process: Comparison of Explainable Regression Models Using Shapley Additive Explanations
Abstract
1. Introduction
2. Machine Learning Models
2.1. Linear Regression (LR)
2.2. k-Nearest Neighbor (KNN) Regression
2.3. Decision Tree Regression (DTR)
2.4. Support Vector Regression (SVR)
2.5. Gradient-Boosting Regression (GBR)
2.6. Random Forest Regression (RFR)
2.7. Multilayer Perceptron (MLP)
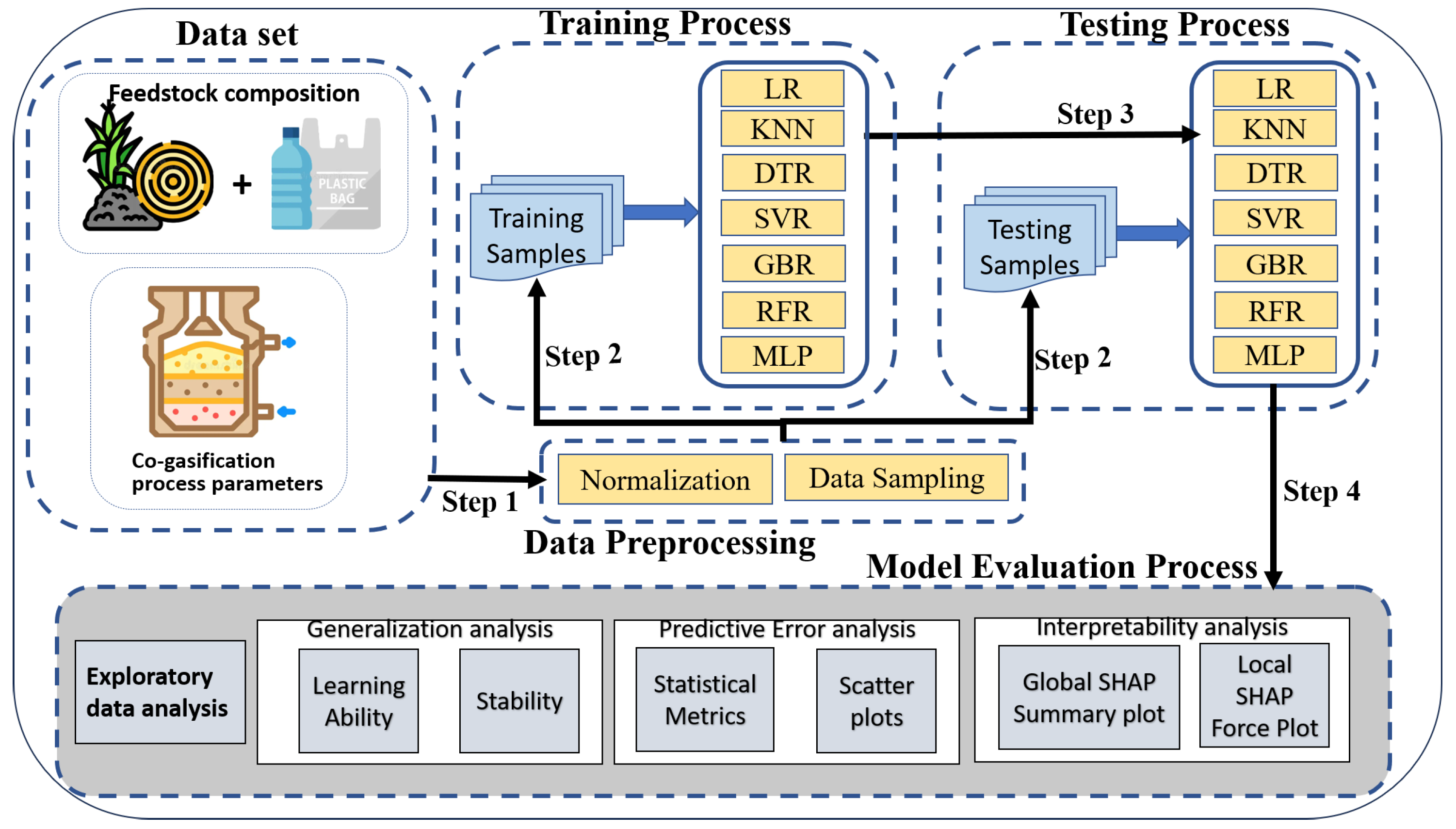
3. Model Design and Implementation
3.1. Data Description
3.2. Data Preparation
3.3. Model Implementation
3.4. Model Hyperparameter Tuning
4. Results and Discussion
4.1. Exploratory Data Analysis (EDA)
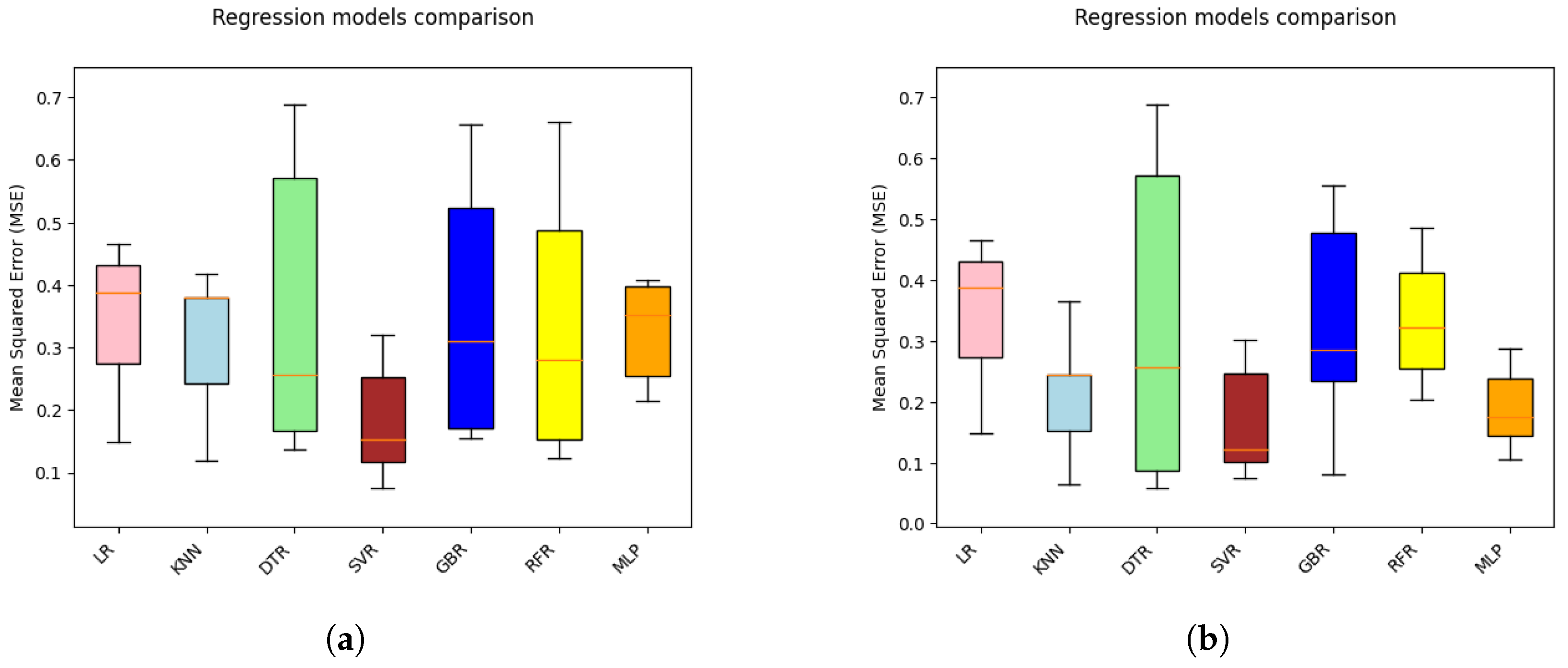
4.2. Model Generalization Analysis
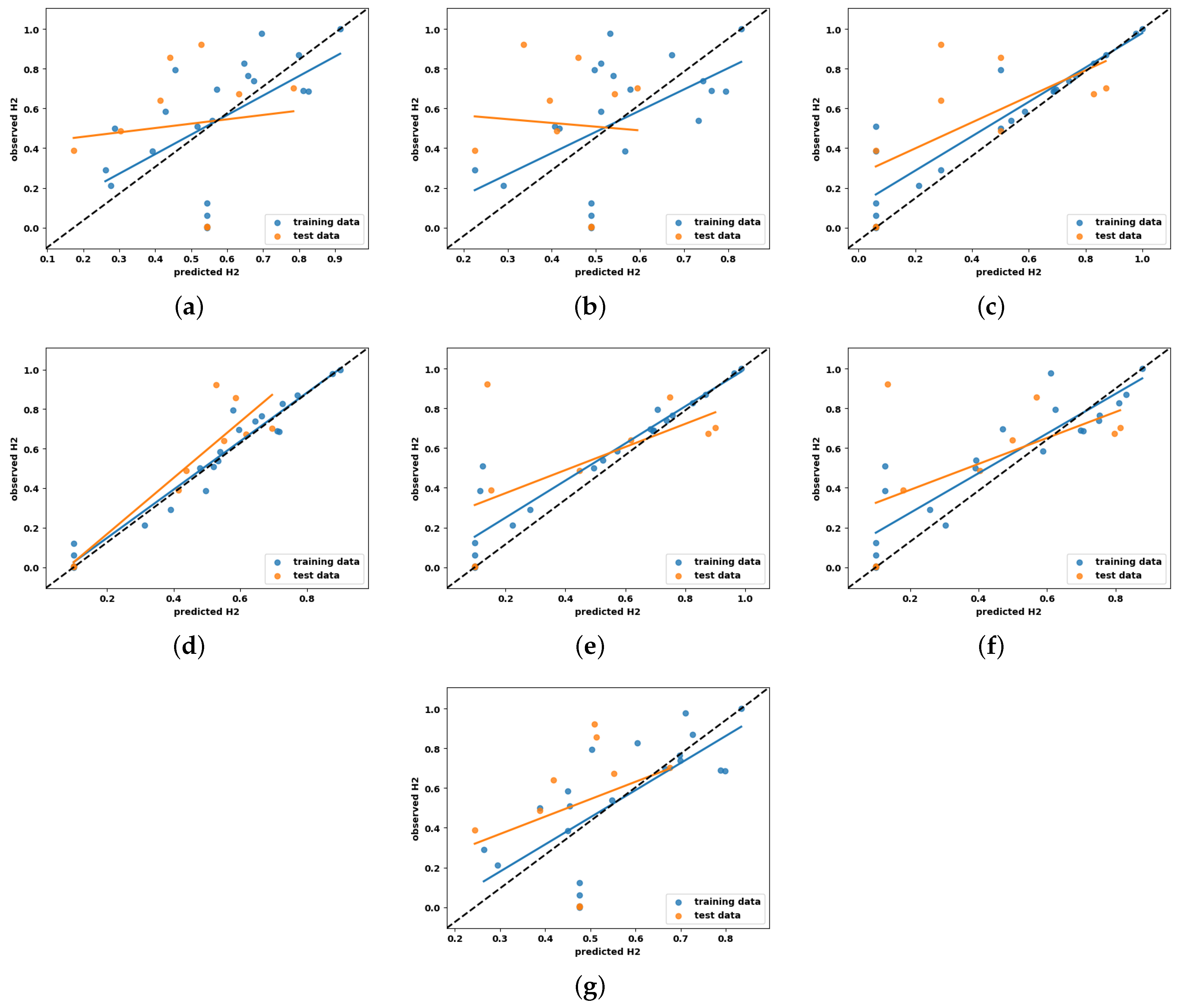
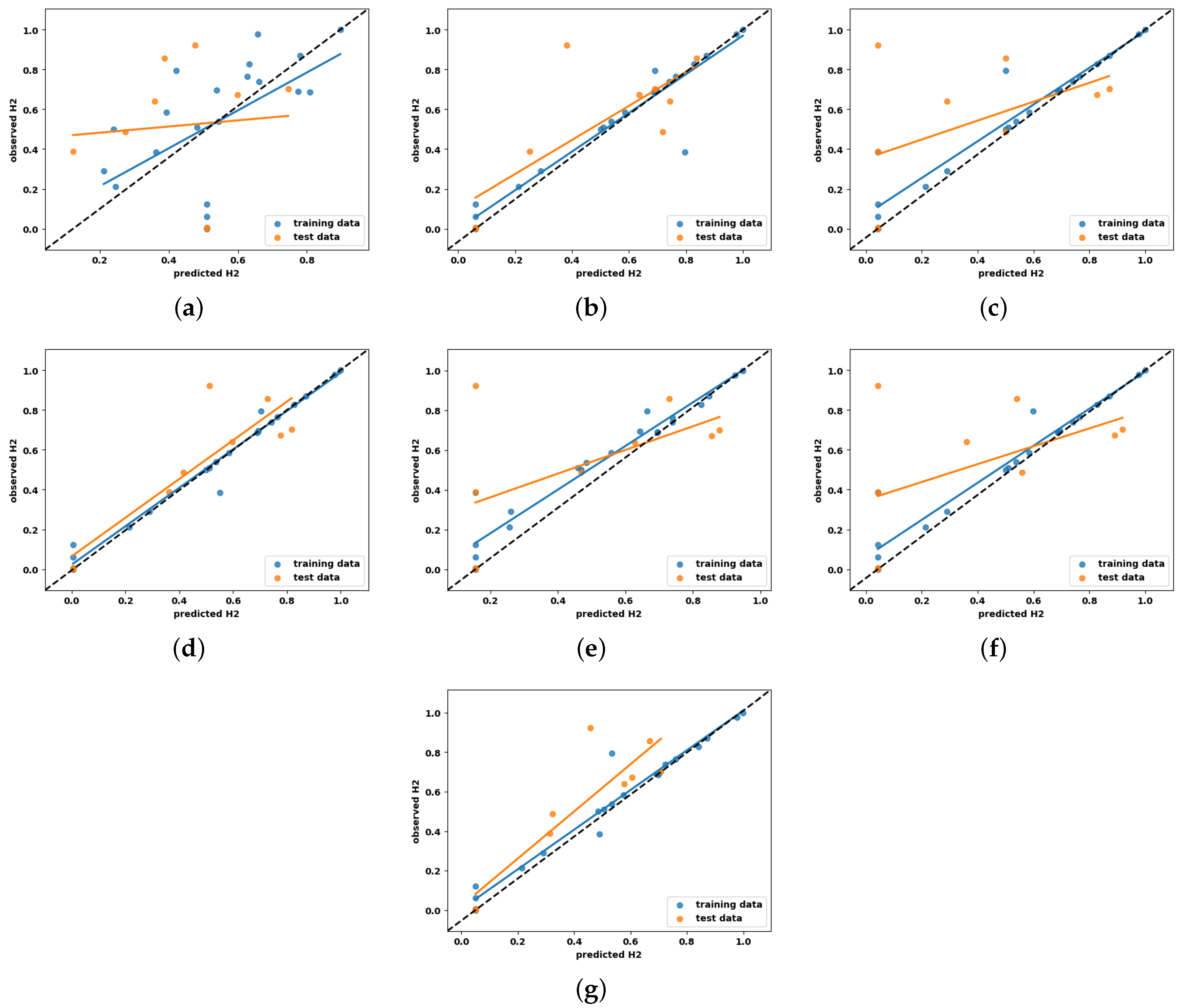
4.2.1. Model Learning Ability
4.2.2. Model Stability
4.3. Prediction Performance Analysis
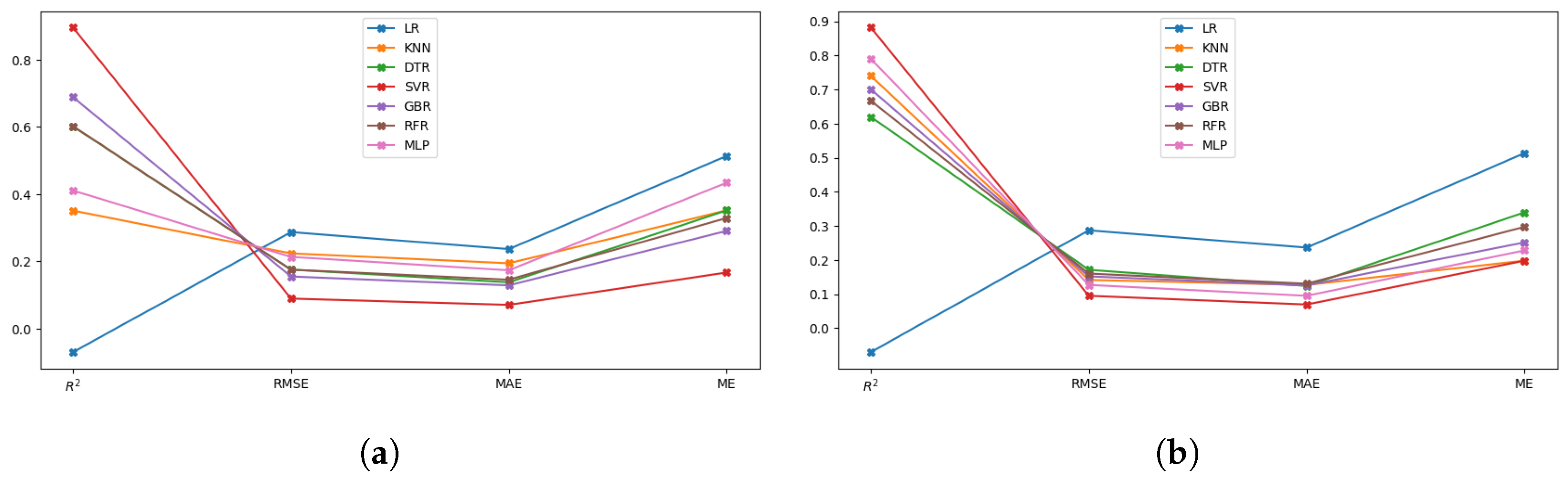
4.3.1. Quantitative Statistical Metrics
4.3.2. Qualitative Scatter Plot
4.4. Model Interpretation
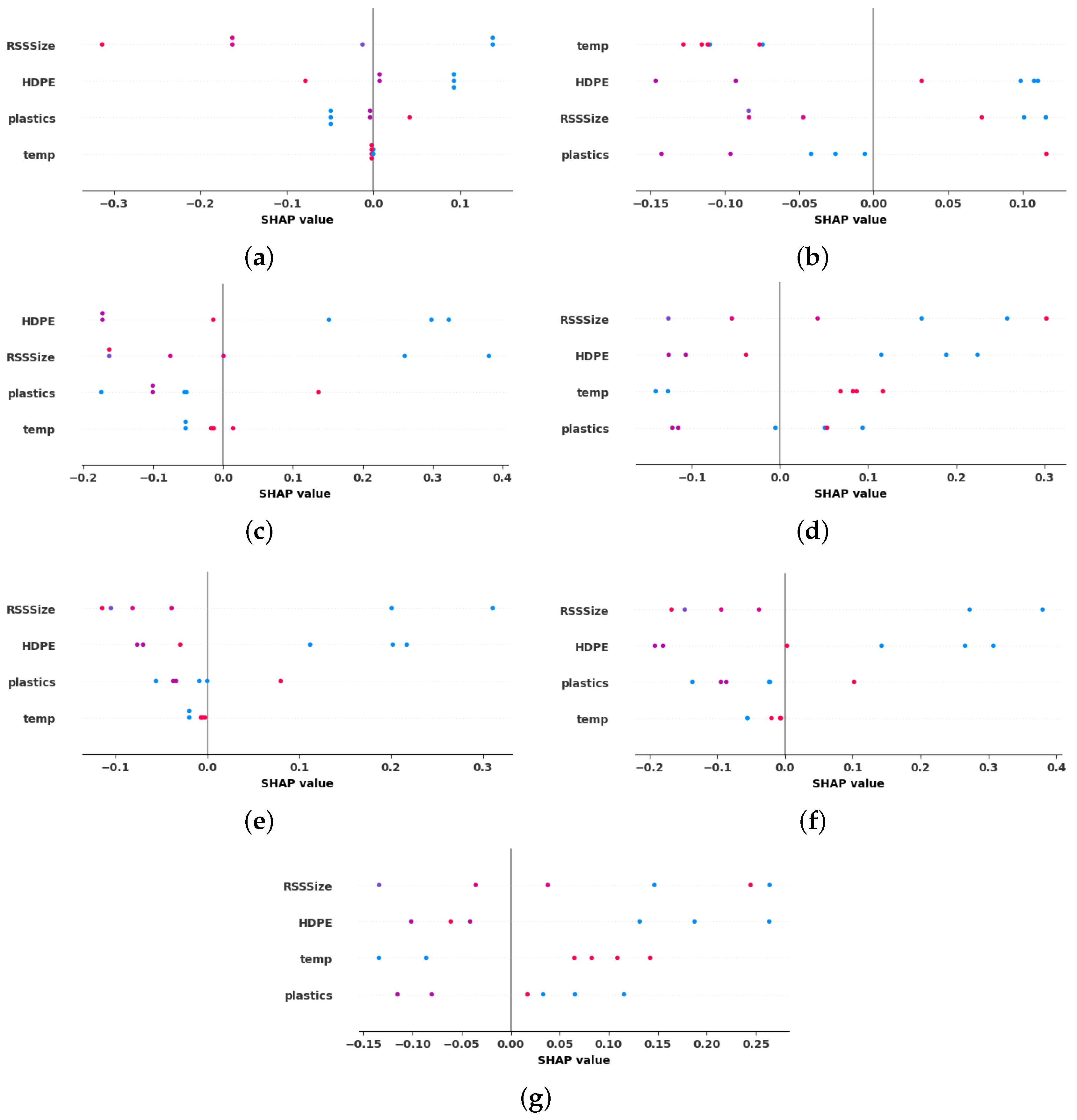
4.4.1. Global Explanation with Summary Plot
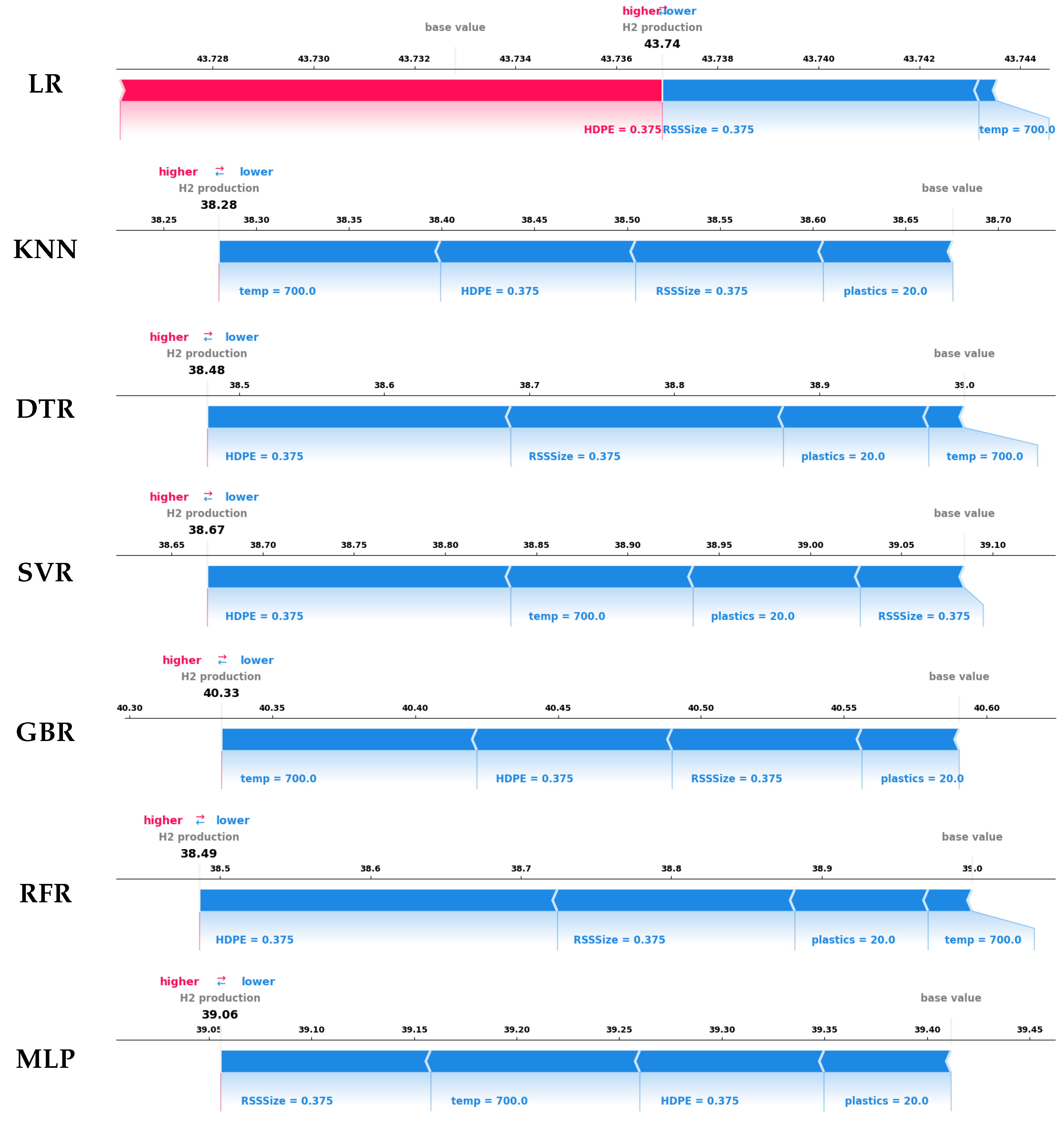
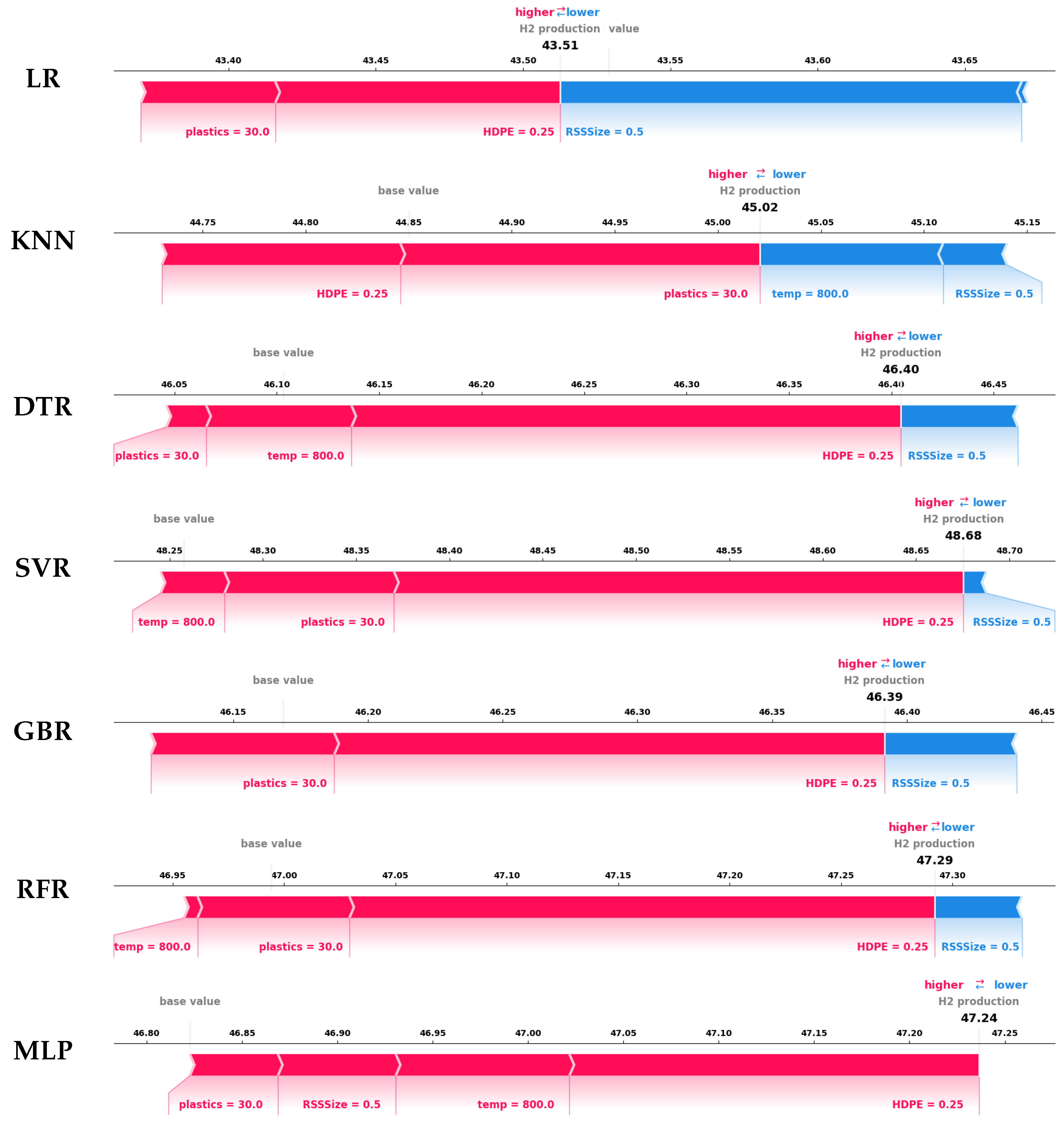
4.4.2. Local Explanation with Force Plot
4.5. Comparative Analysis
4.5.1. Comparison with Related Studies
- (a)
- Model complexity and overfitting mitigation: The exceptionally high values reported in earlier studies may indicate overfitting, particularly given the small dataset size (n = 30). In this study, regularization techniques—such as L1/L2 penalties and early stopping—were applied to mitigate overfitting. Although these measures led to slightly lower values, the resulting models demonstrated improved generalization and stability, essential for deployment in real-world scenarios.
- (b)
- Dataset size and model selection: The limited dataset size presents challenges for complex models like MLP, which typically require larger datasets to generalize effectively. While MLP excels in capturing non-linear relationships, it is prone to overfitting when trained on small datasets. To address this, simpler models such as SVR were prioritized in this study. SVR, which achieved the highest value of 0.86, benefits from kernel functions and built-in regularization, allowing for it to perform reliably with small datasets and enhancing its suitability for hydrogen yield prediction.
4.5.2. Comparison of Model Strengths, Limitations, and Industrial Suitability
5. Conclusions
- The generalization ability analysis conducted through qualitative and quantitative methods using learning curves and CV showed that SVR and MLP models demonstrated superior generalization potential over other competing models, achieving a minimum MSE of approximately 0.025.
- The prediction performance analysis highlights the potential of SVR, with value of approximately 0.9, reflecting its strong ability to model the nonlinear relationship between hydrogen production and process parameters.
- The interpretability analysis of the developed ML models at global and local levels using the SHAP summary plot and force plot, respectively, revealed that the SVR and tree-based models were more successful in reliably elucidating the influence of the process parameters on hydrogen production and concurred with both the experimental observations and the previously published literature.
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yoro, K.O.; Daramola, M.O. CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Elsevier: Amsterdam, The Netherlands, 2020; pp. 3–28. [Google Scholar]
- Mangal, M.; Rao, C.V.; Banerjee, T. Bioplastic: An eco-friendly alternative to non-biodegradable plastic. Polym. Int. 2023, 72, 984–996. [Google Scholar] [CrossRef]
- Thew, C.X.E.; Lee, Z.S.; Srinophakun, P.; Ooi, C.W. Recent advances and challenges in sustainable management of plastic waste using biodegradation approach. Bioresour. Technol. 2023, 374, 128772. [Google Scholar] [CrossRef] [PubMed]
- Züttel, A.; Remhof, A.; Borgschulte, A.; Friedrichs, O. Hydrogen: The future energy carrier. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 3329–3342. [Google Scholar] [CrossRef] [PubMed]
- Ismail, M.M.; Dincer, I. A new renewable energy based integrated gasification system for hydrogen production from plastic wastes. Energy 2023, 270, 126869. [Google Scholar] [CrossRef]
- Sikiru, S.; Oladosu, T.L.; Amosa, T.I.; Olutoki, J.O.; Ansari, M.; Abioye, K.J.; Rehman, Z.U.; Soleimani, H. Hydrogen-powered horizons: Transformative technologies in clean energy generation, distribution, and storage for sustainable innovation. Int. J. Hydrogen Energy 2024, 56, 1152–1182. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.J. Thermochemical conversion of biomass: Potential future prospects. Renew. Sustain. Energy Rev. 2023, 187, 113754. [Google Scholar] [CrossRef]
- Yek, P.N.Y.; Chan, Y.H.; Foong, S.Y.; Mahari, W.A.W.; Chen, X.; Liew, R.K.; Ma, N.L.; Tsang, Y.F.; Sonne, C.; Cheng, Y.W.; et al. Co-processing plastics waste and biomass by pyrolysis–gasification: A review. Environ. Chem. Lett. 2024, 22, 171–188. [Google Scholar] [CrossRef]
- Ramos, A.; Monteiro, E.; Silva, V.; Rouboa, A. Co-gasification and recent developments on waste-to-energy conversion: A review. Renew. Sustain. Energy Rev. 2018, 81, 380–398. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Ullah, Z.; Taqvi, S.A.A.; Khan, M.N.A.; Farooq, W.; Mehran, M.T.; Juchelková, D.; Štěpanec, L. Applications of machine learning in thermochemical conversion of biomass—A review. Fuel 2023, 332, 126055. [Google Scholar]
- Dodo, U.A.; Ashigwuike, E.C.; Abba, S.I. Machine learning models for biomass energy content prediction: A correlation-based optimal feature selection approach. Bioresour. Technol. Rep. 2022, 19, 101167. [Google Scholar] [CrossRef]
- Kabir, M.M.; Roy, S.K.; Alam, F.; Nam, S.Y.; Im, K.S.; Tijing, L.; Shon, H.K. Machine learning-based prediction and optimization of green hydrogen production technologies from water industries for a circular economy. Desalination 2023, 567, 116992. [Google Scholar] [CrossRef]
- Devasahayam, S. Deep learning models in Python for predicting hydrogen production: A comparative study. Energy 2023, 280, 128088. [Google Scholar] [CrossRef]
- Ascher, S.; Wang, X.; Watson, I.; Sloan, W.; You, S. Interpretable machine learning to model biomass and waste gasification. Bioresour. Technol. 2022, 364, 128062. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, X.; Xia, A.; Shah, A.A.; Yan, H.; Huang, Y.; Zhu, X.; Zhu, X.; Liao, Q. Comparison of machine learning methods for predicting the methane production from anaerobic digestion of lignocellulosic biomass. Energy 2023, 263, 125883. [Google Scholar] [CrossRef]
- Ozbas, E.E.; Aksu, D.; Ongen, A.; Aydin, M.A.; Ozcan, H.K. Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms. Int. J. Hydrogen Energy 2019, 44, 17260–17268. [Google Scholar] [CrossRef]
- Wen, H.T.; Lu, J.H.; Phuc, M.X. Applying artificial intelligence to predict the composition of syngas using rice husks: A comparison of artificial neural networks and gradient boosting regression. Energies 2021, 14, 2932. [Google Scholar] [CrossRef]
- Xue, L.; Liu, Y.; Xiong, Y.; Liu, Y.; Cui, X.; Lei, G. A data-driven shale gas production forecasting method based on the multi-objective random forest regression. J. Pet. Sci. Eng. 2021, 196, 107801. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Rubio-Bellido, C.; Solís-Guzmán, J.; Oliveira, M.J. Experimental characterisation of the periodic thermal properties of walls using artificial intelligence. Energy 2020, 203, 117871. [Google Scholar] [CrossRef]
- Chin, B.L.F.; Yusup, S.; Al Shoaibi, A.; Kannan, P.; Srinivasakannan, C.; Sulaiman, S.A. Optimization study of catalytic co-gasification of rubber seed shell and high density polyethylene waste for hydrogen production using response surface methodology. In Advances in Bioprocess Technology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 209–223. [Google Scholar]
- Ayodele, B.V.; Mustapa, S.I.; Kanthasamy, R.; Zwawi, M.; Cheng, C.K. Modeling the prediction of hydrogen production by co-gasification of plastic and rubber wastes using machine learning algorithms. Int. J. Energy Res. 2021, 45, 9580–9594. [Google Scholar] [CrossRef]
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Bisong, E.; Bisong, E. Google colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Apress: New York, NY, USA, 2019; pp. 59–64. [Google Scholar]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Data, M.C.; Komorowski, M.; Marshall, D.C.; Salciccioli, J.D.; Crutain, Y. Exploratory data analysis. In Secondary Analysis of Electronic Health Records; Springer: Berlin/Heidelberg, Germany, 2016; pp. 185–203. [Google Scholar]
- McDonald, J.H.; Dunn, K.W. Statistical tests for measures of colocalization in biological microscopy. J. Microsc. 2013, 252, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Perlich, C. Learning Curves in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wong, T.T.; Yeh, P.Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]
- Vaiyapuri, T.; Elashmawi, W.H.; Shridevi, S.; Asiedu, W. VAE-CNN: Deep Learning on Small Sample Dataset Improves Hydrogen Yield Prediction in Co-gasification. J. Comput. Cogn. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Nguyen, Q.V.; Miller, N.; Arness, D.; Huang, W.; Huang, M.L.; Simoff, S. Evaluation on interactive visualization data with scatterplots. Vis. Inform. 2020, 4, 1–10. [Google Scholar] [CrossRef]
- Das, D.; Ito, J.; Kadowaki, T.; Tsuda, K. An interpretable machine learning model for diagnosis of Alzheimer’s disease. PeerJ 2019, 7, e6543. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Nguyen, V.G.; Sharma, P.; Ağbulut, Ü.; Le, H.S.; Cao, D.N.; Dzida, M.; Osman, S.M.; Le, H.C.; Tran, V.D. Improving the prediction of biochar production from various biomass sources through the implementation of eXplainable machine learning approaches. Int. J. Green Energy 2024, 21, 2771–2798. [Google Scholar] [CrossRef]
- Chen, H.; Lundberg, S.M.; Lee, S.I. Explaining a series of models by propagating Shapley values. Nat. Commun. 2022, 13, 4512. [Google Scholar] [CrossRef] [PubMed]
- Giudici, P.; Raffinetti, E. Shapley-Lorenz eXplainable artificial intelligence. Expert Syst. Appl. 2021, 167, 114104. [Google Scholar] [CrossRef]
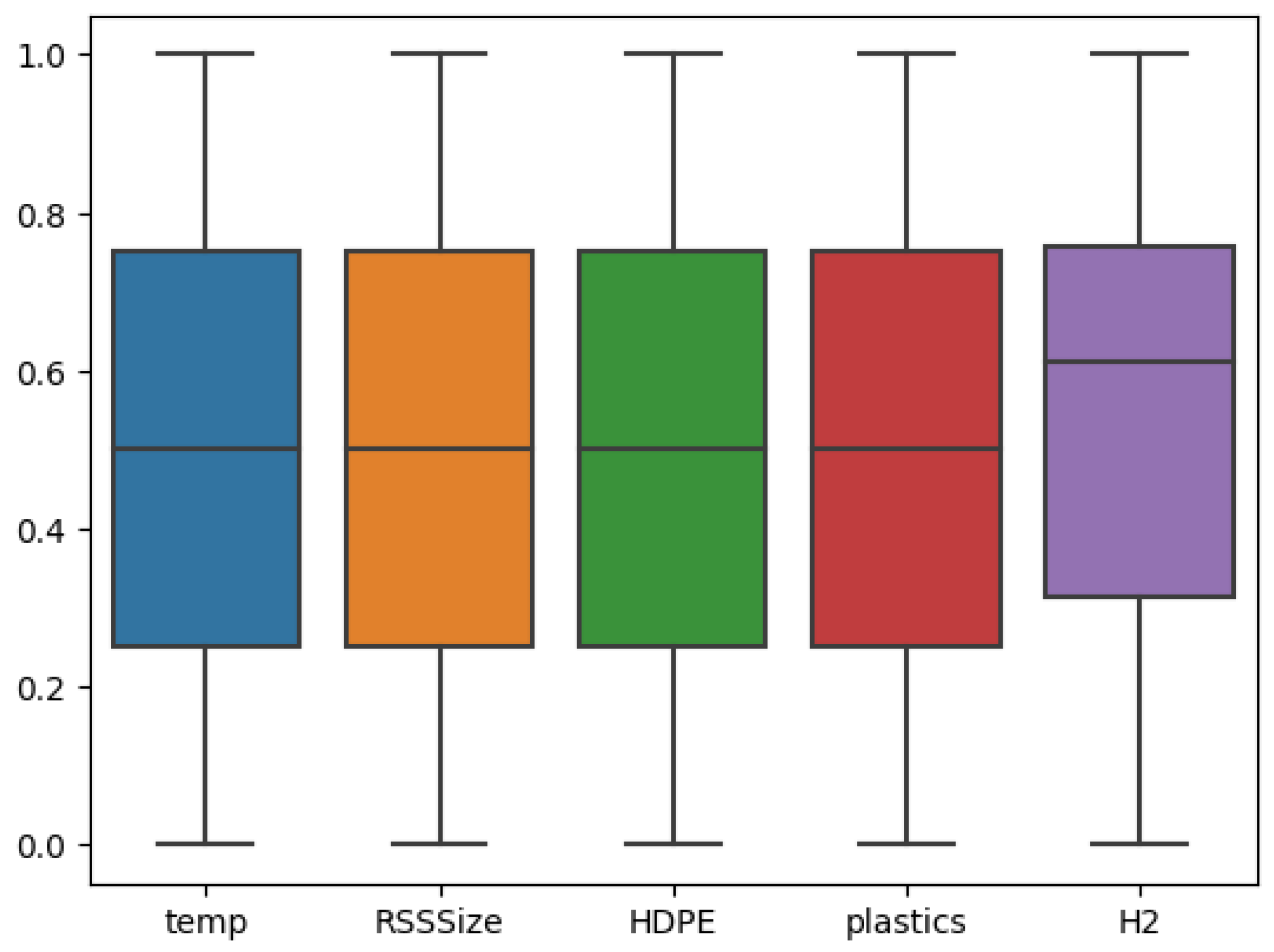
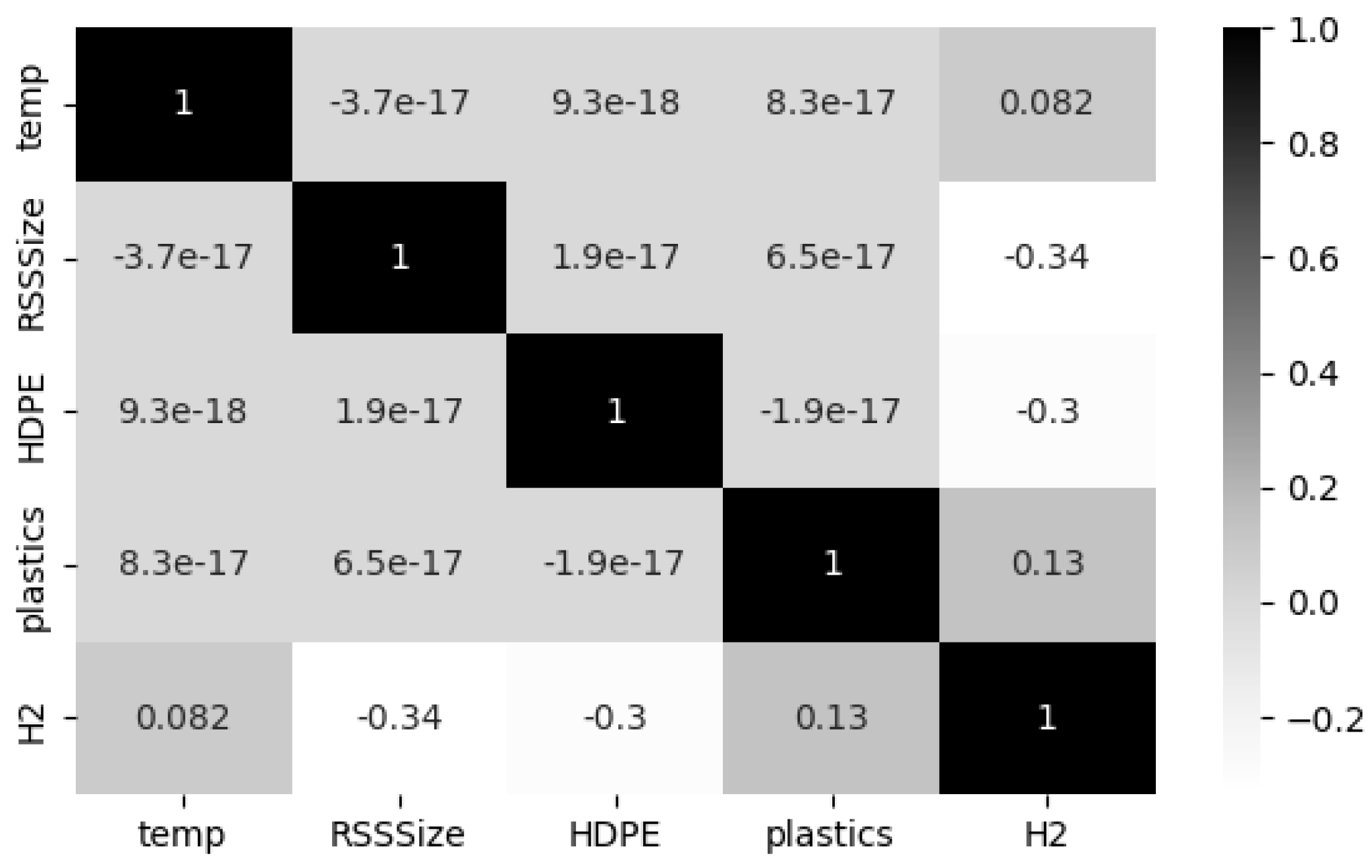


| Temp °C | RSS Size mm | HDPE mm | Plastics wt. % | H2 vol. % | |
|---|---|---|---|---|---|
| count | 30.00 | 30.00 | 30.00 | 30.00 | 30.00 |
| mean | 700.00 | 0.38 | 0.38 | 20.00 | 44.71 |
| std | 90.97 | 0.11 | 0.11 | 9.10 | 3.65 |
| min | 500.00 | 0.12 | 0.12 | 0.00 | 38.57 |
| 25% | 600.00 | 0.25 | 0.25 | 10.00 | 42.21 |
| 50% | 700.00 | 0.38 | 0.38 | 20.00 | 45.64 |
| 75% | 800.00 | 0.50 | 0.50 | 30.00 | 47.33 |
| max | 900.00 | 0.62 | 0.62 | 40.00 | 50.12 |
| Sample | Proximate Analysis Wt. %, Dry Basis | Ultimate Analysis Wt. %, Dry Basis | |||||||
|---|---|---|---|---|---|---|---|---|---|
| V | FC | A | M | C | H | N | O | S | |
| HDPE | 99.46 | 0 | 0.34 | 0 | 81.45 | 12.06 | 0.34 | 0.79 | 5.36 |
| RSS | 80.98 | 6.62 | 3.81 | 8.59 | 44.31 | 4.38 | 0.51 | 50.67 | 0.13 |
| ML Models | Hyperparameters | Search Range | Selected Value |
|---|---|---|---|
| KNN | n_neighbors | [2, 3, 4, 5, 7, 9, 11] | 2 |
| weights | [‘uniform’, ‘distance’] | ‘distance’ | |
| metric | [‘minkowski’, ‘euclidean’,‘manhattan’] | ‘euclidean’ | |
| DTR | max_depth | [3, 5, 7, 9, 11, 15] | 9 |
| min_samples_split | [2, 3, 4, 5] | 2 | |
| criterion | [‘gini’,‘entropy’] | ‘gini’ | |
| SVR | gamma | [1, 1.5, 2, 2.5] | 1.5 |
| C | [3, 4, 4.5, 5, 5.5] | 4.5 | |
| epsilon | [0.1, 0.01, 0.5, 1] | 0.01 | |
| GBR | loss | [‘squared_error’, ‘absolute_error’] | ‘squared_error’ |
| learning_rate | [0.1, 0.01, 0.5, 1] | 0.1 | |
| max_depth | [3, 5, 7, 9, 11, 15] | 5 | |
| n_estimators | [50, 100, 200, 250, 300] | 250 | |
| RFR | max_depth | [3, 5, 7, 9, 11, 15] | 5 |
| max_features | [2, 3, 4, 5] | 4 | |
| criterion | [‘gini’,‘entropy’] | ‘gini’ | |
| n_estimators | [10, 15, 20, 25, 30] | 15 | |
| MLP | hidden_layer_sizes | [(100, 50, 25), (50, 25), (50)] | (50) |
| learning_rate_init | [0.1, 0.01, 0.5, 1] | 0.01 | |
| power_t | [0.1, 0.5, 1] | 0.5 | |
| max_iter | [250, 500, 1000] | 500 |
| ML Models | MSE with Default Hyperparameters | MSE with Tuned Hyperparameters | ||
|---|---|---|---|---|
| Mean | Std | Mean | Std | |
| LR | 0.34 | 0.12 | 0.34 | 0.12 |
| KNN | 0.31 | 0.11 | 0.23 | 0.10 |
| DTR | 0.36 | 0.22 | 0.35 | 0.24 |
| SVR | 0.18 | 0.09 | 0.17 | 0.09 |
| GBR | 0.36 | 0.20 | 0.32 | 0.15 |
| RFR | 0.34 | 0.20 | 0.33 | 0.10 |
| MLP | 0.33 | 0.08 | 0.24 | 0.09 |
| ML Models | Hydrogen Yield Prediction with Default Hyperparameters | Hydrogen Yield Prediction with Optimal Hyperparameters | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | ME | R2 | RMSE | MAE | ME | |
| LR | −0.07 | 0.29 | 0.24 | 0.51 | −0.07 | 0.29 | 0.24 | 0.51 |
| KNN | 0.35 | 0.22 | 0.19 | 0.35 | 0.75 | 0.13 | 0.12 | 0.19 |
| DTR | 0.6 | 0.17 | 0.14 | 0.35 | 0.64 | 0.15 | 0.13 | 0.28 |
| SVR | 0.86 | 0.10 | 0.09 | 0.17 | 0.9 | 0.09 | 0.07 | 0.15 |
| GBR | 0.56 | 0.18 | 0.14 | 0.35 | 0.71 | 0.14 | 0.13 | 0.21 |
| RFR | 0.66 | 0.16 | 0.13 | 0.33 | 0.68 | 0.16 | 0.13 | 0.3 |
| MLP | 0.41 | 0.21 | 0.17 | 0.43 | 0.82 | 0.11 | 0.09 | 0.18 |
| Models | Model Type | Hyper Parameters | Performance on Non-Linear Data | Generalizability | Explainable Ability | Industrial Suitability |
|---|---|---|---|---|---|---|
| LR | Linear | Low | Poor | prone to overfitting | Poor | Low |
| KNN | Instance-based | Low | Good | Good generalization with cross-validation | Excellent | High |
| DTR | Tree-based | Moderate | Moderate | Pruning improves generalization | Moderate | Moderate |
| SVR | Kernel-based | High | Excellent | Strong generalization with regularization | Excellent | High |
| GBR | Ensemble-based | High | Good | Good generalization with boosting | Good | High |
| RFR | Ensemble-based | Moderate | Moderate | Averaging improves generalization | Moderate | Moderate |
| MLP | Neural Network | High | Excellent | Dropout and early stopping improves generalization | Good | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaiyapuri, T. Optimizing Hydrogen Production in the Co-Gasification Process: Comparison of Explainable Regression Models Using Shapley Additive Explanations. Entropy 2025, 27, 83. https://doi.org/10.3390/e27010083
Vaiyapuri T. Optimizing Hydrogen Production in the Co-Gasification Process: Comparison of Explainable Regression Models Using Shapley Additive Explanations. Entropy. 2025; 27(1):83. https://doi.org/10.3390/e27010083
Chicago/Turabian StyleVaiyapuri, Thavavel. 2025. "Optimizing Hydrogen Production in the Co-Gasification Process: Comparison of Explainable Regression Models Using Shapley Additive Explanations" Entropy 27, no. 1: 83. https://doi.org/10.3390/e27010083
APA StyleVaiyapuri, T. (2025). Optimizing Hydrogen Production in the Co-Gasification Process: Comparison of Explainable Regression Models Using Shapley Additive Explanations. Entropy, 27(1), 83. https://doi.org/10.3390/e27010083








