Multipartite Correlations in Parikh–Wilczek Non-Thermal Spectrum
Abstract
1. Introduction
2. Parikh–Wilczek Model and Information Conservation
3. Correlations without Quantum Correction
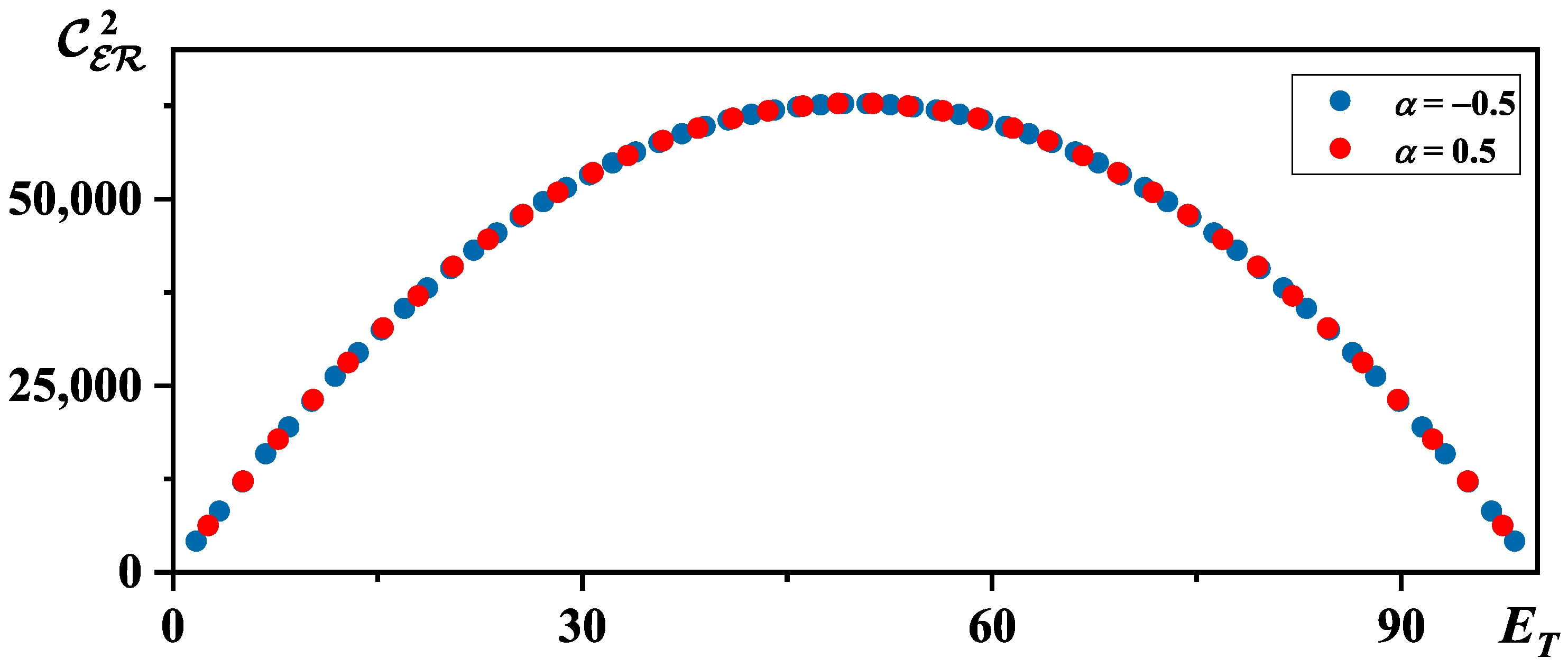
4. Correlations with Quantum Correction
5. Correlations in Black Hole Radiation and Information Conservation
6. Discussion and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Cai, Q.-Y.; You, L.; Zhan, M.S. Hidden messenger revealed in Hawking radiation: A resolution to the paradox of black hole information loss. Phys. Lett. B 2009, 675, 98–101. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, Q.-Y.; Zhan, M.S.; You, L. Entropy is conserved in Hawking radiation as tunneling: A revisit of the black hole information loss paradox. Ann. Phys. 2011, 326, 350. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, Q.-Y.; Zhan, M.S.; You, L. Noncommutative information is revealed from Hawking radiation as tunneling. Europhys. Lett. 2011, 94, 20002. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, Q.-Y.; Zhan, M.S.; You, L. Information conservation is fundamental: Recovering the lost information in Hawking radiation. Int. J. Mod. Phys. D 2013, 22, 1341014. [Google Scholar] [CrossRef]
- Zhang, B.; Cai, Q.-Y.; Zhan, M.S.; You, L. Correlation, entropy, and information transfer in black hole radiation. Chin. Sci. Bull. 2014, 59, 1057–1065. [Google Scholar] [CrossRef][Green Version]
- He, D.S.; Cai, Q.-Y. Gravitational correlation, black hole entropy, and information conservation. Sci. China-Phys. Mech. Astron. 2017, 60, 040011. [Google Scholar] [CrossRef]
- Han, T.S. Nonnegative entropy measures of multivariate symmetric correlations. Inf. Control 1978, 36, 133–156. [Google Scholar] [CrossRef]
- Kumar, A. Multiparty quantum mutual information: An alternative definition. Phys. Rev. A 2017, 96, 012332. [Google Scholar] [CrossRef]
- Page, D.N. Information in black hole radiation. Phys. Rev. Lett. 1993, 71, 3743. [Google Scholar] [CrossRef] [PubMed]
- Page, D.N. Time dependence of Hawking radiation entropy. J. Cosmol. Astropart. Phys. 2013, 9, 28. [Google Scholar] [CrossRef]
- Kuwakino, S.; Wen, W.-Y. N-partite information in Hawking radiation. J. High Energ. Phys. 2015, 2015, 99. [Google Scholar] [CrossRef][Green Version]
- Banerjee, R.; Majhi, B.R. Quantum tunneling and back reaction. Phys. Lett. B 2008, 662, 62–65. [Google Scholar] [CrossRef]
- Medved, A.J.M.; Vagenas, E.C. On Hawking radiation as tunneling with logarithmic corrections. Mod. Phys. Lett. A 2005, 20, 1723. [Google Scholar] [CrossRef]
- Chen, Y.X.; Shao, K.N. Information loss and entropy conservation in quantum corrected Hawking radiation. Phys. Lett. B 2009, 678, 131–134. [Google Scholar] [CrossRef][Green Version]
- Zhang, J. Black hole quantum tunnelling and black hole entropy correction. Phys. Lett. B 2008, 668, 353–356. [Google Scholar] [CrossRef]
- Corda, C. Black hole quantum spectrum. Eur. Phys. J. C 2013, 73, 2665. [Google Scholar] [CrossRef]
- Corda, C.; FatehiNia, M.; Molaei, M.R.; Sayyari, Y. Entropy of iterated function systems and their relations with black holes and Bohr-like black holes entropies. Entropy 2018, 20, 56. [Google Scholar] [CrossRef] [PubMed]
- Xiang, L. A note on the black hole remnant. Phys. Lett. B 2007, 647, 207–210. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, X. Multipartite Correlations in Parikh–Wilczek Non-Thermal Spectrum. Entropy 2024, 26, 680. https://doi.org/10.3390/e26080680
Ming X. Multipartite Correlations in Parikh–Wilczek Non-Thermal Spectrum. Entropy. 2024; 26(8):680. https://doi.org/10.3390/e26080680
Chicago/Turabian StyleMing, Xi. 2024. "Multipartite Correlations in Parikh–Wilczek Non-Thermal Spectrum" Entropy 26, no. 8: 680. https://doi.org/10.3390/e26080680
APA StyleMing, X. (2024). Multipartite Correlations in Parikh–Wilczek Non-Thermal Spectrum. Entropy, 26(8), 680. https://doi.org/10.3390/e26080680





