GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework
Abstract
1. Introduction
- Accelerated position update. By considering the second-order information of the Wasserstein probability space, different accelerated position update strategies have been proposed [27,32]: Liu et al. [27] follows the accelerated gradient descent methods in the Wasserstein probability space [34,35] and derives the Wasserstein Nesterov’s (WNES) and Wasserstein Accelerated Gradient (WAG) methods, which update the particles’ positions with an extra momentum. Inspired by the Accelerated Flow on the space [36], the Accelerated Flow (ACCEL) method [32] directly discretizes the Hamiltonian gradient flow in the Wasserstein space and updates the position with the damped velocity field, effectively decreasing the Hamiltonian potential of the particle system. Later, Wang and Li [33] considered the accelerated gradient flow for general information probability spaces [37], and derived novel accelerated position update strategies according to the Kalman–Wasserstein/Stein Hamiltonian flow. Following similar analyses as in [36], they theoretically show that, under mild conditions, the Hamiltonian flow usually converges to the equilibrium faster compared with the original first-order counterpart, aligning with the Nesterov acceleration framework [38]. Numerous experimental studies demonstrate that these accelerated position-update strategies usually drift the particle system to the target distribution more efficiently [27,32,33,39].
- Dynamic weight adjustment. Dynamic weight techniques, developed within Markov Chain Monte Carlo (MCMC) frameworks, have shown significant promise in improving sampling efficiency by adapting the weight of samples throughout the computation process. Building on these foundations, ref. [23] introduces the novel application of dynamic weights within the Wasserstein–Fisher–Rao (WFR) space to develop Dynamic-weight Particle-based Variational Inference (DPVI) methods. Specifically, they derive effective dynamical weight adjustment approaches by mimicking the reaction variational step in a JKO splitting scheme of first-order WFR gradient flow [40,41]. The seminal papers [42,43] provide foundational insights into the WFR geometry, particularly discussing an un-normalized dynamic weight variant based on a novel metric interpolating between the quadratic Wasserstein and the Fisher–Rao metrics, which is critical for developing these dynamic weight adjustment schemes. Compared with the commonly used fixed weight strategy, these dynamical weight adjustment schemes usually lead to less approximation error, especially when the number of particles is limited [23].
1.1. Contribution
- We investigate the convergence property of the SHIFR flow and show that the target distribution is the stationary distribution of the proposed semi-Hamiltonian flow for proper dissimilarity functional . Moreover, our theoretical result also shows that the augmented Fisher–Rao structure yields an additional decrease in the local functional dissipation, compared to the Hamiltonian flow in the vanilla information space.
- We derive an effective finite-particle approximation to the SHIFR flow, which directly evolves the position, weight, and velocity of the particles via a set of ordinary differential equations. The finite particle system is compatible with different dissimilarity and associated smoothing approaches. We prove that the mean-field limit of the proposed particle system converges to the exact SHIFR flow under mild conditions.
- By adopting explicit Euler discretization for the finite-particle system, we create the General Accelerated Dynamic-weight Particle-based Variational Inference (GAD-PVI) framework, which updates positions in an acceleration manner and dynamically adjusts weights. We derive various GAD-PVI instances by using three different dissimilarities and associated smoothing approaches (KL-BLOB, KL-GFSD, and KSD-KSDD) on the Wasserstein/Kalman–Wasserstein/Stein IFR space, respectively.
- Furthermore, we showcase the versatility of our GAD-PVI by extending its applicability to scenarios where the analytic score is unavailable. We illustrate that the GAD-PVI algorithm can be utilized to develop methods for generating new samples from an unknown target distribution, given only a set of i.i.d. samples. This is achieved by employing suitable dissimilarities and their associated approximation approaches, such as Maximum-Mean-Distance–Maximum-Mean-Distance Flow (MMD-MMDF) and Sinkhorn-Divergence–Sinkhorn-Divergence Flow (SD-SDF), in the GAD-PVI framework.
1.2. Notation
2. Related Works
3. Preliminaries
3.1. Wasserstein Gradient Flow and Classical ParVIs
3.2. Hamiltonian Gradient Flows and Accelerated ParVIs
3.3. Wasserstein–Fisher–Rao Flow and Dynamic-Weight ParVIs
3.4. Dissimilarity Functionals
3.4.1. Kullback–Leibler Divergence
3.4.2. Kernel Stein Discrepancy
3.4.3. Maximum Mean Discrepancy
3.4.4. Sinkhorn Divergence
4. Methodology
| Algorithm 1 General Accelerated Dynamic-weight Particle-based Variational Inference (GAD-PVI) framework |
Input: Initial distribution , position adjusting step-size , weight adjusting step-size , velocity field adjusting step-size , velocity damping parameter .
|
4.1. Information–Fisher–Rao Space and Semi-Hamiltonian-Information–Fisher–Rao Flow
4.2. Finite-Particles Formulations to SHIFR Flows
4.3. GAD-PVI Framework
4.3.1. Updating Rules
4.3.2. Dissimilarities and Approximation Approaches
Score-Based Scenario
Sample-Based Scenario
4.3.3. An Alternative Weight Adjusting Approach
4.3.4. GAD-PVI Instances
5. Experiments
5.1. Score-Based Experiments
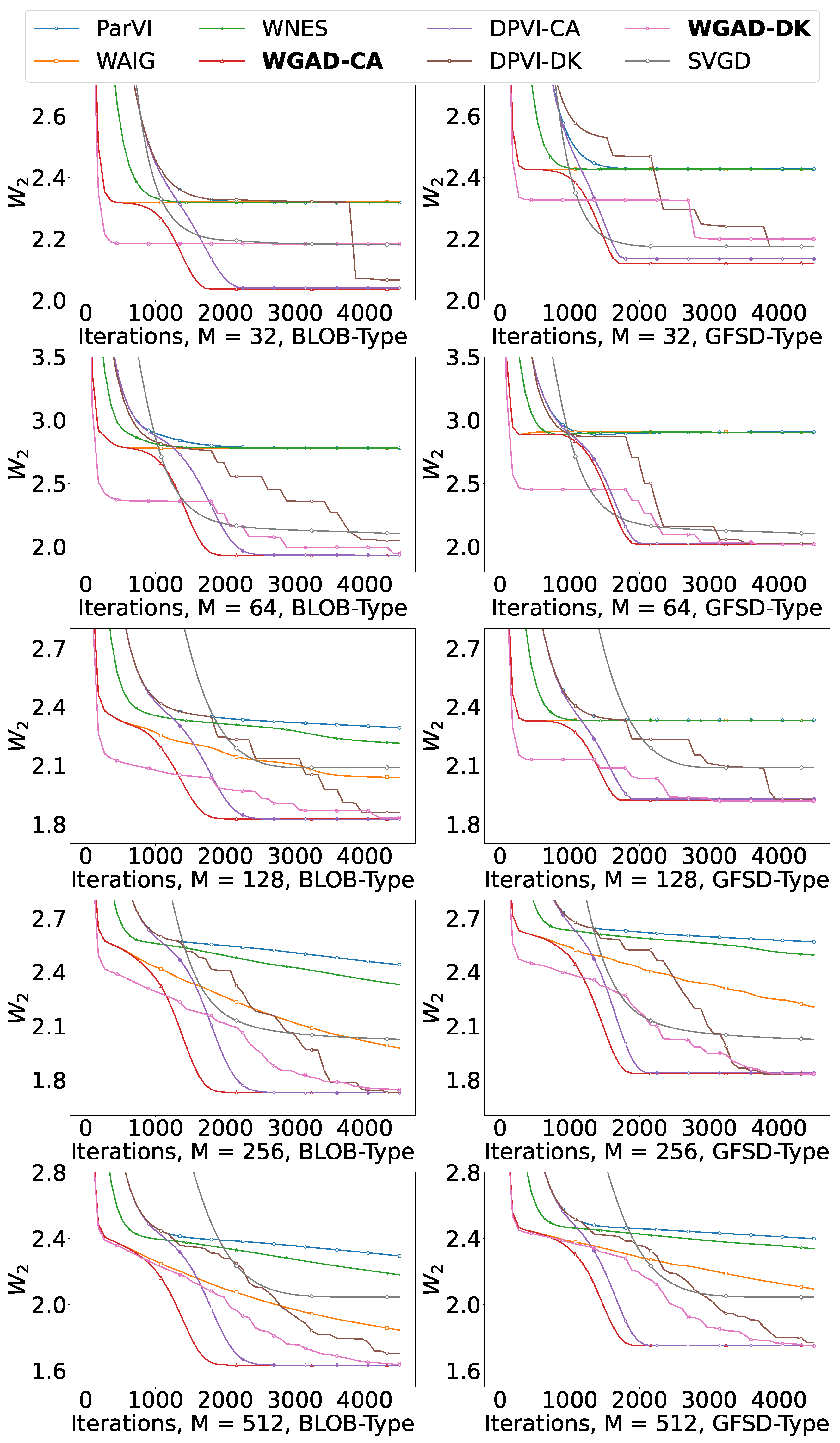
5.1.1. Gaussian Mixture Model
5.1.2. Gaussian Process Regression
5.1.3. Bayesian Neural Network
5.2. Sample-Based Experiments
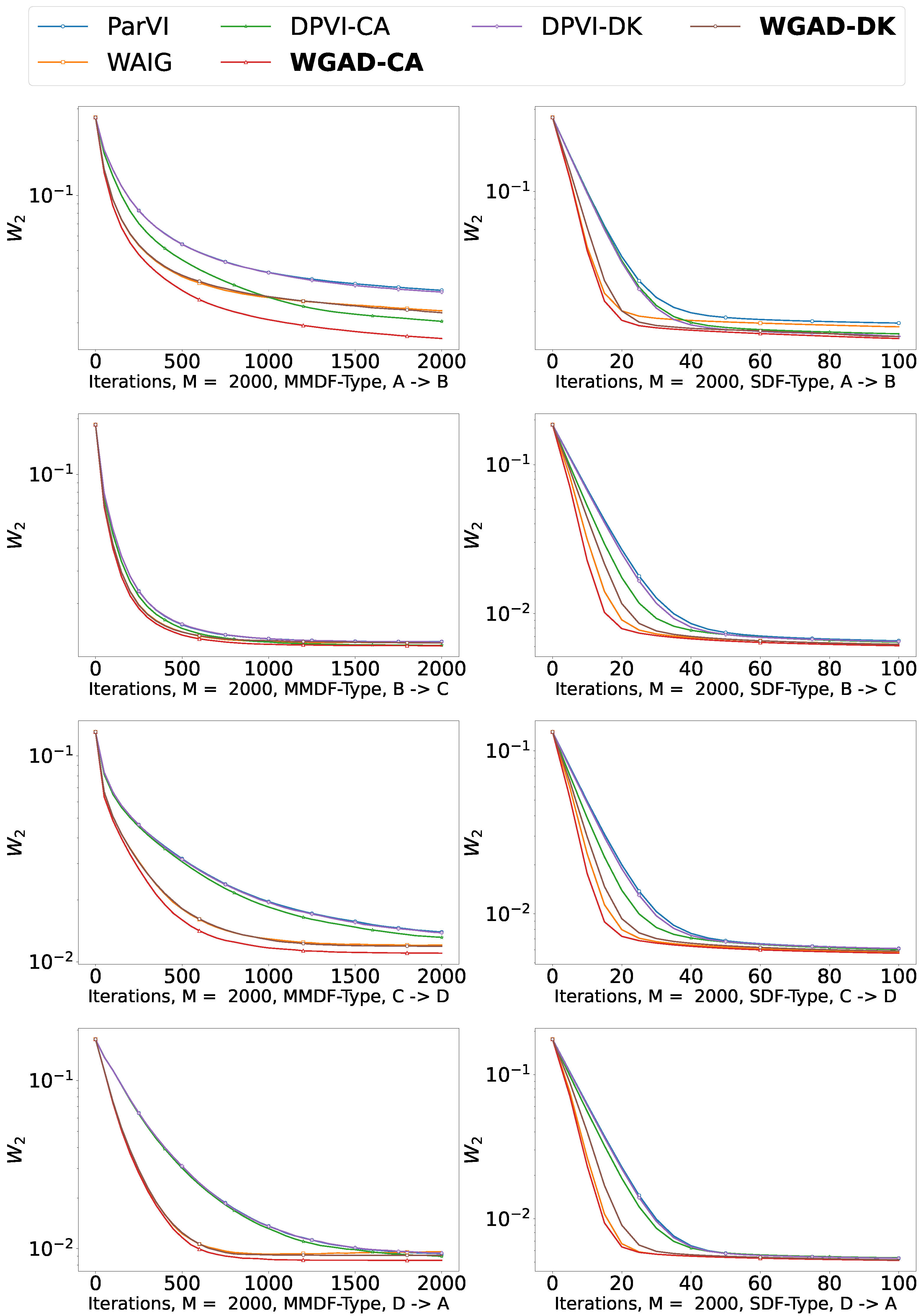
5.2.1. Shape Morphing
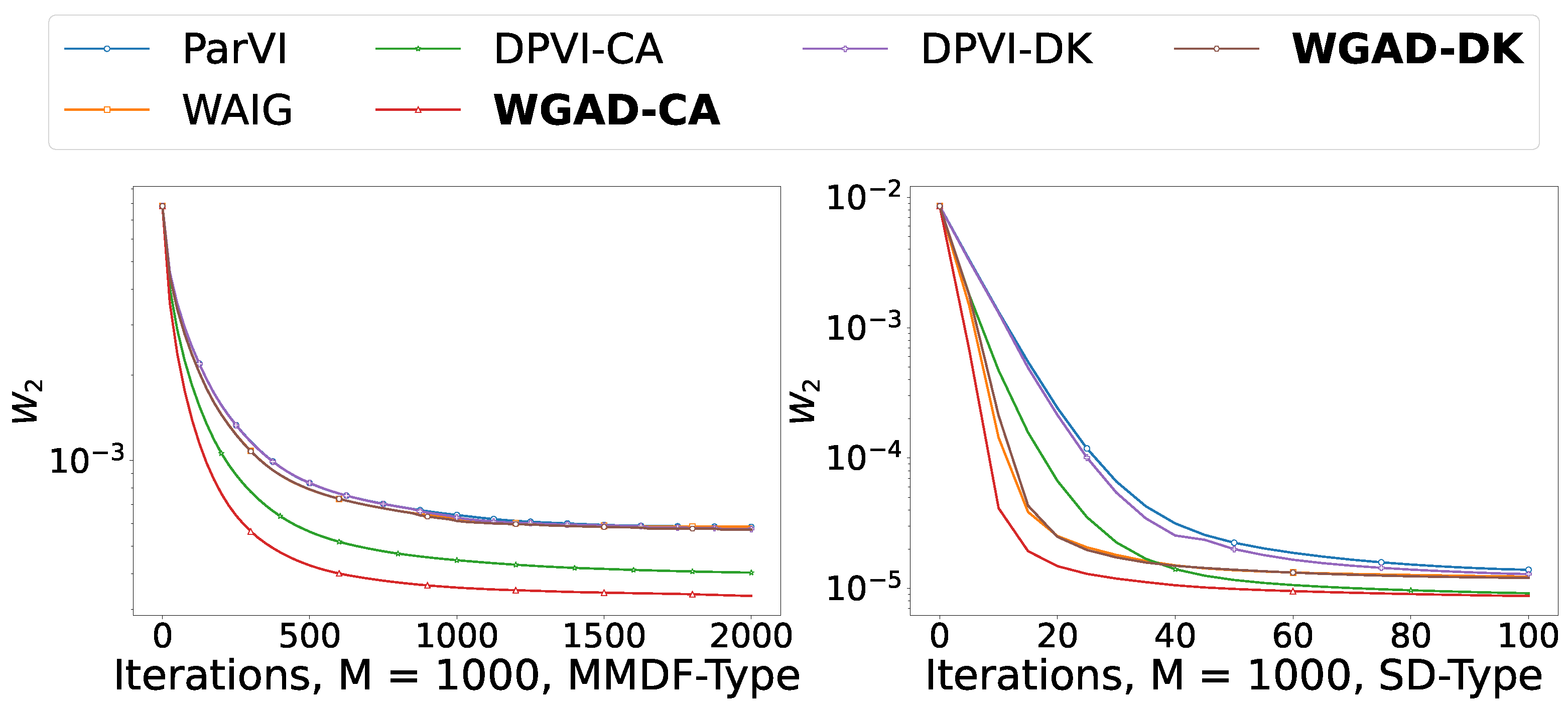
5.2.2. Picture Sketching
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCMC | Markov Chain Monte Carlo |
| ParVI | Particle-based Variational Inference |
| DPVI | Dynamic-weight Particle-based Variational Inference |
| IFR | Information–Fisher–Rao |
| SHIFR | Semi-Hamiltonian Information–Fisher–Rao |
| WFR | Wasserstein–Fisher–Rao |
| GAD-PVI | General Accelerated Dynamic-weight Particle-based Variational Inference |
| SVGD | Stein Variational Gradient Descent |
| GFSD | Gradient Flow with Smoothed Density |
| KSDD | Kernel Setin Discrepancy Descent |
| WAG | Wasserstein Accelerated Gradien |
| ACCEL | The Accelerated Flow method |
| WNES | Wasserstein Nesterov’s |
| AIG | Accelerated Information Gradient Flow |
| MMD | Maximum Mean Distance |
| MMDF | Maximum Mean Distance Flow |
| SD | Sinkhorn Divergence |
| SDF | Sinkhorn Divergence Flow |
| NSGF | Neural Sinkhorn Gradient Flow |
| JSD | J-JKO |
Appendix A. Definitions and Proofs
Appendix A.1. Definition of Information Metric in Probability Space
Appendix A.2. Full Hamiltonian Flow on the IFR Space and the Fisher–Rao Kinetic Energy
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 1
Appendix A.5. Proof of Proposition 2
Appendix B. Detailed Formulations
Appendix B.1. Kalman–Wasserstein–SHIFR Flow and KWGAD-PVI Algorithms
Appendix B.2. Stein-SHIFR Flow and SGAD-PVI Algorithms
Appendix B.3. GAD-PVI Algorithms in Details
| Algorithm A1 General Accelerated Dynamic-weight Particle-based Variational Inference (GAD-PVI) framework in details |
Input: Initial distribution , position adjusting step-size , weight adjusting step-size , velocity field adjusting step-size , velocity damping parameter .
|
Appendix C. Experiment Details
Appendix C.1. Experiments Settings
Appendix C.1.1. Density of the Gaussian Mixture Model
Appendix C.1.2. Density of the Gaussian Process Task
Appendix C.1.3. Training/Validation/Test Dataset in Bayesian Neural Network
Appendix C.1.4. Initialization of Particles’ Positions
Appendix C.1.5. Bandwidth of Kernel Function in Different Algorithms
Appendix C.1.6. WNES and WAG
Appendix C.2. Parameters Tuning
Detailed Settings for ηpos, ηwei, ηvel and γ
| Algorithm | Tasks | |
|---|---|---|
| Single Gaussian | Gaussian Mixture Model | |
| ParVI-BLOB | , –, –, – | , –, –, – |
| WAIG-BLOB | , –, , | , –, , |
| WNES-BLOB | , –, , | , –, , |
| DPVI-CA-BLOB | , , –, – | , , –, – |
| DPVI-DK-BLOB | , , –, – | , , –, – |
| WGAD-CA-BLOB | , , , | , , , |
| WGAD-DK-BLOB | , , , | , , , |
| KWAIG-BLOB | , –, –, – | , –, –, – |
| KWGAD-CA-BLOB | , , , | , , , |
| KWGAD-DK-BLOB | , , , | , , , |
| SAIG-BLOB | , –, –, – | , –, –, – |
| SGAD-CA-BLOB | , , , | , , , |
| SGAD-DK-BLOB | , , , | , , , |
| ParVI-GFSD | , –, –, – | , –, –, – |
| WAIG-GFSD | , –, , | , –, , 0.3 |
| WNES-GFSD | , –, , | , –, , |
| DPVI-CA-GFSD | , , –, – | , , –, – |
| DPVI-DK-GFSD | , , –, – | , , –, – |
| WGAD-CA-GFSD | , , , | , , , |
| WGAD-DK-GFSD | , , , | , , , |
| KWAIG-GFSD | , –, –, – | , –, –, – |
| KWGAD-CA-GFSD | , , , | , , , |
| KWGAD-DK-GFSD | , , , | , , , |
| SAIG-GFSD | , –, –, – | , –, –, – |
| SGAD-CA-GFSD | , , , | , , , |
| SGAD-DK-GFSD | , , , | , , , |
| Algorithm | Smoothing Approaches | |
|---|---|---|
| BLOB | GFSD | |
| ParVI | , –, –, – | , –, –, – |
| WAIG | , –, , | , –, , |
| WNES | , –, , | , –, , |
| DPVI-CA | , , –, – | , , –, – |
| DPVI-DK | , , –, – | , , –, – |
| WGAD-CA | , , , | , , , |
| WGAD-DK | , , , | , , , |
| KWAIG | , –, , | , –, , |
| KWGAD-CA | , , , | , , , |
| KWGAD-DK | , , , | , , , |
| SAIG | , –, , | , –, , |
| SGAD-CA | , , , | , , , |
| SGAD-DK | , , , | , , , |
| Algorithm | Datasets | |||
|---|---|---|---|---|
| Concrete | kin8nm | RedWine | Space | |
| ParVI-BLOB | , –, –, – | , –, –, – | , –, –, – | , –, –, – |
| WAIG-BLOB | , –, , | , –, , | , –, , | , –, , |
| WNES-BLOB | , –, , | , –, , | , –, , | , –, , |
| DPVI-CA-BLOB | , , –, – | , , –, – | , , –, – | , , –, – |
| DPVI-DK-BLOB | , , –, – | , , –, – | , , –, – | , , –, – |
| WGAD-CA-BLOB | , , , | , , , | , , , | , , , |
| WGAD-DK-BLOB | , , , | , , , | , , , | , , , |
| KWAIG-BLOB | , –, , | , –, , | , –, , | , –, , |
| KWGAD-CA-BLOB | , , , | , , , | , , , | , , , |
| KWGAD-DK-BLOB | , , , | , , , | , , , | , , , |
| SAIG-BLOB | , –, , | , –, , | , –, , | , –, , |
| SGAD-CA-BLOB | , , , | , , , | , , , | , , , |
| SGAD-DK-BLOB | , , , | , , , | , , , | , , , |
| ParVI-GFSD | , –, –, – | , –, –, – | , –, –, – | , –, –, – |
| WAIG-GFSD | , –, , | , –, , | , –, , | , –, , |
| WNES-GFSD | , –, , | , –, , | , –, , | , –, , |
| DPVI-CA-GFSD | , , –, – | , , –, – | , , –, – | , , –, – |
| DPVI-DK-GFSD | , , –, – | , , –, – | , , –, – | , , –, – |
| WGAD-CA-GFSD | , , , | , , , | , , , | , , , |
| WGAD-DK-GFSD | , , , | , , , | , , , | , , , |
| KWAIG-GFSD | , –, , | , –, , | , –, , | , –, , |
| KWGAD-CA-GFSD | , , , | , , , | , , , | , , , |
| KWGAD-DK-GFSD | , , , | , , , | , , , | , , , |
| SAIG-GFSD | , –, , | , –, , | , –, , | , –, , |
| SGAD-CA-GFSD | , , , | , , , | , , , | , , , |
| SGAD-DK-GFSD | , , , | , , , | , , , | , , , |
| Algorithms | Sampling Tasks | ||||
|---|---|---|---|---|---|
| A→B | B→C | C→D | D→A | Sketching | |
| ParVI-MMDF | , –, –, – | , –, –, – | , –, –, – | , –, –, – | , –, –, – |
| WAIG-MMDF | , –, , | , –, , | , –, , | , –, , | , –, , |
| DPVI-DK-MMDF | , , –, – | , , –, – | , , –, – | , , –, – | , , –, – |
| DPVI-CA-MMDF | , , –, – | , , –, – | , , –, – | , , –, – | , , –, – |
| WGAD-DK-MMDF | , , , , | , , , , | , , , , | , , , , | , , , , |
| WGAD-CA-MMDF | , , , , | , , , , | , , , , | , , , , | , , , , |
| ParVI-SDF | , –, –, – | , –, –, – | , –, –, – | , –, –, – | , –, –, – |
| WAIG-SDF | , –, , | , –, , | , –, , | , –, , | , –, , |
| DPVI-DK-SDF | , , –, – | , , –, – | , , –, – | , , –, – | , , –, – |
| DPVI-CA-SDF | , , –, – | , , –, – | , , –, – | , , –, – | , , –, – |
| WGAD-DK-SDF | , , , , | , , , , | , , , , | , , , , | , , , , |
| WGAD-CA-SDF | , , , , | , , , , | , , , , | , , , , | , , , , |
Appendix C.3. Additional Experiments Results
Appendix C.3.1. Results for SG
| Algorithm | Number of Particles | ||||
|---|---|---|---|---|---|
| 32 | 64 | 128 | 256 | 512 | |
| ParVI-SVGD | |||||
| ParVI-BLOB | |||||
| WAIG-BLOB | |||||
| WNes-BLOB | |||||
| DPVI-DK-BLOB | |||||
| DPVI-CA-BLOB | |||||
| WGAD-DK-BLOB(Ours) | |||||
| WGAD-CA-BLOB(Ours) | |||||
| KWAIG-BLOB | |||||
| KWGAD-DK-BLOB(Ours) | |||||
| KWGAD-CA-BLOB(Ours) | |||||
| SAIG-BLOB | |||||
| SGAD-DK-BLOB(Ours) | |||||
| SGAD-CA-BLOB(Ours) | |||||
| ParVI-GFSD | |||||
| WAIG-GFSD | |||||
| WNes-GFSD | |||||
| DPVI-DK-GFSD | |||||
| DPVI-CA-GFSD | |||||
| WGAD-DK-GFSD(Ours) | |||||
| WGAD-CA-GFSD(Ours) | |||||
| KWAIG-GFSD | |||||
| KWGAD-DK-GFSD(Ours) | |||||
| KWGAD-CA-GFSD(Ours) | |||||
| SAIG-GFSD | |||||
| SGAD-DK-GFSD(Ours) | |||||
| SGAD-CA-GFSD(Ours) | |||||
Appendix C.3.2. Additional Results for GMM
| Algorithm | Number of Particles | ||||
|---|---|---|---|---|---|
| 32 | 64 | 128 | 256 | 512 | |
| ParVI-SVGD | |||||
| ParVI-BLOB | |||||
| WAIG-BLOB | |||||
| WNes-BLOB | |||||
| DPVI-DK-BLOB | |||||
| DPVI-CA-BLOB | |||||
| WGAD-DK-BLOB(Ours) | |||||
| WGAD-CA-BLOB(Ours) | |||||
| KWAIG-BLOB | |||||
| KWGAD-DK-BLOB(Ours) | |||||
| KWGAD-CA-BLOB(Ours) | |||||
| SAIG-BLOB | |||||
| SGAD-DK-BLOB(Ours) | |||||
| SGAD-CA-BLOB(Ours) | |||||
| ParVI-GFSD | |||||
| WAIG-GFSD | |||||
| WNes-GFSD | |||||
| DPVI-DK-GFSD | |||||
| DPVI-CA-GFSD | |||||
| WGAD-DK-GFSD(Ours) | |||||
| WGAD-CA-GFSD(Ours) | |||||
| KWAIG-GFSD | |||||
| KWGAD-DK-GFSD(Ours) | |||||
| KWGAD-CA-GFSD(Ours) | |||||
| SAIG-GFSD | |||||
| SGAD-DK-GFSD(Ours) | |||||
| SGAD-CA-GFSD(Ours) | |||||
Appendix C.3.3. Additional Results for GP
| Algorithm | Smoothing Strategy | |
|---|---|---|
| BLOB | GFSD | |
| KWAIG | ||
| GAD-KW-DK | ||
| GAD-KW-CA | ||
| SAIG | ||
| GAD-S-DK | ||
| GAD-S-CA | ||
Appendix C.3.4. Additional Results for BNN
| Algorithm | Datasets | |||
|---|---|---|---|---|
| Concrete | kin8nm | RedWine | Space | |
| ParVI-SVGD | ||||
| ParVI-BLOB | ||||
| WAIG-BLOB | ||||
| WNES-BLOB | ||||
| DPVI-DK-BLOB | ||||
| DPVI-CA-BLOB | ||||
| WGAD-DK-BLOB(Ours) | ||||
| WGAD-CA-BLOB(Ours) | ||||
| KWAIG-BLOB | ||||
| KWGAD-DK-BLOB(Ours) | ||||
| KWGAD-CA-BLOB(Ours) | ||||
| SAIG-BLOB | ||||
| SGAD-DK-BLOB(Ours) | ||||
| SGAD-CA-BLOB(Ours) | ||||
| ParVI-GFSD | ||||
| WAIG-GFSD | ||||
| WNES-GFSD | ||||
| DPVI-DK-GFSD | ||||
| DPVI-CA-GFSD | ||||
| WGAD-DK-GFSD(Ours) | ||||
| WGAD-CA-GFSD(Ours) | ||||
| KWAIG-GFSD | ||||
| KWGAD-DK-GFSD(Ours) | ||||
| KWGAD-CA-GFSD(Ours) | ||||
| SAIG-GFSD | ||||
| SGAD-DK-GFSD(Ours) | ||||
| SGAD-CA-GFSD(Ours) | ||||
| Algorithm | Datasets | |||
|---|---|---|---|---|
| Concrete | kin8nm | RedWine | Space | |
| KWAIG-BLOB | ||||
| KWGAD-DK-BLOB(Ours) | ||||
| KWGAD-CA-BLOB(Ours) | ||||
| SAIG-BLOB | ||||
| SGAD-DK-BLOB(Ours) | ||||
| SGAD-CA-BLOB(Ours) | ||||
| KWAIG-GFSD | ||||
| KWGAD-DK-GFSD(Ours) | ||||
| KWGAD-CA-GFSD(Ours) | ||||
| SAIG-GFSD | ||||
| SGAD-DK-GFSD(Ours) | ||||
| SGAD-CA-GFSD(Ours) | ||||
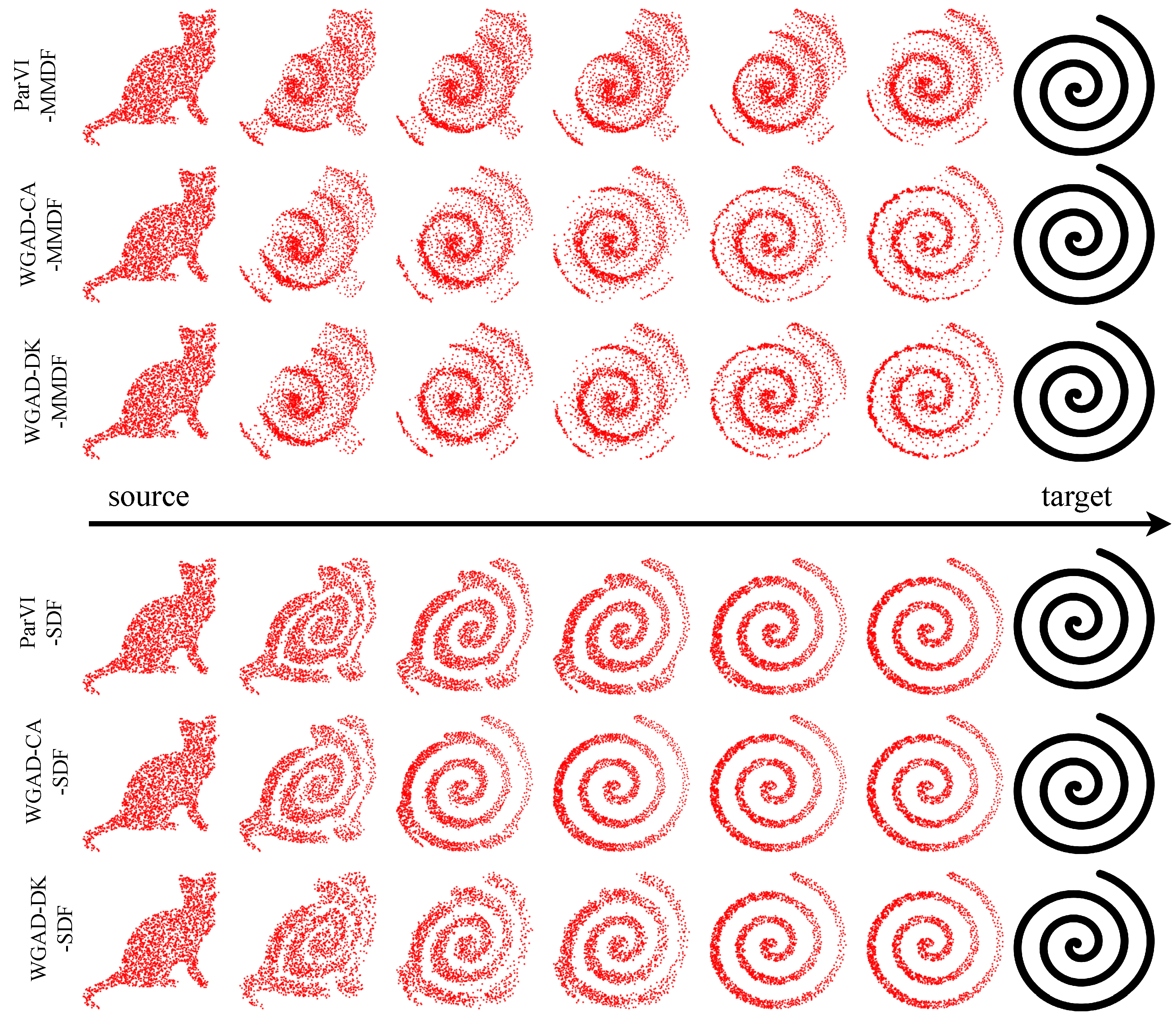

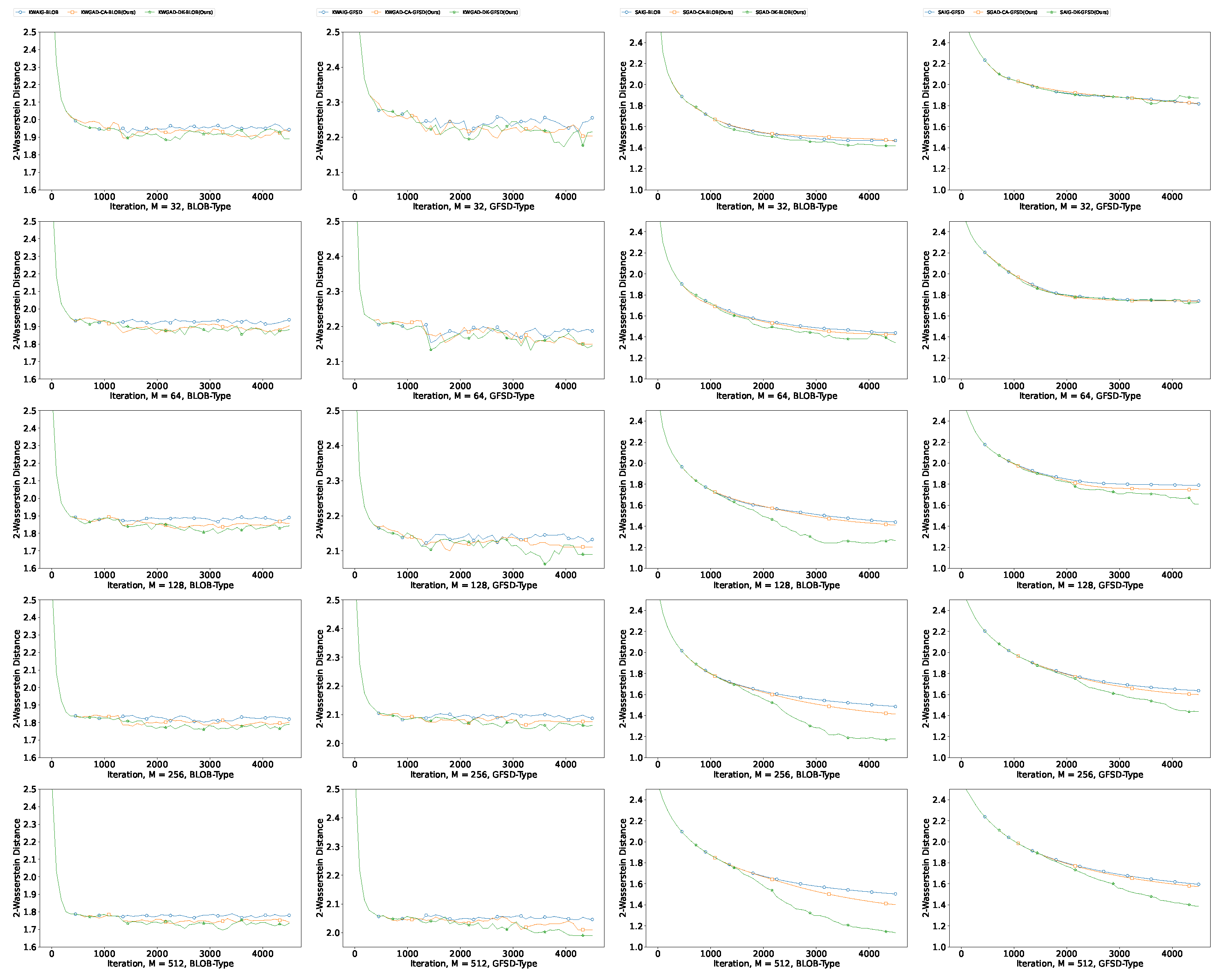
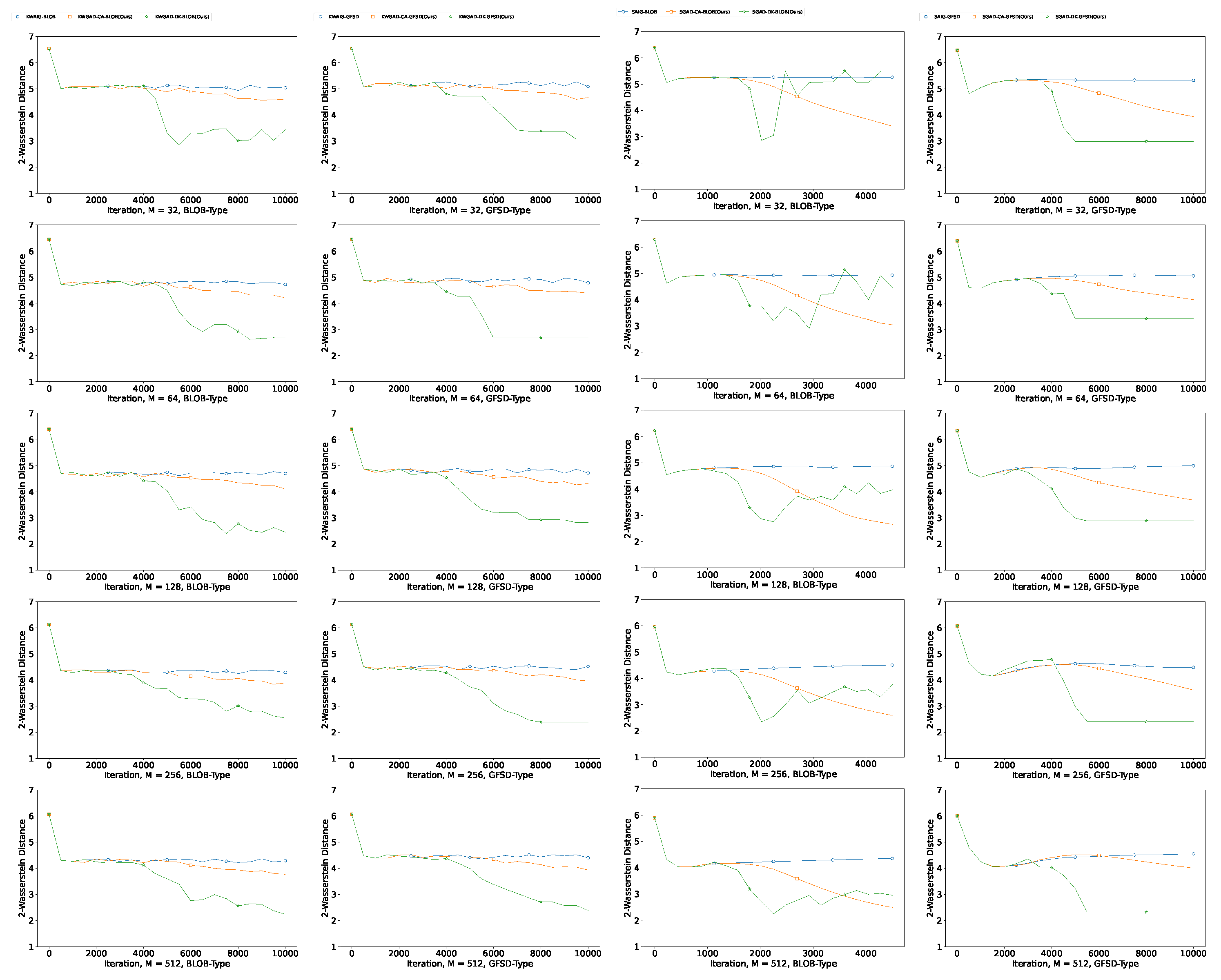
Appendix C.3.5. Results for Morphing
Appendix C.3.6. Results for GAD-KSDD
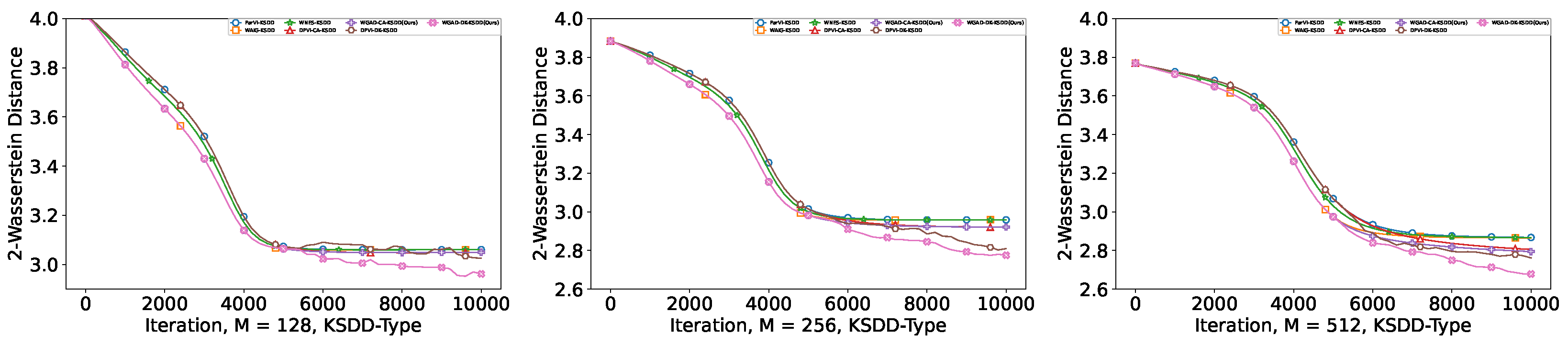
References
- Akbayrak, S.; Bocharov, I.; de Vries, B. Extended variational message passing for automated approximate Bayesian inference. Entropy 2021, 23, 815. [Google Scholar] [CrossRef] [PubMed]
- Sharif-Razavian, N.; Zollmann, A. An overview of nonparametric bayesian models and applications to natural language processing. Science 2008, 71–93. Available online: https://www.cs.cmu.edu/~zollmann/publications/nonparametric.pdf (accessed on 16 August 2023).
- Siddhant, A.; Lipton, Z.C. Deep bayesian active learning for natural language processing: Results of a large-scale empirical study. arXiv 2018, arXiv:1808.05697. [Google Scholar]
- Luo, L.; Yang, J.; Zhang, B.; Jiang, J.; Huang, H. Nonparametric Bayesian Correlated Group Regression With Applications to Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5330–5344. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Du, C.; Huang, L.; He, H. Reconstructing Perceived Images From Human Brain Activities With Bayesian Deep Multiview Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2310–2323. [Google Scholar] [CrossRef] [PubMed]
- Frank, P.; Leike, R.; Enßlin, T.A. Geometric variational inference. Entropy 2021, 23, 853. [Google Scholar] [CrossRef] [PubMed]
- Mohammad-Djafari, A. Entropy, information theory, information geometry and Bayesian inference in data, signal and image processing and inverse problems. Entropy 2015, 17, 3989–4027. [Google Scholar] [CrossRef]
- Jewson, J.; Smith, J.Q.; Holmes, C. Principles of Bayesian inference using general divergence criteria. Entropy 2018, 20, 442. [Google Scholar] [CrossRef] [PubMed]
- Konishi, T.; Kubo, T.; Watanabe, K.; Ikeda, K. Variational Bayesian Inference Algorithms for Infinite Relational Model of Network Data. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2176–2181. [Google Scholar] [CrossRef]
- Chen, Z.; Song, Z.; Ge, Z. Variational Inference Over Graph: Knowledge Representation for Deep Process Data Analytics. IEEE Trans. Knowl. Data Eng. 2023, 36, 730–2744. [Google Scholar] [CrossRef]
- Wang, H.; Fan, J.; Chen, Z.; Li, H.; Liu, W.; Liu, T.; Dai, Q.; Wang, Y.; Dong, Z.; Tang, R. Optimal Transport for Treatment Effect Estimation. In Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems, New Orleans, LO, USA, 10–16 December 2023. [Google Scholar]
- Geyer, C.J. Practical markov chain monte carlo. Stat. Sci. 1992, 7, 473–483. [Google Scholar] [CrossRef]
- Carlo, C.M. Markov chain monte carlo and gibbs sampling. Lect. Notes EEB 2004, 581, 3. [Google Scholar]
- Neal, R.M. MCMC using Hamiltonian dynamics. arXiv 2012, arXiv:1206.1901. [Google Scholar]
- Chen, T.; Fox, E.; Guestrin, C. Stochastic gradient hamiltonian monte carlo. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1683–1691. [Google Scholar]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Doucet, A.; De Freitas, N.; Gordon, N.J. Sequential Monte Carlo Methods in Practice; Springer: Cham, Switzerland, 2001; Volume 1. [Google Scholar]
- Del Moral, P.; Doucet, A.; Jasra, A. Sequential monte carlo samplers. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 411–436. [Google Scholar] [CrossRef]
- Septier, F.; Peters, G.W. Langevin and Hamiltonian based sequential MCMC for efficient Bayesian filtering in high-dimensional spaces. IEEE J. Sel. Top. Signal Process. 2015, 10, 312–327. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, D. Stein variational gradient descent: A general purpose bayesian inference algorithm. arXiv 2016, arXiv:1608.04471. [Google Scholar]
- Zhu, M.; Liu, C.; Zhu, J. Variance Reduction and Quasi-Newton for Particle-Based Variational Inference. In Proceedings of the ICML, Virtual, 13–18 July 2020; pp. 11576–11587. [Google Scholar]
- Shen, Z.; Heinonen, M.; Kaski, S. De-randomizing MCMC dynamics with the diffusion Stein operator. In Proceedings of the Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 17507–17517. [Google Scholar]
- Zhang, C.; Li, Z.; Du, X.; Qian, H. DPVI: A Dynamic-Weight Particle-Based Variational Inference Framework. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22, Vienna, Austria, 23–29 July 2022; pp. 4900–4906. [Google Scholar] [CrossRef]
- Li, L.; Liu, Q.; Korba, A.; Yurochkin, M.; Solomon, J. Sampling with Mollified Interaction Energy Descent. In Proceedings of the The Eleventh International Conference on Learning Representations, Vienna, Austria, 7–11 May 2023. [Google Scholar]
- Galy-Fajou, T.; Perrone, V.; Opper, M. Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation. Entropy 2021, 23, 990. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhang, R.; Wang, W.; Li, B.; Chen, L. A unified particle-optimization framework for scalable Bayesian sampling. arXiv 2018, arXiv:1805.11659. [Google Scholar]
- Liu, C.; Zhuo, J.; Cheng, P.; Zhang, R.; Zhu, J. Understanding and accelerating particle-based variational inference. In Proceedings of the ICML, Long Beach, CA, USA, 9–15 June 2019; pp. 4082–4092. [Google Scholar]
- Korba, A.; Aubin-Frankowski, P.C.; Majewski, S.; Ablin, P. Kernel Stein Discrepancy Descent. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 5719–5730. [Google Scholar]
- Craig, K.; Bertozzi, A. A blob method for the aggregation equation. Math. Comput. 2016, 85, 1681–1717. [Google Scholar] [CrossRef]
- Arbel, M.; Korba, A.; Salim, A.; Gretton, A. Maximum mean discrepancy gradient flow. arXiv 2019, arXiv:1906.04370. [Google Scholar]
- Zhu, H.; Wang, F.; Zhang, C.; Zhao, H.; Qian, H. Neural Sinkhorn Gradient Flow. arXiv 2024, arXiv:2401.14069. [Google Scholar]
- Taghvaei, A.; Mehta, P. Accelerated flow for probability distributions. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6076–6085. [Google Scholar]
- Wang, Y.; Li, W. Accelerated Information Gradient Flow. J. Sci. Comput. 2022, 90, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Shang, F.; Cheng, J.; Cheng, H.; Jiao, L. Accelerated first-order methods for geodesically convex optimization on Riemannian manifolds. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper/2017/hash/6ef80bb237adf4b6f77d0700e1255907-Abstract.html (accessed on 16 August 2023).
- Zhang, H.; Sra, S. An estimate sequence for geodesically convex optimization. In Proceedings of the Conference on Learning Theory, Stockholm, Sweden, 6–9 July 2018; pp. 1703–1723. [Google Scholar]
- Wibisono, A.; Wilson, A.C.; Jordan, M.I. A variational perspective on accelerated methods in optimization. Proc. Natl. Acad. Sci. USA 2016, 113, E7351–E7358. [Google Scholar] [CrossRef]
- Lafferty, J.D. The Density Manifold and Configuration Space Quantization. Trans. Am. Math. Soc. 1988, 305, 699–741. [Google Scholar] [CrossRef]
- Nesterov, Y. Lectures on Convex Optimization; Springer: Cham, Switzerland, 2018; Volume 137. [Google Scholar]
- Carrillo, J.A.; Choi, Y.P.; Tse, O. Convergence to equilibrium in Wasserstein distance for damped Euler equations with interaction forces. Commun. Math. Phys. 2019, 365, 329–361. [Google Scholar] [CrossRef]
- Gallouët, T.O.; Monsaingeon, L. A JKO Splitting Scheme for Kantorovich–Fisher–Rao Gradient Flows. SIAM J. Math. Anal. 2017, 49, 1100–1130. [Google Scholar] [CrossRef]
- Rotskoff, G.; Jelassi, S.; Bruna, J.; Vanden-Eijnden, E. Global convergence of neuron birth-death dynamics. arXiv 2019, arXiv:1902.01843. [Google Scholar]
- Chizat, L.; Peyré, G.; Schmitzer, B.; Vialard, F.X. An interpolating distance between optimal transport and Fisher–Rao metrics. Found. Comput. Math. 2018, 18, 1–44. [Google Scholar] [CrossRef]
- Kondratyev, S.; Monsaingeon, L.; Vorotnikov, D. A new optimal transport distance on the space of finite Radon measures. Adv. Differ. Equ. 2016, 21, 1117–1164. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Liu, Q. Stein variational gradient descent as gradient flow. arXiv 2017, arXiv:1704.07520. [Google Scholar]
- Wang, D.; Liu, Q. Learning to draw samples: With application to amortized mle for generative adversarial learning. arXiv 2016, arXiv:1611.01722. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Li, C.; Han, S.; Carin, L. VAE Learning via Stein Variational Gradient Descent. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Liu, Y.; Ramachandran, P.; Liu, Q.; Peng, J. Stein variational policy gradient. arXiv 2017, arXiv:1704.02399. [Google Scholar]
- Haarnoja, T.; Tang, H.; Abbeel, P.; Levine, S. Reinforcement learning with deep energy-based policies. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 1352–1361. [Google Scholar]
- Liu, W.; Zheng, X.; Su, J.; Zheng, L.; Chen, C.; Hu, M. Contrastive Proxy Kernel Stein Path Alignment for Cross-Domain Cold-Start Recommendation. IEEE Trans. Knowl. Data Eng. 2023, 35, 11216–11230. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, J.; Nolen, J. Accelerating langevin sampling with birth-death. arXiv 2019, arXiv:1905.09863. [Google Scholar]
- Shen, Z.; Wang, Z.; Ribeiro, A.; Hassani, H. Sinkhorn barycenter via functional gradient descent. Adv. Neural Inf. Process. Syst. 2020, 33, 986–996. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. NIPS 2014, 27, 139–144. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Choi, J.; Choi, J.; Kang, M. Scalable Wasserstein Gradient Flow for Generative Modeling through Unbalanced Optimal Transport. arXiv 2024, arXiv:2402.05443. [Google Scholar]
- Ranganath, R.; Gerrish, S.; Blei, D. Black box variational inference. In Proceedings of the Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 814–822. [Google Scholar]
- Ambrosio, L.; Gigli, N.; Savaré, G. Gradient Flows: In Metric Spaces and in the Space of Probability Measures; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport. Cent. Res. Econ. Stat. Work. Pap. 2017. Available online: https://ideas.repec.org/p/crs/wpaper/2017-86.html (accessed on 16 August 2023).
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 64. [Google Scholar]
- Butcher, J.C. Implicit runge-kutta processes. Math. Comput. 1964, 18, 50–64. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Korba, A.; Salim, A.; Arbel, M.; Luise, G.; Gretton, A. A non-asymptotic analysis for Stein variational gradient descent. NeurIPS 2020, 33, 4672–4682. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Proceedings of the Summer School on Machine Learning, Tubingen, Germany, 4–16 August 2003; pp. 63–71. [Google Scholar]
- Chen, W.Y.; Mackey, L.; Gorham, J.; Briol, F.X.; Oates, C. Stein points. In Proceedings of the ICML, Stockholm, Sweden, 10–15 July 2018; pp. 844–853. [Google Scholar]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X.L. Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Cuturi, M.; Doucet, A. Fast computation of Wasserstein barycenters. In Proceedings of the International Conference on Machine Learning, Beijing, China, 22–24 June 2014; pp. 685–693. [Google Scholar]
- Solomon, J.; De Goes, F.; Peyré, G.; Cuturi, M.; Butscher, A.; Nguyen, A.; Du, T.; Guibas, L. Convolutional wasserstein distances: Efficient optimal transportation on geometric domains. ACM Trans. Graph. ToG 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Mroueh, Y.; Sercu, T.; Raj, A. Sobolev descent. In Proceedings of the Artificial Intelligence and Statistics, Okinawa, Japan, 16–18 April 2019; pp. 2976–2985. [Google Scholar]
- Santambrogio, F. {Euclidean, metric, and Wasserstein} gradient flows: An overview. Bull. Math. Sci. 2017, 7, 87–154. [Google Scholar] [CrossRef]
- Von Mises, R.; Geiringer, H.; Ludford, G.S.S. Mathematical Theory of Compressible Fluid Flow; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Mroueh, Y.; Rigotti, M. Unbalanced Sobolev Descent. NeurIPS 2020, 33, 17034–17043. [Google Scholar]
- Garbuno-Inigo, A.; Hoffmann, F.; Li, W.; Stuart, A.M. Interacting Langevin diffusions: Gradient structure and ensemble Kalman sampler. SIAM J. Appl. Dyn. Syst. 2020, 19, 412–441. [Google Scholar] [CrossRef]
- Nüsken, N.; Renger, D. Stein Variational Gradient Descent: Many-particle and long-time asymptotics. arXiv 2021, arXiv:2102.12956. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, R.; Carin, L.; Chen, C. Stochastic particle-optimization sampling and the non-asymptotic convergence theory. In Proceedings of the Artificial Intelligence and Statistics, Online, 26–28 August 2020; pp. 1877–1887. [Google Scholar]


| Features | Accelerated Position Update | Dynamic Weight Adjustment | Dissimilarity and Empirical Approximation | Underlying Probability Space | Target Distribution Accessibility | |
|---|---|---|---|---|---|---|
| Methods | ||||||
| SVGD [20] | ✗ | ✗ | KL-RKHS | Wasserstein | Score | |
| BLOB [29] | ✗ | ✗ | KL-BLOB | Wasserstein | Score | |
| KSDD [28] | ✗ | ✗ | KSD-KSDD | Wasserstein | Score | |
| MMDF [30] | ✗ | ✗ | MMD-MMDF | Wasserstein | Samples | |
| SDF [31] | ✗ | ✗ | SD-SDF | Wasserstein | Samples | |
| ACCEL [32] | ✓ | ✗ | KL-GFSD | Wasserstein | Score | |
| WNES, WAG [27] | ✓ | ✗ | General | Wasserstein | Score | |
| AIG [33] | ✓ | ✗ | KL-GFSD | Information (General) | Score | |
| DPVI [23] | ✗ | ✓ | General | WFR | Score | |
| GAD-PVI (Ours) | ✓ | ✓ | General | IFR (General) | Both | |
| Algorithm | Empirical Strategy | |
|---|---|---|
| BLOB | GFSD | |
| ParVI | ± | ± |
| WAIG | ± | ± |
| WNES | ± | ± |
| DPVI-DK | ± | ± |
| DPVI-CA | ± | ± |
| WGAD-DK | ± | ± |
| WGAD-CA | ± | ± |
| Algorithms | Datasets | |||
|---|---|---|---|---|
| Concrete | kin8nm | RedWine | Space | |
| ParVI-SVGD | 6.323 | 8.020 × | 6.330 × | 9.021 × |
| ParVI-BLOB | 6.313 | 7.891 × | 6.318 × | 8.943 × |
| WAIG-BLOB | 6.063 | 7.791 × | 6.267 × | 8.775 × |
| WNES-BLOB | 6.112 | 7.690 × | 6.264 × | 8.836 × |
| DPVI-DK-BLOB | 6.285 | 7.889 × | 6.294 × | 8.853 × |
| DPVI-CA-BLOB | 6.292 | 7.789 × | 6.298 × | 8.850 × |
| WGAD-DK-BLOB | 6.058 | 7.688 × | 6.267 × | 8.716 × |
| WGAD-CA-BLOB | 6.047 | 7.629 × | 6.263 × | 8.704 × |
| ParVI-GFSD | 6.314 | 7.891 × | 6.317 × | 8.943 × |
| WAIG-GFSD | 6.105 | 7.794 × | 6.265 × | 8.776 × |
| WNES-GFSD | 6.123 | 7.756 × | 6.263 × | 8.836 × |
| DPVI-DK-GFSD | 6.291 | 7.882 × | 6.277 × | 8.851 × |
| DPVI-CA-GFSD | 6.290 | 7.791 × | 6.298 × | 8.852 × |
| WGAD-DK-GFSD | 6.099 | 7.726 × | 6.265 × | 8.708 × |
| WGAD-CA-GFSD | 6.088 | 7.634 × | 6.260 × | 8.710 × |
| Algorithms | Sampling Tasks | ||||
|---|---|---|---|---|---|
| A→B | B→C | C→D | D→A | Sketching | |
| ParVI-MMDF | |||||
| WAIG-MMDF | |||||
| DPVI-DK-MMDF | |||||
| DPVI-CA-MMDF | |||||
| WGAD-DK-MMDF | |||||
| WGAD-CA-MMDF | |||||
| ParVI-SDF | |||||
| WAIG-SDF | |||||
| DPVI-DK-SDF | |||||
| DPVI-CA-SDF | |||||
| WGAD-DK-SDF | |||||
| WGAD-CA-SDF | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhu, H.; Zhang, C.; Zhao, H.; Qian, H. GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework. Entropy 2024, 26, 679. https://doi.org/10.3390/e26080679
Wang F, Zhu H, Zhang C, Zhao H, Qian H. GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework. Entropy. 2024; 26(8):679. https://doi.org/10.3390/e26080679
Chicago/Turabian StyleWang, Fangyikang, Huminhao Zhu, Chao Zhang, Hanbin Zhao, and Hui Qian. 2024. "GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework" Entropy 26, no. 8: 679. https://doi.org/10.3390/e26080679
APA StyleWang, F., Zhu, H., Zhang, C., Zhao, H., & Qian, H. (2024). GAD-PVI: A General Accelerated Dynamic-Weight Particle-Based Variational Inference Framework. Entropy, 26(8), 679. https://doi.org/10.3390/e26080679




