Exergoeconomic Analysis and Optimization of a Biomass Integrated Gasification Combined Cycle Based on Externally Fired Gas Turbine, Steam Rankine Cycle, Organic Rankine Cycle, and Absorption Refrigeration Cycle
Abstract
1. Introduction
- (1)
- Introduction of a novel biomass gasification-based CCP system to enhance the energy utilization efficiency, alongside the development of comprehensive mathematical models to assess system performance from thermodynamic and exergoeconomic perspectives.
- (2)
- Examination of the influence of critical operational parameters on the performance criteria.
- (3)
- Optimization of the system to determine the optimal operational conditions that maximize exergy efficiency while minimizing the LCOE.
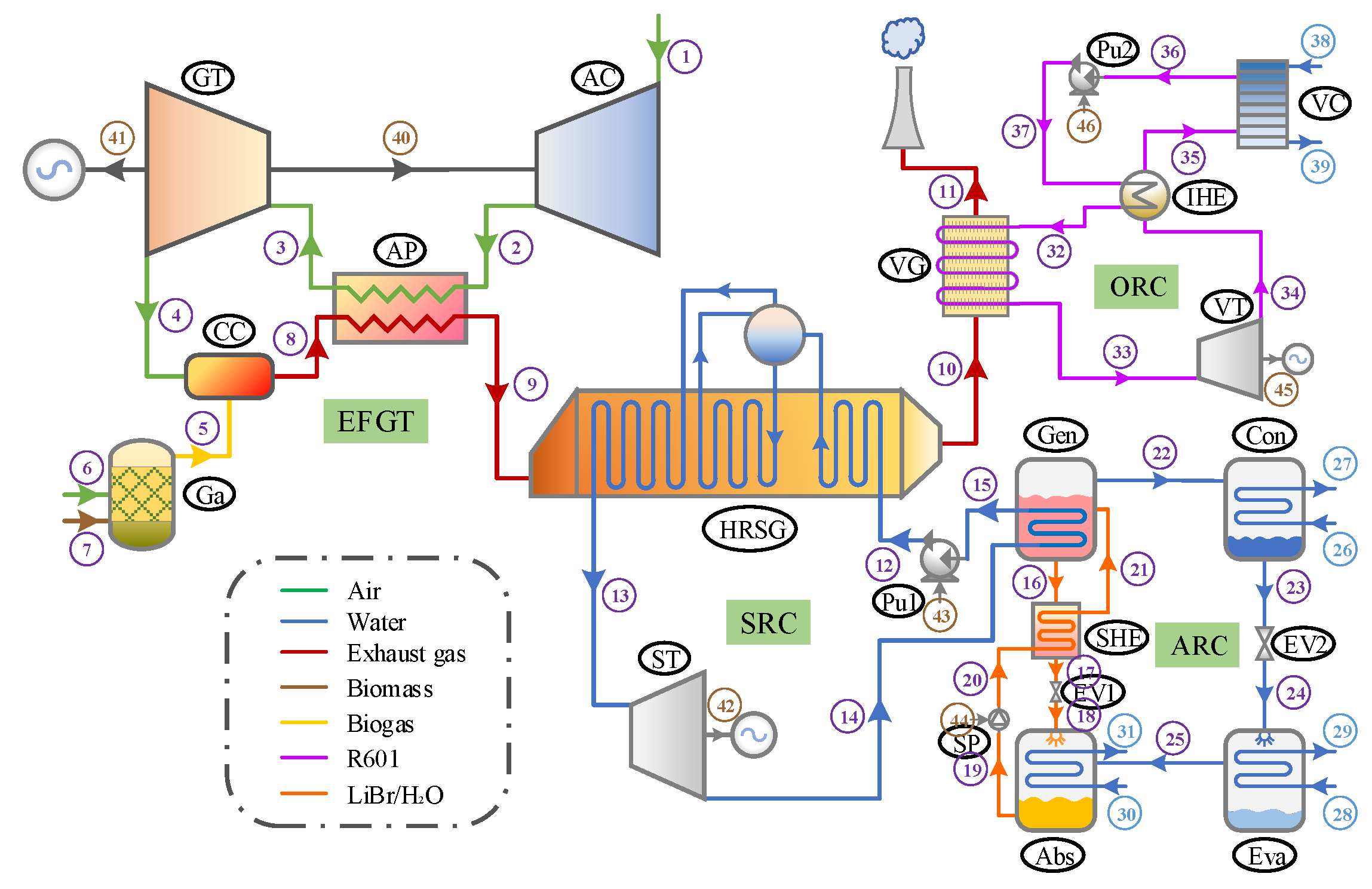
2. System Description
3. Mathematical Modeling
3.1. Assumptions
- Operation of the system is assumed to be in a steady state;
- Changes in kinetic and potential energy within the system are considered negligible;
- The system assumes no heat losses across its various components;
- Pressure variations across piping systems are overlooked;
- The composition of ambient air is taken as 21% oxygen and 79% nitrogen by volume;
- Gas mixtures within the system are treated as ideal gases for the purpose of simulation;
- Within the ARC, fluid streams exit both the evaporator and condenser in a saturated state, and the output solutions from the generator and absorber reach equilibrium at their specific temperatures and concentrations;
- For the ORC, the working fluid departs the vapor generator as saturated vapor and exits the condenser as saturated liquid;
- The performance of compressors, pumps, and turbines is modeled with constant isentropic efficiencies.
3.2. Energy Analysis
3.2.1. Biomass Gasifier
3.2.2. Combustion Chamber
3.2.3. Other System Components
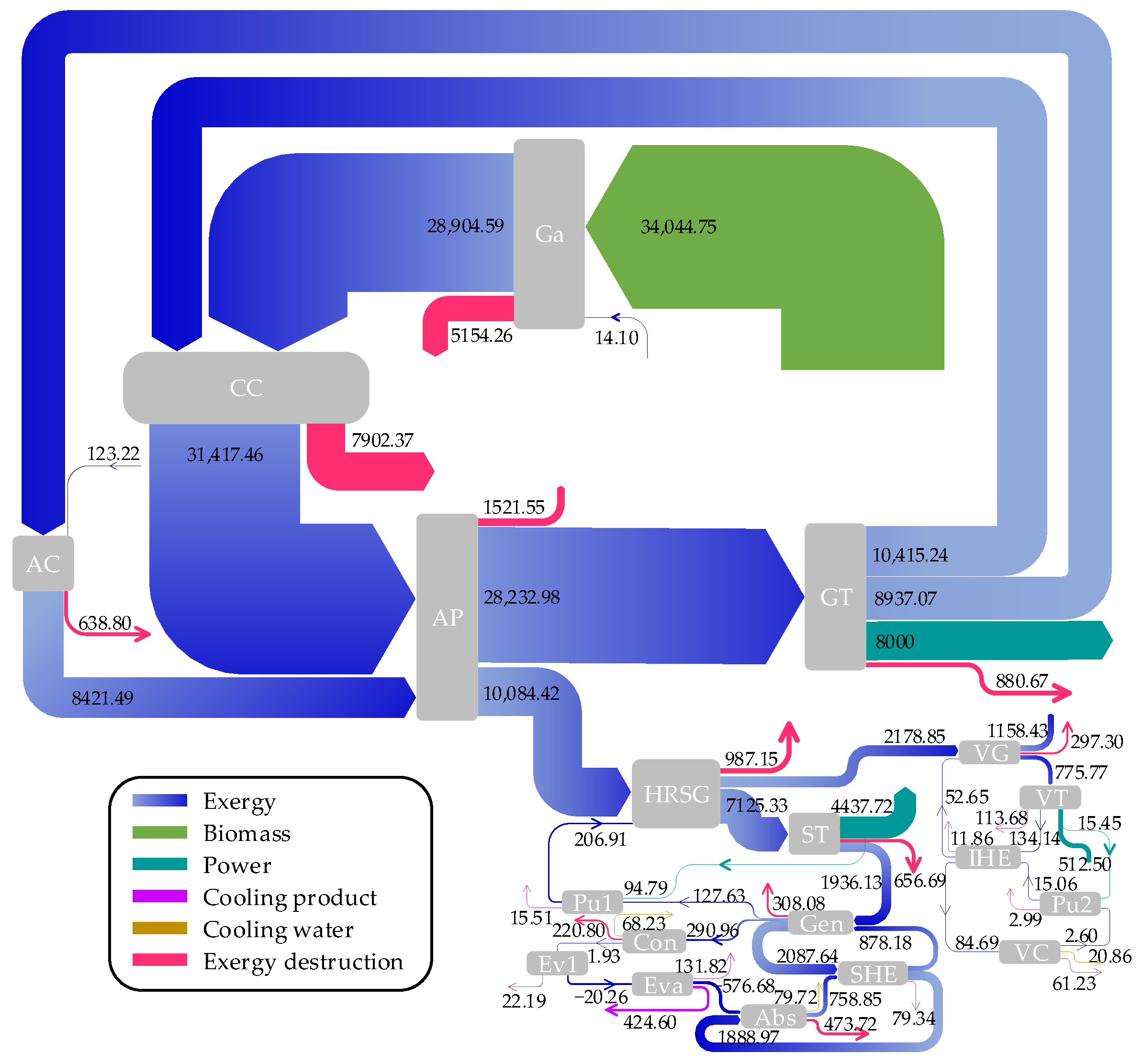
3.3. Exergy Analysis
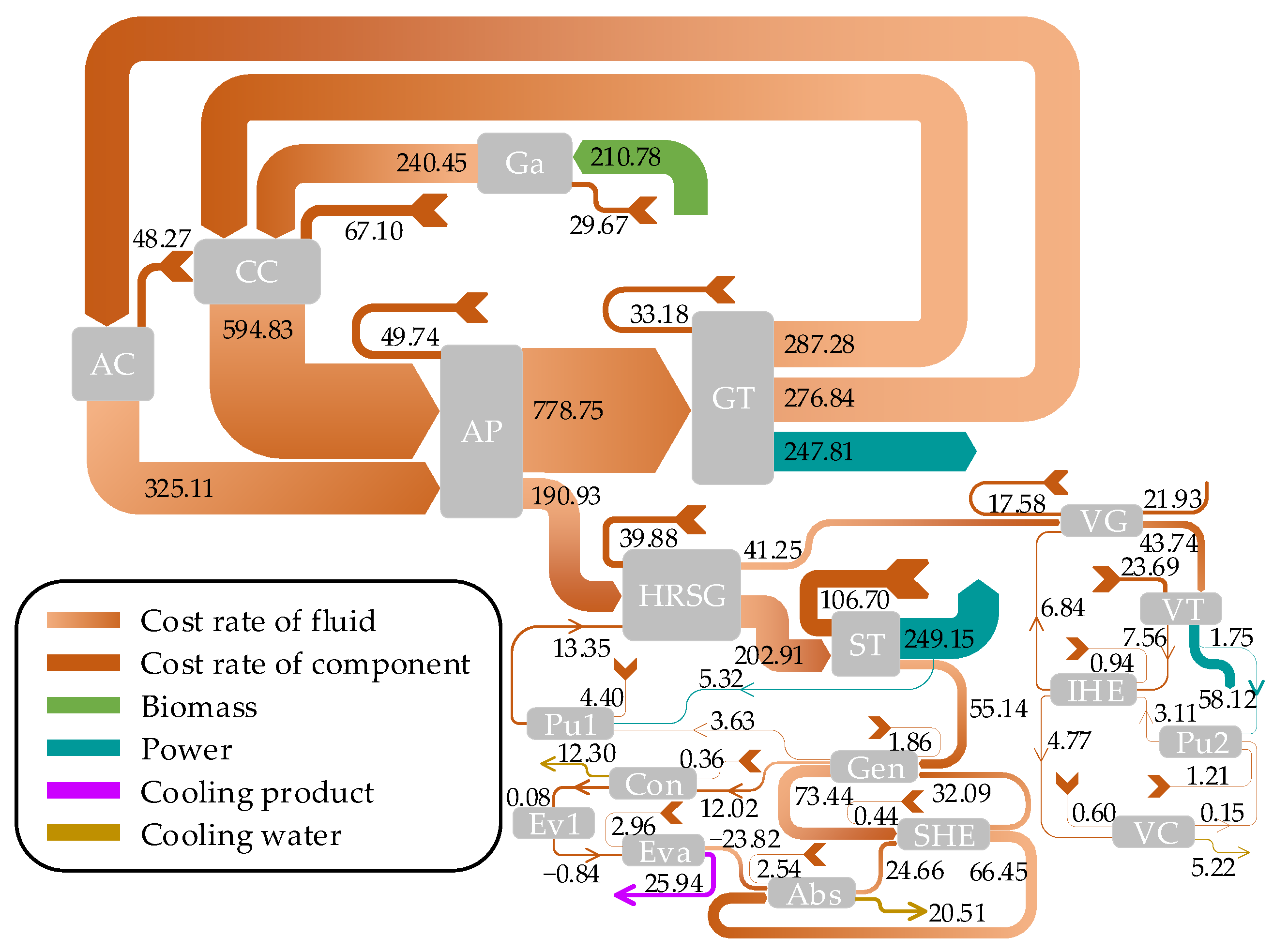
3.4. Exergoeconomic Analysis
3.5. Overall Performance Assessment
3.6. Multi-Objective Optimization
4. Results and Discussion
4.1. Model Validation
4.2. Base Case Results
4.3. Parametric Study
4.3.1. Effect of Air Compressor Pressure Ratio on the System Performance
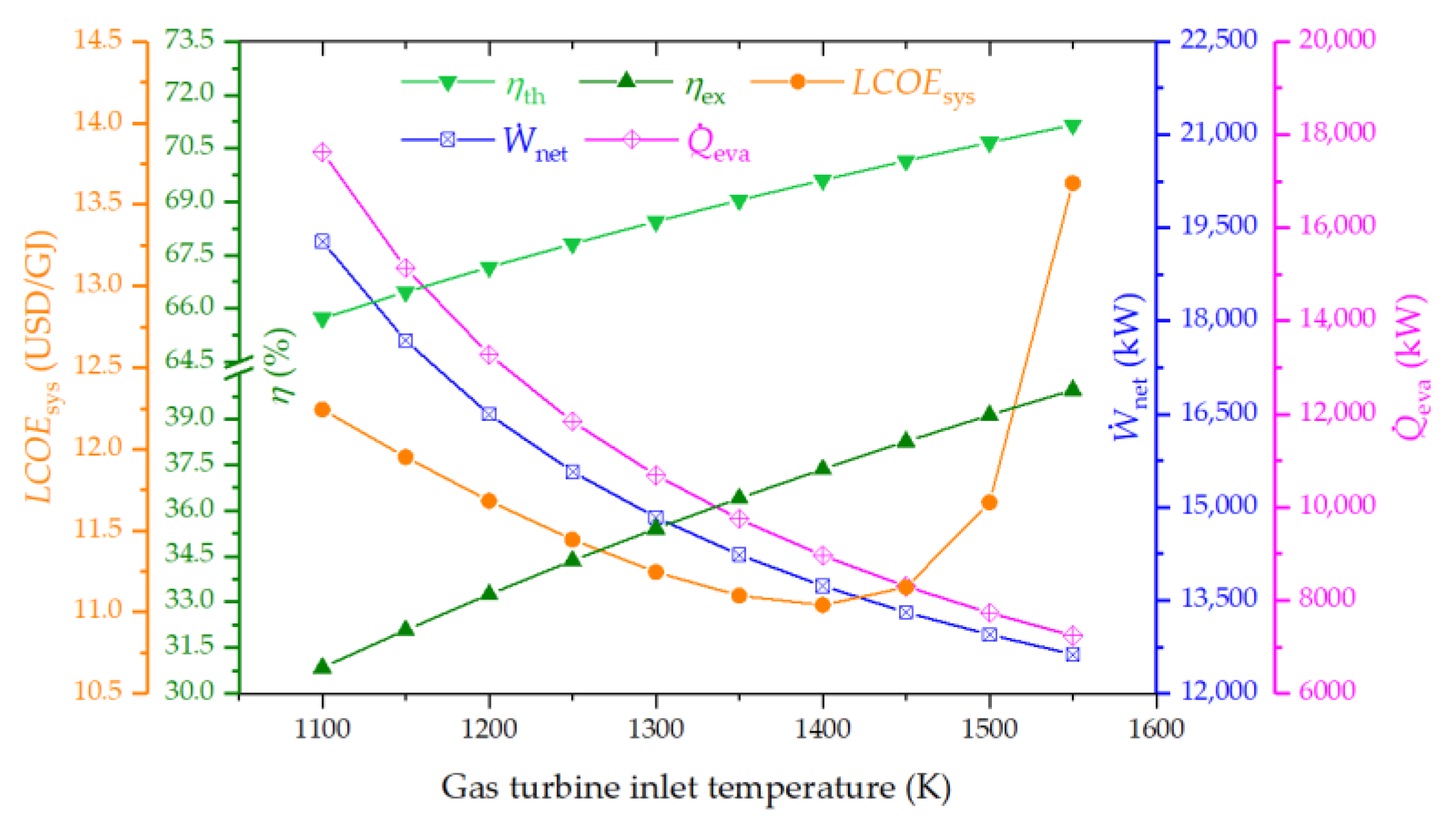
4.3.2. Effect of Gas Turbine Inlet Temperature on the System Performance
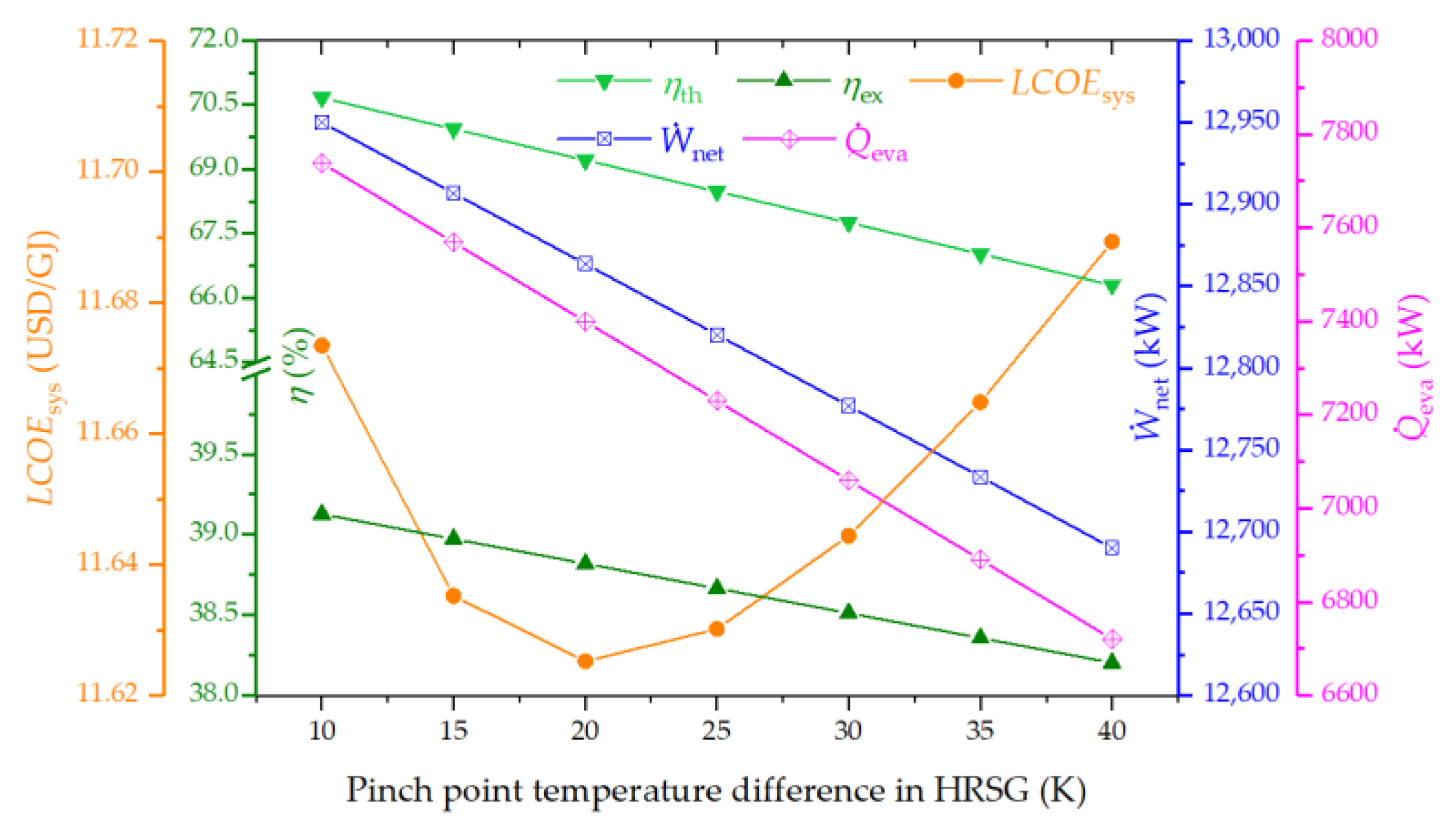
4.3.3. Effect of Pinch Point Temperature Difference in HRSG on the System Performance
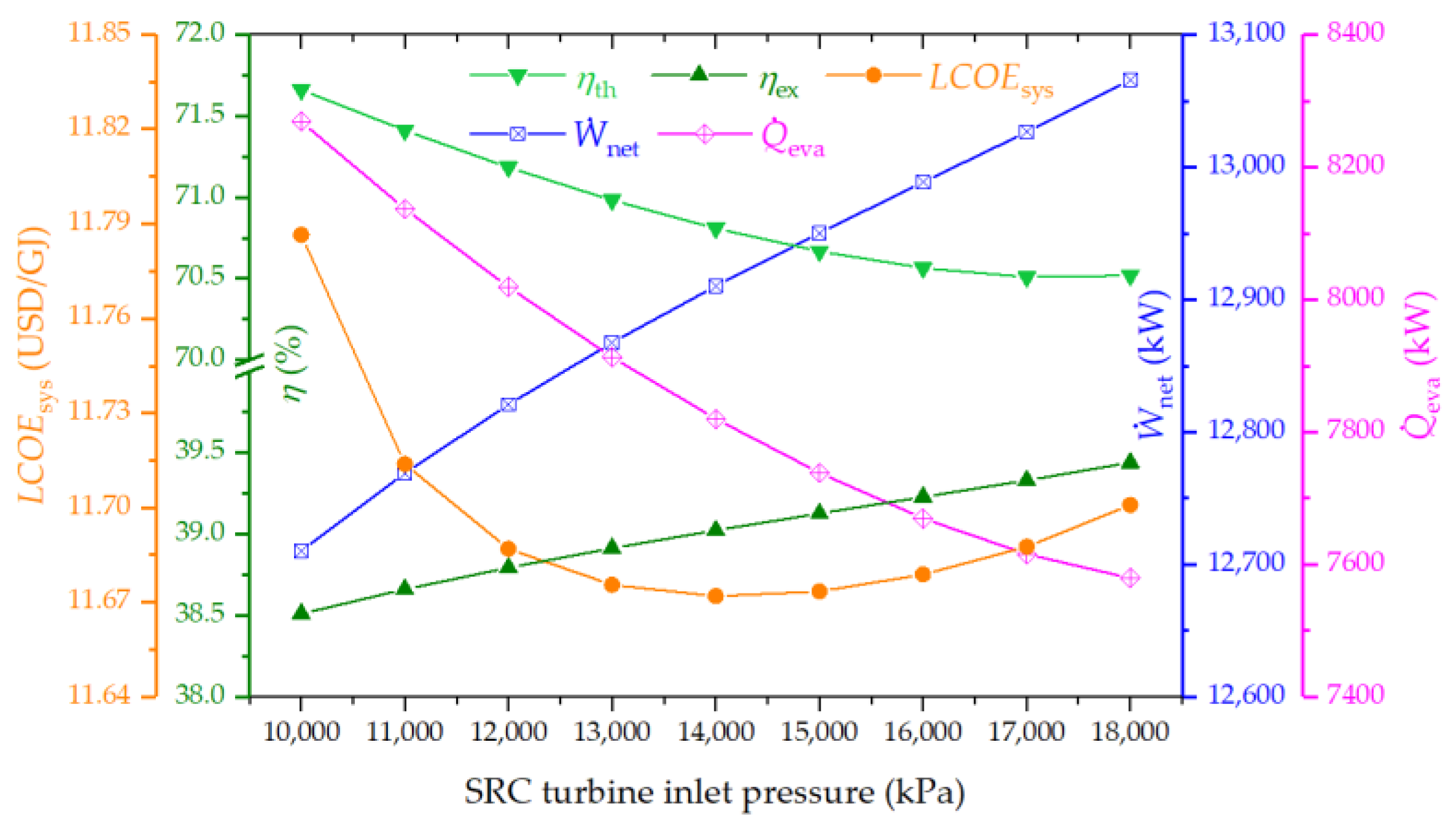
4.3.4. Effect of Steam Turbine Inlet Pressure on the System Performance
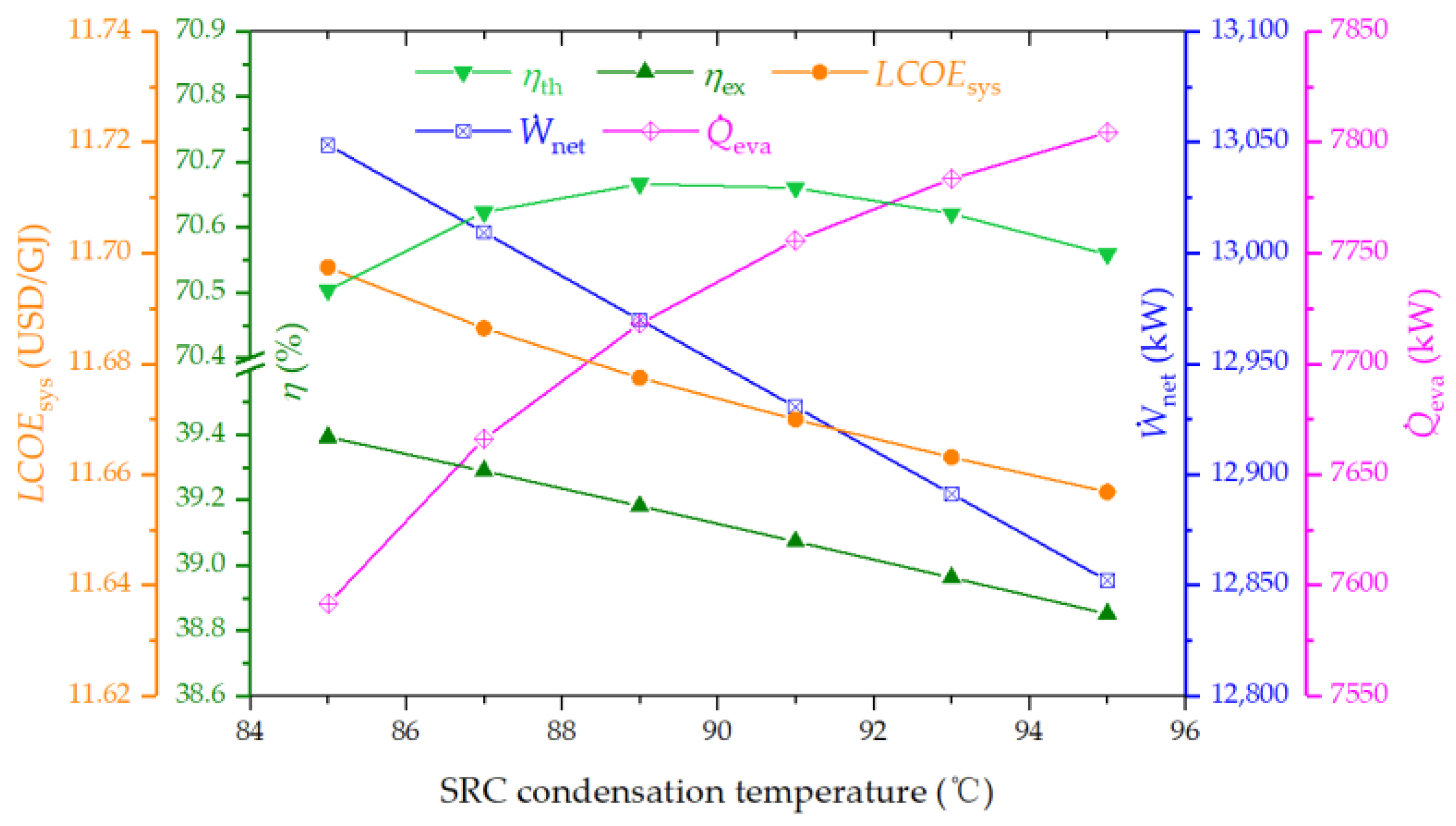
4.3.5. Effect of SRC Condenser Temperature on the System Performance
4.3.6. Effect of ORC Turbine Inlet Pressure on the System Performance
4.4. Optimization Results
4.5. Comprative Study
5. Conclusions
- For the baseline scenario, the system exhibits a thermal efficiency of 70.67%, an exergy efficiency of 39.13%, and an LCOE of 11.67 USD/GJ, alongside generating a net power of 12,950.2 kW and a cooling output of 7738.4 kW.
- Exergy analysis revealed that the highest rate of exergy destruction occurs in the combustion chamber, followed closely by the biomass gasifier. The gas turbine and the absorber demonstrated the best and poorest performances from exergy viewpoint among the system components, respectively.
- The inlet temperature of the gas turbine emerged as a critical factor affecting the system performance. Elevating GTIT significantly boosts both thermal and exergy efficiencies, despite a notable reduction in net power and cooling outputs.
- Superior thermodynamic performance is achieved at a higher air compressor pressure ratio and a gas turbine inlet temperature, or at a lower pinch point temperature difference in the HRSG. Optimizing these parameters also leads to minimized LCOE.
- Under optimal conditions, the CCP system demonstrates a 5.7% reduction in LCOE and a 2.5% decrease in exergy efficiency compared to the baseline scenario, highlighting a trade-off between different optimization criteria. This balance suggests that the optimal solution varies depending on specific engineering applications’ requirements.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area (m2) | COP | coefficient of performance |
| cost per exergy unit (USD·GJ−1) | CRF | capital recovery factor | |
| cost rate (USD·h−1) | EFGT | externally fired gas turbine | |
| ex | exergy per unit mass (kW·kg−1) | EV | expansion valve |
| exergy rate (kW) | eva | evaporator | |
| f | exergoeconomic factor | GA | genetic algorithm |
| h | specific enthalpy (kJ·kg−1) | Ga | gasifier |
| ir | annual interest rate (%) | gen | generator |
| K | equilibrium constant | GT | gas turbine |
| mass flow rate (kg·s−1) | GTIT | gas turbine inlet temperature | |
| n | kilomoles of component (kmol) | HRSG | heat recovery steam generator |
| N | annual operating hours (h) | is | isentropic |
| nt | lifetime of the system | IHE | internal heat exchanger |
| P | pressure (kPa) | LCOE | levelized cost of exergy |
| heat transfer rate (kW) | LHV | lower heating value | |
| r | relative cost difference | MW | molecular weight |
| s | specific entropy (kJ·kg−1·K−1) | ORC | organic Rankine cycle |
| T | temperature (K) | PR | pressure ratio |
| U | heat transfer coefficient (W·m−2·K−1) | pu | pump |
| power (kW) | SHE | solution heat exchanger | |
| exergy destruction ratio (%) | SP | solution pump | |
| Z | investment cost (USD) | SRC | steam Rankine cycle |
| investment cost rate (USD/h) | ST | steam turbine | |
| STIP | steam turbine inlet pressure | ||
| Subscript and abbreviations | VC | vapor condenser | |
| 0 | dead state | VG | vapor generator |
| 1,2,… | state points | VT | vapor turbine |
| abs | absorber | ||
| AC | air compressor | Greek Symbols | |
| AP | air preheater | difference | |
| ARC | absorption refrigeration cycle | η | efficiency |
| CC | combustion chamber | ε | heat exchanger effectiveness |
| CETD | cold end temperature difference | ϕr | maintenance factor |
| con | condenser | chemical exergy coefficient | |
Appendix A
| Parameter | Value | Unit |
|---|---|---|
| Reference temperature (T0) | 298.15 | K |
| Reference pressure (P0) | 101.3 | kPa |
| EFGT [12,51] | ||
| ) | 86 | % |
| ) | 10 | - |
| ) | 86 | % |
| Gas turbine inlet temperature (T3) | 1500 | K |
| Cold end temperature difference (CETD) | 245 | K |
| Pressure drop of the cold side in the AP | 5 | % |
| Pressure drop of the hot side in the AP | 3 | % |
| Pressure drop of the flue gas in the CC | 1 | % |
| Pressure drop of the flue gas in the HRSG | 5 | % |
| Pressure drop of the flue gas in the VG | 5 | % |
| ) | 8000 | kW |
| SRC [52,53] | ||
| Turbine inlet pressure (P13) | 15,000 | kPa |
| Pinch point temperature difference of HRSG (ΔTPP,HRSG) | 30 | K |
| Condenser temperature (T15) | 363.15 | K |
| Steam quality at outlet of the ST | 0.9 | - |
| ) | 85 | % |
| ) | 80 | % |
| ARC [32] | ||
| Generator temperature (T16) | 358.15 | K |
| Absorber temperature (T19) | 308.15 | K |
| Condenser temperature (T23) | 308.15 | K |
| Evaporator temperature (T25) | 278.15 | K |
| Effectiveness of solution heat exchanger | 70 | % |
| Cooling water inlet/outlet temperature in condenser (T26/T27) | 298.15/303.15 | K |
| Cooling water inlet/outlet temperature in evaporator (T28/T29) | 285.15/280.15 | K |
| Cooling water inlet/outlet temperature in absorber (T30/T31) | 298.15/303.15 | K |
| ORC [45] | ||
| Turbine inlet pressure (P33) | 1200 | kPa |
| Condenser temperature (T36) | 308.15 | K |
| ) | 90 | % |
| ) | 80 | % |
| ) | 80 | % |
| Cooling water inlet/outlet temperature in condenser (T38/T39) | 298.15/303.15 | K |
| State | Fluid | T (K) | P (kPa) | (kg/s) | h (kJ/kg) | s (kJ·kg−1·K−1) | (kW) | (USD/h) | c (USD/GJ) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Air | 298.15 | 101.3 | 27.67 | 0 | 6.888 | 123.22 | 0 | 0 |
| 2 | Air | 605.05 | 1013.0 | 27.67 | 323.05 | 6.966 | 8421.49 | 325.11 | 10.72 |
| 3 | Air | 1500 | 962.35 | 27.67 | 1352.89 | 8.018 | 28,232.98 | 778.75 | 7.66 |
| 4 | Air | 978.07 | 116.88 | 27.67 | 740.68 | 8.125 | 10,415.24 | 287.28 | 7.66 |
| 5 | Syngas | 1073.15 | 101.3 | 5.12 | −2710.35 | 10.10 | 28,904.59 | 240.45 | 2.31 |
| 6 | Air | 298.15 | 101.3 | 3.17 | 0 | 6.888 | 14.10 | 0 | 0 |
| 7 | Biomass | 298.15 | 101.3 | 1.95 | −7104.72 | - | 34,044.75 | 210.78 | 1.72 |
| 8 | Comb. gas | 1557.97 | 115.72 | 32.78 | 201.88 | 8.840 | 31,417.46 | 594.83 | 5.26 |
| 9 | Comb. gas | 850.05 | 112.24 | 32.78 | −667.18 | 8.108 | 10,084.42 | 190.93 | 5.26 |
| 10 | Comb. gas | 463.28 | 106.63 | 32.78 | −1110.75 | 7.429 | 2178.85 | 41.25 | 5.26 |
| 11 | Comb. gas | 378.15 | 101.3 | 32.78 | −1203.13 | 7.224 | 1158.43 | 21.93 | 5.26 |
| 12 | Water | 364.99 | 15,000 | 4.92 | 396.31 | 1.203 | 206.91 | 13.35 | 17.93 |
| 13 | Water | 787.84 | 15,000 | 4.92 | 3352.79 | 6.402 | 7125.33 | 202.91 | 7.91 |
| 14 | Water | 363.15 | 70.18 | 4.92 | 2431.28 | 6.850 | 1936.13 | 55.14 | 7.91 |
| 15 | Water | 363.15 | 70.18 | 4.92 | 377.04 | 1.193 | 127.63 | 3.63 | 7.91 |
| 16 | LiBr/H2O | 358.15 | 5.63 | 24.93 | 217.14 | 0.463 | 2087.64 | 73.44 | 9.77 |
| 17 | LiBr/H2O | 323.15 | 5.63 | 24.93 | 152.58 | 0.273 | 1888.97 | 66.45 | 9.77 |
| 18 | LiBr/H2O | 323.15 | 0.87 | 24.93 | 152.58 | 0.273 | 1888.97 | 66.45 | 9.77 |
| 19 | LiBr/H2O | 308.15 | 0.87 | 28.21 | 85.37 | 0.211 | 758.85 | 24.65 | 9.02 |
| 20 | LiBr/H2O | 308.15 | 5.63 | 28.21 | 85.37 | 0.211 | 758.85 | 24.66 | 9.03 |
| 21 | LiBr/H2O | 336.17 | 5.63 | 28.21 | 142.44 | 0.389 | 878.18 | 32.09 | 10.15 |
| 22 | Water | 358.15 | 5.63 | 3.27 | 2659.54 | 8.637 | 290.96 | 12.02 | 11.48 |
| 23 | Water | 308.15 | 5.63 | 3.27 | 146.63 | 0.505 | 1.93 | 0.08 | 11.48 |
| 24 | Water | 278.15 | 0.87 | 3.27 | 146.63 | 0.528 | −20.26 | −0.84 | 11.48 |
| 25 | Water | 278.15 | 0.87 | 3.27 | 2510.06 | 9.025 | −576.68 | −23.82 | 11.48 |
| 26 | Water | 298.15 | 101.3 | 393.63 | 104.92 | 0.367 | 0 | 0 | 0 |
| 27 | Water | 303.15 | 101.3 | 393.63 | 125.82 | 0.437 | 68.23 | 12.30 | 50.09 |
| 28 | Water | 285.15 | 101.3 | 368.84 | 50.51 | 0.181 | 450.89 | 0 | 0 |
| 29 | Water | 280.15 | 101.3 | 368.84 | 29.53 | 0.106 | 875.49 | 25.94 | 8.23 |
| 30 | Water | 298.15 | 101.3 | 459.98 | 104.92 | 0.367 | 0 | 0 | 0 |
| 31 | Water | 303.15 | 101.3 | 459.98 | 125.82 | 0.437 | 79.72 | 20.51 | 71.49 |
| 32 | R601 | 337.80 | 1200 | 6.86 | 70.48 | 0.212 | 52.65 | 6.84 | 36.07 |
| 33 | R601 | 407.57 | 1200 | 6.86 | 512.19 | 1.340 | 775.77 | 43.74 | 15.66 |
| 34 | R601 | 351.24 | 97.70 | 6.86 | 435.19 | 1.396 | 134.14 | 7.56 | 15.66 |
| 35 | R601 | 312.98 | 97.70 | 6.86 | 364.45 | 1.183 | 84.69 | 4.77 | 15.66 |
| 36 | R601 | 308.15 | 97.70 | 6.86 | −2.52 | −0.008 | 2.60 | 0.15 | 15.66 |
| 37 | R601 | 308.73 | 1200 | 6.86 | −0.26 | −0.007 | 15.06 | 3.11 | 57.37 |
| 38 | Water | 298.15 | 101.3 | 120.37 | 104.92 | 0.367 | 0 | 0 | 0 |
| 39 | Water | 303.15 | 101.3 | 120.37 | 125.82 | 0.437 | 20.86 | 5.22 | 69.56 |
| Component | (kW) | (kW) | (kW) | (%) | (USD/h) | (USD/h) | fk | rk |
|---|---|---|---|---|---|---|---|---|
| Air compressor | 8937.07 | 8298.28 | 638.80 | 92.85 | 48.27 | 19.79 | 70.93 | 0.265 |
| Air preheater | 21,333.04 | 19,811.49 | 1521.55 | 92.87 | 49.74 | 28.81 | 63.32 | 0.209 |
| Gas turbine | 17,817.75 | 16,937.07 | 880.67 | 95.06 | 33.18 | 24.29 | 57.73 | 0.123 |
| Combustion chamber | 39,319.83 | 31,417.46 | 7902.37 | 79.90 | 67.10 | 106.06 | 38.75 | 0.411 |
| Biomass gasifier | 34,058.85 | 28,904.59 | 5154.26 | 84.87 | 29.67 | 31.90 | 48.19 | 0.344 |
| HRSG | 7905.57 | 6918.42 | 987.15 | 87.51 | 39.88 | 18.69 | 68.09 | 0.447 |
| Steam turbine | 5189.20 | 4532.51 | 656.69 | 87.35 | 106.70 | 18.70 | 85.09 | 0.972 |
| Pump 1 | 94.79 | 79.29 | 15.51 | 83.64 | 4.40 | 0.87 | 83.47 | 1.183 |
| Generator | 1808.51 | 1500.43 | 308.08 | 82.97 | 1.86 | 8.77 | 17.54 | 0.249 |
| SHE | 198.67 | 119.33 | 79.34 | 60.06 | 0.44 | 2.79 | 13.70 | 0.770 |
| Absorber | 553.45 | 79.72 | 473.72 | 14.41 | 2.54 | 15.39 | 14.17 | 6.923 |
| Condenser | 289.03 | 68.23 | 220.80 | 23.61 | 0.36 | 9.12 | 3.83 | 3.365 |
| Evaporator | 556.42 | 424.60 | 131.82 | 76.31 | 2.96 | 5.45 | 35.21 | 0.479 |
| Vapor generator | 1020.42 | 723.11 | 297.30 | 70.86 | 17.58 | 5.63 | 75.75 | 1.695 |
| Vapor turbine | 641.63 | 527.95 | 113.68 | 82.28 | 23.69 | 6.41 | 78.71 | 1.011 |
| IHE | 49.45 | 37.59 | 11.86 | 76.01 | 0.94 | 0.67 | 58.36 | 0.758 |
| Vapor condenser | 82.09 | 20.86 | 61.23 | 25.41 | 0.60 | 3.45 | 14.73 | 3.442 |
| Pump 2 | 15.45 | 12.47 | 2.99 | 80.68 | 1.21 | 0.34 | 78.18 | 1.097 |
Appendix B
| Item | Value | Unit |
|---|---|---|
| Tube inner diameter, di | 20 | mm |
| Tube outer diameter, do | 25 | mm |
| Tube pitch, STu | 60 | mm |
| Fin height, HF | 12.5 | mm |
| Fin thichness, δF | 1 | mm |
| Fin pitch, YF | 4 | mm |
| Fouling factor [54,55] | ||
| Exhaust gas, rexh | m2·K−1·W | |
| Refrigerant (liquid), rliq | m2·K−1·W | |
| Refrigerant (vapor), rvap | m2·K−1·W | |
| Refrigerant (two-phase), rtp | m2·K−1·W | |
| Tube row alignment | Staggered type | |
| Tube and fin material | Stainless steel 316L | |
| Component | Heat Transfer Coefficient (W·m−2·K−1) |
|---|---|
| Generator | 1500 |
| Condenser | 2500 |
| Evaporator | 1500 |
| Absorber | 700 |
| SHE | 1000 |
References
- Yaghoubi, E.; Xiong, Q.; Doranehgard, M.H.; Yeganeh, M.M.; Shahriari, G.; Bidabadi, M. The effect of different operational parameters on hydrogen rich syngas production from biomass gasification in a dual fluidized bed gasifier. Chem. Eng. Process. Process Intensif. 2018, 126, 210–221. [Google Scholar] [CrossRef]
- Medeiros, D.L.; Sales, E.A.; Kiperstok, A. Energy production from microalgae biomass: Carbon footprint and energy balance. J. Clean. Prod. 2015, 96, 493–500. [Google Scholar] [CrossRef]
- Saidur, R.; Abdelaziz, E.A.; Demirbas, A.; Hossain, M.S.; Mekhilef, S. A review on biomass as a fuel for boilers. Renew. Sustain. Energy Rev. 2011, 15, 2262–2289. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; Bruno, J.C.; Coronas, A. Review and analysis of biomass gasification models. Renew. Sustain. Energy Rev. 2010, 14, 2841–2851. [Google Scholar] [CrossRef]
- Siddiqui, O.; Dincer, I.; Yilbas, B.S. Development of a novel renewable energy system integrated with biomass gasification combined cycle for cleaner production purposes. J. Clean. Prod. 2019, 241, 118345. [Google Scholar] [CrossRef]
- Zang, G.; Tejasvi, S.; Ratner, A.; Lora, E.S. A comparative study of biomass integrated gasification combined cycle power systems: Performance analysis. Bioresour. Technol. 2018, 255, 246–256. [Google Scholar] [CrossRef] [PubMed]
- Soltani, S.; Mahmoudi, S.M.S.; Yari, M.; Rosen, M.A. Thermodynamic analyses of a biomass integrated fired combined cycle. Appl. Therm. Eng. 2013, 59, 60–68. [Google Scholar] [CrossRef]
- Datta, A.; Ganguly, R.; Sarkar, L. Energy and exergy analyses of an externally fired gas turbine (EFGT) cycle integrated with biomass gasifier for distributed power generation. Energy 2010, 35, 341–350. [Google Scholar] [CrossRef]
- Al-Attab, K.A.; Zainal, Z.A. Externally fired gas turbine technology: A review. Appl. Energy 2015, 138, 474–487. [Google Scholar] [CrossRef]
- Soltani, S.; Mahmoudi, S.M.S.; Yari, M.; Rosen, M.A. Thermodynamic analyses of an externally fired gas turbine combined cycle integrated with a biomass gasification plant. Energy Convers. Manag. 2013, 70, 107–115. [Google Scholar] [CrossRef]
- Soltani, S.; Yari, M.; Mahmoudi, S.M.S.; Morosuk, T.; Rosen, M.A. Advanced exergy analysis applied to an externally-fired combined-cycle power plant integrated with a biomass gasification unit. Energy 2013, 59, 775–780. [Google Scholar] [CrossRef]
- Soltani, S.; Mahmoudi, S.M.S.; Yari, M.; Morosuk, T.; Rosen, M.A.; Zare, V. A comparative exergoeconomic analysis of two biomass and co-firing combined power plants. Energy Convers. Manag. 2013, 76, 83–91. [Google Scholar] [CrossRef]
- Mondal, P.; Ghosh, S. Exergo-economic analysis of a 1-MW biomass-based combined cycle plant with externally fired gas turbine cycle and supercritical organic Rankine cycle. Clean Technol. Environ. Policy 2017, 19, 1475–1486. [Google Scholar] [CrossRef]
- Vera, D.; Jurado, F.; Carpio, J.; Kamel, S. Biomass gasification coupled to an EFGT-ORC combined system to maximize the electrical energy generation: A case applied to the olive oil industry. Energy 2018, 144, 41–53. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, F.; Shen, H.; Cai, J.; Liu, Y.; Zhang, J.; Wang, X.; Heydarian, D. Design and analysis of an innovative biomass-powered cogeneration system based on organic flash and supercritical carbon dioxide cycles. Alex. Eng. J. 2023, 80, 623–647. [Google Scholar] [CrossRef]
- Moradi, R.; Cioccolanti, L.; Del Zotto, L.; Renzi, M. Comparative sensitivity analysis of micro-scale gas turbine and supercritical CO2 systems with bottoming organic Rankine cycles fed by the biomass gasification for decentralized trigeneration. Energy 2023, 266, 126491. [Google Scholar] [CrossRef]
- Sharafi Laleh, S.; Fatemi Alavi, S.H.; Soltani, S.; Mahmoudi, S.M.S.; Rosen, M.A. A novel supercritical carbon dioxide combined cycle fueled by biomass: Thermodynamic assessment. Renew. Energy 2024, 222, 119874. [Google Scholar] [CrossRef]
- Kautz, M.; Hansen, U. The externally-fired gas-turbine (EFGT-Cycle) for decentralized use of biomass. Appl. Energy 2007, 84, 795–805. [Google Scholar] [CrossRef]
- Roy, D.; Samanta, S.; Ghosh, S. Techno-economic and environmental analyses of a biomass based system employing solid oxide fuel cell, externally fired gas turbine and organic Rankine cycle. J. Clean. Prod. 2019, 225, 36–57. [Google Scholar] [CrossRef]
- El-Sattar, H.A.; Kamel, S.; Vera, D.; Jurado, F. Tri-generation biomass system based on externally fired gas turbine, organic rankine cycle and absorption chiller. J. Clean. Prod. 2020, 260, 121068. [Google Scholar] [CrossRef]
- Roy, D.; Samanta, S.; Ghosh, S. Performance optimization through response surface methodology of an integrated biomass gasification based combined heat and power plant employing solid oxide fuel cell and externally fired gas turbine. Energy Convers. Manag. 2020, 222, 113182. [Google Scholar] [CrossRef]
- Zhang, G.; Li, H.; Xiao, C.; Sobhani, B. Multi-aspect analysis and multi-objective optimization of a novel biomass-driven heat and power cogeneration system; utilization of grey wolf optimizer. J. Clean. Prod. 2022, 355, 131442. [Google Scholar] [CrossRef]
- Xu, Y.-P.; Lin, Z.-H.; Ma, T.-X.; She, C.; Xing, S.-M.; Qi, L.-Y.; Farkoush, S.G.; Pan, J. Optimization of a biomass-driven Rankine cycle integrated with multi-effect desalination, and solid oxide electrolyzer for power, hydrogen, and freshwater production. Desalination 2022, 525, 115486. [Google Scholar] [CrossRef]
- Du, J.; Zou, Y.; Dahlak, A. Process development and multi-criteria optimization of a biomass gasification unit combined with a novel CCHP model using helium gas turbine, kalina cycles, and dual-loop organic flash cycle. Energy 2024, 291, 130319. [Google Scholar] [CrossRef]
- Yilmaz, F.; Ozturk, M.; Selbas, R. Design and performance evaluation of a biomass-based multigeneration plant with supercritical CO2 brayton cycle for sustainable communities. Int. J. Hydrogen Energy 2024, 59, 1540–1554. [Google Scholar] [CrossRef]
- Zhang, T.; Sobhani, B. Multi-criteria assessment and optimization of a biomass-based cascade heat integration toward a novel multigeneration process: Application of a MOPSO method. Appl. Therm. Eng. 2024, 240, 122254. [Google Scholar] [CrossRef]
- Shu, G.; Liang, Y.; Wei, H.; Tian, H.; Zhao, J.; Liu, L. A review of waste heat recovery on two-stroke IC engine aboard ships. Renew. Sustain. Energy Rev. 2013, 19, 385–401. [Google Scholar] [CrossRef]
- Liang, Y.; Shu, G.; Tian, H.; Liang, X.; Wei, H.; Liu, L. Analysis of an electricity–cooling cogeneration system based on RC–ARS combined cycle aboard ship. Energy Convers. Manag. 2013, 76, 1053–1060. [Google Scholar] [CrossRef]
- Liang, Y.; Shu, G.; Tian, H.; Wei, H.; Liang, X.; Liu, L.; Wang, X. Theoretical analysis of a novel electricity–cooling cogeneration system (ECCS) based on cascade use of waste heat of marine engine. Energy Convers. Manag. 2014, 85, 888–894. [Google Scholar] [CrossRef]
- Ahmadi, P.; Rosen, M.A.; Dincer, I. Greenhouse gas emission and exergo-environmental analyses of a trigeneration energy system. Int. J. Greenh. Gas Control 2011, 5, 1540–1549. [Google Scholar] [CrossRef]
- Sahoo, U.; Kumar, R.; Singh, S.K.; Tripathi, A.K. Energy, exergy, economic analysis and optimization of polygeneration hybrid solar-biomass system. Appl. Therm. Eng. 2018, 145, 685–692. [Google Scholar] [CrossRef]
- Nondy, J.; Gogoi, T.K. Comparative performance analysis of four different combined power and cooling systems integrated with a topping gas turbine plant. Energy Convers. Manag. 2020, 223, 113242. [Google Scholar] [CrossRef]
- Anvari, S.; Khoshbakhti Saray, R.; Bahlouli, K. Conventional and advanced exergetic and exergoeconomic analyses applied to a tri-generation cycle for heat, cold and power production. Energy 2015, 91, 925–939. [Google Scholar] [CrossRef]
- Zoghi, M.; Habibi, H.; Yousefi Choubari, A.; Ehyaei, M.A. Exergoeconomic and environmental analyses of a novel multi-generation system including five subsystems for efficient waste heat recovery of a regenerative gas turbine cycle with hybridization of solar power tower and biomass gasifier. Energy Convers. Manag. 2021, 228, 113702. [Google Scholar] [CrossRef]
- Mussati, S.F.; Gernaey, K.V.; Morosuk, T.; Mussati, M.C. NLP modeling for the optimization of LiBr-H2O absorption refrigeration systems with exergy loss rate, heat transfer area, and cost as single objective functions. Energy Convers. Manag. 2016, 127, 526–544. [Google Scholar] [CrossRef]
- Balafkandeh, S.; Zare, V.; Gholamian, E. Multi-objective optimization of a tri-generation system based on biomass gasification/digestion combined with S-CO2 cycle and absorption chiller. Energy Convers. Manag. 2019, 200, 112057. [Google Scholar] [CrossRef]
- Tezer, Ö.; Karabağ, N.; Öngen, A.; Çolpan, C.Ö.; Ayol, A. Biomass gasification for sustainable energy production: A review. Int. J. Hydrogen Energy 2022, 47, 15419–15433. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.C. Modeling of biomass gasification: A review. Renew. Sustain. Energy Rev. 2014, 39, 806–815. [Google Scholar] [CrossRef]
- Safarian, S.; Unnþórsson, R.; Richter, C. A review of biomass gasification modelling. Renew. Sustain. Energy Rev. 2019, 110, 378–391. [Google Scholar] [CrossRef]
- Silva, I.P.; Lima, R.M.A.; Silva, G.F.; Ruzene, D.S.; Silva, D.P. Thermodynamic equilibrium model based on stoichiometric method for biomass gasification: A review of model modifications. Renew. Sustain. Energy Rev. 2019, 114, 109305. [Google Scholar] [CrossRef]
- Zainal, Z.A.; Ali, R.; Lean, C.H.; Seetharamu, K.N. Prediction of performance of a downdraft gasifier using equilibrium modeling for different biomass materials. Energy Convers. Manag. 2001, 42, 1499–1515. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Misra, R.D.; Sahoo, P.K.; Sahoo, S.; Gupta, A. Thermoeconomic optimization of a single effect water/LiBr vapour absorption refrigeration system. Int. J. Refrig. 2003, 26, 158–169. [Google Scholar] [CrossRef]
- Nazari, N.; Heidarnejad, P.; Porkhial, S. Multi-objective optimization of a combined steam-organic Rankine cycle based on exergy and exergo-economic analysis for waste heat recovery application. Energy Convers. Manag. 2016, 127, 366–379. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Bei, C.; Song, S.; Wang, E. Parametric optimization and performance analysis of ORC (organic Rankine cycle) for diesel engine waste heat recovery with a fin-and-tube evaporator. Energy 2015, 91, 128–141. [Google Scholar] [CrossRef]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Moharamian, A.; Soltani, S.; Rosen, M.A.; Mahmoudi, S.M.S.; Morosuk, T. A comparative thermoeconomic evaluation of three biomass and biomass-natural gas fired combined cycles using organic Rankine cycles. J. Clean. Prod. 2017, 161, 524–544. [Google Scholar] [CrossRef]
- Cao, Y.; Mihardjo, L.W.W.; Dahari, M.; Tlili, I. Waste heat from a biomass fueled gas turbine for power generation via an ORC or compressor inlet cooling via an absorption refrigeration cycle: A thermoeconomic comparison. Appl. Therm. Eng. 2021, 182, 116117. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Barzegaravval, H.; Wahid, M.A.; Ganjehkaviri, A.; Sies, M.M. Thermodynamic assessment of integrated biogas-based micro-power generation system. Energy Convers. Manag. 2016, 128, 104–119. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A. Energy and sizing analyses of parabolic trough solar collector integrated with steam and binary vapor cycles. Energy 2013, 58, 561–570. [Google Scholar] [CrossRef]
- Bet Sarkis, R.; Zare, V. Proposal and analysis of two novel integrated configurations for hybrid solar-biomass power generation systems: Thermodynamic and economic evaluation. Energy Convers. Manag. 2018, 160, 411–425. [Google Scholar] [CrossRef]
- Kazemi, N.; Samadi, F. Thermodynamic, economic and thermo-economic optimization of a new proposed organic Rankine cycle for energy production from geothermal resources. Energy Convers. Manag. 2016, 121, 391–401. [Google Scholar] [CrossRef]
- Tian, H.; Chang, L.; Gao, Y.; Shu, G.; Zhao, M.; Yan, N. Thermo-economic analysis of zeotropic mixtures based on siloxanes for engine waste heat recovery using a dual-loop organic Rankine cycle (DORC). Energy Convers. Manag. 2017, 136, 11–26. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Song, S.; Bei, C.; Wang, H.; Wang, E. Thermoeconomic multi-objective optimization of an organic Rankine cycle for exhaust waste heat recovery of a diesel engine. Energy 2015, 93, 2208–2228. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wang, E.H.; Fan, B.Y. Heat transfer analysis of a finned-tube evaporator for engine exhaust heat recovery. Energy Convers. Manag. 2013, 65, 438–447. [Google Scholar] [CrossRef]
- Gnielinski, V. New equations for heat mass transfer in turbulent pipe and channel flows. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat Mass Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
- Mazzei, M.S.; Mussati, M.C.; Mussati, S.F. NLP model-based optimal design of LiBr–H2O absorption refrigeration systems. Int. J. Refrig. 2014, 38, 58–70. [Google Scholar] [CrossRef]



| Researcher | Year | Biomass Fuel | Configuration | Analysis | Result |
|---|---|---|---|---|---|
| Zhang et al. [15] | 2023 | municipal solid waste | EFGT, SCO2 cycle, OFC | energy, exergy, economic, environmental | energy efficiency of 75.8%, exergy efficiency of 41.21%, net profit of 10.7 M USD, levelized CO2 emission of 0.518 t/kWh |
| Moradi et al. [16] | 2023 | hazelnut shell | GT cycle, SCO2 cycle, ORC | energy | 25% higher electric power output of the SCO2 integrated system |
| Sharafi laleh et al. [17] | 2024 | wood | EFGT, SCO2 cycle | energy | energy efficiency of 41.8% |
| Roy et al. [19] | 2019 | wood, rice husk, paper | EFGT, SOFC, ORC | energy, exergy, economic, environmental | energy efficiency of 49.47%, exergy efficiency of 44.2% |
| El-Sattar et al. [20] | 2020 | bagasse | EFGT, ORC, ARC | energy | thermal efficiency of 43.9% |
| Roy et al. [21] | 2020 | sawdust | EFGT, SOFC, HRSG | exergy, economic | exergy efficiency of 46.58%, levelized cost of exergy of 0.0657 USD/kWh |
| Zhang et al. [22] | 2022 | paddy husk, paper, wood, municipal solid waste | EFGT, SCO2 cycle, Stirling engine, DWH | energy, exergy, exergoeconomic, environmental | exergy efficiency of 46.48%, total cost rate of 401.4 USD/h |
| Xu et al. [23] | 2022 | paddy husk, paper, wood, municipal solid waste | SRC, MED unit, SOEC | energy, exergy, exergoeconomic | exergy efficiency of 17.64%, unit exergy cost of 26 USD/GJ |
| Du et al. [24] | 2024 | wood | helium GT cycle, Kalina cycle, DWH, refrigeration unit, dual-loop OFC | energy, exergy, economic | exergy efficiency of 35.57%, NPV of 15.07 M USD, payback period of 3.97 years |
| Yilmaz et al. [25] | 2024 | pine sawdust | GT cycle, SCO2 cycle, MSFD unit, PEME, DWH | energy, exergy, environmental | energy efficiency of 44.50%, exergy efficiency of 30.01% |
| Zhang et al. [26] | 2024 | carbohydrate | GT cycle, SCO2 cycle, dual-effect ARC, DWH, ORC, RO desalination | energy, exergy, economic | exergy efficiency of 38.54%, SUCP of 30.8 USD/GJ, NPV of 75.17 M USD |
| Biomass | Mass Percentage on Dry Basis (%) | HHV (kJ/kmol) | |||||
|---|---|---|---|---|---|---|---|
| C | H | N | S | O | Ash | ||
| wood | 50 | 6 | 0 | 0 | 44 | 0 | 449,568 |
| Component | Mass and Energy Balance Equations |
|---|---|
| Air compressor | |
| Air preheater | |
| Gas turbine | |
| HRSG | |
| Steam turbine | |
| Pump 1 | |
| Generator | |
| SHE | |
| Absorber | |
| Solution pump | |
| Condenser | |
| Evaporator | |
| Vapor generator | |
| Vapor turbine | |
| IHE | |
| Vapor condenser | |
| Pump 2 | |
| Component | ) | ) | ) |
|---|---|---|---|
| Air compressor | |||
| Air preheater | |||
| Gas turbine | |||
| Combustion chamber | |||
| Biomass gasifier | |||
| HRSG | |||
| Steam turbine | |||
| Pump 1 | |||
| Generator | |||
| SHE | |||
| Absorber | |||
| Solution pump | |||
| Condenser | |||
| Evaporator | |||
| Vapor generator | |||
| Vapor turbine | |||
| IHE | |||
| Vapor condenser | |||
| Pump 2 |
| Component | Cost Balance Equation | Auxiliary Equation |
|---|---|---|
| Air compressor | ||
| Air preheater | ||
| Gas turbine | ||
| Combustion chamber | ||
| Biomass gasifier | ||
| HRSG | ||
| Steam turbine | ||
| Pump 1 | ||
| Generator | ||
| SHE | ||
| Absorber | ||
| Solution pump | ||
| Condenser | ||
| Evaporator | ||
| Vapor generator | ||
| Vapor turbine | ||
| IHE | ||
| Vapor condenser | ||
| Pump 2 |
| Component | Cost Balance Equation |
|---|---|
| Air compressor | |
| Air preheater | |
| Gas turbine | |
| Combustion chamber | |
| Biomass gasifier | |
| HRSG | |
| Steam turbine | |
| Pump 1 | |
| Generator | |
| SHE | |
| Absorber | |
| Condenser | |
| Evaporator | |
| Solution pump | |
| Vapor generator | |
| Vapor turbine | |
| IHE | |
| Vapor condenser | |
| Pump 2 |
| State | Substance | P (kPa) | T (K) | (kg/s) | |||
|---|---|---|---|---|---|---|---|
| Ref. [48] | Present Work | Ref. [48] | Present Work | Ref. [48] | Present Work | ||
| 1 | Air | 101.3 | 101.3 | 298.15 | 298.15 | 9.45 | 9.84 |
| 2 | Air | 911.7 | 911.7 | 589.9 | 583.84 | 9.45 | 9.84 |
| 3 | Air | 884.35 | 884.35 | 1400 | 1400 | 9.45 | 9.84 |
| 4 | Air | 103.83 | 103.88 | 877.6 | 886.18 | 9.45 | 9.84 |
| 5 | Syngas | 101.3 | 101.3 | 1073.15 | 1073.15 | 2.789 | 2.792 |
| 8 | Comb. gas | 102.82 | 102.84 | 1562 | 1578.6 | 12.24 | 12.63 |
| 9 | Comb. gas | 101.3 | 101.3 | 1000 | 1000 | 12.24 | 12.63 |
| Constituent | Roy et al. [19] | Cao et al. [49] | Present Work |
|---|---|---|---|
| H2 (%) | 21.63 | 21.66 | 21.50 |
| CO (%) | 20.25 | 20.25 | 20.21 |
| CH4 (%) | 0.98 | 1.011 | 0.95 |
| CO2 (%) | 12.48 | 12.36 | 12.50 |
| N2 (%) | 44.94 | 44.72 | 44.84 |
| Parameter | Teva (K) | Tcon (K) | Peva (kPa) | Pcon (kPa) | (kg/s) | ηth (%) |
|---|---|---|---|---|---|---|
| Ref. [50] | 373.15 | 303.15 | 5.963 | 0.828 | 16.331 | 13.84 |
| This work | 373.15 | 303.15 | 5.927 | 0.820 | 16.382 | 13.84 |
| Parameter | Ref. [32] | This Work |
|---|---|---|
| Heat capacity of generator (kW) | 4.5999 | 4.6000 |
| Heat capacity of condenser (kW) | 3.7432 | 3.7420 |
| Heat capacity of absorber (kW) | 4.368 | 4.368 |
| Evaporator pressure (kPa) | 1.0021 | 1.0021 |
| Condenser pressure (kPa) | 7.3844 | 7.3849 |
| Weak solution concentration (%) | 62.33 | 62.15 |
| Strong solution concentration (%) | 56.72 | 56.66 |
| Refrigerant mass flow rate (kg/s) | 0.0015 | 0.0015 |
| Weak solution mass flow rate (kg/s) | 0.0151 | 0.0154 |
| Strong solution mass flow rate (kg/s) | 0.0166 | 0.0169 |
| Coefficient of performance | 0.763 | 0.763 |
| Performance Parameters | Unit | Value |
|---|---|---|
| ) | kW | 4532.51 |
| ) | kW | 94.79 |
| ) | kW | 527.95 |
| ) | kW | 15.45 |
| ) | kW | 12,950.2 |
| ) | kW | 7738.4 |
| ) | % | 70.67 |
| ) | % | 39.13 |
| ) | USD/GJ | 8.60 |
| ) | USD/GJ | 15.60 |
| ) | USD/GJ | 31.50 |
| ) | USD/GJ | 8.23 |
| ) | USD/GJ | 11.67 |
| Parameter | Unit | Range |
|---|---|---|
| PRAC | - | |
| T3 | K | |
| CETD | K | |
| ΔTPP, HRSG | K | |
| P13 | kPa | |
| T15 | K | |
| P33 | kPa |
| Parameter | A | B | C |
|---|---|---|---|
| PRAC | 11.03 | 7.86 | 10.62 |
| T3 (K) | 1479.2 | 1374.1 | 1450.2 |
| CETD (K) | 217.7 | 279.5 | 256.2 |
| ΔTPP, HRSG (K) | 19.97 | 11.71 | 14.44 |
| P13 (kPa) | 16,509.9 | 10,257.5 | 16,642.3 |
| T15 (K) | 362.2 | 361.0 | 359.7 |
| P33 (kPa) | 1811.8 | 459.4 | 567.4 |
| (kW) | 12,821.4 | 13,582.6 | 13,660.5 |
| (kW) | 6863.4 | 9807.7 | 8771.8 |
| ηex (%) | 39.40 | 35.66 | 38.15 |
| LCOEsys (USD/GJ) | 11.74 | 10.59 | 11.01 |
| Parameter | Ref. [22] | This Work | Ref. [15] | This Work | Ref. [17] | This Work |
|---|---|---|---|---|---|---|
| PRAC | 10 | 10 | 7 | |||
| GTIT (K) | 1573.15 | 1300 | 1300 | |||
| Energy efficiency (%) | 67.26% | 71.72% | 75.8% | 68.93% | 41.18% | 64.62% |
| Exergy efficiency (%) | 41.08% | 41.31% | 41.21% | 36.58% | - | 37.97% |
| Cost of products (USD/GJ) | 17.17 | 19.32 | 10.2 | 11.74 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Xu, C.; Qian, Z.; Huang, W.; Wang, B. Exergoeconomic Analysis and Optimization of a Biomass Integrated Gasification Combined Cycle Based on Externally Fired Gas Turbine, Steam Rankine Cycle, Organic Rankine Cycle, and Absorption Refrigeration Cycle. Entropy 2024, 26, 511. https://doi.org/10.3390/e26060511
Ren J, Xu C, Qian Z, Huang W, Wang B. Exergoeconomic Analysis and Optimization of a Biomass Integrated Gasification Combined Cycle Based on Externally Fired Gas Turbine, Steam Rankine Cycle, Organic Rankine Cycle, and Absorption Refrigeration Cycle. Entropy. 2024; 26(6):511. https://doi.org/10.3390/e26060511
Chicago/Turabian StyleRen, Jie, Chen Xu, Zuoqin Qian, Weilong Huang, and Baolin Wang. 2024. "Exergoeconomic Analysis and Optimization of a Biomass Integrated Gasification Combined Cycle Based on Externally Fired Gas Turbine, Steam Rankine Cycle, Organic Rankine Cycle, and Absorption Refrigeration Cycle" Entropy 26, no. 6: 511. https://doi.org/10.3390/e26060511
APA StyleRen, J., Xu, C., Qian, Z., Huang, W., & Wang, B. (2024). Exergoeconomic Analysis and Optimization of a Biomass Integrated Gasification Combined Cycle Based on Externally Fired Gas Turbine, Steam Rankine Cycle, Organic Rankine Cycle, and Absorption Refrigeration Cycle. Entropy, 26(6), 511. https://doi.org/10.3390/e26060511








