Hamiltonian Computational Chemistry: Geometrical Structures in Chemical Dynamics and Kinetics
Abstract
1. Introduction
2. Geometrical Structures in Chemical Dynamics
2.1. Canonical Classical Mechanics
2.1.1. Manifolds and Maps
2.1.2. Equations of Motion
- is bilinear,
- antisymmetric,
- , and
- (Jacobi identity).
2.1.3. Integrable Hamiltonian Systems
2.1.4. Complexification of Classical Hamilton’s Equations
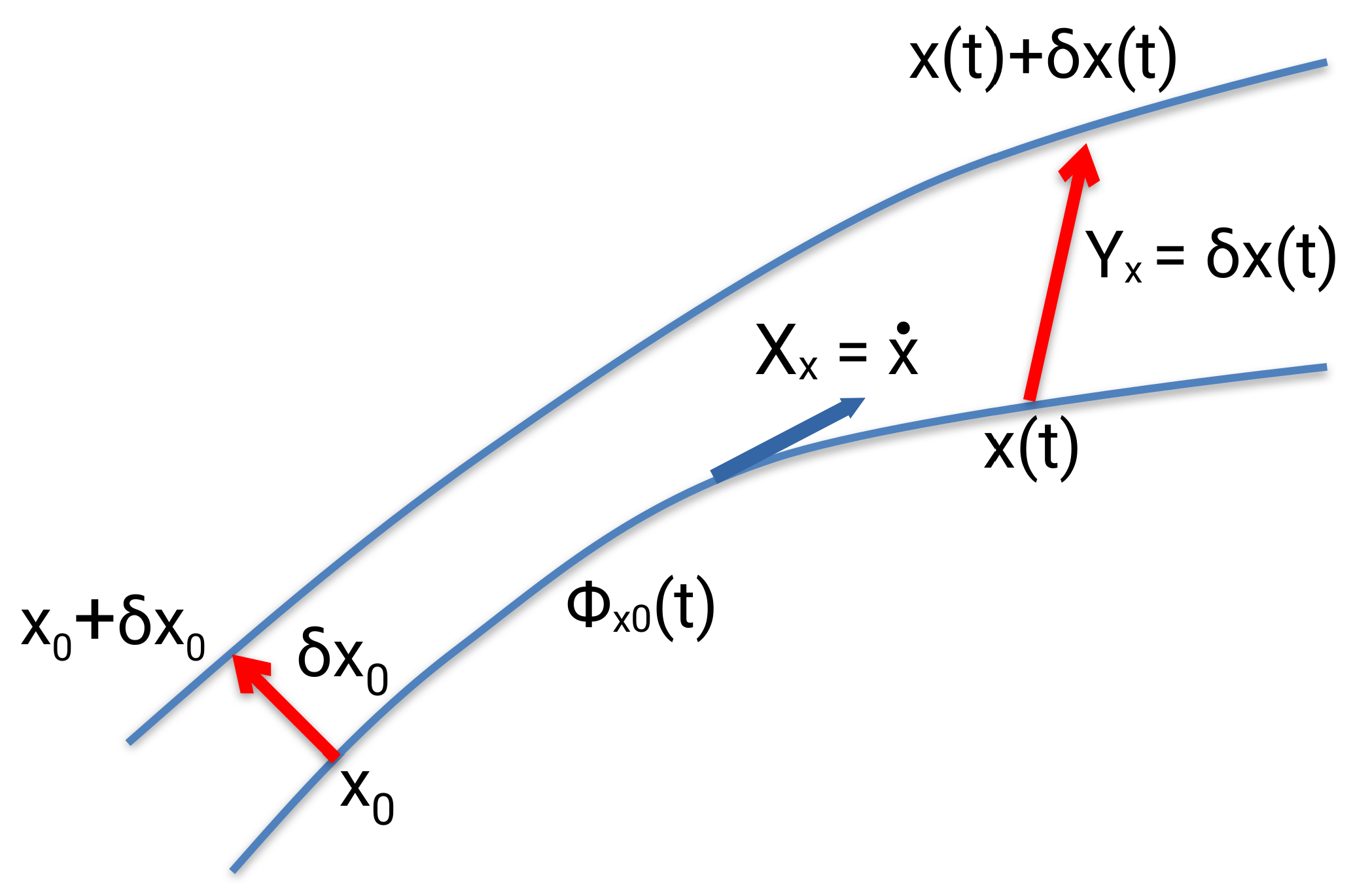
2.1.5. Jacobi Fields and Variational Equations
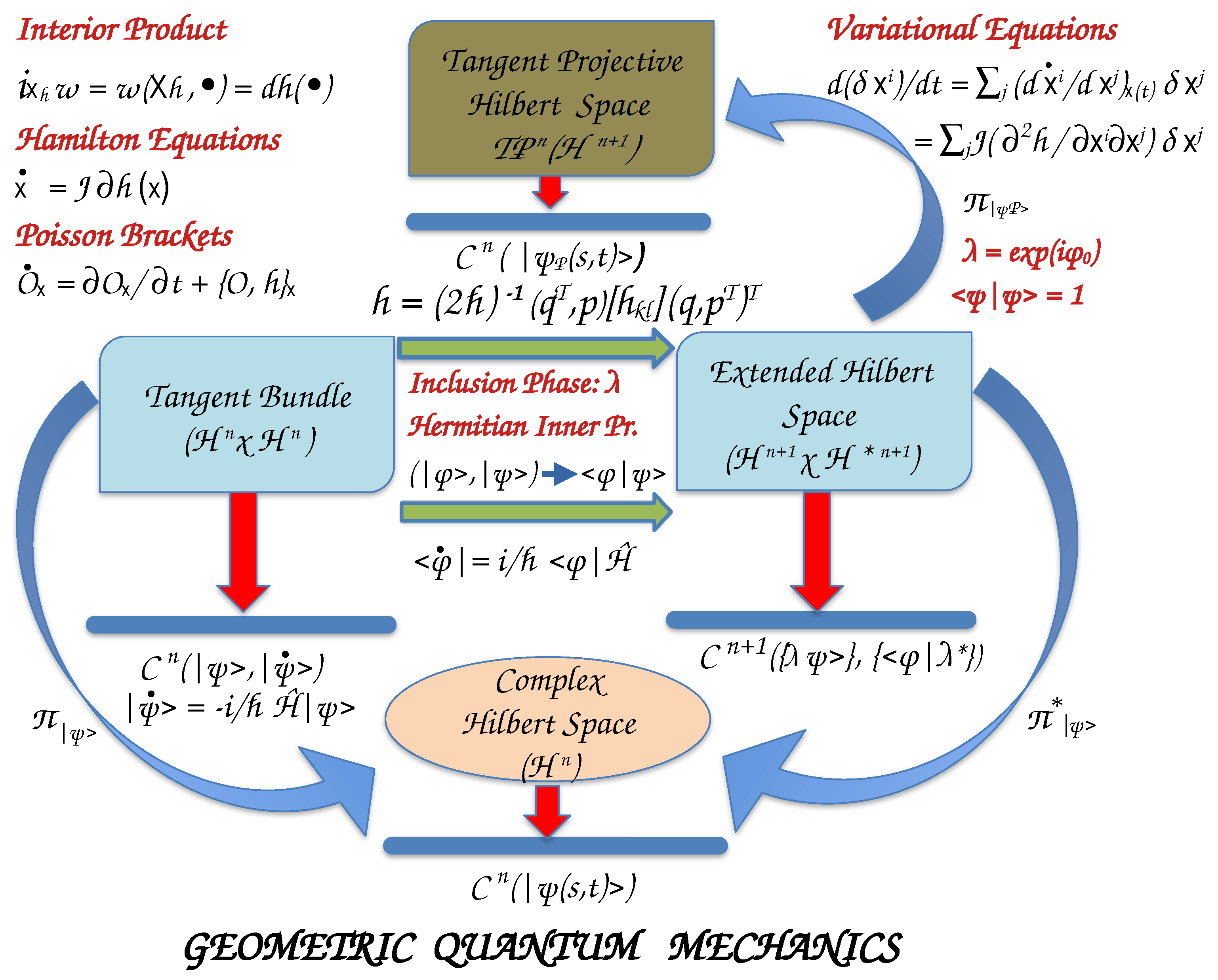
2.2. Geometrical Quantum Mechanics
2.2.1. Manifolds and Maps
2.2.2. Projective Hilbert Space
2.2.3. Realification of Hilbert Space and Kähler Manifolds
2.2.4. Equations of Motion
2.2.5. Quantum Systems as Totally Integrable Hamiltonian Systems
3. Hamiltonian Chemical Thermodynamics
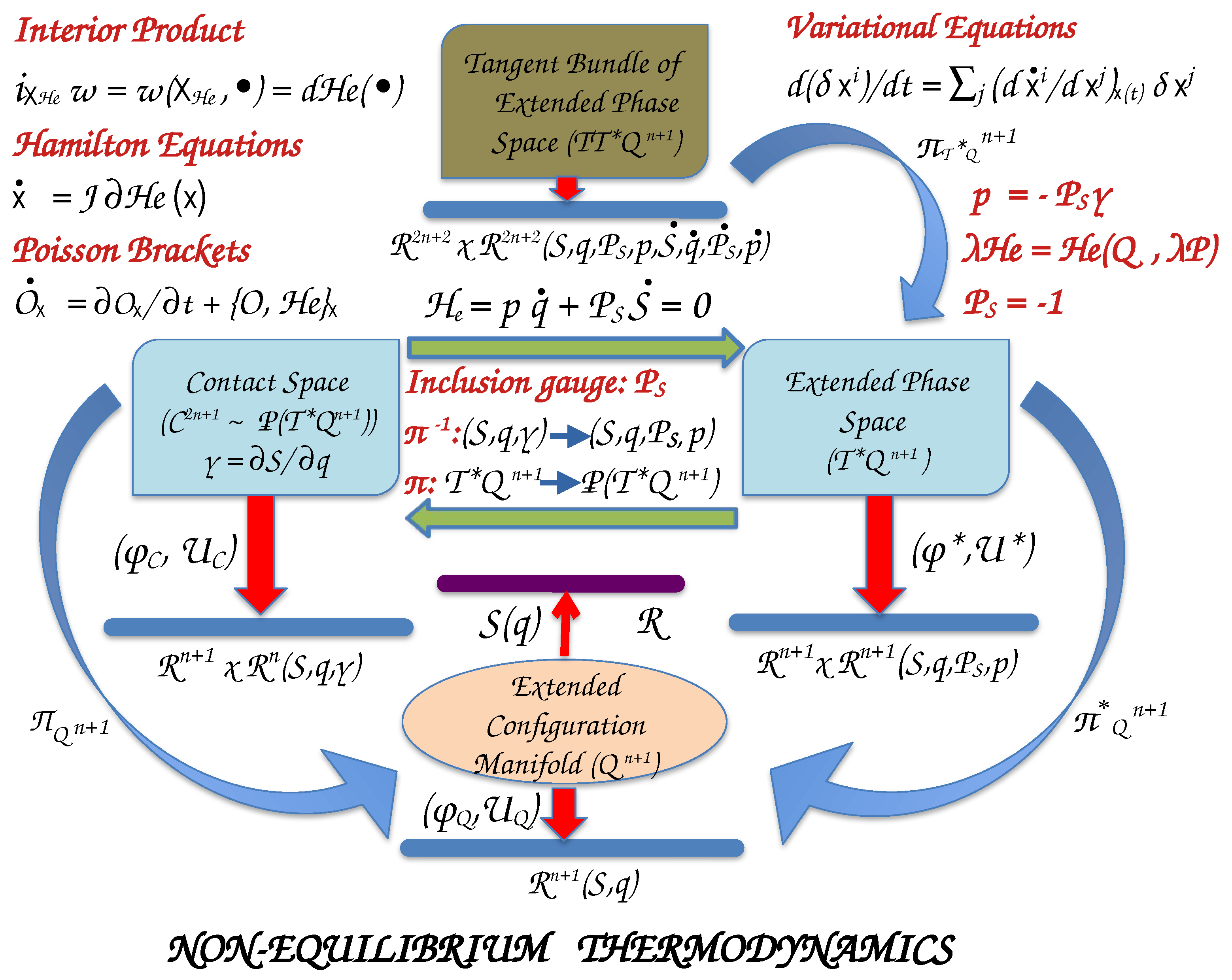
3.1. Manifolds and Maps
3.2. Equations of Motion
3.2.1. Contact Equations of Motion
3.2.2. Riemannian Metric on Lagrangian Submanifold
3.3. Embedding Systems in Homogeneous Media
3.4. Chemical Kinetics
3.4.1. Thermodynamics of Chemical Reactions
3.4.2. Thermodynamic Hamiltonian in Massieu-Gibbs Representation
4. Numerical Implementations
4.1. High-Order Finite-Difference and Pseudospectral Methods
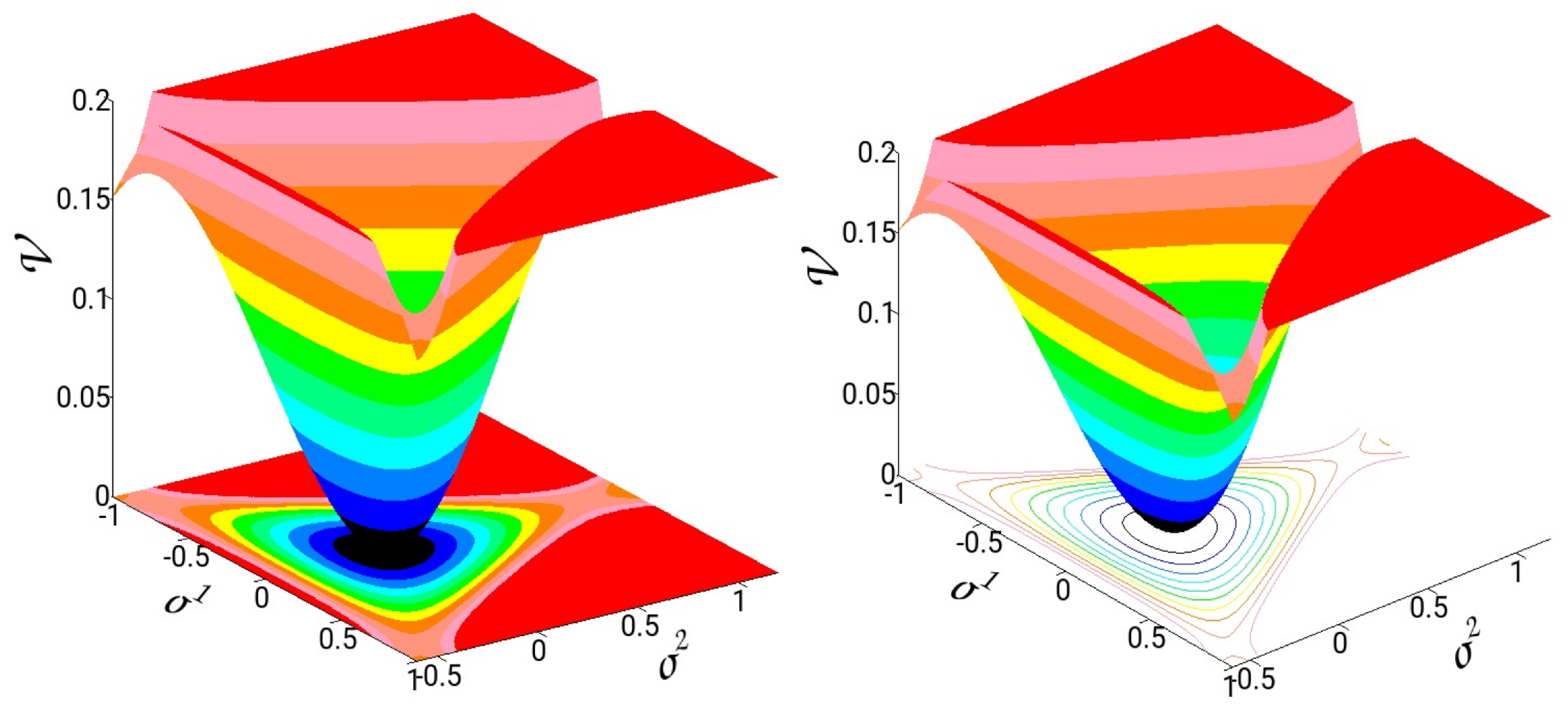
4.2. The Hénon–Heiles Model
4.2.1. A Classical Time-Dependent Hénon–Heiles System
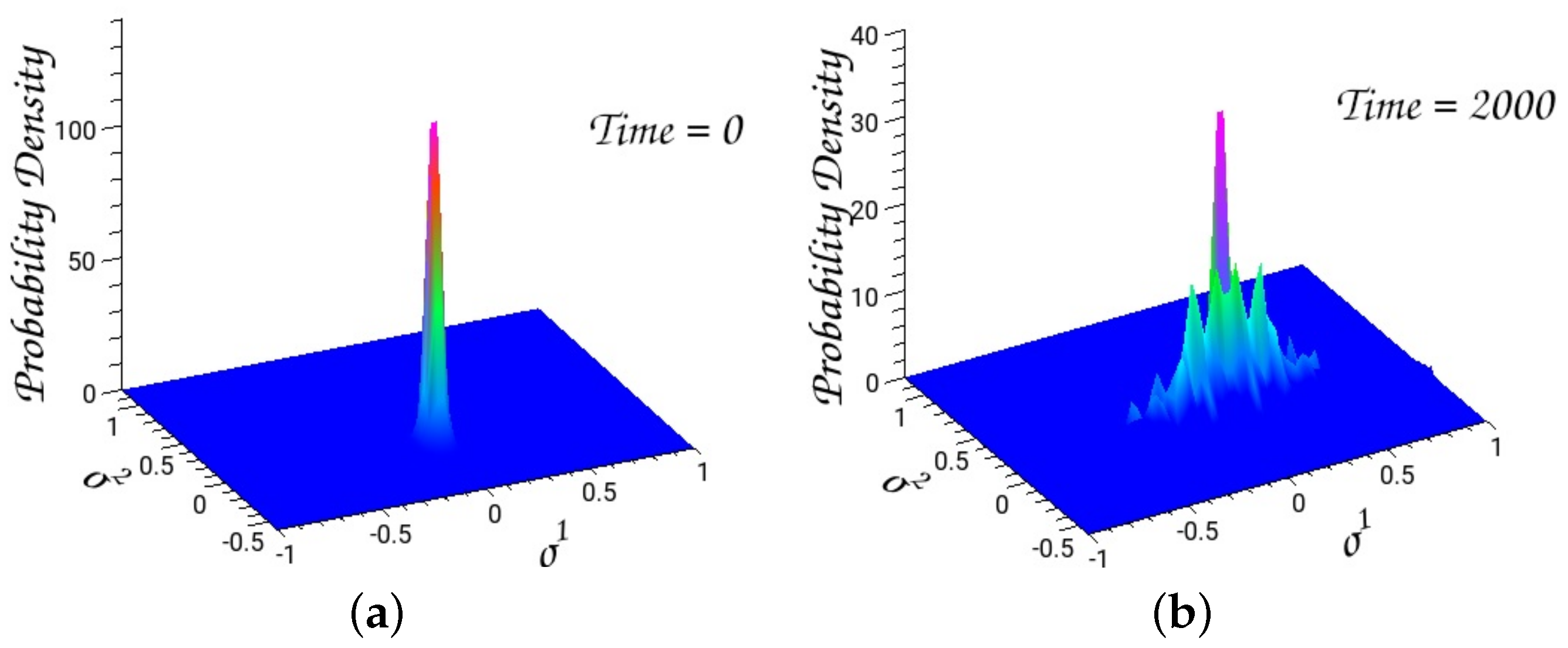
4.2.2. The Quantum Hénon–Heiles System
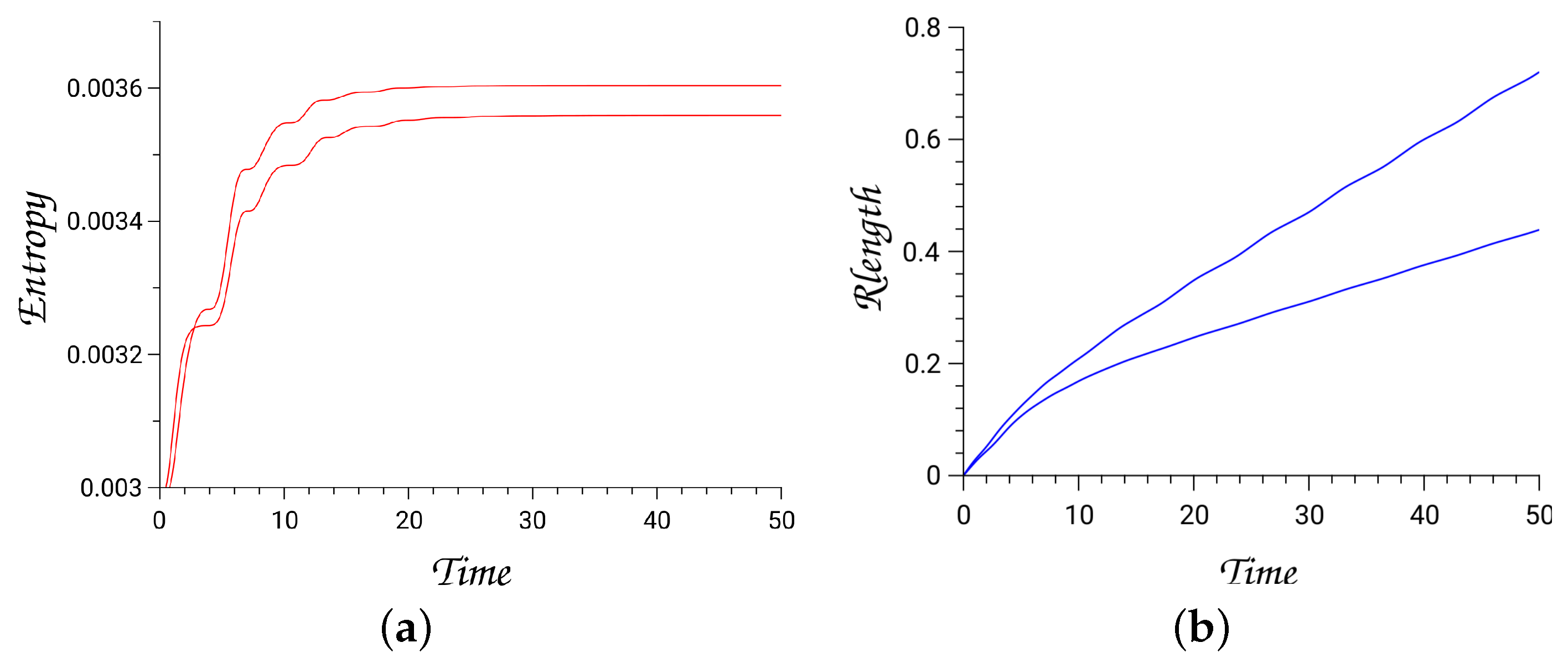
4.2.3. Energy Dissipation of Hénon–Heiles System in Homogeneous Media
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FD | Finite Difference |
| PS | Pseudospectral |
| DOF | degrees of freedom |
| TEPS | Thermodynamic Extended Phase Space |
| TEPSS | Thermodynamic Extended Physical State Submanifold |
| TCS | Thermodynamic Contact Space |
| PTS | Physical Thermodynamic Submanifold |
| ODEs | Ordinary Differential Equations |
| HNN | Hamiltonian neural networks |
| PNN | Physics neural networks |
| nD | dimensional |
Appendix A
Appendix A.1. Proof of Equation (89)
Appendix A.2. Proof of Equation (90)
Appendix A.3. Proof of Equation (152)
Appendix A.4. Tables
Appendix A.4.1. Projection Maps between Thermodynamic Extended Phase Space and Thermodynamic Contact Space
 |
Appendix A.4.2. Thermodynamic Manifolds in Entropy Representation
| Manifold | |||
| Coordinates | |||
| Momenta | |||
| form | |||
| form | |||
| PTS | (TEPSS) | ||
| Metric |
Appendix A.4.3. Thermodynamic Manifolds in Energy Representation
| Manifold | |||
| Coordinates | |||
| Momenta | |||
| form | |||
| form | |||
| PTS | (TEPSS) | ||
| Metric | |||
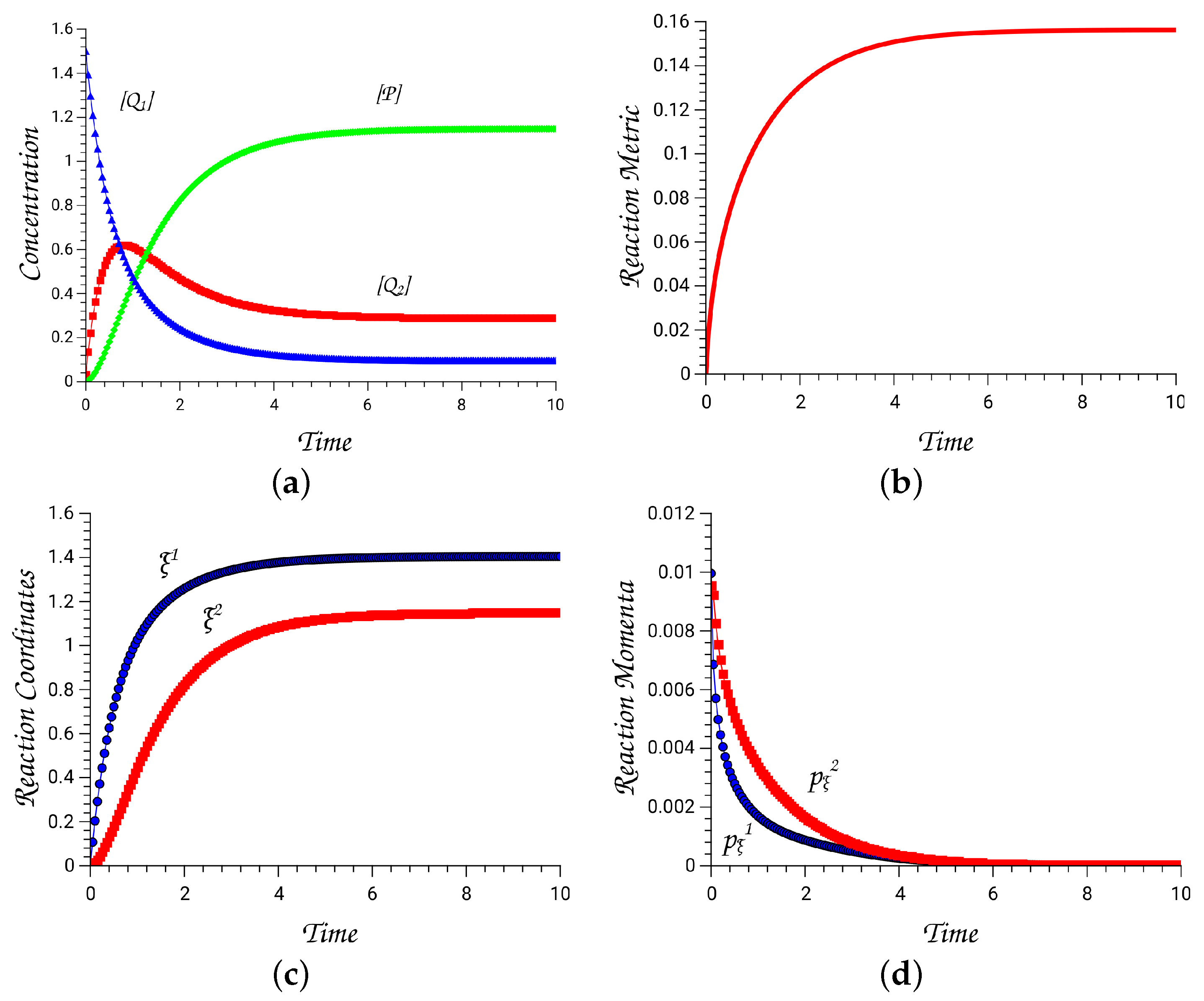
Appendix A.5. Hamiltonian Chemical Kinetics: A Simple Chemical Kinetic Example: Consecutive First-Order Elementary Reactions
Appendix A.5.1. Discussion
References
- Scheck, F. Mechanics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 17. [Google Scholar]
- Meyer, K.R.; Hall, G.R.; Offin, D. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, 2nd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 2009; Volume 90. [Google Scholar]
- Farantos, S.C.; Schinke, R.; Guo, H.; Joyeux, M. Energy Localization in Molecules, Bifurcation Phenomena, and their Spectroscopic Signatures: The Global View. Chem. Rev. 2009, 109, 4248–4271. [Google Scholar] [CrossRef] [PubMed]
- Farantos, S.C. Nonlinear Hamiltonian Mechanics Applied to Molecular Dynamics: Theory and Computational Methods for Understanding Molecular Spectroscopy and Chemical Reactions; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Ashtekar, A.; Schilling, T. Geometrical Formulation of Quantum Mechanics. In On Einstein’s Path: Essays in Honor of Engelbert Schucking; Harvey, A., Ed.; Springer: New York, NY, USA, 1999; pp. 23–65. [Google Scholar] [CrossRef]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef]
- Heydari, H. Geometric formulation of quantum mechanics. arXiv 2016. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics, 2nd ed.; Springer: New York, NY, USA, 1989. [Google Scholar]
- Libermann, P.; Marle, C.M. Symplectic Geometry and Analytical Mechanics; Reidel Publishing Company: Dordrecht, Holland, 1987. [Google Scholar]
- Hermann, R. Geometry, Physics, and Systems. Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Mrugala, R. Geometric formulation of equilibrium phenomenological thermodynamics. Rep. Math. Phys. 1978, 14, 419. [Google Scholar] [CrossRef]
- Mrugala, R. On equivalence of two metrics in classical thermodynamics. Phys. A 1984, 125, 631–639. [Google Scholar] [CrossRef]
- Mrugala, R. Submanifolds in the thermodynamic phase space. Rep. Math. Phys. 1985, 21, 197. [Google Scholar] [CrossRef]
- Mrugala, R.; Nulton, J.; Schoen, J.; Salamon, P. Contact structures in thermodynamic theory. Rep. Math. Phys. 1991, 29, 109–121. [Google Scholar] [CrossRef]
- Peterson, M.A. Analogy between Thermodynamics and Mechanics. Am. J. Phys. 1979, 47, 488–490. [Google Scholar] [CrossRef]
- Salamon, P.; Andresen, B.; Nulton, J.; Konopka, A.K. The Mathematical Structure of Thermodynamics; CRC Press: Boca Raton, FL, USA, 2007; pp. 207–221. [Google Scholar]
- Balian, R.; Valentin, P. Hamiltonian structure of thermodynamics with gauge. Eur. Phys. J. B 2001, 21, 269–282. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Bravetti, A.; Cruz, H.; Tapias, D. Contact Hamiltonian mechanics. Ann. Phys. 2017, 376, 17–39. [Google Scholar] [CrossRef]
- Gay-Balmaz, F.; Yoshimura, H. A Lagrangian variational formulation for nonequilibrium thermodynamics. Part I: Discrete systems. J. Geom. Phys. 2017, 111, 169–193. [Google Scholar] [CrossRef]
- Gay-Balmaz, F.; Yoshimura, H. Dirac structures in nonequilibrium thermodynamics. IFAC Pap. Line 2018, 51, 31–37. [Google Scholar] [CrossRef]
- Liu, Q.; Torres, P.J.; Wang, C. Contact Hamiltonian dynamics: Variational principles, invariants, completeness and periodic behavior. Ann. Phys. 2018, 395, 26–44. [Google Scholar] [CrossRef]
- van der Schaft, A.; Maschke, B. Geometry of Thermodynamic Processes. Entropy 2018, 20, 925. [Google Scholar] [CrossRef] [PubMed]
- Fornberg, B. A Practical Guide to Pseudospectral Methods; Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Hénon, M.; Heiles, C. The Applicability of the Third Integral of Motion: Some Numerical Experiments. Astron. J. 1964, 69, 73–79. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. On the Quantum Theory of Molecules. Ann. Phys. 1927, 84, 457–484. [Google Scholar]
- Frankel, T. The Geometry of Physics: An Introduction; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Farantos, S.C. Hamiltonian Thermodynamics in the Extended Phase Space: A unifying theory for non-linear molecular dynamics and classical thermodynamics. J. Math. Chem. 2020, 58, 1247–1280. [Google Scholar] [CrossRef]
- Farantos, S.C. Hamiltonian classical thermodynamics and chemical kinetics. Phys. D 2021, 417, 132813. [Google Scholar] [CrossRef]
- Sen, D. The uncertainty relations in quantum mechanics. Curr. Sci. 2014, 104, 203–218. [Google Scholar]
- Essex, C.; Andresen, B. The principal equations of state for classical particles, photons, and neutrinos. J. Non-Equilib. Thermodyn. 2013, 38, 293–312. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1999, 20, 1608–1613. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rep. Mod. Phys. 1995, 67, 605–659. [Google Scholar] [CrossRef]
- Weinhold, F. Metric Geometry of Equilibrium THermodynamics. J. Chem. Phys. 1975, 63, 2479–2483. [Google Scholar] [CrossRef]
- Weinhold, F. Classical and Geometrical Theory of Chemical and Phase Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Engelmann, W. Translation: Investigations of Chemical Affinities. Essays by C.M. Guldberg and P. Waage from the Years 1864, 1867, 1879; Wilhelm Engelmann: Leipzig, Germany, 1864. [Google Scholar]
- Voit, E.O.; Martens, H.A.; Omholt, S.W. 150 Years of the Mass Action Law. PLoS Comput. Biol. 2015, 11, e1004012. [Google Scholar] [CrossRef] [PubMed]
- van der Schaft, A.; Rao, S.; Jayawardhana, B. On the Mathematical Structure of Balanced Chemical Reaction Networks Governed by Mass Action Kinetics. SIAM J. Appl. Math. 2013, 73, 953–973. [Google Scholar] [CrossRef]
- van der Schaft, A.; Rao, S.; Jayawardhana, B. Complex and detailed balancing of chemical reaction networks revisited. J. Math. Chem. 2015, 53, 1445–1458. [Google Scholar] [CrossRef][Green Version]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kondepudi, D. Introduction to Modern Thermodynamics; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Salamon, P.; Berry, R.S. Thermodynamic Length and Dissipated Availability. Phys. Rev. Lett. 1983, 51, 1127–1130. [Google Scholar] [CrossRef]
- Andresen, B. Metrics and Energy Landscapes in Irreversible Thermodynamics. Entropy 2015, 17, 6304–6317. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gordon, M.K. Computer Solution of Ordinary Differential Equations: The Initial Value Problem; W. H. Freeman and Company: San Francisco, CA, USA, 1975. [Google Scholar]
- Guantes, R.; Farantos, S.C. High order finite difference algorithms for solving the Schrödinger equation in molecular dynamics. J. Chem. Phys. 1999, 111, 10827. [Google Scholar] [CrossRef][Green Version]
- Guantes, R.; Farantos, S.C. High order finite difference algorithms for solving the Schrödinger equation in molecular dynamics. II. Periodic variables. J. Chem. Phys. 2000, 113, 10429. [Google Scholar] [CrossRef]
- Farantos, S.C. POMULT: A Program for Computing Periodic Orbits in Hamiltonian Systems Based on Multiple Shooting Algorithms. Comput. Phys. Commun. 1998, 108, 240–258. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Serrano, S. Fractal structures in the Hénon-Heiles Hamiltonian. Europhys. Lett. 2008, 82, 10003. [Google Scholar] [CrossRef]
- Kosloff, R. Propagation methods for quantum molecular dynamics. Annu. Rev. Phys. Chem. 1994, 45, 145–178. [Google Scholar] [CrossRef]
- Noether, E. Invariant variation problems. Trans. Theor. Stat. Phys. 1971, 1, 186. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration; Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 31. [Google Scholar]
- Carpenter, B.K.; Ezra, G.S.; Farantos, S.C.; Kramer, Z.C.; Wiggins, S. Empirical Classification of Trajectory Data: An Opportunity for the Use of Machine Learning in Molecular Dynamics. J. Phys. Chem. B 2018, 122, 3230–3241. [Google Scholar] [CrossRef] [PubMed]
- Greydanus, S.; Dzamba, M.; Yosinski, J. Hamiltonian neural networks. In Advances in Neural Information Processing Systems, Hamiltonian Neural Networks; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32, pp. 15379–15389. [Google Scholar]
- Mattheakis, M.; Sondak, D.; Dogra, A.S.; Protopapas, P. Hamiltonian neural networks for solving equations of motion. Phys. Rev. E 2022, 105, 065305. [Google Scholar] [CrossRef]
- Chen, R.; Tao, M. Data-driven Prediction of General Hamiltonian Dynamics via Learning Exactly-Symplectic Maps. arXiv 2021. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farantos, S.C. Hamiltonian Computational Chemistry: Geometrical Structures in Chemical Dynamics and Kinetics. Entropy 2024, 26, 399. https://doi.org/10.3390/e26050399
Farantos SC. Hamiltonian Computational Chemistry: Geometrical Structures in Chemical Dynamics and Kinetics. Entropy. 2024; 26(5):399. https://doi.org/10.3390/e26050399
Chicago/Turabian StyleFarantos, Stavros C. 2024. "Hamiltonian Computational Chemistry: Geometrical Structures in Chemical Dynamics and Kinetics" Entropy 26, no. 5: 399. https://doi.org/10.3390/e26050399
APA StyleFarantos, S. C. (2024). Hamiltonian Computational Chemistry: Geometrical Structures in Chemical Dynamics and Kinetics. Entropy, 26(5), 399. https://doi.org/10.3390/e26050399








