Restoring the Fluctuation–Dissipation Theorem in Kardar–Parisi–Zhang Universality Class through a New Emergent Fractal Dimension
Abstract
1. Introduction
2. The Fluctuation–Dissipation Theorem
2.1. Fractals
2.2. Dimensional Analysis
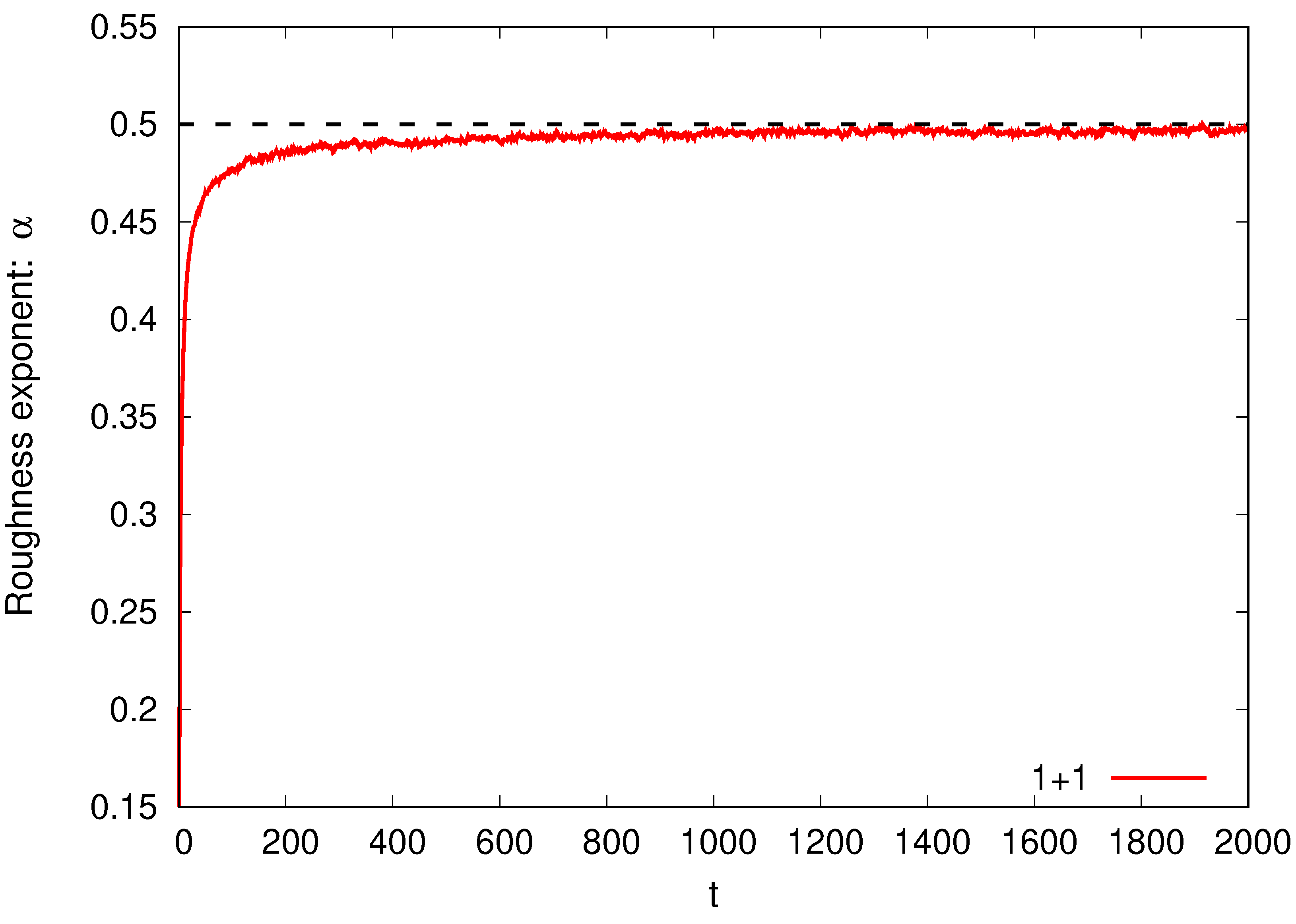
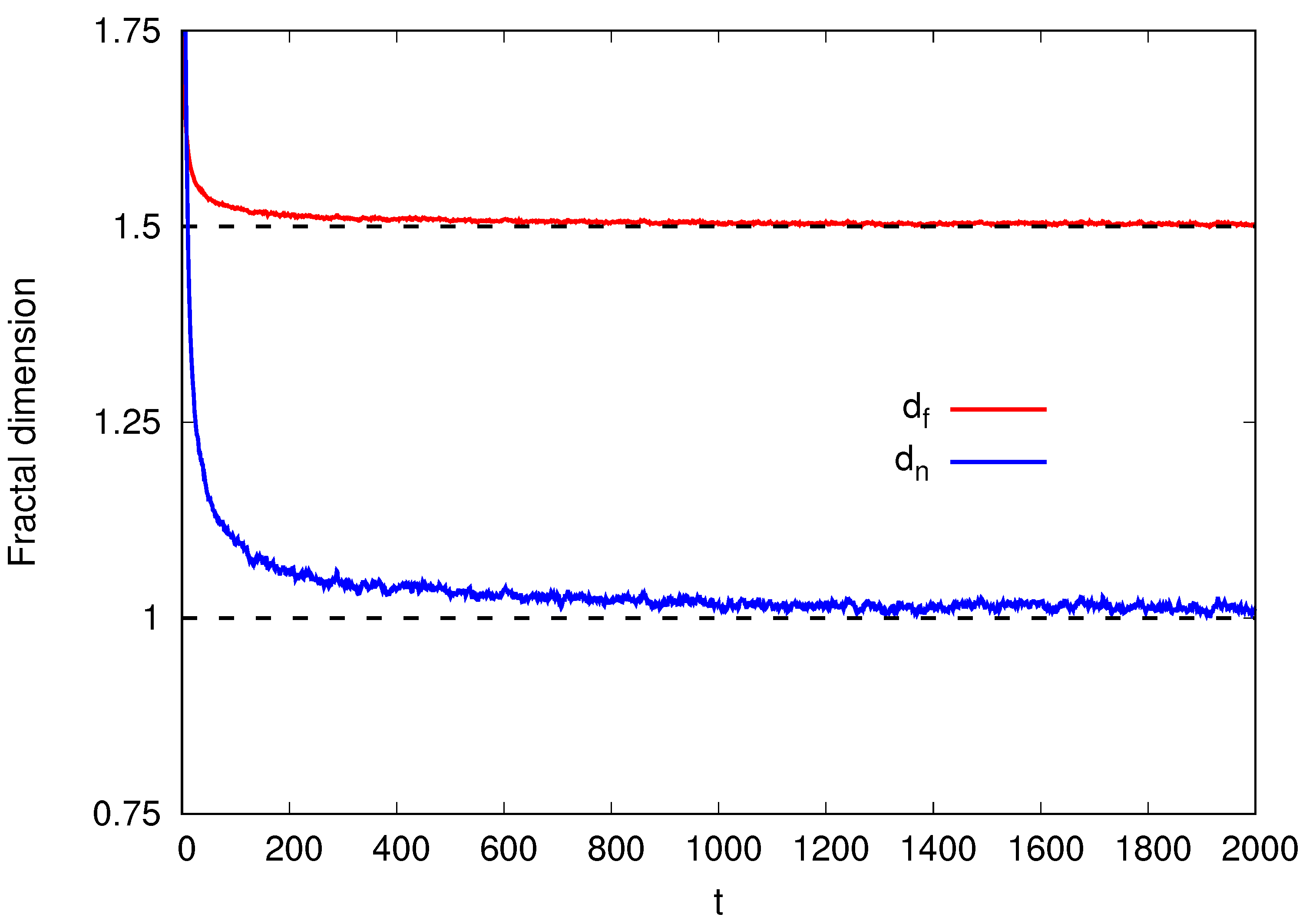
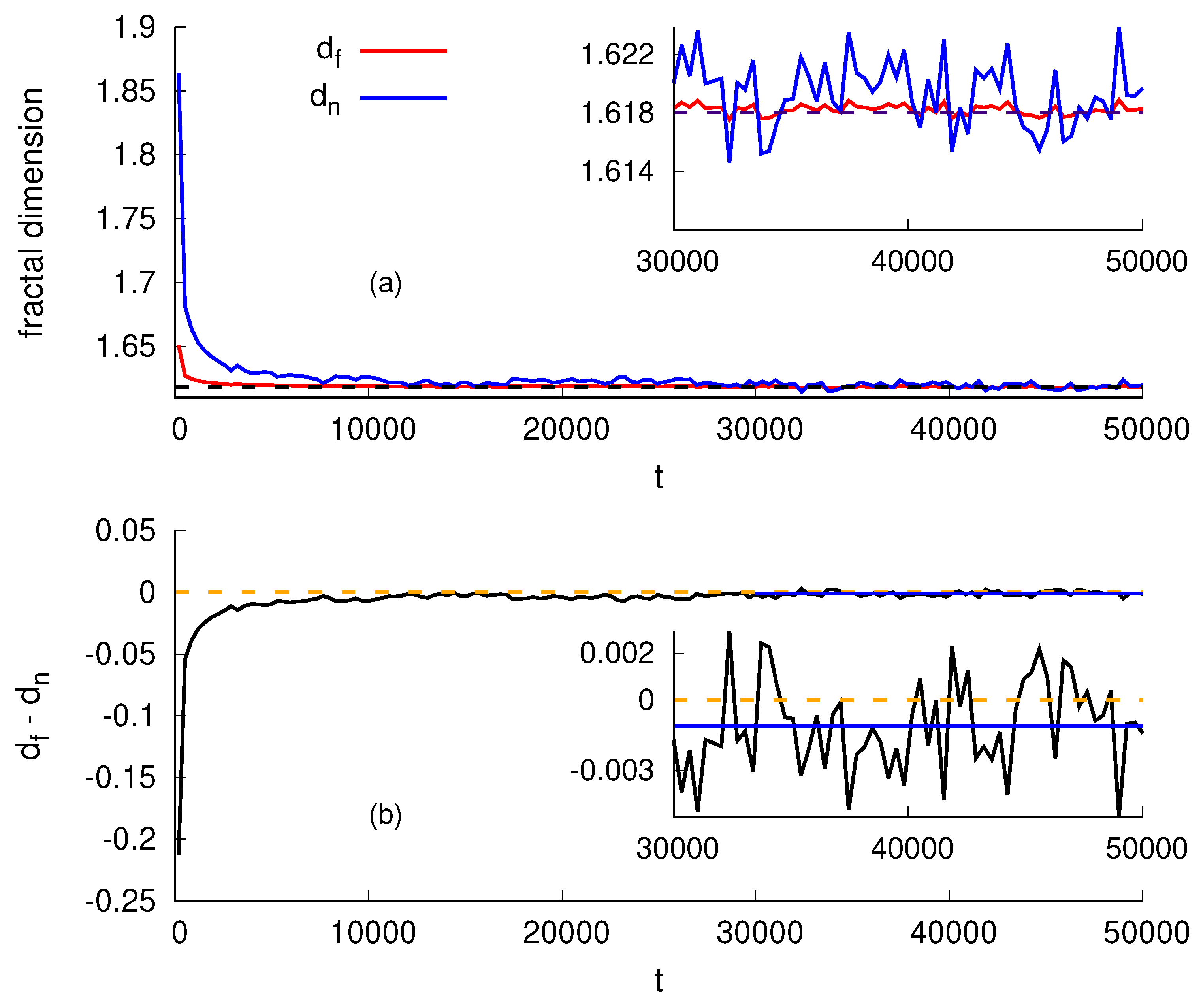
3. Determination of Exponents and Fractal Dimensions
- At time t, randomly choose a site ;
- If is a local minimum, then , with probability p;
- If is a local maximum, then , with probability q.
4. Additional Discussion
4.1. Upper Critical Dimension
4.2. Renormalization
4.3. A Possible Connection between Growth and Phase Transitions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Luis, E.E.M.; de Assis, T.A.; Oliveira, F.A. Unveiling the connection between the global roughness exponent and interface fractal dimension in EW and KPZ lattice models. J. Stat. Mech. Theory Exp. 2022, 2022, 083202. [Google Scholar] [CrossRef]
- Mozo Luis, E.E.; Oliveira, F.A.; de Assis, T.A. Accessibility of the surface fractal dimension during film growth. Phys. Rev. E 2023, 107, 034802. [Google Scholar] [CrossRef]
- Zaslavsky, G.M.; Zaslavskij, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press on Demand: New York, NY, USA, 2005. [Google Scholar]
- Oliveira, F.A.; Ferreira, R.; Lapas, L.C.; Vainstein, M.H. Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.F.; Wilkinson, D. The surface statistics of a granular aggregate. Proc. R. Soc. London. Math. Phys. Sci. 1982, 381, 17–31. [Google Scholar]
- Gomes-Filho, M.S.; Penna, A.L.; Oliveira, F.A. The Kardar-Parisi-Zhang exponents for the 2+1 dimensions. Results Phys. 2021, 26, 104435. [Google Scholar] [CrossRef]
- Barabási, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Merikoski, J.; Maunuksela, J.; Myllys, M.; Timonen, J.; Alava, M.J. Temporal and spatial persistence of combustion fronts in paper. Phys. Rev. Lett. 2003, 90, 024501. [Google Scholar] [CrossRef] [PubMed]
- Le Doussal, P.; Majumdar, S.N.; Rosso, A.; Schehr, G. Exact short-time height distribution in the one-dimensional Kardar-Parisi-Zhang equation and edge fermions at high temperature. Phys. Rev. Lett. 2016, 117, 070403. [Google Scholar] [CrossRef] [PubMed]
- Orrillo, P.A.; Santalla, S.N.; Cuerno, R.; Vázquez, L.; Ribotta, S.B.; Gassa, L.M.; Mompean, F.; Salvarezza, R.C.; Vela, M.E. Morphological stabilization and KPZ scaling by electrochemically induced co-deposition of nanostructured NiW alloy films. Sci. Rep. 2017, 7, 17997. [Google Scholar] [CrossRef]
- Ojeda, F.; Cuerno, R.; Salvarezza, R.; Vázquez, L. Dynamics of Rough Interfaces in Chemical Vapor Deposition: Experiments and a Model for Silica Films. Phys. Rev. Lett. 2000, 84, 3125–3128. [Google Scholar] [CrossRef]
- Chen, L.; Lee, C.F.; Toner, J. Mapping two-dimensional polar active fluids to two-dimensional soap and one-dimensional sandblasting. Nat. Commun. 2016, 7, 12215. [Google Scholar] [CrossRef]
- Rojas-Vega, M.; de Castro, P.; Soto, R. Wetting dynamics by mixtures of fast and slow self-propelled particles. Phys. Rev. E 2023, 107, 014608. [Google Scholar] [CrossRef]
- Family, F.; Vicsek, T. Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. J. Phys. A Math. Gen. 1985, 18, L75. [Google Scholar] [CrossRef]
- Rodrigues, E.A.; Luis, E.E.M.; de Assis, T.A.; Oliveira, F.A. Universal scaling relations for growth phenomena. J. Stat. Mech. Theory Exp. 2024, 2024, 013209. [Google Scholar] [CrossRef]
- Grigera, T.S.; Israeloff, N.E. Observation of Fluctuation-Dissipation-Theorem Violations in a Structural Glass. Phys. Rev. Lett. 1999, 83, 5038. [Google Scholar] [CrossRef]
- Ricci-Tersenghi, F.; Stariolo, D.A.; Arenzon, J.J. Two time scales and violation of the fluctuation-dissipation theorem in a finite dimensional model for structural glasses. Phys. Rev. Lett. 2000, 84, 4473. [Google Scholar] [CrossRef] [PubMed]
- Barrat, A. Monte Carlo simulations of the violation of the fluctuation-dissipation theorem in domain growth processes. Phys. Rev. E 1998, 57, 3629. [Google Scholar] [CrossRef]
- Bellon, L.; Ciliberto, S. Experimental study of the fluctuation dissipation relation during an aging process. Phys. D Nonlinear Phenom. 2002, 168, 325–335. [Google Scholar] [CrossRef][Green Version]
- Hayashi, K.; Takano, M. Violation of the fluctuation-dissipation theorem in a protein system. Biophys. J. 2007, 93, 895–901. [Google Scholar] [CrossRef]
- Perez-Madrid, A.; Lapas, L.C.; Rubi, J.M. Heat exchange between two interacting nanoparticles beyond the fluctuation-dissipation regime. Phys. Rev. Lett. 2009, 103, 048301. [Google Scholar] [CrossRef]
- Costa, I.V.L.; Morgado, R.; Lima, M.V.B.T.; Oliveira, F.A. The Fluctuation-Dissipation Theorem fails for fast superdiffusion. Europhys. Lett. 2003, 63, 173. [Google Scholar] [CrossRef]
- Costa, I.V.; Vainstein, M.H.; Lapas, L.C.; Batista, A.A.; Oliveira, F.A. Mixing, ergodicity and slow relaxation phenomena. Phys. A Stat. Mech. Appl. 2006, 371, 130–134. [Google Scholar] [CrossRef][Green Version]
- Lapas, L.C.; Costa, I.V.L.; Vainstein, M.H.; Oliveira, F.A. Entropy, non-ergodicity and non-Gaussian behaviour in ballistic transport. Europhys. Lett. 2007, 77, 37004. [Google Scholar] [CrossRef][Green Version]
- Lapas, L.C.; Morgado, R.; Vainstein, M.H.; Rubí, J.M.; Oliveira, F.A. Khinchin Theorem and Anomalous Diffusion. Phys. Rev. Lett. 2008, 101, 230602. [Google Scholar] [CrossRef] [PubMed]
- Villa-Torrealba, A.; Chávez-Raby, C.; de Castro, P.; Soto, R. Run-and-tumble bacteria slowly approaching the diffusive regime. Phys. Rev. E 2020, 101, 062607. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, M.A.; Wio, H.S. Stochastic entropies and fluctuation theorems for a discrete one-dimensional Kardar-Parisi-Zhang system. Phys. Rev. E 2019, 100, 032111. [Google Scholar] [CrossRef] [PubMed]
- Gomes-Filho, M.S.; Oliveira, F.A. The hidden fluctuation-dissipation theorem for growth. EPL 2021, 133, 10001. [Google Scholar] [CrossRef]
- dos Anjos, P.H.R.; Gomes-Filho, M.S.; Alves, W.S.; Azevedo, D.L.; Oliveira, F.A. The Fractal Geometry of Growth: Fluctuation–Dissipation Theorem and Hidden Symmetry. Front. Phys. 2021, 9, 566. [Google Scholar] [CrossRef]
- Gomes-Filho, M.S.; Lapas, L.; Gudowska-Nowak, E.; Oliveira, F.A. Fluctuation-Dissipation relations from a modern perspective. arXiv 2023, arXiv:2312.10134. [Google Scholar]
- Vvedensky, D.D. Edwards-Wilkinson equation from lattice transition rules. Phys. Rev. E 2003, 67, 025102. [Google Scholar] [CrossRef]
- Calabrese, P.; Le Doussal, P.; Rosso, A. Free-energy distribution of the directed polymer at high temperature. Europhys. Lett. 2010, 90, 20002. [Google Scholar] [CrossRef]
- Amir, G.; Corwin, I.; Quastel, J. Probability distribution of the free energy of the continuum directed random polymer in 1 + 1 dimensions. Commun. Pur. Appl. Math. 2011, 64, 466–537. [Google Scholar] [CrossRef]
- Prähofer, M.; Spohn, H. Universal distributions for growth processes in 1+ 1 dimensions and random matrices. Phys. Rev. Lett. 2000, 84, 4882. [Google Scholar] [CrossRef] [PubMed]
- Sasamoto, T.; Spohn, H. One-dimensional Kardar-Parisi-Zhang equation: An exact solution and its universality. Phys. Rev. Lett. 2010, 104, 230602. [Google Scholar] [CrossRef]
- Daryaei, E. Universality and crossover behavior of single-step growth models in 1+ 1 and 2+ 1 dimensions. Phys. Rev. E 2020, 101, 062108. [Google Scholar] [CrossRef]
- Kondev, J.; Henley, C.L.; Salinas, D.G. Nonlinear measures for characterizing rough surface morphologies. Phys. Rev. E 2000, 61, 104. [Google Scholar] [CrossRef]
- Lima, H.A.; Luis, E.E.M.; Carrasco, I.S.S.; Hansen, A.; Oliveira, F.A. A geometrical interpretation of critical exponents. arXiv 2024, arXiv:2402.10167. [Google Scholar]
- Jumarie, G. Laplaceś transform of fractional order via the Mittag–Leffler function and modified Riemann–Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Muslih, S.I. Solutions of a particle with fractional delta-potential in a fractional dimensional space. Int. J. Theor. Phys. 2010, 49, 2095–2104. [Google Scholar] [CrossRef]
- Derrida, B. An exactly soluble non-equilibrium system: The asymmetric simple exclusion process. Phys. Rep. 1998, 301, 65–83. [Google Scholar] [CrossRef]
- Meakin, P.; Ramanlal, P.; Sander, L.M.; Ball, R. Ballistic deposition on surfaces. Phys. Rev. A 1986, 34, 5091. [Google Scholar] [CrossRef]
- Mello, B.A.; Chaves, A.S.; Oliveira, F.A. Discrete atomistic model to simulate etching of a crystalline solid. Phys. Rev. E 2001, 63, 041113. [Google Scholar] [CrossRef]
- Rodrigues, E.A.; Oliveira, F.A.; Mello, B.A. On the Existence of an Upper Critical Dimension for Systems Within the KPZ Universality Class. Acta Phys. Pol. B 2015, 46, 1231. [Google Scholar] [CrossRef]
- Alves, W.S.; Rodrigues, E.A.; Fernandes, H.A.; Mello, B.A.; Oliveira, F.A.; Costa, I.V.L. Analysis of etching at a solid–solid interface. Phys. Rev. E 2016, 94, 042119. [Google Scholar] [CrossRef]
- Almeida, R.; Ferreira, S.; Oliveira, T.; Reis, F.A. Universal fluctuations in the growth of semiconductor thin films. Phys. Rev. B 2014, 89, 045309. [Google Scholar] [CrossRef]
- Fusco, D.; Gralka, M.; Kayser, J.; Anderson, A.; Hallatschek, O. Excess of mutational jackpot events in expanding populations revealed by spatial Luria–Delbrück experiments. Nat. Commun. 2016, 7, 12760. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Ahammer, H.; Sabathiel, N.; Reiss, M.A. Is a two-dimensional generalization of the Higuchi algorithm really necessary? Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 073104. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Zhu, H.; Zuo, X.; Yang, J. The three-point sinuosity method for calculating the fractal dimension of machined surface profile. Fractals 2015, 23, 1550016. [Google Scholar] [CrossRef]
- Wolf, D.; Kertesz, J. Surface width exponents for three-and four-dimensional eden growth. Europhys. Lett. 1987, 4, 651. [Google Scholar] [CrossRef]
- Kardar, M. Statistical Physics of Fields; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomes-Filho, M.S.; de Castro, P.; Liarte, D.B.; Oliveira, F.A. Restoring the Fluctuation–Dissipation Theorem in Kardar–Parisi–Zhang Universality Class through a New Emergent Fractal Dimension. Entropy 2024, 26, 260. https://doi.org/10.3390/e26030260
Gomes-Filho MS, de Castro P, Liarte DB, Oliveira FA. Restoring the Fluctuation–Dissipation Theorem in Kardar–Parisi–Zhang Universality Class through a New Emergent Fractal Dimension. Entropy. 2024; 26(3):260. https://doi.org/10.3390/e26030260
Chicago/Turabian StyleGomes-Filho, Márcio S., Pablo de Castro, Danilo B. Liarte, and Fernando A. Oliveira. 2024. "Restoring the Fluctuation–Dissipation Theorem in Kardar–Parisi–Zhang Universality Class through a New Emergent Fractal Dimension" Entropy 26, no. 3: 260. https://doi.org/10.3390/e26030260
APA StyleGomes-Filho, M. S., de Castro, P., Liarte, D. B., & Oliveira, F. A. (2024). Restoring the Fluctuation–Dissipation Theorem in Kardar–Parisi–Zhang Universality Class through a New Emergent Fractal Dimension. Entropy, 26(3), 260. https://doi.org/10.3390/e26030260





