Abstract
We propose and experimentally demonstrate a wireless-channel key distribution scheme based on laser synchronization induced by a common wireless random signal. Two semiconductor lasers are synchronized under injection of the drive signal after electrical-optical conversion and emit irregular outputs that are used to generate shared keys. Our proof-of-concept experiment using a complex drive signal achieved a secure key generation rate of up to 150 Mbit/s with a bit error rate below 3.8 × 10−3. Numerical simulation results show that the proposed scheme has the potential to achieve a distribution distance of several hundred meters. It is believed that common-signal-induced laser synchronization paves the way for high-speed wireless physical-layer key distribution.
1. Introduction
With the increase in wireless communication rates, high-speed key distribution has become more important [1]. Existing key distribution is divided into two types: computational security-based and information-theoretic security-based key distribution. The former presupposes that the eavesdropper’s computational power is constrained, thus an inherent risk of being decoded by using high-performance computers. The latter has attracted increasing attention because of its ability to resist unlimited computational power. It has been proved that two users with access to common random sources can generate a shared secret key by exchanging messages over a public channel [2,3]. Many key distribution schemes based on common random sources have been proposed and investigated [4,5,6,7,8,9,10].
Information-theoretic security key distribution has been successfully demonstrated in the wireless domain [11,12,13], where the channel reciprocity properties of the wireless fading channel provide the common random sources for key establishment. However, limited by the bandwidth of channel randomness, the scheme has limited key rates (bit/s~kbit/s). Although various approaches have been investigated to improve the key rate [14,15,16], the improvement effect is quite limited. Additionally, the key generated in a static or free space environment lacks randomness, rendering it susceptible to prediction.
It has been demonstrated that optical chaos in semiconductor lasers is a promising physical entropy source for generating high-speed random bits at Gbit/s or even Tbit/s [17,18]. The synchronization of optical chaos can be used as a source of common randomness and has been intensively investigated for applications in high-speed secure key distribution [19,20,21,22,23,24]. Uchida et al. firstly experimentally demonstrated a 182-kbit/s key distribution using the chaos synchronization of two optical-feedback lasers driven by a common random light [20]. The security of the scheme is based on information theory and the practical difficulties of completely observing the fast and complex optical process [8,25]. The key rate of the scheme is limited by the chaos synchronization recovery time in the magnitude of tens of nanoseconds. Recently, Wang et al. experimentally demonstrated a 0.75-Gbit/s key distribution by using the open-loop configuration of commonly driven lasers [26]. Nevertheless, the utilization of these schemes in wireless secure communication is restricted due to the presence of optical fiber links among users.
In this paper, we propose and demonstrate a high-speed wireless key distribution scheme based on laser synchronization induced by a common wireless random signal. It enhances the key distribution scheme based on common-signal-induced synchronization to accommodate wireless environments. We successfully achieve synchronization of commonly driven lasers and demonstrate a secure key generation rate of up to 150 Mbit/s while maintaining a bit error rate (BER) below the threshold of 3.8 × 10−3. In addition, the distribution distance of the proposed scheme is studied by numerical simulation.
2. Principle and Experimental Setup
The principle of the proposed scheme is shown in Figure 1a. Two identical nonlinear oscillators are authorized to the legitimate users Alice and Bob. Each nonlinear oscillator has a set V of parameters that can be changed. These parameters can take on one of M possible values. VA and VB are generated by two independent random bit generators (RBG). A complex drive signal is transmitted through an antenna, and then it is received and injected into the nonlinear oscillators to achieve chaos synchronization. Only in the time slots when VA = VB, do the chaotic waveforms synchronize. This process is called random keying. Subsequently, the output signals of the oscillators are sampled and quantized to generate the correlated random bits XA and XB privately and independently. They repeat this procedure many times to acquire sequences of the pairs (VA,i, XA,i) and (VB,i, XB,i), i = 1, 2, …, n, respectively. Next, they exchange the parameters sequences {VA,i} and {VB,i}, i = 1, 2, …, n, over a public channel to sift bits. Only the bits XA,i and XB,i for i such that VA,i = VB,i are retained, otherwise the bits are discarded. These retained bits, denoted as {YA,i} and {YB,i}, i = 1, 2, …, n, are used to generate a common secret key KA = KB by using an information reconciliation protocol and a privacy amplification protocol [27] in post processors.
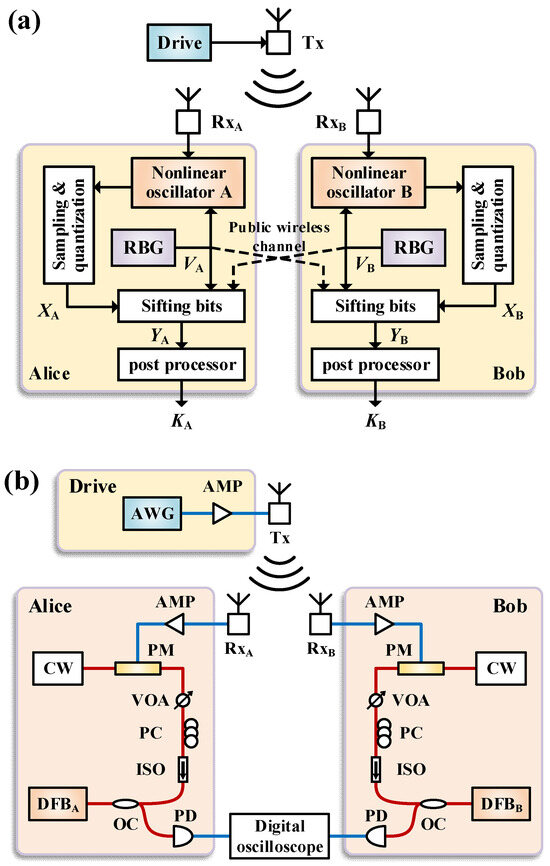
Figure 1.
(a) Principle and (b) experimental setup for wireless-channel key distribution. RBG, random bit generator; AWG, arbitrary waveform generator; AMP, radio frequency amplifier; PM, electro-optic phase modulator; CW, continuous-wave laser; VOA, variable optical attenuator; PC, polarization controller; ISO, optical isolator; OC, optical fiber coupler; DFB, distributed-feedback semiconductor laser; PD, photodetector.
To evaluate the security of this scheme, we assume an eavesdropper, Eve, who can inject the drive signal into one or more nonlinear oscillators. Additionally, we assume that Eve can obtain any information exchanged through a public channel between Alice and Bob. It has been proven that Alice and Bob can generate a key that is completely secret to Eve when Eve has no way of inferring the bits generated by Alice and Bob without errors [8]. In our scheme, we utilize two characteristics of common-signal-induced synchronization to facilitate this condition [28,29]. Firstly, the outputs of two nonlinear oscillators can synchronize under the drive of a common noise signal, while there is no simple functional relationship between the drive signal and the oscillator outputs. This makes it difficult for Eve to obtain sufficient information about the retained bits even if she can get the drive signal from the wireless channel. Secondly, the synchronization is sensitive to the parameter mismatches of the nonlinear oscillators. This means that even if Eve can access all information on the public channel, it is difficult for Eve to obtain enough oscillators with parameter matches to observe the outputs for all possible parameter values. These characteristics give Alice and Bob a certain probability of retaining bits that cannot be obtained by Eve, thus enabling the establishment of a common secret key. It is worth noting that Alice and Bob can further reduce the amount of information obtained by Eve by applying privacy amplification techniques [27], so they do not need to know which bits Eve has obtained.
In the subsequent section, we conduct a proof-of-concept experiment using semiconductor lasers as nonlinear oscillators to verify the feasibility of the scheme and estimate the secure key generation rate under reasonable assumptions.
Figure 1b illustrates the experimental setup for wireless-channel key distribution. Alice and Bob are assigned a pair of parameter-matched distributed-feedback semiconductor lasers (DFB). These lasers were selected from an identical fabrication batch that was supplied by the company Eblana Photonics. An arbitrary waveform generator (AWG) generates a noise signal as the common wireless drive signal, which is broadcasted via an antenna (5.38~8.17 GHz standard gain horn antenna) Tx. The drive signal is transmitted over a 2.5 m wireless link and received by antennas RxA and RxB. Due to the beamwidth of the transmitter, RxA and RxB are placed approximately 0.5 m apart to ensure that the drive signal is successfully received. For each user, the received RF drive signal is first converted into an optical signal using an electro-optic phase modulator (PM) of a continuous-wave laser (CW) light. The resulting phase-random drive light is then injected into the DFB laser. To adjust the modulation depth, a radio frequency amplifier (AMP) is used. The modulation depth is defined as 3σ/Vπ, where σ is the standard deviation of the drive signal and Vπ is the half-wave voltage of the PM. For injection of the drive light, a polarization controller (PC) is used to match injection light polarization to that of the laser, and an optical isolator (ISO) is used to ensure unidirectional injection. A variable optical attenuator (VOA) is used to adjust the injection strength, which is defined as power ratio of DFB free output to drive light. The output of the laser is derived from an optical fiber coupler (OC), detected by a photodetector (PD), and observed using a digital oscilloscope (Keysight Technologies, Santa Rosa, CA, USA, DSAV164A, 16 GHz bandwidth). Although various schemes [20,26,30,31] can accomplish random keying, this does not impact the feasibility of the proposed scheme. Hence, there are no experimental demonstrations of random keying in this work, and our analysis solely focuses on its impact on the key rate.
3. Experimental Results
3.1. Laser Synchronization Induced by a Common Wireless Signal
The drive signal utilized in our experiment is a Gaussian noise characterized by a 3-dB bandwidth of 2.8 GHz and a central frequency of 6.7 GHz. The spectrum of the drive signal is shown in Figure 2a. The generation of broad-spectrum and synchronized outputs by the lasers requires a drive signal with an adequately broad bandwidth. The power loss is 37 dB, as the received power is approximately −24 dBm and the transmit power is 13 dBm. The modulation depth is adjusted to 0.7 with an amplifier gain of 44 dB. The currents for the DFB lasers are set to 24.20 mA (2.12 Ith) and 23.50 mA (2.19 Ith) to achieve identical relaxation oscillation frequencies of 5.5 GHz. The injection strengths are adjusted to −8.43 dB and −8.70 dB to induce injection locking. The optical frequency detuning of the center frequencies of the DFB lasers and drive light is approximately 1.6 GHz, as illustrated in Figure 2b.
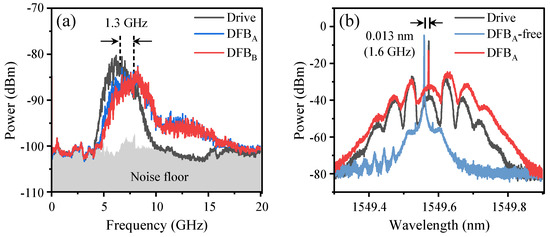
Figure 2.
(a) RF spectra for the drive signal and the DFB laser outputs. (b) Optical spectra for the drive light and the DFBA output with and without optical injection.
As shown in Figure 2a, the laser outputs exhibit broad spectra characterized by a 3-dB bandwidth of approximately 2 GHz. This characteristic renders them suitable for the generation of high-speed random bits. The laser outputs have center frequencies that are approximately 1.3 GHz greater than those of the drive signal. This phenomenon arises as a result of the drive signal’s spectrum encompassing the laser’s relaxation oscillation frequency, thereby generating a light injection effect that enhances the relaxation oscillation frequency [32]. The spectral characteristics of the laser output and the drive light exhibit a comparable configuration, as illustrated in Figure 2b. The laser output maintains a fixed center frequency in accordance with that of the drive light.
We introduce a measure of cross-correlation to evaluate the quality of the laser synchronization and the correlation between the laser output and the drive signal. The cross-correlation of temporal waveforms x(t) and y(t) is defined as
where <·> denotes time average, and are the mean values, σx and σy are the standard deviations. If CCxy = 1, it indicates that x(t) and y(t) are completely identical. Conversely, if CCxy = 0, it means that they are completely uncorrelated.
Figure 3a shows the temporal waveforms of the transmitted wireless drive signal, the signals received by antennas RxA and RxB, and the response outputs of the DFB lasers. The received signals of both users maintain a high similarity, which satisfies the conditions for common-signal-induced synchronization. The temporal waveforms produced by the lasers demonstrate a significant resemblance. The corresponding linear correlation shown in Figure 3b is also evident in their corresponding correlation plot, which has a cross-correlation of 0.95. This observation demonstrates that Alice and Bob have successfully executed high-quality chaotic synchronization. In addition, as shown in Figure 3c, the cross-correlation between the laser output and the drive signal is 0.67, which is comparatively lower than that between the laser outputs. This indicates that only limited information about the synchronized outputs can be obtained from the drive signal, which satisfies our condition for key distribution.
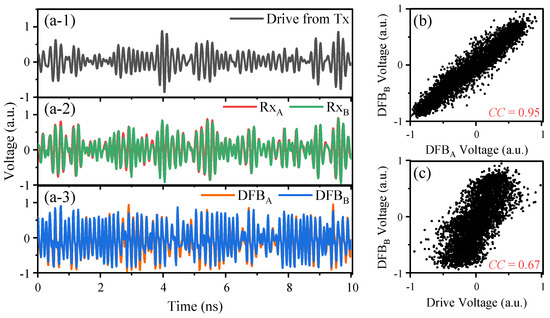
Figure 3.
Temporal waveforms of (a-1) the drive signal, (a-2) signals received by antennas RxA and RxB, and (a-3) the DFB laser outputs. (b) Correlation plots for the DFBA and DFBB outputs. (c) Correlation plots for the drive signal and DFBB output.
The effects of external parameter mismatches, such as center wavelength, bias current, and injection power, on the cross-correlation between laser outputs is illustrated in Figure 4. A mismatch of these external parameters for the lasers between Alice and Bob would lead to the reduction of the cross-correlation coefficient. To maintain laser synchronization with cross-correlation exceeding 0.9, the discrepancy ranges for injection power, bias current, and center wavelength are as follows: −0.010~0.004 nm, −7.7~3.4%, and −10~23%, respectively. These tolerated mismatches demonstrate that laser synchronization is less sensitive to external operations and imply synchronization robustness. Nevertheless, a high sensitivity of chaos synchronization to mismatches in laser inner parameters is required to ensure security, which poses difficulties for Eve in obtaining a parameter-matched laser. It has been shown that synchronization is only achievable within a maximum tolerance of ±1% for laser inner parameters, such as active region length, linear gain coefficient, transparency carrier density, and so on [26]. This means that achieving synchronization necessitates the use of lasers manufactured on the same wafer, which is typically unattainable for Eve [33]. It is worth noting that the cross-correlation between two lasers with mismatched internal parameters is significantly lower than the cross-correlation between their outputs and the drive signal. Therefore, extracting information about the key from lasers with mismatched internal parameters is no more effective than extracting it directly from the drive signal.
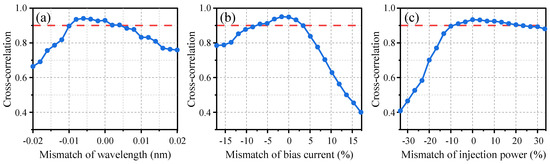
Figure 4.
Effects of external parameters mismatch on laser synchronization: (a) center wavelength mismatch, (b) bias current mismatch, and (c) injection power mismatch. Original settings: center wavelength λA = λB = 1549.559 nm, bias current IA = 24.20 mA, IB = 23.50 mA, injection power PjA = PjB = 300 μW.
3.2. Secure Key Generation Rate
In this section, we analyze the key generation rate of the scheme based on the previous assumptions. The secret bit rate, which is defined as the ratio of the number of secret bits to the raw samples, can be estimated using the following formula [20]:
where ME is the number of parameter-matched lasers that Eve can manipulate, IE is the information per bit that Eve knows about Alice or Bob’s retained bits when Eve’s random keying parameter VE does not match that of Alice and Bob, Rfail is the BER caused by imperfect synchronization between Alice and Bob, and h(·) is the binary entropy function defined by h(x) = −xlog(x) − (1 − x)log(1 − x). 1/M represents the probability of Alice and Bob matching the parameter VA = VB, while 1 − ME/M represents the probability for Eve to match a different parameter from Alice and Bob when VA = VB. h(Rfail) estimates the rate loss caused by the error bits. When the conditions
are satisfied, the value of Rb will be positive, indicating that secure key distribution is possible. Next, we will calculate Rb and the key rate based on experimental results and some reasonable assumptions.
If Alice and Bob introduce a binary random keying parameter, the number of possible values of the parameter set is M = 2. Considering the sensitivity of the laser’s inner parameters to synchronization, we assume that Eve is unable to obtain a third laser with matching parameters [26], resulting in ME = 0. Therefore, Eve can only try to extract information from the drive signal. We further assume Eve can obtain bits XE,i by sampling and quantizing the drive signal using a single threshold [34], and retained those for i such that VA,i = VB,i. In this case, IE can be estimated by
where YE is Eve’s retained bits, I(X;Y) is the mutual information between random bits X and Y, defined as
where P(x) is the probability of X = x, P(y) is the probability of Y = y, and P(x,y) is the joint probability of X = x and Y = y. In practical operation, due to the limited number of available antennas, the drive signal used for estimating IE is obtained by partitioning a portion of Alice’s received signal.
A robust dual-threshold quantization method [34] is used to reduce the BER of between Alice and Bob. We set the upper threshold Vth,u and the lower threshold Vth,l as
where m and σ are the mean and standard deviation of the temporal waveform, and C+ and C− are the threshold coefficients. A sampling point will be quantized to bit “1” if its voltage is larger than Vth,u, and quantized to bit “0” if its voltage is smaller than Vth,l; otherwise, it will be discarded. To guarantee a nearly uniform distribution of the quantized bit stream, C+ and C− are tuned to satisfy
where p[x(t)] is the probability density function of the temporal waveform x(t). In this robust quantization method, only a certain proportion of the sampled points are used to generate the key. The variation of the retained ratio Rdt in relation to the quantization threshold coefficients C+ is illustrated in Figure 5a. Given this fact, the key rate can be calculated using
where fs is raw sample rate. Considering the bandwidth of the laser output, the raw sampling rate is set to fs = 1.0 GHz to ensure the randomness of the generated key.
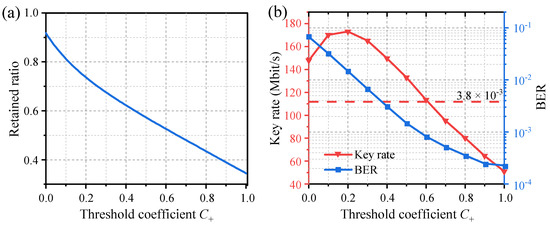
Figure 5.
Effects of quantization threshold coefficients on (a) the retained ratio, (b) the BER between Alice and Bob, and the key generation rate.
Figure 5b shows the key rate and the BER between Alice and Bob (Rfail) in relation to the quantization threshold coefficients C+. Rfail decreases as C+ increases and remains below the BER threshold of 3.8 × 10−3 for hard-decision forward-error correction (HD-FEC) when C+ > 0.4. When C+ is excessively small or large, the key rate will decrease due to a high BER or low retained ratio. The maximum key generation rate that satisfies the BER threshold is achieved when C+ = 0.4, resulting in 150 Mbit/s. In this configuration, we summarized statistical measures of secure key generation in Table 1.

Table 1.
Statistical evaluation on the generated bits. The threshold coefficients for the dual-threshold quantization are set to C+ = 0.400 and C− = 0.408.
Considering the influence of uncertain factors such as noise interference, one can enhance the robustness of the system by increasing the threshold coefficient, at the cost of reducing the key rate. For example, when C+ = 0.8, the BER decreases to 3.6 × 10−4, while the key generation rate decreases to 80 Mbit/s.
In order to verify the randomness of the generated keys, we employed the National Institute of Standards and Technology Special Publication 800-22 statistical tests (NIST SP800-22) to test the generated keys. As shown in Figure 6, the p-values are all greater than 0.01, indicating that the generated keys successfully pass all the 15 NIST tests and thereby verify their randomness.
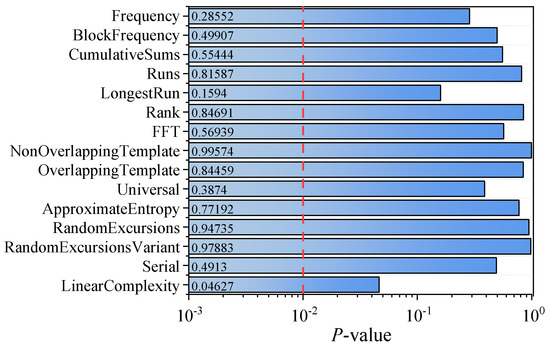
Figure 6.
NIST statistical tests results for p-value. Using 1 Mbit data and a significant level of α = 0.01, the p-value should be greater than 0.01 to pass the test.
4. Numerical Results
We carried out numerical simulations to verify our experimental observations and investigate the impact of transmission distance. For simplicity, we exclusively consider the scenario in free space. The path loss of free space is given by Friis transmission formula [35]
where d is transmission distance, λ is the wavelength of the drive signal, LM is the atmospheric attenuation, and Gt and Gr are the antenna gains of the transmitting and receiving antennas, respectively. The atmospheric attenuation is given by LM = γa·d, where γa is the attenuation coefficient. Assuming perfect polarization matching between the transmitting and receiving antennas, the transfer function of free space is given by [36]
The impulse response of the channel is defined as
where F−1{·} is the inverse Fourier transform. The received signal Sr(t, d) can be obtained by using
where St(t) is the drive signal, is the convolution operator, and n(t) is the noise from the receiving antenna output, given by
where ξ(t) is the normalized Gaussian noise, k = 1.38 × 10−23 J/K is the Boltzmann’s constant, Ta is the equivalent noise temperature of the receiving antenna, and B is the bandwidth of the receiving antenna. The drive light injected into the DFB laser can be represented by
where E0(t) is the CW light input to the phase modulator, and ga is the voltage gain of the amplifier. In our simulations, it’s used the transmission line laser model (TLLM) in VPItransmissionMaker software (Version 9.1) to simulate the dynamic response of DFB lasers to light injection [37,38].
The parameter values used in our simulations are as follows: Gt = 10 dBi, Gr = 10 dBi, γa = 0.01 dB/km, Ta = 303.15 K, B = 2.8 GHz. The center wavelength of the drive signal is 6.7 GHz, and the bandwidth is 2.8 GHz. The transmission power Pt of the drive signal is 13 dBm, and the modulation depth of the phase modulator is set to 0.7. The laser inner parameters are listed in Table 2. The laser current is set to I = 2.4 Ith, where the current threshold Ith is 20 mA. With this configuration, the relaxation oscillation frequency of the laser is 5.5 GHz. The injection strength is set to −8.5 dB, and the optical frequency detuning of the center frequencies of the DFB lasers and drive light is set to 1.6 GHz. We also use a raw sample rate of fs = 1 GHz and a dual-threshold quantization method to generate bits.

Table 2.
Parameter values of DFB lasers used in simulations.
First, let us consider the case where the distance from the drive to Alice (dDA) is equal to the distance from the drive to Bob (dDB). The simulation results are shown in Figure 7. With the increase in transmission distance d, the cross-correlation between the laser outputs decreases, and the BER between Alice and Bob increases. This degradation in performance is due to the decrease in received power as the distance increases, leading to a deterioration of the receiver’s signal-to-noise ratio (SNR), which ultimately affects laser synchronization. When the transmit power of the drive signal is set to Pt = 13 dBm, the maximum transmission distance that satisfies a cross-correlation greater than 0.9 and BER lower than 3.8 × 10−3 is approximately 200 m. We can improve the received SNR to extend the maximum distance by increasing the transmit power. When Pt is set to 27 dBm, the maximum distance can reach 1000 m. It is worth noting that the distribution distance between Alice and Bob (dAB) depends on their orientation relative to the drive. If the drive is positioned exactly in the middle between Alice and Bob, dAB will be twice the transmission distance.
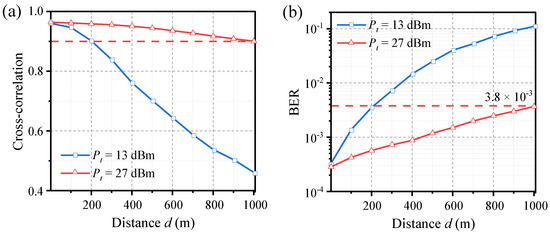
Figure 7.
Effects of transmission distance d on the (a) laser synchronization and (b) BER between Alice and Bob. The distance from the drive to Alice and Bob is equal (dDA = dDB = d). The threshold coefficient of dual-threshold quantization is set to C+ = 0.8.
Continuing with the more general case where the distance from the drive to Alice and Bob is unequal, the simulation results are shown in Figure 8. The distance from the drive to Bob (dDB) is adjusted while maintaining the distance from the drive to Alice at dDA = 100 m. When dDB is less than 240 m, the cross-correlation of the laser outputs remains above 0.9. This indicates that synchronization exhibits robustness to unequal distances. Therefore, it is also feasible to place the drive at either Alice or Bob, in which case the distribution distance dAB is equal to the transmission distance.
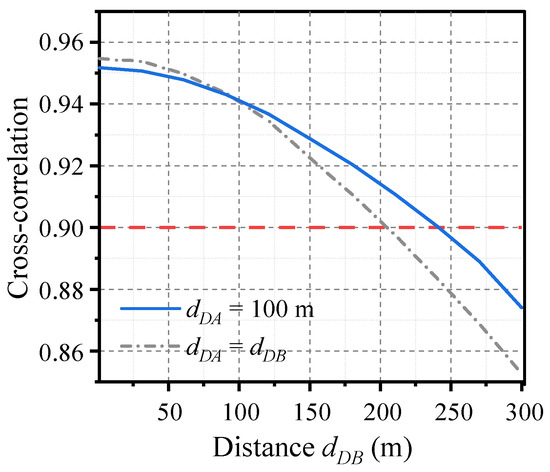
Figure 8.
Effect of unequal distances on laser synchronization. The distance from the drive to Alice is fixed at dDA = 100 m (solid blue curve). As a reference, the results for equal distances from the drive to Alice and Bob (dDA = dDB) are also plotted (dashed gray curve). The transmit power is set to Pt = 13 dBm.
5. Discussion
In this work, we have successfully demonstrated laser synchronization induced by a common wireless signal, achieving a cross-correlation of 0.95. This finding supports the feasibility of common-signal-induced laser synchronization when there is no direct optical connection between the drive source and response laser. It enables us to achieve high-speed key distribution over wireless links utilizing the wideband synchronized output of the laser. Moreover, it is worth noting that the key rate can be further improved by using a wider bandwidth drive signal, thanks to the positive correlation between the laser output and the drive signal’s bandwidth. Nevertheless, the channel bandwidth remains the primary limiting factor in determining the achievable key rate, as it dictates the maximum bandwidth of the drive signal that can be transmitted.
While we utilized a frequency band centered around 6.7 GHz for the drive signal in our experiment, it is not a strict requirement. We observed that when the center frequency of the drive signal is close to the laser’s relaxation oscillation frequency, it is easier to achieve synchronization and obtain a stronger response intensity. Typically, the relaxation oscillation frequency of a laser can be adjusted within the range of 1 to 10 GHz by varying the bias current, allowing for the usability of frequency bands within this range [39].
Our results demonstrate the feasibility of wireless key distribution at high speeds using common-signal-induced laser synchronization. When operating in a free space environment, the method of generating keys based on channel measurements is ineffective. In such cases, our scheme could serve as a valuable alternative, offering a high-speed key distribution rate. Within complex environments, such as multipath fading channels, severe changes in the receiving signal may significantly impair the efficacy of laser synchronization, ultimately leading to a reduction in key rate. By utilizing a digital signal as the drive signal, this difficulty may be resolved in an innovative manner. In combination with the robustness of digital wireless communication and the privacy of laser synchronization, high-speed security key distribution is expected in complex environments, and related work is currently under investigation.
6. Conclusions
In this paper, we propose a high-speed wireless key distribution scheme based on the chaos synchronization of nonlinear oscillators and experimentally demonstrate it using DFB lasers. Our experiments demonstrate laser synchronization induced by a common wireless signal with a cross-correlation coefficient of 0.95. Based on the broadband synchronization responses of the lasers, a secure key generation rate of up to 150 Mbit/s with a BER below 3.8 × 10−3 is accomplished. Our numerical results show that the distribution distance of the scheme can reach several hundred meters in a free space. The findings of our study indicate that the utilization of common-signal-induced laser synchronization holds promise as a viable approach for attaining high-speed wireless key distribution.
Author Contributions
Conceptualization, Y.W. and A.W.; methodology, J.X. and A.W.; validation, J.X. and Y.S.; investigation, J.X., X.Z., L.M. and Y.Z.; writing—original draft preparation, J.X.; writing—review and editing, A.W. and Y.W.; supervision, Y.W. and Y.Q.; project administration, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (Grant No. 62035009); Program for Guangdong Introducing Innovative and Enterpreneurial Teams; and Guangdong Provincial Key Laboratory of Photonics Information Technology (Grant No. 2020B121201011).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszar, I. Common randomness in information theory and cryptography. I. Secret sharing. IEEE Trans. Inf. Theory 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless information-theoretic security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Hassan, A.A.; Stark, W.E.; Hershey, J.E.; Chennakeshu, S. Cryptographic Key Agreement for Mobile Radio. Digit. Signal Process. 1996, 6, 207–212. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Bangalore, India, 9–12 December 1984. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Muramatsu, J.; Yoshimura, K.; Davis, P. Information Theoretic Security Based on Bounded Observability. In Information Theoretic Security; Kurosawa, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 128–139. [Google Scholar]
- Cachin, C.; Maurer, U. Unconditional Security against Memory-Bounded Adversaries; Springer: Berlin/Heidelberg, Germany, 1997; pp. 292–306. [Google Scholar]
- Rabin, M.O. Provably unbreakable hyper-encryption in the limited access model. In Proceedings of the IEEE Information Theory Workshop, Awaji Isl, Japan, 16–19 October 2005; 2005; pp. 34–37. [Google Scholar]
- Aono, T.; Higuchi, K.; Ohira, T.; Komiyama, B.; Sasaoka, H. Wireless secret key generation exploiting reactance-domain scalar response of multipath fading channels. IEEE Trans. Antennas Propag. 2005, 53, 3776–3784. [Google Scholar] [CrossRef]
- Patwari, N.; Croft, J.; Jana, S.; Kasera, S.K. High-Rate Uncorrelated Bit Extraction for Shared Secret Key Generation from Channel Measurements. IEEE Trans. Mob. Comput. 2010, 9, 17–30. [Google Scholar] [CrossRef]
- Ye, C.X.; Mathur, S.; Reznik, A.; Shah, Y.; Trappe, W.; Mandayam, N.B. Information-Theoretically Secret Key Generation for Fading Wireless Channels. IEEE Trans. Inf. Forensics Secur. 2010, 5, 240–254. [Google Scholar]
- Madiseh, M.G.; Neville, S.W.; McGuire, M.L. Applying Beamforming to Address Temporal Correlation in Wireless Channel Characterization-Based Secret Key Generation. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1278–1287. [Google Scholar] [CrossRef]
- Aldaghri, N.; Mahdavifar, H. Physical Layer Secret Key Generation in Static Environments. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2692–2705. [Google Scholar] [CrossRef]
- Lu, X.J.; Lei, J.; Shi, Y.X.; Li, W. Intelligent Reflecting Surface Assisted Secret Key Generation. IEEE Signal Process. Lett. 2021, 28, 1036–1040. [Google Scholar] [CrossRef]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Sakuraba, R.; Iwakawa, K.; Kanno, K.; Uchida, A. Tb/s physical random bit generation with bandwidth-enhanced chaos in three-cascaded semiconductor lasers. Opt. Express 2015, 23, 1470–1490. [Google Scholar] [CrossRef] [PubMed]
- Kanter, I.; Butkovski, M.; Peleg, Y.; Zigzag, M.; Aviad, Y.; Reidler, I.; Rosenbluh, M.; Kinzel, W. Synchronization of random bit generators based on coupled chaotic lasers and application to cryptography. Opt. Express 2010, 18, 18292–18302. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, K.; Muramatsu, J.; Davis, P.; Harayama, T.; Okumura, H.; Morikatsu, S.; Aida, H.; Uchida, A. Secure Key Distribution Using Correlated Randomness in Lasers Driven by Common Random Light. Phys. Rev. Lett. 2012, 108, 5. [Google Scholar] [CrossRef] [PubMed]
- Porte, X.; Soriano, M.C.; Brunner, D.; Fischer, I. Bidirectional private key exchange using delay-coupled semiconductor lasers. Opt. Lett. 2016, 41, 2871–2874. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.X.; Cheng, M.F.; Luo, C.K.; Deng, L.; Zhang, M.M.; Fu, S.N.; Tang, M.; Shum, P.; Liu, D.M. Semiconductor-laser-based hybrid chaos source and its application in secure key distribution. Opt. Lett. 2019, 44, 2605–2608. [Google Scholar] [CrossRef]
- Argyris, A.; Pikasis, E.; Syvridis, D. Gb/s One-Time-Pad Data Encryption With Synchronized Chaos-Based True Random Bit Generators. J. Lightwave Technol. 2016, 34, 5325–5331. [Google Scholar] [CrossRef]
- Bohm, F.; Sahakian, S.; Dooms, A.; Verschaffelt, G.; Van der Sande, G. Stable High-Speed Encryption Key Distribution via Synchronization of Chaotic Optoelectronic Oscillators. Phys. Rev. Appl. 2020, 13, 10. [Google Scholar] [CrossRef]
- Muramatsu, J.; Yoshimura, K.; Davis, P.; Uchida, A.; Harayama, T. Secret-Key Distribution Based on Bounded Observability. Proc. IEEE 2015, 103, 1762–1780. [Google Scholar] [CrossRef]
- Gao, H.; Wang, A.B.; Wang, L.S.; Jia, Z.W.; Guo, Y.Y.; Gao, Z.S.; Yan, L.S.; Qin, Y.W.; Wang, Y.C. 0.75 Gbit/s high-speed classical key distribution with mode-shift keying chaos synchronization of Fabry-Perot lasers. Light-Sci. Appl. 2021, 10, 9. [Google Scholar] [CrossRef] [PubMed]
- Muramatsu, J.; Yoshimura, K.; Arai, K.; Davis, P. Secret key capacity for optimally correlated sources under sampling attack. IEEE Trans. Inf. Theory 2006, 52, 5140–5151. [Google Scholar] [CrossRef]
- Toral, R.; Mirasso, C.R.; Hernandez-Garcia, E.; Piro, O. Analytical and numerical studies of noise-induced synchronization of chaotic systems. CHAOS 2001, 11, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Kanno, K.; Uchida, A. Consistency and complexity in coupled semiconductor lasers with time-delayed optical feedback. Phys. Rev. E 2012, 86, 9. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Xue, C.P.; Liu, D.; Lv, Y.X.; Qiu, K. Secure key distribution based on chaos synchronization of VCSELs subject to symmetric random-polarization optical injection. Opt. Lett. 2017, 42, 1055–1058. [Google Scholar] [CrossRef]
- Wang, L.S.; Chao, M.; Wang, A.B.; Gao, H.; Li, S.S.; Guo, Y.Y.; Wang, Y.C.; Yan, L.S. High-speed physical key distribution based on dispersion-shift-keying chaos synchronization in commonly driven semiconductor lasers without external feedback. Opt. Express 2020, 28, 37919–37935. [Google Scholar] [CrossRef]
- Murakami, A.; Kawashima, K.; Atsuki, K. Cavity resonance shift and bandwidth enhancement in semiconductor lasers with strong light injection. IEEE J. Quantum Electron. 2003, 39, 1196–1204. [Google Scholar] [CrossRef]
- Argyris, A.; Grivas, E.; Hamacher, M.; Bogris, A.; Syvridis, D. Chaos-on-a-chip secures data transmission in optical fiber links. Opt. Express 2010, 18, 5188–5198. [Google Scholar] [CrossRef]
- Koizumi, H.; Morikatsu, S.; Aida, H.; Nozawa, T.; Kakesu, I.; Uchida, A.; Yoshimura, K.; Muramatsu, J.; Davis, P. Information-theoretic secure key distribution based on common random-signal induced synchronization in unidirectionally-coupled cascades of semiconductor lasers. Opt. Express 2013, 21, 17869–17893. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2001; Volume 2. [Google Scholar]
- Promwong, S.; Panthap, P. Experimental evaluation of complex form Friis’ transmission formula with indoor/outdoor for ultra wideband inpulse radio. In Proceedings of the International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 13–15 May 2008; 2008; pp. 1037–1041. [Google Scholar]
- Lowery, A.J. New dynamic semiconductor laser model based on the transmission-line modelling method. IEE Proc. J. (Optoelectron.) 1987, 134, 281–289. [Google Scholar] [CrossRef]
- Duzgol, O.; Kyritsis, G.; Zakhleniuk, N. Travelling-wave modelling of the modulation dynamic performance of wavelength-tunable laser diodes using the integrated VPI and PICS3D software. IET Optoelectron. 2017, 11, 66–72. [Google Scholar] [CrossRef]
- Ohtsubo, J. Semiconductor Lasers: Stability, Instability and Chaos, 4th ed.; Springer: Cham, Switzerland, 2017; pp. 51–55. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).