Chaos-Assisted Tunneling
Abstract
1. Introduction
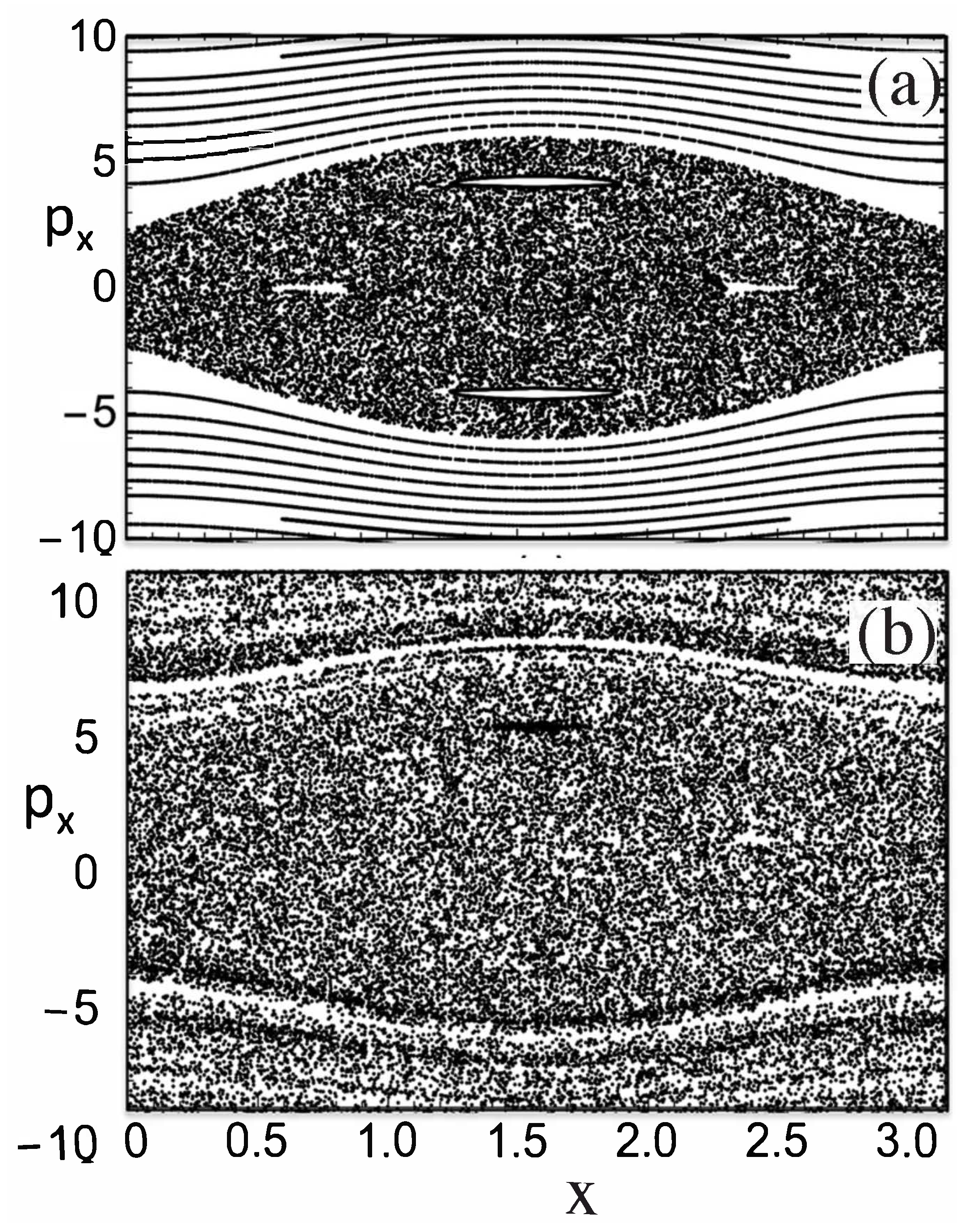
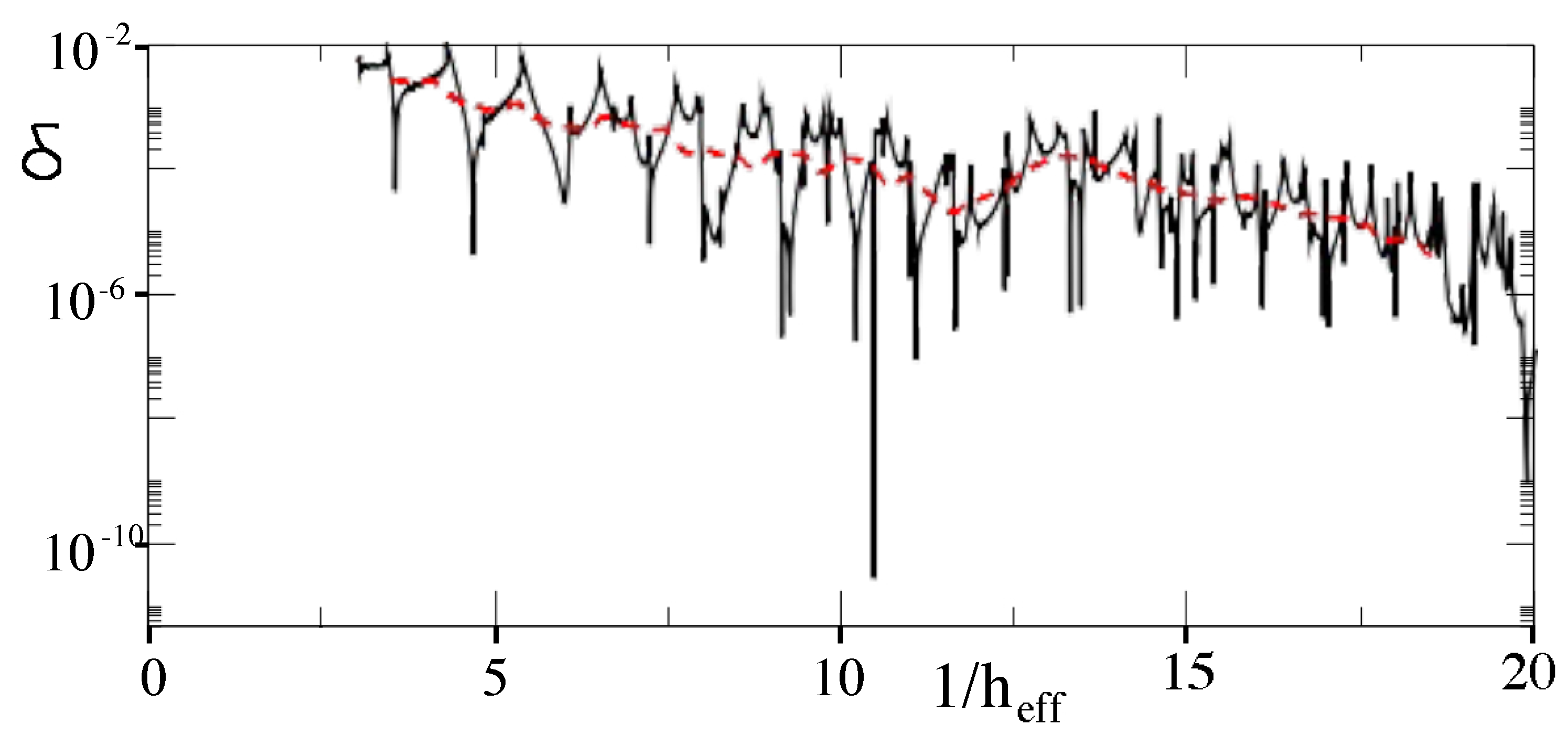
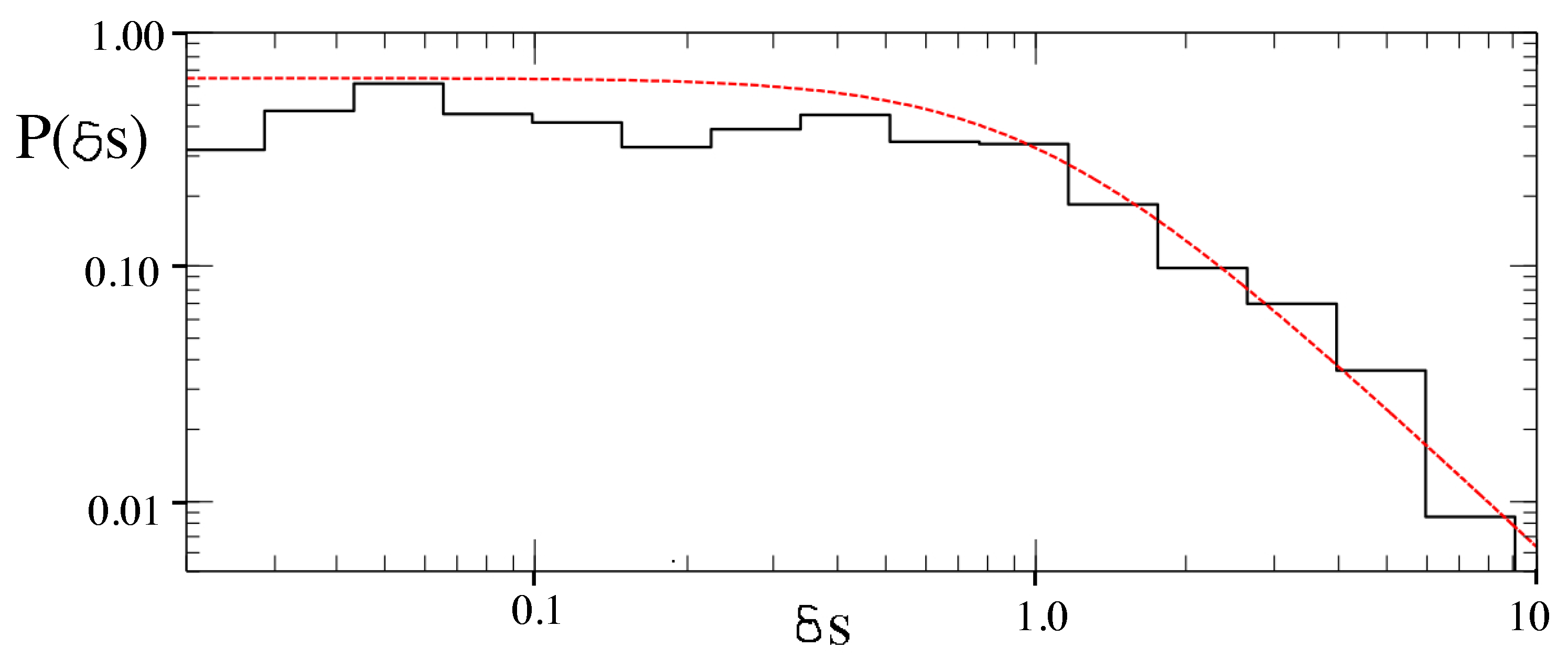
2. Chaos-Assisted Tunneling in 2D Systems
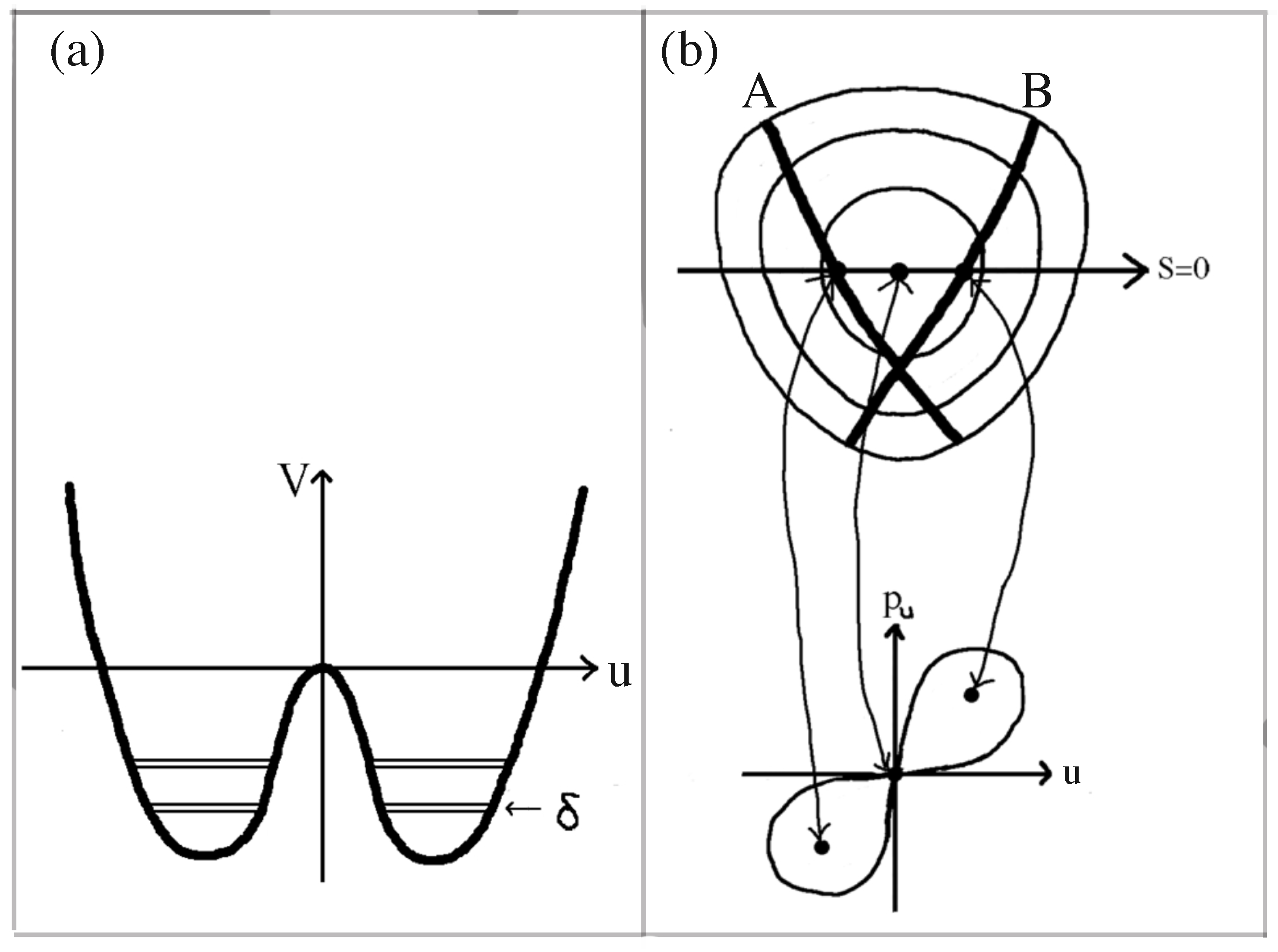
2.1. Anharmonic Oscillators
2.2. Time-Periodic 1D Systems
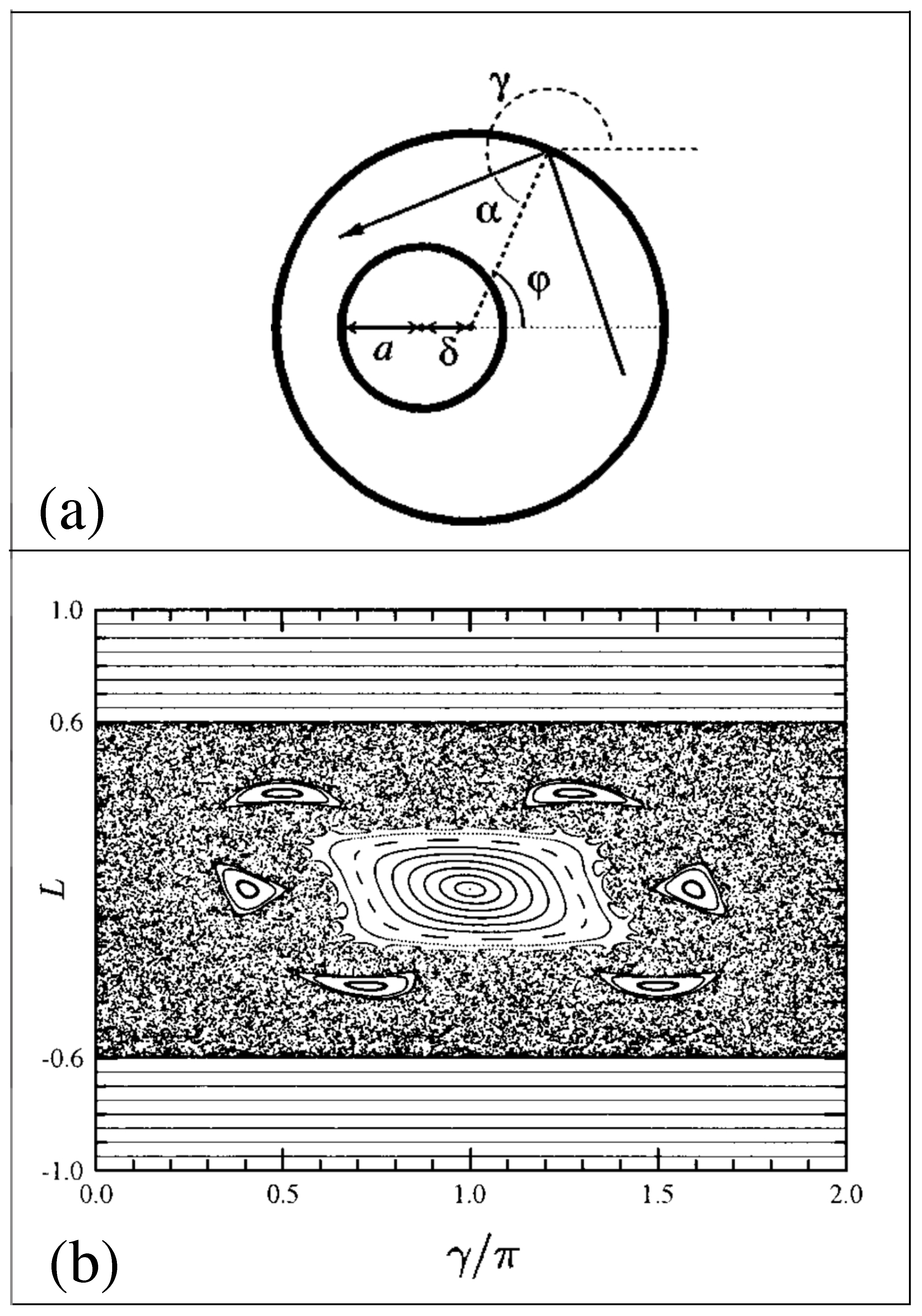
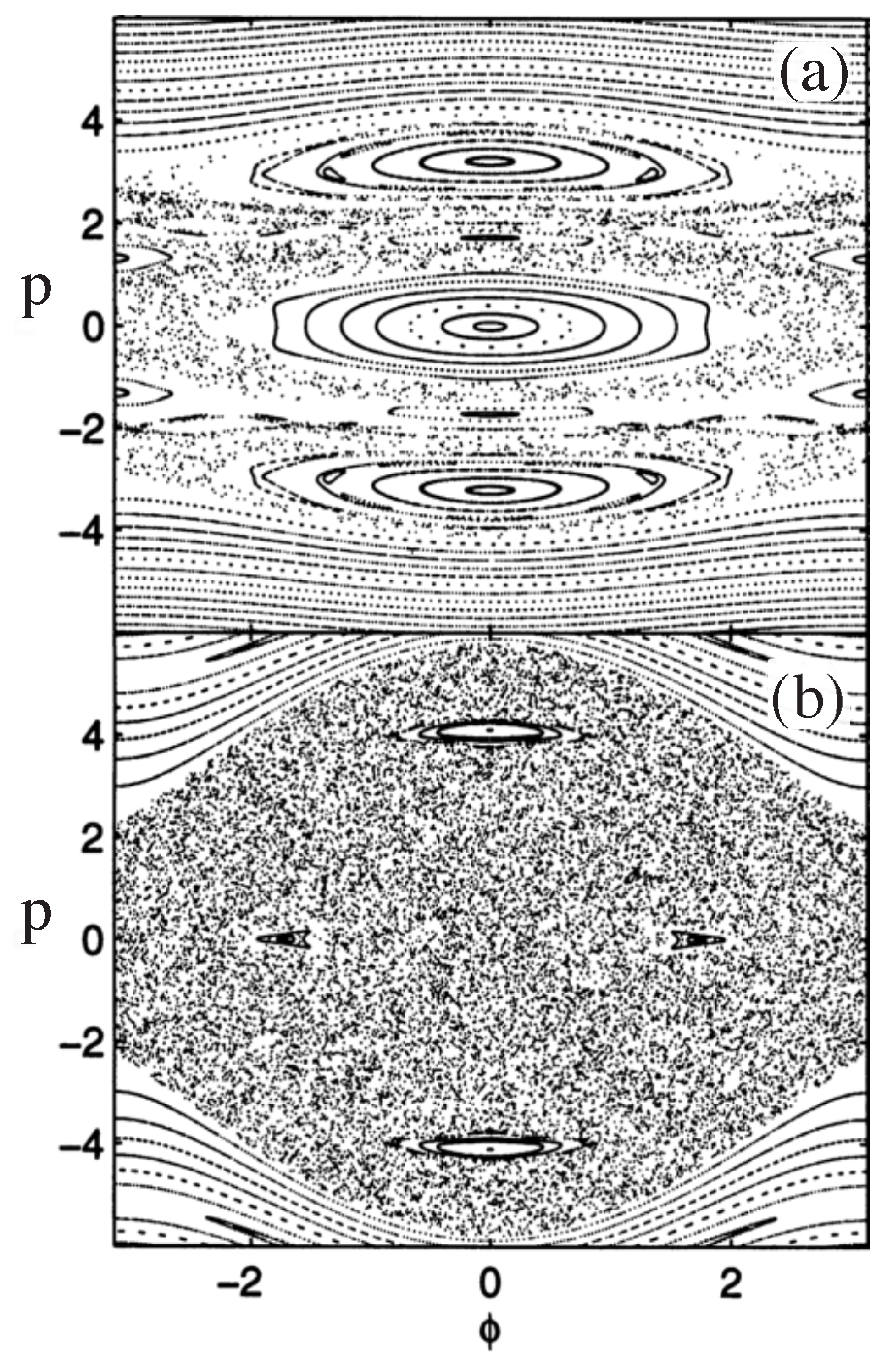
2.3. Billiards
2.3.1. Microwave Cavities
2.3.2. Optical Cavities
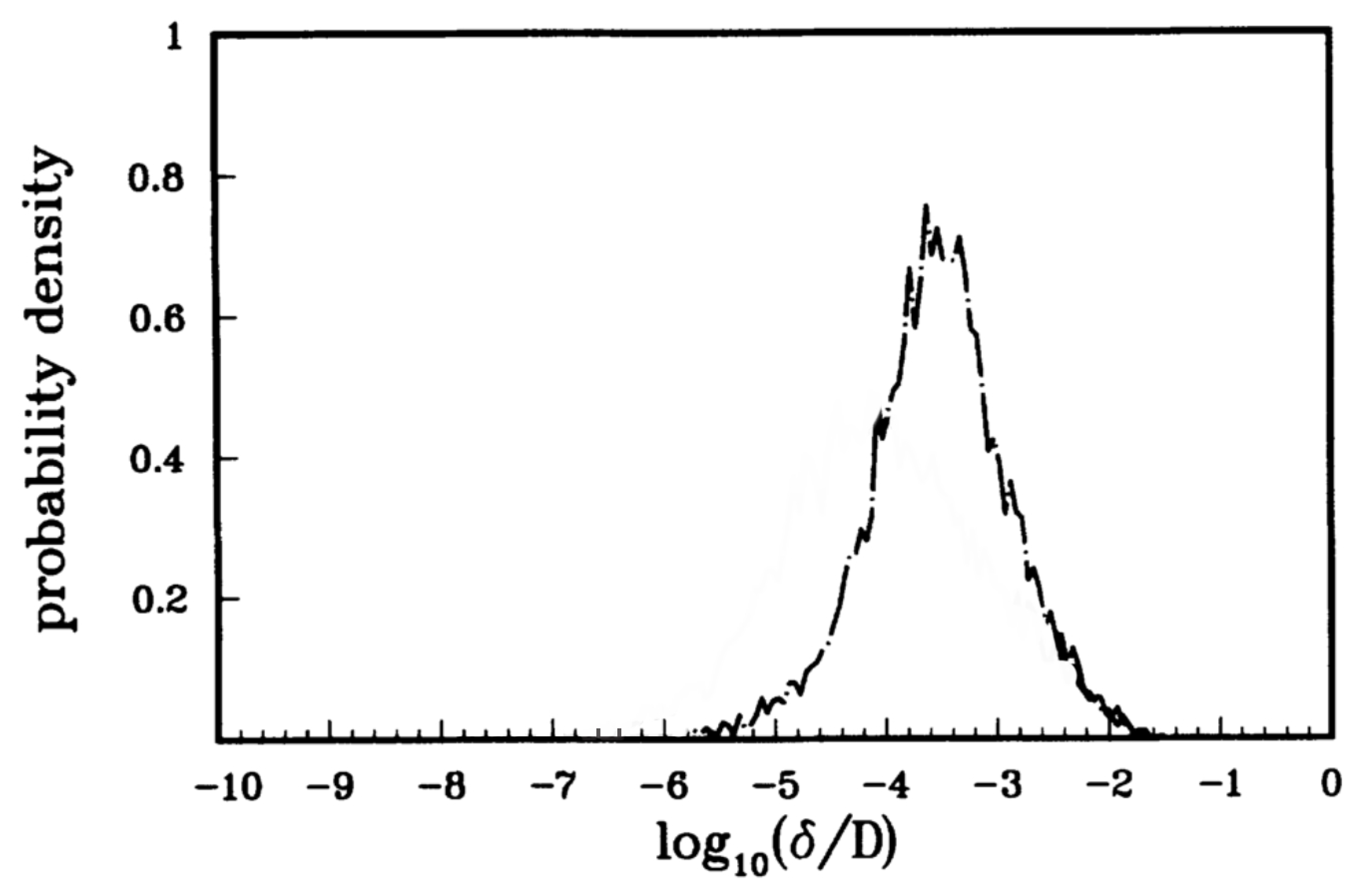
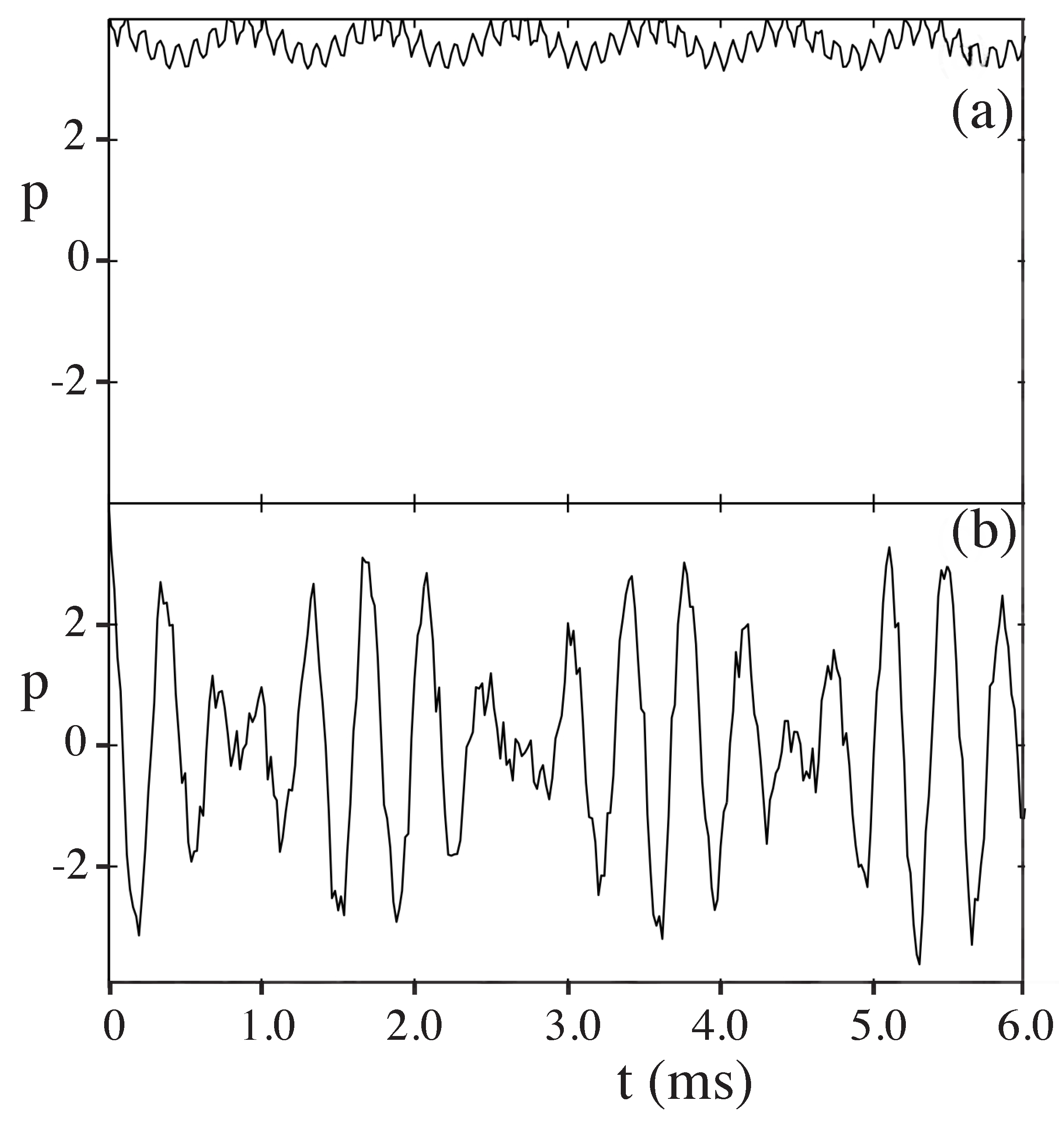
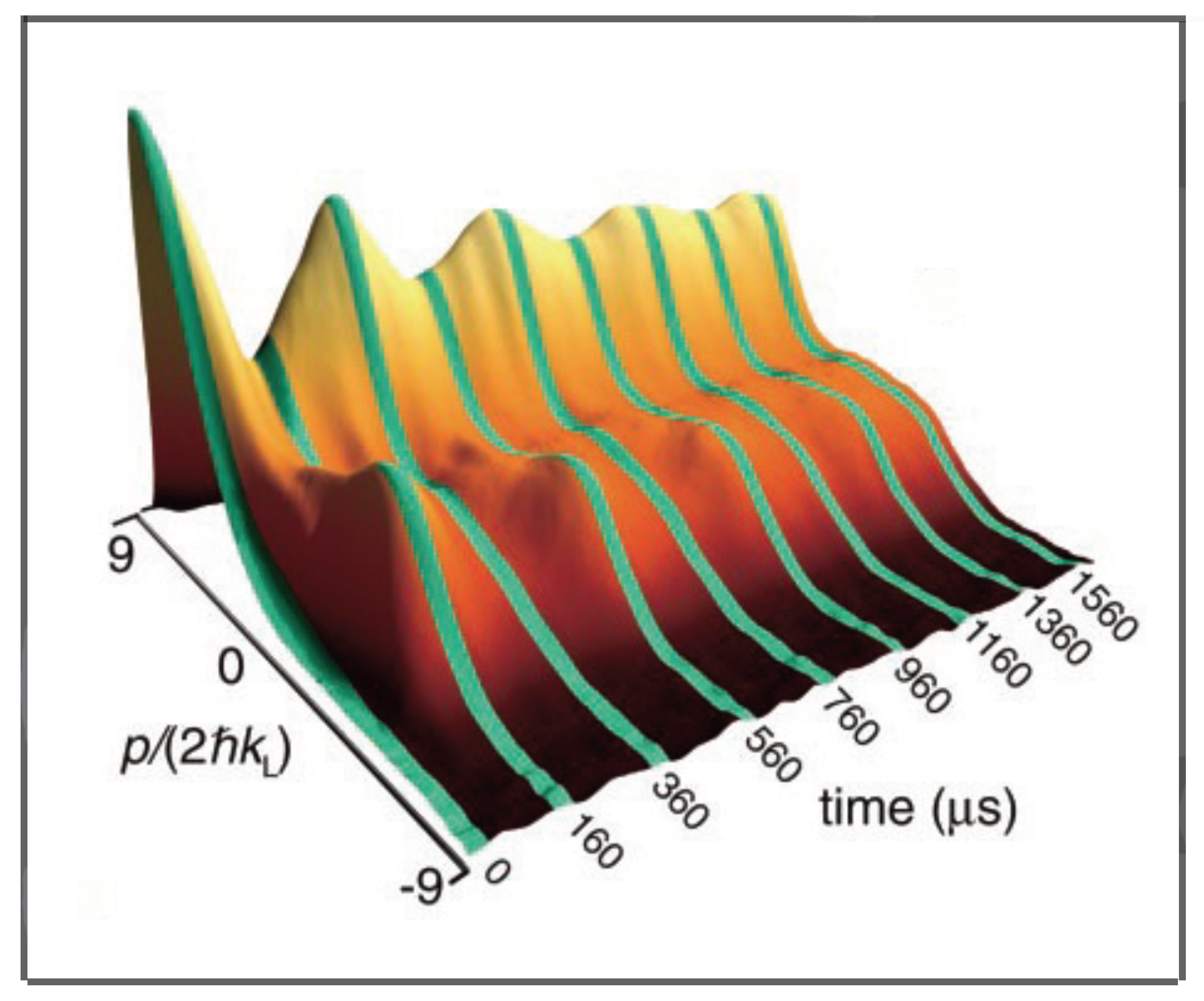
2.4. Cold Atoms
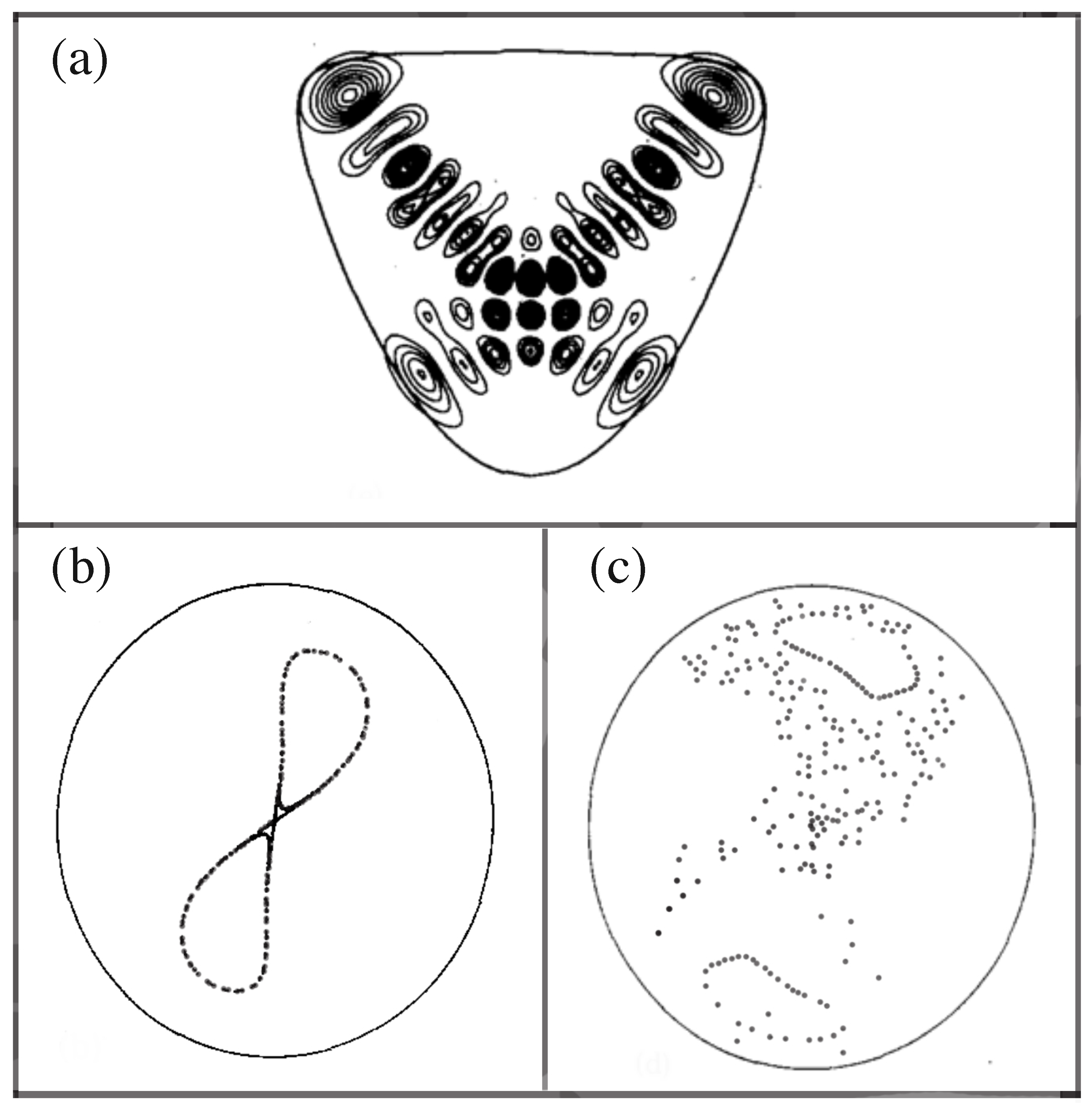
3. Three or More Degrees of Freedom
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Newton, I. The Principia: The Mathematical Principles of Natural Philosophy; Patristic Publishing: Omaha, NE, USA, 2019; English translation of the 1686 Latin language version. [Google Scholar]
- Poincaré, H. Les Méthodes Nouvlles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1899; Volume 3. [Google Scholar]
- Lichtenberg, A.J.; Lieberman, M.A. Regular and Chaotic Motion, 2nd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 1992; Volume 38. [Google Scholar]
- Sinai, Y.G. On the foundations of the ergodic hypothesis for a dynamical system of statistical mechanics. Sov. Math. Dokl. 1963, 4, 1818–1822. [Google Scholar]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888. [Google Scholar] [CrossRef]
- Reichl, L.E. The Transition to Chaos, 3rd ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Kolmogorov, A.N. The General Theory of Dynamical Systems and Classical Mechanics. In Proceedings of the International Congress of Mathematicians, Amsterdam, The Netherlands, 2–9 September 1954; English translation in Appendic D of Abraham, R. and Marsden, J.E.; Foundations of Mechanics, 2nd ed.. Routledge: New York, NY, USA, 1978. [Google Scholar]
- Arnol’d, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. Russ. Math. Surv. 1963, 18, 85. [Google Scholar] [CrossRef]
- Arnol’d, V.I.; Avez, A. Ergodic Problems of Classical Mechanics; W.A. Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Moser, J. Stable and Random Motions in Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Ree, S.; Reichl, L.E. Classical and quantum chaos in a circular billiard with a straight cut. Phys. Rev. E 1999, 60, 1607. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.J.; Heller, E.J. Quantum dynamical tunneling in bound states. J. Chem. Phys. 1981, 75, 246–254. [Google Scholar] [CrossRef]
- Tomsovic, S.; Ullmo, D. Chaos Assisted Tunneling. Phys. Rev. E 1994, 50, 145. [Google Scholar] [CrossRef] [PubMed]
- Heller, E.J.; Davis, M.J. Quantum Dynamical Tunneling in Large Molecules. A Plausible Conjecture. J. Phys. Chem. 1981, 85, 307–309. [Google Scholar] [CrossRef]
- Bohigas, O.; Tomsovic, S.; Ullmo, D. Manifestations of Classical Phase Space Structures in Quantum Mechanics. Phys. Rep. 1993, 223, 43–133. [Google Scholar] [CrossRef]
- Leyvraz, F.; Ullmo, D. The level splitting distribution in chaos-assisted tunnelling. J. Phys. A Math. Gen. 1996, 29, 2529. [Google Scholar] [CrossRef][Green Version]
- Dubertrand, R.; Billy, J.; Guéry-Odelin, D.; Georgeot, B.; Lemarixex, G. Routes towards the experimental observation of the large fluctuations due to chaos-assisted tunneling effects with cold atoms. Phys. Rev. A 2016, 94, 043621. [Google Scholar] [CrossRef]
- Lin, W.A.; Ballentine, L.E. Quantum tunneling and regular and irregular quantum dynamics of a driven double-well oscillator. Phys. Rev. A 1992, 45, 3637. [Google Scholar] [CrossRef] [PubMed]
- Latka, M.; Grigolini, P.; West, B.J. Chaos and avoided crossings. Phys. Rev. E 1994, 50, 596. [Google Scholar] [CrossRef]
- Roncaglia, R.; Bonci, L.; Izrailev, F.M.; West, B.J.; Grigolini, P. Tunneling versus Chaos in the Kicked Harper Model. Phys. Rev. Lett. 1994, 73, 802. [Google Scholar] [CrossRef] [PubMed]
- Doron, E.; Frischat, S.D. Semiclassical Description of Tunneling n Mixed Systems: Case of the Annular Billiard. Phys. Rev. Lett. 1995, 75, 1421. [Google Scholar] [CrossRef]
- Frischat, S.D.; Doron, E. Dynamical tunneling in mixed systems. Phys. Rev. E 1998, 57, 1421. [Google Scholar] [CrossRef]
- Hackenbroich, G.; Nöckel, J.U. Dynamical tunneling in optical cavities. Europhys. Lett. 1997, 39, 371. [Google Scholar] [CrossRef]
- Dembowski, C.; Gräf, H.-D.; Heine, A.; Hofferbert, R.; Rehfeld, H.; Richter, A. First Experimental Evidence for Chaos-Assisted Tunneling in a Microwave Annular Billiard. Phys. Rev. Lett. 2000, 84, 867. [Google Scholar] [CrossRef]
- Hofferbert, R.; Alt, H.; Dembowski, C.; Gräf, H.-D.; Harney, H.L.; Heine, A.; Rehfeld, H.; Richter, A. Experimental investigations of chaos-assisted tunneling in a microwave annular billiard. Phys. Rev. E 2005, 71, 046201. [Google Scholar] [CrossRef]
- Bäcker, A.; Ketzmerick, R.; Löck, S.; Vidmar, M.R.G.; Hxoxhmann, R.; Kuhl, U.; Stxoxckmann, H.-J. Dynamical Tunneling in Mushroom Billiards. Phys. Rev. Lett. 2008, 100, 174103. [Google Scholar] [CrossRef]
- Nöckel, J.U.; Stone, A.D.; Chang, R.K. Q spoiling and directionality in deformed ring cavities. Opt. Lett. 1994, 19, 1693–1695. [Google Scholar] [CrossRef] [PubMed]
- Nöckel, J.U.; Stone, A.D. Ray and wave chaos in asymmetric resonant optical cavities. Nature 1997, 385, 45–47. [Google Scholar] [CrossRef]
- Nöckel, J.U.; Stone, A.D.; Chen, G.; Grossman, H.L.; Chang, R.K. Directional emission from asymmetric resonant cavities. Opt. Lett. 1996, 21, 1609–1611. [Google Scholar] [CrossRef]
- Jiang, X.-F.; Zou, C.-L.; Wang, L.; Gong, Q.; Xiao, Y.-F. Whispering-gallery microcavities with unidirectional laser emission. Laser Photonics Rev. 2016, 10, 40. [Google Scholar] [CrossRef]
- Mekis, A.; Nöckel, J.U.; Chen, G.; Stone, A.D.; Chang, R.K. Ray Chaos and Q Spoiling in Lasing Droplets. Phys. Rev. Lett. 1995, 75, 2682. [Google Scholar] [CrossRef]
- Shinohara, S.; Harayama, T.; Fukushima, T.; Hentschel, M.; Sasaki, T.; Narimanov, E.E. Chaos-Assisted Directional Light Emission from Microcavity Lasers. Phys. Rev. Lett. 2010, 104, 163902. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, S.; Harayama, T.; Fukushima, T.; Hentschel, M.; Sunada, S.; Narimanov, E.E. Chaos-assisted emission from asymmetric resonant cavity microlasers. Phys. Rev. A. 2011, 83, 053837. [Google Scholar] [CrossRef]
- Kim, M.W.; Rim, S.; Yi, C.H.; Kim, C.M. Chaos-assisted tunneling in a deformed microcavity laser. Opt. Express 2013, 21, 32508–32515. [Google Scholar] [CrossRef]
- Xiao, Y.-F.; Jiang, X.-F.; Yang, Q.-F.; Wang, L.; Shi, K.; Li, Y.; Gong, Q. Tunneling-induced transparency in a chaotic microcavity. Laser Photonics Rev. 2013, 7, L51–L54. [Google Scholar] [CrossRef]
- Qian, Y.J.; Liu, H.; Cao, Q.T.; Kullig, J.; Rong, K.; Qiu, C.W.; Wiersig, J.; Gong, Q.; Chen, J.; Xiao, Y.F. Regulated Photon Transport in Chaotic Microcavities by Tailoring Phase Space. Phys. Rev. Lett. 2021, 127, 273902. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Liu, Y.; Xiao, S.; Wang, Z.; Fan, Y.; Han, J.; Ge, L.; Song, Q. Direct observation of chaotic resonances in optical microcavities. Light Sci. Appl. 2021, 10, 135. [Google Scholar] [CrossRef]
- Graham, R.; Schlautmann, M.; Zoller, P. Dynamical localization of atomic-beam defection by a modulated standing light wave. Phys. Rev. A 1992, 45, R19. [Google Scholar] [CrossRef]
- Steck, D.A.; Oskay, W.H.; Raizen, M.G. Observation of Chaos-Assisted Tunneling Between Islands of Stablity. Science 2001, 293, 274. [Google Scholar] [CrossRef]
- Steck, D.A.; Oskay, W.H.; Raizen, M.G. Fluctuations and Decoherence in Chaos-Assisted Tunneling. Phys. Rev. Lett. 2002, 88, 120406. [Google Scholar] [CrossRef] [PubMed]
- Keshavamurthy, S.; Schlagheck, P. (Eds.) Dynamical Tunneling, Theory and Experiment; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hensinger, W.K.; Häffner, H.; Browaeys, A.; Heckenberg, N.R.; Helmerson, K.; McKenzie, C.; Milburn, G.J.; Phillips, W.D.; Rolston, S.L.; Rubinsztein-Dunlop, H.; et al. Dynamical tunneling of ultracold atoms. Nature 2001, 412, 52. [Google Scholar] [CrossRef]
- Hensinger, W.K.; Mouchet, A.; Julienne, P.S.; Delande, D.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Analysis of dynamical tunneling experiments with a Bose-Einstein condensate. Phys. Rev. A 2004, 70, 013408. [Google Scholar] [CrossRef]
- Luter, R.; Reichl, L.E. Floquet analysis of atom-optics tunneling experiments. Phys. Rev. A 2002, 66, 053615. [Google Scholar] [CrossRef]
- Luter, R.; Reichl, L.E. Tunneling between Floquet states in atom-optics experiments. Int. J. Mod. Phys B 2003, 17, 4101. [Google Scholar] [CrossRef]
- Mouchet, A.; Miniatura, C.; Kaiser, R.; Gremaud, B.; Delande, D. Chaos-assisted tunneling with cold atoms. Phys. Rev. E 2001, 64, 016221. [Google Scholar] [CrossRef]
- Mouchet, A.; Delande, D. Signatures of chaotic tunneling. Phys. Rev. E 2003, 67, 046216. [Google Scholar] [CrossRef] [PubMed]
- Arnal, M.; Chatelain, G.; Martinez, M.; Dupont, N.; Giraud, O.; Ullmo, D.; Georgeot, B.; Lemarié, G.; Billy, J.; Guéry-Odelin, D. Chaos-assisted tunneling resonances in a synthetic Floquet superlattice. Sci. Adv. 2020, 6, eabc4886. [Google Scholar] [CrossRef]
- Boretz, Y.; Reichl, L.E. Arnold diffusion in a driven optical lattice. Phys. Rev. E 2016, 93, 032214. [Google Scholar] [CrossRef] [PubMed]
- Froeschlé, C.; Guzzo, M.; Lega, E. Grapical Evolution of the Arnold Web: From Order to Chaos. Science 2000, 289, 2108. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-D.; Reichl, L.E.; Jung, C. The vibrational dynamics of 3D HOCl above dissociation. J. Chem. Phys. 2015, 142, 124304. [Google Scholar] [CrossRef] [PubMed]
- Krithika, V.R.; Santhanam, M.S.; Mahesh, T.S. NMR investigations of dynamical tunneling in spin systems. Phys. Rev. A 2023, 108, 032207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reichl, L.E. Chaos-Assisted Tunneling. Entropy 2024, 26, 144. https://doi.org/10.3390/e26020144
Reichl LE. Chaos-Assisted Tunneling. Entropy. 2024; 26(2):144. https://doi.org/10.3390/e26020144
Chicago/Turabian StyleReichl, Linda E. 2024. "Chaos-Assisted Tunneling" Entropy 26, no. 2: 144. https://doi.org/10.3390/e26020144
APA StyleReichl, L. E. (2024). Chaos-Assisted Tunneling. Entropy, 26(2), 144. https://doi.org/10.3390/e26020144