Performance Analysis of Troposphere Scattering Communication Channel with Chirp-BOK Modulation
Abstract
1. Introduction
2. System Model with Chirp-BOK Modulation
2.1. Chirp Signal Model
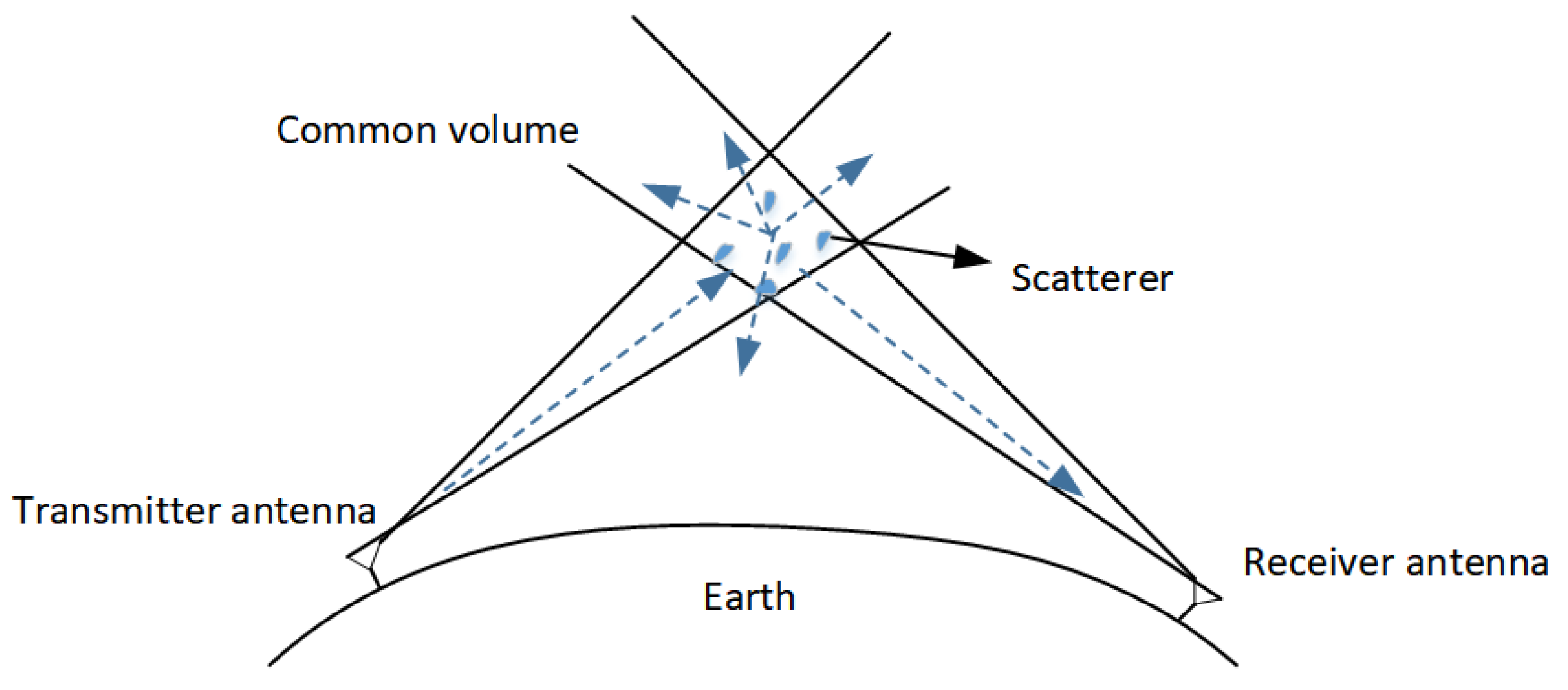
2.2. Troposcatter Channel Model
2.3. Chirp-BOK System Model
| Algorithm 1: Chirp-BOK modulation algorithm. |
 |
| Algorithm 2: Chirp-BOK demodulation algorithm. |
 |
3. Theoretical Analysis for Bit Error Rate
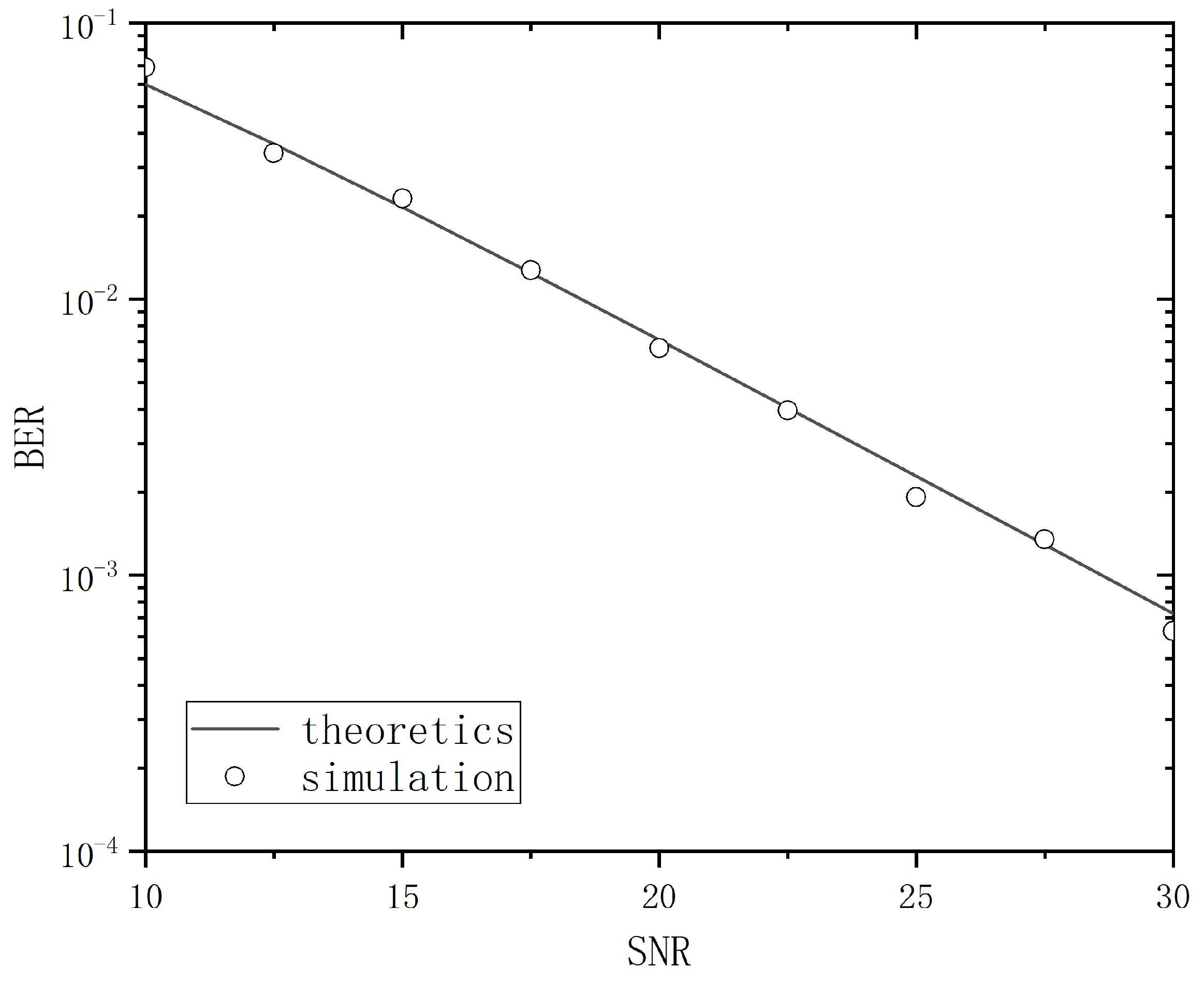
3.1. Rayleigh Flat Fading
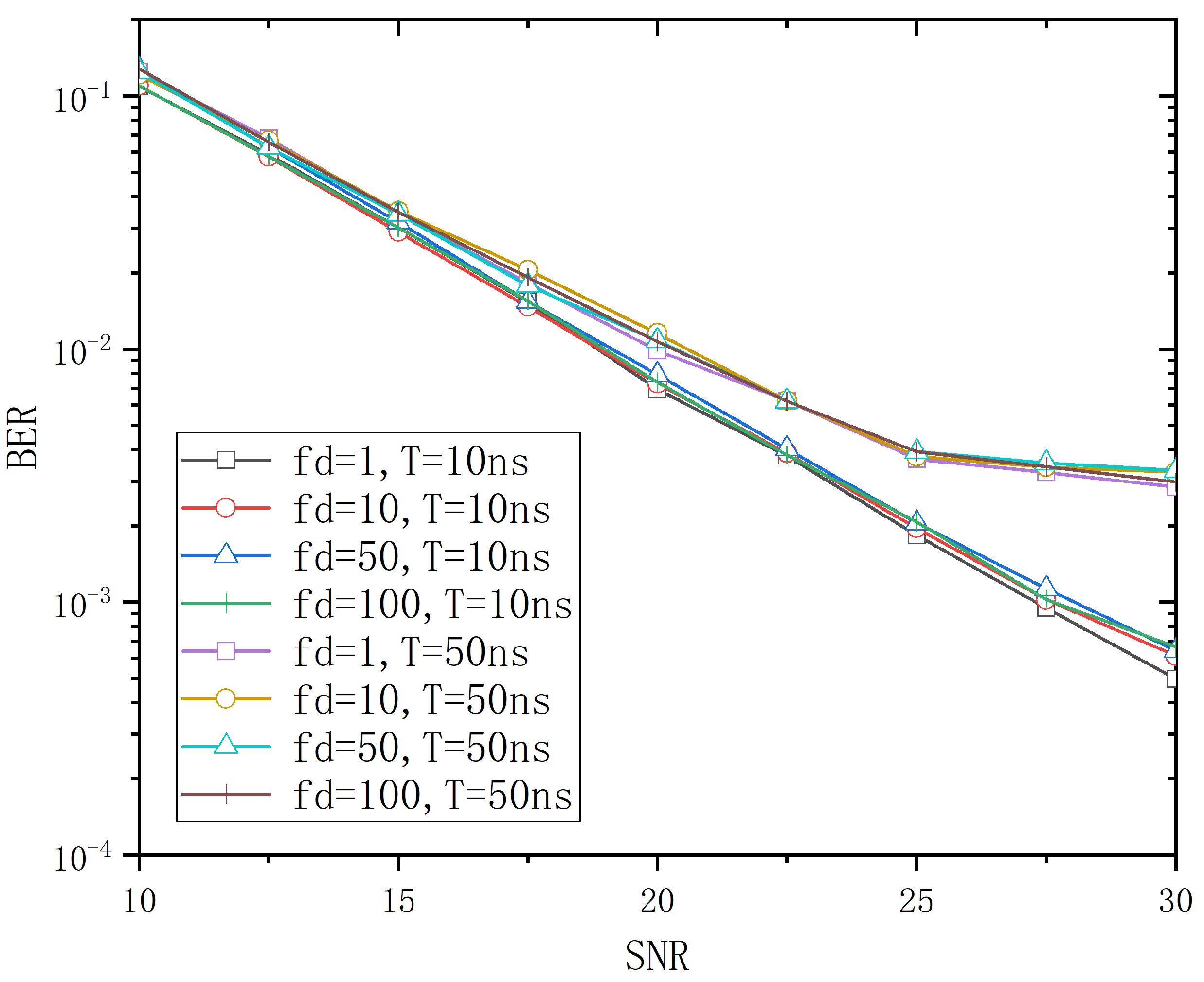
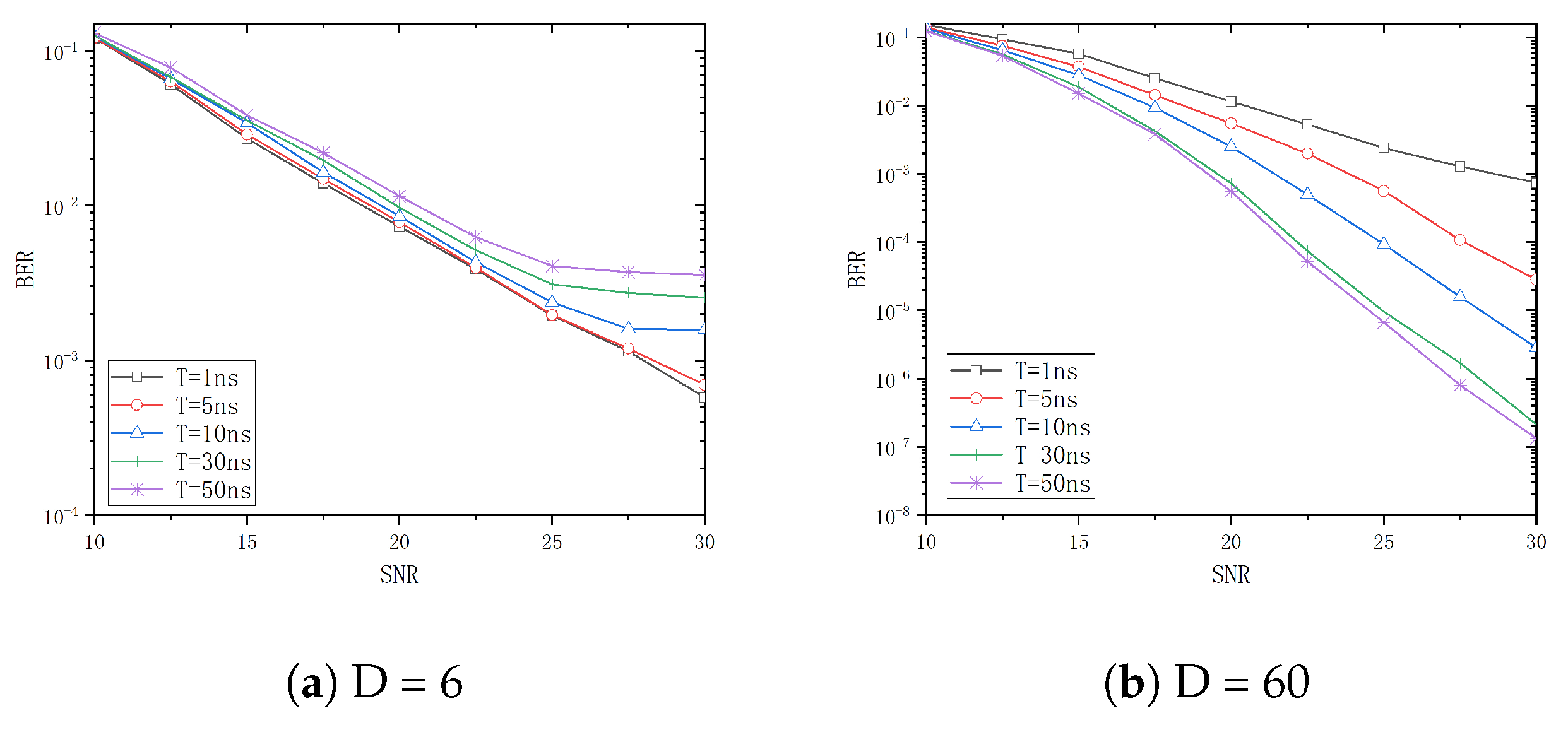
3.2. Frequency-Selective Fading
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSS | Chirp spread spectrum |
| BOK | Binary orthogonal keying |
| ISI | Inter-symbol interference |
| BER | Bit error rate |
| SNR | Signal-to-noise power ratio |
| Probability density function | |
| CDF | Cumulative distribution function |
References
- Li, C.; Chen, X.; Liu, X. Cognitive Tropospheric Scatter Communication. IEEE. Trans. Vehic. Technol. 2017, 67, 1482–1491. [Google Scholar] [CrossRef]
- IEEE. Std. 802.15.4a-2007; IEEE Standard for Information Technology—Local and Metropolitan Area Networks—Specific Requirements—Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs): Amendment 1: Add Alternate PHYs. IEEE: Piscataway, NJ, USA, 2007; pp. 1–210. [CrossRef]
- Winkler, M. Chirp signals for communications. In Proceedings of the 1962 IEEE Western Electronic Show and Convention Conference (WESCON), Los Angeles, CA, USA, 21–24 August 1962; pp. 14–17. [Google Scholar]
- Lee, H.; Kim, T.H.; Choi, J.W. Chirp signal-based aerial acoustic communication for smart devices. In Proceedings of the 2015 IEEE Conference on Computer Communications(INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 2407–2415. [Google Scholar] [CrossRef]
- Zhao, Q.M.; Zhang, Q.Y.; Zhang, N.T. Multiple chirp-rate modulation based on fractional fourier transform. In Proceedings of the 2010 First International Conference on Pervasive Computing, Signal Processing and Applications (PCSPA), Harbin, China, 17–19 September 2010; pp. 688–691. [Google Scholar] [CrossRef]
- Kaihan, Z.; Keyu, C.; Fei, Y.; Jinwang, Y. Chirp FSK based on FRFT for underwater acoustic communication. In Proceedings of the 2017 7th IEEE International Conference on Electronics Information and Emergency Communication (ICEIEC), Macau, China, 21–23 July 2017; pp. 49–52. [Google Scholar] [CrossRef]
- Vangelista, L. Frequency shift chirp modulation: The LoRa modulation. IEEE. SPL 2017, 24, 1818–1821. [Google Scholar] [CrossRef]
- Yuyang, J. Performance Study of LFM-Based Shared Signal for Radar and Communications. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. (In Chinese). [Google Scholar] [CrossRef]
- Jianxun, H. Research on Radar Communication Signal Integration and Beamforming. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. (In Chinese). [Google Scholar] [CrossRef]
- Reynders, B.; Meert, W.; Pollin, S. Range and coexistence analysis of long range unlicensed communication. In Proceedings of the International Conference on Telecommunications(ICT), Thessaloniki, Greece, 16–18 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Reynders, B.; Pollin, S. Chirp spread spectrum as a modulation technique for long range communication. In Proceedings of the 2016 Symposium on Communications and Vehicular Technologies (SCVT), Mons, Belgium, 22–22 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Zhang, Y.; Zhao, X. Performance Analysis of LoRa Modulation with Residual Frequency Offset. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018; pp. 835–839. [Google Scholar] [CrossRef]
- Jia, W.; Wang, W.Q.; Cheng, J.; Hau, Y.; Kang, Z. Low PAPR OFDM-Chirp Modulation Signaling Scheme. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7963–7966. [Google Scholar] [CrossRef]
- Jia, Z.; Zheng, W.; Yuan, F. A Two-Dimensional Chirp-MFCSK Modulation Method for Underwater LoRa System. IEEE. Intern. Thin. J. 2022, 9, 24388–24397. [Google Scholar] [CrossRef]
- Zhao, Z. The Multiple Access PSK-Chirp System and the Demodulation Based on FrFT. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 77–83. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, S.; Wang, X.; Zhu, Y. Fractional Chirp Rate Based Non-Orthogonal Transmission for Chirp Spread Spectrum Modulation. In Proceedings of the 2023 International Conference on Intelligent Communication and Networking (ICN), Changzhou, China, 10–12 November 2023; pp. 111–115. [Google Scholar] [CrossRef]
- Gupta, A.; Agarwal, S.; Chakravarty, S. Non-Coherent Distributed Transmission with Chirp Spread Spectrum Modulation. In Proceedings of the 2024 IEEE International Conference on Communications Workshops (ICC Workshops), Denver, CO, USA, 9–13 June 2024; pp. 51–56. [Google Scholar] [CrossRef]
- Bacioccola, A.; Cicconetti, C.; Eklund, C.; Lenzini, L.; Li, Z.; Mingozzi, E. IEEE 802.16: History, status and future trends. Comput. Commun. 2010, 33, 113–123. [Google Scholar] [CrossRef]
- Xuemei, S.; Xudong, Z. Research on tropospheric scattering for radar signal beyond line-of-sight transmission. Modern Radar 2011, 33, 9–12. [Google Scholar] [CrossRef]
- Mengnan, W. Research on Beyond-Line-of-Sight Wideband Array Signal Beamforming Technology. Master’s Thesis, National University of Defense Technology, Changsha, China, 2013. (In Chinese). [Google Scholar]
- Garg, A.; Das, S.S. Design of troposcatter broadband link based on SCFDE. In Proceedings of the 2017 IEEE International Conference on Advanced Networks and Telecommunications System(ANTS), Bhubaneswar, India, 17–20 December 2017. [Google Scholar] [CrossRef]
- Biscarini, M.; De Sanctis, K.; Di Fabio, S.; Montopoli, M.; Milani, L.; Marzano, F.S. Assessment and Uncertainty Estimation of Weather-Forecast Driven Data Transfer for Space Exploration at Ka- and X-Band. IEEE. Trans. Antenn. Propag. 2019, 67, 3308–3322. [Google Scholar] [CrossRef]
- Binsong, S.; Jiancun, Q.; Wencheng, R. A new scattering communication method based on frequency hopping and simulation research. J. Jilin Univ. 2020, 50, 1870–1875. [Google Scholar] [CrossRef]
- ITU-R Recommendation P.617-5, Propagation Prediction Techniques and Data Required for the Design of Trans-Horizon Radio-Relay Systems. 2019. Available online: https://1f8a81b9b0707b63-19211.webchannel-proxy.scarabresearch.com/rec/R-REC-P.617/en (accessed on 4 September 2024).
- Annavajjala, R.; Zagami, J. Design and Performance Evaluation of High-Capacity Mobile Troposcatter Links Under Mobility, Frequency Selectivity, and Antenna Pointing Errors. In Proceedings of the 2018 IEEE Military Communications Conference (MILCOM), Los Angeles, CA, USA, 29–31 October 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Dong, H.; Liu, H. Anti-disturbance filter design for a class of stochastic systems with fading channels. Sci. China Inf. Sci. 2020, 63, 327–329. [Google Scholar] [CrossRef]
- Minggao, Z. Troposphere Scatter Propagation; Publishing House of Electronics Industry: Beijing, China, 2004; ISBN 9787121003820. [Google Scholar]
- Tranter, W.; Shanmugan, K.; Rappaport, T.; Kosbar, K. Principles of Communication Systems Simulation with Wireless Applications; Prentice Hall: London, UK, 2003; ISBN 0134947908. [Google Scholar]
- Hashemi, H. The indoor radio propagation channel. Proc. IEEE 1993, 81, 943–968. [Google Scholar] [CrossRef]
- Kailath, T. Channel characterization: Time-variant dispersive channels. Lect. Commun. Syst. Theor. 1961, 95–123. [Google Scholar]
- Alsharef, M.; Rao, R.K. M-ary chirp modulation for coherent and non-coherent data transmission. In Proceedings of the 2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 3–6 May 2015; pp. 213–219. [Google Scholar] [CrossRef]
- Eng, T.; Milstein, L.B. Coherent DS-CDMA perfomance in Nakagami multipath fading. IEEE Trans. Commun. 1995, 43, 1134–1143. [Google Scholar] [CrossRef]

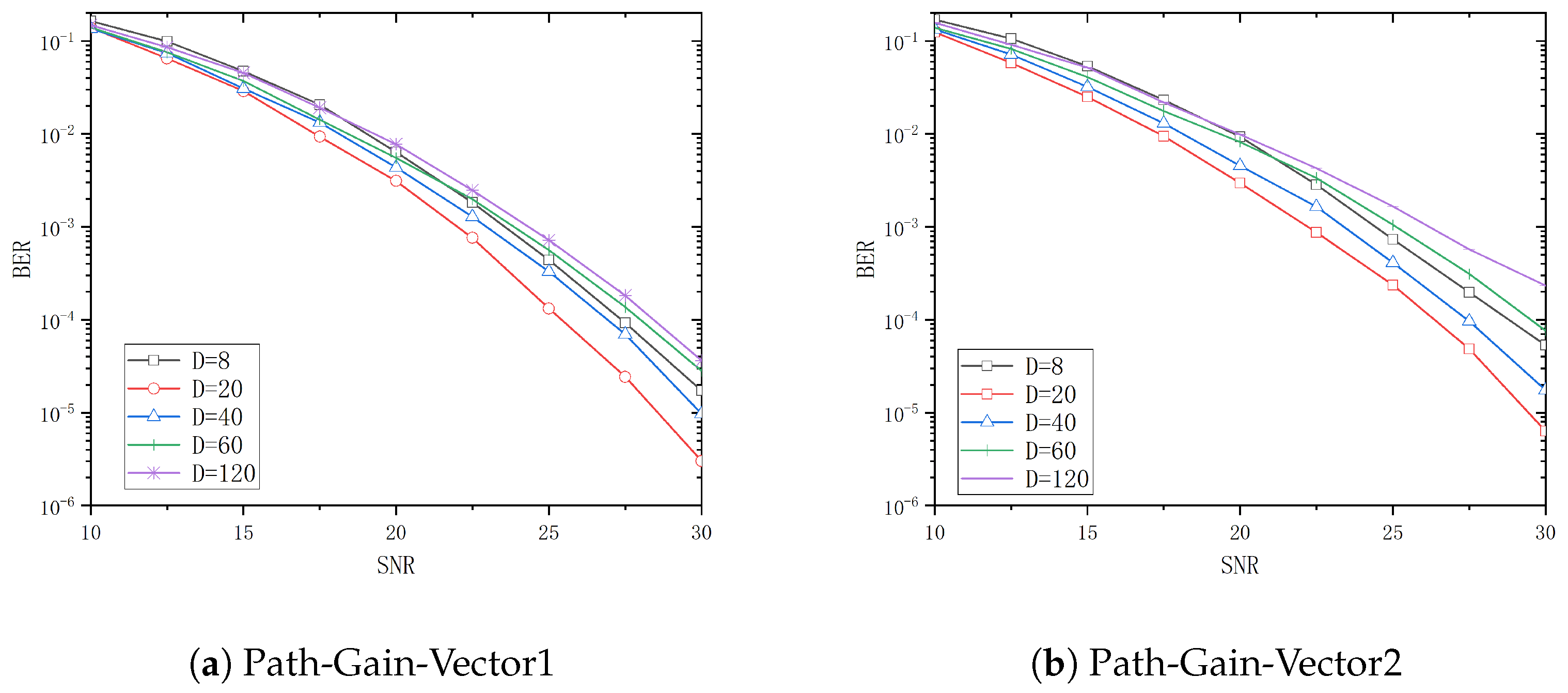
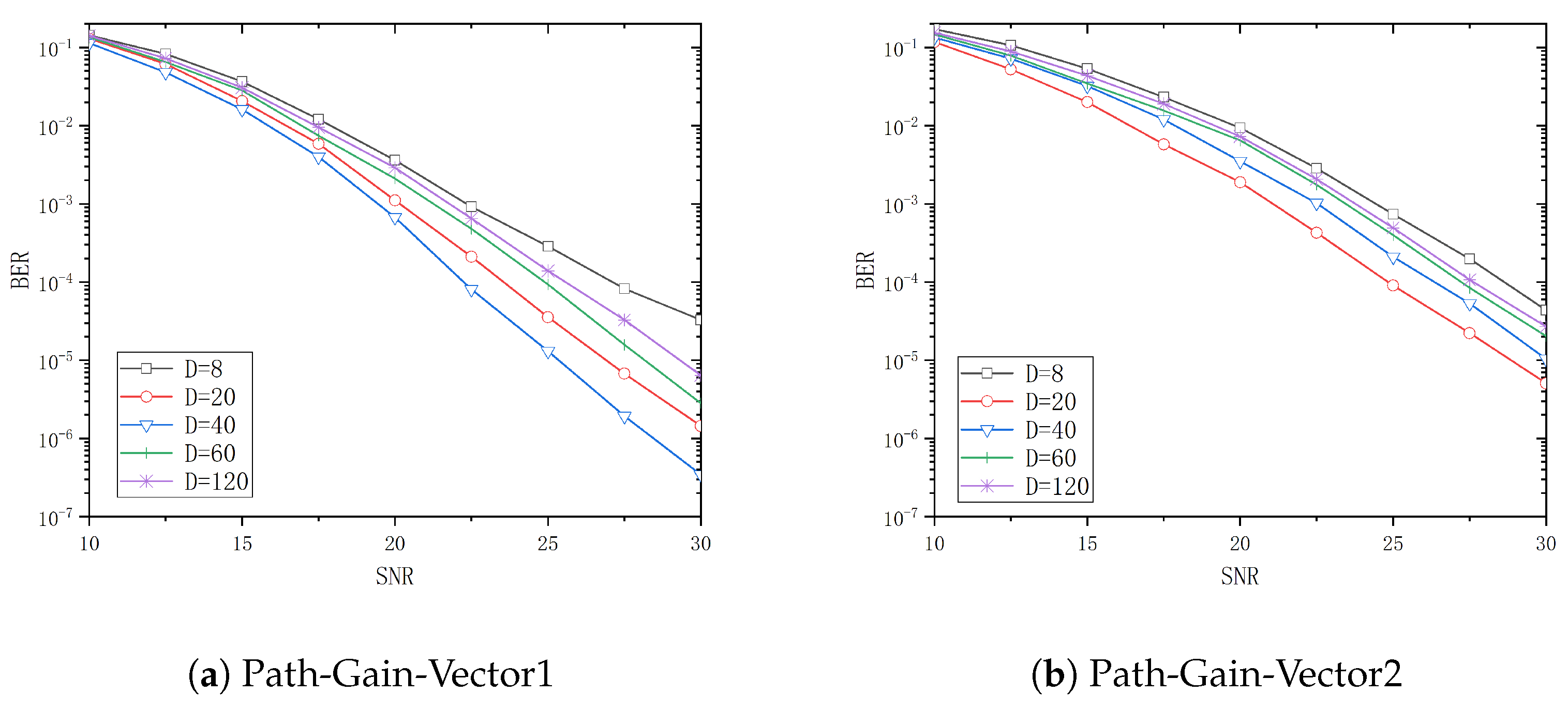



| Parameter | Value |
|---|---|
| Maximum Doppler Shift | |
| Delay-Vector | |
| Path-Gain-Vector1 | |
| Path-Gain-Vector2 | |
| Time–Bandwidth Product |
| Path-Gain-Vector1 | ||||
|---|---|---|---|---|
| 27.2 | 27.5 | 31.9 | 32.5 | |
| 25.5 | 24.0 | 23.5 | 25.0 | |
| 26.8 | 22.5 | 22.8 | 22.7 | |
| 28.2 | 25.0 | 22.4 | 22.5 | |
| 28.8 | 25.8 | 25.0 | 21.4 |
| Path-Gain-Vector2 | ||||
|---|---|---|---|---|
| 28.7 | 28.7 | 30.4 | 32.7 | |
| 26.0 | 24.8 | 22.7 | 23.4 | |
| 27.5 | 26.9 | 25.1 | 22.9 | |
| 29.1 | 27.4 | 26.3 | 25.4 | |
| 32.6 | 27.7 | 27.4 | 25.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, J.; Liu, Z.; Liu, Y.; Xie, T. Performance Analysis of Troposphere Scattering Communication Channel with Chirp-BOK Modulation. Entropy 2024, 26, 1052. https://doi.org/10.3390/e26121052
Shao J, Liu Z, Liu Y, Xie T. Performance Analysis of Troposphere Scattering Communication Channel with Chirp-BOK Modulation. Entropy. 2024; 26(12):1052. https://doi.org/10.3390/e26121052
Chicago/Turabian StyleShao, Junhu, Zaiping Liu, Yishuo Liu, and Tianjiao Xie. 2024. "Performance Analysis of Troposphere Scattering Communication Channel with Chirp-BOK Modulation" Entropy 26, no. 12: 1052. https://doi.org/10.3390/e26121052
APA StyleShao, J., Liu, Z., Liu, Y., & Xie, T. (2024). Performance Analysis of Troposphere Scattering Communication Channel with Chirp-BOK Modulation. Entropy, 26(12), 1052. https://doi.org/10.3390/e26121052







