A Three-Dimensional Time-Varying Channel Model for THz UAV-Based Dual-Mobility Channels
Abstract
1. Introduction
2. Modeling of Uav-Based Dual-Mobility Wireless Channels in the Thz Band
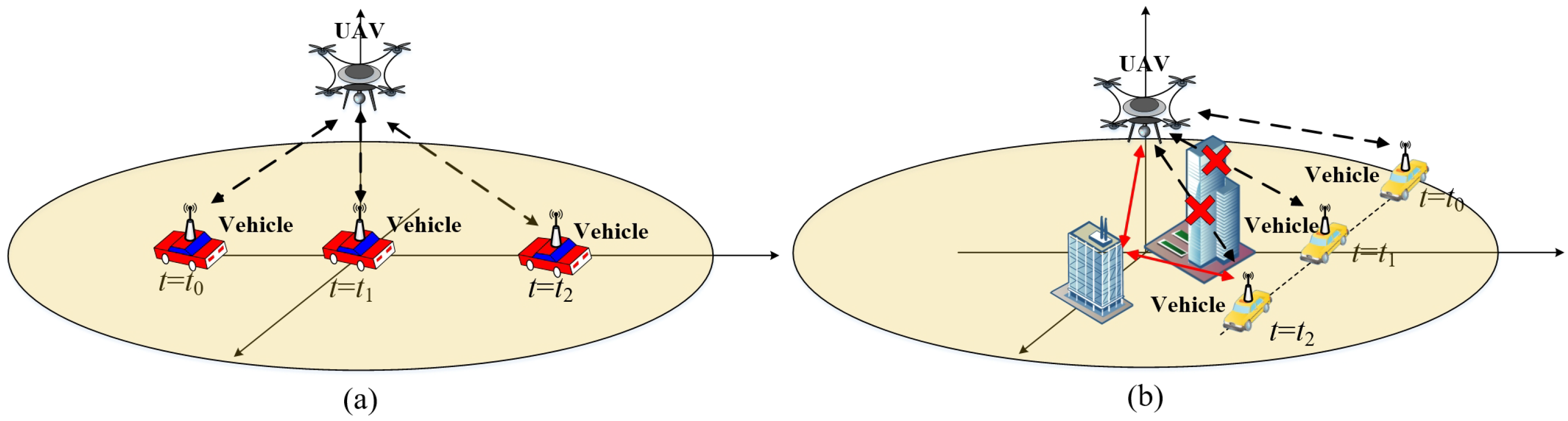
2.1. Description of the Wireless Communication System
2.2. Time-Varying Small-Scale Fading Coefficient of the NLoS Path on the Rough Surfaces
2.3. Atmospheric Molecule Absorption Attenuation of Radio-Wave for the Wireless Channel
2.3.1. Attenuation Coefficient of Oxygen Molecule to Radio-Wave
2.3.2. Attenuation Coefficient of Water Vapor Molecule to Radio-Wave
2.4. Propagation Scenarios for the Time-Varying Channel
2.4.1. LoS Propagation Path
2.4.2. NLoS Propagation Path
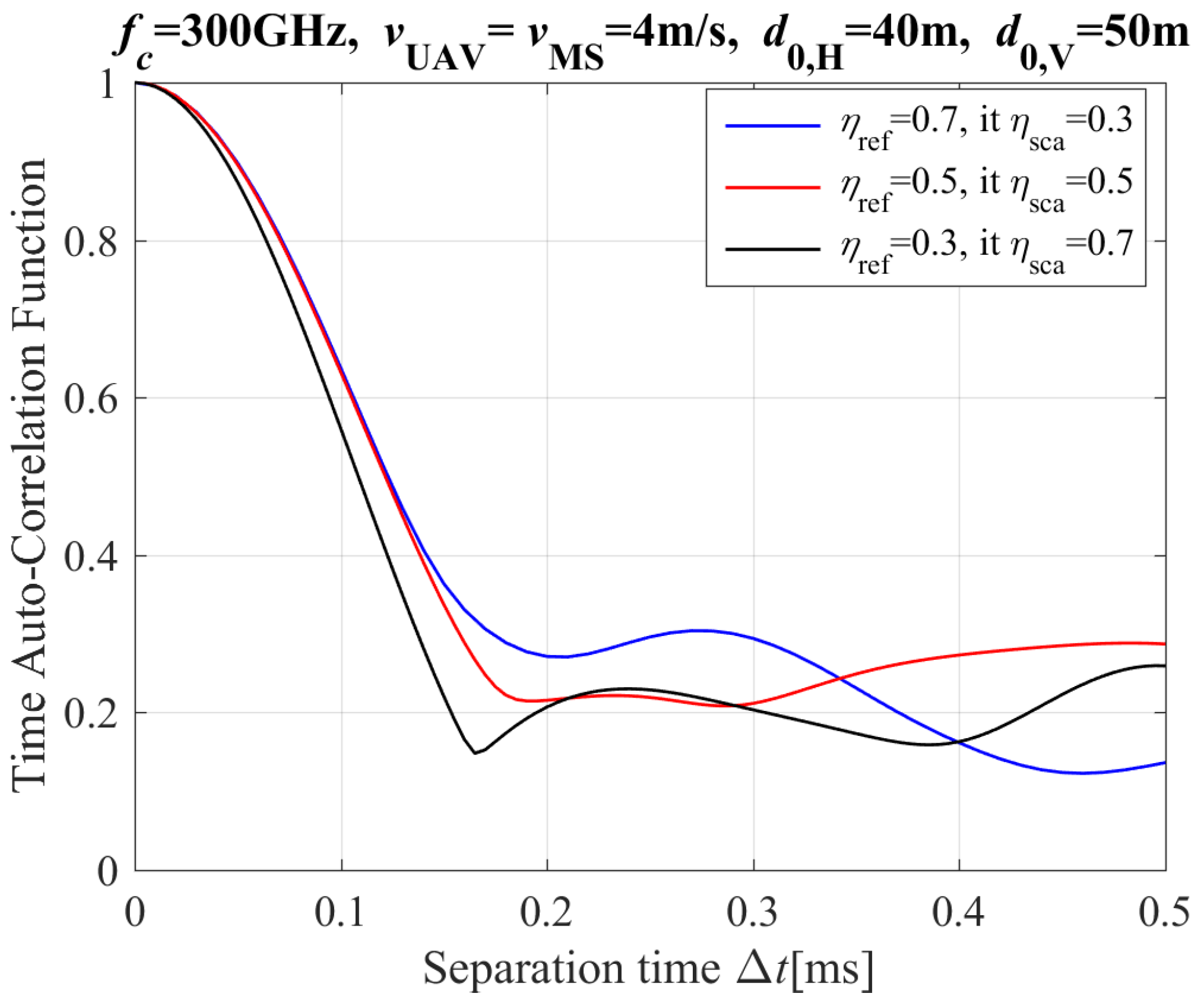
2.4.3. Time Auto-Correlation Function
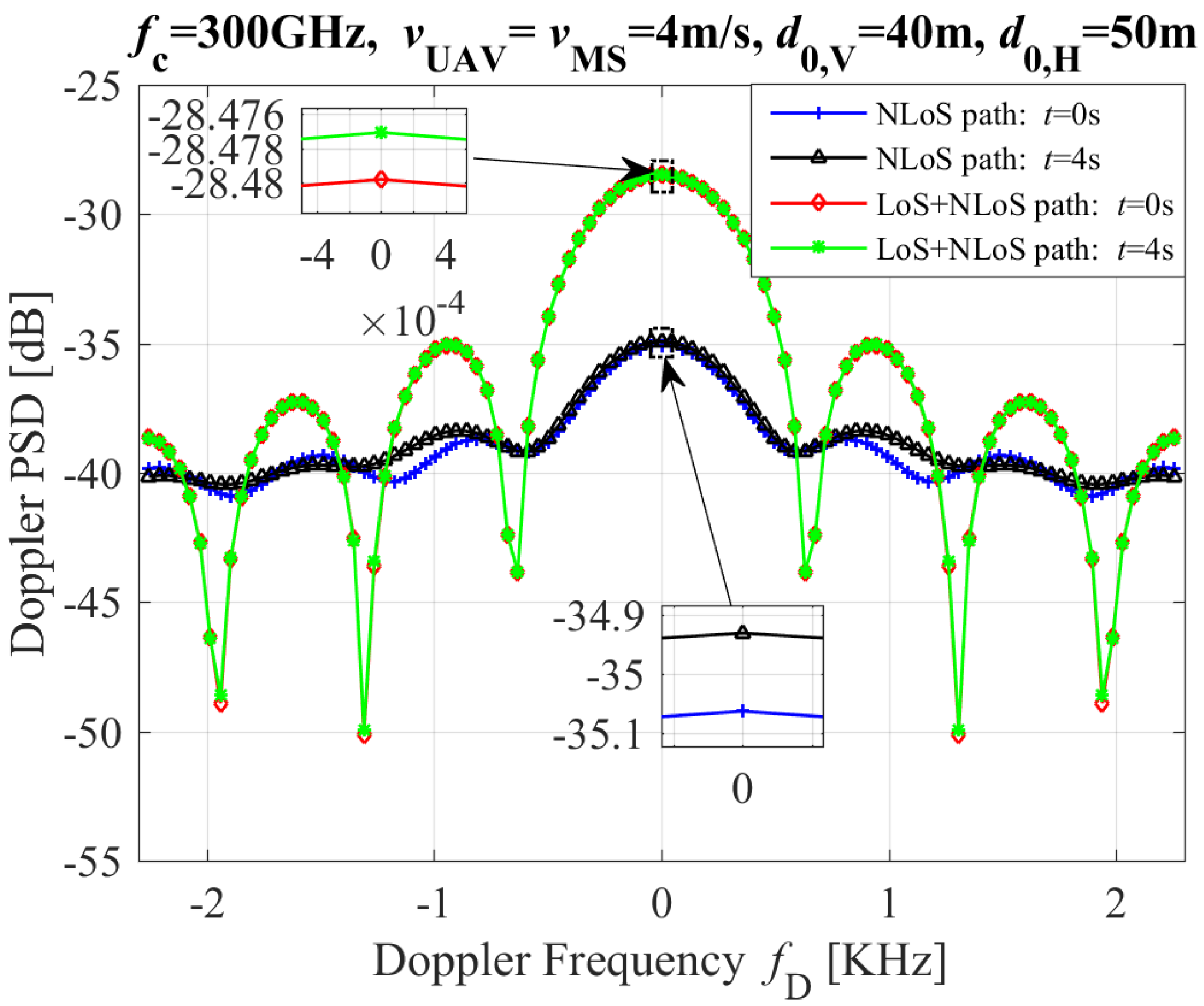
2.5. Doppler Power Spectrum Density
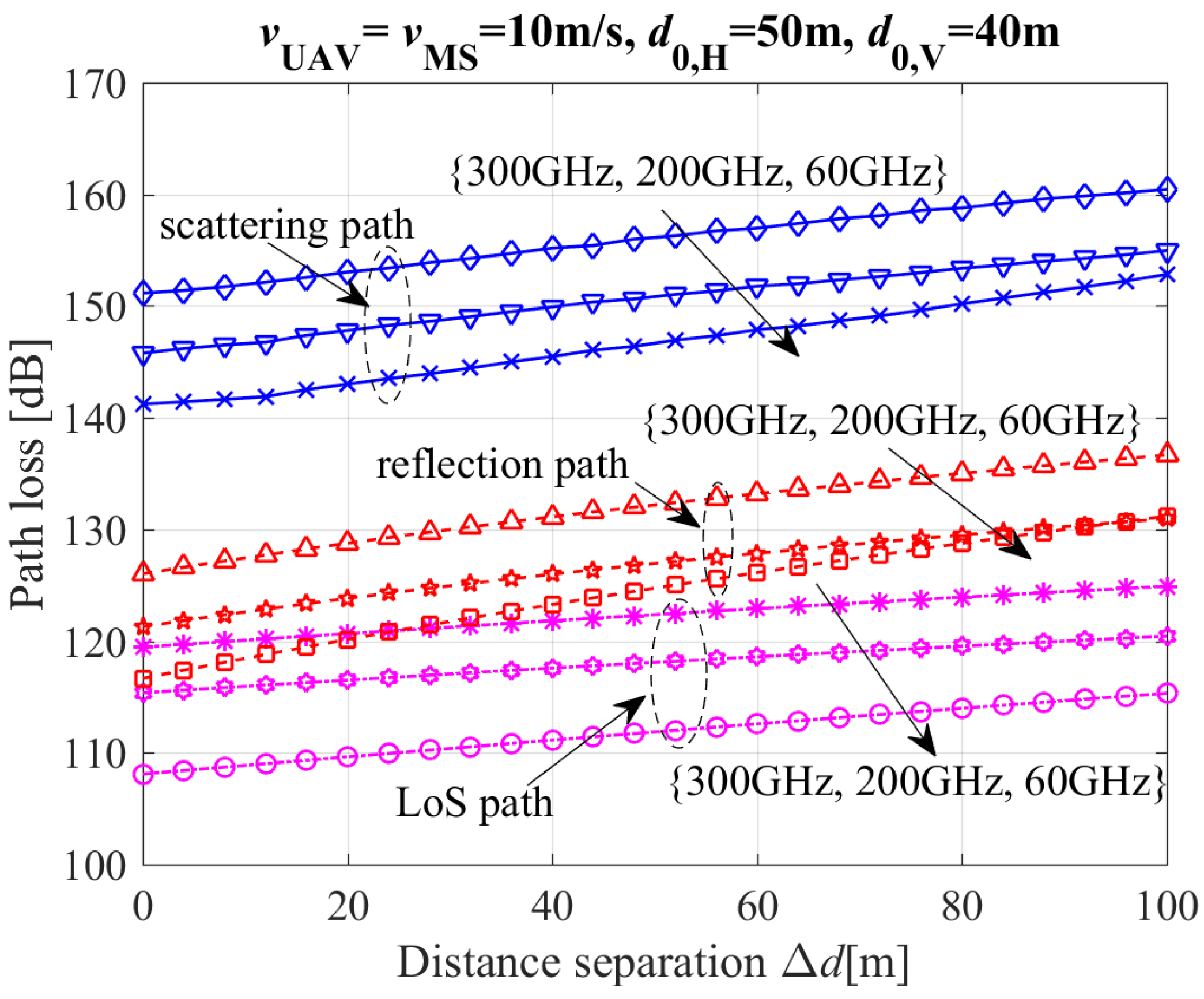
3. Numerical Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Description |
| UAV | Unmanned aerial vehicle |
| THz | Terahertz |
| 3D | Three-dimensional |
| T-ACF | Time autocorrelation function |
| DPSD | Doppler power spectrum density |
| mm-wave | Millimeter wave |
| SAGNs | Space–air–ground integrate networks |
| 6G | Sixth generation |
| A2G | Air to ground |
| A2A | Air to air |
| AFD | Average fading duration |
| STC | Space–time correlation |
| STFC | Space–time–frequency correlation |
| GBSM | Geometry-based stochastic model |
| Tx | Transmitter |
| Rx | Receiver |
| LoS | Line-of-sight |
| NLoS | Non-line-of-sight |
| CIR | Channel impulse response |
| MPCs | Multipath components |
References
- Wang, C.X.; Huang, J.; Wang, H.; Gao, X.; You, X.; Hao, Y. 6G wireless channel measurements and models trends and challenges. IEEE Veh. Technol. Mag. 2020, 15, 22–32. [Google Scholar] [CrossRef]
- Yuan, Y.; He, R.; Ai, B.; Ma, Z.; Miao, Y.; Niu, Y.; Zhang, J.; Chen, R.; Zhong, Z. A 3D geometry-based THz channel model for 6G ultra massive MIMO systems. IEEE Trans. Veh. Technol. 2022, 71, 2251–2266. [Google Scholar] [CrossRef]
- Valavanis, K.P.; Vachtsevanos, G.J. Handbook of Unmanned Aerial Vehicle; Springer: Berlin, Germany, 2015; p. 2077. [Google Scholar]
- Namuduri, K.; Chaumette, S.; Kim, J.H.; Sterbenz, J.P. UAV Networks and Communications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tut. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Klaine, P.V.; Nadas, J.P.; Souza, R.D.; Imran, M.A. Distributed drone base station positioning for emergency cellular networks using reinforcement learning. Cogn. Comput. 2018, 10, 790–804. [Google Scholar] [CrossRef] [PubMed]
- Jayakody, D.N.K.; Perera, T.D.P.; Ghrayeb, A.; Hasna, M.O. Selfenergized UAV-assisted scheme for cooperative wireless relay networks. IEEE Trans Veh. Technol. 2020, 69, 578–592. [Google Scholar] [CrossRef]
- Song, Y.; Lim, S.H.; Jeon, S.W.; Baek, S. On cooperative achievable rates of UAV assisted cellular networks. IEEE Trans. Veh. Technol. 2020, 69, 9882–9895. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.X.; Liu, Y.; Tian, J.; Qiao, J.; Zheng, X. 3D Non-Stationary Wideband UAV-to-Ground MIMO Channel Models Based on Aeronautic Random Mobility Model. IEEE Trans. Veh. Technol. 2021, 70, 11154–11168. [Google Scholar] [CrossRef]
- Lian, Z.; Su, Y.; Wang, Y.; Jiang, L.; Zhang, Z.; Xie, Z.; Li, S. A Non-Stationary 3-D Wideband Channel Model for Low Altitude UAV-MIMO Communication Systems. IEEE Internet Things J. 2022, 9, 5290–5303. [Google Scholar] [CrossRef]
- Bai, L.; Huang, Z.; Zhang, X.; Cheng, X. A Non-Stationary 3D Model for 6G Massive MIMO mmWave UAV Channels. IEEE Trans. Wireless Commun. 2021, 1–14. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Zhong, Z.; Yang, M. A Non-Stationary Geometry-Based MIMO Channel Model for Millimeter-Wave UAV Networks. IEEE J. Sel. Areas Commun. 2021, 39, 2960–2974. [Google Scholar] [CrossRef]
- Bai, L.; Han, R.; Liu, J.; Yu, Q.; Choi, J.; Zhang, W. Air-to-Ground Wireless Links for High-Speed UAVs. IEEE J. Sel. Areas Commun. 2020, 38, 2918–2930. [Google Scholar] [CrossRef]
- Yu, X.; Jia, S.; Hu, H.; Galili, M.; Morioka, T.; Jepsen, P.U.; Oxenløwe, L.K. 160 Gbit/s photonics wireless transmission in the 300–500 GHz band. APL Photon. 2016, 1, 081301. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Wang, S.; Lu, Z.; Yang, Z.; Liu, S.; Qiao, M.; He, Y.; Pang, X.; Zhang, X.; et al. Tbit/s multi-dimensional multiplexing THz-over-fiber for 6G wireless communication. J. Lightw. Technol. 2021, 39, 5783–5790. [Google Scholar] [CrossRef]
- Wang, C.X.; Bian, J.; Sun, J.; Zhang, W.; Zhang, M. A survey of 5G channel measurements and models. IEEE Commun. Surveys Tuts. 2018, 20, 3142–3168. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.X.; Huang, J.; Wang, H.; Gao, X. A General 3D Space-Time-Frequency Non-Stationary THz Channel Model for 6G Ultra-Massive MIMO Wireless Communication Systems. IEEE J. Sel. Areas Commun. 2021, 39, 1576–1589. [Google Scholar] [CrossRef]
- Han, C.; Bicen, A.O.; Akyildiz, I.F. Multiray channel modeling and wideband characterization for wireless communications in the terahertz band. IEEE Trans. Wireless Commun. 2015, 14, 2402–2412. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, L.; He, Z. A 3-D hybrid dynamic channel model for indoor THz communications. China Commun. 2021, 18, 50–65. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.X.; Huang, J.; Wang, H.; Gao, X.; You, X.; Hao, Y. A novel 3D non-stationary GBSM for 6G THz ultra-massive MIMO wireless systems. IEEE Trans. Veh. Technol. 2021, 70, 12312–12324. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Zhang, C.; Yu, X.; Dong, Y. Three-dimensional non-stationary geometry-based modeling of sub-THz MIMO channels for UAV air-to-ground communications. In Proceedings of the IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023. [Google Scholar]
- Zhang, K.; Wang, H.; Zhang, C.; Yu, X.; Dong, Y. Three dimensional geometry based stochastic model for sub-terahertz air to air UAV-MIMO channels. In Proceedings of the IEEE/CIC lnternational Conference on Communications, Dalian, China, 10–12 August 2023. [Google Scholar]
- Zhang, K.; Zhang, C.; Wang, H.; Yang, Z.; Yu, X.; Li, Y. Nonstationary Channel Modeling for Wireless Communications Underlaying UAV-Based RelayAssisted IIoT Networks in the Subterahertz Band. IEEE Internet Things J. 2024, 11, 26888–26900. [Google Scholar] [CrossRef]
- International Telecommunication Union, Radio Communication Sector (ITU-R), Recommendation P.676-11, Attenuation by Atmospheric GASES. 2016. Available online: https://www.itu.int/rec/R-REC-P.676-11-201609-I (accessed on 20 July 2024).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, F.; Li, Y.; Wang, X.; Yang, Z.; Liu, Y.; Zhang, C.; Li, X. A Three-Dimensional Time-Varying Channel Model for THz UAV-Based Dual-Mobility Channels. Entropy 2024, 26, 924. https://doi.org/10.3390/e26110924
Zhang K, Zhang F, Li Y, Wang X, Yang Z, Liu Y, Zhang C, Li X. A Three-Dimensional Time-Varying Channel Model for THz UAV-Based Dual-Mobility Channels. Entropy. 2024; 26(11):924. https://doi.org/10.3390/e26110924
Chicago/Turabian StyleZhang, Kai, Fenglei Zhang, Yongjun Li, Xiang Wang, Zhaohui Yang, Yuanhao Liu, Changming Zhang, and Xin Li. 2024. "A Three-Dimensional Time-Varying Channel Model for THz UAV-Based Dual-Mobility Channels" Entropy 26, no. 11: 924. https://doi.org/10.3390/e26110924
APA StyleZhang, K., Zhang, F., Li, Y., Wang, X., Yang, Z., Liu, Y., Zhang, C., & Li, X. (2024). A Three-Dimensional Time-Varying Channel Model for THz UAV-Based Dual-Mobility Channels. Entropy, 26(11), 924. https://doi.org/10.3390/e26110924






