Image Forensics in the Encrypted Domain
Abstract
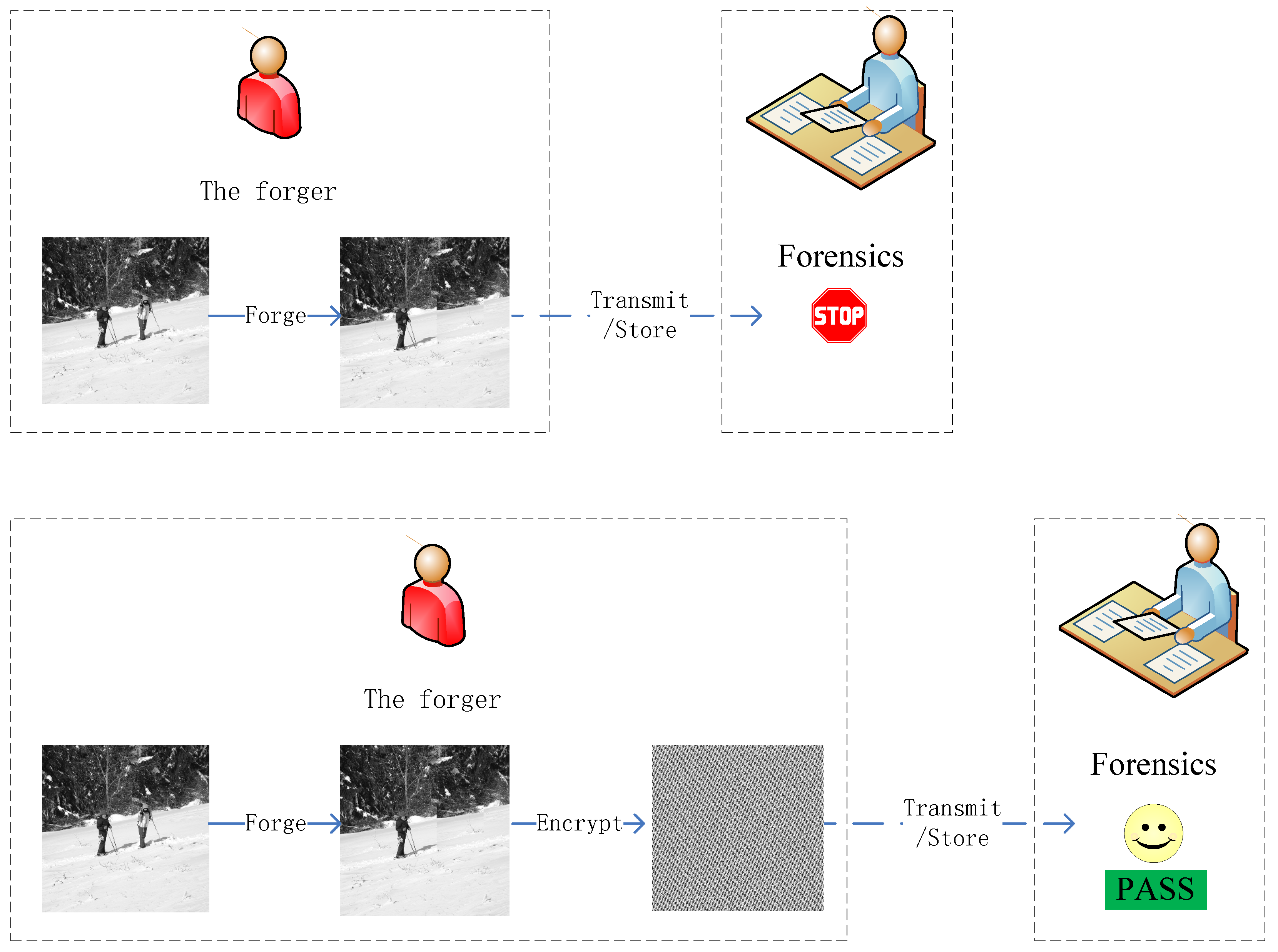
1. Introduction
- Image forensics in the encrypted domain is introduced, including its problem description, formal definition, and evaluation metrics.
- A deep learning-based IFED algorithm, namely LEFN, is proposed to deal with the issue of copy–move detection, where the encryption technique of classic permutation is used. Experiments and analyses are employed to validate the proposed algorithm.
- Compared with the traditional forensic tools that usually rely on hand-crafted features, the proposed deep learning-based LEFN can extract higher dimensional statistical features to depict the target’s potential characteristics, thus achieving possible forensics.
2. Preliminaries
2.1. A Copy–Move Forgery
2.2. Arnold Permutation
3. IFED Definition
- 1.
- Source detection or identification: To detect or identify the device used to acquire the encrypted image, like a camera or scanner.
- 2.
- Forgery detection: To validate whether the encrypted image has been forged.
- 3.
- Processing operations identification: To identify the sequence of image processing.
- 4.
- Forgery cracking: To crack or recover the original image.
- 5.
- Forgery attack: To render the encrypted (forged) image unusable
- 1.
- Accuracy: The proportion of accurately classified encrypted (forged) images out of all encrypted (forged) images, represented by Equation (2).where , and represent the quantities of true positive, true negative, false negative, and false positive classifications of encrypted (forged) images, respectively.
- 2.
- Precision: The percentage of correctly classified positive encrypted (forged) images among all encrypted (forged) images classified as positive, as shown in Equation (3).
- 3.
- Area under the curve (AUC) score: The possibility that a randomly selected positive encrypted (forged) image takes precedence over a randomly selected negative encrypted image.Assuming there are n positive encrypted images and m negative encrypted images, AUC can be estimated through the following steps: For each positive encrypted image, compare its predicted value with the predicted values of all negative encrypted images. If the predicted value of a positive encrypted image is higher than that of a negative encrypted image, then increment the counter by one. Finally, divide the total count by the product of the number of positive encrypted images n and the number of negative encrypted images m to obtain AUC. The formulaic expression is as follows:where I is an indicator function that returns 1 when the condition is met, otherwise it returns 0; represents the predicted score of the ith positive sample; represents the predicted score of the jth negative sample. The AUC value represents the area under the ROC curve, and its range is from 0 to 1. An ideal classifier should have an AUC value close to 1, while a classifier that guesses randomly would have an AUC value of about 0.5.
- For a given forged style, the encryption algorithm, and its EI are significant factors in evaluating an IFED method.
- The user can select the metrics according to the practical forensic problem.
4. The Proposed LEFN-Based IFED Algorithm
4.1. Design Idea and Overall Architecture
- A powerful feature-extraction module to extract high-level abstract features and more distinguished features between the encrypted normal image and the encrypted forged image.
- A preprocessing module designed to better guide the feature-extraction module in focusing on sharply changing regions.
- An enhancement module with a large receptive field to capture both local and long-range correlations, as well as the overall feature information.
4.2. Specific Module Frameworks
4.2.1. FE Module
4.2.2. KV Kernel
4.2.3. RFE Module
5. Experimental Results and Analyses
5.1. Datasets and Experimental Settings
5.2. Ablation Study on the Network Design
- Modules FE-A and FE-B highlight the crucial function of the average pooling operation in LEFN. This operation retains the comprehensive feature information and captures statistical characteristics by progressively condensing the feature maps. Furthermore, the additional average pooling operation behind the convolution layer will further provide stronger constraints for the local or overall correlations of the extracted feature maps, thus greatly improving the detection accuracy.
- Modules FE-B and KV-FE-B verify the effectiveness of the KV kernel, it works as a high-pass filter to screen the high-frequency residual signal in the tampered region and conduct the next FE module to locate the important clues for feature extraction, thus speeding up network training and learning.
- Modules KV-FE-B and RFE-KV-FE-B showcase the vital importance of the RFE module within LEFN. This module proficiently expands the receptive field to encompass distant surrounding information and global semantic details, thereby markedly enhancing the model’s learning efficiency and detection accuracy.
- Figure 8b indicates that our designed full model is lightweight with only 0.065 M parameters, and the designed modules significantly enhance the network performance without dramatically increasing the model parameters.
5.3. Influence of CR on IFED
- Generally, higher CR means higher detection accuracy. When CR is lower than 9%, the encrypted forged image is less likely to be detected, when CR is higher than 9%, so the encrypted forged image is more likely to be detected. Because higher CR means larger modifications and more distinguishable features.
- Due to the integrated modules, the comprehensive RFE-KV-FE-B model attains the highest detection performance, aligning with the findings depicted in Figure 8a.
5.4. Influence of EI on IFED
5.5. Deal with the Increase of EI
- Increasing the feature channels will increase the network parameters and the detection accuracy is accordingly improved.
- Enlarging the kernel size will dramatically increase the network parameters; however, it also significantly boosts the detection accuracy.
5.6. Discussions
- More digital image processing operations can be tested, such as splicing, rotating, and compressing. Their corresponding datasets can be set up.
- Some other encrypted techniques will be exploited and used, such as Paillier cryptosystem-based proxy encryption, homomorphic wavelet transform, and Lattice-based homomorphic cryptosystems.
- Since image encryption might not modify the EXIF (exchangeable image file format) information, source detection or identification of IFED will be possible.
- A specific deep learning network for IFED will be designed.
- We can design more forensic methods for IFED. One potential approach is as follows: IFED is analogous to a ciphertext-only attack, where some plaintext is replaced within a given encryption algorithm. Therefore, we may achieve IFED from the perspective of cryptanalysis.
- Real-time IFED based on traffic is significant.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castillo Camacho, I.; Wang, K. A Comprehensive Review of Deep-Learning-Based Methods for Image Forensics. J. Imaging 2021, 7, 69. [Google Scholar] [CrossRef]
- Zhong, J.L.; Pun, C.M. An End-to-End Dense-InceptionNet for Image Copy-Move Forgery Detection. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2134–2146. [Google Scholar] [CrossRef]
- Ng, T.T.; Chang, S.F.; Lin, C.Y.; Sun, Q. 15 - Passive-blind Image Forensics. In Multimedia Security Technologies for Digital Rights Management; Zeng, W., Yu, H., Lin, C.Y., Eds.; Academic Press: Burlington, VT, USA, 2006; pp. 383–412. [Google Scholar] [CrossRef]
- Yang, F.; Li, J.; Lu, W.; Weng, J. Copy-move forgery detection based on hybrid features. Eng. Appl. Artif. Intell. 2017, 59, 73–83. [Google Scholar] [CrossRef]
- Kalker, T. Considerations on watermarking security. In Proceedings of the 2001 IEEE Fourth Workshop on Multimedia Signal Processing (Cat. No.01TH8564), Cannes, France, 3–5 October 2001; pp. 201–206. [Google Scholar] [CrossRef]
- Lukas, J.; Fridrich, J.; Goljan, M. Digital camera identification from sensor pattern noise. IEEE Trans. Inf. Forensics Secur. 2006, 1, 205–214. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, J. Fast and Effective Image Copy-Move Forgery Detection via Hierarchical Feature Point Matching. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1307–1322. [Google Scholar] [CrossRef]
- Chen, B.; Tan, W.; Coatrieux, G.; Zheng, Y.; Shi, Y.Q. A Serial Image Copy-Move Forgery Localization Scheme with Source/Target Distinguishment. IEEE Trans. Multimed. 2021, 23, 3506–3517. [Google Scholar] [CrossRef]
- Barni, M.; Phan, Q.T.; Tondi, B. Copy Move Source-Target Disambiguation through Multi-Branch CNNs. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1825–1840. [Google Scholar] [CrossRef]
- Bohme, R.; Kirchner, M. Counter-Forensics: Attacking Image Forensics. In Digital Image Forensics: There Is More to a Picture than Meets the Eye; Springer: New York, NY, USA, 2013; pp. 327–366. [Google Scholar] [CrossRef]
- Nowroozi, E.; Dehghantanha, A.; Parizi, R.M.; Choo, K.K.R. A survey of machine learning techniques in adversarial image forensics. Comput. Secur. 2021, 100, 102092. [Google Scholar] [CrossRef]
- Barni, M.; Cancelli, G.; Esposito, A. Forensics aided steganalysis of heterogeneous images. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 1690–1693. [Google Scholar] [CrossRef]
- Cao, G.; Zhao, Y.; Ni, R.; Tian, H. Anti-Forensics of Contrast Enhancement in Digital Images. In Proceedings of the 12th ACM Workshop on Multimedia and Security, Rome, Italy, 9–10 September 2010; MM& Sec ’10. pp. 25–34. [Google Scholar] [CrossRef]
- Barni, M. Steganography in Digital Media: Principles, Algorithms, and Applications (Fridrich, J. 2010) [Book Reviews]. IEEESignal Process. Mag. 2011, 28, 142–144. [Google Scholar] [CrossRef]
- Valenzise, G.; Nobile, V.; Tagliasacchi, M.; Tubaro, S. Countering JPEG anti-forensics. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 1949–1952. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, X.; Gong, L.; Wang, S.; Niu, X.; Shen, L. Late Fusion Multiple Kernel Clustering with Local Kernel Alignment Maximization. IEEE Trans. Multimed. 2021, 25, 993–1007. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J.S.; Liu, S.Q. Permutation transform of images. Chin. J. Comput. 1998, 21, 6. [Google Scholar]
- Qian, Y.; Dong, J.; Wang, W.; Tan, T. Deep learning for steganalysis via convolutional neural networks. In Proceedings of the Media Watermarking, Security, and Forensics 2015, San Francisco, CA, USA, 9–11 February 2015; Alattar, A.M., Memon, N.D., Heitzenrater, C.D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2015; Volume 9409, pp. 171–180. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Yin, Z.; Xiang, Y.; Zhang, X. Reversible Data Hiding in Encrypted Images Based on Multi-MSB Prediction and Huffman Coding. IEEE Trans. Multimed. 2020, 22, 874–884. [Google Scholar] [CrossRef]
- Xiong, L.; Zhong, X.; Yang, C.N.; Han, X. Transform Domain-Based Invertible and Lossless Secret Image Sharing With Authentication. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2912–2925. [Google Scholar] [CrossRef]
- Jiang, R.; Zhou, H.; Zhang, W.; Yu, N. Reversible Data Hiding in Encrypted Three-Dimensional Mesh Models. IEEE Trans. Multimed. 2018, 20, 55–67. [Google Scholar] [CrossRef]









| Notation | Description |
|---|---|
| The size of the image | |
| The original (normal) image | |
| The encrypted original image | |
| The forged image | |
| The encrypted forged image | |
| The encryption intensity | |
| The copy–move forgery rate | |
| IFED | Image forensics in the encrypted domain |
| LEFN | Lightweight enhanced forensic network |
| Model Name | Model Description |
|---|---|
| FE-A | Model featuring only the FE module from Figure 5a |
| FE-B | Model containing solely the FE module shown in Figure 5b |
| KV-FE-B | Model incorporating the KV kernel and FE module depicted in Figure 5b |
| RFE-KV-FE-B | Model equipped with the RFE module, KV kernel, and FE module as shown in Figure 5b |
| CR (%) | 0.25 | 1 | 2.25 | 4 | 6.25 | 9 | 12.25 | 16 | 20.25 | 25 |
| FE-A | 62% | 65% | 70% | 74% | 68% | 75% | 75% | 73% | 71% | 73% |
| FE-B | 63% | 71% | 67% | 74% | 71% | 83% | 75% | 81% | 77% | 79% |
| KV-FE-B | 66% | 70% | 67% | 79% | 72% | 80% | 76% | 82% | 79% | 79% |
| RFE-KV-FE-B | 67% | 72% | 70% | 77% | 77% | 83% | 81% | 83% | 80% | 86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Lu, Y.; Li, L.; Chen, F.; Yan, X. Image Forensics in the Encrypted Domain. Entropy 2024, 26, 900. https://doi.org/10.3390/e26110900
Yu Y, Lu Y, Li L, Chen F, Yan X. Image Forensics in the Encrypted Domain. Entropy. 2024; 26(11):900. https://doi.org/10.3390/e26110900
Chicago/Turabian StyleYu, Yongqiang, Yuliang Lu, Longlong Li, Feng Chen, and Xuehu Yan. 2024. "Image Forensics in the Encrypted Domain" Entropy 26, no. 11: 900. https://doi.org/10.3390/e26110900
APA StyleYu, Y., Lu, Y., Li, L., Chen, F., & Yan, X. (2024). Image Forensics in the Encrypted Domain. Entropy, 26(11), 900. https://doi.org/10.3390/e26110900






