Neural Geometrodynamics, Complexity, and Plasticity: A Psychedelics Perspective
Abstract
1. Introduction
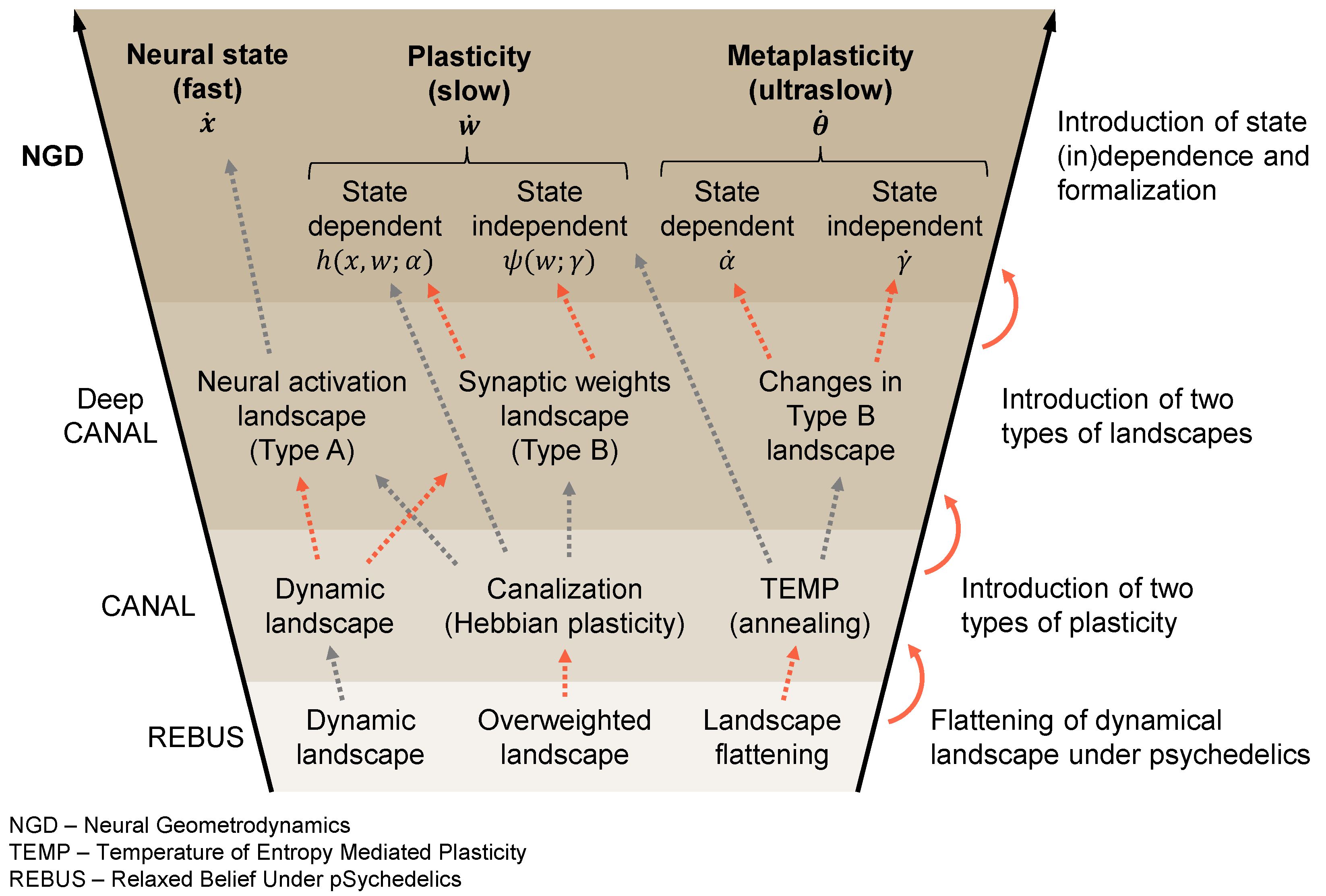
2. Dynamics across Timescales
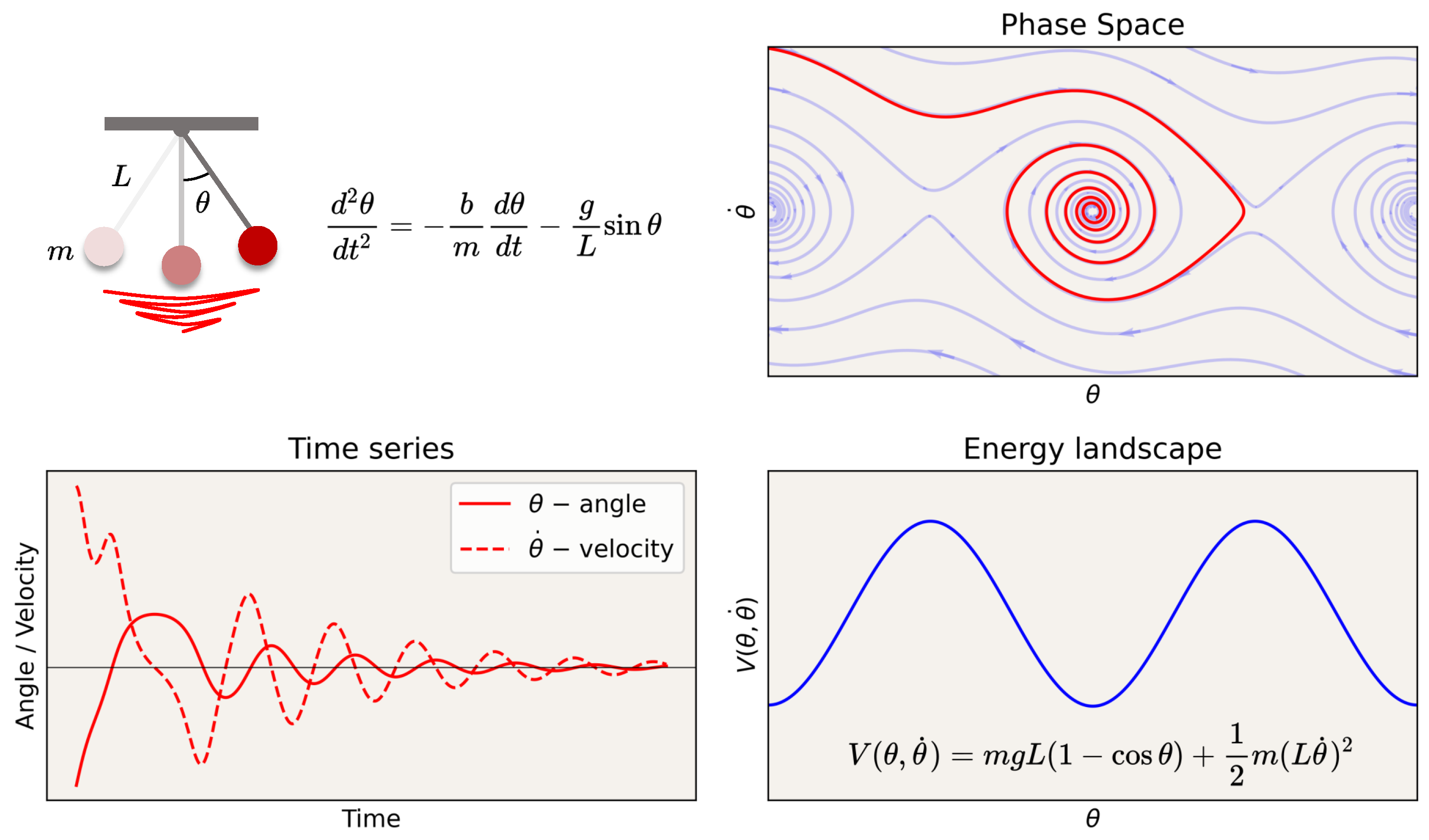
2.1. Fast Time: Neural Dynamics
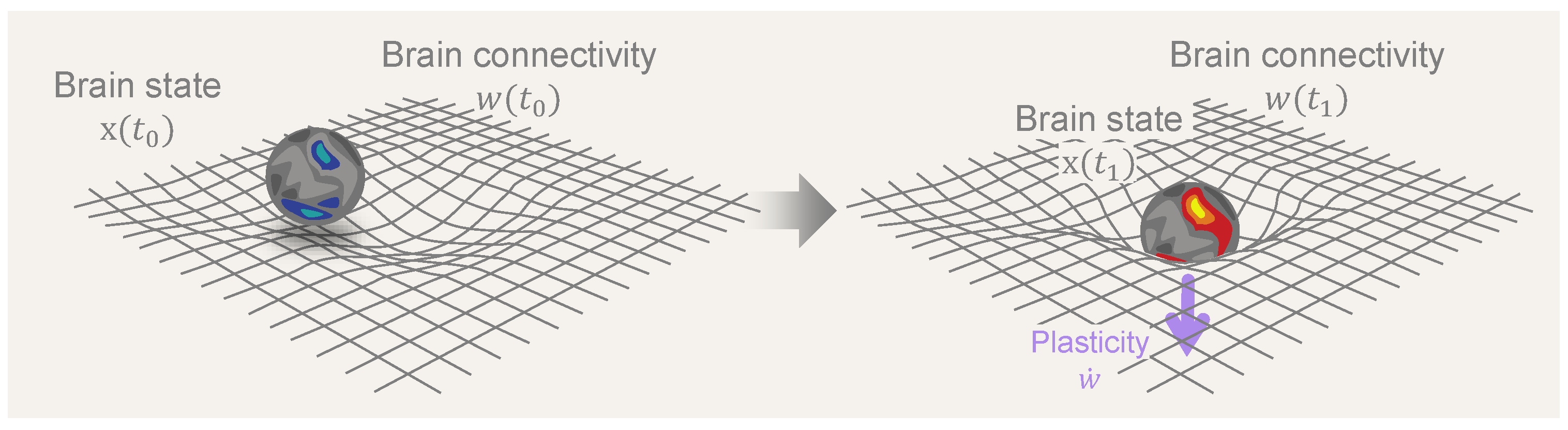
2.2. Slow Time: Connectodynamics
2.3. Ultraslow Time: Metaplasticity
Metaplasticity […] is manifested as a change in the ability to induce subsequent synaptic plasticity, such as long-term potentiation or depression. Thus, metaplasticity is a higher-order form of synaptic plasticity.[73]
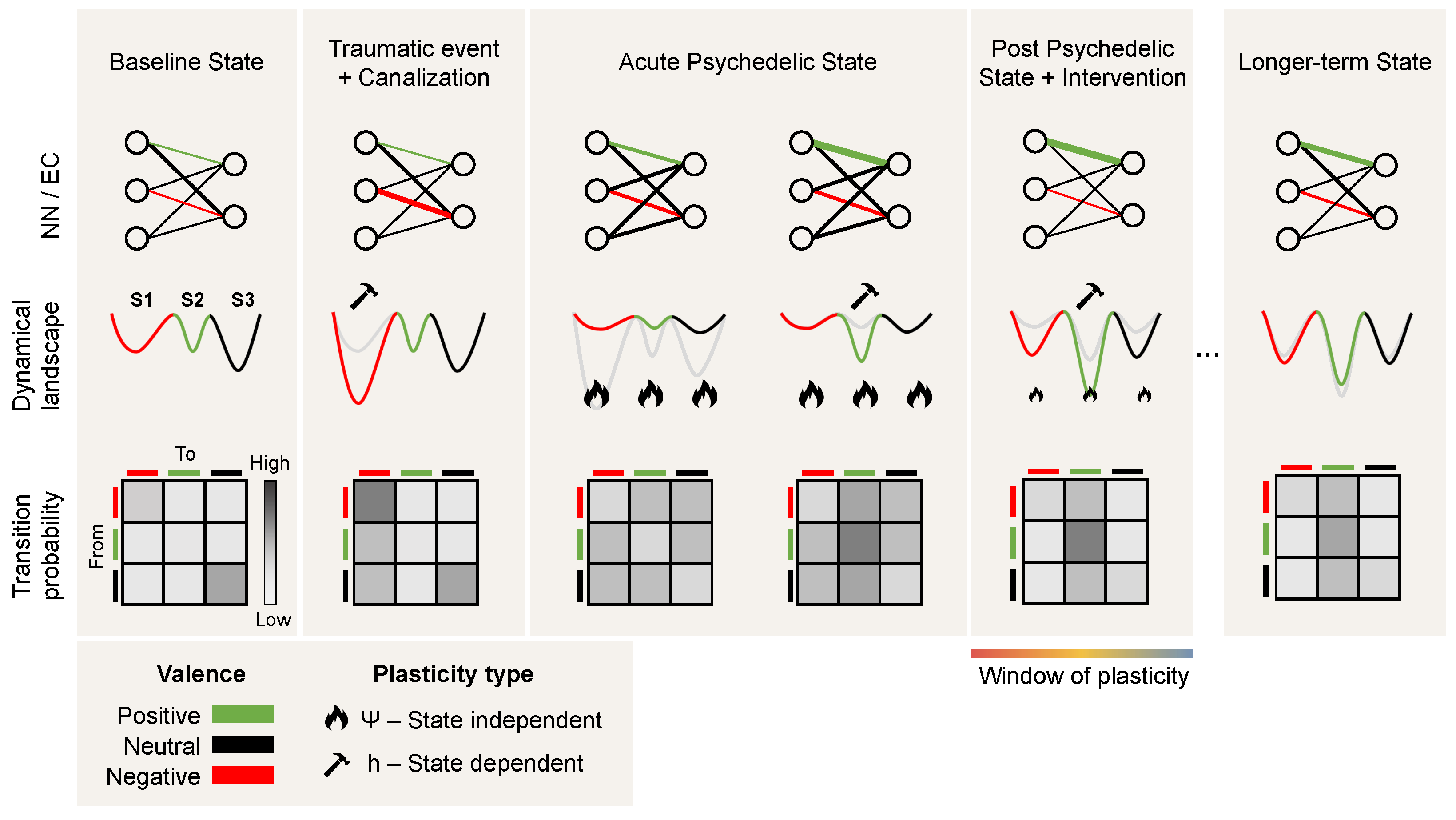
3. Dynamics under Psychedelics
Dynamics of Psychedelics and Psychopathology
4. Neural Geometrodynamics and General Relativity
4.1. Metaplasticity and Variable Constants in Cosmology
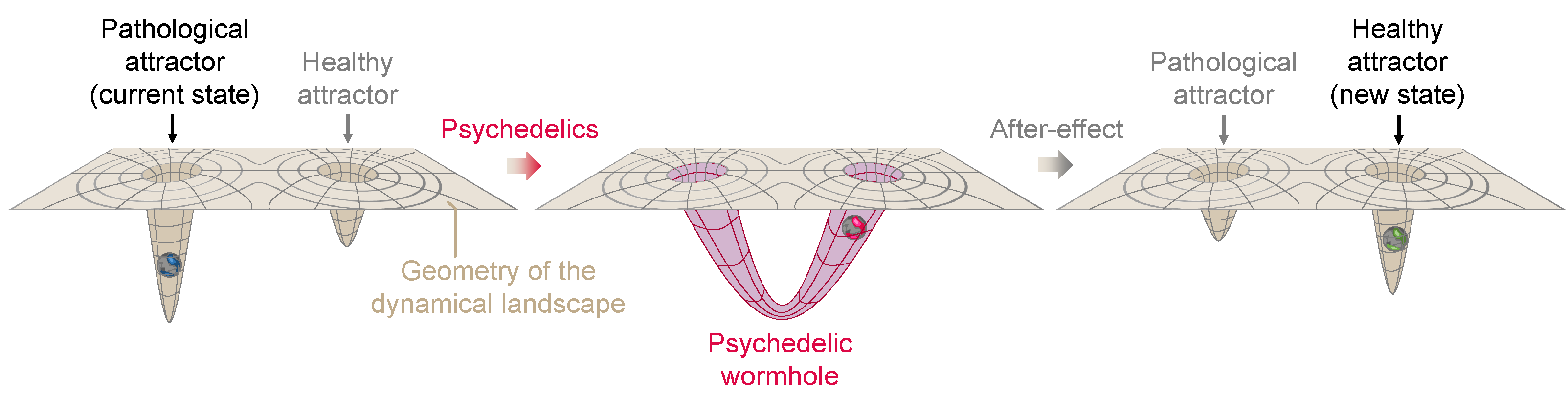
4.2. Psychedelics as Wormholes in the Neural Landscape
4.3. Characterizing the Landscape
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. A Nautical Analogy
Appendix A.2. Classical Dynamics of Particles and Fields
Appendix A.2.1. Non-Relativistic Electrodynamics
Appendix A.2.2. Relativistic Equations
Appendix A.3. Modeling Plasticity in Neural Mass Models
| Type | Time Scale | Mechanism | Effects | State-Dependence |
|---|---|---|---|---|
| Functional or dynamical Plasticity | Milliseconds to minutes | Changes in strength/efficiency of synapses (e.g., Hebbian plasticity, LTP, LTD) | Short and long-term memory, fine-tuning of connections | State-dependent (h) |
| Acute Psychedelic-induced Plasticity | Minutes to Hours | Targeting of serotonergic neuroreceptors especially the 5- with a result in overall excitability [7,11,12,81] | Flattens or de-weights the dynamical landscape | State-independent () |
| Homeostatic Plasticity | Hours to days | Regulation of overall excitability to maintain stability (e.g., adjusting synapse strength for E/I balance) | Balances and stabilizes network | State-dependent (h) |
| Structural Plasticity (e.g., post-acute psychedelic-induced plasticity) | Hours to years | Larger physical changes in neurons (e.g., dendrite growth, synapse formation) through an increase of endogenous BDNF and via TrkB binding (the receptor of BDNF) [82] | Long-term memory, development | Depends on context |
| Metaplasticity | Various, often longer-term | Changes in mechanisms governing synaptic plasticity (e.g., modulation of thresholds/rules) | Regulates other forms of plasticity, “plasticity of plasticity” [73] | Depends on context |
Appendix A.3.1. Functional Plasticity
Appendix A.3.2. Homeostatic Plasticity
Appendix A.3.3. Structural Plasticity
Appendix A.3.4. Empirically-Derived Structural Plasticity
References
- Deco, G.; Jirsa, V.K.; Robinson, P.A.; Breakspear, M.; Friston, K. The dynamic brain: From spiking neurons to neural masses and cortical fields. PLoS Comput. Biol. 2008, 4, e1000092. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. NeuroImage 2017, 160, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.L.; Whybrow, P.C.; Logothetis, N.K.; Kringelbach, M.L. Whole-brain multimodal neuroimaging model using serotonin receptor maps explains non-linear functional effects of LSD. Curr. Biol. 2018, 28, 3065–3074. [Google Scholar] [CrossRef]
- Kringelbach, M.L.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.; Whybrow, P.C.; Logothetis, N.K.; Deco, G. Dynamic coupling of whole-brain neuronal and neurotransmitter systems. Proc. Natl. Acad. Sci. USA 2020, 117, 9566–9576. [Google Scholar] [CrossRef] [PubMed]
- Aday, J.S.; Mitzkovitz, C.M.; Bloesch, E.K.; Davoli, C.C.; Davis, A.K. Long-term effects of psychedelic drugs: A systematic review. Neurosci. Biobehav. Rev. 2020, 113, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Nichols, D.E. Psychedelics. Pharmacol. Rev. 2016, 68, 264–355. [Google Scholar] [CrossRef]
- de Vos, C.M.H.; Mason, N.L.; Kuypers, K.P.C. Psychedelics and Neuroplasticity: A Systematic Review Unraveling the Biological Underpinnings of Psychedelics. Front. Psychiatry 2021, 12, 724606. [Google Scholar] [CrossRef]
- Moliner, R.; Girych, M.; Brunello, C.A.; Kovaleva, V.; Biojone, C.; Enkavi, G.; Antenucci, L.; Kot, E.F.; Goncharuk, S.A.; Kaurinkoski, K.; et al. Psychedelics promote plasticity by directly binding to BDNF receptor TrkB. Nat. Neurosci. 2023, 26, 1032–1041. [Google Scholar] [CrossRef]
- Nardou, R.; Sawyer, E.; Song, Y.J.; Wilkinson, M.; Padovan-Hernandez, Y.; de Deus, J.L.; Wright, N.; Lama, C.; Faltin, S.; Goff, L.A.; et al. Psychedelics reopen the social reward learning critical period. Nature 2023, 618, 790–798. [Google Scholar] [CrossRef]
- Carhart-Harris, R.L.; Chandaria, S.; Erritzoe, D.E.; Gazzaley, A.; Girn, M.; Kettner, H.; Mediano, P.A.M.; Nutt, D.J.; Rosas, F.E.; Roseman, L.; et al. Canalization and plasticity in psychopathology. Neuropharmacology 2023, 226, 109398. [Google Scholar] [CrossRef]
- Carhart-Harris, R.L.; Friston, K.J. REBUS and the Anarchic Brain: Toward a Unified Model of the Brain Action of Psychedelics. Pharmacol. Rev. 2019, 71, 316–344. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Carhart-Harris, R.L. The entropic brain—Revisited. Neuropharmacology 2018, 142, 167–178. [Google Scholar] [CrossRef]
- Girn, M.; Rosas, F.E.; Daws, R.E.; Gallen, C.L.; Gazzaley, A.; Carhart-Harris, R.L. A complex systems perspective on psychedelic brain action. Trends Cogn. Sci. 2023, 27, 433–445. [Google Scholar] [CrossRef] [PubMed]
- Ruffini, G.; Lopez-Sola, E. AIT foundations of structured experience. J. AI Consci. 2022, 9, 153–191. [Google Scholar] [CrossRef]
- Geyer, M.A.; Vollenweider, F.X. Serotonin research: Contributions to understanding psychoses. Trends Pharmacol. Sci. 2008, 29, 445–453. [Google Scholar] [CrossRef]
- Hipólito, I.; Mago, J.; Rosas, F.E.; Carhart-Harris, R. Pattern breaking: A complex systems approach to psychedelic medicine. Neurosci. Conscious. 2023, 2023, niad017. [Google Scholar] [CrossRef]
- Carhart-Harris, R.L.; Erritzoe, D.; Williams, T.; Stone, J.M.; Reed, L.J.; Colasanti, A.; Tyacke, R.J.; Leech, R.; Malizia, A.L.; Murphy, K.; et al. Neural correlates of the psychedelic state as determined by fMRI studies with psilocybin. Proc. Natl. Acad. Sci. USA 2012, 109, 2138–2143. [Google Scholar] [CrossRef]
- Carhart-Harris, R.L.; Leech, R.; Hellyer, P.J.; Shanahan, M.; Feilding, A.; Tagliazucchi, E.; Chialvo, D.R.; Nutt, D. The entropic brain: A theory of conscious states informed by neuroimaging research with psychedelic drugs. Front. Hum. Neurosci. 2014, 8, 20. [Google Scholar] [CrossRef]
- Carhart-Harris, R.L.; Muthukumaraswamy, S.; Roseman, L.; Kaelen, M.; Droog, W.; Murphy, K.; Tagliazucchi, E.; Schenberg, E.E.; Nest, T.; Orban, C.; et al. Neural correlates of the LSD experience revealed by multimodal neuroimaging. Proc. Natl. Acad. Sci. USA 2016, 113, 4853–4858. [Google Scholar] [CrossRef]
- Atasoy, S.; Roseman, L.; Kaelen, M.; Kringelbach, M.L.; Deco, G.; Carhart-Harris, R.L. Connectome-harmonic decomposition of human brain activity reveals dynamical repertoire re-organization under LSD. Sci. Rep. 2017, 7, 17661. [Google Scholar] [CrossRef] [PubMed]
- Atasoy, S.; Vohryzek, J.; Deco, G.; Carhart-Harris, R.L.; Kringelbach, M.L. Common neural signatures of psychedelics: Frequency-specific energy changes and repertoire expansion revealed using connectome-harmonic decomposition. Prog. Brain Res. 2018, 242, 97–120. [Google Scholar]
- Luppi, A.I.; Vohryzek, J.; Kringelbach, M.L.; Mediano, P.A.; Craig, M.M.; Adapa, R.; Carhart-Harris, R.L.; Roseman, L.; Pappas, I.; Finoia, P.; et al. Distributed harmonic patterns of structure-function dependence orchestrate human consciousness. Commun. Biol. 2023, 6, 117:1–117:19. [Google Scholar] [CrossRef] [PubMed]
- Singleton, S.P.; Luppi, A.I.; Carhart-Harris, R.L.; Cruzat, J.; Roseman, L.; Nutt, D.J.; Deco, G.; Kringelbach, M.L.; Stamatakis, E.A.; Kuceyeski, A. LSD and psilocybin flatten the brain’s energy landscape: Insights from receptor-informed network control theory. bioRxiv 2022. [Google Scholar] [CrossRef]
- Preller, K.H.; Burt, J.B.; Ji, J.L.; Schleifer, C.H.; Adkinson, B.D.; Stämpfli, P.; Seifritz, E.; Repovs, G.; Krystal, J.H.; Murray, J.D.; et al. Changes in global and thalamic brain connectivity in LSD-induced altered states of consciousness are attributable to the 5-HT2A receptor. eLife 2018, 7, e35082. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Roseman, L.; Kaelen, M.; Orban, C.; Muthukumaraswamy, S.D.; Murphy, K.; Laufs, H.; Leech, R.; McGonigle, J.; Crossley, N.; et al. Increased global functional connectivity correlates with LSD-induced ego dissolution. Curr. Biol. 2016, 26, 1043–1050. [Google Scholar] [CrossRef]
- McCulloch, D.E.W.; Knudsen, G.M.; Barrett, F.S.; Doss, M.K.; Carhart-Harris, R.L.; Rosas, F.E.; Deco, G.; Kringelbach, M.L.; Preller, K.H.; Ramaekers, J.G.; et al. Psychedelic resting-state neuroimaging: A review and perspective on balancing replication and novel analyses. Neurosci. Biobehav. Rev. 2022, 138, 104689. [Google Scholar] [CrossRef]
- Varley, T.F.; Carhart-Harris, R.; Roseman, L.; Menon, D.K.; Stamatakis, E.A. Serotonergic Psychedelics LSD & Psilocybin Increase the Fractal Dimension of Cortical Brain Activity in Spatial and Temporal Domains. NeuroImage 2020, 220, 117049. [Google Scholar] [CrossRef]
- Toker, D.; Pappas, I.; Lendner, J.D.; Frohlich, J.; Mateos, D.M.; Muthukumaraswamy, S.; Carhart-Harris, R.; Paff, M.; Vespa, P.M.; Monti, M.M.; et al. Consciousness is supported by near-critical slow cortical electrodynamics. Proc. Natl. Acad. Sci. USA 2022, 119, e2024455119. [Google Scholar] [CrossRef]
- Schartner, M.M.; Carhart-Harris, R.L.; Barrett, A.B.; Seth, A.K.; Muthukumaraswamy, S.D. Increased Spontaneous MEG Signal Diversity for Psychoactive Doses of Ketamine, LSD and Psilocybin. Sci. Rep. 2017, 7, 46421. [Google Scholar] [CrossRef] [PubMed]
- Ezaki, T.; Watanabe, T.; Ohzeki, M.; Masuda, N. Energy landscape analysis of neuroimaging data. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375, 20160287. [Google Scholar] [CrossRef] [PubMed]
- Ezaki, T.; Fonseca Dos Reis, E.; Watanabe, T.; Sakaki, M.; Masuda, N. Closer to critical resting-state neural dynamics in individuals with higher fluid intelligence. Commun. Biol. 2020, 3, 52. [Google Scholar] [CrossRef] [PubMed]
- Ruffini, G.; Damiani, G.; Lozano-Soldevilla, D.; Deco, N.; Rosas, F.E.; Kiani, N.A.; Ponce-Alvarez, A.; Kringelbach, M.L.; Carhart-Harris, R.; Deco, G. LSD-induced increase of Ising temperature and algorithmic complexity of brain dynamics. PLoS Comput. Biol. 2023, 19, e1010811. [Google Scholar] [CrossRef]
- Ruffini, G.; Deco, G. The 2D Ising model, criticality and AIT. bioRxiv 2021. [Google Scholar] [CrossRef]
- Ruffini, G. An algorithmic information theory of consciousness. Neurosci. Conscious. 2017, 3, nix019. [Google Scholar] [CrossRef] [PubMed]
- Ruffini, G. Structured dynamics in the algorithmic agent. bioRxiv 2023. [Google Scholar] [CrossRef]
- Margulies, D.S.; Ghosh, S.S.; Goulas, A.; Falkiewicz, M.; Huntenburg, J.M.; Langs, G.; Bezgin, G.; Eickhoff, S.B.; Castellanos, F.X.; Petrides, M.; et al. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci. USA 2016, 113, 44. [Google Scholar] [CrossRef]
- Xu, Y.; Long, X.; Feng, J.; Gong, P. Interacting spiral wave patterns underlie complex brain dynamics and are related to cognitive processing. Nat. Hum. Behav. 2023, 7, 1196–1215. [Google Scholar] [CrossRef]
- Vézquez-Rodríguez, B.; Liu, Z.Q.; Hagmann, P.; Misic, B. Signal propagation via cortical hierarchies. Netw. Neurosci. 2020, 4, 1072–1090. [Google Scholar] [CrossRef]
- Deco, G.; Sanz Perl, Y.; Bocaccio, H.; Tagliazucchi, E.; Kringelbach, M.L. The INSIDEOUT framework provides precise signatures of the balance of intrinsic and extrinsic dynamics in brain states. Commun. Biol. 2022, 5, 572. [Google Scholar] [CrossRef] [PubMed]
- Kringelbach, M.L.; Perl, Y.S.; Tagliazucchi, E.; Deco, G. Toward naturalistic neuroscience: Mechanisms underlying the flattening of brain hierarchy in movie-watching compared to rest and task. Sci. Adv. 2023, 9, eade6049. [Google Scholar] [CrossRef] [PubMed]
- Lynn, C.W.; Cornblath, E.J.; Papadopoulos, L.; Bertolero, M.A.; Bassett, D.S. Broken detailed balance and entropy production in the human brain. Proc. Natl. Acad. Sci. USA 2021, 118, e2109889118. [Google Scholar] [CrossRef]
- Girn, M.; Roseman, L.; Bernhardt, B.; Smallwood, J.; Carhart-Harris, R.; Spreng, R.N. Serotonergic psychedelic drugs LSD and psilocybin reduce the hierarchical differentiation of unimodal and transmodal cortex. NeuroImage 2022, 256, 119220. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Liu, H.; Lei, X.; He, Y.; Wu, Q.; Yan, Y.; Zhou, X.; Tian, X.; Peng, Y.; Huang, S.; et al. Hierarchical fluctuation shapes a dynamic flow linked to states of consciousness. Nat. Commun. 2023, 14, 3238. [Google Scholar] [CrossRef]
- Vohryzek, J.; Cabral, J.; Timmermann, C.; Atasoy, S.; Roseman, L.; Nutt, D.; Carhart-Harris, R.; Deco, G.; Kringelbach, M.L. Harmonic decomposition of spacetime (HADES) framework characterises the spacetime hierarchy of the DMT brain state. bioRxiv 2023. [Google Scholar] [CrossRef]
- Vohryzek, J.; Cabral, J.; Vuust, P.; Deco, G.; Kringelbach, M.L. Understanding brain states across spacetime informed by whole-brain modelling. Philos. Trans. R. Soc. A 2022, 380, 20210247. [Google Scholar] [CrossRef]
- Juliani, A.; Safron, A.; Kanai, R. Deep CANALs: A Deep Learning Approach to Refining the Canalization Theory of Psychopathology. Psyarxiv Prepr. 2023. [Google Scholar] [CrossRef]
- Nichols, D.E.; Johnson, M.W.; Nichols, C.D. Psychedelics as medicines: An emerging new paradigm. Clin. Pharmacol. Ther. 2017, 101, 209–219. [Google Scholar] [CrossRef]
- Kuo, M.F.; Nitsche, M.A. Effects of transcranial electrical stimulation on cognition. Clin. EEG Neurosci. 2012, 43, 192–199. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 1st ed.; Westview Press: Boulder, CO, USA, 2001. [Google Scholar]
- Cayton, L. Algorithms for Manifold Learning; Technical Report; Department of Computer Science & Engineering: San Diego, CA, USA, 2008. [Google Scholar]
- Konz, N.; Gu, H.; Dong, H.; Mazurowski, M.A. Correction to: The intrinsic manifolds of radiological images and their role in deep learning. In Lecture Notes in Computer Science; Springer Nature Switzerland: Cham, Swizerland, 2022; p. C1. [Google Scholar]
- Perl, Y.S.; Bocaccio, H.; Pérez-Ipiña, I.; Zamberlán, F.; Piccinini, J.; Laufs, H.; Kringelbach, M.; Deco, G.; Tagliazucchi, E. Generative Embeddings of Brain Collective Dynamics Using Variational Autoencoders. Phys. Rev. Lett. 2020, 125, 238101. [Google Scholar] [CrossRef]
- Sanz Perl, Y.; Fittipaldi, S.; Gonzalez Campo, C.; Moguilner, S.; Cruzat, J.; Fraile-Vazquez, M.E.; Herzog, R.; Kringelbach, M.L.; Deco, G.; Prado, P.; et al. Model-based whole-brain perturbational landscape of neurodegenerative diseases. eLife 2023, 12, e83970. [Google Scholar] [CrossRef]
- Jefferys, J.G. Nonsynaptic modulation of neuronal activity in the brain: Electric currents and extracellular ions. Physiol. Rev. 1995, 75, 689–723. [Google Scholar] [CrossRef]
- Anastassiou, C.A.; Perin, R.; Markram, H.; Koch, C. Ephaptic coupling of cortical neurons. Nat. Neurosci. 2011, 14, 217–223. [Google Scholar] [CrossRef]
- Ruffini, G.; Salvador, R.; Tadayon, E.; Sanchez-Todo, R.; Pascual-Leone, A.; Santarnecchi, E. Realistic modeling of mesoscopic ephaptic coupling in the human brain. PLoS Comput. Biol. 2020, 16, e1007923. [Google Scholar] [CrossRef]
- Pinotsis, D.A.; Miller, E.K. In vivo ephaptic coupling allows memory network formation. Cereb. Cortex 2023, 33, 9877–9895. [Google Scholar] [CrossRef]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; John Wiley and Sons: New York, NY, USA, 1949. [Google Scholar]
- Turrigiano, G.G.; Leslie, K.R.; Desai, N.S.; Rutherford, L.C.; Nelson, S.B. Activity-Dependent Scaling of Quantal Amplitude in Neocortical Neurons. Nature 1998, 391, 892–896. [Google Scholar] [CrossRef]
- Turrigiano, G.G.; Nelson, S.B. Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 2004, 5, 97–107. [Google Scholar] [CrossRef]
- Maffei, A.; Nelson, S.B.; Turrigiano, G.G. Selective Reconfiguration of Layer 4 Visual Cortical Circuitry by Visual Deprivation. Nat. Neurosci. 2004, 7, 1353–1359. [Google Scholar] [CrossRef]
- Hengen, K.B.; Lambo, M.E.; Van Hooser, S.D.; Katz, D.B.; Turrigiano, G.G. Firing Rate Homeostasis in Visual Cortex of Freely Behaving Rodents. Neuron 2013, 80, 335–342. [Google Scholar] [CrossRef]
- Hellyer, P.J.; Jachs, B.; Clopath, C.; Leech, R. Local Inhibitory Plasticity Tunes Macroscopic Brain Dynamics and Allows the Emergence of Functional Brain Networks. NeuroImage 2016, 124, 85–95. [Google Scholar] [CrossRef]
- Ma, Z.; Turrigiano, G.G.; Wessel, R.; Hengen, K.B. Cortical Circuit Dynamics Are Homeostatically Tuned to Criticality In Vivo. Neuron 2019, 104, 655–664.e4. [Google Scholar] [CrossRef]
- Chistiakova, M.; Bannon, N.M.; Bazhenov, M.; Volgushev, M. Heterosynaptic plasticity: Multiple mechanisms and multiple roles. Neuroscientist 2014, 20, 483–498. [Google Scholar] [CrossRef]
- Lepow, L.; Morishita, H.; Yehuda, R. Critical period plasticity as a framework for psychedelic-assisted psychotherapy. Front. Neurosci. 2021, 15, 710004. [Google Scholar] [CrossRef]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.A.; Hudspeth, A.J. Principles of Neural Science, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2013; ISBN 978-1-259-64223-4. [Google Scholar]
- Rosenberg, S.M.; Hastings, P.J. Stress-Induced Mutagenesis in Bacteria. Science 2003, 300, 1404–1409. [Google Scholar] [CrossRef]
- Vose, L.R.; Stanton, P.K. Synaptic plasticity, metaplasticity and depression. Curr. Neuropharmacol. 2017, 15, 71–86. [Google Scholar] [CrossRef]
- Voss, P.; Thomas, M.E.; Cisneros-Franco, J.M.; de Villers-Sidani, É. Dynamic brains and the changing rules of neuroplasticity: Implications for learning and recovery. Front. Psychol. 2017, 8, 1657. [Google Scholar] [CrossRef]
- Abraham, W.C.; Bear, M.F. Metaplasticity: The plasticity of synaptic plasticity. Trends Neurosci. 1996, 19, 126–130. [Google Scholar] [CrossRef]
- Pickersgill, J.W.; Turco, C.V.; Ramdeo, K.; Rehsi, R.S.; Foglia, S.D.; Nelson, A.J. The combined influences of exercise, diet and sleep on neuroplasticity. Front. Psychol. 2022, 13, 831819. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Carhart-Harris, R.L.; Nutt, D. Serotonin and brain function: A tale of two receptors. J. Psychopharmacol. 2017, 31, 1091–1120. [Google Scholar] [CrossRef]
- Carhart-Harris, R.; Giribaldi, B.; Watts, R.; Baker-Jones, M.; Murphy-Beiner, A.; Murphy, R.; Martell, J.; Blemings, A.; Erritzoe, D.; Nutt, D.J. Trial of psilocybin versus escitalopram for depression. N. Engl. J. Med. 2021, 384, 1402–1411. [Google Scholar] [CrossRef]
- Burstein, E.S. Relevance of 5-HT2A receptor modulation of pyramidal cell excitability for dementia-related psychosis: Implications for pharmacotherapy. CNS Drugs 2021, 35, 727–741. [Google Scholar] [CrossRef]
- Andrade, R. Serotonergic regulation of neuronal excitability in the prefrontal cortex. Neuropharmacology 2011, 61, 382–386. [Google Scholar] [CrossRef]
- Lau, Z.J.; Pham, T.; Chen, S.H.A.; Makowski, D. Brain Entropy, Fractal Dimensions and Predictability: A Review of Complexity Measures for EEG in Healthy and Neuropsychiatric Populations. Eur. J. Neurosci. 2022, 56, 5047–5069. [Google Scholar] [CrossRef]
- Kwan, A.C.; Olson, D.E.; Preller, K.H.; Roth, B.L. The neural basis of psychedelic action. Nat. Neurosci. 2022, 25, 1407–1419. [Google Scholar] [CrossRef]
- Calder, A.E.; Hasler, G. Towards an understanding of psychedelic-induced neuroplasticity. Neuropsychopharmacology 2023, 48, 104–112. [Google Scholar] [CrossRef]
- Rucker, J.J.; Iliff, J.; Nutt, D.J. Psychiatry & the psychedelic drugs. Past, present & future. Neuropharmacology 2018, 142, 200–218. [Google Scholar]
- Calvey, T.; Howells, F.M. An introduction to psychedelic neuroscience. Prog. Brain Res. 2018, 242, 1–23. [Google Scholar]
- Petri, G.; Expert, P.; Turkheimer, F.; Carhart-Harris, R.; Nutt, D.; Hellyer, P.J.; Vaccarino, F. Homological scaffolds of brain functional networks. J. R. Soc. Interface 2014, 11, 20140873. [Google Scholar] [CrossRef]
- Santos, F.A.N.; Raposo, E.P.; Coutinho-Filho, M.D.; Copelli, M.; Stam, C.J.; Douw, L. Topological phase transitions in functional brain networks. Phys. Rev. E 2019, 100, 032414. [Google Scholar] [CrossRef]
- Charó, G.D.; Chekroun, M.D.; Sciamarella, D.; Ghil, M. Noise-driven topological changes in chaotic dynamics. Chaos 2021, 31, 103115. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Zurek, W.H. John Wheeler, relativity, and quantum information. Phys. Today 2009, 62, 40–46. [Google Scholar] [CrossRef]
- do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice-Hall: Upper Saddle River, NJ, USA, 1976. [Google Scholar]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Luminet, J.P. The Status of Cosmic Topology after Planck Data. Universe 2016, 2, 1. [Google Scholar] [CrossRef]
- Gilmore, R. Topological analysis of chaotic dynamical systems. Rev. Mod. Phys. 1998, 70, 1455–1529. [Google Scholar] [CrossRef]
- Carlsson, G. Topological pattern recognition for point cloud data. Acta Numer. 2014, 23, 289–368. [Google Scholar] [CrossRef]
- Giusti, C.; Ghrist, R.; Bassett, D.S. Two’s company, three (or more) is a simplex: Algebraic-topological tools for understanding higher-order structure in neural data. J. Comput. Neurosci. 2016, 41, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Reimann, M.W.; Nolte, M.; Scolamiero, M.; Turner, K.; Perin, R.; Chindemi, G.; Dłotko, P.; Levi, R.; Hess, K.; Markram, H. Cliques of neurons bound into cavities provide a missing link between structure and function. Front. Comput. Neurosci. 2017, 11, 48. [Google Scholar] [CrossRef]
- Perea, J.A. Topological time series analysis. Not. Am. Math. Soc. 2019, 66, 686–694. [Google Scholar] [CrossRef]
- Sciamarella, D.; Mindlin, G.B. Topological structure of chaotic flows from human speech data. Phys. Rev. Lett. 1999, 82, 1450–1453. [Google Scholar] [CrossRef]
- Billings, J.; Saggar, M.; Hlinka, J.; Keilholz, S.; Petri, G. Simplicial and topological descriptions of human brain dynamics. Netw. Neurosci. 2021, 5, 549–568. [Google Scholar] [CrossRef]
- Bai, X.; Yu, C.; Zhai, J. Topological data analysis of the firings of a network of stochastic spiking neurons. Front. Neural Circuits 2024, 17, 1308629. [Google Scholar] [CrossRef] [PubMed]
- Coleman, A.J. The Betti numbers of the simple Lie groups. Canad. J. Math. 1958, 10, 349–356. [Google Scholar] [CrossRef]
- Meunier, D.; Lambiotte, R.; Bullmore, E.T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 2010, 4, 200. [Google Scholar] [CrossRef] [PubMed]
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, V.J.H. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Gralla, S.E.; Harte, A.I.; Wald, R.M. Rigorous derivation of electromagnetic self-force. Phys. Rev. 2009, 80, 024031. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: Nashville, TN, USA, 1998. [Google Scholar]
- Deco, G.; Cruzat, J.; Cabral, J.; Tagliazucchi, E.; Laufs, H.; Logothetis, N.K.; Kringelbach, M.L. Awakening: Predicting external stimulation to force transitions between different brain states. Proc. Natl. Acad. Sci. USA 2019, 116, 18088–18097. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruffini, G.; Lopez-Sola, E.; Vohryzek, J.; Sanchez-Todo, R. Neural Geometrodynamics, Complexity, and Plasticity: A Psychedelics Perspective. Entropy 2024, 26, 90. https://doi.org/10.3390/e26010090
Ruffini G, Lopez-Sola E, Vohryzek J, Sanchez-Todo R. Neural Geometrodynamics, Complexity, and Plasticity: A Psychedelics Perspective. Entropy. 2024; 26(1):90. https://doi.org/10.3390/e26010090
Chicago/Turabian StyleRuffini, Giulio, Edmundo Lopez-Sola, Jakub Vohryzek, and Roser Sanchez-Todo. 2024. "Neural Geometrodynamics, Complexity, and Plasticity: A Psychedelics Perspective" Entropy 26, no. 1: 90. https://doi.org/10.3390/e26010090
APA StyleRuffini, G., Lopez-Sola, E., Vohryzek, J., & Sanchez-Todo, R. (2024). Neural Geometrodynamics, Complexity, and Plasticity: A Psychedelics Perspective. Entropy, 26(1), 90. https://doi.org/10.3390/e26010090







