An Information Theoretic Condition for Perfect Reconstruction
Abstract
| A movement is accomplished in six stages |
| And the seventh brings return. |
| The seven is the number of the young light |
| It forms when darkness is increased by one. |
| Change returns success |
| Going and coming without error. |
| Action brings good fortune. |
| Sunset, sunrise. |
| Syd Barrett, Chapter 24 (Pink Floyd). |
1. Introduction
2. What Is Information? A Detailed Study of Shannon’s Information Lattice
2.1. Definition of the “True” Information
- Reflexivity: so .
- Antisymmetry: If and , a.s., and a.s. for deterministic functions f and g, so .
- Transitivity: If and , then there exist two deterministic functions f and g such that: a.s. and a.s. Then, a.s.; hence, . □
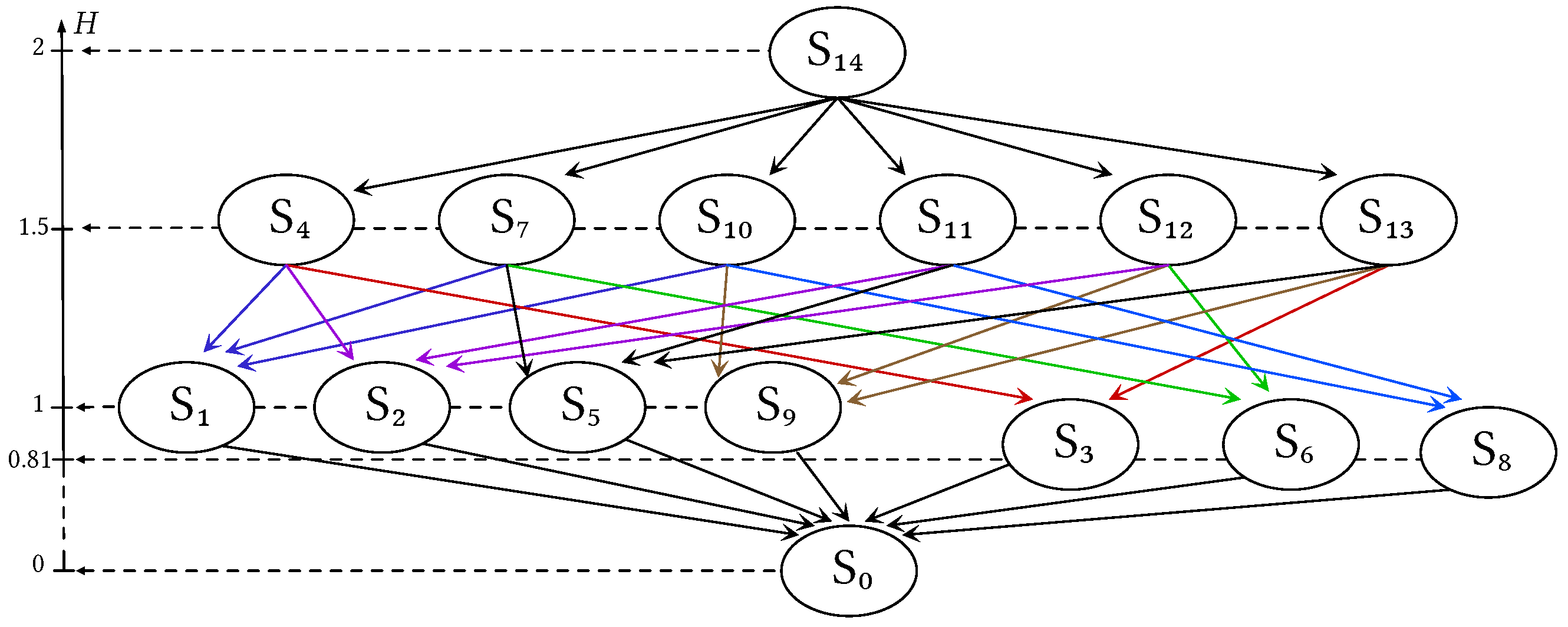
2.2. Structure of the Information Lattice: Joint Information; Common Information
2.3. Computing Common Information
| Algorithm 1: Algorithm to compute the common information. |
|
2.4. Boundedness and Complementedness: Null, Total, and Complementary Information
- The minimal element 0 (“null information”) is the equivalence class of all deterministic variables. Thus, means that X is a deterministic variable.
- The maximal element 1 (“total information”) of the lattice is the equivalence class of the identity function on Ω.
2.5. Computing the Complementary Information
| Algorithm 2: Algorithm for computing the complementary information. |
|
2.6. Relationship between Complementary Information and Functional Representation
2.7. Is the Information Lattice a Boolean Algebra?
3. Metric Properties of the Information Lattice
3.1. Information and Information Measures
- Entropy: If , there exist functions f and g such that a.s. (hence, ) and a.s. (hence, ). Thus, .
- Conditional entropy: Let with f and g be two functions such that and a.s. Then, . Similarly, . Therefore, . Finally, if with two functions h and k such that and a.s., then and likewise . Therefore, .
- Mutual information: Since , compatibility follows from the two previous cases. □
3.2. Common Information vs. Mutual Information
3.3. Submodularity of Entropy on the Information Lattice
3.4. Two Entropic Metrics: Shannon Distance; Rajski Distance
- Positivity: As just noted above, vanishes only when .
- Symmetry: is obvious by the commutativity of addition.
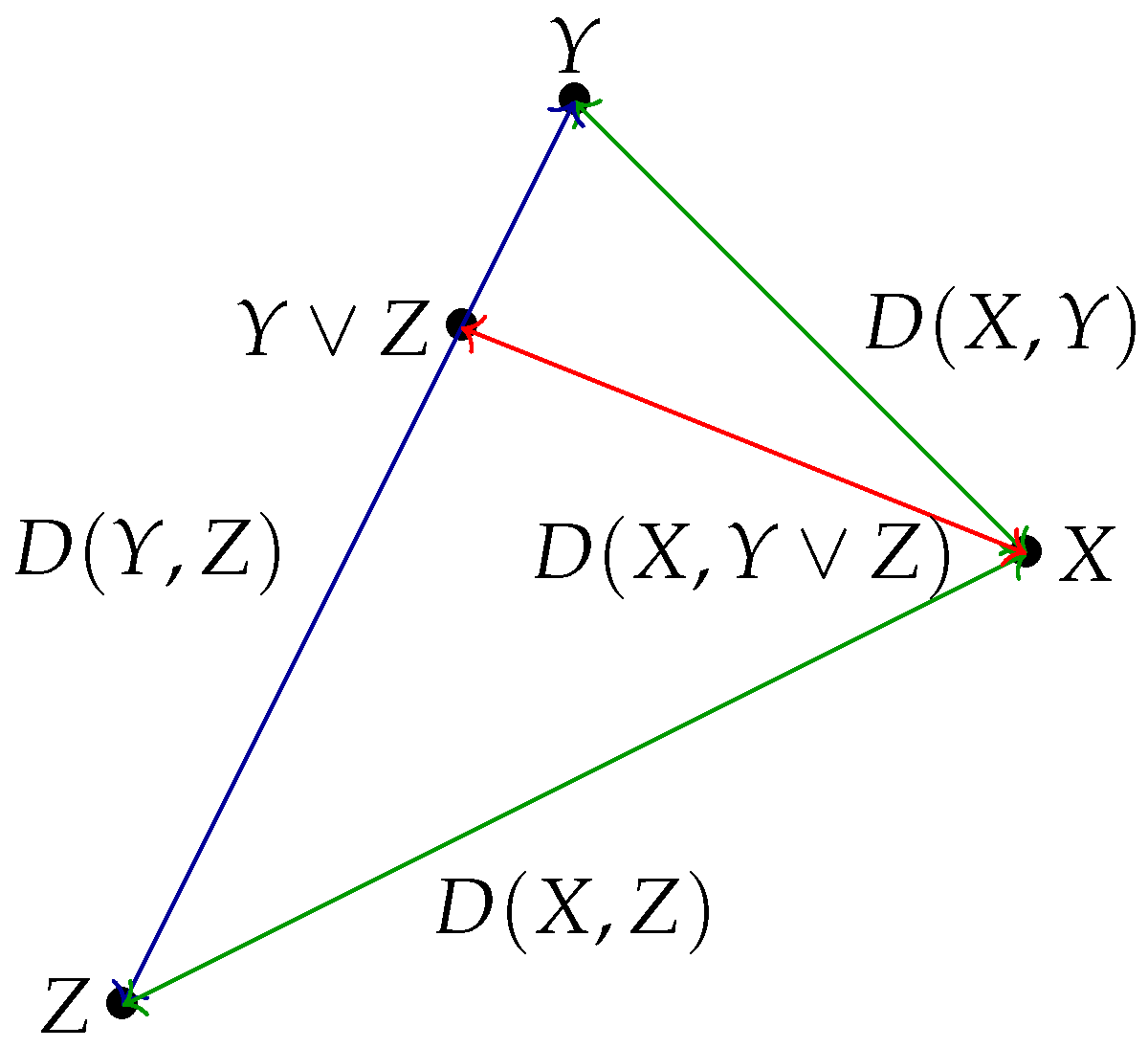
- Triangular inequality: First note that . By permuting X and Z, we also obtain that . Summing up the two inequalities, we obtain the triangular inequality . □
3.5. Dependency Coefficient
3.6. Discontinuity and Continuity Properties
- (i)
- .
- (ii)
- .
- (iii)
- .
- (iv)
- .
- (i)
- By the chain rule: , hence .
- (ii)
- Applying the inequality (i) to the variables and , we obtain . From the continuity of joint information (Proposition 20), one can further bound .
- (iii)
- By the chain rule, . The conclusion now follows from (i) and (ii).
- (iv)
- By the chain rule, . The conclusion follows from bounding each of the three terms in the sum using (i) and (ii). □
4. Geometric Properties of the Information Lattice
4.1. Alignments of Random Variables
4.2. Convex Sets of Random Variables in the Information Lattice
4.3. The Lattice Generated by a Random Variable
4.4. Properties of Rajski and Shannon Distances in the Lattice Generated by a Random Variable
4.5. Triangle Properties of the Shannon Distance
5. The Perfect Reconstruction Problem
5.1. Problem Statement
5.2. A Necessary Condition for Perfect Reconstruction
5.3. A Sufficient Condition for Perfect Reconstruction
- Either , and perfect reconstruction is possible;
- Or , and perfect reconstruction is impossible.
- Either , and perfect reconstruction is possible;
- Or , and perfect reconstruction is impossible.
5.4. Approximate Reconstruction
6. Examples and Applications
6.1. Reconstruction from Sign and Absolute Value
6.2. Linear Transformation over a Finite Field
6.3. Integer Prime Factorization
6.4. Chinese Remainder Theorem
6.5. Optimal Sort
7. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Shannon, C.E. The lattice theory of information. Trans. Ire Prof. Group Inf. Theory 1953, 1, 105–107. [Google Scholar] [CrossRef]
- Fano, R.M. Interview by Aftab, Cheung, Kim, Thkkar, Yeddanapudi, 6.933 Project History, Massachusetts Institute of Technology. November 2001. [Google Scholar]
- Fano, R.M. Class Notes for Course 6.574: Transmission of Information; MIT: Cambridge, MA, USA, 1952. [Google Scholar]
- Cherry, E.C. A history of the theory of information. Proc. Inst. Electr. Eng. 1951, 98, 383–393. [Google Scholar]
- Shannon, C.E. The bandwagon (editorial). In IRE Transactions on Information Theory; Institute for Radio Engineers, Inc.: New York, NY, USA, 1956; Volume 2, p. 3. [Google Scholar]
- Shannon, C.E. Some Topics on Information Theory. In Proceedings of the International Congress of Mathematicians, Cambridge, MA, USA, 30 August–6 September 1950; Volume II. pp. 262–263. [Google Scholar]
- Rioul, O.; Béguinot, J.; Rabiet, V.; Souloumiac, A. La véritable (et méconnue) théorie de l’information de Shannon. In Proceedings of the 28e Colloque GRETSI 2022, Nancy, France, 6–9 September 2022. [Google Scholar]
- Rajski, C. A metric space of discrete probability distributions. Inf. Control 1961, 4, 371–377. [Google Scholar] [CrossRef]
- Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control Inf. Theory 1973, 2, 149–162. [Google Scholar]
- Gamal, A.E.; Kim, Y.-H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wyner, A.D. The common information of two dependent random variables. IEEE Trans. Inf. Theory 1975, 21, 163–179. [Google Scholar] [CrossRef]
- Nakamura, Y. Entropy and semivaluations on semilattices. Kodai Math. Semin. Rep. 1970, 22, 443–468. [Google Scholar] [CrossRef]
- Yeung, R.W. Information Theory and Network Coding; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Horibe, Y. A note on entropy metrics. Inf. Control 1973, 22, 403. [Google Scholar] [CrossRef][Green Version]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Société Vaudoise Des Sci. Nat. 1901, 37, 241–272. [Google Scholar]
- Csiszár, I.; Körner, J. Information Theory. Coding Theorems for DiscreteMemoryless Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Donderi, D.C. Information measurement of distinctiveness and similarity. Percept. Psychophys. 1988, 44, 576–584. [Google Scholar] [CrossRef] [PubMed]
- Donderi, D.C. An information theory analysis of visual complexity and dissimilarity. Perception 2006, 35, 823–835. [Google Scholar] [CrossRef] [PubMed]
- Rioul, O. Théorie de l’information et du Codage; Hermes Science—Lavoisier: London, UK, 2007. [Google Scholar]
- Pierce, J.R. The early days of information theory. IEEE Trans. Inf. Theory 1973, 19, 3–8. [Google Scholar] [CrossRef]
- Malacaria, P. Algebraic foundations for quantitative information flow. Math. Struct. Comput. Sci. 2015, 25, 404–428. [Google Scholar] [CrossRef][Green Version]
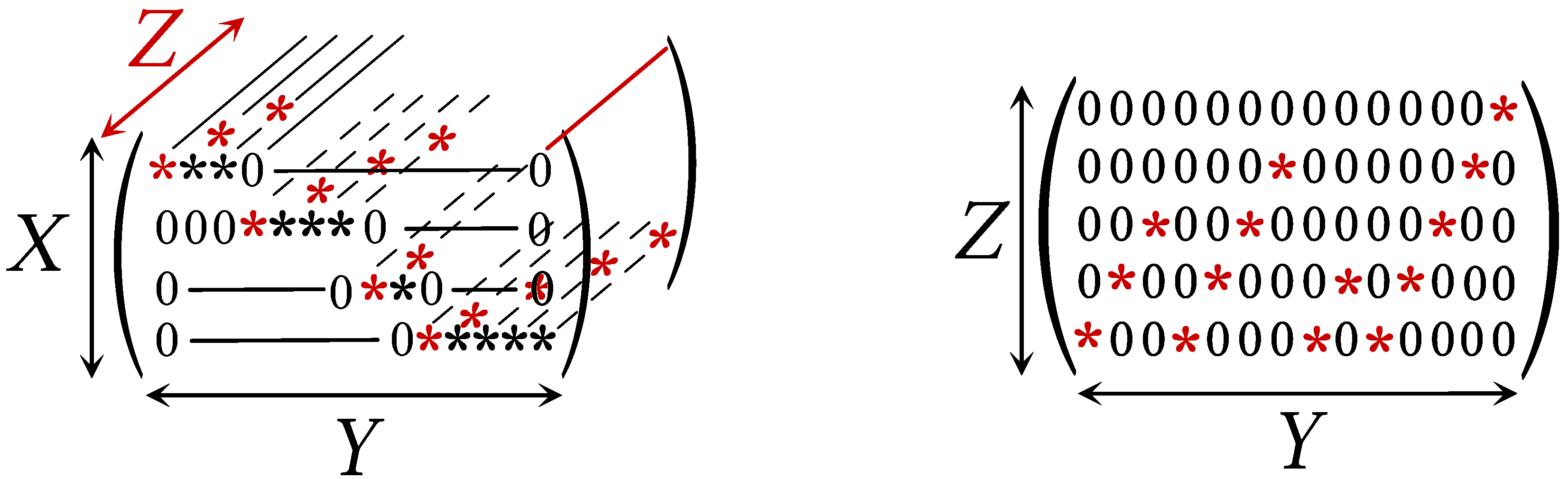
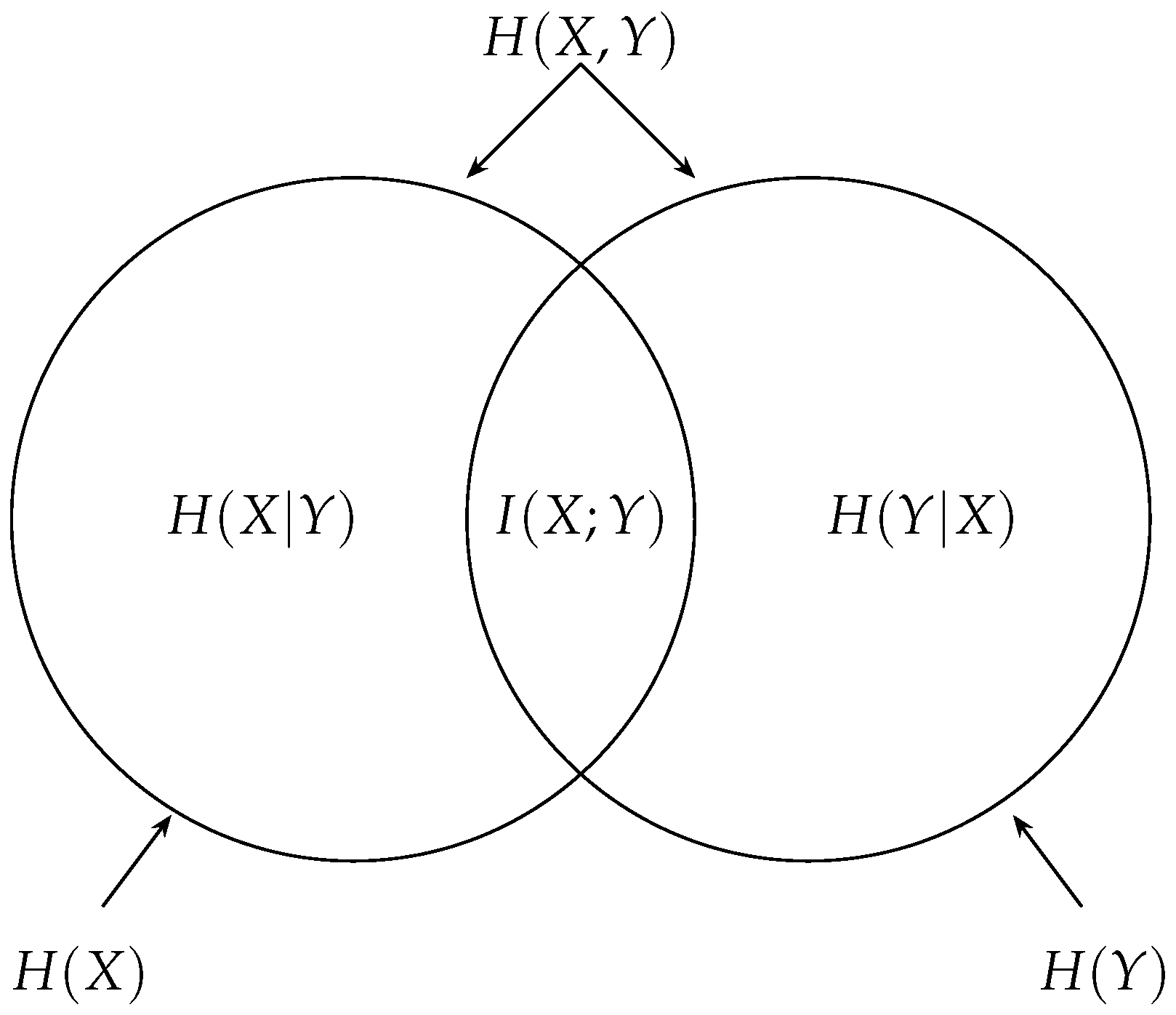
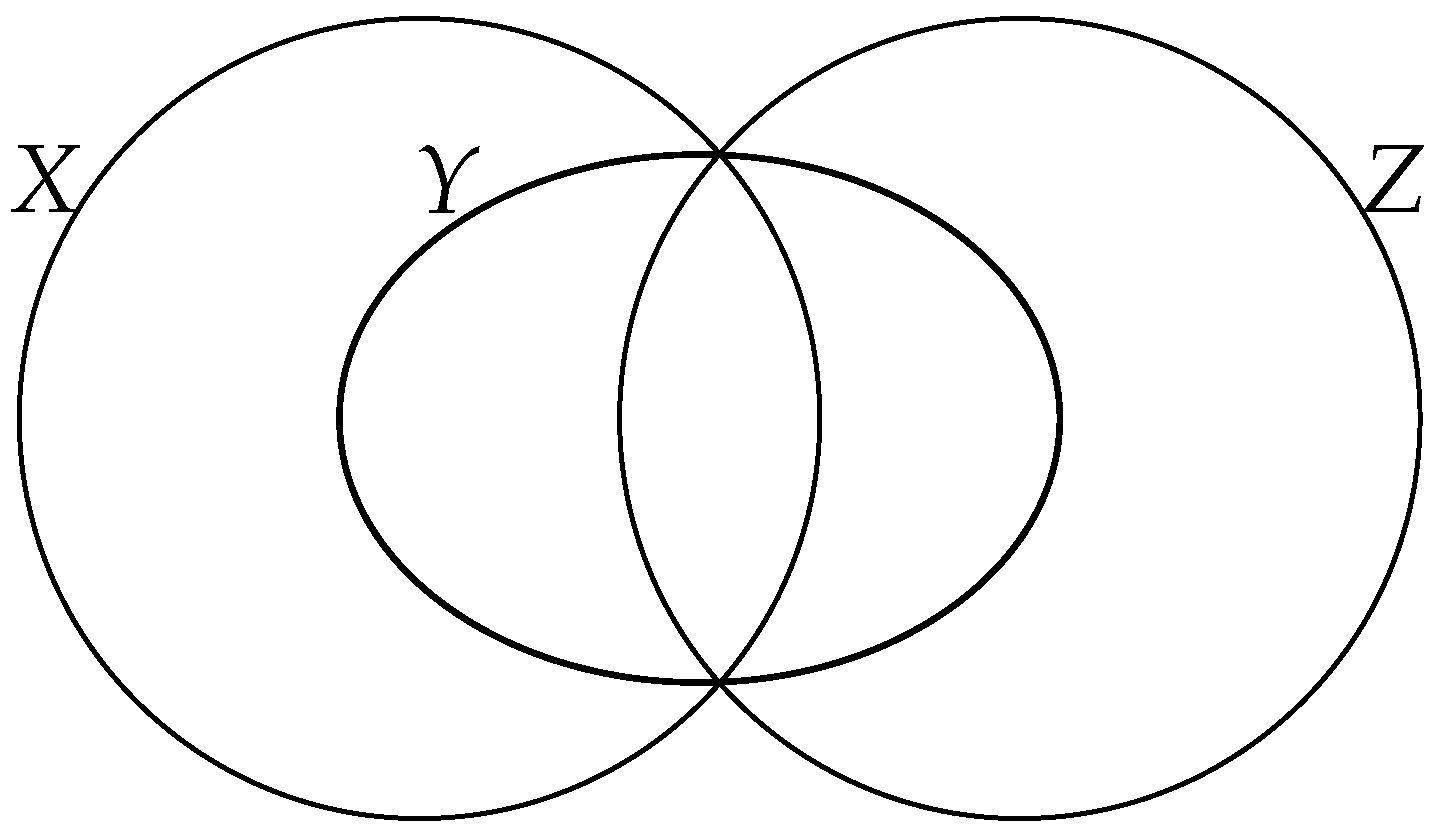

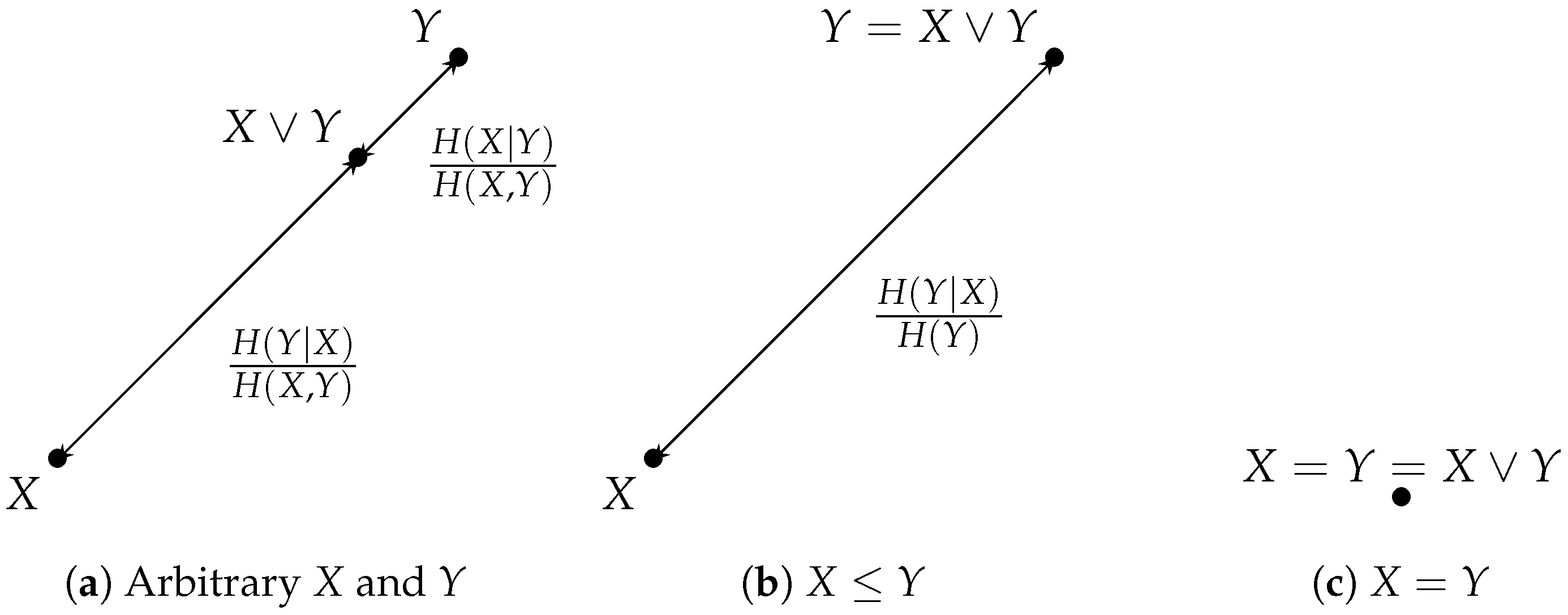
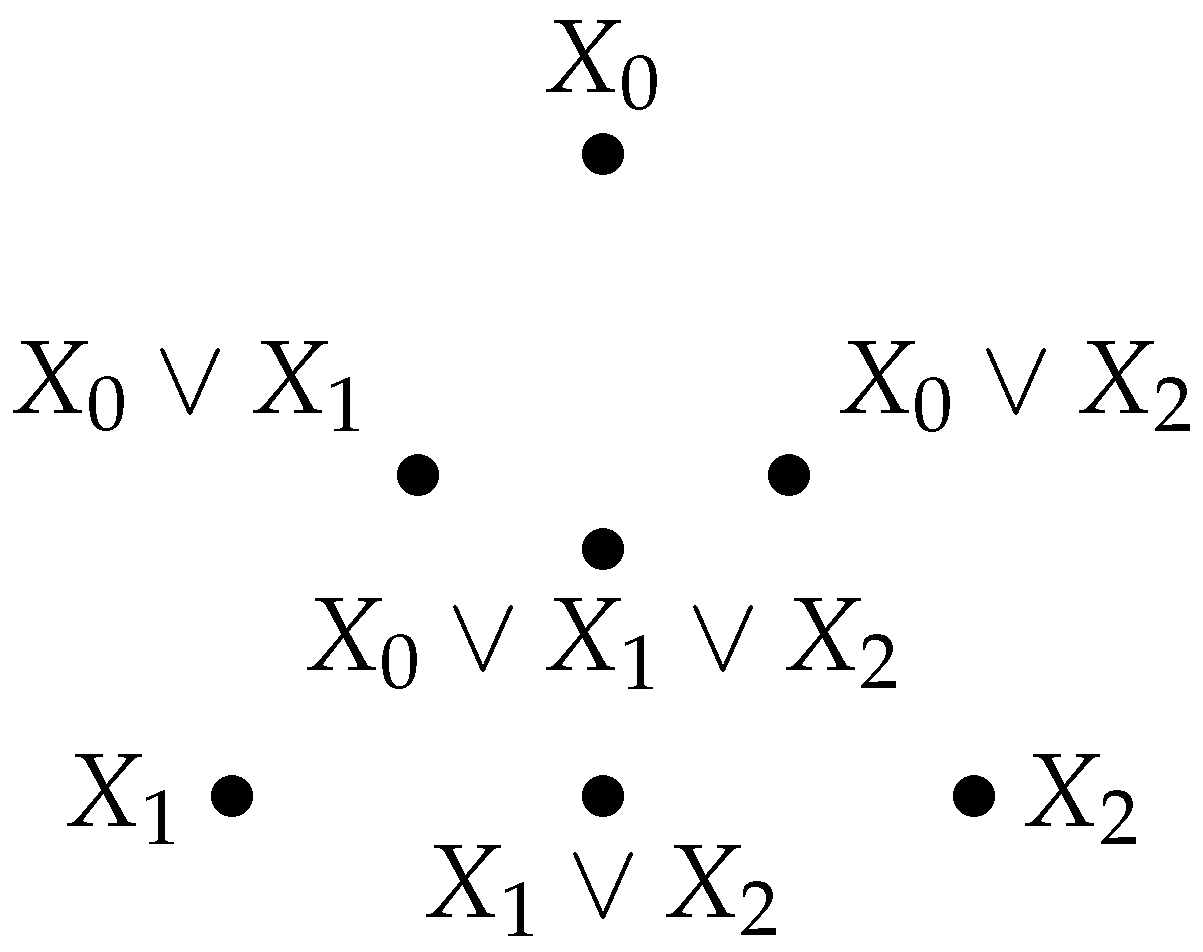
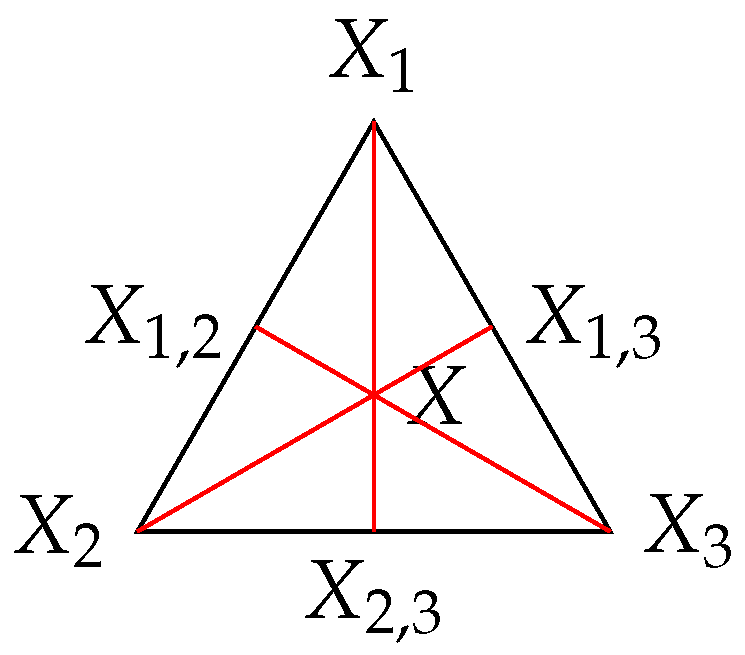
| 0 | 1 | 2 | 3 | |
| X | 0 | 1 | 0 | 1 |
| 1 | 1 | 2 | 2 | |
| 2 | 1 | 1 | 2 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delsol , I.; Rioul , O.; Béguinot, J.; Rabiet , V.; Souloumiac , A. An Information Theoretic Condition for Perfect Reconstruction. Entropy 2024, 26, 86. https://doi.org/10.3390/e26010086
Delsol I, Rioul O, Béguinot J, Rabiet V, Souloumiac A. An Information Theoretic Condition for Perfect Reconstruction. Entropy. 2024; 26(1):86. https://doi.org/10.3390/e26010086
Chicago/Turabian StyleDelsol , Idris, Olivier Rioul , Julien Béguinot, Victor Rabiet , and Antoine Souloumiac . 2024. "An Information Theoretic Condition for Perfect Reconstruction" Entropy 26, no. 1: 86. https://doi.org/10.3390/e26010086
APA StyleDelsol , I., Rioul , O., Béguinot, J., Rabiet , V., & Souloumiac , A. (2024). An Information Theoretic Condition for Perfect Reconstruction. Entropy, 26(1), 86. https://doi.org/10.3390/e26010086










