Robustness of Wave–Particle Duality under Unruh Effect
Abstract
:1. Introduction
2. Fulling–Davies–Unruh Effect
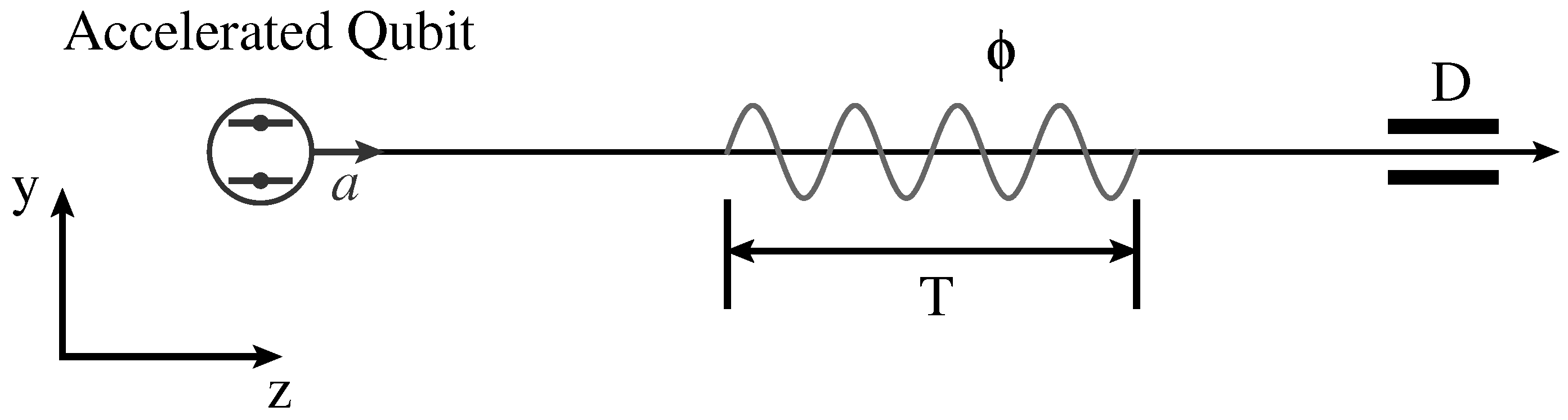
3. Setup A: Accelerated Qubit
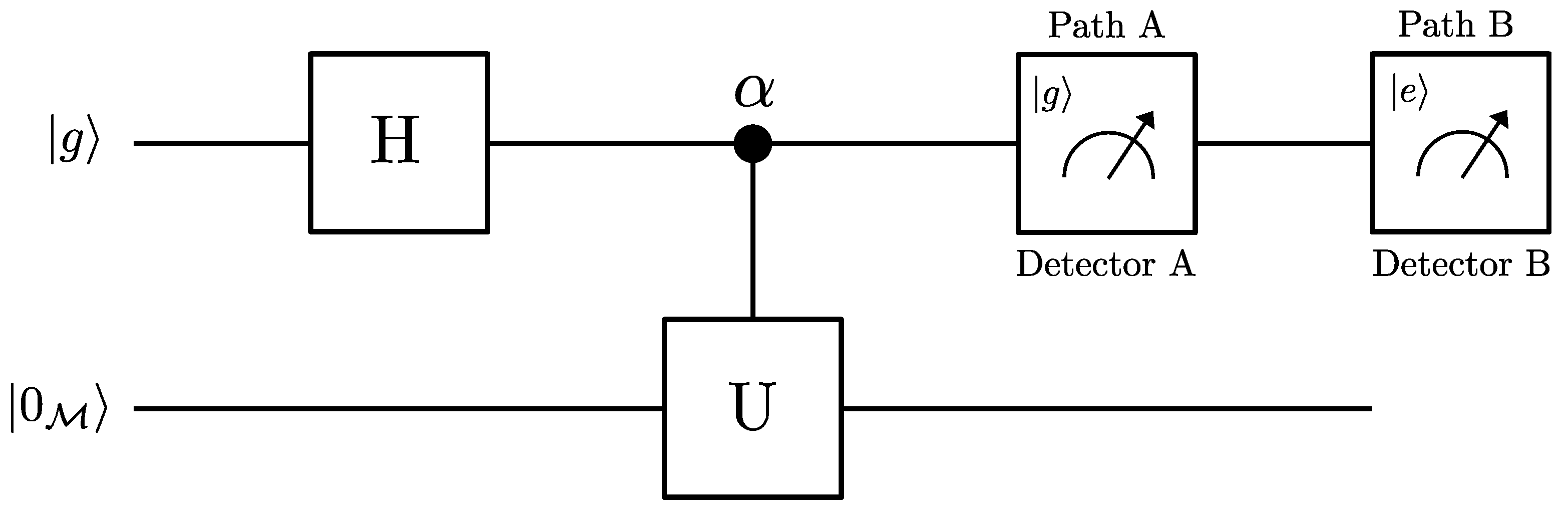
4. Setup B: Quantum Interferometric Circuit
4.1. Quantum Coherence and Visibility
4.2. Which-Path Distinguishability
4.3. Complementarity Relation
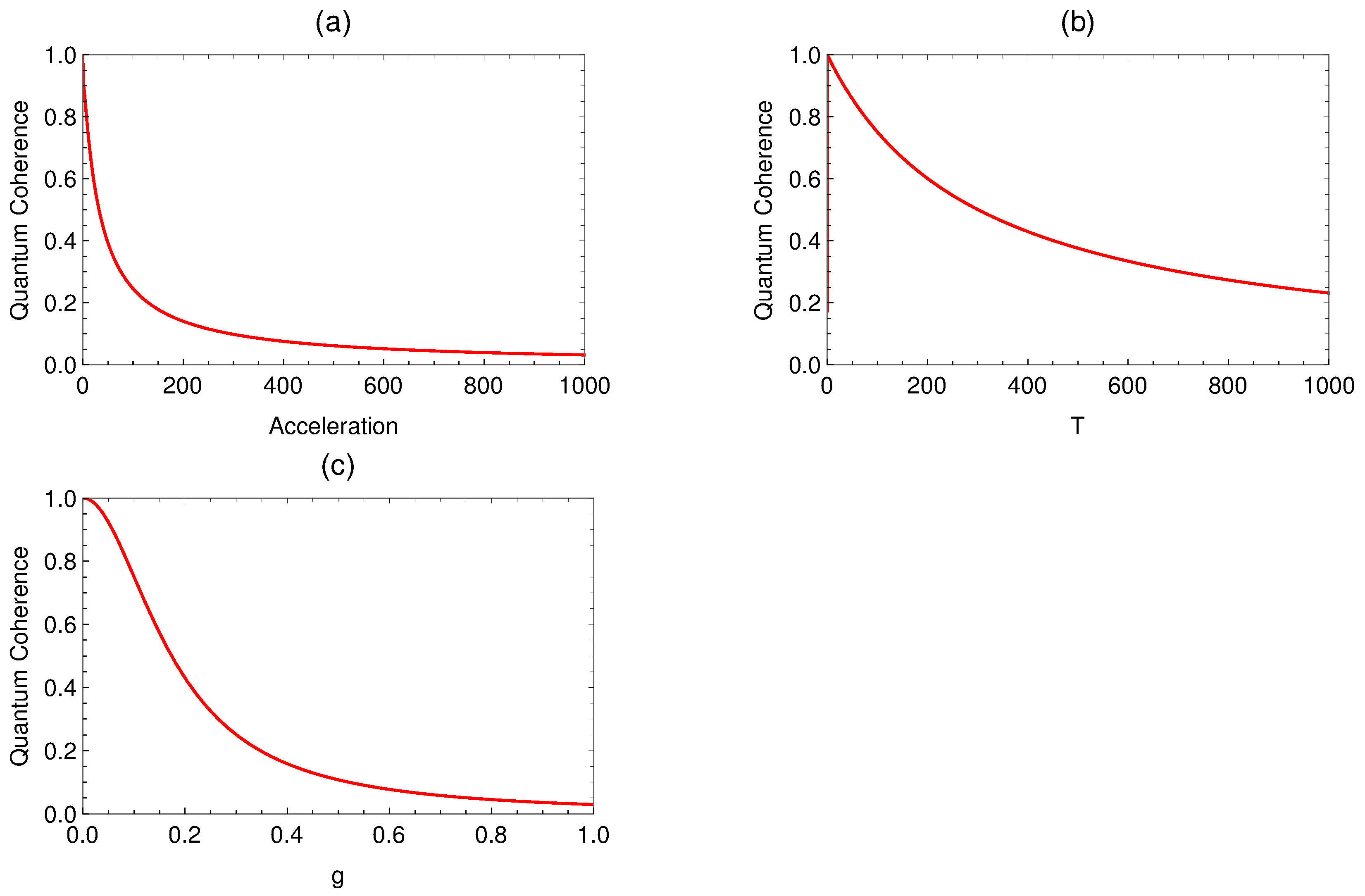
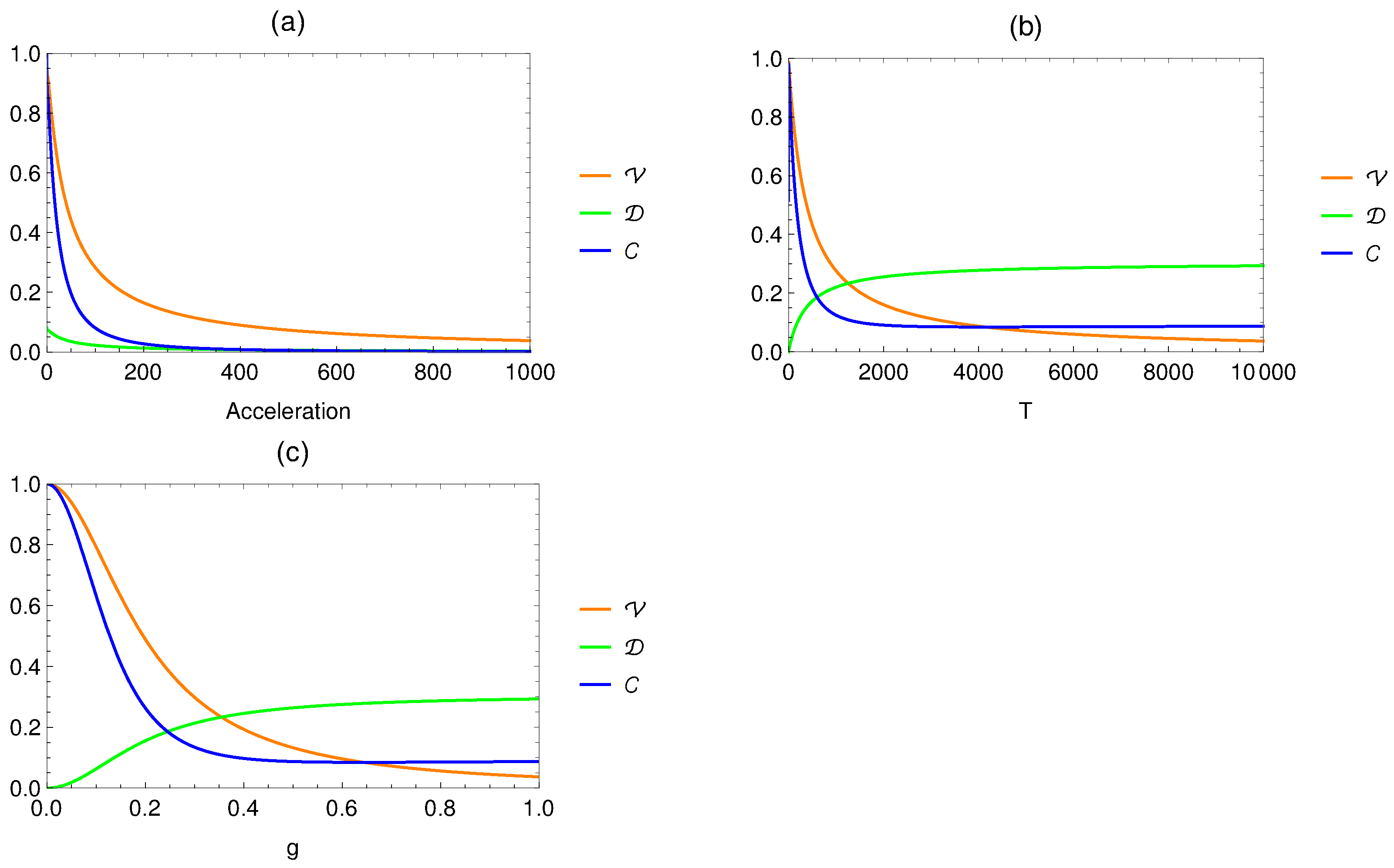
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Gedik, Z.; Silva, I.A.; Çakmak, B.; Karpat, G.; Vidoto, E.L.G.; Soares-Pinto, D.O.; deAzevedo, E.R.; Fanchini, F.F. Computational speed-up with a single qudit. Sci. Rep. 2015, 5, 14671. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.; Zeilinger, A. The Physics of Quantum Information; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Liuzzo-Scorpo, P.; Mari, A.; Giovannetti, V.; Adesso, G. Optimal Continuous Variable Quantum Teleportation with Limited Resources. Phys. Rev. Lett. 2017, 119, 120503. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Hou, Z.; Tang, J.-F.; Streltsov, A.; Xiang, G.-Y.; Li, C.-F.; Guo, G.-C. Direct estimation of quantum coherence by collective measurements. NPJ Quantum Inf. 2020, 6, 46. [Google Scholar] [CrossRef]
- Ge, W.; Jacobs, K.; Asiri, S.; Foss-Feig, M.; Zubairy, M.S. Operational resource theory of nonclassicality via quantum metrology. Phys. Rev. Res. 2020, 6, 023400. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Unurh, W.G.; Wald, R.M. What happens when an accelerating observer detects a Rindler particle. Phys. Rev. D 1984, 29, 1047. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Fulling, S.A. Nonuniqueness of Canonical Field Quantization in Riemannian Space-Time. Phys. Rev. D 1973, 7, 2850. [Google Scholar] [CrossRef]
- Davies, P. Scalar particle production in Schwarzschild and Rindler metrics. J. Phys. A 1975, 8, 609. [Google Scholar] [CrossRef]
- Huang, Z.; Situ, H. Quantum coherence behaviors of fermionic system in non-inertial frame. Quantum Inf. Process 2018, 17, 95. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W. Quantum Coherence Behaviors for a Uniformly Accelerated Atom Immersed in Fluctuating Vacuum Electromagnetic Field with a Boundary. Braz. J. Phys. 2019, 49, 161. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Yang, T. Quantum coherence of a circularly accelerated atom in a spacetime with a reflecting boundary. Sci. Rep. 2022, 12, 12577. [Google Scholar] [CrossRef] [PubMed]
- Salton, G.; Mann, R.B.; Menicucci, N.C. Acceleration-assisted entanglement harvesting and rangefinding. New J. Phys. 2015, 17, 035001. [Google Scholar] [CrossRef]
- Pozas-Kerstjens, A.; Martín-Martínez, E. Harvesting correlations from the quantum vacuum. Phys. Rev. D 2015, 92, 064042. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Yu, H. Entanglement harvesting of accelerated detectors versus static ones in a thermal bath. Phys. Rev. D 2023, 107, 045010. [Google Scholar] [CrossRef]
- Martín-Martínez, E.; Sutherland, C. Quantum gates via relativistic remote control. Phys. Lett. B 2014, 739, 74. [Google Scholar] [CrossRef]
- Martín-Martínez, E.; Aasen, D.; Kempf, A. Processing Quantum Information with Relativistic Motion of Atoms. Phys. Rev. Lett. 2013, 110, 160501. [Google Scholar] [CrossRef]
- Jonsson, R.H.; Martín-Martínez, E.; Kempf, A. Quantum signaling in cavity QED. Phys. Rev. A 2014, 89, 022330. [Google Scholar] [CrossRef]
- Jonsson, R.H.; Martín-Martínez, E.; Kempf, A. Information Transmission without Energy Exchange. Phys. Rev. Lett. 2015, 114, 110505. [Google Scholar] [CrossRef]
- Martín-Martínez, E. Causality issues of particle detector models in QFT and quantum optics. Phys. Rev. D 2015, 92, 104019. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Entanglement generation in uniformly accelerating atoms: Reexamination of the Unruh effect. Phys. Rev. A 2004, 70, 012112. [Google Scholar] [CrossRef]
- Svaiter, B.F.; Svaiter, N.F. Inertial and noninertial particle detectors and vacuum fluctuations. Phys. Rev. D 1992, 46, 5267. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, A.; Matsas, G.E.A.; Peres, C.B. Uniformly accelerated finite-time detectors. Phys. Rev. D 1993, 48, 3731. [Google Scholar] [CrossRef] [PubMed]
- Sriramkumar, L.; Padmanabhan, T. Finite-time response of inertial and uniformly accelerated Unruh—DeWitt detectors. Class. Quantum Grav. 1996, 13, 2061. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space. Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Padmanabhan, T. General covariance, accelarated frames and the particle concept. Astrophys. Space. Sci. 1982, 83, 247. [Google Scholar] [CrossRef]
- Letaw, J.R.; Pfautsch, J.D. Quantized scalar field in the stationary coordinate systems of flat spacetime. Phys. Rev. D 1982, 24, 1491. [Google Scholar] [CrossRef]
- Rindler, W. Kruskal Space and the Uniformly Accelerated Frame. Am. J. Phys. 1966, 34, 1174. [Google Scholar] [CrossRef]
- Scully, M.O.; Kocharovsky, V.V.; Belyanin, A.; Fry, E.; Capasso, F. Enhancing Acceleration Radiation from Ground-State Atoms via Cavity Quantum Electrodynamics. Phys. Rev. Lett. 2003, 91, 243004. [Google Scholar] [CrossRef]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley: Berlin, Germany, 2001. [Google Scholar]
- Audretsch, J.; Mensky, M.; Müller, R. Continuous measurement and localization in the Unruh effect. Phys. Rev. D 1995, 51, 1716. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Wu, K.D.; Theurer, T.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Plenio, M.B.; Streltsov, A. Detecting non-Markovianity via quantified coherence: Theory and experiments. NPJ Quantum Inf. 2020, 6, 55. [Google Scholar] [CrossRef]
- Rossatto, D.Z.; Pires, D.P.; Paula, F.M.D.; Neto, O.P.d. Quantum coherence and speed limit in the mean-field Dicke model of superradiance. Phys. Rev. A 2020, 102, 053716. [Google Scholar] [CrossRef]
- Warnes, J.H.; de Paula, F.M.; Costa, N.C.; Neto, O.P.d.S. Dynamics of quantum coherence in the Jaynes—Cummings model with quenched disorder. Phys. Open 2023, 15, 100146. [Google Scholar] [CrossRef]
- Costa, H.A.S.; da Paz, I.G.; Carvalho, P.R.S.; Sampaio, M. Ramsey interferometry as a witness of acceleration radiation. Ann. Phys. 2020, 416, 168158. [Google Scholar] [CrossRef]
- Lopes, H.T.; da Paz, I.G.; Carvalho, P.R.S.; Costa, H.A.S. Thermal signature of the Unruh effect in the interference pattern. Phys. Lett. A 2021, 409, 127483. [Google Scholar] [CrossRef]
- Neto, O.P.d.; Oliveira, M.C.D.; Caldeira, A.O. Generation of superposition states and charge-qubit relaxation probing in a circuit. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 135503. [Google Scholar] [CrossRef]
- Neto, O.P.d.; Oliveira, M.C.D. Quantum bit encoding and information processing with field superposition states in a circuit. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 185505. [Google Scholar] [CrossRef]
- Ramsey, N.F. A New Molecular Beam Resonance Method. Phys. Rev. 1949, 76, 996. [Google Scholar] [CrossRef]
- Souza, A.M.; Oliveira, I.S.; Sarthour, R.S. A scattering quantum circuit for measuring Bell’s time inequality: A nuclear magnetic resonance demonstration using maximally mixed states. New J. Phys. 2011, 13, 053023. [Google Scholar] [CrossRef]
- Negrevergne, C.; Somma, R.; Ortiz, G.; Knill, E.; Laflamme, R. Liquid-state NMR simulations of quantum many-body problems. Phys. Rev. A 2005, 71, 032344. [Google Scholar] [CrossRef]
- Leonhardt, U. Quantum-state tomography and discrete Wigner function. Phys. Rev. Lett. 1995, 74, 4101. [Google Scholar] [CrossRef] [PubMed]
- Miquel, C.; Paz, J.P.; Saraceno, M.; Knill, E.; Laflamme, R.; Negrevergne, C. Interpretation of tomography and spectroscopy as dual forms of quantum computation. Nature 2002, 418, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Batalhão, T.; Souza, A.M.; Mazzola, L.; Auccaise, R.; Oliveira, I.S.; Goold, J.; Chiara, G.D.; Paternostro, M.; Serra, R.M. Experimental reconstruction of work distribution and verification of fluctuation relations at the full quantum level. Phys. Rev. Lett. 2014, 113, 140601. [Google Scholar] [CrossRef] [PubMed]
- Jakob, M.; Bergou, J.A. Quantitative complementarity relations in bipartite systems: Entanglement as a physical reality. Opt. Commun. 2010, 283, 827. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barros, P.H.M.; da Paz, I.G.; Neto, O.P.d.S.; Costa, H.A.S. Robustness of Wave–Particle Duality under Unruh Effect. Entropy 2024, 26, 1. https://doi.org/10.3390/e26010001
Barros PHM, da Paz IG, Neto OPdS, Costa HAS. Robustness of Wave–Particle Duality under Unruh Effect. Entropy. 2024; 26(1):1. https://doi.org/10.3390/e26010001
Chicago/Turabian StyleBarros, Pedro H. M., Irismar G. da Paz, Olimpio P. de Sá Neto, and Helder A. S. Costa. 2024. "Robustness of Wave–Particle Duality under Unruh Effect" Entropy 26, no. 1: 1. https://doi.org/10.3390/e26010001
APA StyleBarros, P. H. M., da Paz, I. G., Neto, O. P. d. S., & Costa, H. A. S. (2024). Robustness of Wave–Particle Duality under Unruh Effect. Entropy, 26(1), 1. https://doi.org/10.3390/e26010001





