Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions
Abstract
1. Introduction
2. Governing Equations
3. Derivation of the KdV Burgers Type Equation
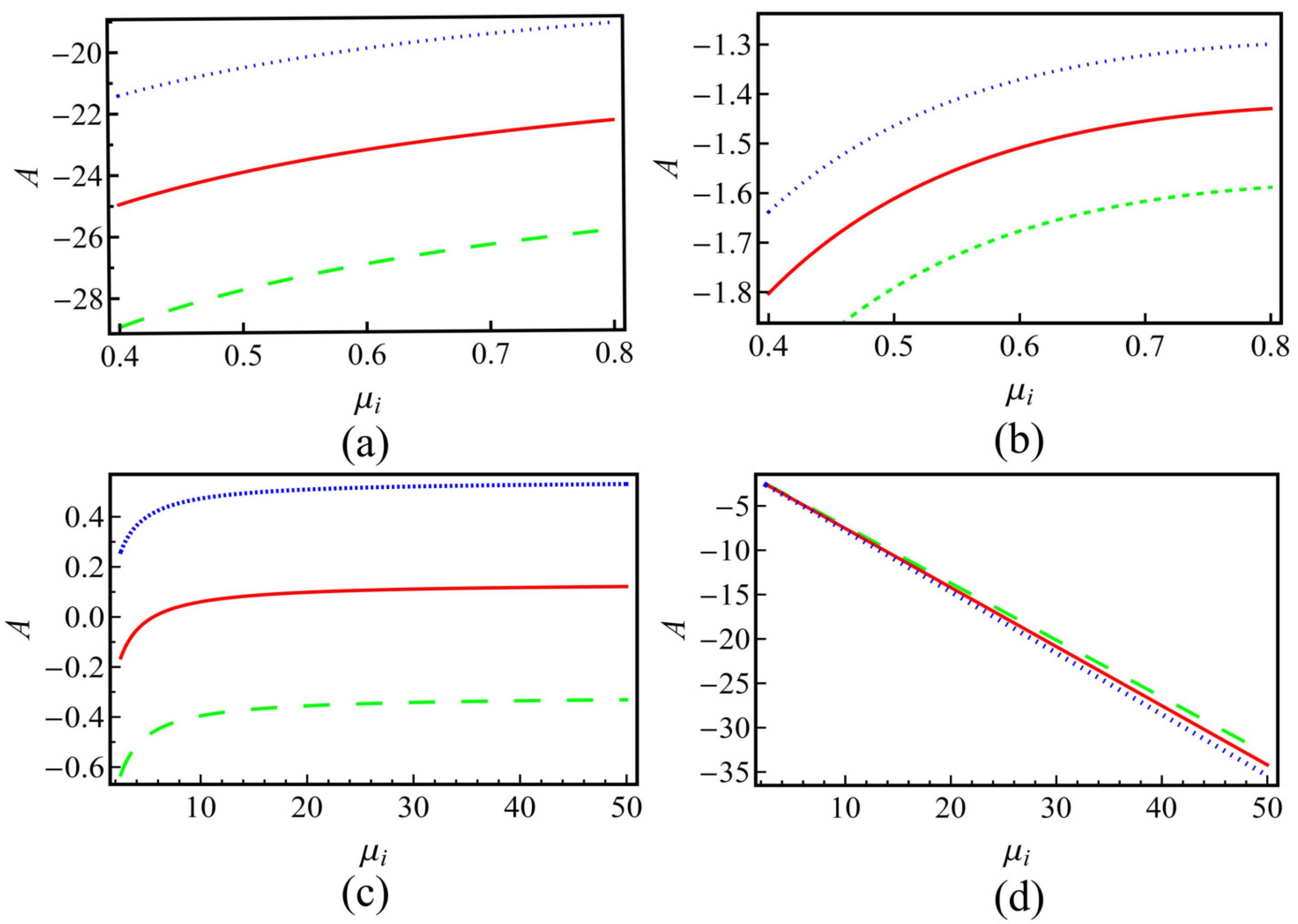
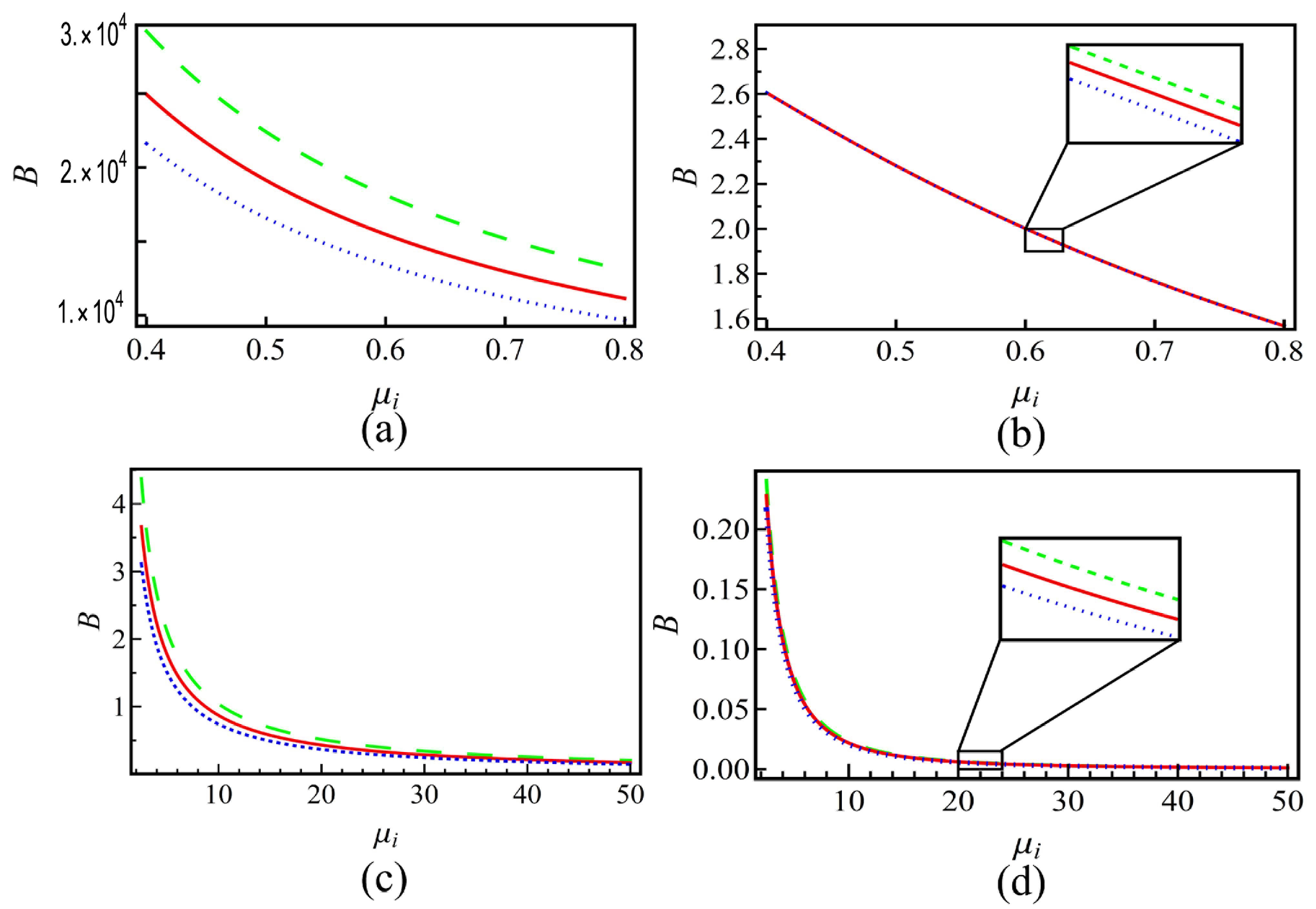
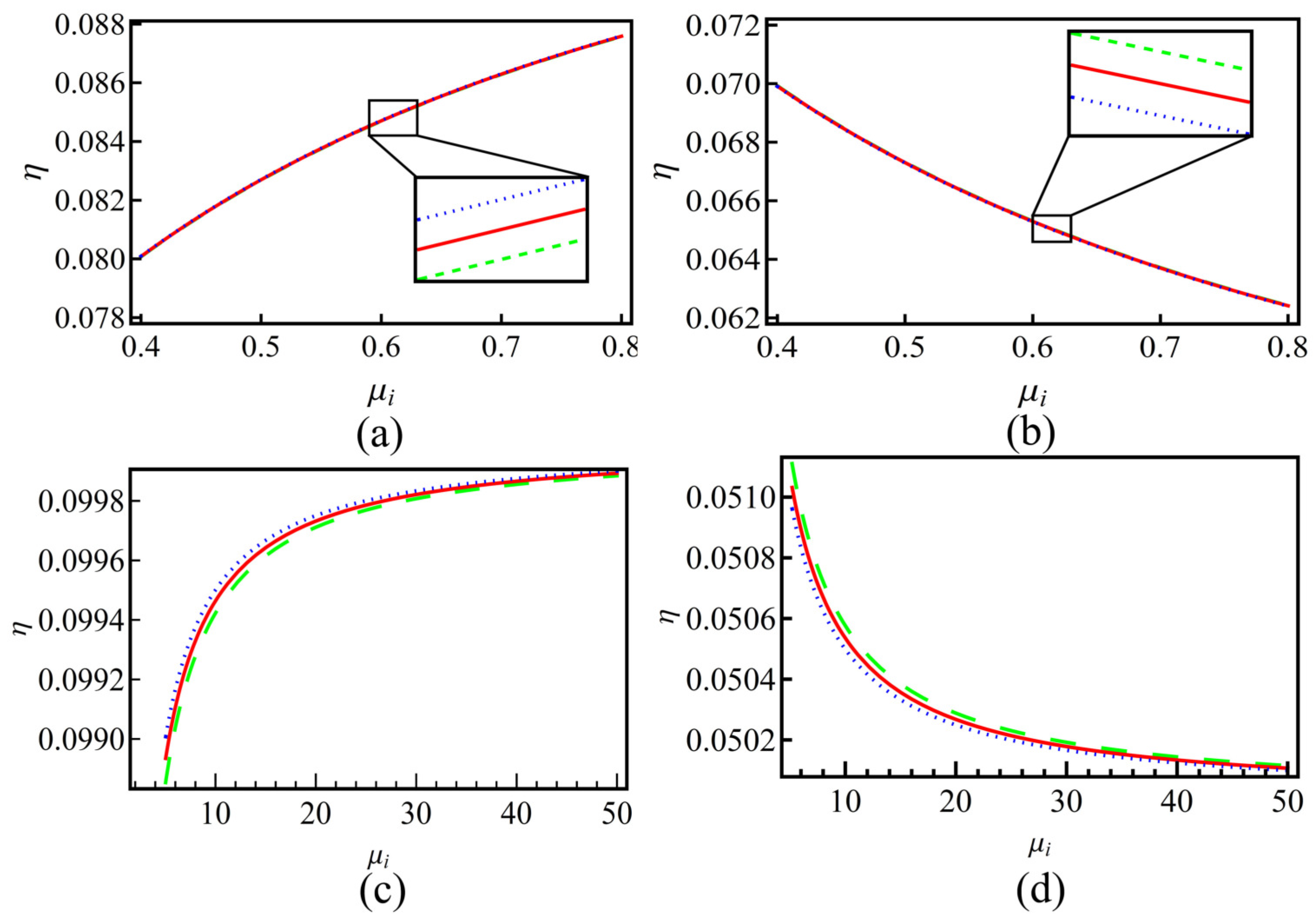
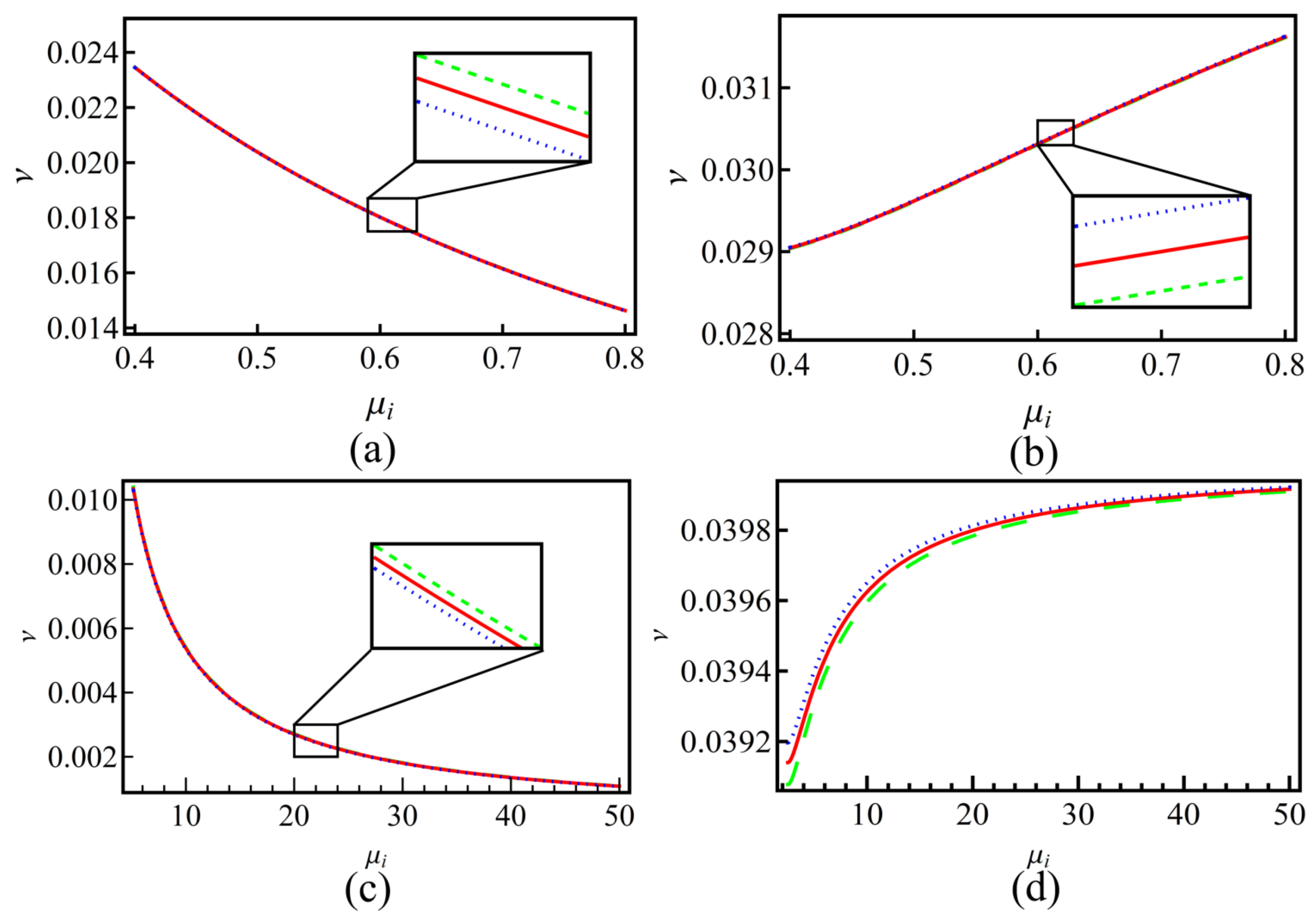
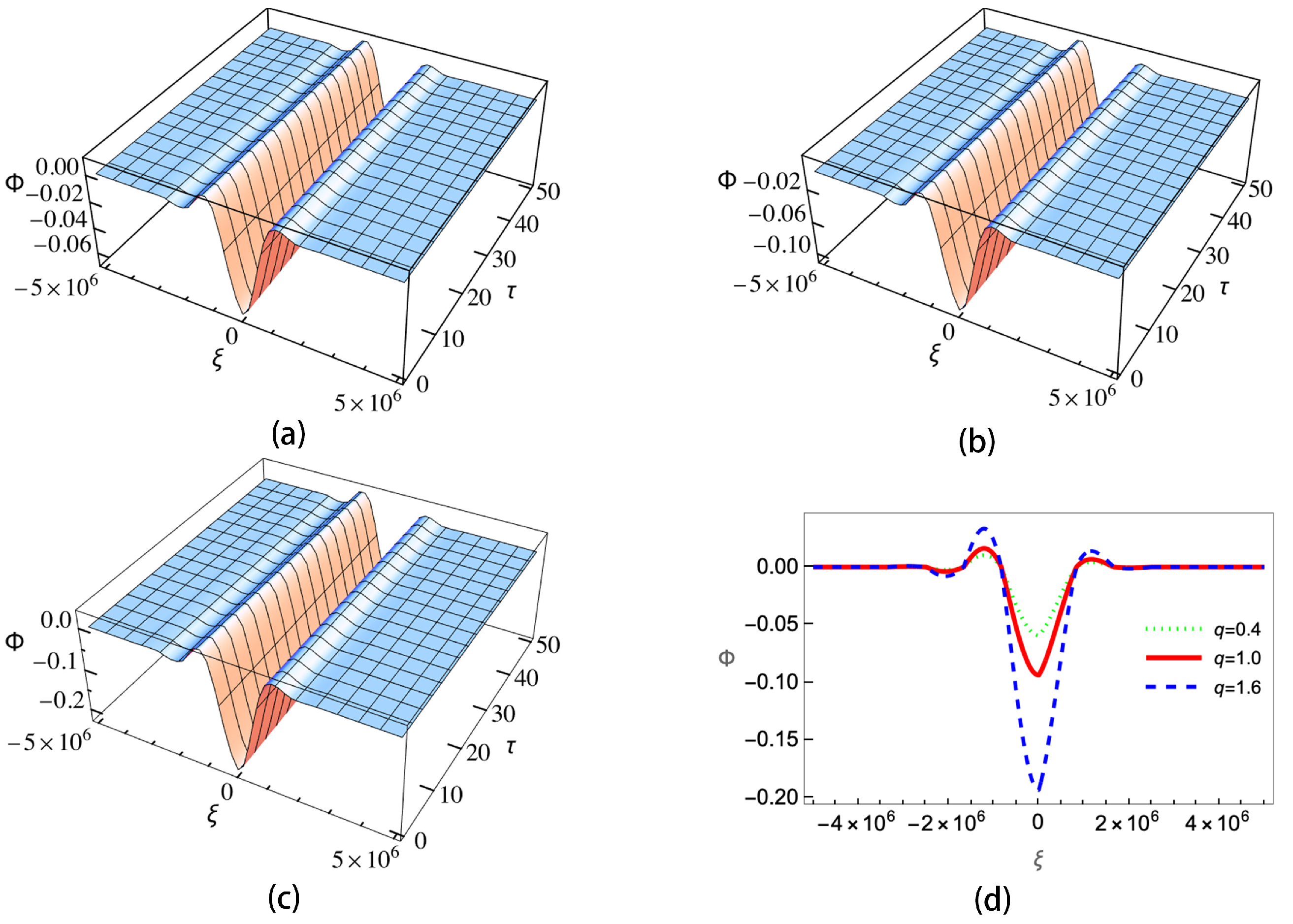
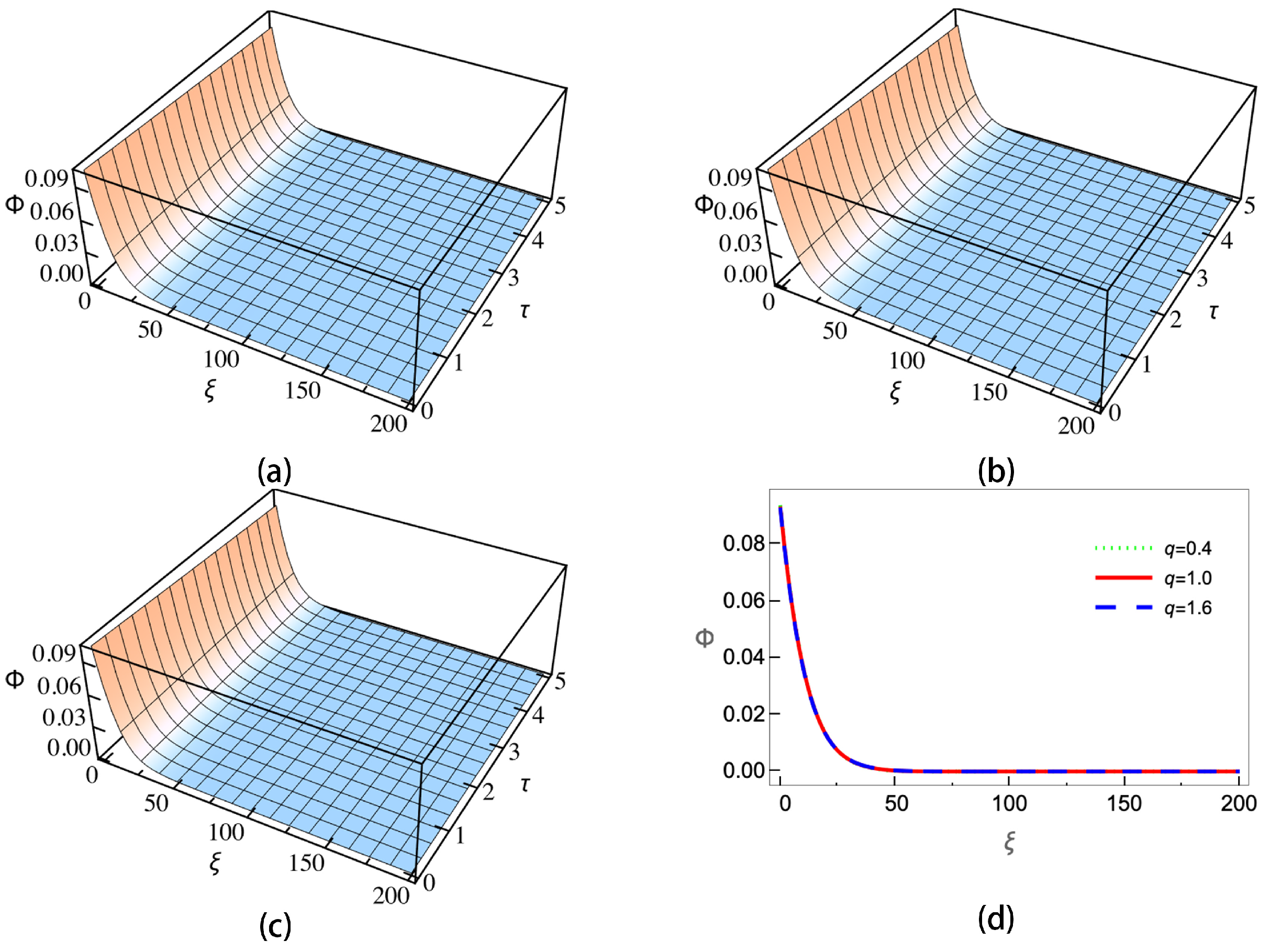
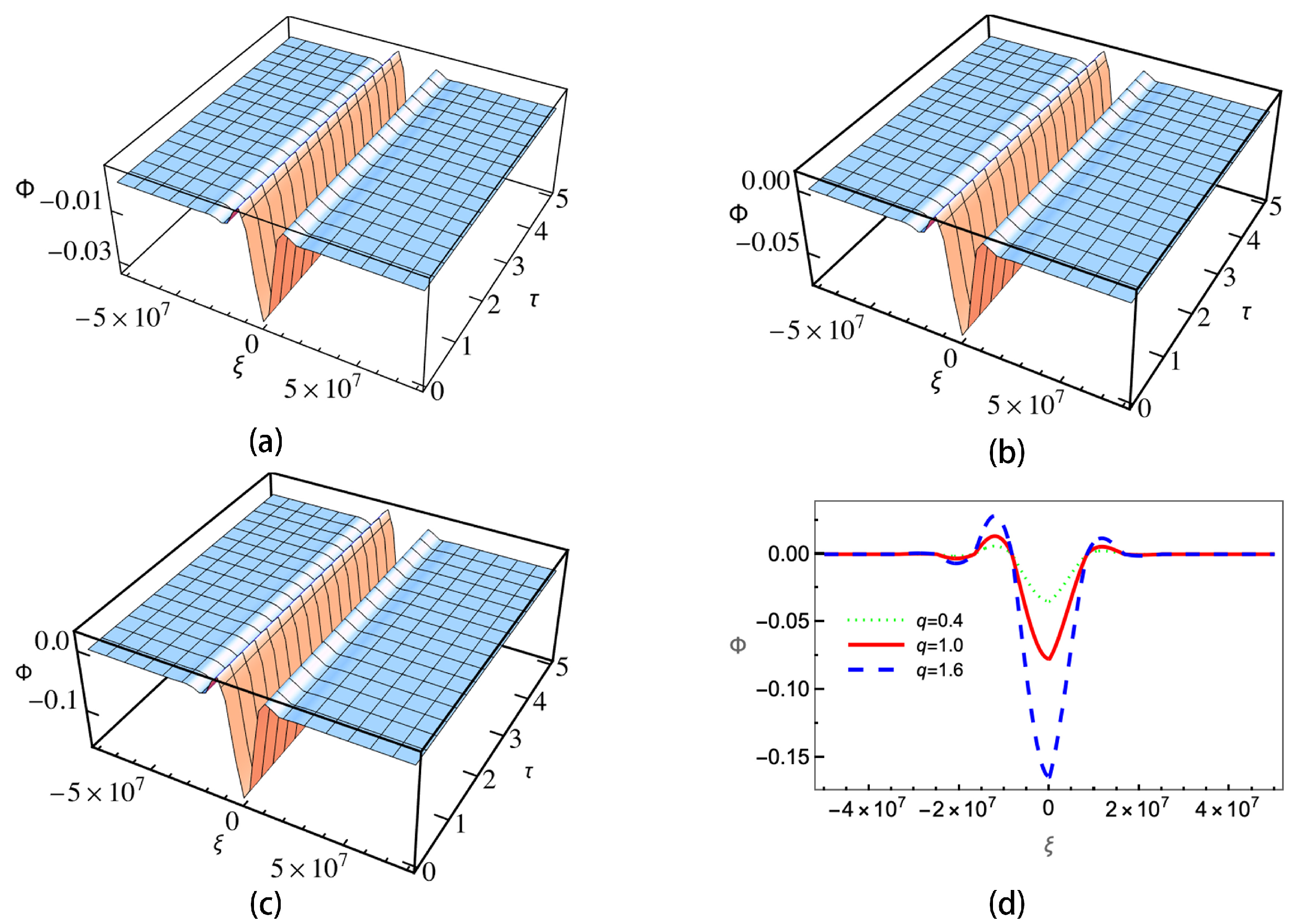
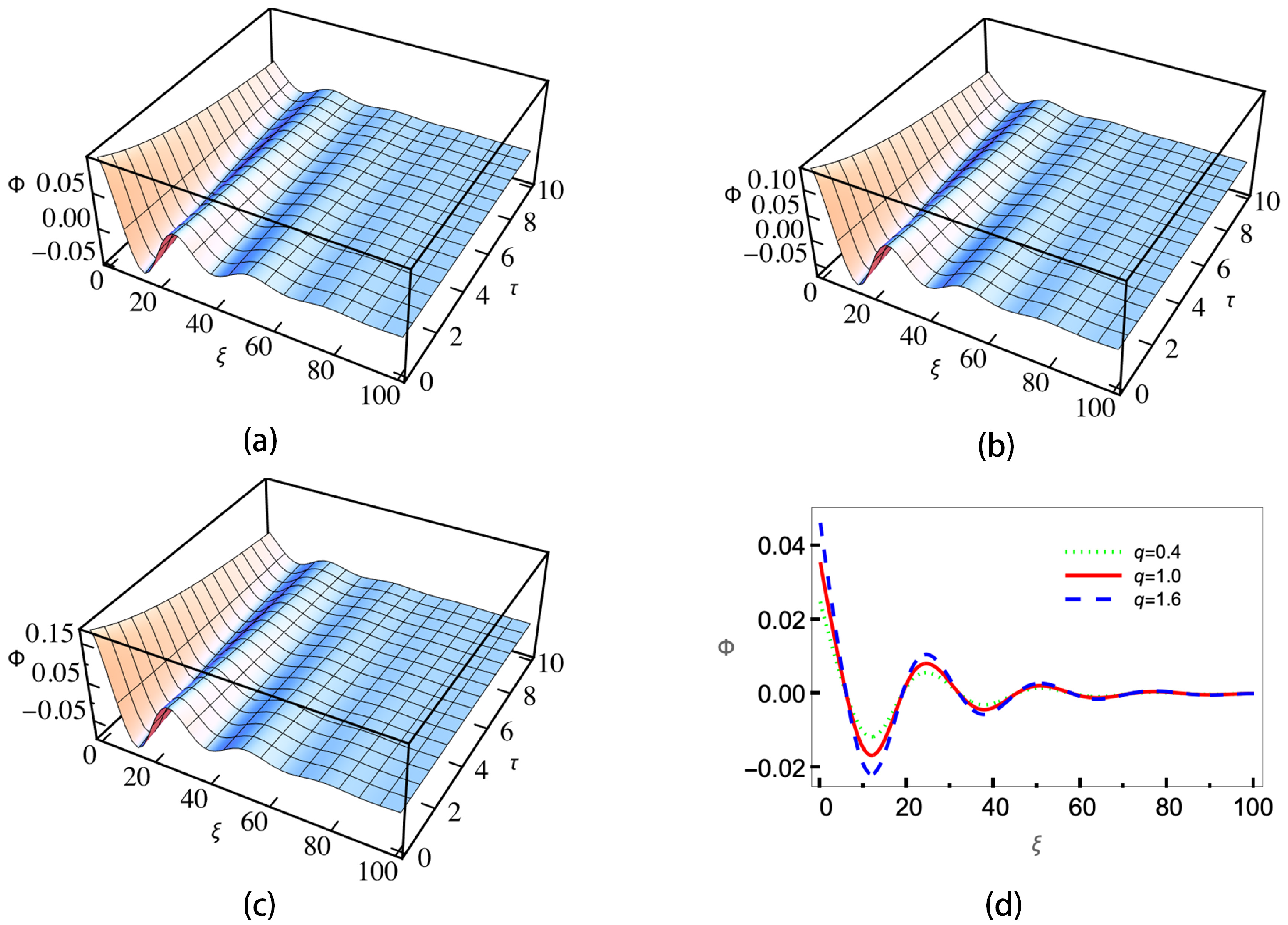
4. Numerical Results and Discussion
5. Summary and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IAW | Ion Acoustic Wave |
| DIAW | Dust–Ion Acoustic Wave |
| IASWS | Ion Acoustic Solitary Wave and Shocks |
| KdVB | Korteweg–de Vries Burgers |
References
- Lee, M.J.; Jung, Y.D. Temperature effects on the propagation and Landau damping of the dust surface waves. Phys. Plasmas 2019, 26, 032103. [Google Scholar] [CrossRef]
- Bilal, M.; Rehman, A.U.; Mahmood, S.; Shahzad, M.A.; Sarfraz, M. Landau damping of ion-acoustic waves with simultaneous effects of non-extensivity and non-thermality in the presence of hybrid Cairns-Tsallis distributed electrons. Contrib. Plasma Phys. 2023, 63, e202200102. [Google Scholar] [CrossRef]
- Beving, L.P.; Hopkins, M.M.; Baalrud, S.D. Simulations of ion heating due to ion-acoustic instabilities in presheaths. Phys. Plasmas 2021, 28, 123516. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.; Menietti, J.D. Effective collision frequency due to ion-acoustic instability: Theory and simulations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Khalid, M. Oblique ion-acoustic solitary waves in anisotropic plasma with Tsallis distribution. Europhys. Lett. 2022, 138, 53003. [Google Scholar] [CrossRef]
- Madhukalya, B.; Das, R.; Hosseini, K.; Baleanu, D.; Salahshour, S. Small amplitude ion-acoustic solitary waves in a magnetized ion-beam plasma under the effect of ion and beam temperatures. Euro. Phys. J. Plus 2023, 138, 315. [Google Scholar] [CrossRef]
- Biskamp, D.; Parkinson, D. Ion Acoustic Shock Waves. Phys. Fluids 1970, 13, 2295–2299. [Google Scholar] [CrossRef]
- Ikezi, H.; Taylor, R.; Baker, D. Formation and interaction of ion-acoustic solitions. Phys. Rev. Lett. 1970, 25, 11. [Google Scholar] [CrossRef]
- Das, G.C. Ion-acoustic solutions and shock waves in multicomponent plasmas. Plasma Phys. 1979, 21, 257. [Google Scholar] [CrossRef]
- Shukla, P.K.; Silin, V.P. Dust ion-acoustic wave. Phys. Scr. 1992, 45, 508. [Google Scholar] [CrossRef]
- Saleem, H.; Shan, S.A. Solar wind interaction with dusty plasma produces electrostatic instabilities and solitons. Astrophys. Space Sci. 2021, 366, 41. [Google Scholar] [CrossRef]
- Bansal, S.; Aggarwal, M.; Gill, T.S. Nonplanar ion acoustic waves in dusty plasma with two temperature electrons: Application to Saturn’s E ring. Phys. Plasmas 2020, 27, 083704. [Google Scholar] [CrossRef]
- Hirashita, H. Dust growth in the interstellar medium: How do accretion and coagulation interplay? Mon. Not. R. Astron. Soc. 2012, 422, 1263–1271. [Google Scholar] [CrossRef]
- Mann, I.; Gunnarsdottir, T.; Häggström, I.; Eren, S.; Tjulin, A.; Myrvang, M.; Rietveld, M.; Dalin, P.; Jozwicki, D.; Trollvik, H. Radar studies of ionospheric dusty plasma phenomena. Contrib. Plasma Phys. 2019, 59, e201900005. [Google Scholar] [CrossRef]
- Merlino, R. Dusty plasmas: From Saturn’s rings to semiconductor processing devices. Adv. Phys. X 2021, 6, 1873859. [Google Scholar] [CrossRef]
- Long, J.M.; Ou, J. Dust particle surface potential in fusion plasma with supra-thermal electrons. Phys. Plasmas 2022, 29. [Google Scholar] [CrossRef]
- El-Labany, S.; Moslem, W.M.; Mowafy, A. Effects of trapped electron temperature, dust charge variations, and grain radius on the existence of the dust-ion-acoustic waves. Phys. Plasmas 2003, 10, 4217–4223. [Google Scholar] [CrossRef]
- Vranješ, J.; Pandey, B.; Poedts, S. Ion–acoustic waves in dusty plasma with charge fluctuations. Phys. Plasmas 2002, 9, 1464–1467. [Google Scholar] [CrossRef]
- El-Labany, S.; El-Siragy, N.; El-Taibany, W.; El-Shamy, E.; Behery, E. Linear and nonlinear quantum dust ion acoustic wave with dust size distribution effect. Phys. Plasmas 2010, 17, 053705. [Google Scholar] [CrossRef]
- Chutia, B.; Deka, T.; Bailung, Y.; Sharma, D.; Sharma, S.; Bailung, H. Spatiotemporal evolution of a self-excited dust density wave in a nanodusty plasma under strong Havnes effect. Phys. Plasmas 2021, 28, 123702. [Google Scholar] [CrossRef]
- Sharma, R.; Bhardwaj, S.; Dhiman, J.S. Effects of dust temperature and radiative heat-loss functions on the magnetogravitational instability of viscoelastic dusty plasma. Astrophys. Space Sci. 2020, 365, 106. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Xu, A.; Zhang, G.; Zhang, Y.; Succi, S. Discrete Boltzmann trans-scale modeling of high-speed compressible flows. Phys. Rev. E 2018, 97, 053312. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.B.; Xu, A.G.; Zhang, G.C.; Lin, C.D.; Lai, H.L.; Liu, Z.P. Nonequilibrium and morphological characterizations of Kelvin–Helmholtz instability in compressible flows. Front. Phys. 2019, 14, 43602. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Lai, H.; Li, W.; Sun, G.; Succi, S. Discrete Boltzmann multi-scale modelling of non-equilibrium multiphase flows. J. Fluid Mech. 2022, 951, A8. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, L.; Du, J. A nonextensive approach for the instability of current-driven ion-acoustic waves in space plasmas. Phys. Plasmas 2009, 16, 072111. [Google Scholar] [CrossRef]
- Liu, Z.; Du, J. Dust acoustic instability driven by drifting ions and electrons in the dust plasma with Lorentzian kappa distribution. Phys. Plasmas 2009, 16, 123707. [Google Scholar] [CrossRef]
- Liu, Z.; Song, J.; Xu, A.; Zhang, Y.; Xie, K. Discrete Boltzmann modeling of plasma shock wave. Proc. IMechE Part C J. Mech. Eng. Sci. 2023, 237, 2532–2548. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Leubner, M.P. A Nonextensive Entropy Approach to Kappa-Distributions. Astrophys. Space Sci. 2002, 282, 573–579. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D. Exploring transitions of space plasmas out of equilibrium. Astrophys. J. 2010, 714, 971. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D. Invariant kappa distribution in space plasmas out of equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Du, J. What does the nonextensive parameter stand for in self-gravitating systems? Astrophys. Space Sci. 2006, 305, 247–251. [Google Scholar] [CrossRef][Green Version]
- Deppman, A.; Megías, E.P.; Menezes, D. Fractal Structures of Yang–Mills Fields and Non-Extensive Statistics: Applications to High Energy Physics. Physics 2020, 2, 455–480. [Google Scholar] [CrossRef]
- Megías, E.; Timóteo, V.; Gammal, A.; Deppman, A. Bose–Einstein condensation and non-extensive statistics for finite systems. Phys. A 2022, 585, 126440. [Google Scholar] [CrossRef]
- Du, J. Nonextensivity in nonequilibrium plasma systems with Coulombian long-range interactions. Phys. Lett. A 2004, 329, 262–267. [Google Scholar] [CrossRef]
- Du, J. The nonextensive parameter and Tsallis distribution for self-gravitating systems. Europhys. Lett. 2004, 67, 893. [Google Scholar] [CrossRef]
- Du, J. Nonextensivity and the power-law distributions for the systems with self-gravitating long-range interactions. Astrophys. Space Sci. 2007, 312, 47–55. [Google Scholar] [CrossRef]
- Yu, H.; Du, J. The nonextensive parameter for the rotating astrophysical systems with power-law distributions. Europhys. Lett. 2017, 116, 60005. [Google Scholar] [CrossRef][Green Version]
- Gong, J.; Du, J. Dust charging processes in the nonequilibrium dusty plasma with nonextensive power-law distribution. Phys. Plasmas 2012, 19, 023704. [Google Scholar] [CrossRef]
- Gong, J.; Liu, Z.; Du, J. Dust-acoustic waves and stability in the permeating dusty plasma. II. Power-law distributions. Phys. Plasmas 2012, 19, 083706. [Google Scholar] [CrossRef]
- Du, J. Transport coefficients in Lorentz plasmas with the power-law kappa-distribution. Phys. Plasmas 2013, 20, 092901. [Google Scholar] [CrossRef]
- Wang, L.; Du, J. The diffusion of charged particles in the weakly ionized plasma with power-law kappa-distributions. Phys. Plasmas 2017, 24, 102305. [Google Scholar] [CrossRef]
- Wang, Y.; Du, J. The viscosity of charged particles in the weakly ionized plasma with power-law distributions. Phys. Plasmas 2018, 25, 062309. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G. Statistical Uncertainties of Space Plasma Properties Described by Kappa Distributions. Entropy 2020, 22, 541. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Silva, R.; Santos, J. Plasma oscillations and nonextensive statistics. Phys. Rev. E 2000, 61, 3260–3263. [Google Scholar] [CrossRef]
- Younsi, S.; Tribeche, M. Arbitrary amplitude electron-acoustic solitary waves in the presence of excess superthermal electrons. Astrophys. Space Sci. 2010, 330, 295–300. [Google Scholar] [CrossRef]
- El-Awady, E.; Moslem, W. On a plasma having nonextensive electrons and positrons: Rogue and solitary wave propagation. Phys. Plasmas 2011, 18, 082306. [Google Scholar] [CrossRef]
- Yasmin, S.; Asaduzzaman, M.; Mamun, A. Dust ion-acoustic shock waves in nonextensive dusty plasma. Astrophys. Space Sci. 2013, 343, 245–250. [Google Scholar] [CrossRef]
- Misra, A.P.; Adhikary, N.C.; Shukla, P.K. Ion-acoustic solitary waves and shocks in a collisional dusty negative-ion plasma. Phys. Rev. E 2012, 86, 056406. [Google Scholar] [CrossRef] [PubMed]
- Pakzad, H.R.; Javidan, K. Dust acoustic solitary and shock waves in strongly coupled dusty plasmas with nonthermal ions. Pramana 2009, 73, 913–926. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z. Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions. Entropy 2023, 25, 1363. https://doi.org/10.3390/e25091363
Liu Z. Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions. Entropy. 2023; 25(9):1363. https://doi.org/10.3390/e25091363
Chicago/Turabian StyleLiu, Zhipeng. 2023. "Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions" Entropy 25, no. 9: 1363. https://doi.org/10.3390/e25091363
APA StyleLiu, Z. (2023). Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions. Entropy, 25(9), 1363. https://doi.org/10.3390/e25091363





