A Novel Joint Channel Estimation and Symbol Detection Receiver for Orthogonal Time Frequency Space in Vehicular Networks
Abstract
:1. Introduction
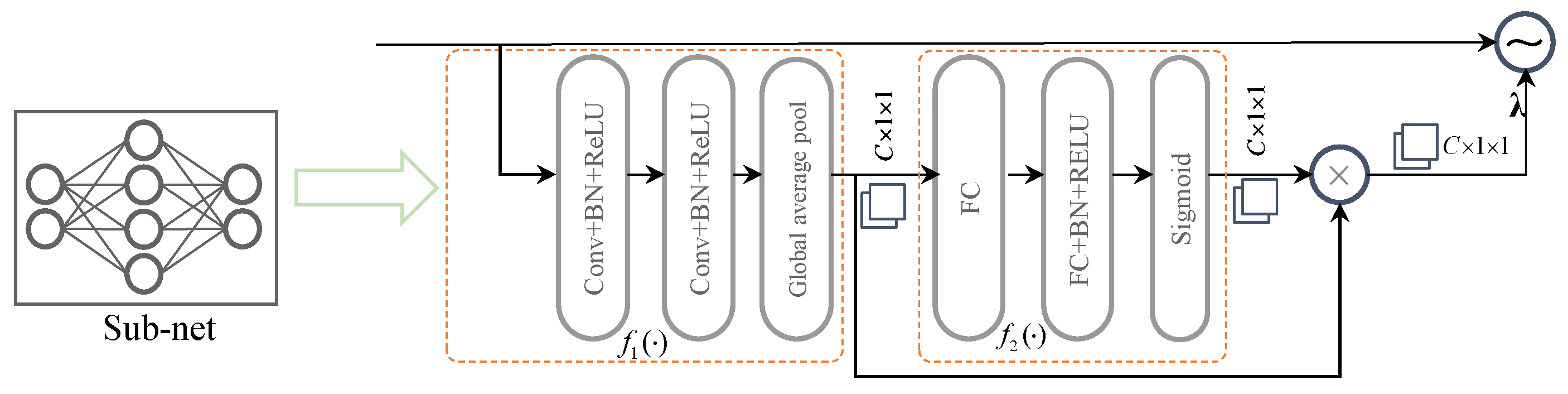
- We propose an integrated OTFS-ISAC system that leverages a novel deep residual denoising network and OAMP algorithm for joint channel estimation and symbol detection. Specifically, we design a DNN-based denoising module, incorporating an element-by-element subtraction operation that concurrently exploits the spatial attributes of noise-infected channel matrices as well as the additive character of the perturbation. In addition, a subnetwork that can generate thresholds is utilized to eliminate irrelevant features, thereby enhancing the estimation accuracy.
- We employ the OAMP detector to carry out the OTFS symbol detection, as it has the potential for MMSE optimality and exhibits excellent detection performance.
- We demonstrate the effectiveness of the proposed system through simulations and compare its performance with traditional communication systems. The proposed system shows superior performance in challenging environments such as a high Doppler frequency and delay spread, making it a promising solution for future wireless communication systems.
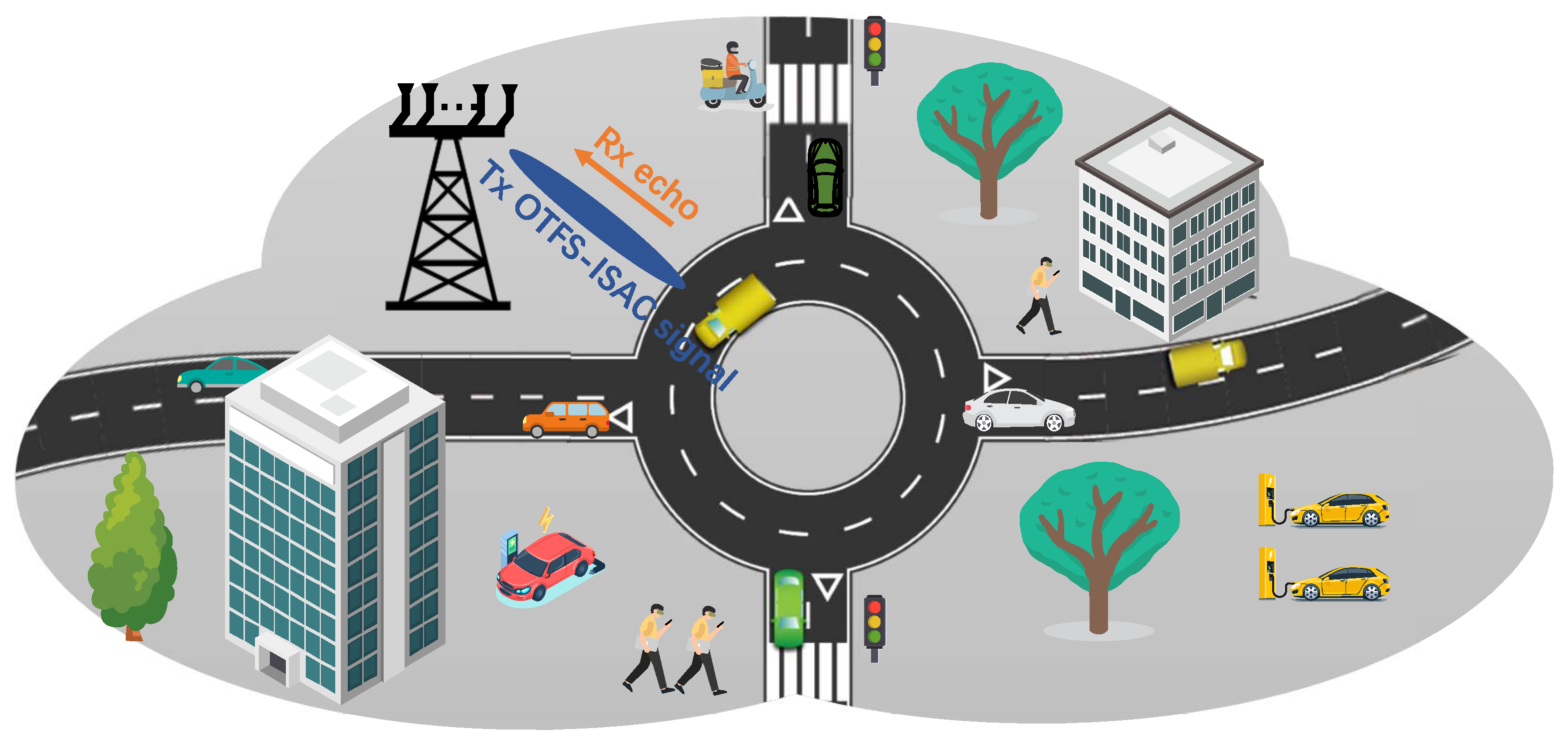
2. System Model
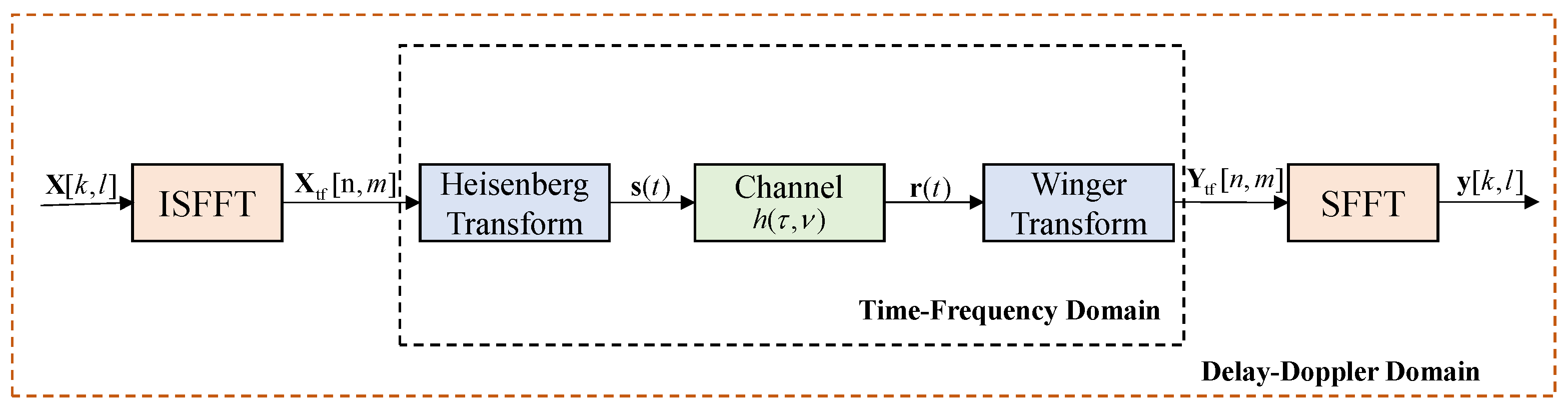
2.1. The Modulation of OTFS Signal
2.2. Communication Signal
2.3. Sensing Signal
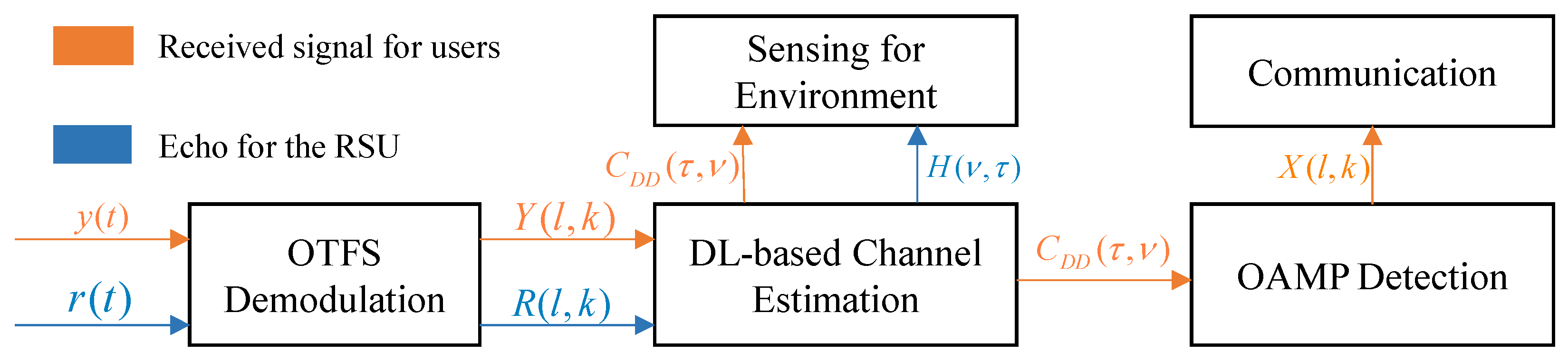
2.4. JCESD for OTFS-Based Vehicular Networks
3. The Joint Channel Estimation and Symbol Detection
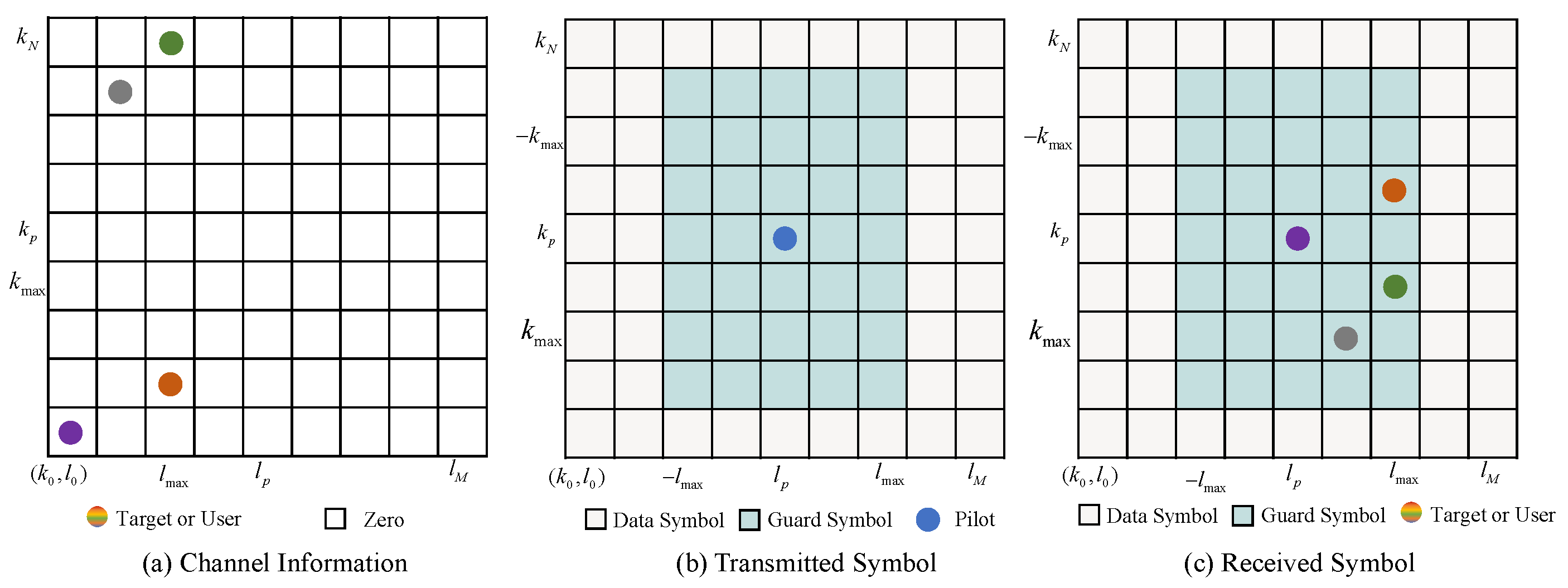
3.1. Pilot Placement
3.2. The Architecture of the DL Network
3.3. Estimation of Neural Network
3.4. Communication Symbol Detection
4. Simulation Result
4.1. Simulation Setups
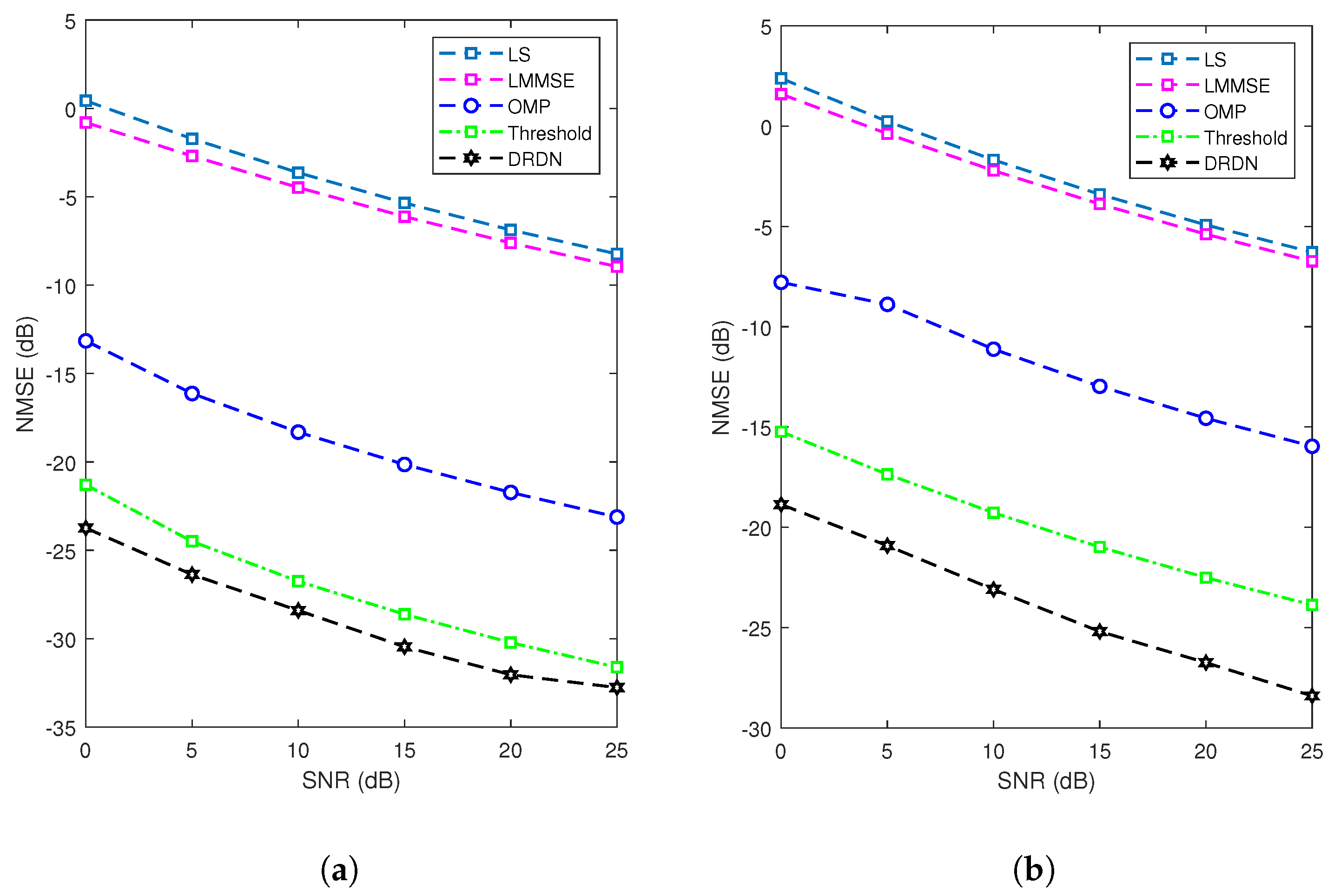
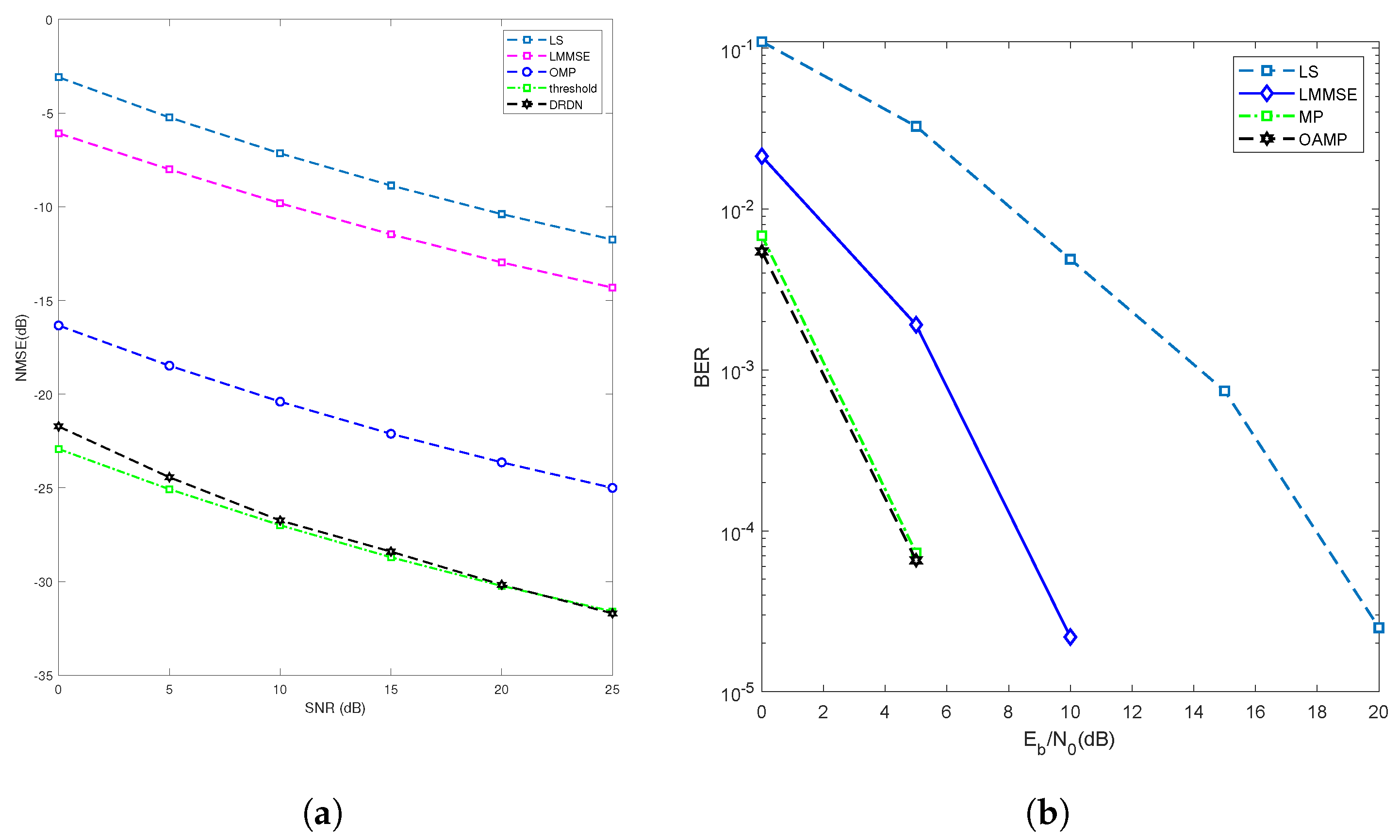
4.2. Sensing Channel Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Xu, B.; Wang, X.; Zheng, K.; Chi, K.; Tian, X. Impacts of sensing energy and data availability on throughput of energy harvesting cognitive radio networks. IEEE Trans. Veh. Technol. 2022, 72, 747–759. [Google Scholar] [CrossRef]
- Yuan, W.; Li, S.; Wei, Z.; Jiang, J.; Zhang, H.; Fan, P. A Survey on Orthogonal Time Frequency Space: New Delay Doppler Communications Paradigm in 6G era. arXiv 2022, arXiv:2211.12955. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Ng, D.W.K. Off-grid channel estimation with sparse bayesian learning for OTFS systems. IEEE Trans. Wirel. Commun. 2022, 21, 7407–7426. [Google Scholar] [CrossRef]
- Li, S.; Yuan, W.; Liu, C.; Wei, Z.; Yuan, J.; Bai, B.; Ng, D.W.K. A novel ISAC transmission framework based on spatially-spread orthogonal time frequency space modulation. IEEE J. Sel. Areas Commun. 2022, 40, 1854–1872. [Google Scholar] [CrossRef]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Towards dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Li, S.; Yuan, J.; Ng, D.W.K. Integrated sensing and communication-assisted orthogonal time frequency space transmission for vehicular networks. IEEE J. Sel. Top. Signal Process. 2021, 15, 1515–1528. [Google Scholar] [CrossRef]
- Hadani, R.; Monk, A. OTFS: A new generation of modulation addressing the challenges of 5G. arXiv 2018, arXiv:1802.02623. [Google Scholar]
- Yuan, W.; Li, S.; Wei, Z.; Yuan, J.; Ng, D.W.K. Bypassing channel estimation for OTFS transmission: An integrated sensing and communication solution. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Nanjing, China, 29 March 2021; pp. 1–5. [Google Scholar]
- Xiong, Y.; Liu, F.; Cui, Y.; Yuan, W.; Han, T.X. Flowing the information from Shannon to Fisher: Towards the fundamental tradeoff in ISAC. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Nanjing, China, 29 March 2021; pp. 5601–5606. [Google Scholar]
- Dong, F.; Wang, W.; Hu, Z.; Hui, T. Low-complexity beamformer design for joint radar and communications systems. IEEE Commun. Lett. 2020, 25, 259–263. [Google Scholar] [CrossRef]
- Meng, X.; Liu, F.; Lu, S.; Chepuri, S.P.; Masouros, C. RIS-assisted integrated sensing and communications: A subspace rotation approach. arXiv 2022, arXiv:2210.13987. [Google Scholar]
- Li, Z.; Yuan, W.; Zhou, L. UAMP-Based Channel Estimation for OTFS in the Presence of the Fractional Doppler with HMM Prior. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Foshan, China, 11–13 August 2022; pp. 304–308. [Google Scholar]
- Zhang, K.; Yuan, W.; Li, S.; Liu, F.; Gao, F.; Fan, P.; Cai, Y. Radar Sensing via OTFS Signaling: A Delay Doppler Signal Processing Perspective. arXiv 2023, arXiv:2301.09909. [Google Scholar]
- Zheng, K.; Jia, X.; Chi, K.; Liu, X. DDPG-based joint time and energy management in ambient backscatter-assisted hybrid underlay CRNs. IEEE Trans. Commun. 2022, 71, 441–456. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Ng, D.W.K.; Yuan, J. Deep residual learning for channel estimation in intelligent reflecting surface-assisted multi-user communications. IEEE Trans. Wirel. Commun. 2021, 21, 898–912. [Google Scholar] [CrossRef]
- Kim, T.K.; Min, M. Reinforcement Learning-Aided Channel Estimator in Time-Varying MIMO Systems. Sensors 2023, 23, 5689. [Google Scholar] [CrossRef] [PubMed]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Li, S.; Yuan, W.; Wei, Z.; Yuan, J.; Bai, B.; Ng, D.W.K.; Xie, Y. Hybrid MAP and PIC detection for OTFS modulation. IEEE Trans. Veh. Technol. 2021, 70, 7193–7198. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Yuan, J.; Ng, D.W.K. A Simple Variational Bayes Detector for Orthogonal Time Frequency Space (OTFS) Modulation. IEEE Trans. Veh. Technol. 2020, 69, 7976–7980. [Google Scholar] [CrossRef]
- Wen, H.; Yuan, W.; Wu, N.; Wen, J. A Low-Complexity Cross-Domain OAMP Detector for OTFS: (Invited Paper). In Proceedings of the 2022 International Symposium on Wireless Communication Systems (ISWCS), Hangzhou, China, 19–22 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, F.; Yuan, W.; Guo, Q.; Wang, Z.; Yuan, J. Iterative Detection for Orthogonal Time Frequency Space Modulation With Unitary Approximate Message Passing. IEEE Trans. Wirel. Commun. 2022, 21, 714–725. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded pilot-aided channel estimation for OTFS in delay–Doppler channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Zhang, X.; Yuan, W.; Liu, C. Deep Residual Learning for OTFS Channel Estimation with Arbitrary Noise. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Foshan, China, 11–13 August 2022; pp. 320–324. [Google Scholar]
- Zhang, X.; Yuan, W.; Liu, C.; Liu, F.; Wen, M. Deep Learning with a Self-Adaptive Threshold for OTFS Channel Estimation. In Proceedings of the 2022 International Symposium on Wireless Communication Systems (ISWCS), Hangzhou, China, 19–22 October 2022; pp. 1–5. [Google Scholar]
- Liu, C.; Wei, Z.; Ng, D.W.K.; Yuan, J.; Liang, Y.C. Deep transfer learning for signal detection in ambient backscatter communications. IEEE Trans. Wirel. Commun. 2020, 20, 1624–1638. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Li, Y.; Vucetic, B.; Ng, D.W.K. Deep Residual Learning-Assisted Channel Estimation in Ambient Backscatter Communications. IEEE Wirel. Commun. Lett. 2021, 10, 339–343. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Hoyer, P.; Oja, E. Sparse code shrinkage: Denoising by nonlinear maximum likelihood estimation. Adv. Neural Inf. Process. Syst. 1998, 11. [Google Scholar]
- Ma, J.; Ping, L. Orthogonal AMP. IEEE Access 2017, 5, 2020–2033. [Google Scholar] [CrossRef]
- Li, S.; Yuan, J.; Yuan, W.; Wei, Z.; Bai, B.; Ng, D.W.K. Performance analysis of coded OTFS systems over high-mobility channels. IEEE Trans. Wirel. Commun. 2021, 20, 6033–6048. [Google Scholar] [CrossRef]
- Liu, C.; Li, S.; Yuan, W.; Liu, X.; Ng, D.W.K. Predictive precoder design for OTFS-enabled URLLC: A deep learning approach. IEEE J. Sel. Areas Commun. 2023, 41, 2245–2260. [Google Scholar] [CrossRef]
- Li, Q.; Gong, Y.; Meng, F.; Li, Z.; Miao, L.; Xu, Z. Residual learning based channel estimation for OTFS system. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Foshan, China, 11–13 August 2022; pp. 275–280. [Google Scholar]
- Moustakas, A.L.; Simon, S.H.; Sengupta, A.M. MIMO capacity through correlated channels in the presence of correlated interferers and noise: A (not so) large N analysis. IEEE Trans. Inf. Theory 2003, 49, 2545–2561. [Google Scholar] [CrossRef]
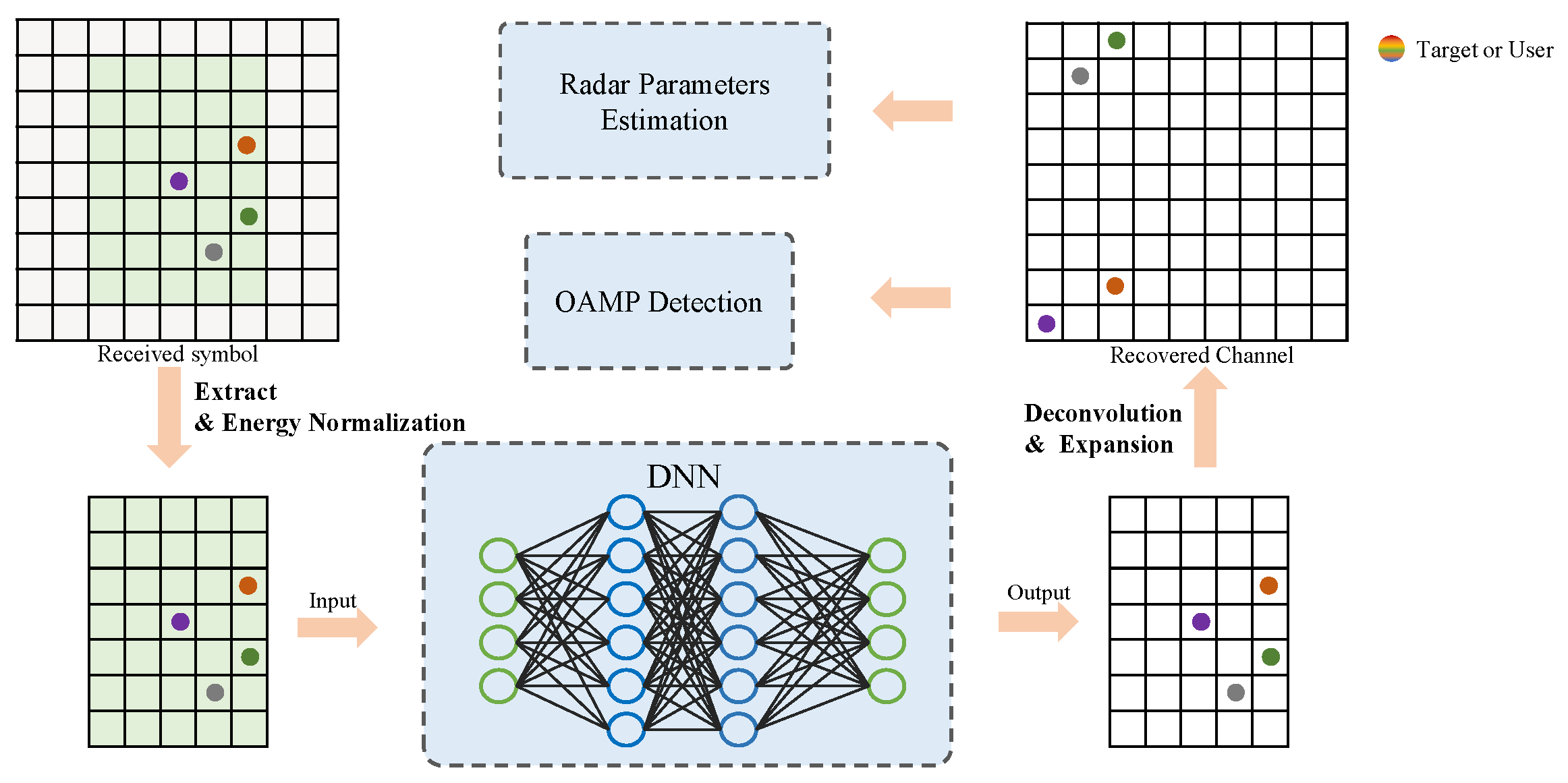

| Input layer: real-valued matrix with dimension | ||
| Denoising Module: D denoising blocks share the same construction | ||
| Layers | Operation | Filter size |
| 1 | Conv + BN + ReLU | |
| 2~ | Conv + BN + ReLU | |
| 3 | Conv | |
| Subnetwork: generate the threshold array | ||
| Module Name | Operation | Parameters |
| Conv + BN + ReLU | ||
| FC + BN + ReLU | ||
| Output layer: recovery channel matrix of size | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wen, H.; Yan, Z.; Yuan, W.; Wu, J.; Li, Z. A Novel Joint Channel Estimation and Symbol Detection Receiver for Orthogonal Time Frequency Space in Vehicular Networks. Entropy 2023, 25, 1358. https://doi.org/10.3390/e25091358
Zhang X, Wen H, Yan Z, Yuan W, Wu J, Li Z. A Novel Joint Channel Estimation and Symbol Detection Receiver for Orthogonal Time Frequency Space in Vehicular Networks. Entropy. 2023; 25(9):1358. https://doi.org/10.3390/e25091358
Chicago/Turabian StyleZhang, Xiaoqi, Haifeng Wen, Ziyu Yan, Weijie Yuan, Jun Wu, and Zhongjie Li. 2023. "A Novel Joint Channel Estimation and Symbol Detection Receiver for Orthogonal Time Frequency Space in Vehicular Networks" Entropy 25, no. 9: 1358. https://doi.org/10.3390/e25091358
APA StyleZhang, X., Wen, H., Yan, Z., Yuan, W., Wu, J., & Li, Z. (2023). A Novel Joint Channel Estimation and Symbol Detection Receiver for Orthogonal Time Frequency Space in Vehicular Networks. Entropy, 25(9), 1358. https://doi.org/10.3390/e25091358







