Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials
Abstract
:1. Introduction
2. Fundamental Concepts
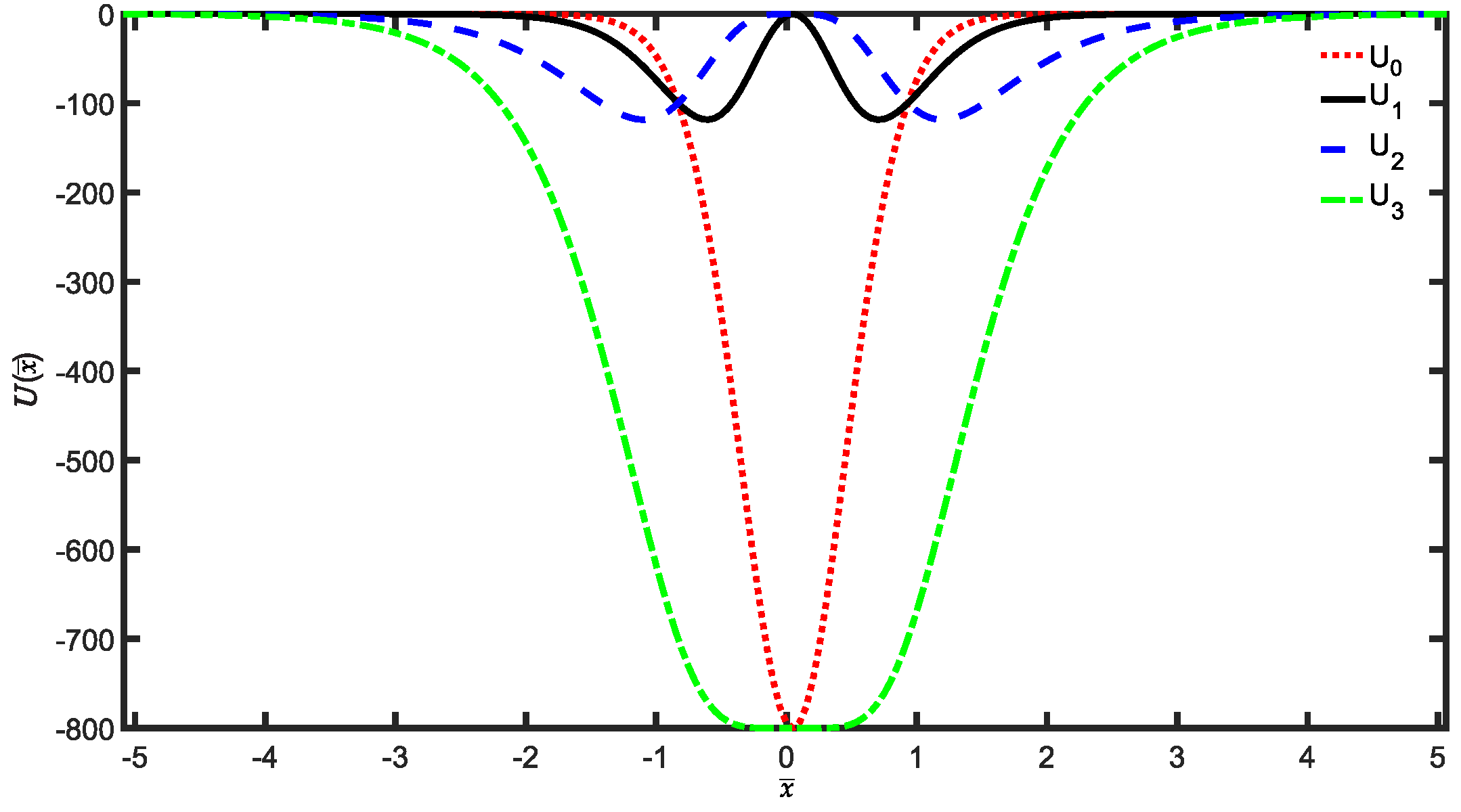
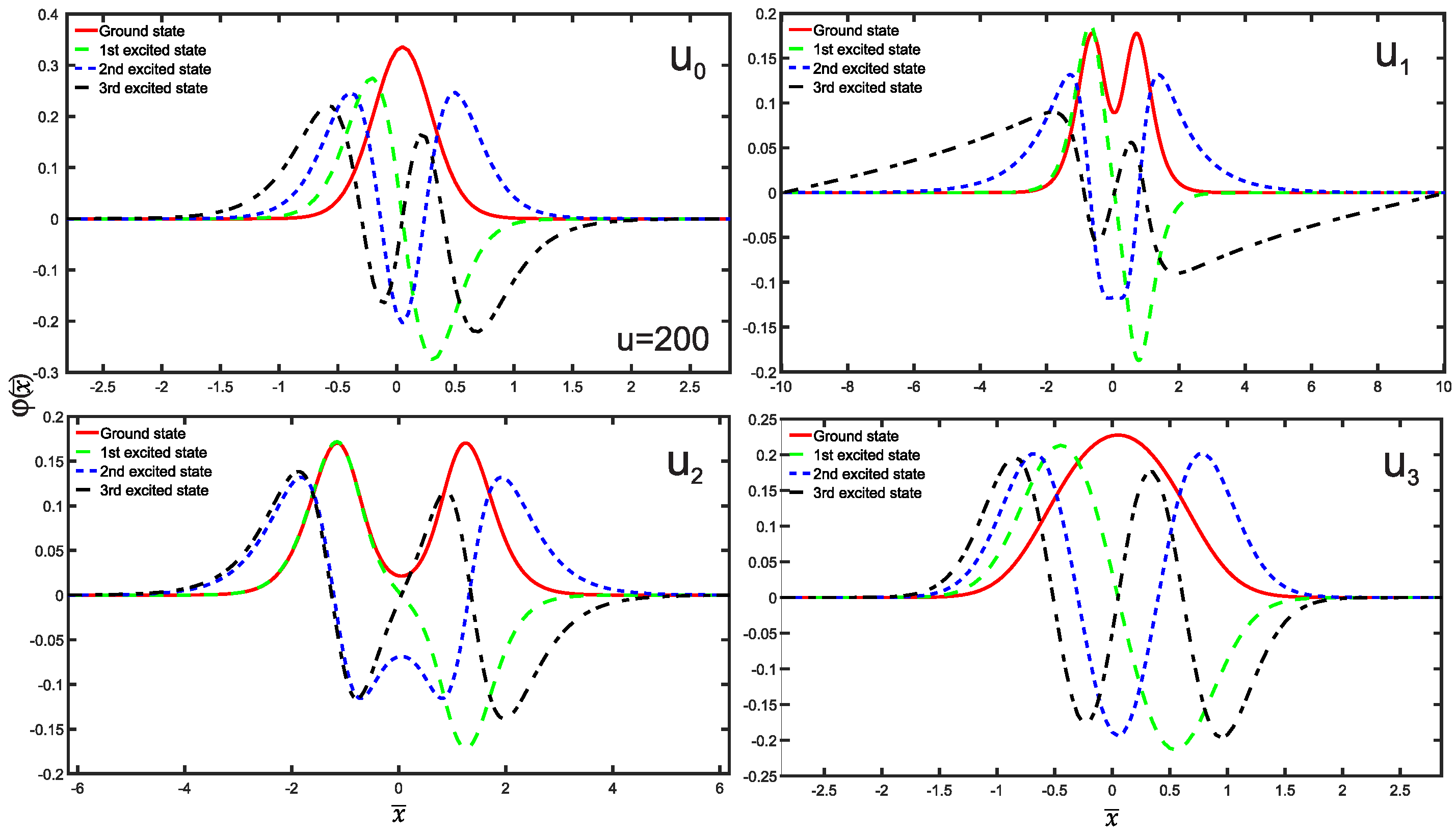
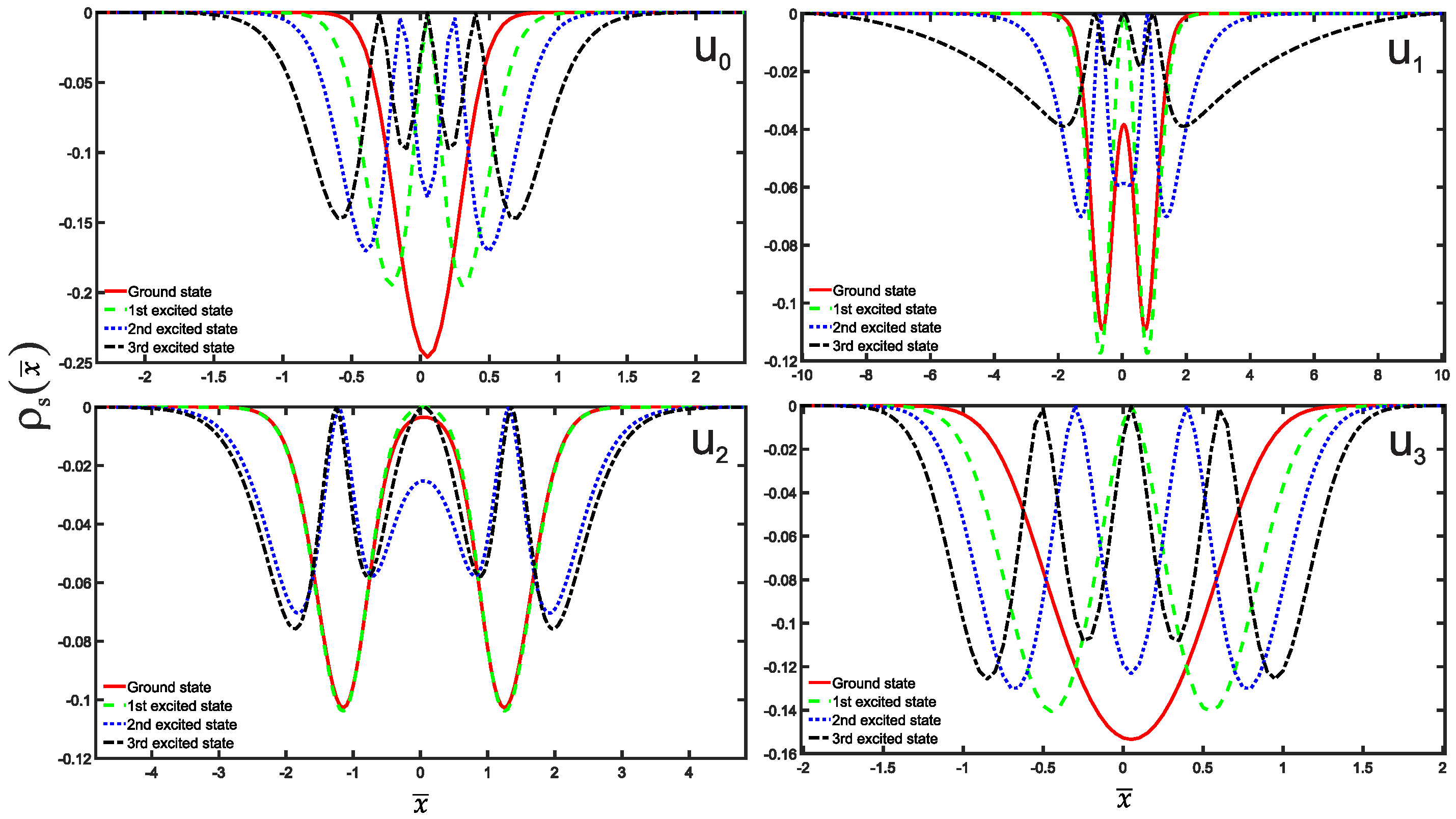
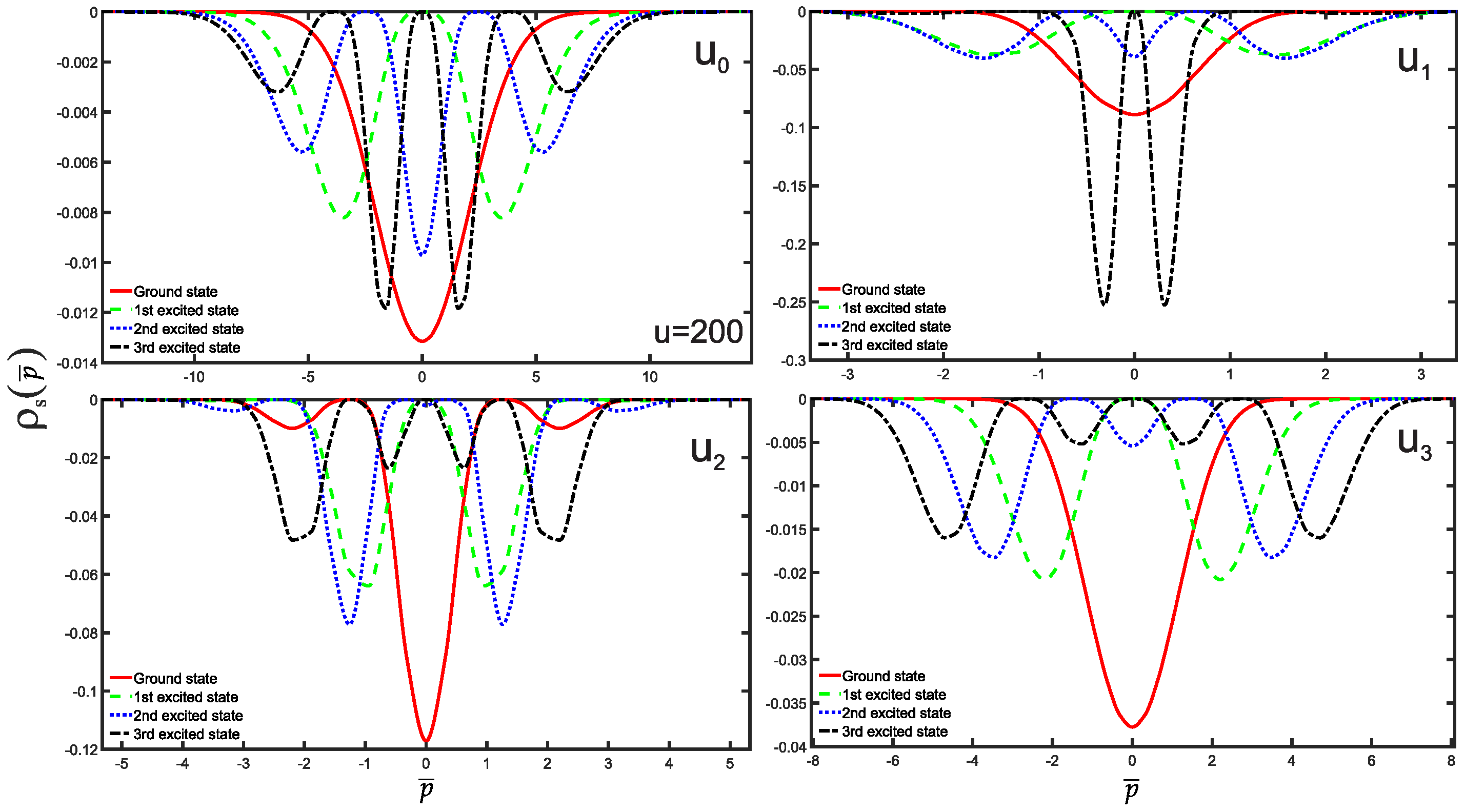
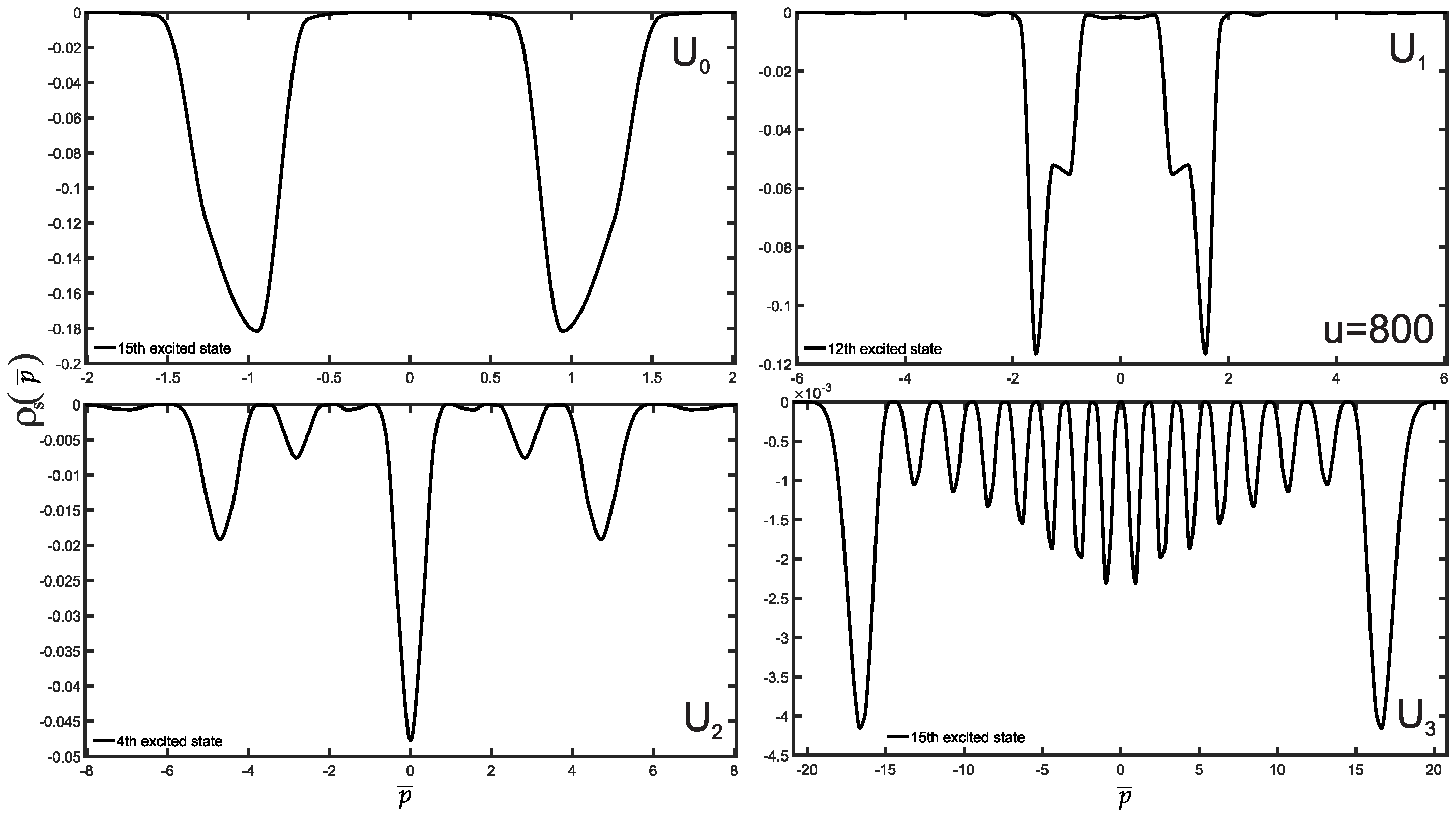
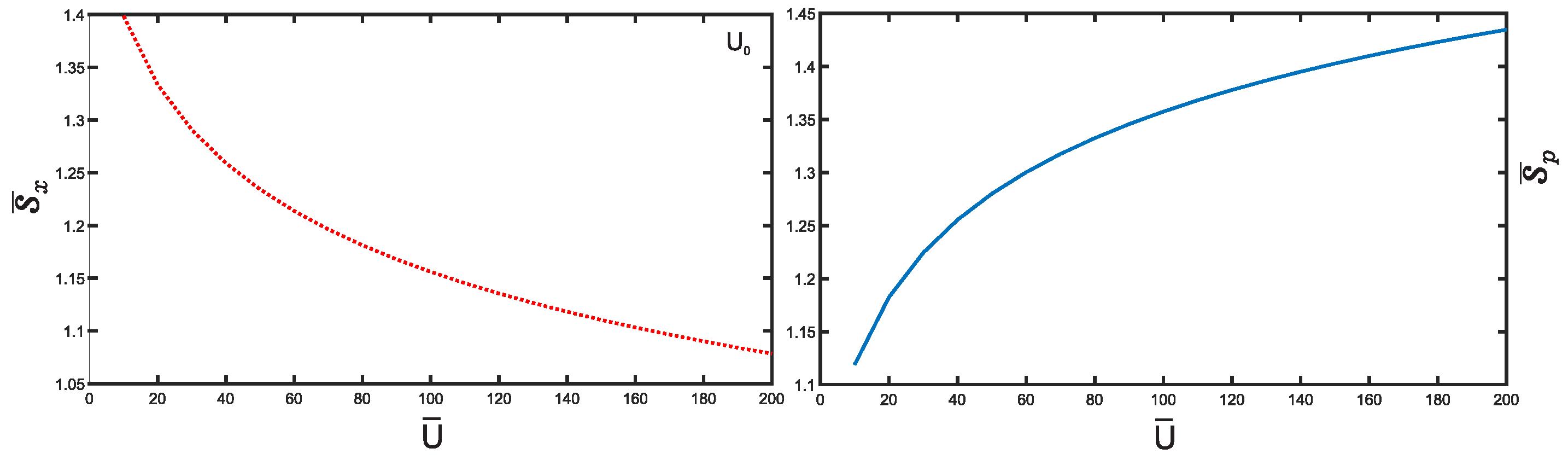
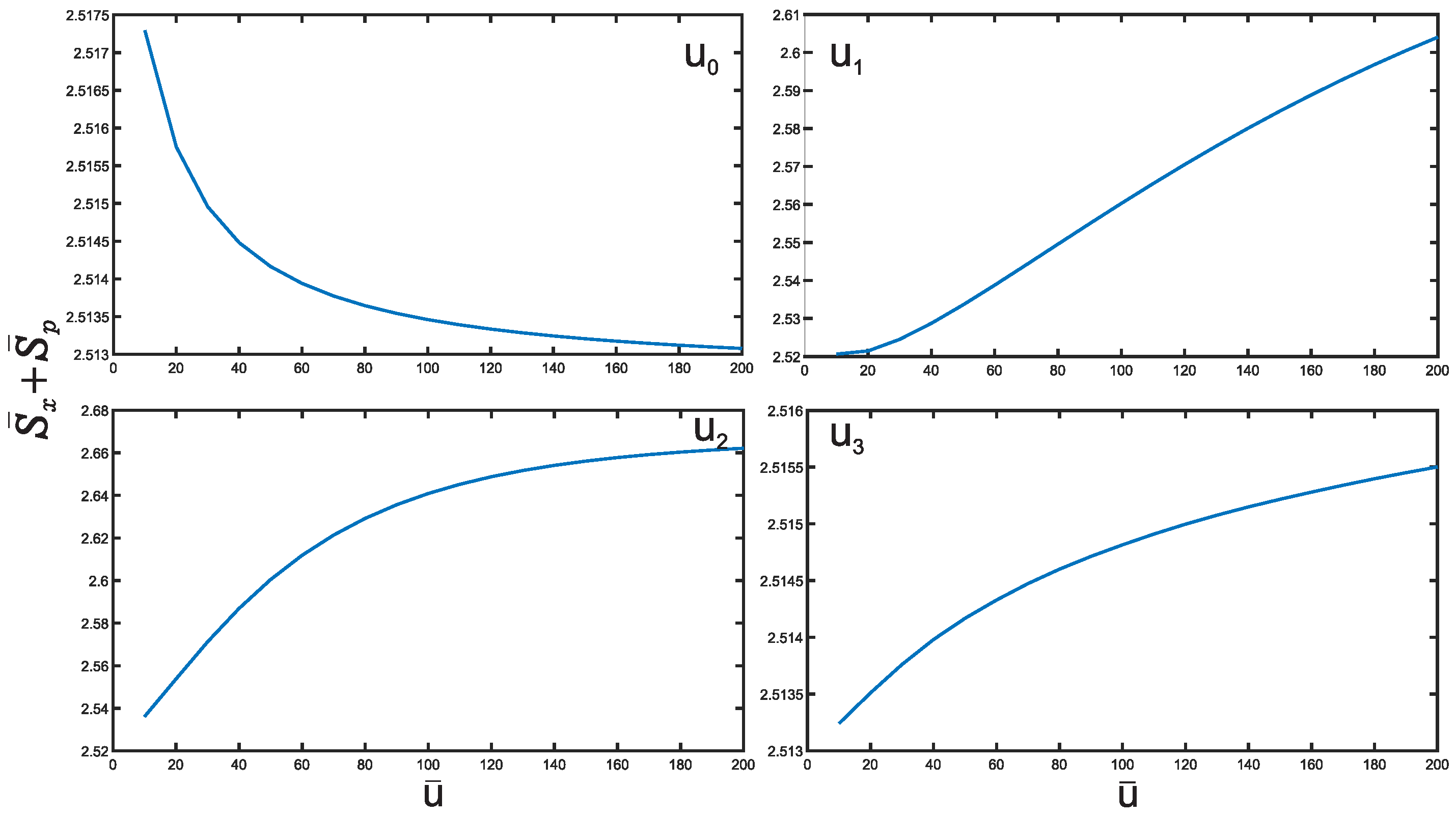
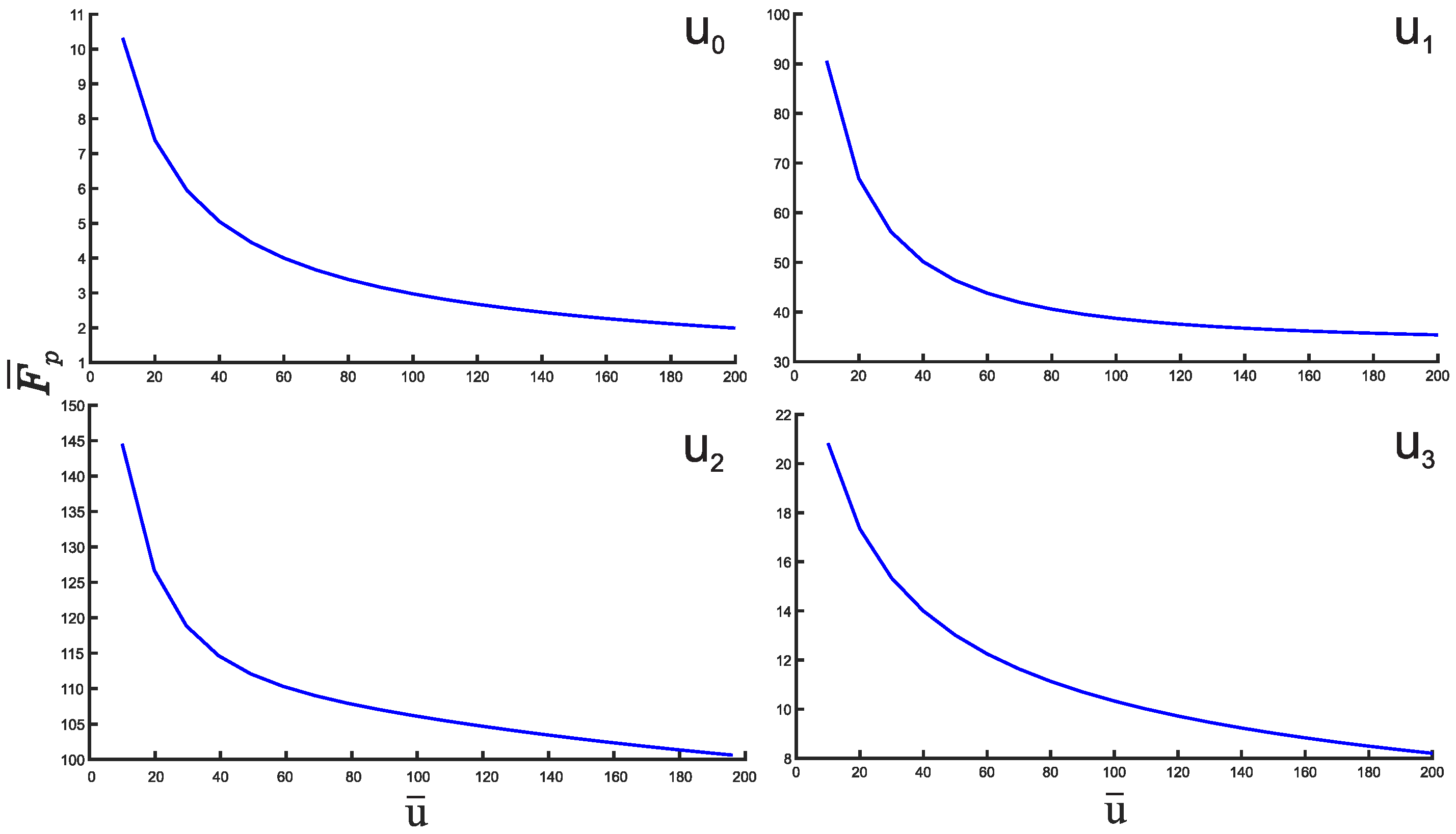
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Martinez-Finkelshtein, A.; Sorokin, V.N. Information-theoretic measures for Morse and Pöschl-Teller potentials. Mol. Phys. 2006, 104, 613. [Google Scholar] [CrossRef]
- Aydiner, E.; Orta, C.; Sever, R. Quantum information entropies of the eigenstates of the Morse potential. Int. J. Mod. Phys. B 2008, 22, 231. [Google Scholar] [CrossRef]
- Yañez, R.J.; van Assche, W.; Dehesa, J.S. Position and momentum information entropies of the D-dimensional harmonic oscillator and hydrogen atom. Phys. Rev. A 1994, 50, 3065. [Google Scholar] [CrossRef] [PubMed]
- Majernik, V.; Opatrny, T. Entropic uncertainty relations for a quantum oscillator. J. Phys. A 1996, 29, 2187. [Google Scholar] [CrossRef]
- Coffey, M.W. Semiclassical position and momentum information entropy for sech2 and a family of rational potentials. Can. J. Phys. 2007, 85, 733. [Google Scholar] [CrossRef]
- Patil, S.H.; Sen, K.D. Net information measures for modified Yukawa and Hulthén potentials. Int. J. Quant. Chem. 2007, 107, 1864. [Google Scholar] [CrossRef]
- Sun, G.H.; Dong, S.H. Quantum information entropies of the eigenstates for a symmetrically trigonometric Rosen-Morse potential. Phys. Scr. 2013, 87, 045003. [Google Scholar] [CrossRef]
- Yañez-Navarro, G.; Sun, G.H.; Dytrich, T.; Launey, K.D.; Dong, S.H.; Draayer, J.P. Quantum information entropies for position-dependent mass Schrödinger problem. Ann. Phys. 2014, 348, 153. [Google Scholar] [CrossRef]
- Hazra, R.K.; Ghosh, M.; Bhattacharyya, S.P. Information entropy and level-spacing distribution based signatures of quantum chaos in electron doped 2D single carrier quantum dots. Chem. Phys. Lett. 2008, 460, 209. [Google Scholar] [CrossRef]
- Sun, G.H.; Dong, S.H.; Launey, K.D.; Dytrych, T.; Draayer, J.P. Shannon information entropy for a hyperbolic double-well potential. Int. J. Quant. Chem. 2015, 115, 891. [Google Scholar] [CrossRef]
- Majernik, V.; Majernikova, E. Standard and entropic uncertainty relations of the finite well. J. Phys. A 2002, 35, 5751. [Google Scholar]
- Song, X.D.; Sun, G.H.; Dong, S.H. Shannon information entropy for an infinite circular well. Phys. Lett. A 2015, 379, 1402. [Google Scholar] [CrossRef]
- Sun, G.H.; Popov, D.; Camacho-Nieto, O.; Dong, S.H. Shannon information entropies for position-dependent mass Schrödinger problem with a hyperbolic well. Chin. Phys. B 2015, 24, 100303. [Google Scholar]
- Sun, G.H.; Dong, S.H.; Saad, N. Quantum information entropies for an asymmetric trigonometric Rosen-Morse potential. Ann. Phys. 2013, 525, 934. [Google Scholar] [CrossRef]
- Sun, G.H.; Avila Aoki, M.; Dong, S.H. Quantum information entropies of the eigenstates for the Pöschl-Teller-like potential. Chin. Phys. B 2013, 22, 050302. [Google Scholar] [CrossRef]
- Song, X.D.; Dong, S.H.; Zhang, Y. Quantum information entropy for one-dimensional system undergoing quantum phase transition. Chin. Phys. B 2016, 25, 050302. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolin, J.; Zarzo, A.; Cuchi, J.C. Maximum-entropy technique with logarithmic constraints: Estimation of atomic radial densities. Eur. Phys. J. D 1999, 7, 479. [Google Scholar] [CrossRef]
- Orlowski, A. Information entropy and squeezing of quantum fluctuations. Phys. Rev. A 1997, 56, 2545. [Google Scholar] [CrossRef]
- Salazar, S.J.C.; Laguna, H.G.; Prasad, V.; Sagar, R.P. Shannon-information entropy sum in the confined hydrogenic atom. Int. J. Quan. Phys. 2020, 120, e26188. [Google Scholar] [CrossRef]
- Ikot, A.N.; Rampho, G.J.; Amadi, P.O.; Okorie, U.S.; Sithole, M.J.; Lekala, M.L. Theoretic quantum information entropies for the generalized hyperbolic potential. Int. J. Quan. Phys. 2020, 120, e26410. [Google Scholar] [CrossRef]
- Onate, C.A.; Onyeaju, M.C.; Abolarinwa, A.; Lukman, A.F. Analytical determination of theoretic quantities for multiple potential. Sci. Rep. 2020, 10, 17542. [Google Scholar] [CrossRef] [PubMed]
- Salazar, S.J.C.; Laguna, H.G.; Dahiya, B.; Prasad, V.; Sagar, R.P. Shannon information entropy sum of the confined hydrogenic atom under the influence of an electric field. Eur. Phys. J. D 2021, 75, 127. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Belega, E.D.; Toranzo, I.V.; Aptekarev, A.I. The Shannon entropy of high-dimensional hydrogenic and harmonic systems. Int. J. Quan. Chem. 2019, 119, e25977. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures in free and confined hydrogen atom. Int. J. Quan. Chem. 2018, 118, e25596. [Google Scholar] [CrossRef]
- Ghosal, A.; Mukherjee, N.; Roy, A.K. Information entropic measures of a quantum harmonic oscillator in symmetric and asymmetric confinement within an impenetrable box. Ann. Phys. 2016, 528, 796. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, L.Y.; Tong, P.Q. The geometric mean density of states and its application to one-dimensional nonuniform systems. Eur. Phys. J. B 2011, 80, 485. [Google Scholar] [CrossRef]
- Hiramoto, H.; Kohmoto, M. New Localization in a Quasiperiodic System. Phys. Rev. Lett. 1989, 62, 2714. [Google Scholar] [CrossRef]
- Gil-Barrera, C.A.; Santana-Carrillo, R.; Sun, G.H.; Dong, S.H. Quantum Information Entropies on Hyperbolic Single Potential Wells. Entropy 2022, 24, 604. [Google Scholar] [CrossRef]
- Santana-Carrillo, R.; Dong, Q.; Sun, G.H.; Silva-Ortigoza, R.; Dong, S.H. Shannon entropy of asymmetric rectangular multiple well with unequal width barrier. Results Phys. 2022, 33, 105109. [Google Scholar] [CrossRef]
- Carrillo, R.S.; Gil-Barrera, C.A.; Sun, G.H.; Solaimani, M.; Dong, S.H. Shannon entropies of asymmetric multiple quantum well systems with a constant total length. Eur. Phys. J. Plus 2022, 136, 1060. [Google Scholar] [CrossRef]
- Shi, Y.J.; Sun, G.H.; Tahir, F.; Ahmadov, A.I.; He, B.; Dong, S.H. Quantum information measures of infinite spherical well. Mod. Phys. Lett. A 2018, 16, 1850088. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Hartmann, R.R.; Robinson, N.J.; Portnoi, M.E. Smooth electron waveguides in graphene. Phys. Rev. B 2010, 81, 245431. [Google Scholar] [CrossRef]
- Downing, C.A.; Portnoi, M.E. One-dimensional Coulomb problem in Dirac materials. Phys. Rev. A 2014, 90, 052116. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Portnoi, M.E. Quasi-exact solution to the Dirac equation for the hyperbolic-secant potential. Phys. Rev. A 2014, 89, 012101. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Zarrinkamar, S.; Yazarloo, B.H. The nonrelativistic oscillator strength of a hyperbolic-type potential. Chin. Phys. B 2013, 22, 060202. [Google Scholar] [CrossRef]
- Santana-Carrillo, R.; González-Flores, J.S.; Magaña-Espinal, E.; Quezada, L.F.; Sun, G.H.; Dong, S.H. Quantum Information Entropy of Hyperbolic Potentials in Fractional Schrödinger. Entropy 2022, 24, 1516. [Google Scholar] [CrossRef]
- Santana-Carrillo, R.; Peto, J.V.; Sun, G.H.; Dong, S.H. Quantum Information Entropy for a Hyperbolic Double Well Potential in the Fractional Schrödinger Equation. Entropy 2023, 25, 988. [Google Scholar] [CrossRef]
- Wang, X.H.; Chen, C.Y.; You, Y.; Lu, F.L.; Sun, D.S.; Dong, S.H. Exact solutions of the Schrödinger equation for a class of hyperbolic potential well. Chin. Phys. B 2022, 31, 040301. [Google Scholar] [CrossRef]
- Wang, X.H.; Chen, C.Y.; You, Y.; Sun, D.S.; Lu, F.L.; Dong, S.H. Exact solutions of the Schrödinger equation for another class of hyperbolic potential wells. Phys. Scr. 2023, 98, 055404. [Google Scholar] [CrossRef]
- Obi-Tayo, B. Finite Difference Solution of the Schrödinger Equation. 2019. Available online: https://medium.com/modern-physics/finite-difference-solution-of-the-schrodinger-equation-c49039d161a8 (accessed on 30 July 2023).
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flanner, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, NY, USA, 2007. [Google Scholar]
- Beckner, W. Inequalities in Fourier Analysis. Ann. Math. 1975, 102, 159. [Google Scholar] [CrossRef]
- Bialynicki–Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129. [Google Scholar] [CrossRef]
- Sears, S.B.; Parr, R.G.; Dinur, U. On the Quantum-Mechanical Kinetic Energy as a Measure of the Information in a Distribution. Isr. J. Chem. 1980, 19, 165. [Google Scholar] [CrossRef]
- Falaye, B.J.; Serrano, F.A.; Dong, S.H. Fisherinformation for the position-dependent mass Schrödinger system. Phys. Lett. A 2016, 380, 267. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700. [Google Scholar] [CrossRef]

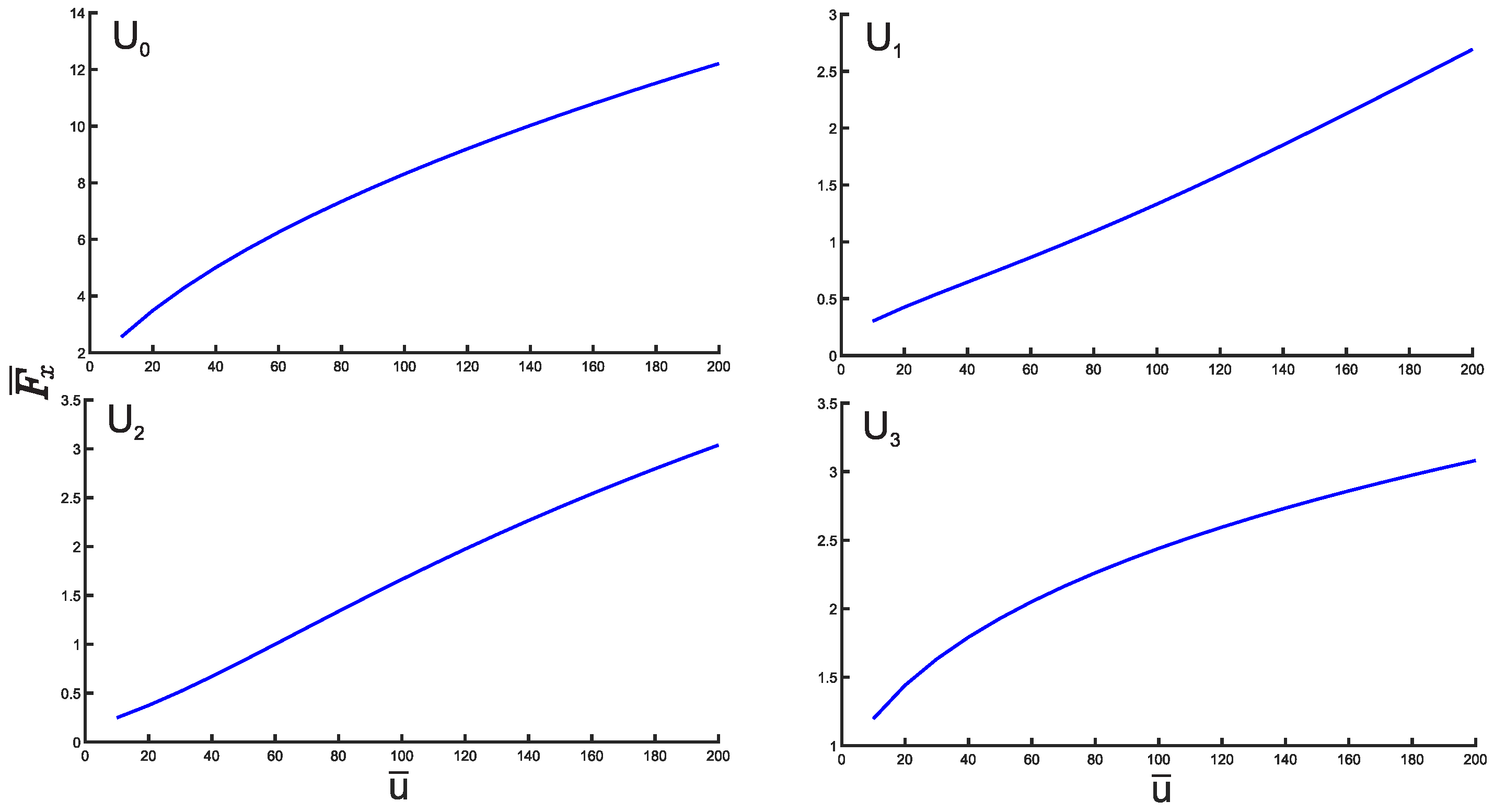
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santana-Carrillo, R.; de J. León-Montiel, R.; Sun, G.-H.; Dong, S.-H. Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials. Entropy 2023, 25, 1296. https://doi.org/10.3390/e25091296
Santana-Carrillo R, de J. León-Montiel R, Sun G-H, Dong S-H. Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials. Entropy. 2023; 25(9):1296. https://doi.org/10.3390/e25091296
Chicago/Turabian StyleSantana-Carrillo, R., Roberto de J. León-Montiel, Guo-Hua Sun, and Shi-Hai Dong. 2023. "Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials" Entropy 25, no. 9: 1296. https://doi.org/10.3390/e25091296
APA StyleSantana-Carrillo, R., de J. León-Montiel, R., Sun, G.-H., & Dong, S.-H. (2023). Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials. Entropy, 25(9), 1296. https://doi.org/10.3390/e25091296








