Comparative Study of Variations in Quantum Approximate Optimization Algorithms for the Traveling Salesman Problem
Abstract
:1. Introduction
2. Traveling Salesman Problem
2.1. TSP Formulation as an Optimization Problem
2.2. Improved TSP by Eliminating Rotational Symmetry
3. Quantum Approximate Optimization Algorithm (QAOA)
3.1. QAOA Workflow
- State initialization with initial state .
- Parameterized unitary ansatz , a variational ansatz of p layers for the TSP, based on two alternating Hamiltonians, and , using respective parameters and .
- Measurement and optimization of the cost expectation for the final state , where an optimizer on a classical computer is used for the minimization.
3.2. From Binary Decision Variables to Qubits
3.3. State Initialization
3.4. Variational Ansatzes
3.4.1. Problem Hamiltonian
3.4.2. Mixer Hamiltonian
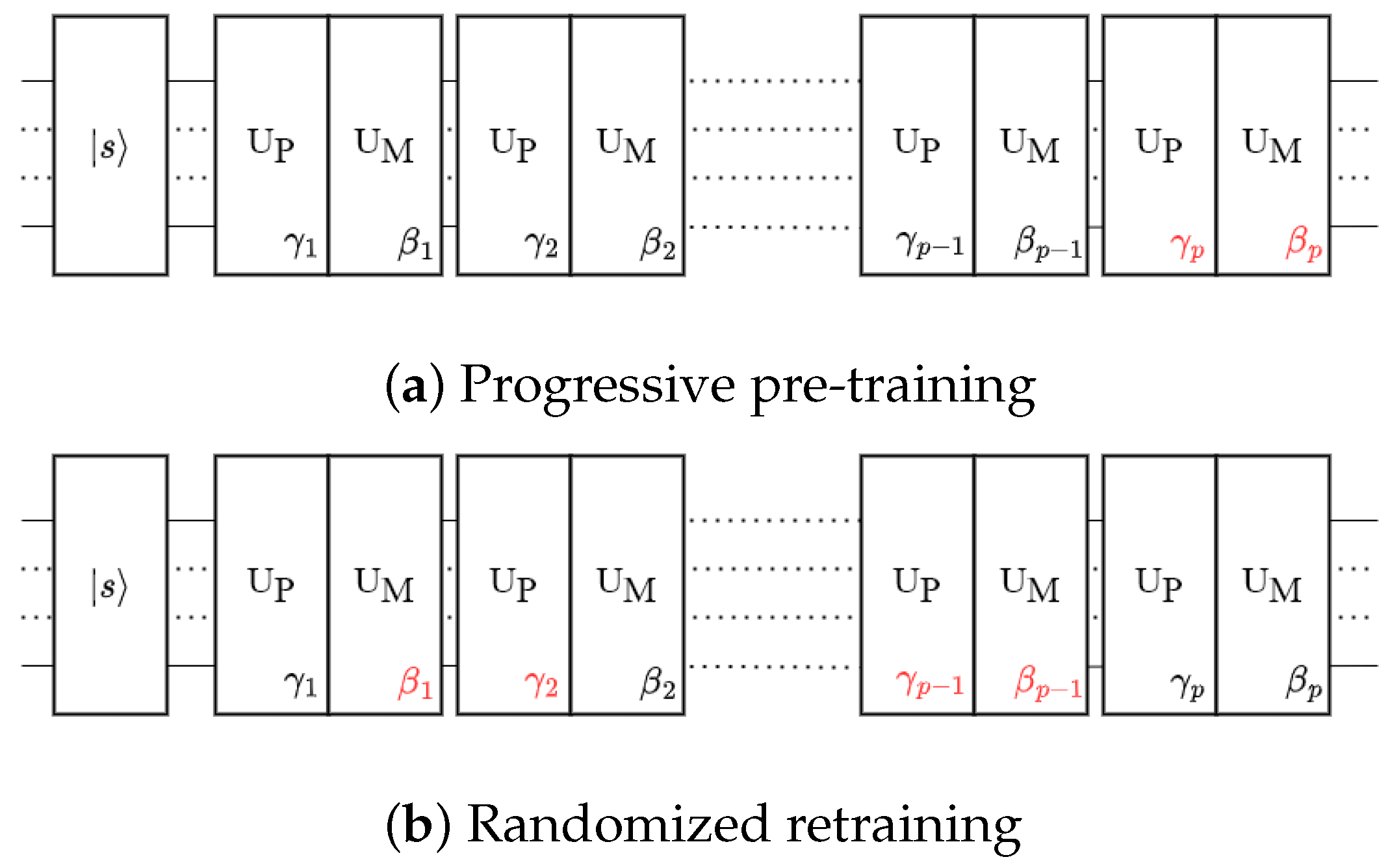
3.5. Measurement and Optimization Protocol
- (A)
- Progressive pre-training: In the first part (Figure 1a), we construct the QAOA ansatz by gradually adding layers. Initially, we train and optimize over the leading few layers (typically two layers). Then, for a p-layer QAOA simulation, we freeze the parameters in the first -th layers, obtained from previous simulations, and exclusively optimize the parameters in the p-th layer. Optimal parameters of the current layer that yield the lowest cost expectation are selected. Note the initial values for the parameters of the p-th layer are zero. If no lower cost is found at the p-th layer compared with previous costs, we use zeros for the parameters of that layer. In this way, the cost is always non-increasing over the entire simulation. This progressive optimization protocol proves to be efficient and leads to an increasingly optimized solution as the number of layers increases. It also reduces the computational cost in parameter searching for very thick layers. We denote this protocol with the letter A and an integer to indicate the depth being optimized.
- (B)
- Randomized retraining: In the second part (Figure 1b), we take the pre-trained QAOA ansatz from part (A) and randomly select a larger portion of the parameters to be trained at a time. Typically, we free 50% of the parameters in each iteration of retraining. Although it is more computationally expensive, this retraining is still less costly than the CDL, which allows us to train the QAOA ansatz as a whole. This mitigates the risk of becoming trapped in local minima, which could occur when using the protocol of part (A) exclusively. We use the protocol of part (B) with a number to indicate which iteration of retraining is being conducted.
4. Numerical Results
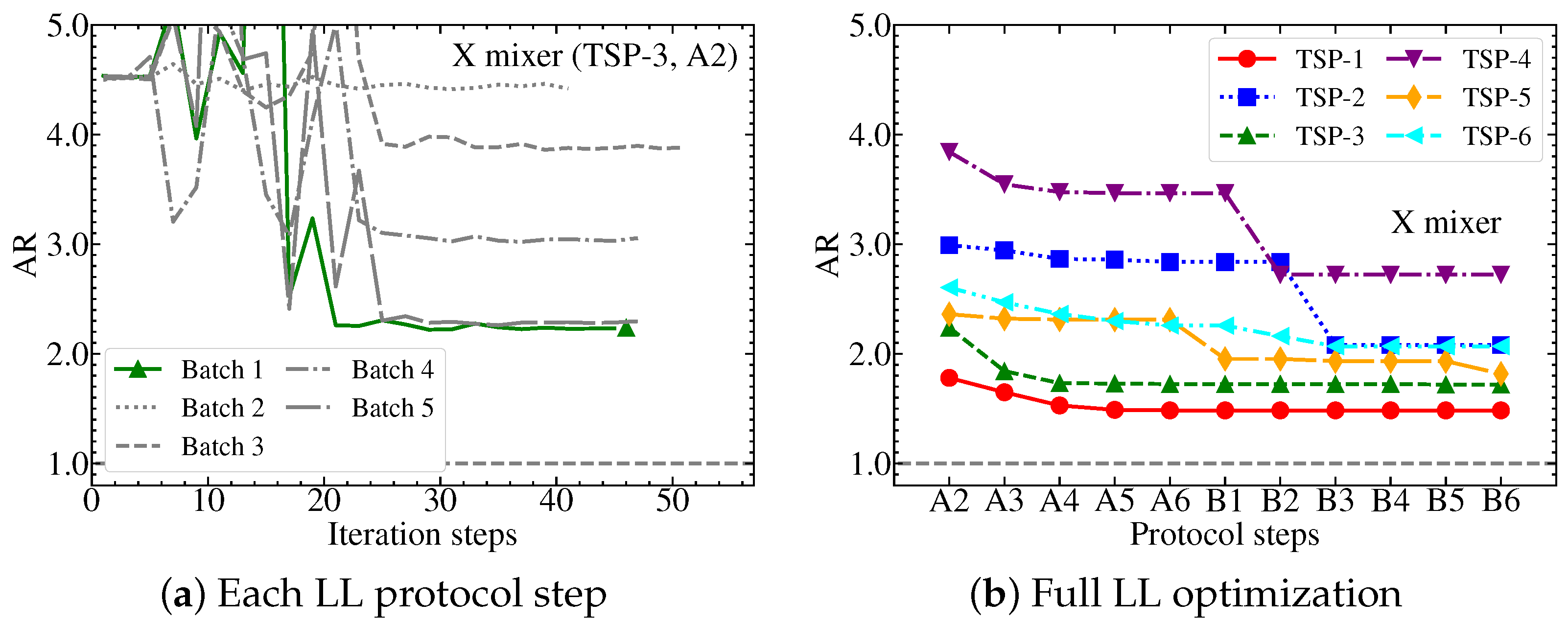
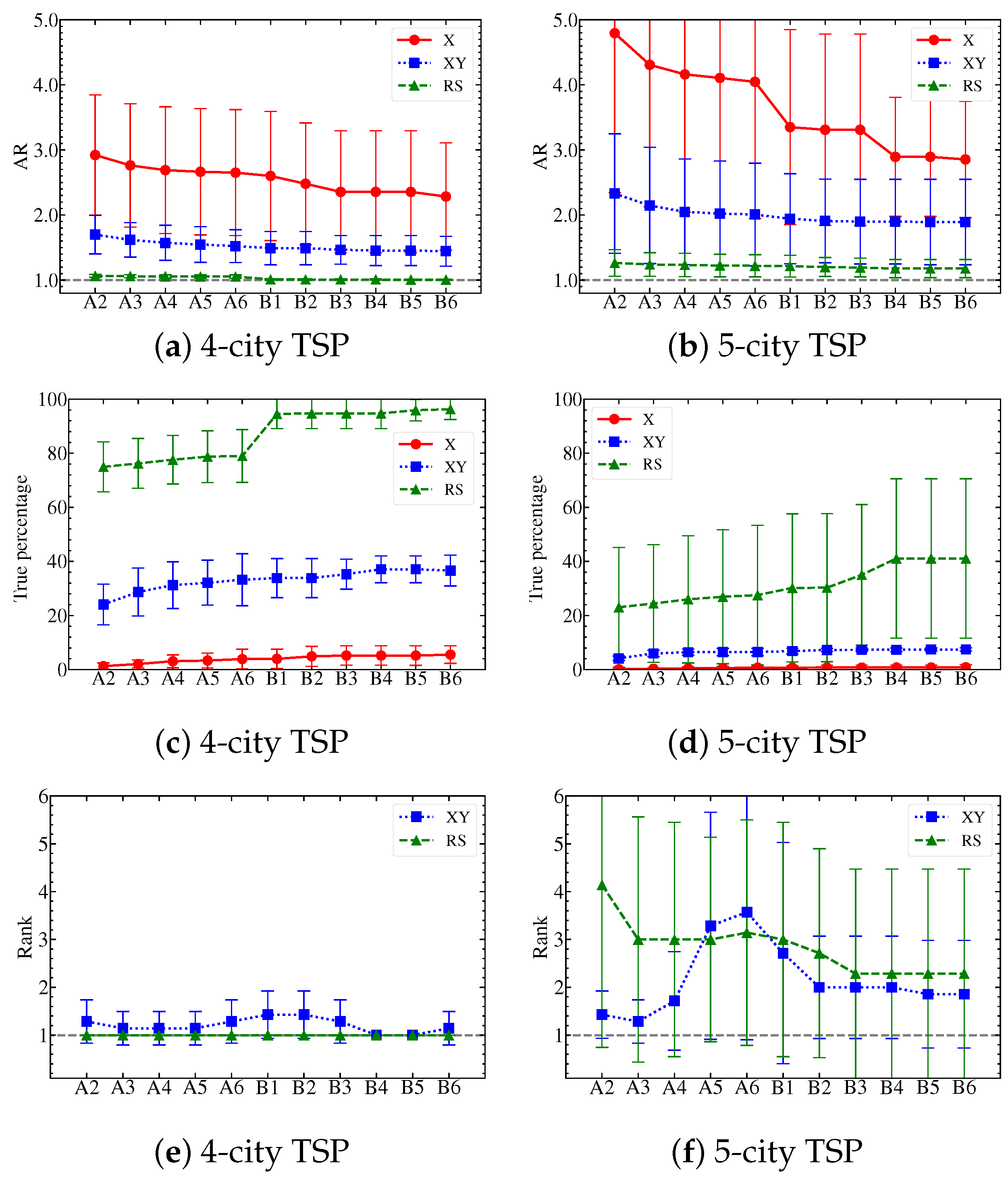
4.1. Simulation Accuracy
4.2. Resource Evaluations
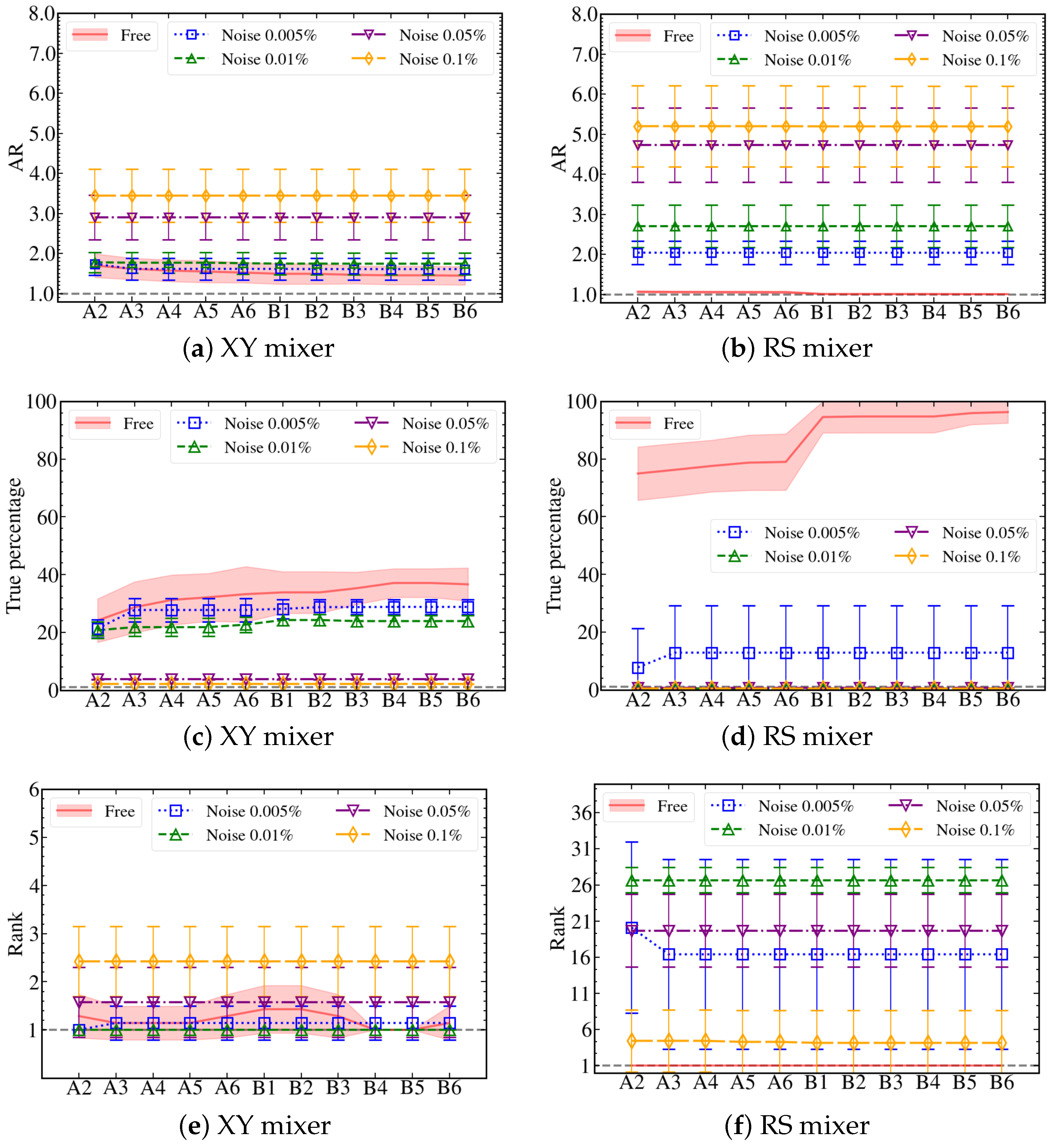
4.3. Robustness against Noise
4.4. Problem Dependence
5. Summary and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TSP | Traveling Salesman Problem |
| QA | Quantum Annealing |
| QAOA | Quantum Approximate Optimization Algorithm |
| VQA | Variational Quantum Algorithm |
| NISQ | Noisy Intermediate-Scale Quantum |
| AQC | Adiabatic Quantum Computation |
| VQE | Variational Quantum Eigensolver |
| DC-QAOA | Digitized-Counterdiabatic QAOA |
| RS mixer | Row-Swap Mixer |
| LL | Layer-wise Learning |
| BP | Barren Plateaus |
| CDL | Complete Depth Learning |
| AR | Approximation Ratio |
Appendix A. Pauli Gates
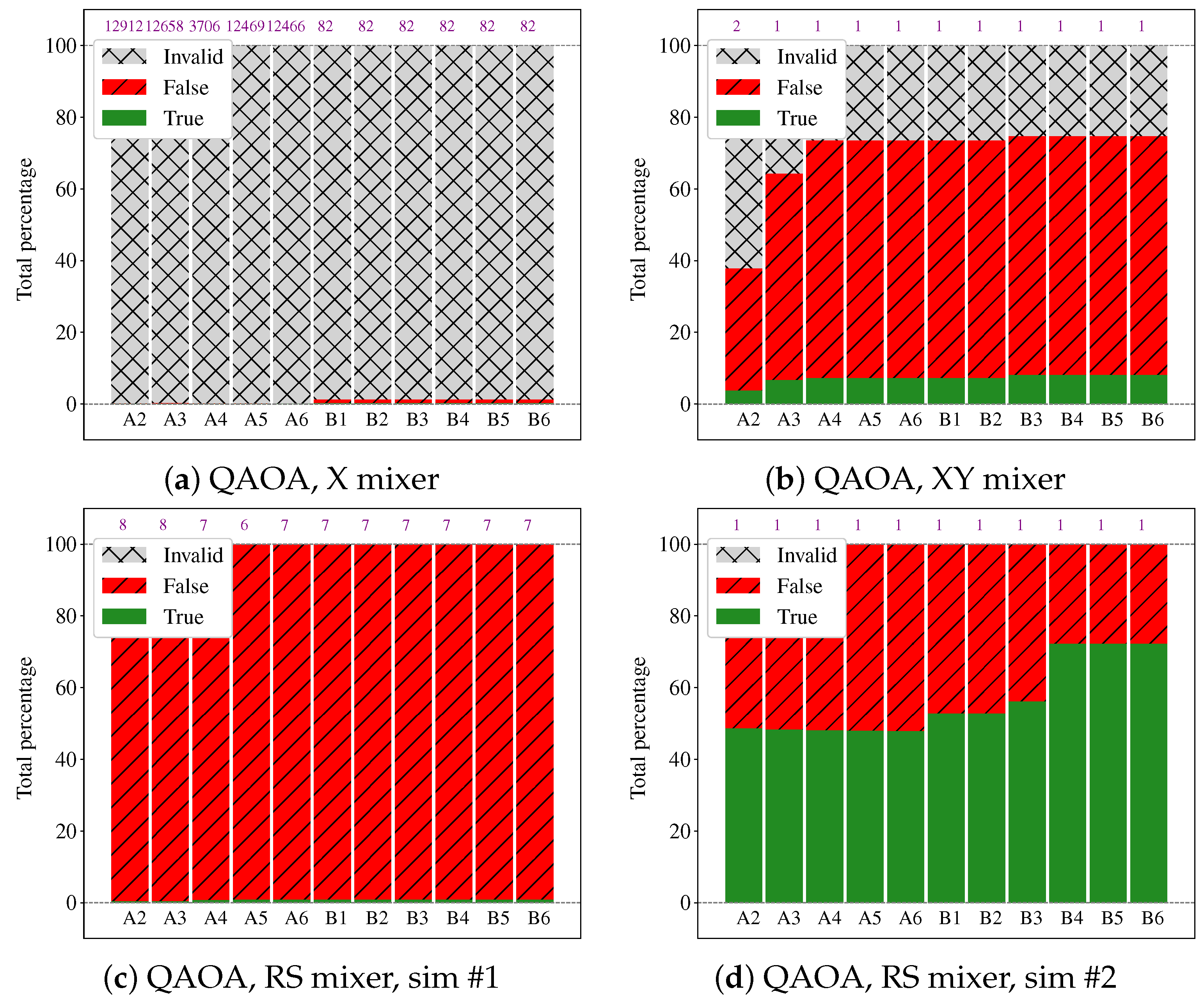
Appendix B. Comparison of the Three Mixers on a Single TSP Instance
References
- Biggs, N.; Lloyd, E.K.; Wilson, R.J. Graph Theory, 1736–1936; Clarendon Press: Cary, NC, USA, 1986. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Ambainis, A.; Balodis, K.; Iraids, J.; Kokainis, M.; Prūsis, K.; Vihrovs, J. Quantum Speedups for Exponential-Time Dynamic Programming Algorithms. In Proceedings of the SODA ’19: Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 6–9 January 2019; pp. 1783–1793. [Google Scholar]
- Finnila, A.; Gomez, M.; Sebenik, C.; Stenson, C.; Doll, J. Quantum annealing: A new method for minimizing multidimensional functions. Chem. Phys. Lett. 1994, 219, 343–348. [Google Scholar] [CrossRef]
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355–5363. [Google Scholar] [CrossRef]
- Warren, R.H. Solving combinatorial problems by two D-Wave hybrid solvers: A case study of traveling salesman problems in the TSP Library. arXiv 2021, arXiv:2106.05948. [Google Scholar] [CrossRef]
- Jain, S. Solving the Traveling Salesman Problem on the D-Wave Quantum Computer. Front. Phys. 2021, 9, 760783. [Google Scholar] [CrossRef]
- Villar-Rodriguez, E.; Osaba, E.; Oregi, I. Analyzing the behaviour of D’WAVE quantum annealer: Fine-tuning parameterization and tests with restrictive Hamiltonian formulations. In Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence (SSCI), Singapore, 4–7 December 2022. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.; Gambetta, J. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef]
- Qian, W.; Basili, R.; Pal, S.; Luecke, G.; Vary, J.P. Solving hadron structures using the basis light-front quantization approach on quantum computers. Phys. Rev. Res. 2022, 4, 043193. [Google Scholar] [CrossRef]
- Egger, D.J.; Gambella, C.; Marecek, J.; McFaddin, S.; Mevissen, M.; Raymond, R.; Simonetto, A.; Woerner, S.; Yndurain, E. Quantum Computing for Finance: State-of-the-Art and Future Prospects. IEEE Trans. Quantum Eng. 2020, 1, 3101724. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. arXiv 2018, arXiv:1801.00862. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices. Phys. Rev. X 2020, 10, 021067. [Google Scholar] [CrossRef]
- Mesman, K.; Al-Ars, Z.; Möller, M. QPack: Quantum Approximate Optimization Algorithms as universal benchmark for quantum computers. arXiv 2021, arXiv:2103.17193. [Google Scholar]
- Harrigan, M.P.; Sung, K.J.; Neeley, M.; Satzinger, K.J.; Arute, F.; Arya, K.; Atalaya, J.; Bardin, J.C.; Barends, R.; Boixo, S.; et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 2021, 17, 332–336. [Google Scholar] [CrossRef]
- Cook, J.; Eidenbenz, S.; Bärtschi, A. The Quantum Alternating Operator Ansatz on Maximum k-Vertex Cover. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 83–92. [Google Scholar] [CrossRef]
- Azad, U.; Behera, B.K.; Ahmed, E.A.; Panigrahi, P.K.; Farouk, A. Solving Vehicle Routing Problem Using Quantum Approximate Optimization Algorithm. IEEE Trans. Intell. Transp. Syst. 2022, 24, 7564–7573. [Google Scholar] [CrossRef]
- Sarkar, A.; Al-Ars, Z.; Bertels, K. QuASeR: Quantum Accelerated de novo DNA sequence reconstruction. PLoS ONE 2021, 16, e0249850. [Google Scholar] [CrossRef]
- Fingerhuth, M.; Babej, T.; Ing, C. A quantum alternating operator ansatz with hard and soft constraints for lattice protein folding. arXiv 2018, arXiv:1810.13411. [Google Scholar]
- Khumalo, M.T.; Chieza, H.A.; Prag, K.; Woolway, M. An investigation of IBM Quantum Computing device performance on Combinatorial Optimisation Problems. Neural Comput. Appl. 2022, 1–16. [Google Scholar] [CrossRef]
- Hadfield, S.; Wang, Z.; O’Gorman, B.; Rieffel, E.G.; Venturelli, D.; Biswas, R. From the Quantum Approximate Optimization Algorithm to a Quantum Alternating Operator Ansatz. Algorithms 2019, 12, 34. [Google Scholar] [CrossRef]
- Hadfield, S.; Wang, Z.; Rieffel, E.G.; O’Gorman, B.; Venturelli, D.; Biswas, R. Quantum Approximate Optimization with Hard and Soft Constraints. In Proceedings of the Second International Workshop on Post Moores Era Supercomputing, Denver, CO, USA, 12–17 November 2017. [Google Scholar]
- Streif, M.; Leib, M. Comparison of QAOA with quantum and simulated annealing. arXiv 2019, arXiv:1901.01903. [Google Scholar]
- Martoňák, R.; Santoro, G.E.; Tosatti, E. Quantum annealing of the traveling-salesman problem. Phys. Rev. E 2004, 70, 057701. [Google Scholar] [CrossRef]
- Jiang, Z.; Rieffel, E.G.; Wang, Z. Near-optimal quantum circuit for Grover’s unstructured search using a transverse field. Phys. Rev. A 2017, 95, 062317. [Google Scholar] [CrossRef]
- Skolik, A.; McClean, J.R.; Mohseni, M.; van der Smagt, P.; Leib, M. Layerwise learning for quantum neural networks. Quantum Mach. Intell. 2021, 3, 5. [Google Scholar] [CrossRef]
- ANIS, M.S.; Abraham, H.; AduOffei; Agarwal, R.; Agliardi, G.; Aharoni, M.; Akhalwaya, I.Y.; Aleksandrowicz, G.; Alexander, T.; Amy, M.; et al. Qiskit: An Open-source Framework for Quantum Computing, 2021. Available online: https://zenodo.org/record/8190968 (accessed on 18 August 2023).
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer Programming Formulation of Traveling Salesman Problems. J. ACM 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Gonzalez-Bermejo, S.; Alonso-Linaje, G.; Atchade-Adelomou, P. GPS: A New TSP Formulation for Its Generalizations Type QUBO. Mathematics 2022, 10, 416. [Google Scholar] [CrossRef]
- Zhu, J.; Gao, Y.; Wang, H.; Li, T.; Wu, H. A Realizable GAS-Based Quantum Algorithm for Traveling Salesman Problem. arXiv 2022, arXiv:2212.02735. [Google Scholar]
- Glos, A.; Krawiec, A.; Zimborás, Z. Space-efficient binary optimization for variational computing. arXiv 2020, arXiv:2009.07309. [Google Scholar] [CrossRef]
- Bakó, B.; Glos, A.; Salehi, O.; Zimborás, Z. Near-Optimal Circuit Design for Variational Quantum Optimization. arXiv 2022, arXiv:2209.03386. [Google Scholar]
- Albash, T.; Lidar, D.A. Adiabatic quantum computation. Rev. Mod. Phys. 2018, 90, 015002. [Google Scholar] [CrossRef]
- Blekos, K.; Brand, D.; Ceschini, A.; Chou, C.H.; Li, R.H.; Pandya, K.; Summer, A. A Review on Quantum Approximate Optimization Algorithm and Its Variants. arXiv 2023, arXiv:2306.09198. [Google Scholar]
- Herrman, R.; Lotshaw, P.C.; Ostrowski, J.; Humble, T.S.; Siopsis, G. Multi-angle quantum approximate optimization algorithm. Sci. Rep. 2022, 12, 1–10. [Google Scholar]
- Chandarana, P.; Hegade, N.N.; Paul, K.; Albarrán-Arriagada, F.; Solano, E.; del Campo, A.; Chen, X. Digitized-counterdiabatic quantum approximate optimization algorithm. Phys. Rev. Res. 2022, 4, 013141. [Google Scholar] [CrossRef]
- Wurtz, J.; Love, P.J. Counterdiabaticity and the quantum approximate optimization algorithm. Quantum 2022, 6, 635. [Google Scholar] [CrossRef]
- Zhu, L.; Tang, H.L.; Barron, G.S.; Calderon-Vargas, F.A.; Mayhall, N.J.; Barnes, E.; Economou, S.E. Adaptive quantum approximate optimization algorithm for solving combinatorial problems on a quantum computer. Phys. Rev. Res. 2022, 4, 033029. [Google Scholar] [CrossRef]
- Hadfield, S. On the Representation of Boolean and Real Functions as Hamiltonians for Quantum Computing. ACM Trans. Quantum Comput. 2021, 2, 1–21. [Google Scholar] [CrossRef]
- Cruz, D.; Fournier, R.; Gremion, F.; Jeannerot, A.; Komagata, K.; Tosic, T.; Thiesbrummel, J.; Chan, C.L.; Macris, N.; Dupertuis, M.A.; et al. Efficient quantum algorithms for GHZ and W states, and implementation on the IBM quantum computer. Adv. Quantum Technol. 2019, 2, 1900015. [Google Scholar] [CrossRef]
- Diker, F. Deterministic construction of arbitrary W states with quadratically increasing number of two-qubit gates. arXiv 2016, arXiv:1606.09290. [Google Scholar]
- Cervera-Lierta, A. Exact Ising model simulation on a quantum computer. Quantum 2018, 2, 114. [Google Scholar] [CrossRef]
- LaRose, R.; Rieffel, E.; Venturelli, D. Mixer-phaser Ansätze for quantum optimization with hard constraints. Quantum Mach. Intell. 2022, 4, 17. [Google Scholar] [CrossRef]
- Bärtschi, A.; Eidenbenz, S. Grover Mixers for QAOA: Shifting Complexity from Mixer Design to State Preparation. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 72–82. [Google Scholar] [CrossRef]
- Wang, Z.; Rubin, N.C.; Dominy, J.M.; Rieffel, E.G. XY mixers: Analytical and numerical results for the quantum alternating operator ansatz. Phys. Rev. A 2020, 101, 012320. [Google Scholar] [CrossRef]
- Borgsten, C. Quantum Approximate Optimization Using SWAP Gates for Mixing. Ph.D Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2021. [Google Scholar]
- Powell, M.J.D. Direct search algorithms for optimization calculations. Acta Numer. 1998, 7, 287–336. [Google Scholar] [CrossRef]
- Powell, M. A View of Algorithms for Optimization without Derivatives. Math. Today 2007, 43, 1–12. [Google Scholar]
- Powell, M.J.D. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J.P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar] [CrossRef]
- Spall, J. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Autom. Control. 1992, 37, 332–341. [Google Scholar] [CrossRef]
- Spall, J. Accelerated second-order stochastic optimization using only function measurements. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; Volume 2, pp. 1417–1424. [Google Scholar] [CrossRef]
- Rakyta, P.; Zimborás, Z. Approaching the theoretical limit in quantum gate decomposition. Quantum 2022, 6, 710. [Google Scholar] [CrossRef]
- Campos, E.; Rabinovich, D.; Akshay, V.; Biamonte, J. Training saturation in layerwise quantum approximate optimization. Phys. Rev. A 2021, 104, L030401. [Google Scholar] [CrossRef]
- Atsushi, M.; Yudai, S.; Shigeru, Y. Problem-specific Parameterized Quantum Circuits of the VQE Algorithm for Optimization Problems. arXiv 2020, arXiv:2006.05643. [Google Scholar]
- Basili, R.; Qian, W.; Tang, S.; Castellino, A.; Eshaghian-Wilner, M.; Khokhar, A.; Luecke, G.; Vary, J.P. Performance Evaluations of Noisy Approximate Quantum Fourier Arithmetic. In Proceedings of the 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lyon, France, 30 May 2022–3 June 2022; pp. 435–444. [Google Scholar] [CrossRef]
- Abrams, D.; Didier, N.; Johnson, B.; Silva, M.; Ryan, C. Implementation of XY entangling gates with a single calibrated pulse. Nat. Electron. 2020, 3, 744–750. [Google Scholar] [CrossRef]
- Joanes, D.N.; Gill, C.A. Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 183–189. [Google Scholar] [CrossRef]
- Kokoska, S.; Zwillinger, D. CRC Standard Probability and Statistics Tables and Formulae; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Kübler, J.M.; Arrasmith, A.; Cincio, L.; Coles, P.J. An Adaptive Optimizer for Measurement-Frugal Variational Algorithms. Quantum 2020, 4, 263. [Google Scholar] [CrossRef]
- Qian, W.; Basili, R.; Eshaghian-Wilner, M.; Khokhar, A.; Luecke, G.; Vary, J.P. Comparative study on the variations of quantum approximate optimization algorithms to the Traveling Salesman Problem. In Proceedings of the 2023 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPS), St. Petersburg, FL, USA, 15–19 May 2023; IEEE Computer Society: Washington, DC, USA, 2023; pp. 541–551. [Google Scholar] [CrossRef]

| After Pre-Training | After Retraining | ||||||
|---|---|---|---|---|---|---|---|
| # City | Mixers | AR | True % | Rank | AR | True % | Rank |
| 3 | VQE | 1.02 (0.02) | 87.6 (28.6) | 1.1 (0.3) | 1.01 (0.02) | 90.9 (20.2) | 1.1 (0.4) |
| X | 1.34 (0.14) | 38.5 (24.8) | 2.3 (2.2) | 1.28 (0.10) | 44.2 (28.2) | 1.9 (1.4) | |
| XY | 1.00 (0) | 100.0 (0) | 1.0 (0) | 1.00 (0) | 100.0 (0) | 1.0 (0) | |
| 4 | VQE | 2.23 (0.29) | 12.8 (13.3) | 35.6 (44.1) | 2.19 (0.37) | 11.8 (13.9) | 39.1 (42.2) |
| X | 2.65 (0.97) | 3.9 (3.6) | 67.7 (140.8) | 2.33 (0.83) | 5.5 (3.2) | 4.7 (5.3) | |
| XY | 1.52 (0.25) | 33.2 (9.6) | 1.3 (0.5) | 1.44 (0.23) | 36.6 (5.7) | 1.1 (0.4) | |
| RS | 1.05 (0.03) | 79.0 (9.8) | 1.0 (0) | 1.01 (0.01) | 96.3 (3.8) | 1.0 (0) | |
| 5 | X | 4.05 (2.10) | 0.7 (0.8) | 1814.1 (4348.8) | 2.85 (0.90) | 0.9 (1.0) | 94.3 (105.0) |
| XY | 2.01 (0.79) | 6.5 (1.3) | 3.6 (2.7) | 1.89 (0.66) | 7.4 (0.6) | 1.9 (1.1) | |
| RS | 1.22 (0.17) | 27.6 (25.8) | 3.1 (2.4) | 1.18 (0.14) | 41.1 (29.5) | 2.3 (2.2) | |
| # City | # Qubits | Mixers | Circuit Depth | Single-Qubit Gates | Double-Qubit Gates |
|---|---|---|---|---|---|
| 3 | 4 | X | 5 | 20 | 0 |
| XY | 26 | 64 | 16 | ||
| 4 | 9 | X | 5 | 45 | 0 |
| XY | 37 | 144 | 36 | ||
| RS | 668 | 477 | 432 | ||
| 5 | 16 | X | 5 | 80 | 0 |
| XY | 48 | 256 | 64 | ||
| RS | 1553 | 1808 | 1728 | ||
| n | X | 5 | 0 | ||
| XY | |||||
| RS |
| XY Mixer | RS Mixer | ||||||
|---|---|---|---|---|---|---|---|
| Noise % | Protocol | AR | True % | Rank | AR | True % | Rank |
| 0.1 | A2 | 3.44 (0.67) | 2.09 (0.03) | 2.43 (0.73) | 5.20 (1.02) | 0.4 (0.1) | 4.4 (4.3) |
| A6 | 3.44 (0.67) | 2.09 (0.03) | 2.43 (0.73) | 5.20 (1.02) | 0.4 (0.1) | 4.3 (4.4) | |
| B6 | 3.44 (0.67) | 2.09 (0.03) | 2.43 (0.73) | 5.19 (1.00) | 0.4 (0.1) | 4.1 (4.5) | |
| 0.05 | A2 | 2.90 (0.56) | 3.7 (0.1) | 1.6 (0.7) | 4.73 (0.92) | 0.6 (0.1) | 19.7 (5.1) |
| A6 | 2.90 (0.56) | 3.7 (0.1) | 1.6 (0.7) | 4.73 (0.92) | 0.6 (0.1) | 19.7 (5.1) | |
| B6 | 2.90 (0.56) | 3.7 (0.1) | 1.6 (0.7) | 4.73 (0.92) | 0.6 (0.1) | 19.7 (5.1) | |
| 0.01 | A2 | 1.78 (0.25) | 20.8 (2.9) | 1.0 (0) | 2.70 (0.53) | 0.6 (0) | 26.7 (1.8) |
| A6 | 1.76 (0.27) | 22.7 (2.7) | 1.0 (0) | 2.70 (0.53) | 0.6 (0) | 26.7 (1.8) | |
| B6 | 1.74 (0.27) | 23.9 (2.0) | 1.0 (0) | 2.70 (0.53) | 0.6 (0) | 26.7 (1.8) | |
| 0.005 | A2 | 1.74 (0.29) | 21.3 (3.1) | 1.0 (0) | 2.04 (0.29) | 7.7 (13.5) | 20.1 (11.8) |
| A6 | 1.62 (0.27) | 27.8 (4.0) | 1.1 (0.4) | 2.04 (0.29) | 12.9 (16.3) | 16.4 (13.1) | |
| B6 | 1.61 (0.28) | 28.8 (2.5) | 1.1 (0.4) | 2.04 (0.29) | 12.9 (16.3) | 16.4 (13.1) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, W.; Basili, R.A.M.; Eshaghian-Wilner, M.M.; Khokhar, A.; Luecke, G.; Vary, J.P. Comparative Study of Variations in Quantum Approximate Optimization Algorithms for the Traveling Salesman Problem. Entropy 2023, 25, 1238. https://doi.org/10.3390/e25081238
Qian W, Basili RAM, Eshaghian-Wilner MM, Khokhar A, Luecke G, Vary JP. Comparative Study of Variations in Quantum Approximate Optimization Algorithms for the Traveling Salesman Problem. Entropy. 2023; 25(8):1238. https://doi.org/10.3390/e25081238
Chicago/Turabian StyleQian, Wenyang, Robert A. M. Basili, Mary Mehrnoosh Eshaghian-Wilner, Ashfaq Khokhar, Glenn Luecke, and James P. Vary. 2023. "Comparative Study of Variations in Quantum Approximate Optimization Algorithms for the Traveling Salesman Problem" Entropy 25, no. 8: 1238. https://doi.org/10.3390/e25081238
APA StyleQian, W., Basili, R. A. M., Eshaghian-Wilner, M. M., Khokhar, A., Luecke, G., & Vary, J. P. (2023). Comparative Study of Variations in Quantum Approximate Optimization Algorithms for the Traveling Salesman Problem. Entropy, 25(8), 1238. https://doi.org/10.3390/e25081238







