1. Introduction
The problem of Private Information Retrieval (PIR), initially introduced in Chor et al. (1995) [
1], revolves around the confidential retrieval of data from distributed servers. Users aim to retrieve a specific file from a collection of files stored across these servers while keeping the servers unaware of the file’s identity. Sun et al. (2017) [
2] present a PIR scheme that minimizes the user’s download cost. Subsequently, the PIR problem has been addressed in various other settings. For instance, in [
3], PIR is studied with colluding servers, and in [
4], weakly private information retrieval is studied where some information about the user demand is allowed to be known to the servers. In [
5], the user is allowed to have files stored as side information.
Currently, PIR is being explored in conjunction with coded caching for content delivery scenarios. As first proposed in [
6], the coded caching problem includes a number of users, each with their own cache memories and a single server hosting a number of files. Users fill their caches while the network is not busy, and during periods of high network traffic, they request files from the server. The server broadcasts coded transmissions that benefit multiple users simultaneously. Users can use the content in their caches to decode the files they requested after receiving the broadcasts. A cache-aided PIR technique was recently put up by Caire et al. [
7], in which many users, each with access to their own dedicated caches, attempt to privately recover files from non-colluding servers. The advantages of coded caching from [
2,
6] are combined to provide an order-optimal MuPIR strategy.
In this paper, we use a variation of coded caching known as multi-access coded caching in PIR. In multi-access coded caching, users do not have access to dedicated caches. Instead, there are helper cache nodes, which are accessed by the users. Multiple users can access one helper cache, and a user can access multiple caches. This paper uses a multi-access setup with cyclic wraparound cache access. In cyclic wraparound cache access, the number of users and cache nodes are equal. Multi-access systems with cyclic wraparound cache access are widely studied in the literature. In [
8], Hachem et al. derive an order-optimal caching scheme which judiciously shares cache memory among files with different popularities. This idea was extended to a multi-access setup with cyclic-wraparound cache access. In [
9], Reddy et al. studied a multi-access coded caching design and proposed a new achievable rate within a multiplicative gap of at most 2 compared to the lower bound for the said problem provided uncoded placement. In [
10], a delivery scheme is proposed for the decentralized multi-access coded caching problem where each user is connected to multiple consecutive caches in a cyclic wrap-around fashion. A lower bound on the delivery rate is also obtained for the decentralized multi-access coded caching problem using techniques from index coding. In [
11], Cheng et al. propose a transformation approach to generalize the MAN scheme to the multi-access caching systems, such that the results of [
8] remain achievable in full generality. In [
12], the authors generalize one of the cases in [
13], which proposes novel caching and coded delivery schemes maximizing the local caching gain.
Notation 1. Consider integers a and b. Then, . . For a set of size and an integer , . For set and , denotes the set . For the set of integers we define to be the set .
The following subsections briefly explain the PIR, coded caching and multi-user PIR problems. Firstly, we explain the single-user PIR problem of [
2] and introduce the concept of private retrieval from distributed servers. Then, we introduce the coded caching problem [
6] and its different variations, i.e., dedicated cache and multi-access coded caching problems. We provide motivation behind the cyclic-wraparound multi-access model in
Section 1.3. Then, the combination of the dedicated cache-aided coded caching problem and the PIR problem as described in [
7] is introduced in
Section 1.4. Finally, the contribution of this paper, which considers a combination of PIR with a multi-access coded caching problem, is summarized in
Section 1.5.
1.1. Private Information Retrieval
The protocol of Private Information Retrieval [
2] allows for the retrieval of a specific file from a set of
N files
. These files are replicated across
S non-colluding servers, with each file being of equal size. The objective of PIR is to retrieve the desired file, denoted as
, without disclosing its identity to the servers. In other words, the user intends to conceal the index
from the servers. To achieve this, the user generates
S queries
and sends query
to server
s. Upon receiving their respective queries, the servers generate answers based on the query received and the files they possess. Server
s generates the answer
and sends it back to the user. After receiving answers from all
S servers, the user should be able to decode the desired file. The PIR protocol must satisfy privacy and correctness conditions, which are formally defined as follows:
The transmission cost of PIR is defined as
A PIR scheme is provided in [
2], which incurs the minimum possible transmission cost,
is given as a function of the number of servers
S and the number of files is denoted as
N.
In the scheme provided in [
2], every file has to be divided into
subfiles, and every server performs a transmission of size
.
Note: In the literature, the term rate is used for the transmission cost (e.g., [
6]) as we use it here, whereas sometimes (e.g., [
2]) the term rate is used for teh mean the inverse of the transmission cost as used by us. We use the term “transmission cost” instead of rate in this paper as in most of the coded caching literature [
6,
14,
15].
1.2. Coded Caching
The authors in [
6] propose a centralized coded caching system consisting of a server storing
N independent files
of unit size and
K users with a dedicated cache memory of size
M files. However, in recent years, multi-access coded caching systems have been gaining attention, where
C cache nodes exist, and each user can access several of them.
Coded caching systems work in two phases. In the delivery phase, which corresponds to low network traffic, the server fills the caches with the contents of the files. Then, in the delivery phase, all users wish to retrieve some files from the servers, increasing the network traffic. User k wishes to retrieve file where . Each user conveys to the server the index of the file they want. The server broadcasts coded transmissions of size in the unit of files after receiving the user requests. The transmission is a function of the files stored at the server and user demand. All users should be able to retrieve their chosen files using the caches they can access after receiving the coded transmission . The quantity is defined as the rate of the coded caching system, and it measures the size of the server’s transmissions.
1.3. Multi-Access Coded Caching with Cyclic Wraparound Cache Access
Several approaches exist for users to access cache nodes in multi-access coded caching systems. In [
15], multi-access schemes are derived from cross-resolvable designs, and the authors of [
14] propose a system where each user can access
L unique caches, resulting in
users. This multi-access setting was further generalized in [
16], showing that the rate achieved in [
14] is optimal for certain cases. In this paper, we focus on a cyclic wraparound cache access approach where
and each user accesses
L neighboring cache nodes. This approach is reminiscent of circular wraparound networks, also known as ring networks, that have been extensively studied in the literature. For example, circular soft-handoff (SH) models in cellular networks [
17] arrange nodes (base stations) in a circle, where users access only two nodes, their local node, and the node in the left neighboring cell. Another variant is the circular Wyner model, where nodes are arranged in a circle and users access three nodes (base stations), its local node, and nodes in two neighboring cells. Such settings were studied in [
18], and Shannon-theoretic limits for a very simple cellular multiple-access system were obtained. In [
19], the Wyner model was studied again, and upper and lower bounds on the per-user multiplexing gain of Wyner’s circular soft-handoff model were presented. In [
20], achievable rates were derived for the uplink channel of a cellular network with joint multicell processing. The rates were given in closed form for the classical Wyner model and the soft-handover model. There is extensive research on circular wraparound cache access in multi-access coded caching settings [
8,
9,
10,
11,
12,
13]. Like in cellular networks discussed above, this can occur when cache nodes are arranged in a circular manner and users access the
L nearest cache nodes.
1.4. Dedicated Cache Aided MuPIR
In the dedicated cache setup described in [
7], there is a collection of
N files denoted as
, which are replicated across
S servers. The system involves
K users, each equipped with a dedicated cache capable of storing
M files. The users aim to retrieve their desired files from the servers. The system operates in two distinct phases.
In the
Placement Phase, the cache of each user is populated with certain content. This cache content is determined based on the files stored across the servers and is independent of the future demands of the users. Subsequently, in the
Private Delivery Phase, each user independently selects a file and seeks to privately retrieve their respective file from the servers. To achieve this, the users collaboratively generate
S queries and transmit them to the servers. Upon receiving their respective queries, the servers respond with answers. The users should be able to decode their desired files using the transmitted answers and the content stored in their caches. In [
7], an achievable scheme known as the
product design is proposed. The product design results in a transmission cost denoted as
, where
whenever
for some integer
. For other memory points, lower convex envelope of points
is achieved by memory sharing.
Cache-aided multi-user PIR setups with multi-access caches are also considered in [
21,
22].
1.5. Our Contributions
This paper presents a PIR scheme that enables multiple users, aided by multi-access cache nodes, to privately retrieve data from distributed servers. The proposed scheme focuses on the multi-access setup with cyclic wraparound cache access where there are multiple non-colluding servers and all messages are replicated across these servers. The servers are connected with the users through noiseless broadcast links.
The contributions of this paper are as follows.
The paper comprehensively describes the system model for the MACAMuPIR setup with cyclic wraparound cache access. It outlines the key components and mechanisms involved in the scheme.
The paper presents an achievable scheme for the multi-access problem described above and characterizes its transmission cost.
A comparison is made between the transmission costs of the multi-access setup and a dedicated cache setup proposed in previous work. The results show that the multi-access setup outperforms the dedicated cache setup.
The paper includes proofs that validate the privacy guarantees and transmission costs mentioned in the scheme description. These proofs demonstrate the scheme’s ability to preserve user privacy and ensure accurate retrieval of requested data.
1.6. Paper Organization
The rest of the paper is organized as follows:
In
Section 2, the problem statement is described, along with formal descriptions of transmission cost, privacy and correctness conditions.
Then, in
Section 3, the main results of the paper are summarized. The achieved rate is mentioned in this section.
Section 4 has the scheme to achieve the transmission load mentioned in
Section 3. We first explain the scheme using a concrete example in
Section 4.1. Then, we extend the description to encompass general parameters in
Section 4.2. We then specialize the scheme to the context of cyclic wraparound cache access in
Section 4.3. Then, proof of privacy and calculation of subpacketization level follows.
After the specialized description of
Section 4.3, we arrive at the critical observation that to calculate the rate, it is essential to characterize the number of
-sized subsets of
that contain at least
L consecutive integers, with wrapping around
K allowed. Here,
. This is calculated in
Section 4.4 onward.
Section 5 contains a discussion about the results and scope for future research, and
Section 6 concludes the paper.
2. System Model: MACAMuPIR with Cyclic Wraparound Caches
The system consists of
K users and
N independent files, denoted as
, which are replicated across
servers. Each file has a unit size. There are
C cache nodes available, and each cache can store up to
M files. Each user is connected to a unique set of
cache nodes through links with infinite capacity. User
k is connected to cache nodes indexed by
. The system follows a multi-access setup with cyclic wraparound cache access. In this setup, the number of users equals the number of cache nodes, i.e.,
. Each user accesses
L consecutive caches in a cyclic wraparound fashion. Specifically, user
accesses caches indexed by
. We consider
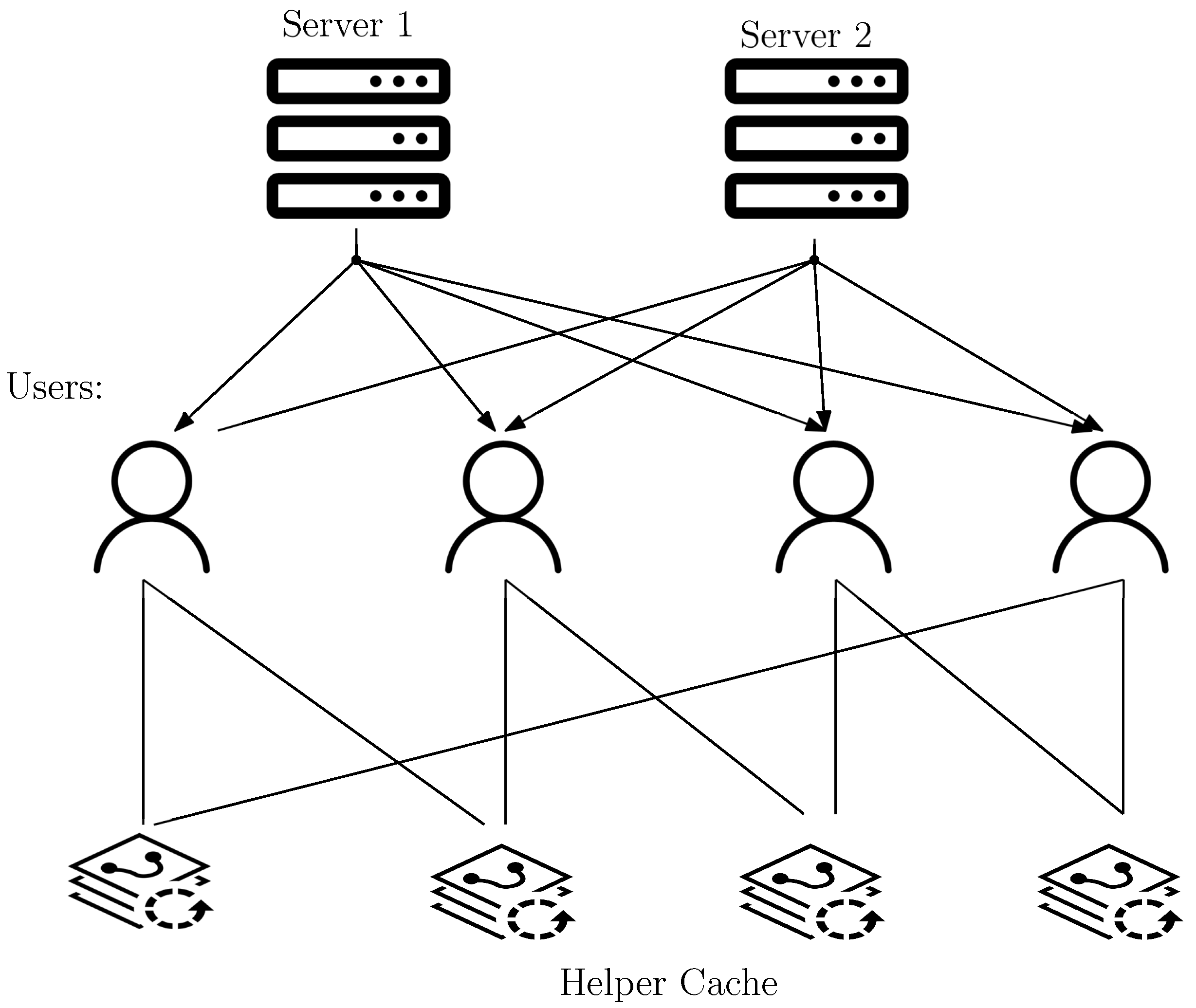
Figure 1; it is a multi-access system with cyclic wraparound access. In this system, we have
servers and
users. There are four cache nodes, and every user is accessing
cache nodes. The system operates in two phases described below.
Placement Phase: During this phase, all C cache nodes are populated. We let denote the content stored in cache . The content is determined based on the files , and all servers possess knowledge of the content stored in each helper cache.
Private Delivery Phase: In this phase, each user aims to retrieve a specific file from the servers. User k selects and desires to privately retrieve from the servers. The demand vector is denoted as . To retrieve their desired files from the servers while preserving privacy, users cooperatively generate S queries based on their demands and the content stored in helper caches. These queries are designed in a way that they do not disclose the demand vector to any of the servers. After generating the queries, each query is sent to server . Upon receiving their respective queries, each server , broadcasts the answer to the users. The answer is a function of the query and the files . After receiving all S answers , each user k, decodes using the caches accessible to that user.
To ensure the privacy of the user demands, the following condition must be satisfied:
This condition, known as the privacy condition, ensures that none of the servers have any information about user demands. And
known as the correctness condition, ensures that users experience no ambiguity concerning their desired file.
We define the transmission cost
R as the amount of data that has to be transmitted by all the servers in order to satisfy the user demand.
Our goal is to design cache placement and private delivery schemes that satisfy privacy and correctness conditions and minimize the transmission cost.
4. Achievable Scheme: Proof of Theorem 1
4.1. Example
In this section, we present an achievable scheme using an example. Let us consider a cache-aided system with
files denoted as
,
cache nodes, and
users. Each user has access to
cache nodes in a cyclic wraparound manner. Since each user is connected to a unique set of three cache nodes, we can index each user with a subset of
of size 3. For instance, the user connected to cache nodes indexed by six, seven, and eight can be denoted as
. Here is the list of all eight users:
Placement Phase: We let
. We divide each file into
subfiles, each indexed by integers in
.
Then, we fill the cache nodes as follows:
Delivery Phase: In this phase, every user chooses one of the file indexes. We enumerate the demands of the users:
For privately retrieving the files, users cooperatively generate queries as follows. For every
, such that
is the superset of at least one user index set, users generate sub-queries. For example, for
, we have users
and
as a subset of
. Therefore, the users generate
corresponding to
, where
are the queries generated by the users in a single-user PIR setup if the demand is
and the set of files are
, whereas there is no user for which
is a superset; therefore, no queries can be generated corresponding to
.
Then, for
, server
s transmits
where
is the answer of server
s in a single-user PIR setup if the received query is
and the set of files is
.
Decoding
We consider user
and subfiles
and
. Subfile
is available to the user from the cache node 4. Subfile
has to be decoded from the transmissions. Consider the transmissions corresponding to
from (
7):
User
has access to subfiles
, and therefore it can reconstruct
using the contents in Cache 6. After removing
from the transmission corresponding to
, user
obtains
. As these are the answers of a single-user PIR setup for demand
and files
, user
can decode
.
4.2. General Scheme: K Users, Each Connected to a Unique Arbitrary Set of L Caches
Consider
N independent unit size files
replicated across the
S servers. There are
C cache nodes, each capable of storing
M files, and
K users each connected to a unique set of
L cache nodes. As each user is connected to a unique set of the
L cache, we index them with an
L-sized subset of
. Specifically, user
, where
, is the user connected to cache nodes indexed by
. We let
be the set of all users where
Note that, for the special case of cyclic wraparound cache access,
and
where
.
Placement Phase: We let
be an integer. Then, we divide each file into
subfiles, each indexed by a
t-sized subset of
.
Then, we fill cache node
c with
Delivery Phase: In this phase, every user chooses one of the file indexes. We let user
choose index
. User
then wishes to retrieve file
from the servers without reveling the index of the demanded file to the servers. We let
be the demand vector. Users do not want the servers to obtain any information about the demand vector. For privately retrieving the files, the users cooperatively generate
S queries
as follows. For every
, such that
for at least one
, the users generate sub-queries
where the sub-sub-query
is the query sent to server
s in a single-user PIR setup of [
2] if the user demand is
. We note that
for all
and for all
are generated independently. The query sent to server
s is
Now, for every
, server
s transmits
where
is the answer of server
s in a single-user PIR setup if the received query is
and the set of files is
.
Now, we proceed to show that all the users are able to decode their required file from these transmissions and the caches they have access to.
4.2.1. Decoding
We consider user
(i.e., the user connected to cache nodes indexed by
) and subfile index
. If
, then the subfile
is available to the user from the cache. If
, then the subfiles have to be decoded from the transmissions. We consider transmissions corresponding to
.
User
has access to all the subfiles in the second term of RHS above, and therefore it can recover the first term from the above expression. After obtaining
for all
, user
can recover subfile
from the transmissions.
4.2.2. Proof of Privacy
Now, we show that query
sent to server
s is independent of the demand vector
,
. For some
, we consider
in (
8). We show that
is independent of the demand vector. From the privacy of the single-user PIR scheme, the demand of user
, i.e.,
is independent of sub-sub-query
. Also, other sub-sub-queries in
are similarly independent of
as they correspond to the users other than
. This means that
is independent of the demands of the users in
. Moderover, all
for any
and
are constructed independently, so these are also independent of the demands of users in
. This shows that
is independent of the demand vector
. Same analysis is true for any
where
for at least one
, which completes the proof of privacy for our scheme.
4.2.3. Subpacketization
As we can see, each file is divided into subfiles. According to the single-user PIR scheme, each of these subfiles has to be further divided into sub-subfiles. Therefore, the subpacketization level is
4.3. General Scheme: Cyclic Wraparound Cache Access
For cyclic wraparound cache access systems, we have
and
. Therefore, transmissions are performed only for those
for which
for at least one
. This is the same as the number of
-sized subsets of
that contain at least
L consecutive integers, with wrapping around
K allowed. As shown in
Section 4.4, there are
such subsets of
. Now,
transmissions are performed by each of the
S servers, and every transmission is of size
units; therefore, the transmission cost incurred is
Also, note that user
k of the dedicated cache setup and that of the multi-access setup with a cyclic wraparound cache access are accessing cache node
k. In a dedicated cache setup
, transmissions are required to satisfy user demands. Therefore, when
, we perform placement and transmissions as conducted for a dedicated cache setup. In this scenario, the transmission cost incurred in a multi-access setup is only as high as the transmission cost of a dedicated cache scenario with same cache sizes. For
, the transmission cost of a multi-access setup would be
We demonstrate our claim using an example for
caches and users,
servers,
files and
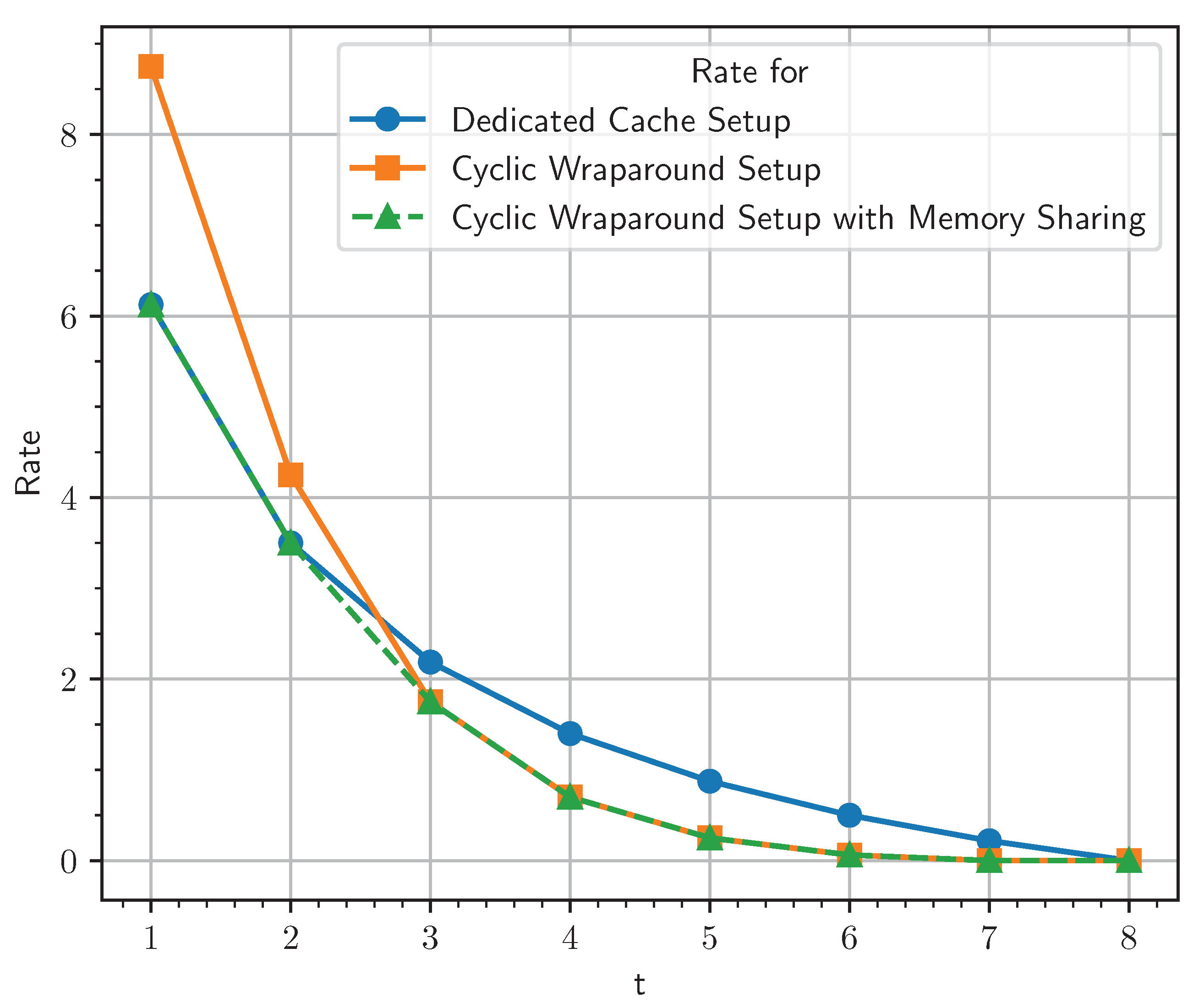
. In
Figure 3, we see that for smaller values of the
t cyclic wraparound, cache access is incurring more transmission cost than the dedicated cache setup. For instance, when
or
,
, transmissions are performed for cyclic wraparound cache access without memory sharing (and incurring transmission cost
) compared to
transmissions in a dedicated cache setup (and incurring transmission cost
). Therefore, when
, transmissions corresponding to dedicated cache setup are performed. But when
or
, a multi-access system with a cyclic wraparound cache access satisfy user demand with 56 transmissions (and an incurring transmission cost
) compared to a dedicated cache setup which requires 70 transmissions (and sn incurring transmission cost
), and therefore transmissions, as described here, are performed. For cache memory
M,
, memory sharing between these two schemes can incur transmission cost lower than either of these schemes.
4.4. Proving the Expression for
In this section, we show that the number of ways of choosing
k integers from the set
, such that there is a subset of at least
m consecutive integers, with cyclic wrapping around
n allowed, is
as defined in (
4).
First, for every , we denote as the length of consecutive runs of integers inside and is the length of consecutive run of integers outside . For instance, if and , then corresponding to elements in , corresponding to not in , corresponding to element in , corresponding to not in and corresponding to in . Now, every can be uniquely determined by a sequence of positive integers consisting of and where every integer provides the length of consecutive runs of integers inside or outside , provided it is known if 1 is inside or outside . For example, with and , if we are given the sequence of lengths of consecutive runs of the integers inside and outside as and it is known that , then we can uniquely figure out .
Now, the set of all k-sized subsets of with at least m cyclically consecutive integers can be partitioned into four disjoint sets as follows:
and . This corresponds to sequences of the form where for all , , , such that , . We let the set of all such k-sized subsets be .
and . This corresponds to sequences of the form where for all , , , such that , . We let the set of all such k-sized subsets be .
and . This corresponds to sequences of the form where for all , , and such that , . The set of all such k-sized subsets is denoted by .
and . This corresponds to sequences of the form where for all , , and such that or , . We let the set of all such k-sized subsets be denoted by .
Now, we have . We proceed to calculate the size of these sets individually.
4.4.1. Calculation of
Sets in correspond to the positive integer sequences of the form . Here, and , and at least one and r takes all possible values in .
We let
denote the set of tuples of
r positive integers with the sum of integers equal to
k and teh
integer greater than or equal to
m, i.e.,
For a given
r,
is the set of all
r length sequences,
, of positive integers such that
. For all such sequences
there also exist
sequences of positive integers
such that
. Therefore,
From the inclusion–exclusion principle, we know that
where
which implies
4.4.2. Calculation of
By the definition of the set
and from the sequence of integers
corresponding to
, it is clear that
4.4.3. Calculation of
Here, we again see that we need a sequence of positive integers
such that
and
for which
. We have already calculated this quantity for
, but for every such sequence of integers, there exist
sequences
of positive integers such that
. Therefore,
4.4.4. Calculation of
We consider all sequences of integers corresponding to such that for all , , and and such that OR . can be partitioned into two disjoint subsets, corresponding to sequences where and for at lest one and corresponding to sequences where . Again, and . We proceed to calculate the cardinality of both these sets separately.
Calculation of
We consider the set of all
r length positive integer sequences
such that
and
and
for some
. We note that, for such sequences,
. The number of such sequences is
For every such
r length sequence, there exist
positive integer sequences
such that
, and we obtain
Calculation of
We consider the set of all
length positive integer sequences
such that
and
. The number of such sequences is
For every such
r length sequence, there exist
positive integer sequences
such that
, and when
, there are
possible pairs of positive integers
which provides
, leading to
Finally, we have
Defining
if
or if
or
, the expression above can be simplified to (
4).
5. Discussion
In this paper, we proposed an efficient and privacy-preserving scheme for multi-user retrieval scenarios. By leveraging the benefits of multi-access setups with cyclic wraparound cache access, we demonstrated improved transmission costs compared to the dedicated cache setup. We conducted a comprehensive comparison with prior works that utilize dedicated cache systems. Our results demonstrate the superior performance of our proposed scheme.
Moreover, the placement and delivery schemes designed for dedicated cache-aided MuPIR scenarios are applicable in our MAC-MuPIR scenarios with cyclic wraparound cache access. This adaptability leads to consistently lower rates in our scheme compared to the product design. Hence, we achieved even lower rates by utilizing memory sharing between our setup and the dedicated cache-aided setup. For instance, if we consider
Figure 3, specifically for points
and 4. At
, the dedicated cache setup of [
7] achieves a lower rate than the scheme provided in
Section 4.3, so placement and delivery, as described in [
7], are performed, which still work in our setting. At
, the scheme provided in
Section 4.3 has a lower rate, so placement and delivery are performed as described in the section mentioned above. At
, we can perform memory sharing between dedicated cache and multi-access cache schemes and achieve a rate lower than both of the schemes (dotted line in
Figure 3, referring to scheme with memory sharing below the lines corresponding to dedicated cache scheme and scheme mentioned in
Section 4.3).
However, it is important to acknowledge some limitations of our study. Firstly, we focused on noiseless broadcast links, which may not reflect real-world scenarios where channel impairments exist. Future research could investigate the impact of channel conditions on the performance of the proposed scheme. Additionally, we assumed non-colluding servers and replicated messages across the servers. Exploring the scheme’s resilience in the presence of adversarial behaviors or server failures could be an interesting direction for further investigation.
6. Conclusions
In this study, we introduced a PIR scheme that enables multiple users to securely retrieve data from distributed servers using a multi-access setup with cyclic wraparound cache access. We described the system model, formally defined the privacy and correctness constraints, and presented the transmission cost associated with our proposed scheme.
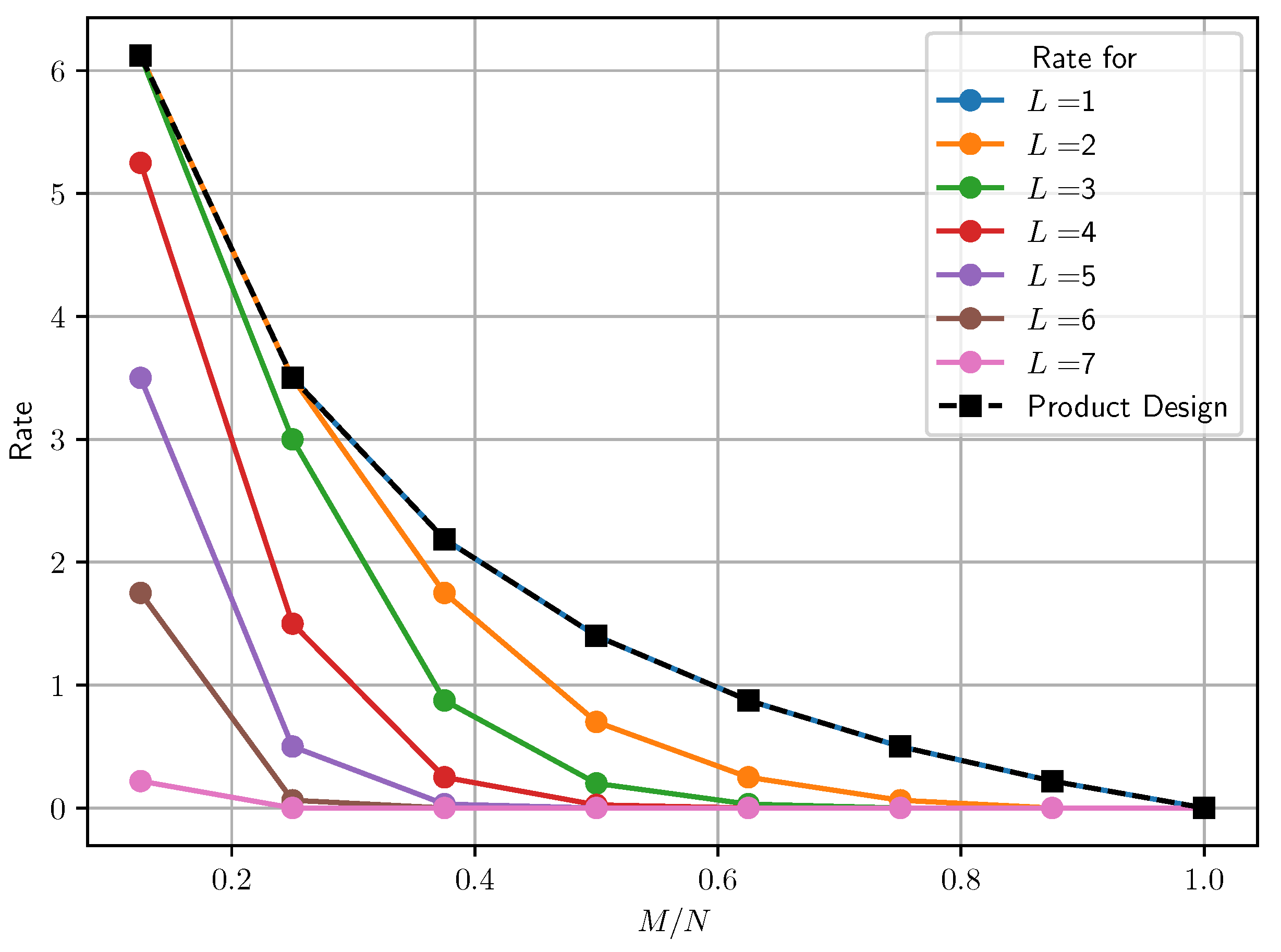
Our findings indicate that the multi-access setup with cyclic wraparound cache access offers significant advantages over the dedicated cache setup. By comparing the transmission costs of both setups, we demonstrated that the multi-access setup outperforms the dedicated cache setup, making it a more efficient and reliable approach for multi-user PIR scenarios. For instance, in
Figure 2, for caching ratio
, we see that for
the cyclic wraparound system and the dedicated cache system both achieve a rate of three. But the rate decreases as cache access degree
L increases and users have access to more caches. For
and 7, the rate of our scheme is
and 0, respectively. More than a twofold improvement in download cost is shown compared to that of the dedicated cache setup from
onward, i.e., accessing half of the available caches.
Furthermore, our scheme provides strong privacy guarantees, ensuring that users can retrieve data without revealing their individual retrieval patterns or compromising the privacy of the data. The proofs presented in
Section 4.2.2 validate the privacy and transmission costs associated with our scheme, reinforcing its effectiveness and security.