An Ensemble Outlier Detection Method Based on Information Entropy-Weighted Subspaces for High-Dimensional Data
Abstract
1. Introduction
1.1. Neighborhood-Based Detection
1.2. Subspace-Based Detection
1.3. Ensemble-Based Detection
- By employing a subsampling technique based on ensemble thinking, this study introduces diversity into the ensemble of density-based unsupervised anomaly detection methods. In each subsample, the densities around each data point in the dataset are determined to compute their respective anomaly scores. This approach provides diversified detection results, reduces global variance through ensemble learning, and enhances the robustness of the algorithm model.
- To tackle the redundancy and irrelevance of the numerous subspaces present in high-dimensional data, this paper proposes a weighted subspace outlier detection algorithm based on information entropy. This algorithm determines the corresponding weighted subspaces based on the information entropy of data points in each dimension. It redefines the distances between data points, thereby reducing the noise impact caused by high-dimensional data and improving density-based outlier detection performance for high-dimensional data.
- This study optimizes algorithm implementation based on the LOF (Local Outlier Factor) algorithm framework, enhancing the differentiation between normal and anomalous data, as well as making anomalous behavior more salient. This improvement results in an overall enhancement of the algorithm model’s anomaly detection performance.
2. Materials and Methods
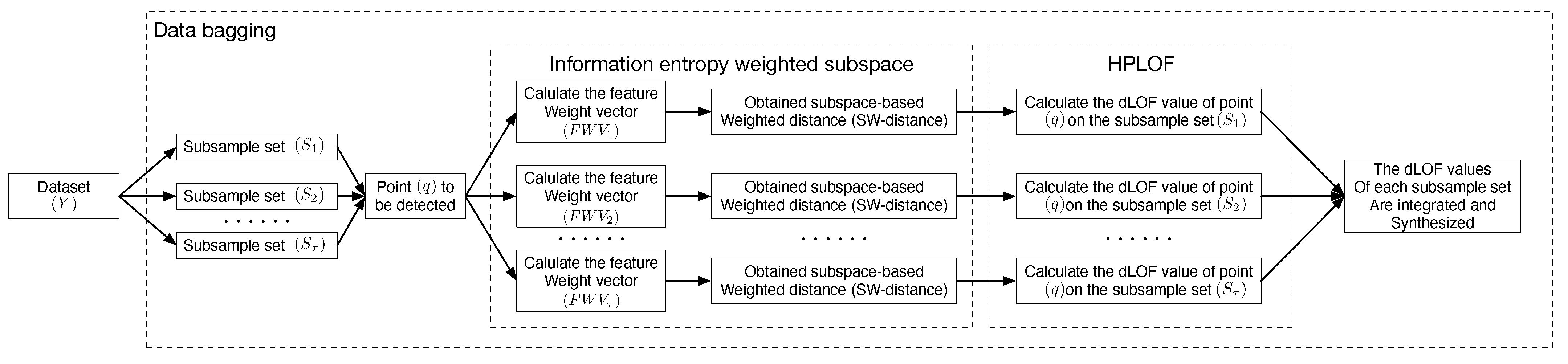
3. EOEH
3.1. Subsampling
3.2. Information Entropy-Weighted Subspace
3.3. HPLOF
3.4. Algorithm Implementation
| Algorithm 1 EOEH |
| Input: dataset Y with dimension n and sample number m, number of subsample sets T, number of samples in each subsample set , abnormal entropy weight , normal entropy weight , neighborhood parameter K Output: Integrate exception score set O
|
4. Algorithm Experiment
4.1. Experimental Environment
4.2. Experimental Metrics
4.3. Experimental Data
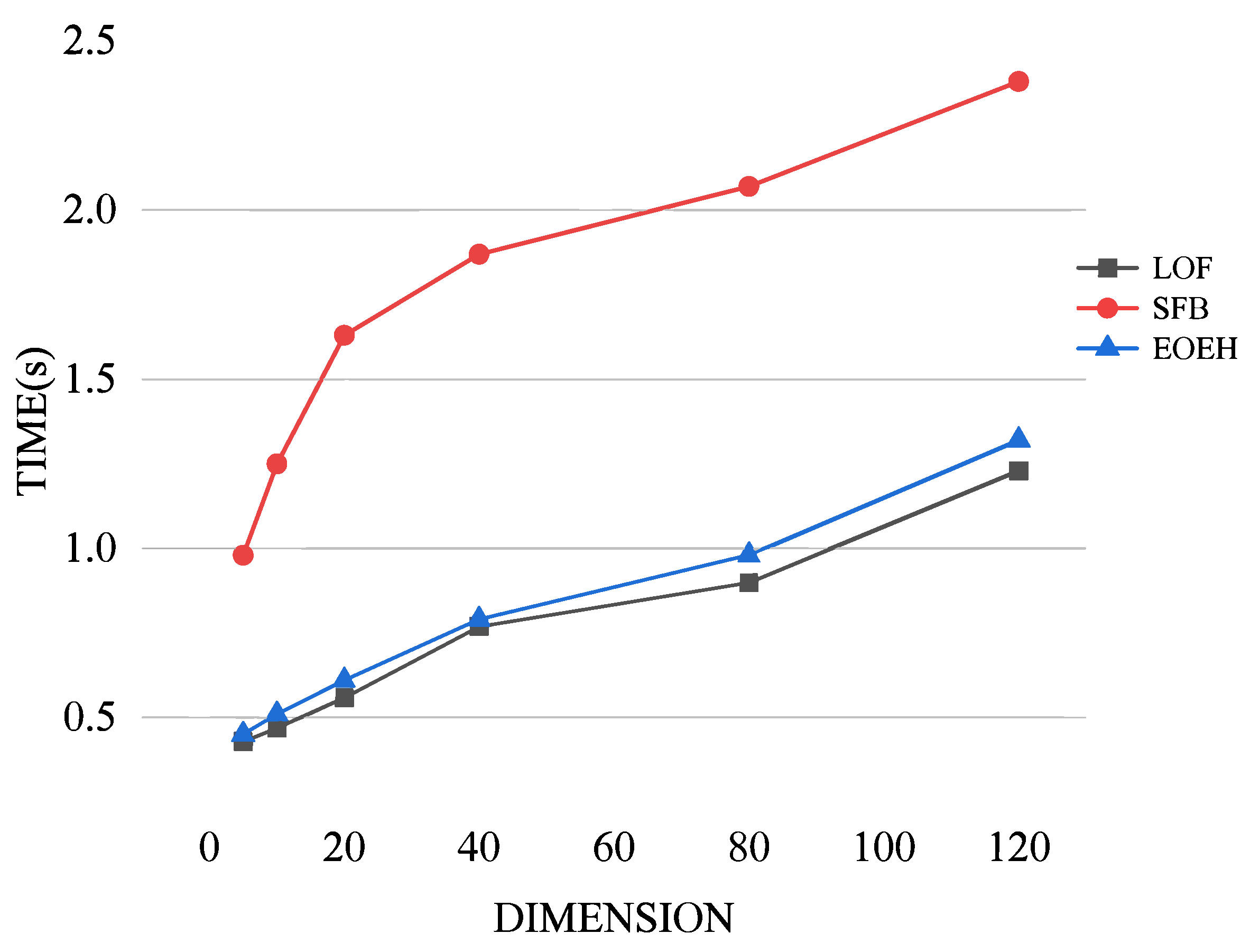
4.4. Experimental Contents
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boukerche, A.; Zheng, L.; Alfandi, O. Outlier detection: Methods, models, and classification. ACM Comput. Surv. CSUR 2020, 53, 1–37. [Google Scholar] [CrossRef]
- Goldstein, M. Special Issue on Unsupervised Anomaly Detection. Appl. Sci. 2023, 13, 5916. [Google Scholar] [CrossRef]
- Kou, A.; Huang, X.; Sun, W. Outlier Detection Algorithms for Open Environments. Wirel. Commun. Mob. Comput. 2023, 2023, 5162254. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y. Density-Distance Outlier Detection Algorithm Based on Natural Neighborhood. Axioms 2023, 12, 425. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, H.; Li, T.; Liu, J.; Wang, S. Fuzzy information entropy-based adaptive approach for hybrid feature outlier detection. Fuzzy Sets Syst. 2021, 421, 1–28. [Google Scholar] [CrossRef]
- Yu, J.; Kang, J. Clustering ensemble-based novelty score for outlier detection. Eng. Appl. Artif. Intell. 2023, 121, 106164. [Google Scholar] [CrossRef]
- Lu, Y.C.; Chen, F.; Wang, Y.; Lu, C.T. Discovering anomalies on mixed-type data using a generalized student-t based approach. IEEE Trans. Knowl. Data Eng. 2016, 28, 2582–2595. [Google Scholar] [CrossRef]
- Bouguessa, M. A practical outlier detection approach for mixed-attribute data. Expert Syst. Appl. 2015, 42, 8637–8649. [Google Scholar] [CrossRef]
- Souiden, I.; Omri, M.N.; Brahmi, Z. A survey of outlier detection in high dimensional data streams. Comput. Sci. Rev. 2022, 44, 100463. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Aggarwal, C.C. High-dimensional outlier detection: The subspace method. In Outlier Analysis; Springer: Berlin/Heidelberg, Germany, 2017; pp. 149–184. [Google Scholar]
- Wichitaksorn, N.; Kang, Y.; Zhang, F. Random feature selection using random subspace logistic regression. Expert Syst. Appl. 2023, 217, 119535. [Google Scholar] [CrossRef]
- Chung, H.C.; Ahn, J. Subspace rotations for high-dimensional outlier detection. J. Multivar. Anal. 2021, 183, 104713. [Google Scholar] [CrossRef]
- Muhr, D.; Affenzeller, M. Little data is often enough for distance-based outlier detection. Procedia Comput. Sci. 2022, 200, 984–992. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y. A robust supervised subspace learning approach for output-relevant prediction and detection against outliers. J. Process Control 2021, 106, 184–194. [Google Scholar] [CrossRef]
- Zhang, P.; Li, T.; Wang, G.; Wang, D.; Lai, P.; Zhang, F. A multi-source information fusion model for outlier detection. Inf. Fusion 2023, 93, 192–208. [Google Scholar] [CrossRef]
- Wang, B.; Mao, Z. A dynamic ensemble outlier detection model based on an adaptive k-nearest neighbor rule. Inf. Fusion 2020, 63, 30–40. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, Q.; Luo, J.; Zhu, F. Local dynamic neighborhood based outlier detection approach and its framework for large-scale datasets. Egypt. Inform. J. 2021, 22, 125–132. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Schubert, E.; Zimek, A. Outlier detection in axis-parallel subspaces of high dimensional data. In Advances in Knowledge Discovery and Data Mining: 13th Pacific-Asia Conference, PAKDD 2009, Bangkok, Thailand, 27–30 April 2009; Proceedings 13; Springer: Berlin/Heidelberg, Germany, 2009; pp. 831–838. [Google Scholar]
- Zhang, J.; Jiang, Y.; Chang, K.H.; Zhang, S.; Cai, J.; Hu, L. A concept lattice based outlier mining method in low-dimensional subspaces. Pattern Recognit. Lett. 2009, 30, 1434–1439. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Chang, K.H.; Qin, X. An outlier mining algorithm based on constrained concept lattice. Int. J. Syst. Sci. 2014, 45, 1170–1179. [Google Scholar] [CrossRef]
- Müller, E.; Schiffer, M.; Seidl, T. Adaptive outlierness for subspace outlier ranking. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management, Toronto, ON, Canada, 26–30 October 2010; pp. 1629–1632. [Google Scholar]
- Müller, E.; Schiffer, M.; Seidl, T. Statistical selection of relevant subspace projections for outlier ranking. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 434–445. [Google Scholar]
- Dutta, J.K.; Banerjee, B.; Reddy, C.K. RODS: Rarity based outlier detection in a sparse coding framework. IEEE Trans. Knowl. Data Eng. 2015, 28, 483–495. [Google Scholar] [CrossRef]
- Van Stein, B.; Van Leeuwen, M.; Bäck, T. Local subspace-based outlier detection using global neighbourhoods. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 1136–1142. [Google Scholar]
- Xu, X.; Liu, H.; Yao, M. Recent progress of anomaly detection. Complexity 2019, 2019, 2686378. [Google Scholar] [CrossRef]
- Lazarevic, A.; Kumar, V. Feature bagging for outlier detection. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 21–24 August 2005; pp. 157–166. [Google Scholar]
- Nguyen, H.V.; Ang, H.H.; Gopalkrishnan, V. Mining outliers with ensemble of heterogeneous detectors on random subspaces. In Database Systems for Advanced Applications: 15th International Conference, DASFAA 2010, Tsukuba, Japan, 1–4 April 2010; Proceedings, Part I 15; Springer: Berlin/Heidelberg, Germany, 2010; pp. 368–383. [Google Scholar]
- Wang, B.; Wang, W.; Meng, G.; Meng, T.; Song, B.; Wang, Y.; Guo, Y.; Qiao, Z.; Mao, Z. Selective Feature Bagging of one-class classifiers for novelty detection in high-dimensional data. Eng. Appl. Artif. Intell. 2023, 120, 105825. [Google Scholar] [CrossRef]
- Zimek, A.; Campello, R.J.; Sander, J. Ensembles for unsupervised outlier detection: Challenges and research questions a position paper. ACM Sigkdd Explor. Newsl. 2014, 15, 11–22. [Google Scholar] [CrossRef]
- Pasillas-Díaz, J.R.; Ratté, S. Bagged subspaces for unsupervised outlier detection. Comput. Intell. 2017, 33, 507–523. [Google Scholar] [CrossRef]
- Chen, L.; Wang, W.; Yang, Y. CELOF: Effective and fast memory efficient local outlier detection in high-dimensional data streams. Appl. Soft Comput. 2021, 102, 107079. [Google Scholar] [CrossRef]
- Yan, Y.; Cao, L.; Rundensteiner, E.A. Scalable top-n local outlier detection. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1235–1244. [Google Scholar]
- Tang, J.; Chen, Z.; Fu, A.W.C.; Cheung, D.W. Enhancing effectiveness of outlier detections for low density patterns. In Advances in Knowledge Discovery and Data Mining: 6th Pacific-Asia Conference, PAKDD 2002, Taipei, Taiwan, 6–8 May 2002; Proceedings 6; Springer: Berlin/Heidelberg, Germany, 2002; pp. 535–548. [Google Scholar]
- Papadimitriou, S.; Kitagawa, H.; Gibbons, P.B.; Faloutsos, C. Loci: Fast outlier detection using the local correlation integral. In Proceedings of the 19th International Conference on Data Engineering (Cat. No. 03CH37405), Bangalore, India, 5–8 March 2003; pp. 315–326. [Google Scholar]
- Kriegel, H.P.; Kröger, P.; Schubert, E.; Zimek, A. LoOP: Local outlier probabilities. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; pp. 1649–1652. [Google Scholar]
- Su, S.; Xiao, L.; Ruan, L.; Gu, F.; Li, S.; Wang, Z.; Xu, R. An efficient density-based local outlier detection approach for scattered data. IEEE Access 2018, 7, 1006–1020. [Google Scholar] [CrossRef]
- Riahi-Madvar, M.; Azirani, A.A.; Nasersharif, B.; Raahemi, B. A new density-based subspace selection method using mutual information for high dimensional outlier detection. Knowl.-Based Syst. 2021, 216, 106733. [Google Scholar] [CrossRef]
- Wang, G.; Wei, D.; Li, X.; Wang, N. A novel method for local anomaly detection of time series based on multi entropy fusion. Phys. A Stat. Mech. Appl. 2023, 615, 128593. [Google Scholar] [CrossRef]
- Maheshwari, R.; Mohanty, S.K.; Mishra, A.C. DCSNE: Density-based Clustering using Graph Shared Neighbors and Entropy. Pattern Recognit. 2023, 137, 109341. [Google Scholar] [CrossRef]
- Bohm, C.; Railing, K.; Kriegel, H.P.; Kroger, P. Density connected clustering with local subspace preferences. In Proceedings of the Fourth IEEE International Conference on Data Mining (ICDM’04), Brighton, UK, 1–4 November 2004; pp. 27–34. [Google Scholar]
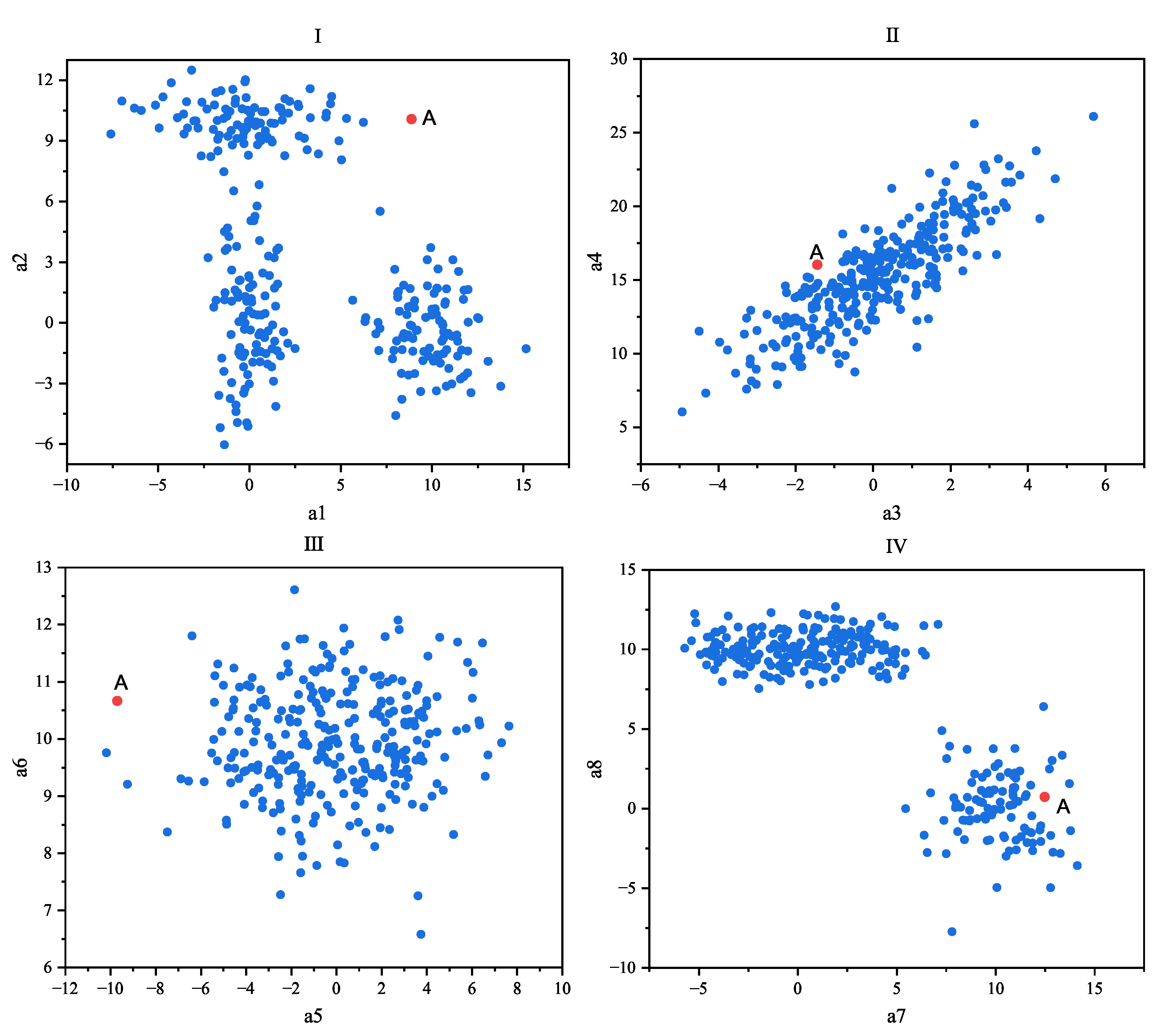

| Real Class | Prediction Class | Index |
|---|---|---|
| 1 | 1 | True Positive () |
| 0 | 1 | False Positive () |
| 1 | 0 | False Negative () |
| 0 | 0 | True Negative () |
| Data Set | Data Size (Anomaly %) | Dimension | Classes |
|---|---|---|---|
| Musk | 3062 (0.03) | 166 | 5 |
| Movement | 360 (0.06) | 90 | 15 |
| Coil2000 | 9389 (0.05) | 85 | 2 |
| Optdigits | 1014 (0.28) | 64 | 10 |
| Spambase | 4597 (0.01) | 57 | 2 |
| Spectfheart | 267 (0.21) | 44 | 2 |
| Texture | 4755 (0.009) | 40 | 7 |
| Satimage | 4577 (0.008) | 36 | 6 |
| Thyroid | 7036 (0.01) | 21 | 3 |
| Ring | 4564 (0.06) | 20 | 2 |
| Twonorm | 4144 (0.08) | 20 | 2 |
| Pendigits | 6870 (0.02) | 16 | 10 |
| Data Set | Data Size (Anomaly %) | Dimension |
|---|---|---|
| A | 5000 (0.1) | 5 |
| B | 5000 (0.1) | 10 |
| C | 5000 (0.1) | 20 |
| D | 5000 (0.1) | 40 |
| E | 5000 (0.1) | 80 |
| F | 5000 (0.1) | 160 |
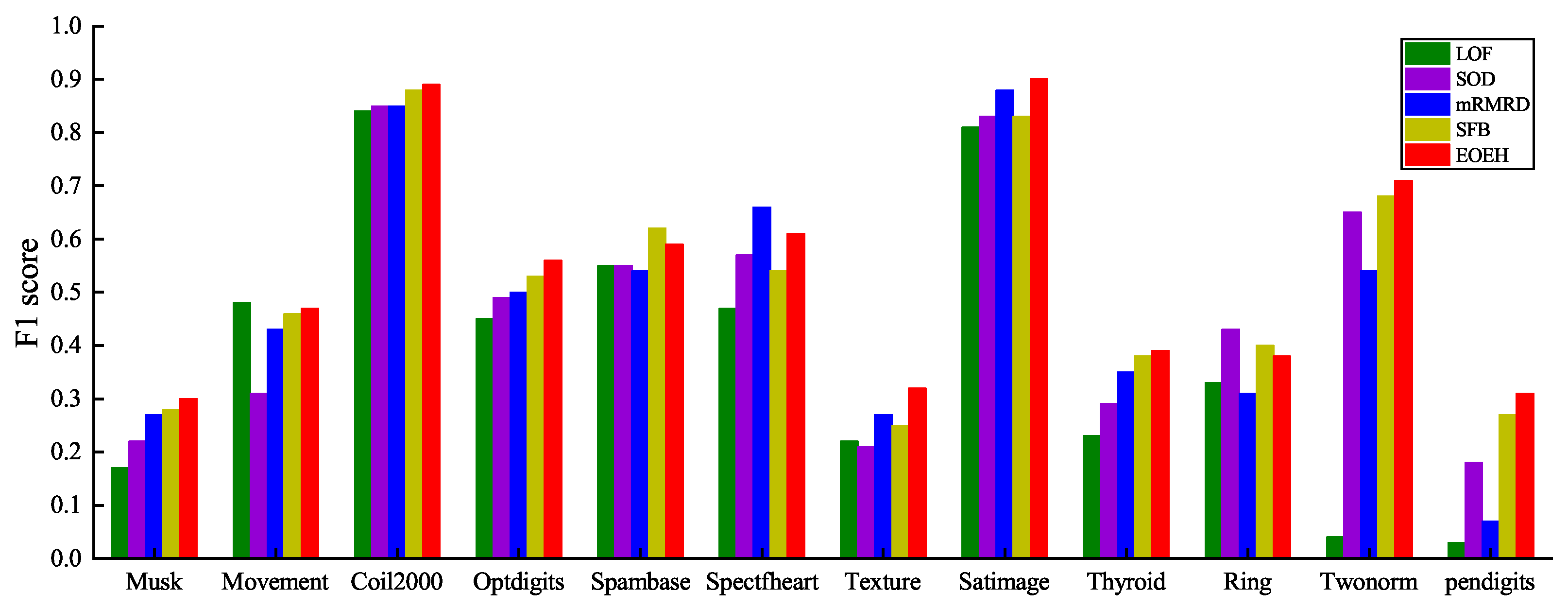
| Data Set | LOF | SOD | mRMRD | SFB | EOEH |
|---|---|---|---|---|---|
| Musk | 0.17 | 0.22 | 0.27 | 0.28 | 0.30 |
| Movement | 0.48 | 0.31 | 0.43 | 0.46 | 0.47 |
| Coil2000 | 0.84 | 0.85 | 0.85 | 0.88 | 0.89 |
| Optdigits | 0.45 | 0.49 | 0.50 | 0.53 | 0.56 |
| Spambase | 0.55 | 0.55 | 0.54 | 0.62 | 0.59 |
| Spectfheart | 0.47 | 0.57 | 0.66 | 0.54 | 0.61 |
| Texture | 0.22 | 0.21 | 0.27 | 0.25 | 0.32 |
| Satimage | 0.81 | 0.83 | 0.88 | 0.83 | 0.90 |
| Thyroid | 0.23 | 0.29 | 0.35 | 0.38 | 0.39 |
| Ring | 0.33 | 0.43 | 0.31 | 0.40 | 0.38 |
| Twonorm | 0.04 | 0.65 | 0.54 | 0.68 | 0.71 |
| Pendigits | 0.03 | 0.18 | 0.07 | 0.27 | 0.31 |
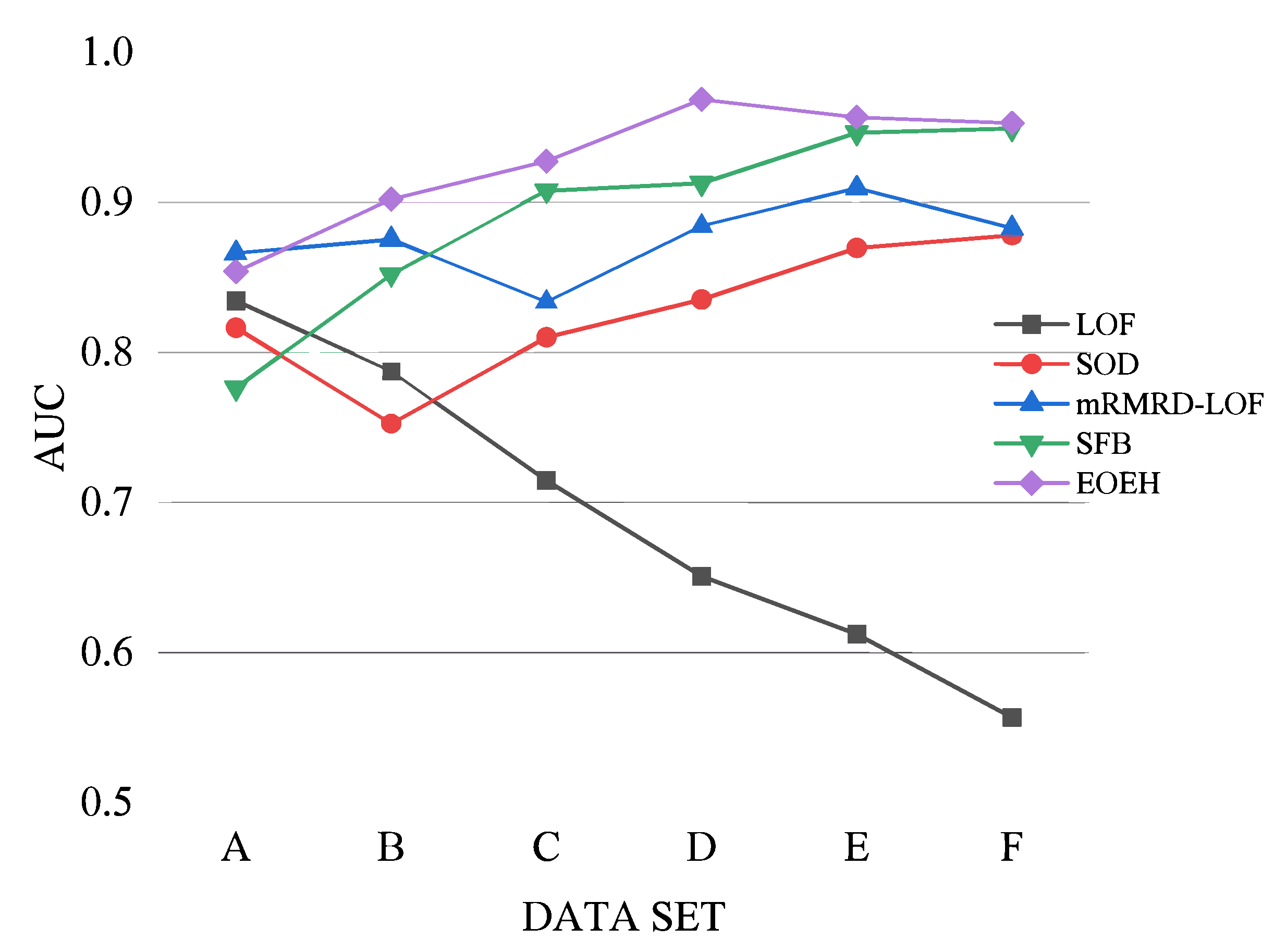
| Data Set | LOF | SOD | mRMRD | SFB | EOEH |
|---|---|---|---|---|---|
| A | 0.8344 | 0.8165 | 0.8661 | 0.7764 | 0.8541 |
| B | 0.7875 | 0.7528 | 0.8754 | 0.8517 | 0.8517 |
| C | 0.7148 | 0.8101 | 0.8338 | 0.9077 | 0.9273 |
| D | 0.6509 | 0.8353 | 0.8844 | 0.9129 | 0.9684 |
| E | 0.6123 | 0.8697 | 0.9094 | 0.9465 | 0.9566 |
| F | 0.5569 | 0.8782 | 0.8827 | 0.9493 | 0.9527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, L. An Ensemble Outlier Detection Method Based on Information Entropy-Weighted Subspaces for High-Dimensional Data. Entropy 2023, 25, 1185. https://doi.org/10.3390/e25081185
Li Z, Zhang L. An Ensemble Outlier Detection Method Based on Information Entropy-Weighted Subspaces for High-Dimensional Data. Entropy. 2023; 25(8):1185. https://doi.org/10.3390/e25081185
Chicago/Turabian StyleLi, Zihao, and Liumei Zhang. 2023. "An Ensemble Outlier Detection Method Based on Information Entropy-Weighted Subspaces for High-Dimensional Data" Entropy 25, no. 8: 1185. https://doi.org/10.3390/e25081185
APA StyleLi, Z., & Zhang, L. (2023). An Ensemble Outlier Detection Method Based on Information Entropy-Weighted Subspaces for High-Dimensional Data. Entropy, 25(8), 1185. https://doi.org/10.3390/e25081185






