Experimental Evidence for Double Quaternary Azeotropy’s Existence
Abstract
1. Introduction
2. Materials and Methods
2.1. Thermodynamic Modeling
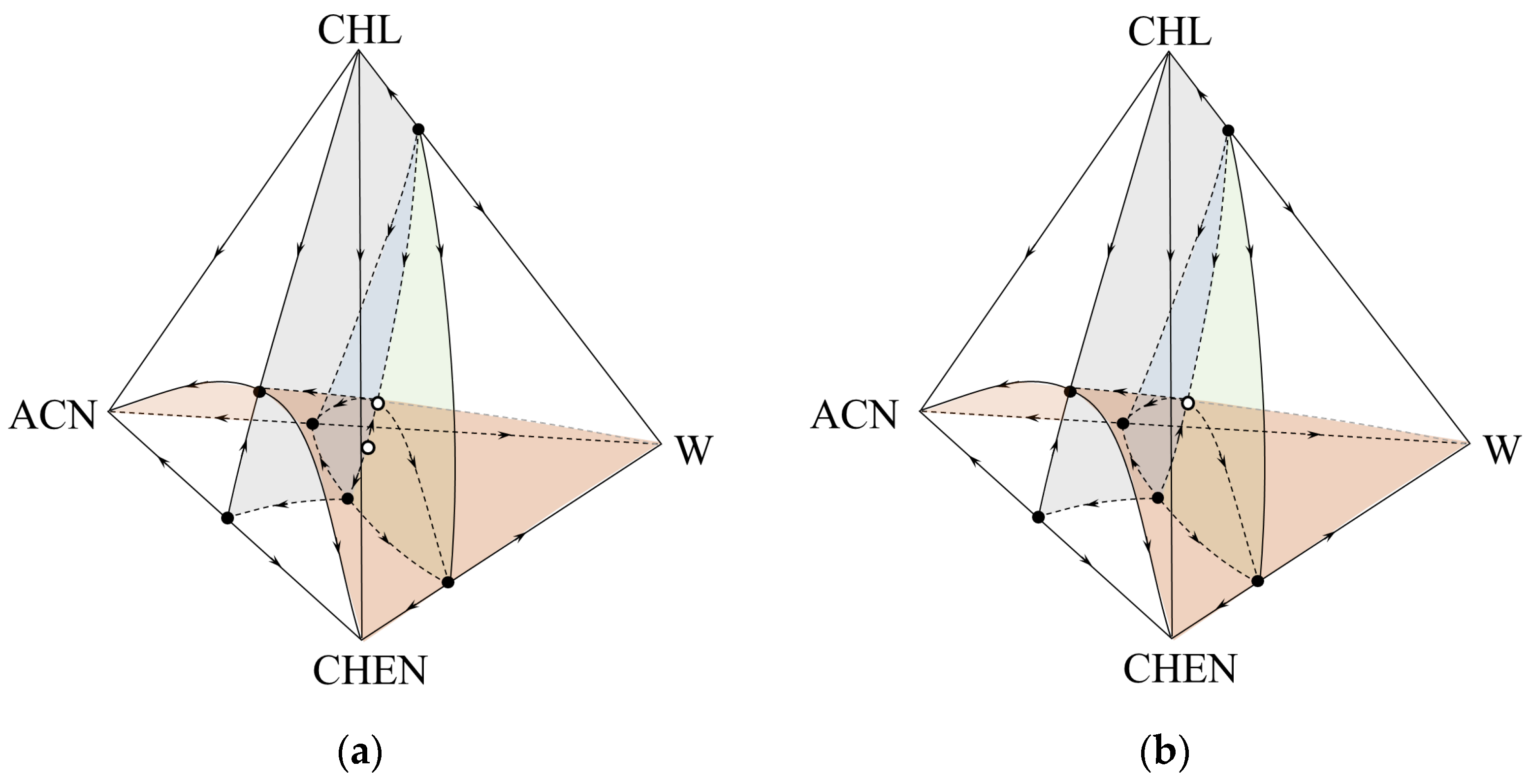
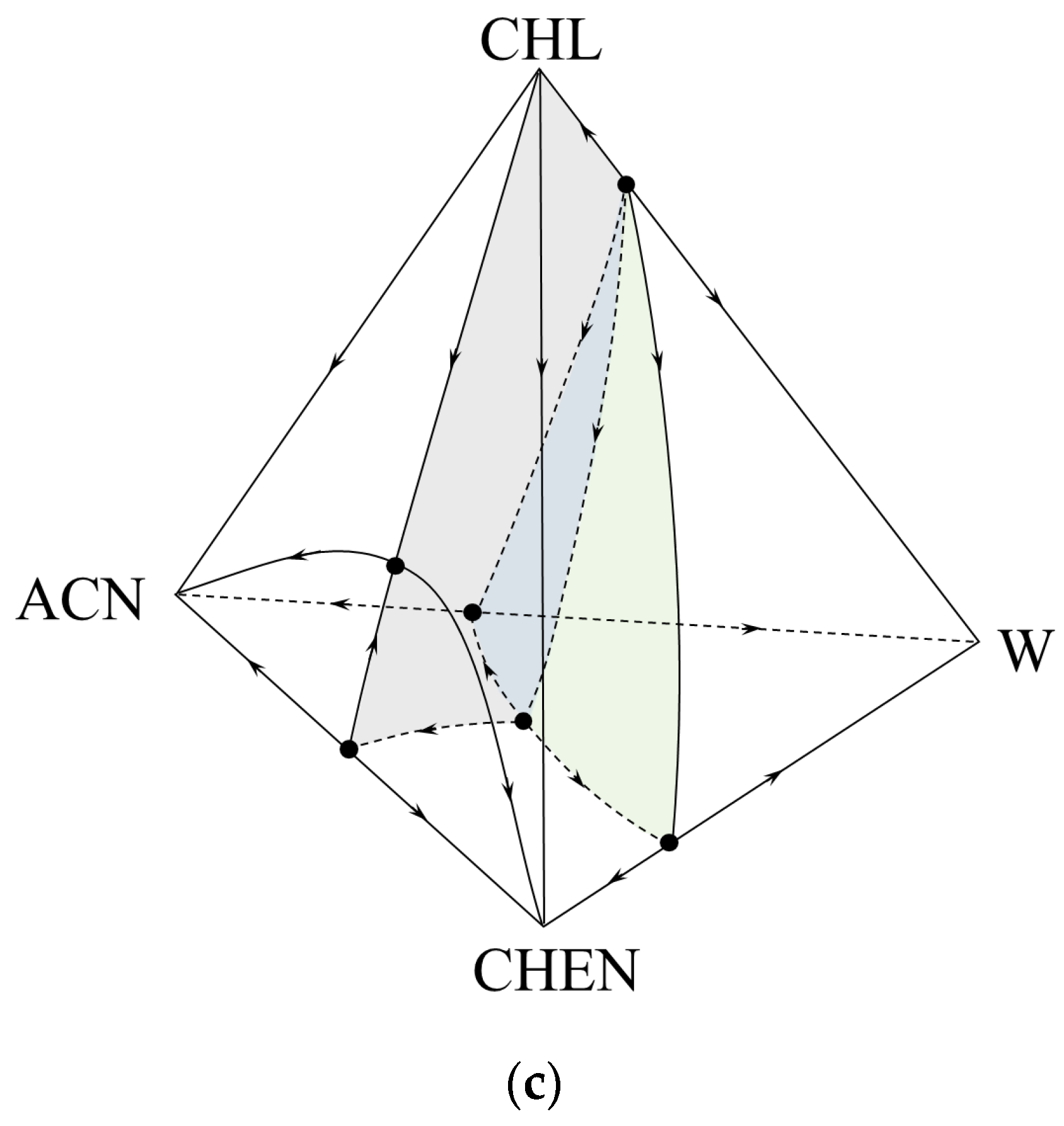
2.2. Thermodynamic-Topological Analysis
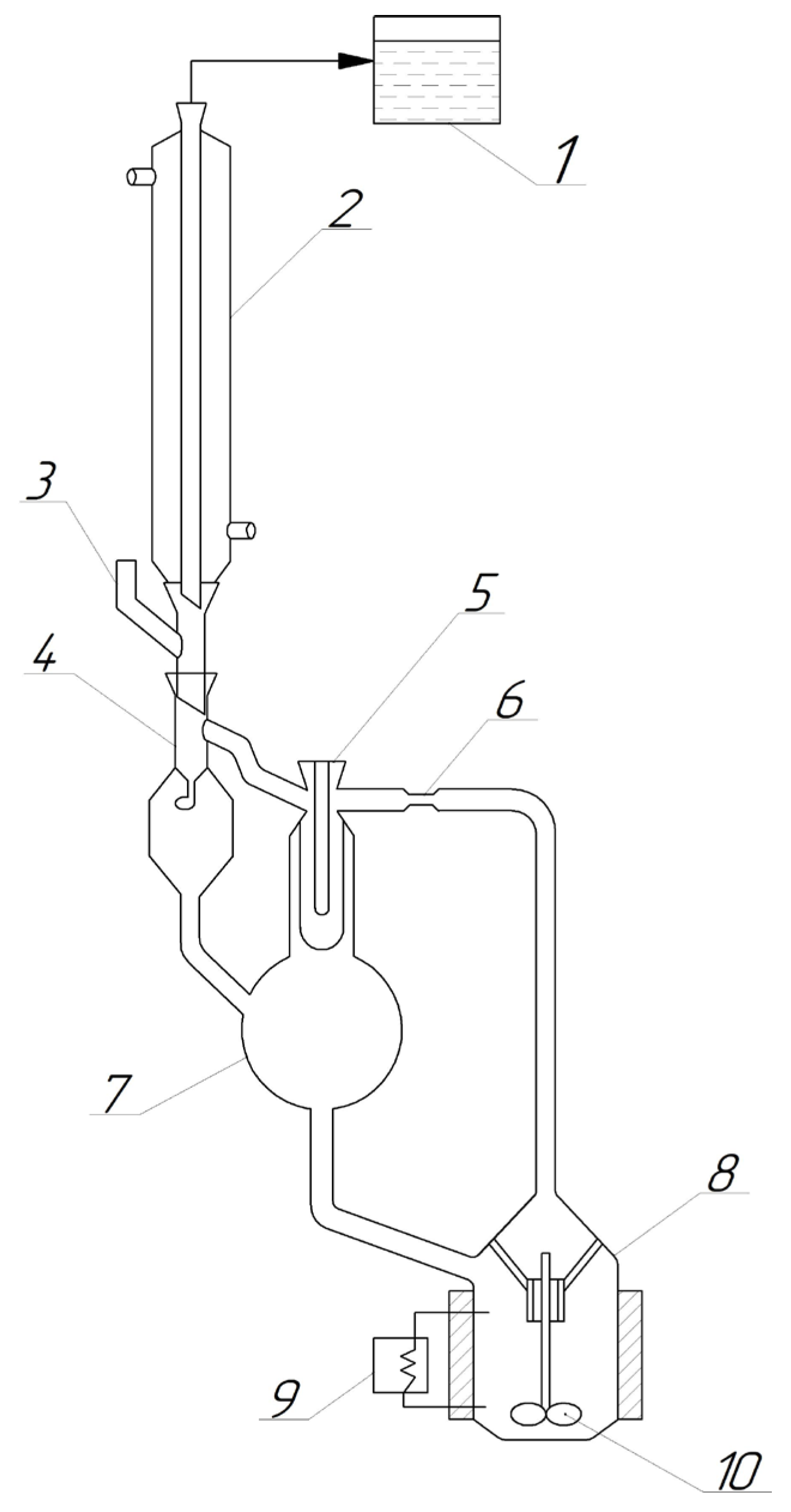
2.3. Experimental Procedures
2.3.1. Chemicals
2.3.2. Ebulliometric Titration
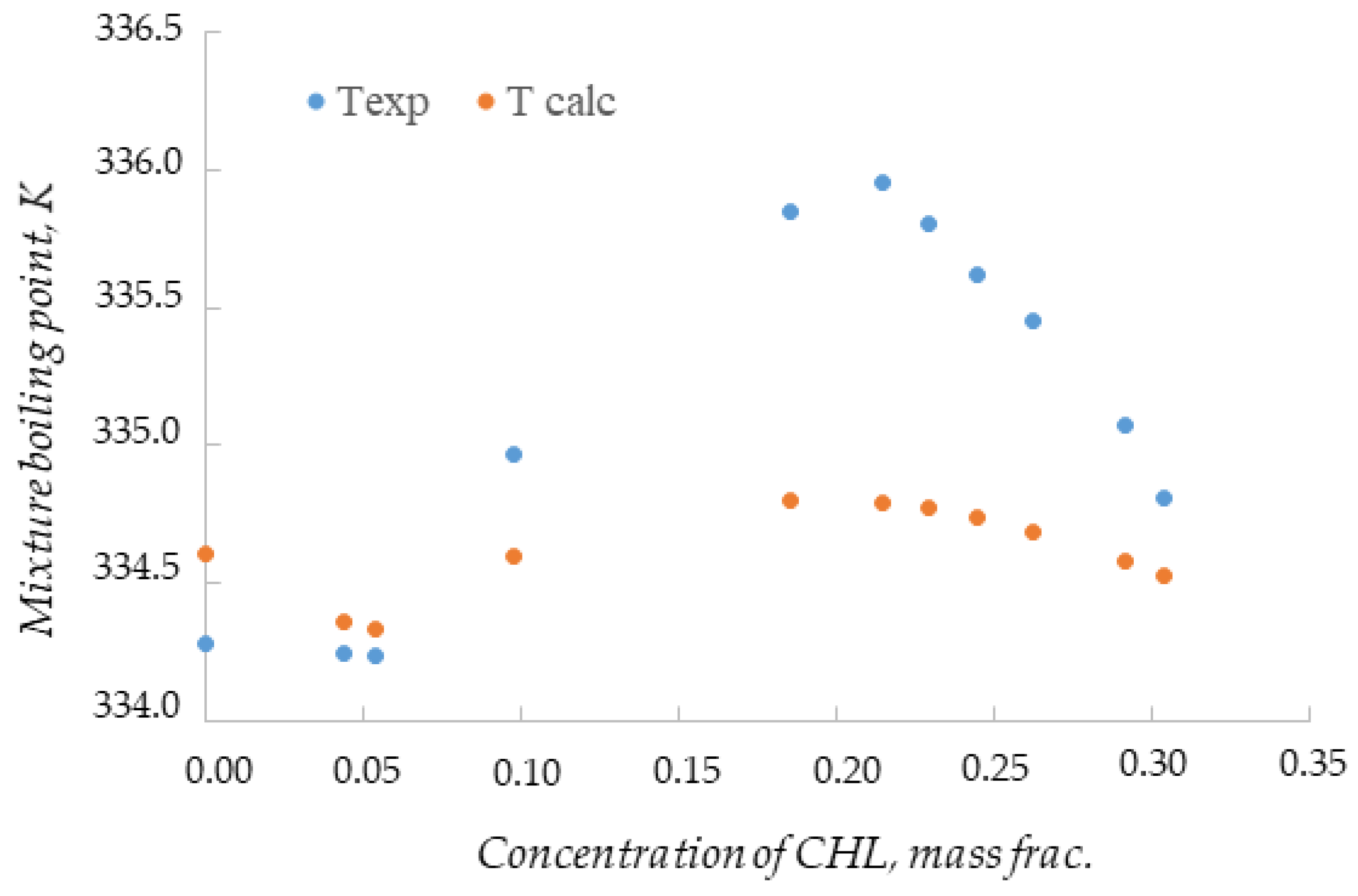
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Frolkova, A.V.; Ososkova, T.E.; Frolkova, A.K. Thermodynamic and topological analysis of phase diagrams of quaternary systems with internal singular points. Theor. Found. Chem. Eng. 2020, 54, 407–419. [Google Scholar] [CrossRef]
- Fernández, L.; Ortega, J.; Sosa, A. Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation. Thermo 2022, 2, 267–288. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilib. 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Frolkova, A.V.; Fertikova, V.G.; Rytova, E.V.; Frolkova, A.K. Evaluation of the adequacy of phase equilibria modeling based on various sets of experimental data. Fine Chem. Technol. 2021, 16, 457–464. [Google Scholar] [CrossRef]
- Kontogeorgis, G.M.; Folas, G.K. Activity Coefficient Models Part 2: Local Composition Models, from Wilson and NRTL to UNIQUAC and UNIFAC. In Thermodynamic Models for Industrial Applications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Korotkova, T.G. Parameters of the UNIQUAC model for describing the vapor-liquid phase equilibrium of D2-T2, D2-DT, DT-T2 hydrogen isotope mixtures. Fine Chem. Technol. 2022, 17, 459–472. [Google Scholar] [CrossRef]
- Zharov, V.T.; Serafimov, L.A. Physicochemical Foundations of Simple Distillation and Rectification; Chemistry Publishing, Co.: Lenningrad, Russia, 1975; 240p. (In Russian) [Google Scholar]
- Serafimov, L.A.; Frolkova, A.V.; Medvedev, D.V.; Semin, G.A. Determining the structure of the distillation line diagram from its geometric development for four-component mixtures. Theor. Found. Chem. Eng. 2012, 46, 120–127. [Google Scholar] [CrossRef]
- Serafimov, L.; Frolkova, A. Determination of vapor-liquid equilibrium diagrams of multicomponent systems. Chem. Pap. 2016, 70, 1578–1589. [Google Scholar] [CrossRef]
- Serafimov, L.A. Thermodynamic and topological analysis of heterogeneous equilibrium diagrams of multicomponent mixtures. Russ. J. Phys. Chem. A 2002, 76, 1211–1224. [Google Scholar]
- Serafimov, L.A. State of the art in the thermodynamic and topological analysis of phase diagrams. Theor. Found. Chem. Eng. 2009, 43, 268–278. [Google Scholar] [CrossRef]
- Frolkova, A.K.; Maevskii, M.A.; Oshanina, I.V.; Frolkova, A.V. Cyclohexanone: The main methods of obtaining and extracting target products from a reaction mixture. Theor. Found. Chem. Eng. 2018, 52, 653–660. [Google Scholar] [CrossRef]
- Temkin, O.N.; Bruk, L.G.; Zakharova, D.S.; Odintsov, K.Y.; Katsman, E.A.; Petrov, I.V.; Istomina, O.Y. Kinetics of cyclohexene oxidation by p-quinones in aqueous-organic solutions of cationic palladium (II) complexes. Kinet. Catal. 2010, 51, 691–703. [Google Scholar] [CrossRef]
- Hori, T.; Fujinaga, T. Analytical use of solvent extraction with acetonitrile/water/chloroform and 1-propanol/water/cyclohexane mixtures. Talanta 1985, 32, 735–743. [Google Scholar] [CrossRef]
- Zhu, Z.; Bai, W.; Qi, P.; Dai, Y.; Wang, Y.; Cui, P.; Gao, J. Liquid Liquid Equilibrium Data for the Separation of Acetone from n-Heptane Using Four Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2019, 64, 1202–1208. [Google Scholar] [CrossRef]
- Frolkova, A.V.; Balbenov, S.A.; Frolkova, A.K.; Akishina, A.A. Phase equilibrium in the system water–acetonitrile–cyclohexene–cyclohexanone. Russ. Chem. Bull. 2015, 64, 2330–2336. [Google Scholar] [CrossRef]
- Frolkova, A.V.; Zakharova, D.S.; Frolkova, A.K.; Balbenov, S.A. Liquid—Liquid and liquid—Liquid equilibrium for ternary system water—Acetonitrile—Cyclohexene at 298.15 K. Fluid Ph. Equilib. 2016, 408, 10–14. [Google Scholar] [CrossRef]
- Frenkel, M.; Chirico, R.D.; Diky, V.; Kazakov, A.F.; Muzny, C.D.; Magee, J.W.; Abdulagatov, I.; Kroenlein, K.; Kang, J.W. NIST Thermo Data Engine, NIST Standard Reference Database 103b-Pure Compounds, Binary Mixtures, and Chemical Reactions, Version 5.0; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Wang, B.; Ge, X.; Zheng, H.; Qiu, T.; Wu, Y. Liquid–liquid equilibrium for the system water + cyclohexene + cyclohexanol over the temperature range of (303.2 to 403.2) K. J. Chem. Eng. Data 2010, 55, 2529–2531. [Google Scholar] [CrossRef]
- Dadmohammadi, Y.; Gebreyohannes, S.; Neely, B.J.; Gasem, K.A.M. Application of Modified NRTL Models for Binary LLE Phase Characterization. Ind. Eng. Chem. Res. 2018, 57, 7282–7290. [Google Scholar] [CrossRef]
- Ogorodnikov, S.K.; Lesteva, T.M.; Kogan, V.B. Azeotropnye smesi. Spravochnik (Azeotropic Mixtures: A Handbook); Chemistry Publishing Co.: Lenningrad, Russia, 1971; 848p. (In Russian) [Google Scholar]
- Reinders, W.J.; de Minjer, C.H. Vapour-liquid equilibria in ternary systems. VI. the system water-acetone-chloroform. Recl. Trav. Chim. 1947, 66, 573–604. [Google Scholar] [CrossRef]
- Stephenson, R.M. Mutual solubilities: Water-ketones, water-ethers, and water-gasoline-alcohols. J. Chem. Eng. Data 1992, 37, 80–95. [Google Scholar] [CrossRef]
- Polak, J.; Lu, B.C.-Y. Mutual Solubilities of Hydrocarbons and Water at 0 and 25 °C. Can. J. Chem. 1973, 51, 4018–4023. [Google Scholar] [CrossRef]
- ALDRICH Chemistry (2012–2014); Sigma-Aldrich: St. Louis, MO, USA, 2011.
- Zhuchkov, V.I.; Frolkova, A.K.; Nazanskiy, S.L. Experimental research and mathematical modeling of vapor-liquid equilibrium in the ternary benzene—Hexafluorobenzene—Dimethyl sulfoxide system. Russ. Chem. Bull. 2018, 67, 200–205. [Google Scholar] [CrossRef]
- Zhuchkov, V.I.; Malyugin, A.A.; Frolkova, A.V.; Frolkova, A.K. Double ternary azeotrope in the benzene + perfluorobenzene + water system at 101 kPa. J. Chem. Eng. Data 2020, 65, 2002–2007. [Google Scholar] [CrossRef]
- Aucejo, A.; Monton, J.B.; Munoz, R.; Wisniak, J. Double azeotropy in the benzene+ hexafluorobenzene system. J. Chem. Eng. Data 1996, 41, 21–24. [Google Scholar] [CrossRef]
- Kao, C.-P.C.; Paulaitis, M.E.; Yokozeki, A. Double azeotropy in binary mixtures of NH3 and CHF2CF3. Fluid Ph. Equilib. 1997, 127, 191–203. [Google Scholar]

| Component/Azeotrope | Experimental Data | Calculated Data | The Relative Standard Uncertainty | |||
|---|---|---|---|---|---|---|
| X1 (X2), Mole Frac. | T, K | X1 (X2/X3), Mole Frac. | T, K | for X1 (X2) | for T | |
| ACN | 1.0000 | 354.75 | 1.0000 | 354.80 | - | 0.0001 |
| CHEN | 1.0000 | 356.15 | 1.0000 | 356.03 | - | 0.0003 |
| W | 1.0000 | 373.15 | 1.0000 | 373.15 | - | 0.000 |
| CHL | 1.0000 | 334.30 | 1.0000 | 334.25 | - | 0.0001 |
| ACN + W | 0.6810 | 349.35 | 0.6735 | 350.06 | 0.011 | 0.002 |
| ACN + CHEN | - | 339.55 | 0.4874 | 338.85 | - | 0.002 |
| CHEN + W | 0.6910 | 343.95 | 0.6822 | 343.90 | 0.013 | 0.0001 |
| CHL + W | 0.8397 | 329.23 | 0.8360 | 329.29 | 0.004 | 0.0002 |
| ACN + W + CHEN | - | 334.35 | 0.3461 (0.1960) | 334.61 | - | 0.0008 |
| ACN + CHEN + CHL | - | - | 0.3669 (0.3721) | 340.23 | - | - |
| ACN + W + CHEN + CHL | - | - | 0.2901 (0.1968/0.3571) | 334.61 | - | - |
| Chemicals (CAS Number) | Source | Purity, Mass Frac. | Density ρ, g·cm−3 | T, K | ||
|---|---|---|---|---|---|---|
| Exp. | Lit. [28] | Exp. | Lit. [28] | |||
| ACN (75-05-8) | Merck | ≥0.9900 | 0.7862 | 0.7860 | 354.61 | 354.15 |
| CHEN (110-83-8) | Merck | ≥0.9900 | 0.8114 | 0.8110 | 326.20 | 356.15 |
| W (7732-18-5) | - | 1.0000 | 0.9990 | 1.0000 | 373.12 | 373.15 |
| CHL (67-66-3) | Merck | >0.9900 | 1.4785 | 1.4800 | 334.39 | 334.65 |
| Singular Point | ACN | CHEN | W | CHL | CHL + W | ACN + CHEN | ACN + W |
|---|---|---|---|---|---|---|---|
| Type | Nst | Nst | Nst | S | Nunst | S | S |
| Poincaré index | +1 | +1 | +1 | 0 | –1 | 0 | –1 |
| Singular Point | CHEN + W | ACN + CHL + CHEN | ACN + CHEN + W | ACN + CHEN + W + CHL | |||
| Type | S | S | S | S | |||
| Poincaré index | –1 | –1 | +1 | +1 | |||
| The sum of Poincaré indexes is +2 | |||||||
| Mass CHL, g | Mixture Mass, g | Mixture Composition, Mass Frac. | Texp, K | Tcalc, K | ur | |||
|---|---|---|---|---|---|---|---|---|
| CHEN | ACN | W | CHL | |||||
| 0.0000 | 48.9263 | 0.6795 | 0.2568 | 0.0637 | 0.0000 | 334.28 | 334.61 | 0.0010 |
| 2.2357 | 51.1620 | 0.6498 | 0.2456 | 0.0609 | 0.0437 | 334.25 | 334.36 | 0.0003 |
| 2.7596 | 51.6859 | 0.6433 | 0.2431 | 0.0603 | 0.0534 | 334.24 | 334.33 | 0.0003 |
| 5.2943 | 54.2206 | 0.6132 | 0.2317 | 0.0574 | 0.0976 | 334.97 | 334.60 | 0.0011 |
| 11.1418 | 60.0681 | 0.5535 | 0.2092 | 0.0519 | 0.1855 | 335.85 | 334.80 | 0.0031 |
| 13.3445 | 62.2708 | 0.5339 | 0.2018 | 0.0500 | 0.2143 | 335.95 | 334.79 | 0.0035 |
| 14.5139 | 63.4402 | 0.5241 | 0.1981 | 0.0491 | 0.2288 | 335.80 | 334.77 | 0.0031 |
| 15.7888 | 64.7151 | 0.5137 | 0.1942 | 0.0481 | 0.2440 | 335.62 | 334.74 | 0.0026 |
| 17.4032 | 66.3295 | 0.5012 | 0.1894 | 0.0470 | 0.2624 | 335.45 | 334.69 | 0.0023 |
| 20.0747 | 69.0010 | 0.4818 | 0.1821 | 0.0451 | 0.2909 | 335.07 | 334.58 | 0.0015 |
| 21.3615 | 70.2878 | 0.4730 | 0.1788 | 0.0443 | 0.3039 | 334.81 | 334.53 | 0.0008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frolkova, A.; Zhuchkov, V.; Frolkova, A. Experimental Evidence for Double Quaternary Azeotropy’s Existence. Entropy 2023, 25, 980. https://doi.org/10.3390/e25070980
Frolkova A, Zhuchkov V, Frolkova A. Experimental Evidence for Double Quaternary Azeotropy’s Existence. Entropy. 2023; 25(7):980. https://doi.org/10.3390/e25070980
Chicago/Turabian StyleFrolkova, Anastasia, Valeriy Zhuchkov, and Alla Frolkova. 2023. "Experimental Evidence for Double Quaternary Azeotropy’s Existence" Entropy 25, no. 7: 980. https://doi.org/10.3390/e25070980
APA StyleFrolkova, A., Zhuchkov, V., & Frolkova, A. (2023). Experimental Evidence for Double Quaternary Azeotropy’s Existence. Entropy, 25(7), 980. https://doi.org/10.3390/e25070980







