Unveiling the Connectivity of Complex Networks Using Ordinal Transition Methods
Abstract
1. Introduction
2. Model and Methods
2.1. Model
2.2. Methods
2.2.1. Ordinal Permutation Entropy
2.2.2. Ordinal Transition Entropy
2.2.3. Synchronization Measures
3. Results
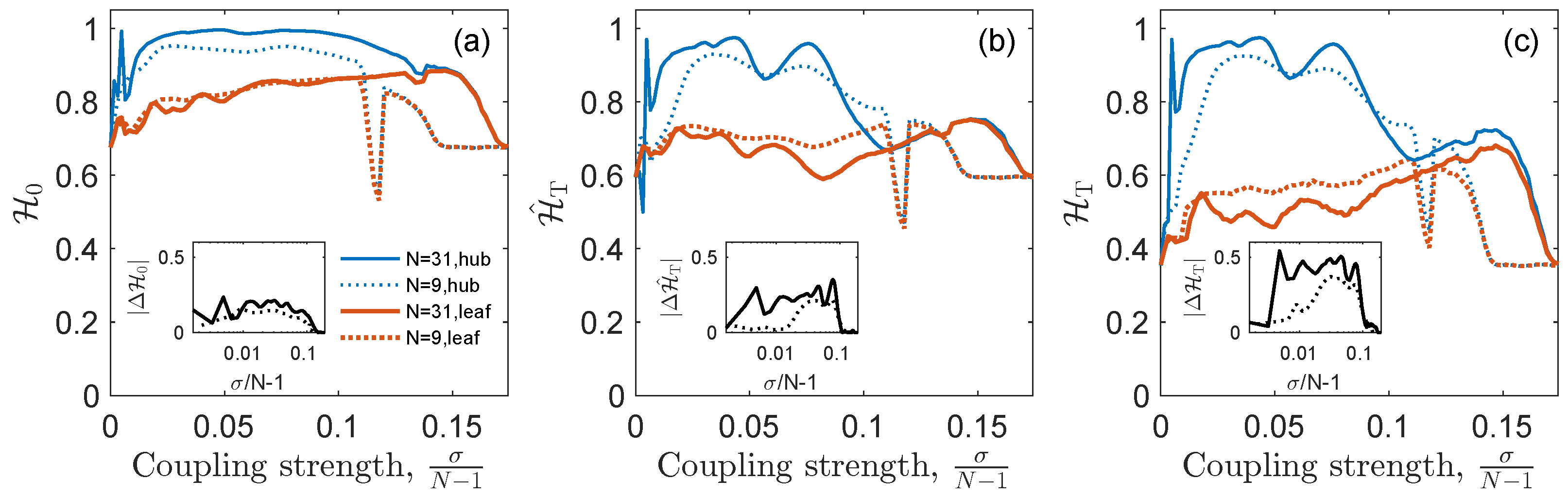
3.1. Star Network
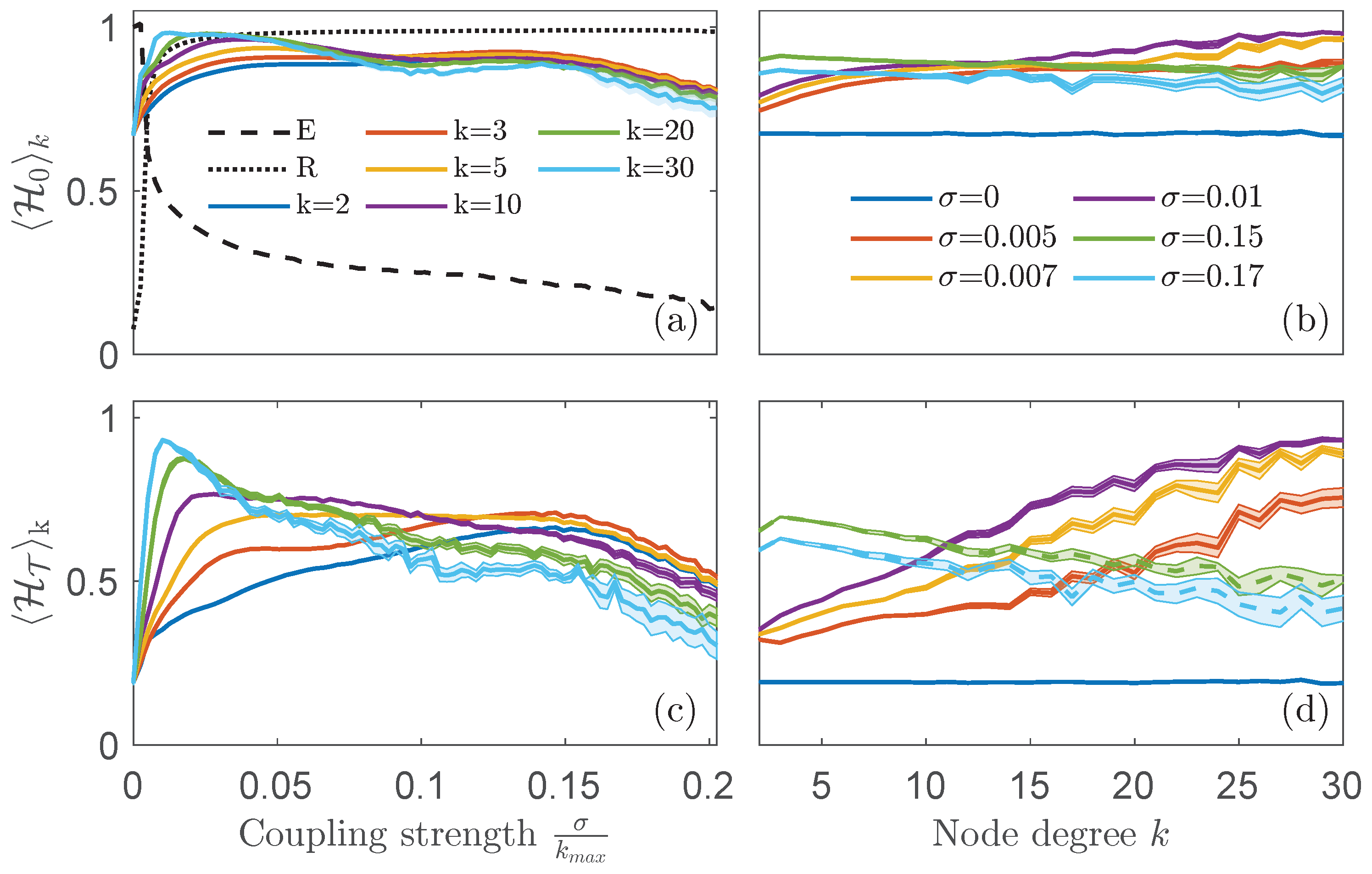
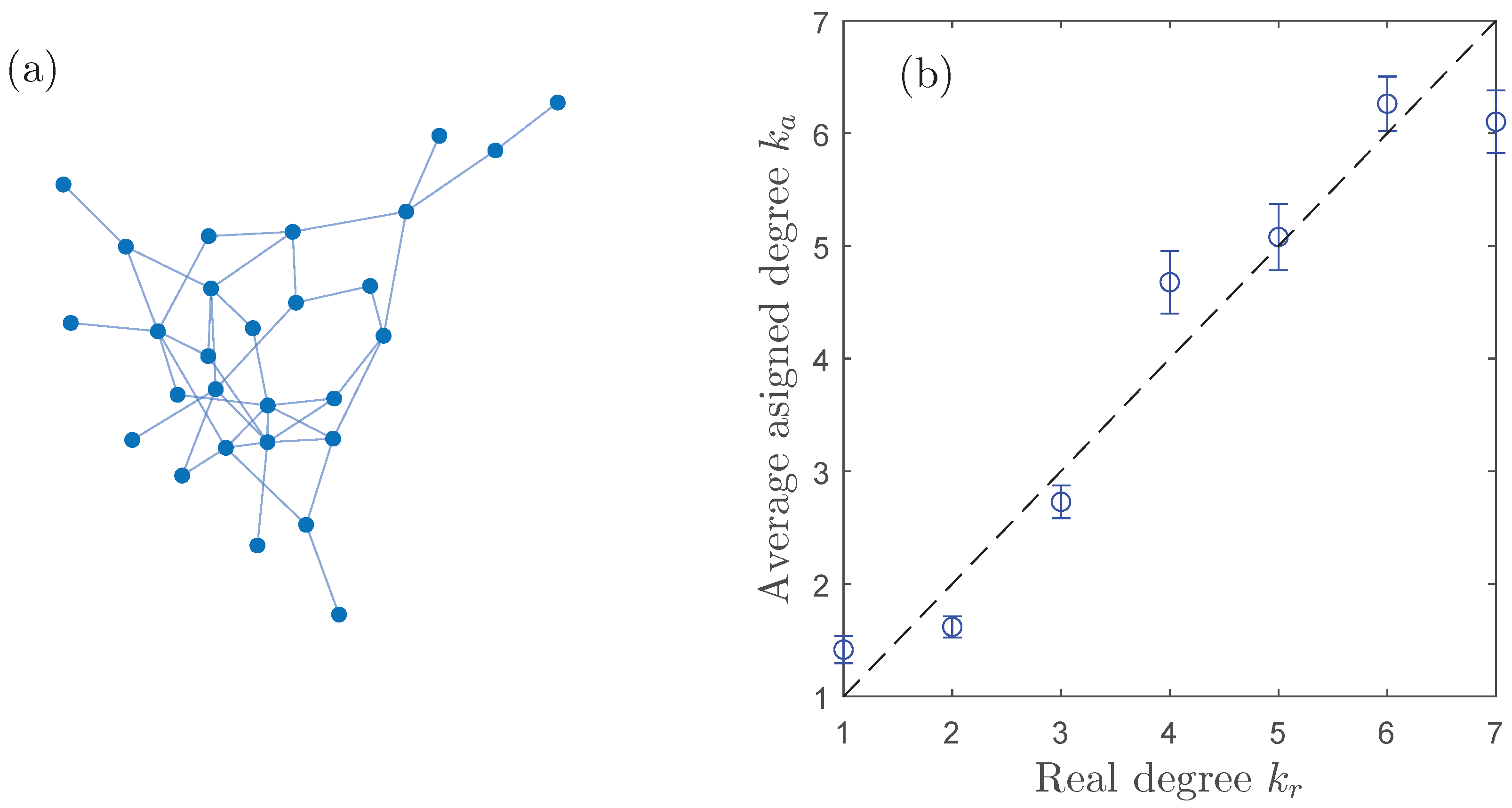
3.2. Scale-Free Network
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Leyva, I.; Martínez, J.H.; Masoller, C.; Rosso, O.A.; Zanin, M. 20 years of ordinal patterns: Perspectives and challenges. Europhys. Lett. 2022, 138, 31001. [Google Scholar] [CrossRef]
- Tlaie, A.; Ballesteros-Esteban, L.; Leyva, I.; Sendiña-Nadal, I. Statistical complexity and connectivity relationship in cultured neural networks. Chaos Solitons Fractals 2019, 119, 284–290. [Google Scholar] [CrossRef]
- Lehnertz, K. Ordinal methods for a characterization of evolving functional brain networks. Chaos 2023, 33, 022101. [Google Scholar] [CrossRef] [PubMed]
- Tiana-Alsina, J.; Quintero-Quiroz, C.; Masoller, C. Comparing the dynamics of periodically forced lasers and neurons. New J. Phys. 2019, 21, 103039. [Google Scholar] [CrossRef]
- Buldú, J.M.; Gómez, M.Á.; Herrera-Diestra, J.L.; Martínez, J.H. Nonlinear dynamics and networks in sports. Chaos Solitons Fractals 2021, 142, 110518. [Google Scholar] [CrossRef]
- Small, M. Complex networks from time series: Capturing dynamics. In Proceedings of the IEEE International Symposium on Circuits and Systems, Beijing, China, 19–23 May 2013; pp. 2509–2512. [Google Scholar] [CrossRef]
- Sun, X.; Small, M.; Zhao, Y.; Xue, X. Characterizing system dynamics with a weighted and directed network constructed from time series data. Chaos 2014, 24, 24402. [Google Scholar] [CrossRef]
- McCullough, M.; Small, M.; Stemler, T.; Ho, H.; Iu, C.; Iu, H.H.C. Time lagged ordinal partition networks for capturing dynamics of continuous dynamical systems. Chaos 2015, 25, 53101. [Google Scholar] [CrossRef]
- Pessa, A.A.; Ribeiro, H.V. Characterizing stochastic time series with ordinal networks. Phys. Rev. E 2019, 100, 42304. [Google Scholar] [CrossRef]
- Olivares, F.; Zanin, M.; Zunino, L.; Pérez, D.G. Contrasting chaotic with stochastic dynamics via ordinal transition networks. Chaos 2020, 30, 063101. [Google Scholar] [CrossRef]
- Borges, J.B.; Ramos, H.S.; Mini, R.A.; Rosso, O.A.; Frery, A.C.; Loureiro, A.A. Learning and distinguishing time series dynamics via ordinal patterns transition graphs. Appl. Math. Comput. 2019, 362, 124554. [Google Scholar] [CrossRef]
- Cardoso-Pereira, I.; Borges, J.B.; Barros, P.H.; Loureiro, A.F.; Rosso, O.A.; Ramos, H.S. Leveraging the self-transition probability of ordinal patterns transition network for transportation mode identification based on GPS data. Nonlinear Dyn. 2022, 107, 889–908. [Google Scholar] [CrossRef]
- Huang, M.; Sun, Z.; Donner, R.V.; Zhang, J.; Guan, S.; Zou, Y. Characterizing dynamical transitions by statistical complexity measures based on ordinal pattern transition networks. Chaos 2021, 31, 33127. [Google Scholar] [CrossRef]
- Varley, T.F.; Denny, V.; Sporns, O.; Patania, A. Topological analysis of differential effects of ketamine and propofol anaesthesia on brain dynamics. R. Soc. Open Sci. 2021, 8, 201971. [Google Scholar] [CrossRef] [PubMed]
- Kulp, C.W.; Chobot, J.M.; Freitas, H.R.; Sprechini, G.D. Using ordinal partition transition networks to analyze ECG data. Chaos 2016, 26, 073114. [Google Scholar] [CrossRef]
- Wang, X.; Han, X.; Chen, Z.; Bi, Q.; Guan, S.; Zou, Y. Multi-scale transition network approaches for nonlinear time series analysis. Chaos Solitons Fractals 2022, 159, 112026. [Google Scholar] [CrossRef]
- Peng, K.; Shang, P. Characterizing ordinal network of time series based on complexity-entropy curve. Pattern Recognit. 2022, 124, 108464. [Google Scholar] [CrossRef]
- Nicolis, G.; Cantú, A.G.; Nicolis, C. Dynamical aspects of interaction networks. Int. J. Bifurc. Chaos 2005, 15, 3467–3480. [Google Scholar] [CrossRef]
- Zhang, J.; Small, M. Complex Network from Pseudoperiodic Time Series: Topology versus Dynamics. Phys. Rev. Lett. 2006, 96, 238701. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuño, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Silva, V.F.; Silva, M.E.; Ribeiro, P.; Silva, F. Time series analysis via network science: Concepts and algorithms. WIREs Data Min. Knowl. Discov. 2021, 11, e1404. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.; Tang, M.; Guo, H.; Small, M.; Zou, Y. Constructing ordinal partition transition networks from multivariate time series. Sci. Rep. 2017, 7, 7795. [Google Scholar] [CrossRef] [PubMed]
- Shahriari, Z.; Small, M. Permutation Entropy of State Transition Networks to Detect Synchronization. Int. J. Bifurc. Chaos 2020, 30, 2050154. [Google Scholar] [CrossRef]
- Subramaniyam, N.P.; Donner, R.V.; Caron, D.; Panuccio, G.; Hyttinen, J. Causal coupling inference from multivariate time series based on ordinal partition transition networks. Nonlinear Dyn. 2021, 105, 555–578. [Google Scholar] [CrossRef]
- Ruan, Y.; Donner, R.V.; Guan, S.; Zou, Y. Ordinal partition transition network based complexity measures for inferring coupling direction and delay from time series. Chaos 2019, 29, 043111. [Google Scholar] [CrossRef]
- Ren, H.; Yuan, Q.; Semba, S.; Weng, T.; Gu, C.; Yang, H. Pattern interdependent network of cross-correlation in multivariate time series. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2020, 384, 126781. [Google Scholar] [CrossRef]
- Echegoyen, I.; Vera-Ávila, V.; Sevilla-Escoboza, R.; Martínez, J.H.; Buldú, J.M. Ordinal synchronization: Using ordinal patterns to capture interdependencies between time series. Chaos Solitons Fractals 2019, 119, 8–18. [Google Scholar] [CrossRef]
- Tlaie, A.; Leyva, I.; Sevilla-Escoboza, R.; Vera-Avila, V.P.; Sendiña Nadal, I. Dynamical complexity as a proxy for the network degree distribution. Phys. Rev. E 2019, 99, 012310. [Google Scholar] [CrossRef]
- Letellier, C.; Leyva, I.; Sendiña Nadal, I. Dynamical complexity measure to distinguish organized from disorganized dynamics. Phys. Rev. E 2020, 101, 022204. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Gómez-Gardeñes, J.; Moreno, Y.; Arenas, A. Synchronizability determined by coupling strengths and topology on complex networks. Phys. Rev. E 2007, 75, 066106. [Google Scholar] [CrossRef] [PubMed]
- Shahriari, Z.; Algar, S.D.; Walker, D.M.; Small, M. Ordinal Poincaré sections: Reconstructing the first return map from an ordinal segmentation of time series. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 053109. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. True and false forbidden patterns in deterministic and random dynamics. Europhys. Lett. 2007, 79, 50001. [Google Scholar] [CrossRef]
- Masoller, C.; Hong, Y.; Ayad, S.; Gustave, F.; Barland, S.; Pons, A.J.; Gómez, S.; Arenas, A. Quantifying sudden changes in dynamical systems using symbolic networks. New J. Phys. 2015, 17, 023068. [Google Scholar] [CrossRef]
- McCullough, M.; Small, M.; Iu, H.H.C.; Stemler, T. Multiscale ordinal network analysis of human cardiac dynamics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160292. [Google Scholar] [CrossRef]
- Unakafov, A.M.; Keller, K. Conditional entropy of ordinal patterns. Phys. D Nonlinear Phenom. 2014, 269, 94–102. [Google Scholar] [CrossRef]
- Zanin, M.; Olivares, F. Ordinal patterns-based methodologies for distinguishing chaos from noise in discrete time series. Commun. Phys. 2021, 4, 190. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Zhou, C.; Kurths, J. Hierarchical synchronization in complex networks with heterogeneous degrees. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 015104. [Google Scholar] [CrossRef] [PubMed]
- Pereira, T. Hub synchronization in scale-free networks. Phys. Rev. E 2010, 82, 036201. [Google Scholar] [CrossRef] [PubMed]
- Vera-Ávila, V.; Sevilla-Escoboza, R.; Lozano-Sánchez, A.; Rivera-Durón, R.; Buldú, J.M. Experimental datasets of networks of nonlinear oscillators: Structure and dynamics during the path to synchronization. Data Brief 2020, 28, 105012. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almendral, J.A.; Leyva, I.; Sendiña-Nadal, I. Unveiling the Connectivity of Complex Networks Using Ordinal Transition Methods. Entropy 2023, 25, 1079. https://doi.org/10.3390/e25071079
Almendral JA, Leyva I, Sendiña-Nadal I. Unveiling the Connectivity of Complex Networks Using Ordinal Transition Methods. Entropy. 2023; 25(7):1079. https://doi.org/10.3390/e25071079
Chicago/Turabian StyleAlmendral, Juan A., I. Leyva, and Irene Sendiña-Nadal. 2023. "Unveiling the Connectivity of Complex Networks Using Ordinal Transition Methods" Entropy 25, no. 7: 1079. https://doi.org/10.3390/e25071079
APA StyleAlmendral, J. A., Leyva, I., & Sendiña-Nadal, I. (2023). Unveiling the Connectivity of Complex Networks Using Ordinal Transition Methods. Entropy, 25(7), 1079. https://doi.org/10.3390/e25071079







