Predicting the Popularity of Information on Social Platforms without Underlying Network Structure
Abstract
1. Introduction
2. Materials and Methods
2.1. Empirical Data Analysis
2.2. The Activation-Decay Model
2.2.1. The Hill Equation and BiHill Equation
2.2.2. The Activation-Decay Model
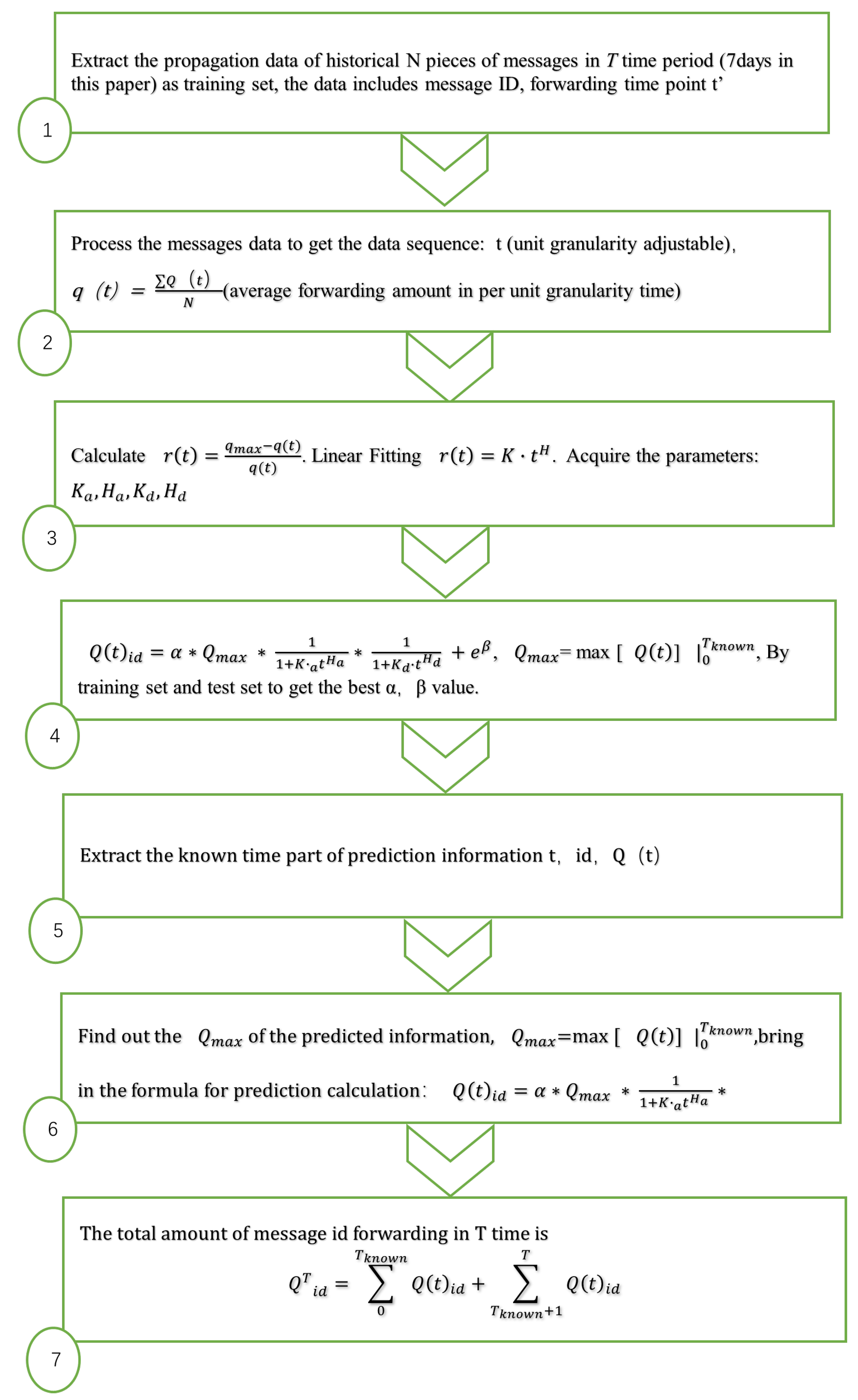
2.2.3. The Algorithm for Popularity Prediction Based on Activation-Decay Model
- Step 1
- Gaining model parameters from historical data sets, , as shown in Figure 2 ①–③:
- (1)
- Taking the time of each message generation as the zero time, obtain the forward amount in every unit time (unit granularity adjustable). Process N messages’ forward amount in T period into data sequence, t, , .
- (2)
- Calculate the average amount of these N messages in T period time , which yields date sequence t, .
- (3)
- Step 2
- Obtaining best parameters, and , by training set and test set, as shown in Figure 2 ④.
- (1)
- The training set data are divided into two parts, with the known maximum time (which can be set by oneself): the part is the known information set, and the part is the information set for prediction. e.g., if the information propagation data of 10 min is known, i.e., the data within 0–10 min are available, and the rest is a test set.
- (2)
- Find out the , calculate the total propagation amount of each message from Equation (11). The calculated value of the propagation amount of each message is compared with the actual propagation amount and calculates the average absolute error . When is minimum, the parameters and are the optimal parameters.
- Step 3
- Put the Related parameters () into the AD algorithm to predict the propagation quantity of the information to be predicted, as shown in Figure 2 ⑤–⑦.
2.3. Evaluation Metrics for the Prediction Algorithm
2.3.1. APE and MAPE
2.3.2. TIC
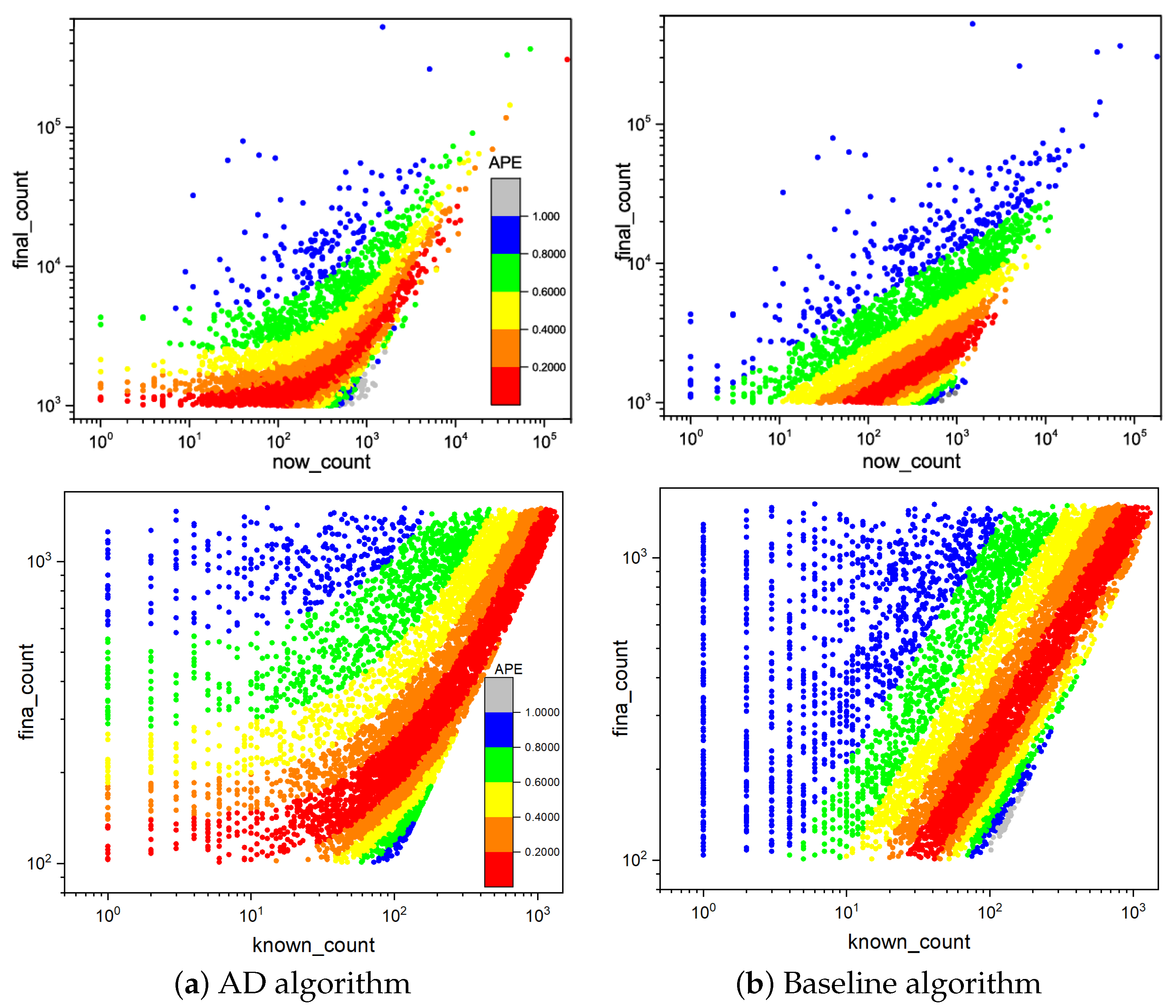
2.4. Baseline Algorithm
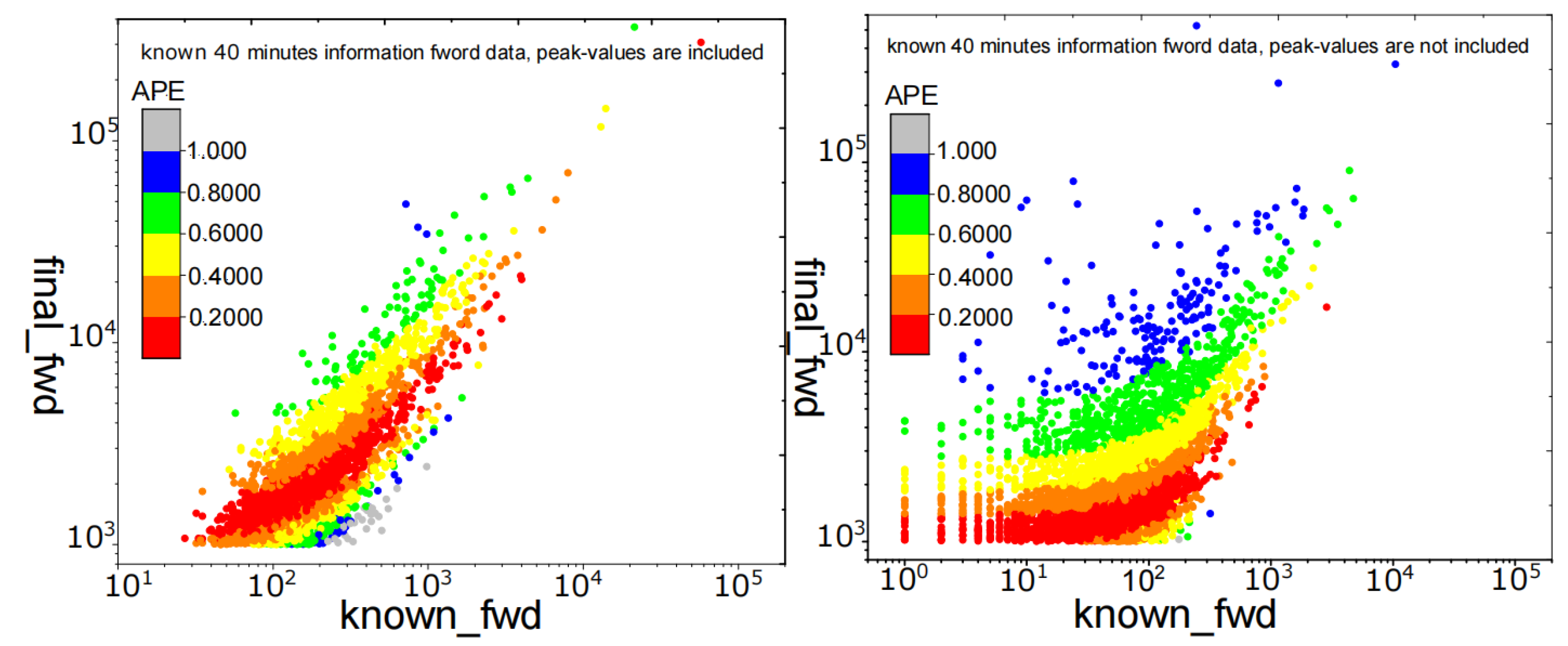
3. Experimental Results
3.1. Prediction of the Popularity of Information
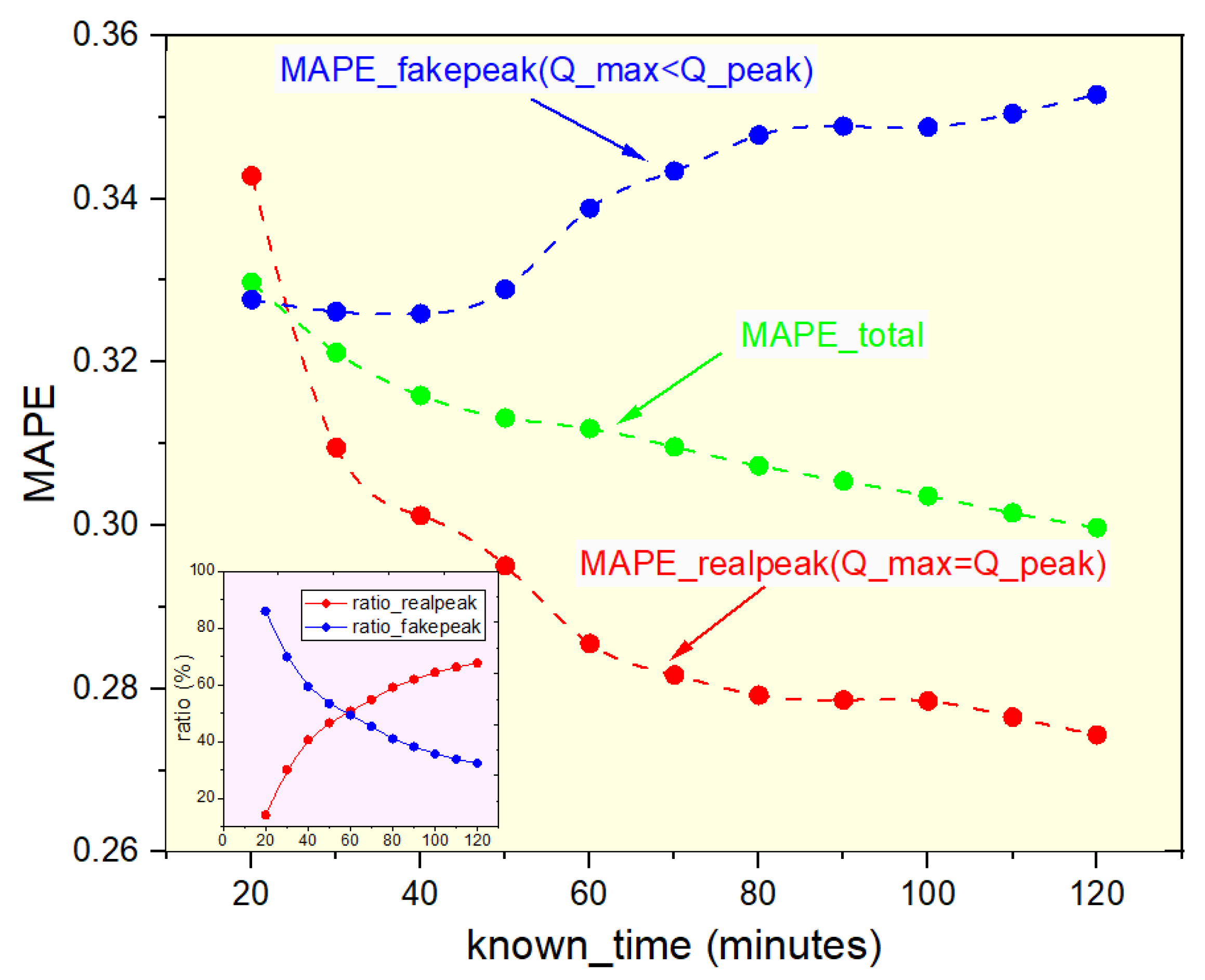
3.2. Determine the Peak
Peak Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Brady, W.J.; McLoughlin, K.; Doan, T.N.; Crockett, M.J. How social learning amplifies moral outrage expression in online social networks. Sci. Adv. 2021, 7, eabe5641. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, J.; Xu, K. Weak ties: Subtle role of information diffusion in online social networks. Phys. Rev. E 2010, 82, 016105. [Google Scholar] [CrossRef]
- Lazer, D.; Pentland, A.; Adamic, L.; Aral, S.; Barabási, A.L.; Brewer, D.; Christakis, N.; Contractor, N.; Fowler, J.; Gutmann, M.; et al. Life in the network: The coming age of computational social science. Science 2009, 323, 721–723. [Google Scholar] [CrossRef]
- Freelon, D.; Marwick, A.; Kreiss, D. False equivalencies: Online activism from left to right. Science 2020, 369, 1197–1201. [Google Scholar] [CrossRef] [PubMed]
- Wasserman, S. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Aggarwal, C.C. An introduction to social network data analytics. In Social Network Data Analytics; Springer: New York, NY, USA, 2011; pp. 1–15. [Google Scholar]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- Brockmann, D.; Helbing, D. The hidden geometry of complex, network-driven contagion phenomena. Science 2013, 342, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Giles, J. Making the links. Nature 2012, 488, 448–450. [Google Scholar] [CrossRef] [PubMed]
- Conte, R.; Gilbert, N.; Bonelli, G.; Cioffi-Revilla, C.; Deffuant, G.; Kertesz, J.; Loreto, V.; Moat, S.; Nadal, J.P.; Sanchez, A.; et al. Manifesto of computational social science. Eur. Phys. J. Spec. Top. 2012, 214, 325–346. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Szabo, G.; Huberman, B.A. Predicting the popularity of online content. Commun. ACM 2010, 53, 80–88. [Google Scholar] [CrossRef]
- Cheng, J.; Adamic, L.; Dow, P.A.; Kleinberg, J.M.; Leskovec, J. Can cascades be predicted? In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Republic of Korea, 7–11 April 2014; pp. 925–936. [Google Scholar]
- Liao, D.; Xu, J.; Li, G.; Huang, W.; Liu, W.; Li, J. Popularity prediction on online articles with deep fusion of temporal process and content features. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 200–207. [Google Scholar]
- Chen, X.; Zhou, F.; Zhang, K.; Trajcevski, G.; Zhong, T.; Zhang, F. Information diffusion prediction via recurrent cascades convolution. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 770–781. [Google Scholar]
- Zhou, F.; Xu, X.; Trajcevski, G.; Zhang, K. A survey of information cascade analysis: Models, predictions, and recent advances. ACM Comput. Surv. (CSUR) 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Yu, L.; Liu, C.; Zhang, Z.K. Multi-linear interactive matrix factorization. Knowl.-Based Syst. 2015, 85, 307–315. [Google Scholar] [CrossRef]
- Yu, L.; Huang, J.; Zhou, G.; Liu, C.; Zhang, Z.K. TIIREC: A tensor approach for tag-driven item recommendation with sparse user generated content. Inf. Sci. 2017, 411, 122–135. [Google Scholar] [CrossRef]
- Prasse, B.; Mieghem, P.V. Predicting network dynamics without requiring the knowledge of the interaction graph. Proc. Natl. Acad. Sci. USA 2022, 119, e2205517119. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Erdogdu, M.A.; He, H.Y.; Rajaraman, A.; Leskovec, J. SEISMIC: A self-exciting point process model for predicting tweet popularity. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1513–1522. [Google Scholar]
- Bao, P.; Shen, H.W.; Huang, J.; Cheng, X.Q. Popularity prediction in microblogging network: A case study on sina weibo. In Proceedings of the 22nd International Conference on World Wide Web (WWW’13 Companion), Rio de Janeiro, Brazil, 13–17 May 2013; ACM: New York, NY, USA, 2013; pp. 177–178. [Google Scholar]
- Gao, S.; Ma, J.; Chen, Z. Modeling and predicting retweeting dynamics on microblogging platforms. In Proceedings of the Eighth ACM International Conference on Web Search and Data Mining, Shanghai, China, 2–6 February 2015; pp. 107–116. [Google Scholar]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Gao, J.; Shen, H.; Liu, S.; Cheng, X. Modeling and predicting retweeting dynamics via a mixture process. In Proceedings of the 25th International Conference Companion on World Wide Web, Montreal, QC, Canada, 11–15 April 2016; International World Wide Web Conferences Steering Committee: Geneva, Switzerland, 2016; pp. 33–34. [Google Scholar]
- Yu, H.; Hu, Y.; Shi, P. A prediction method of peak time popularity based on Twitter hashtags. IEEE Access 2020, 8, 61453–61461. [Google Scholar] [CrossRef]
- Wu, B.; Cheng, W.H.; Liu, P.; Liu, B.; Zeng, Z.; Luo, J. Smp challenge: An overview of social media prediction challenge 2019. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2667–2671. [Google Scholar]
- Zhang, X.; Aravamudan, A.; Anagnostopoulos, G.C. Anytime Information Cascade Popularity Prediction via Self-Exciting Processes. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 26028–26047. [Google Scholar]
- Wang, J.; Jiang, W.; Li, K.; Wang, G.; Li, K. Incremental group-level popularity prediction in online social networks. ACM Trans. Internet Technol. (TOIT) 2021, 22, 1–26. [Google Scholar] [CrossRef]
- Chen, T.; Guo, J.; Wu, W. Graph representation learning for popularity prediction problem: A survey. arXiv 2022, arXiv:2203.07632. [Google Scholar] [CrossRef]
- Hill, A.V. The possible effects of the aggregation of the molecules of hæmoglobin on its dissociation curves. J. Physiol. 1910, 40, i–vii. [Google Scholar]
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill equation: A review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 2008, 22, 633–648. [Google Scholar] [CrossRef] [PubMed]
- Frank, S.A. Input-output relations in biological systems: Measurement, information and the Hill equation. Biol. Direct 2013, 8, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.; Lehninger, A.; Cox, M. Lehninger Principles of Biochemistry; W. H. Freeman: New York, NY, USA, 2008. [Google Scholar]
- He, X.; Gao, M.; Kan, M.Y.; Liu, Y.; Sugiyama, K. Predicting the popularity of web 2.0 items based on user comments. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Madrid, Spain, 11–15 July 2014; pp. 233–242. [Google Scholar]
- Bandari, R.; Asur, S.; Huberman, B. The pulse of news in social media: Forecasting popularity. In Proceedings of the International AAAI Conference on Web and Social Media, Dublin, Ireland, 4–7 June 2012; Volume 6, pp. 26–33. [Google Scholar]
- Kupavskii, A.; Ostroumova, L.; Umnov, A.; Usachev, S.; Serdyukov, P.; Gusev, G.; Kustarev, A. Prediction of retweet cascade size over time. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 2335–2338. [Google Scholar]
- Li, H.; Ma, X.; Wang, F.; Liu, J.; Xu, K. On popularity prediction of videos shared in online social networks. In Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 169–178. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Yi, L.; Ren, X.-L.; Lü, L. Predicting the Popularity of Information on Social Platforms without Underlying Network Structure. Entropy 2023, 25, 916. https://doi.org/10.3390/e25060916
Wu L, Yi L, Ren X-L, Lü L. Predicting the Popularity of Information on Social Platforms without Underlying Network Structure. Entropy. 2023; 25(6):916. https://doi.org/10.3390/e25060916
Chicago/Turabian StyleWu, Leilei, Lingling Yi, Xiao-Long Ren, and Linyuan Lü. 2023. "Predicting the Popularity of Information on Social Platforms without Underlying Network Structure" Entropy 25, no. 6: 916. https://doi.org/10.3390/e25060916
APA StyleWu, L., Yi, L., Ren, X.-L., & Lü, L. (2023). Predicting the Popularity of Information on Social Platforms without Underlying Network Structure. Entropy, 25(6), 916. https://doi.org/10.3390/e25060916






