Abstract
There are mostly semi-honest agents in cloud computing, so agents may perform unreliable calculations during the actual execution process. In this paper, an attribute-based verifiable conditional proxy re-encryption (AB-VCPRE) scheme using a homomorphic signature is proposed to solve the problem that the current attribute-based conditional proxy re-encryption (AB-CPRE) algorithm cannot detect the illegal behavior of the agent. The scheme implements robustness, that is the re-encryption ciphertext, can be verified by the verification server, showing that the received ciphertext is correctly converted by the agent from the original ciphertext, thus, meaning that illegal activities of agents can be effectively detected. In addition, the article demonstrates the reliability of the constructed AB-VCPRE scheme validation in the standard model, and proves that the scheme satisfies CPA security in the selective security model based on the learning with errors (LWE) assumption.
1. Introduction
As a new resource sharing in the field of information, cloud computing is constantly changing people’s lives. As an important technology in cloud computing, cloud storage is used to organize a series of different types of network storage devices to facilitate data sharing. To ensure the confidentiality of data, before being uploaded to a cloud server, user data are encrypted, however, this poses difficulties in sharing data between different users. When dealing with a significant quantity of data recipients, general encryption algorithms can significantly increase the computational and communication expenses incurred by the data owner. Proxy re-encryption (PRE) effectively solves this problem.
In 1998, Blaze et al. [1] first introduced the concept of PRE at the Euromonitor Conference. PRE is a data cipher conversion in cloud computing, which ensures both user data security and flexible access and sharing of data. However, in the traditional PRE system, it is usually one delegator that corresponds to another delegator, that is, a one-to-one model; this implies that only one client’s message can be re-encrypted at a time, necessitating a large amount of communication overhead and computation expense, which is contrary to the initial aim of cloud computing customers wanting to save money. In 2007, GREEN et al. [2] simplified the public key certificate authentication process by proposing an encryption scheme based on user identity information instead of a public key. However, the encryption process is specific to particular users and requires explicit information about the recipient. In 2009, JIAN et al. [3] suggested a strategy for conditional PRE (CPRE) based on identity proxy re-encryption. By designing a conditional ciphertext conversion method, the ciphertext can only be converted when the ciphertext meets the set conditions, enabling the assignment of partial decryption rights, but it is still in the form of a one-to-one assignment between the authorizer and the authorized person, which not only severely restricts users’ ability to selectively share data with other users at a fine-grained level, but it also has the problems of high communication costs and high computational overhead when a large number of users need to access that shared data, as well as wasting a large amount of local memory space to hold a large number of decryption keys.
Being a novel cryptographic technique that differs from conventional public key cryptography, attribute-based encryption (ABE) [4] is ideally suited for resolving data confidentiality protection and access control of ciphertext problems in cloud storage applications [5]. ABE technology can provide an effective one-to-many, fine-grained ciphertext access control solution for cloud storage data security. AB-CPRE schemes have been presented that demonstrate the advantages and properties of ABE and CPRE. However, the existing AB-PRE schemes and AB-CPRE schemes are mostly based on constructs such as linear mappings or discrete logarithmic puzzles [6,7]. Due to the advent of quantum computers, the security of traditional number theory puzzles is threatened and these schemes will become insecure. To solve this problem, a lattice cipher is proposed. It is believed that lattice-based cryptography can resist quantum attacks and has high computational efficiency. Therefore, lattice-based public key cryptography schemes have attracted wide attention in recent years.
However, all the AB-CPRE schemes [8,9,10] that are currently in use are semi-trusted agents, so they may perform unreliable calculations, which bring security problems to data sharing. Most AB-CPRE efforts focus on data privacy and access control without considering re-encryption authentication, which can lead to incorrect results for users.
Therefore, it is of interest to ensure that the re-encryption ciphertext is converted correctly from the original ciphertext. In a homomorphic encryption algorithm, the user can perform some kind of secure proxy calculation with the untrusted remote server. In this process, the server cannot see any private information. The homomorphic signature algorithm supports the signature operation consistent with the message, and the generated signature does not disclose any information related to the data set, which can meet the security requirements in the cloud environment, and is very suitable for the sensor network, network coding, and other message operation scenarios to ensure information security. This paper introduces homomorphic signature techniques in AB-CPRE, provides a verification mechanism for re-encryption performed by a verification server, and proposes a verifiable PRE scheme.
Our main contributions in this article are as follows:
- An AB-VCPRE scheme based on LWE is proposed. The scheme ensures by verification that the re-encryption ciphertext is correctly converted from the encryption ciphertext;
- Fine-grained access control is implemented. In combination with fully homomorphic encryption, the delegation policy supports any polynomial-depth boolean circuit;
- Robustness is achieved. The scheme uses a validation algorithm to achieve robustness. Forged or incorrectly shared ciphertexts can be detected by validating the re-encryption ciphertext with a validation server;
- The scheme satisfies CPA security. The ciphertext in our scheme needs to be signed and verified using an unforgeable homomorphic signature. This paper demonstrates that the constructed AB-VCPRE scheme is CPA security based on a LWE problem.
The rest of the paper is organized into seven sections. In Section 2, the related studies are described. In Section 3, the relevant definitions are introduced. In Section 4 and Section 5, we state the details of the scheme and the security analysis. Section 6 presents the efficiency analysis. The last section is a summary of the paper.
2. Related Work
Liang et al. [7] present an AB-PRE cryptographic primitive based on the augmented decisional bilinear Diffie–Hellman (DBDH) problem combining ABE and PRE for the first time, which empowers users to authorize in an access control environment. Li et al. [11] propose a proxy re-encryption scheme for a re-splitable threshold multi-agent, which is different from the encryption scheme on the ciphertext input and output plane and the re-encryption surface, which means the noise boundary has a wider range of choices and can ensure the security of the re-encryption key. Nunez et al. [12] propose a typical threshold proxy re-encryption scheme, which is based on a DBDH assumption, vulnerable to quantum attacks. Luo et al. [13] construct a standard lattice multi-hop AB-PRE scheme, which supports circuit access, has a short key, the key size is dependent on the depth of the circuit policy, and satisfies CPA security requirements based on the LWE problem in the selection security model. However, these PRE schemes may not show sufficient flexibility and practicality when the data owner wishes to select some but not all of the data for dissemination to certain users. Weng et al. [3] proposed a CPRE scheme where only those that satisfy the conditions can be re-encrypted, but it can only be applied to simple keyword-based conditions and will be limited in practical applications. Then, Yang et al. [8] propose a ciphertext policy-based AB-CPRE scheme, which supports a fine-grained decryption delegation. The ciphertext in the scheme is related to the access policy while the re-encryption key is related to the attributes, and the ciphertext can be re-encrypted only when the access policy satisfies the attributes. Huang et al. [14] propose PRECISE, which combines AB-CPRE with IBBE to support fine-grained re-encryption conditions for IBBE ciphertexts. Yao et al. [15] combine ciphertext authorization, key update, and ciphertext evolution to propose an improved revocable, identity-based ciphertext evolution conditional proxy re-encryption scheme for secure and efficient cloud data sharing.
The universal CPRE algorithm cannot ensure the cloud server’s integrity during the re-encryption procedure, while the homomorphic signature algorithm has unforgettable security and privacy, which can effectively verify the honesty of the proxy during the re-encryption. Therefore, this paper uses a homomorphic signature algorithm to propose a PRE scheme with encryption validating on the lattice, which can effectively detect the illegal behavior of the proxy and provide a guarantee for the safe sharing of data.
3. Preliminaries
3.1. Lattice
Definition 1 (lattice).
The lattice is a linear combination of group ’s linearly independent vectors’ integer coefficients in m-dimensional Euclidean space , which is defined as:
Lemma 1
([16]). Take integer , , , there exists a algorithm that generates a matrix and a trapdoor for the lattice , i.e., there is , such that the distribution statistics satisfied by the matrix are close to a uniform distribution on , and holds by an absolute margin.
Lemma 2
([17]). Let and . Select three uniform matrices , , and at random for some polynomials with . Distribution and are statistically indistinguishable for any vector .
LWE is a difficult problem under lattice. Regev [18] first proposed this in 2005 and proved that the average case is just as difficult to solve for several standard cells.
Definition 2 (LWE).
Given positive integer , integer and , choosing uniform random matrix and vector , vector follows the error distribution. Given , the LWE problem is to find with non-negligible probability.
Definition 3 (Small integer solutions problem, SIS).
Let the defining parameters be , is a prime number, given positive integers and , select a matrix at random, solve for a non-zero vector of integers with . In 1996, Ajtai presented the SIS problem in the literature [16]. The homomorphic signature used for robustness in the paper is based on the SIS problem.
3.2. Related Functions and Tools
3.2.1. Functions of Bits and Power2
According to the article [19], decomposing the vector into the form of an inner product can effectively control the error range of the vector. The following describes how to decompose vectors into bit representations.
For any , let , . Output vector , where . For any , where is a column vector, output matrix
It can be verified that for any , there is .
3.2.2. Discrete Gaussian Distribution
For integer vectors , , the discrete Gaussian distribution on the m-dimensional lattice is:
Lemma 3
([17]). Let , is a matrix over and . Let is the base of , . For , there are:
- Set the rank of is , , , . Let , PPT algorithms , where is the base of , output a short base statistical distribution to ;
- : There is trapdoor of lattice , the real number , for any vector , a PPT algorithm capable of generating a vector from a distribution that is statistically close to , satisfying ;
- Let the rank of be , , a low-dimensional matrix , a trapdoor for the lattice , and . PPT algorithm output a short base with a statistical distribution close to .
3.3. Key Homomorphism
By embedding algorithmic circuits in LWE matrices, Boneh et al. suggested an ABE approach for algorithmic circuits in their paper [20], and the method was used in many LWE-based structures, for example, predicate encryption [21], constraint PRFs [22], watermarks for PRFs [23], etc.
Definition 4.
For any positive integer , , a of boolean circuit, defining families of functions .
Lemma 4
(Fully homomorphic encryption [20,24]). Given parameters , where is a B-bounded noise distribution, is a security parameter, . For any matrices , any boolean circuit for any depth, , matrix , vector , for , if ,
- : Taking a circuit , matrices as input, outputs a matrix ;
- : Given a circuit , matrices , a vector and vectors , outputs a vector , satisfying , where , with all but negligible probability;
- : On input a circuit , a vector , matrices , a matrix , outputs a matrix satisfying , where with all but negligible probability.
3.4. Homomorphic Signature
A homomorphic signature is a valid signature that permits any entity to conduct a sequence of operations on the original message and its signature without the signing private key.
Definition 5 (Homomorphic signature).
The probabilistic polynomial-time algorithm is included in the following tuple is the homomorphic signature (HS) scheme:
- : Take a safety parameter , a circuit depth , and a message length as input, output a signature private key and a verification key ;
- : Accept as inputs the message requiring signature and , output the signature ;
- : Take an evaluation circuit and signature as input, output a homomorphic calculation signature ;
- : Take , a message , a circuit and a signature , the verification algorithm either accepts the signature (outputs 1) or rejects it (outputs 0).
Correctness. On input , , , , any circuit with a depth , , the equation below holds:
3.5. Robustness
A key component of the AB-VCPRE design is robustness. The fundamental tenet is that by re-encryption key sharing, an adversary cannot create ciphertext that is falsely obtained yet can be correctly authenticated. The following game describes the robustness of the AB-VCPRE scheme.
During the guessing phase, the adversary outputs the appropriate ciphertext satisfies while , , , and interact as specified in Definition 6.
The adversary’s advantage is characterized as
4. The Model of AB-VCPRE with Re-Encryption Verification
4.1. Scheme Definition
An AB-VCPRE scheme consists of seven algorithms. The specific flow chart is shown in Figure 1. In comparison to the standard AB-VCPRE, a verification method called is added to check for an honest transformation of the ciphertext. The algorithm is publicly verifiable because all that is required are the original ciphertext and the corresponding re-encryption ciphertext.
- : Input security parameter , output public parameters ;
- : Given , output the public/private key pair for user ;
- : Taking , , plaintext , and an attribute vector as input, output a related ciphertext with ;
- : Taking , , and as input, output a message ;
- : Input , of user , of user , and a control policy/function , returns the re-encryption key related to and the corresponding signature, outputs the re-encryption verification key from user to user ;
- : With , of user , associated with , and as input. When remains constant, output the converted ciphertext , otherwise output ;
- : If the original ciphertext’s conversion to the re-encryption ciphertext is performed correctly, the output of the authentication algorithm is valid, otherwise output (invalid ciphertext).
Correctness. In an AB-VCPRE scheme, correctness has the following two requirements:
- Decryption correctness.
For security parameter n, attribute vectors , message , the equations below hold
where the decryption error is negligible.
- 2.
- Verification correctness.
Verification correctness is satisfied using an AB-VCPRE scheme. We have the probability if all converted ciphertexts are produced by the re-encryption keys and .
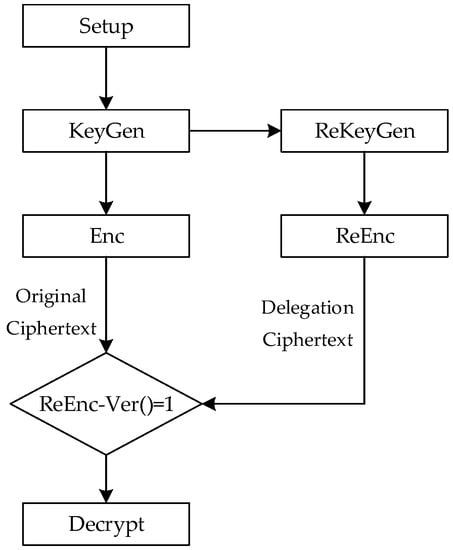
Figure 1.
Flow chart of AB-VCPRE.
4.2. Security Model
Definition 6.
To demonstrate the CPA security of the AB-VCPRE scheme, the game between challenger and adversary is used.
Init. Before seeing the public parameter , adversary declares a vector of attributes .
Setup. Initialize the public parameters in Challenger and use the algorithm to obtain , and transmit and to .
Query phase 1. chooses some queries as the following:
- : performs a key query. runs to produce the ;
- : runs to provide when receives a re-encryption key query, where and . And responds with verification key by running algorithm ;
- : sends to where and , computes a re-encryption key as in and returns a re-encrypted ciphertext by running .
Challenge phase. chooses two messages of the same length and (), executives , where , and gives back the original ciphertext from to .
Query phase 2. Similar to phase 1, keeps asking the query.
Guess. is guessed by , and if , the game winner is .
The benefits of are described as
5. Our Scheme
5.1. Our Scheme Composition
Using the LWE difficulty problem as a basis and the homomorphic signature algorithm, this paper proposes an AB-VCPRE scheme.
Let security parameters , where , .
- Central agency generates random security parameters prime , an error sampling algorithm for B-bounded distributions, . The boolean circuit’s maximum depth is , the number of attributes is , and the Gaussian parameter is , ;
- Create the corresponding trapdoor matrix and the matrix by running algorithm ;
- Select uniform matrices with random.
- Output public parameters .
- 2.
Randomly select a matrix , and run , such that .
Output .
- 3.
- Given the plaintext , attribute vectors , where . Select random vectors , error vectors ;
- Compute :
- should be set to if is null or none. Or else randomly choose uniform matrices at random, calculate
Output ciphertext ;
- 4.
Input , .
- Compute . Set for if , or else set .
Output ;
- 5.
Input , , , a policy .
- Randomly selected matrices , , is the Gaussian parameter, and .
- Let , . Running . Generate the basic for .
- Execute algorithm to produce , in order to obtain , of which . Compute the re-encryption key:
- Creating the verification key using algorithm and signature private key , parse each line of as , then use the signature algorithm to sign as ;
- To validate the signature, publish . Deliver and the associated signature across a secure channel to the proxy server;
- 6.
Input , , .
- Output if or , or else , . The proxy performs the ciphertext conversion ;
- The valuation circuit is , and the evaluation algorithm from HS creates a signature .
Output as converted ciphertext;
- 7.
Input verification key , original ciphertext , converted ciphertext .
Verification algorithm output .
Figure 2 depicts the new AB-VCPRE scheme’s workflow. If Bob wants to share Alice’s content stored on the cloud server, first KGC generates a public key and private key for Alice and Bob and sends the keys to them. Then, Alice generates the re-encryption key and original ciphertext, which are sent to the cloud server and executes the re-encryption algorithm. The cloud server delivers both the original and the re-encryption ciphertext to the authentication server after the re-encryption operation is finished. The authentication server verifies the algorithm for re-encryption. If the verification algorithm outputs 1, the authentication server sends Bob the ciphertext, Bob recovers the message by decrypting the ciphertext matching to it, otherwise output .
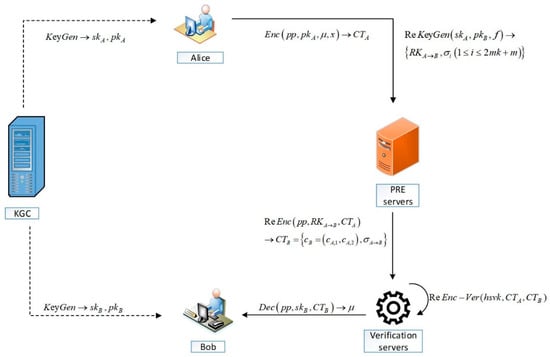
Figure 2.
The workflow of AB-VCPRE.
5.2. Correctness and Parameters
5.2.1. The Correctness of the Original Ciphertext
With the private key , the original ciphertext can be decrypted.
Only if the error does not exceed the decryption algorithm is able to correctly recover the plaintext . In fact, .
5.2.2. Correctness of Conversion Ciphertext
After passing one conversion, the corresponding conversion cipher is decrypted as follows:
Where and are the user ‘s public keys, , , with overwhelming probability. By the theorem we have:
where , with overwhelming probability.
The conversion ciphertext is decrypted by the private key .
where:
with overwhelming probability. Therefore, the value of can be decrypted correctly, i.e., the transformed ciphertext can be decrypted correctly.
In fact, the algorithm can only obtain single-hop, because in , we set , which means that the re-encryption ciphertext cannot be encrypted again. This design is our first work and we will investigate this problem and extend it to multi-hop schemes in future work.
5.2.3. Correctness of Ciphertext Verification
In the HS scheme, the re-encryption verifiability is carried out using the algorithm . In , input the ciphertext and the re-encryption key , using as a valuation circuit, re-encryption key as circuit input, can be seen as some computation at the message level and in , with signature as input, and it can be interpreted as a computation of the signature level. If is in fact the outcome of an honest computation based on , the concept of correctness for homomorphic signature schemes holds. Then can pass the verification and the verification algorithm’s accuracy is demonstrated.
5.3. Security
Theorem 1 (Security).
The scheme we construct is CPA security under assumption.
Proof of Theorem 1.
A game-based approach is used in this proof. A challenger can be built to resolve the LWE presumption if it is possible for an adversary to breach the CPA’s security.
Game 0: In the original CPA attack paradigm described in Section 3, this is a true game between and .
Game 1: Same as game 0, but with a change in the way the common matrix is generated. On receipt of , generates uniformly random small parametric matrices , calculate where . □
Lemma 5.
Game 0 is statistically indistinguishable from game 1.
Proof of Lemma 5.
In game 0, is a random uniform matrix on . In the challenge query, is the construction of the generated challenge ciphertext random matrix. However, in game 1, serves as the error vector and is used to generate and . By Lemma 2, the distribution and are statistically equivalent for any . Hence, no statistically significant difference exists between the common matrix in games 0 and 1. This shows that there is no statistically significant difference between games 0 and 1. □
Game 2: Challenger randomly selects on with no trapdoor and utilizes the to produce and its trapdoor .
KeyGen query . performs a key query. run to produce the , output to .
ReKeyGen query . When adversary interrogates to make , challenger executes of Lemma 4 to create a re-encryption key.
- , , policy , set , a policy ;
- Run to make . It follows from the definition of that there is ;
- executive to generate short basic of . Run to produce , hence, an equals ;
- When , let , matrix , , create the matrix
- 5.
- When , let , matrix , , select a random uniform distribution matrix , create the matrix
Then send the challenger some re-encryption verification questions, who will then carry out the operation honestly and report the results to the adversary .
ReEnc query . output .
Lemma 6.
Game 1 is computationally indistinguishable from game 2.
Proof of Lemma 6.
The technique employed to generate the re-encryption key differs between games 1 and 2. When hold, here is the re-encryption key:
Corollary 1.
By applying the standard mixing parameters, the ensuing distributions cannot be distinguished computationally. Otherwise, there is a useful algorithm for resolving the problem.
- 1.
- and , where , , , ;
- 2.
- and , where , ;
- 3.
- and , where , , , for , .
By Corollary 1, under the LWE assumption, it is evident that game 1 and game 2 are computationally indistinguishable.
Additionally, the private key creation mechanism is undetected from game 1 to game 2, and the produced private key continues to satisfy , while the re-encryption key is selected from the uniform distribution, which is similar to the standard LWE distribution. Furthermore, because homomorphic signatures are non-negligible, the adversary in the CPA game cannot offer an invalid ciphertext to pass re-encryption verification, that is, re-encryption verification provides no auxiliary capacity to the adversary.
On the other side, to demonstrate it, if succeeds in the re-encryption verifiability game, then by interacting with challenger , the simulator can break the homomorphic signature’s unforgeability.
The verification key is first acquired by the simulator from . The re-encryption key is then chosen by adversary as the one it wants to assault, and the simulator s is provided by . To create the signature, asks the message for a homomorphic signature to obtain and then gives it back to . The challenger then calculates whenever outputs a false re-encryption ciphertext after the simulator has parsed it, where is an evaluation circuit converted from the original ciphertext.
If wins the verifiability of re-encryption, the forgery of ‘s signature can pass , which also counts as a valid homomorphic signature. Therefore, breaking the unforgeability of the homomorphic signature provides the same advantage as breaking the re-encryption verifiability of the AB-VCPRE scheme. When all of the aforementioned factors are considered, game 1 and game 2 are similar from the standpoint of the adversary. □
Game 3: Similar to game 2, except that the challenge cipher given to the opponent is no longer honestly generated, but chosen evenly and randomly in . Due to the fact that the challenge cipher is a random factor in the cipher space, it is independent of and , so there is zero advantage to the in this game.
Lemma 7.
Game 2 is statistically indistinguishable from game 3.
Proof of Lemma 7.
If distinguishes game 2 from game 3 with a non-negligible advantage, then there is a simulator that can use the information acquired by to resolve the problem. □
LWE instance. The simulator requests the LWE prophesy device to acquire an LWE instance , possibly is a truly random distribution or is a pseudo-random distribution of noise from the LWE.
Public parameters. Let , sample a uniform matrix to generate a randomly identified public key , select random matrices , and let for . Then the common matrix , public key .
Queries. As with game 2, answers all of ‘s queries.
Challenge ciphertext. Generate challenge cipher via LWE instance
The answer to is then returned. In this case, the distribution of the challenge cipher is the same as that of game 2.
where , , .
Challenge ciphertext:
Then through , there is
Statistically, the challenge ciphertext is indistinguishable in the alternative scenario if and are chosen consistently, according to the leftover hash lemma [25].
Output. The simulator outputs ‘s guess after predicts whether it interacts with game 2 or game 3. can solve the problem with the same probability if can distinguish between games 2 and 3. However, the problem is mysterious, so game 3 cannot be won by .
The Proof of Theorem 1 is completed by considering game 0 to game 3.
Theorem 2 (Robustness).
The new AB-VCPRE scheme fulfills robustness if the homomorphic signature satisfies unforgeability.
Proof of Theorem 2.
Using a randomly selected evaluation circuit, a dishonest proxy server is able to obtain an invalid re-encryption ciphertext share and corresponding signature. However, the original ciphertext should describe the right evaluation circuit. When the correct evaluation circuit diverges from the forgery, verification fails, allowing the proxy server to convert the data truthfully.
Homomorphic signatures can be used to demonstrate the robustness of the new scheme. If can defeat the game outlined in Definition 6, then by collaborating with in the homomorphic signature security model, it is able to build a simulator that compromises the homomorphic signatures’ unforgeability. Here is the procedure.
picks the re-encryption key it wishes to attack once the simulator receives the challenger ‘s verification key . When sends simulator a forged re-encryption ciphertext share , processes it to obtain and submits it to an oracle as a forged homomorphic signature.
If succeeds in the robustness game, then , but , this also means that was able to pass the verification, so the simulator successfully forged an illegal signature, which will be submitted to oracle later. This indicates that the homomorphic signature algorithm’s unforgeability has been compromised.
Thus, if the homomorphic signature algorithm meets the requirement for unforgeability, the signature is considered unforgeable. The new AB-VCPRE is capable of achieving robustness. □
Theorem 3 (Weak collusion resistance).
The new AB-VCPRE scheme can realize weak collusion resistance, if the LWE problem is difficult.
Proof of Theorem 3.
Weak collusion resistance is that when an agent with a re-encryption key colludes with a trustee with a re-encryption key, the agent obtains only an approximate result, not an exact result.
The re-encryption key is and , which can be further expressed as
This is a standard LWE distribution that is not different from unified distribution, nor can anyone obtain any useful information about private keys. After collusion, Bob encrypted the above equation with his private key and got . As the noise generated during re-encryption is very low, the encryption message can be well restored by . Therefore, in the case of collusion, the private key seems to have all been compromised. However, this is not the case. We can restore an equivalent private key, but this equivalent private key is different from the original private key. We provide the following two explanations. On the one hand, any data that can initially be decrypted by can be easily re-encrypted and read by an enemy who possesses both and . On the other hand, they are unable to determine the delegator’s precise private key from the equation above. Although Power2 is an easy-to-reverse feature, because it contains some noise from , you cannot obtain an exact private key from the first n-line of . Therefore, the method proposed in this project has weak collusion resistance. □
6. Efficiency Analysis
Paper [15] proposed a CPRE algorithm based on DBDH, which supports fine-grained authorization and collision resistance security, however, it cannot achieve robustness. Paper [11] and paper [12] are PRE schemes with verification, both of which are robust and the method for achieving robustness is zero-knowledge proof with a decisional discrete logarithm tool, but are not as low complexity as the schemes in this paper. In addition, paper [12] is based on discrete logarithmic constructions and is not resistant to quantum attacks. Although paper [11] is a scheme using lattice construction, which seems to be resistant to quantum attacks, the robustness verification tool is a decisional discrete logarithm, so in general the scheme is not resistant to quantum attacks. Table 1 demonstrates that the approach presented in this paper is not only robust to proxy re-encryption but also simple to implement and resistant to quantum attacks.

Table 1.
Comparison of related work.
In Table 2, the efficiency of the scheme is analyzed through plaintext space, size of ciphertext, size of re-encryption key, encryption complexity, re-encryption complexity, and robustness verification complexity. represents an integer on modulo q. , , , , and denote the computation of pairing, modular exponentiation, signature, ciphertext verification, and multiplication operation, respectively. , , respectively, represent the time spent for the hash function and the GVP algorithm. Table 2 demonstrates that the computational complexity of the literature [15] is worse than that of the proposed scheme, and is not robust. In terms of robustness verification complexity, when a boolean circuit evaluates the original signature, homomorphic signature computation is a boolean operation that is more straightforward and effective. Here, we choose the linear homomorphic signature scheme based on the difficult problem of SIS on the lattice proposed in paper [26] for comparison. Compared with the scheme [12], the proposed scheme has better re-encryption complexity, encryption complexity, and robustness verification complexity. Compared with the scheme [11], the proposed scheme in this paper only needs to pay some extra cost to encrypt the message vector, and the robustness verification complexity is lower.

Table 2.
Computational and communication complexity comparison.
7. Conclusions
By using homomorphic signatures, this paper proposes an AB-VCPRE scheme, which solves the problem of being unable to detect illegal proxy behavior in traditional PRE schemes. The scheme is robust enough to allow proxy servers that have sent invalid transformed ciphertext shares to be detected. In terms of security, the scheme is CPA security based on a LWE problem and is resistant to quantum attacks. In terms of efficiency, the scheme has advantages in re-encryption and robustness verification computational efficiency. In addition, there is some room for improvement in the performance of our solutions, and constructing a multi-hopping PRE scheme will be the focus of our next work.
Author Contributions
Conceptualization, Y.T., M.J. and H.M.; methodology, M.J. and H.M.; validation, M.J., Y.T. and H.M.; formal analysis, M.J. and L.Y.; writing—original draft preparation, M.J.; writing—review and editing, H.M., C.Z. and L.Y.; supervision, H.M. and C.Z.; funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the Henan Key Laboratory of Network Cryptography Technology (LNCT2022-A11) and the Shaanxi Key Laboratory of Information Communication Network and Security (ICNS202006).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Proceedings of the Advances in Cryptology—EUROCRYPT’98: International Conference on the Theory and Application of Cryptographic Techniques, Espoo, Finland, 31 May–4 June 1998; pp. 127–144. [Google Scholar] [CrossRef]
- Green, M.; Ateniese, G. Identity-based proxy re-encryption. In Proceedings of the Applied Cryptography and Network Security: 5th International Conference, ACNS 2007, Zhuhai, China, 5–8 June 2007; pp. 288–306. [Google Scholar] [CrossRef]
- Weng, J.; Deng, R.H.; Ding, X.; Chu, C.-K.; Lai, J. Conditional proxy re-encryption secure against chosen-ciphertext attack. In Proceedings of the 4th International Symposium on Information, Computer, and Communications Security, Sydney, Australia, 10–12 March 2009; pp. 322–332. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Advances in Cryptology–EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 24–26 May 2005; pp. 457–473. [Google Scholar] [CrossRef]
- Zamite, J.; Domingos, D.; Silva, M.J.; Santos, C. Group-based discretionary access control in health related repositories. J. Inf. Technol. Res. JITR 2014, 7, 78–94. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, D.; Zhang, Z. Attribute-based conditional proxy re-encryption with chosen-ciphertext security. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Liang, X.; Cao, Z.; Lin, H.; Shao, J. Attribute based proxy re-encryption with delegating capabilities. In Proceedings of the 4th International Symposium on Information, Computer, and Communications Security, Sydney, Australia, 10–12 March 2009; pp. 276–286. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Weng, J.; Zhang, Y.; Sakurai, K. Fine-grained conditional proxy re-encryption and application. In Proceedings of the Provable Security: 8th International Conference, ProvSec 2014, Hong Kong, China, 9–10 October 2014; pp. 206–222. [Google Scholar] [CrossRef]
- Mao, X.; Li, X.; Wu, X.; Wang, C.; Lai, J. Anonymous attribute-based conditional proxy re-encryption. In Proceedings of the Network and System Security: 12th International Conference, NSS 2018, Hong Kong, China, 27–29 August 2018; pp. 95–110. [Google Scholar] [CrossRef]
- Ge, C.; Susilo, W.; Wang, J.; Huang, Z.; Fang, L.; Ren, Y. A key-policy attribute-based proxy re-encryption without random oracles. Comput. J. 2016, 59, 970–982. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Zhao, Q. Resplittable threshold multi-broker proxy re-encryption scheme from lattices. J. Commun. 2017, 38, 157–164. [Google Scholar]
- Nunez, D. Umbral: A Threshold Proxy Re-Encryption Scheme; NuCypher Inc. and NICS Lab, University of Malaga: Málaga, Spain, 2018. [Google Scholar]
- Luo, F.; Al-Kuwari, S.; Wang, F.; Chen, K. Attribute-based proxy re-encryption from standard lattices. Theor. Comput. Sci. 2021, 865, 52–62. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, Y.; Fu, J. PRECISE: Identity-based private data sharing with conditional proxy re-encryption in online social networks. Future Gener. Comput. Syst. 2018, 86, 1523–1533. [Google Scholar] [CrossRef]
- Yao, S.; Dayot, R.V.J.; Kim, H.-J.; Ra, I.-H. A novel revocable and identity-based conditional proxy re-encryption scheme with ciphertext evolution for secure cloud data sharing. IEEE Access 2021, 9, 42801–42816. [Google Scholar] [CrossRef]
- Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar] [CrossRef]
- Agrawal, S.; Boneh, D.; Boyen, X. Efficient lattice (h) ibe in the standard model. In Proceedings of the Eurocrypt 2010, Berlin, Heidelberg, 30 May–3 June 2010; pp. 553–572. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM JACM 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Aono, Y.; Boyen, X.; Phong, L.T.; Wang, L. Key-private proxy re-encryption under LWE. In Proceedings of the Progress in Cryptology–INDOCRYPT 2013: 14th International Conference on Cryptology in India, Mumbai, India, 7–10 December 2013; pp. 1–18. [Google Scholar] [CrossRef]
- Boneh, D.; Gentry, C.; Gorbunov, S.; Halevi, S.; Nikolaenko, V.; Segev, G.; Vaikuntanathan, V.; Vinayagamurthy, D. Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In Proceedings of the Advances in Cryptology–EUROCRYPT 2014: 33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Copenhagen, Denmark, 11–15 May 2014; pp. 533–556. [Google Scholar] [CrossRef]
- Gorbunov, S.; Vaikuntanathan, V.; Wee, H. Predicate encryption for circuits from LWE. In Proceedings of the Advances in Cryptology—CRYPTO 2015: 35th Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; pp. 503–523. [Google Scholar] [CrossRef]
- Brakerski, Z.; Vaikuntanathan, V. Constrained Key-Homomorphic PRFs from Standard Lattice Assumptions: Or: How to Secretly Embed a Circuit in Your PRF. In Proceedings of the Theory of Cryptography: 12th Theory of Cryptography Conference, TCC 2015, Warsaw, Poland, 23–25 March 2015; pp. 1–30. [Google Scholar] [CrossRef]
- Kim, S.; Wu, D.J. Watermarking PRFs from lattices: Stronger security via extractable PRFs. In Proceedings of the Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; pp. 335–366. [Google Scholar] [CrossRef]
- Liang, X.; Weng, J.; Yang, A.; Yao, L.; Jiang, Z.; Wu, Z. Attribute-based conditional proxy re-encryption in the standard model under LWE. In Proceedings of the Computer Security–ESORICS 2021: 26th European Symposium on Research in Computer Security, Darmstadt, Germany, 4–8 October 2021; pp. 147–168. [Google Scholar] [CrossRef]
- Håstad, J.; Impagliazzo, R.; Levin, L.A.; Luby, M. A pseudorandom generator from any one-way function. SIAM J. Comput. 1999, 28, 1364–1396. [Google Scholar] [CrossRef]
- Deng, Y. A Linearly Homomorphic Signature Scheme on Lattice. Henan Sci. 2015, 33, 1346–1351. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).