Swarming Transition in Super-Diffusive Self-Propelled Particles
Abstract
1. Introduction
2. The Model
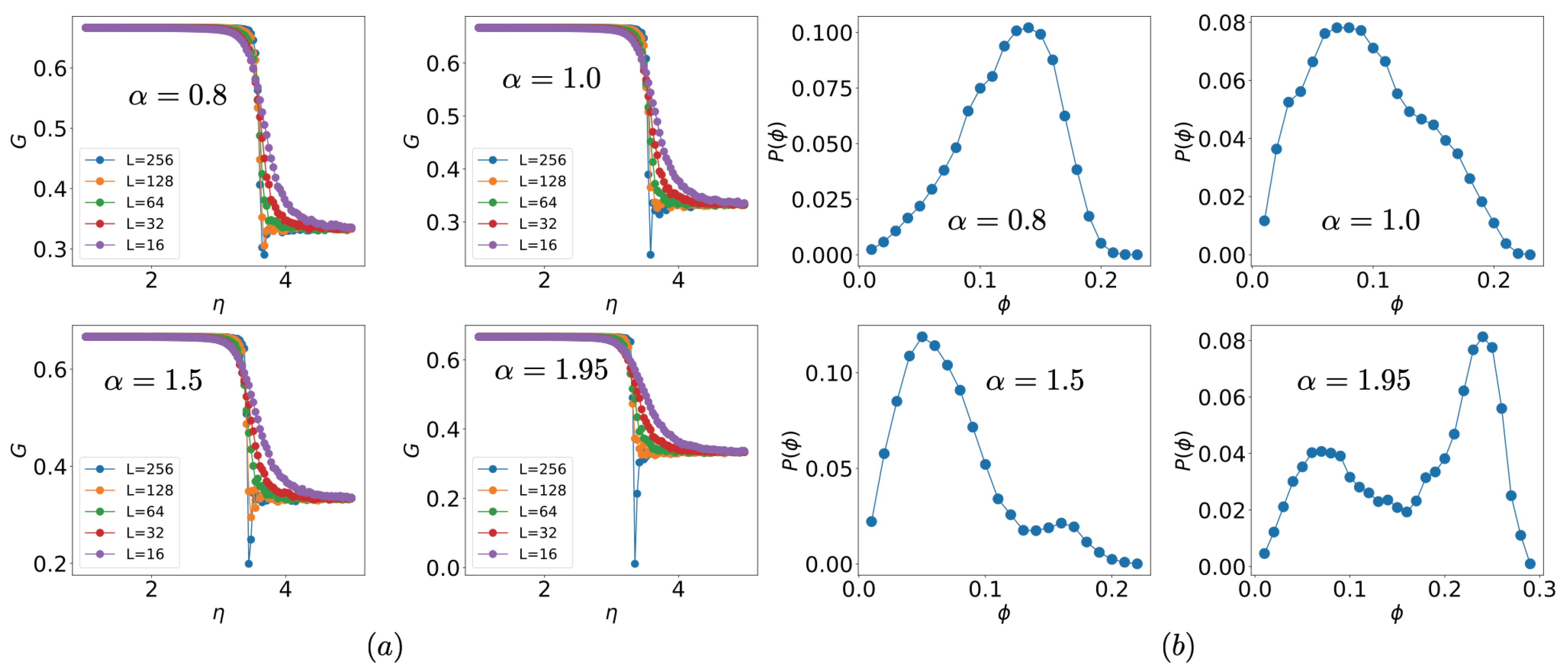
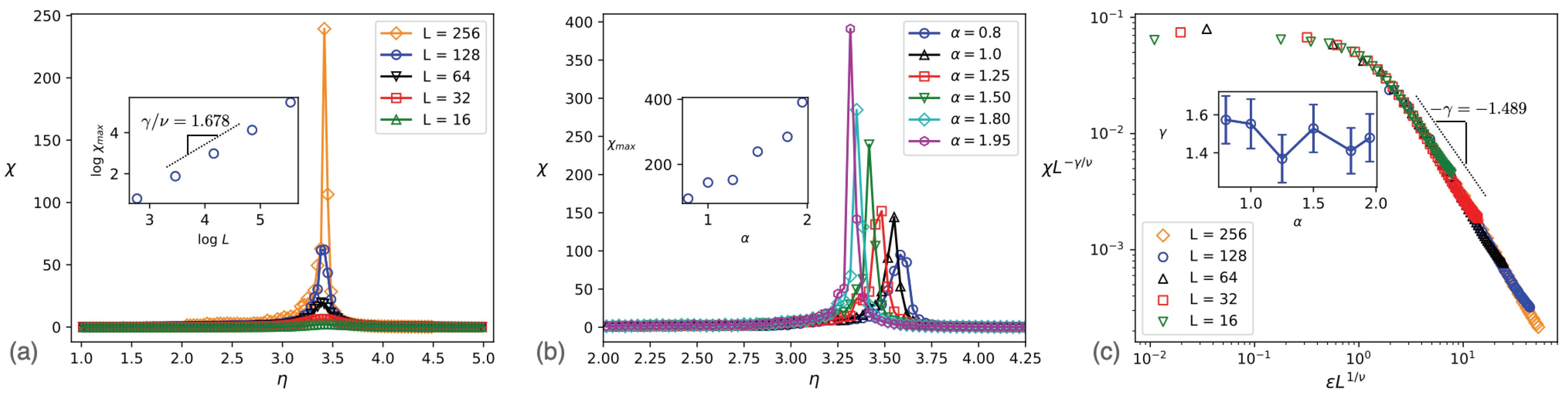
3. Simulation Results
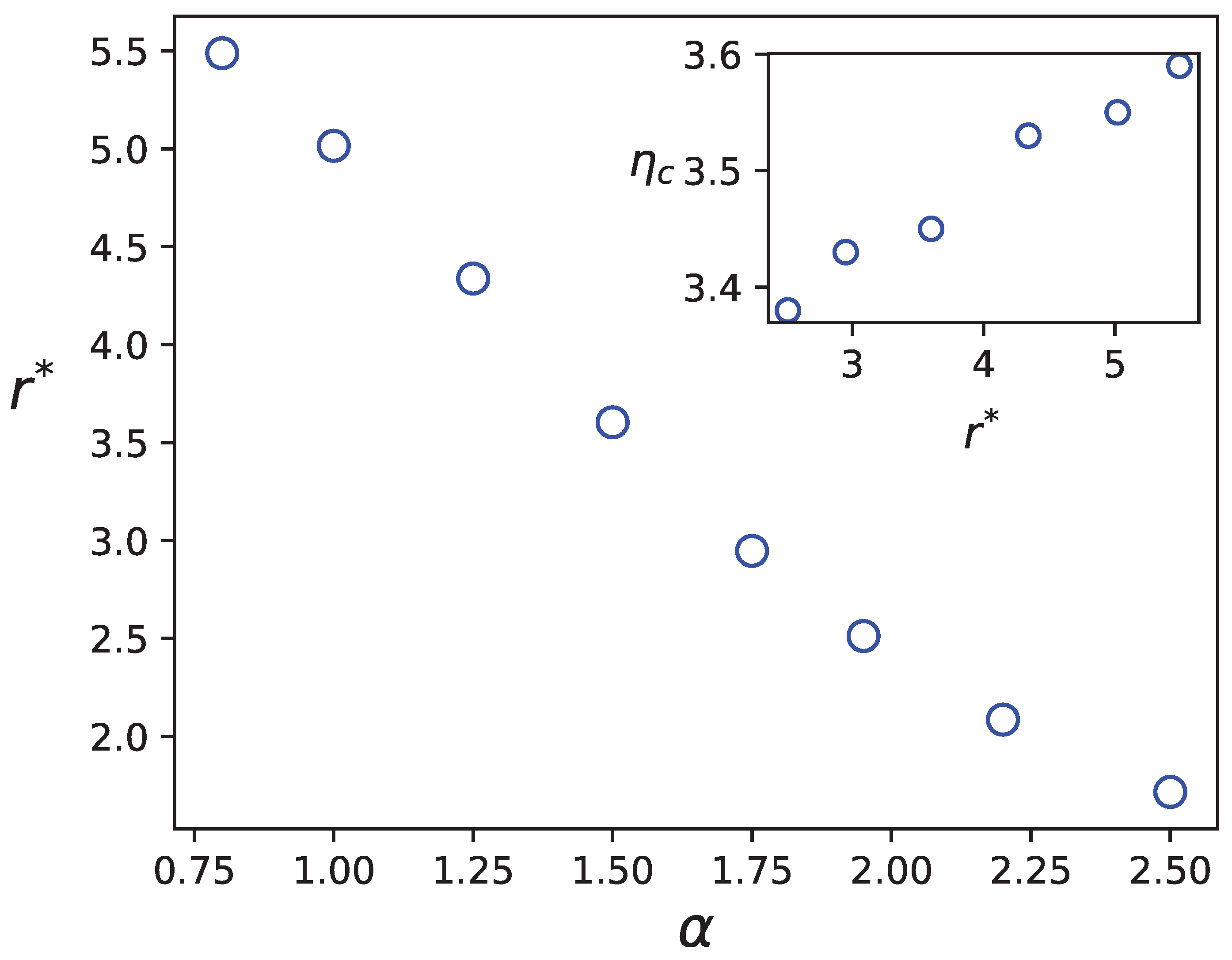
4. Mean Field Arguments
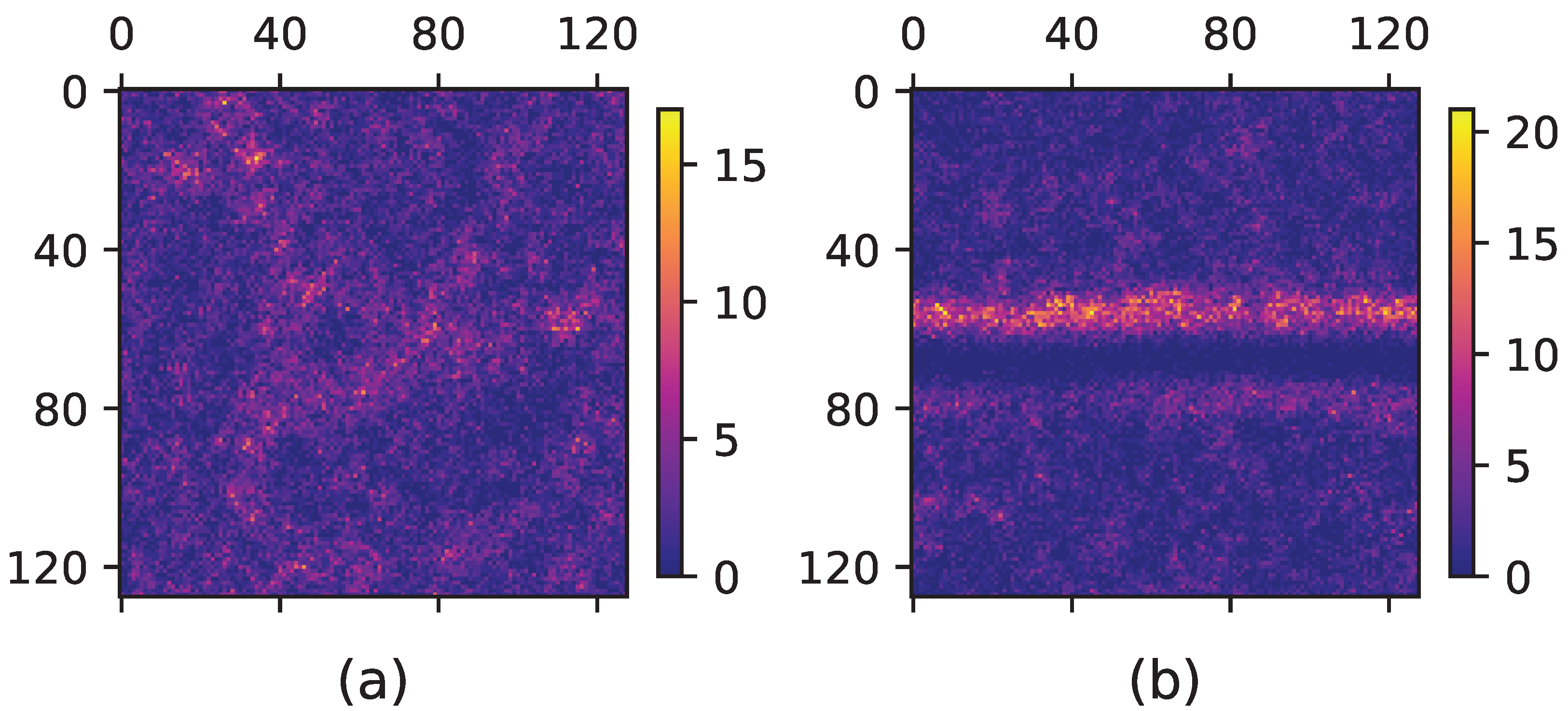
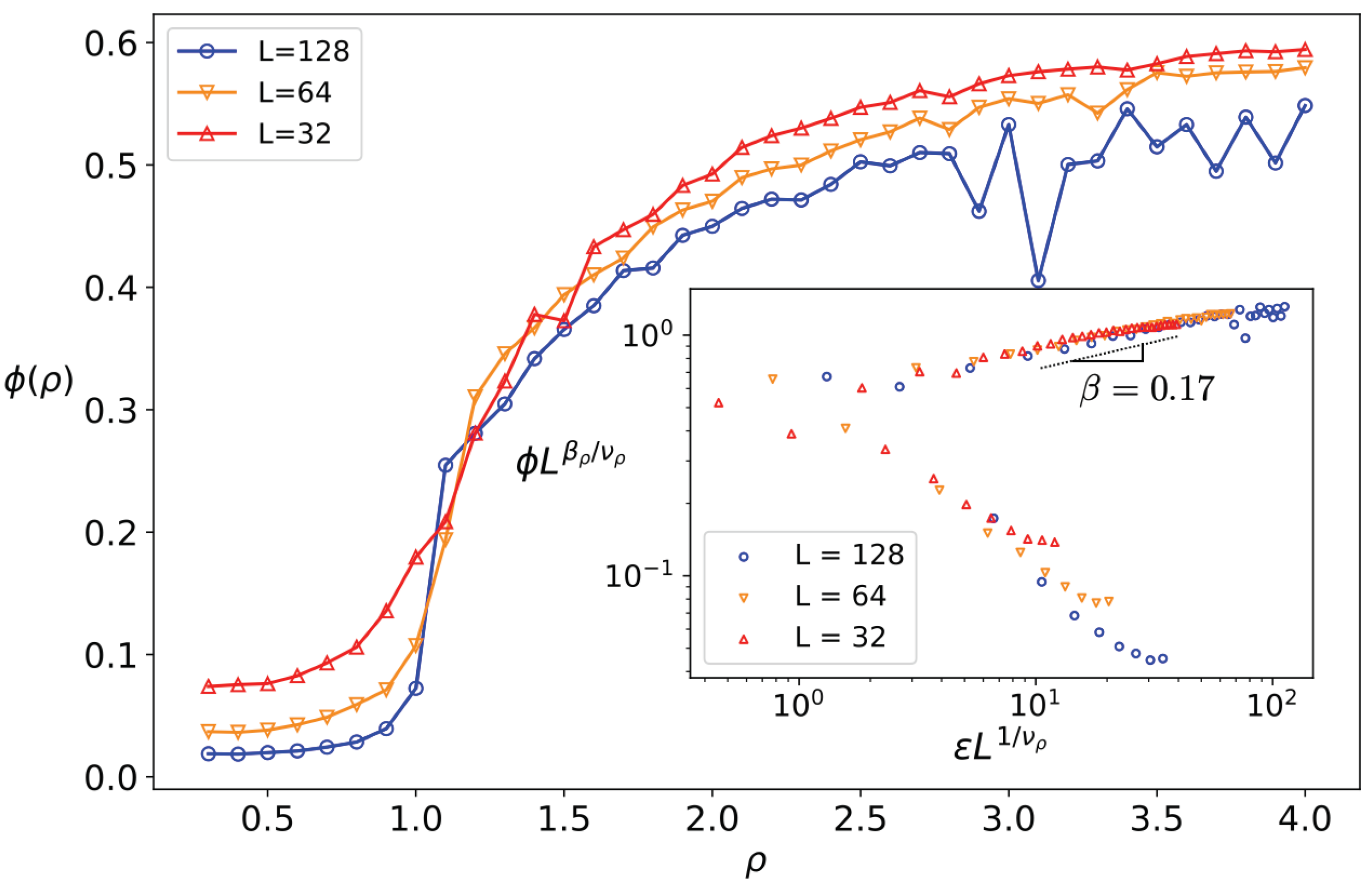
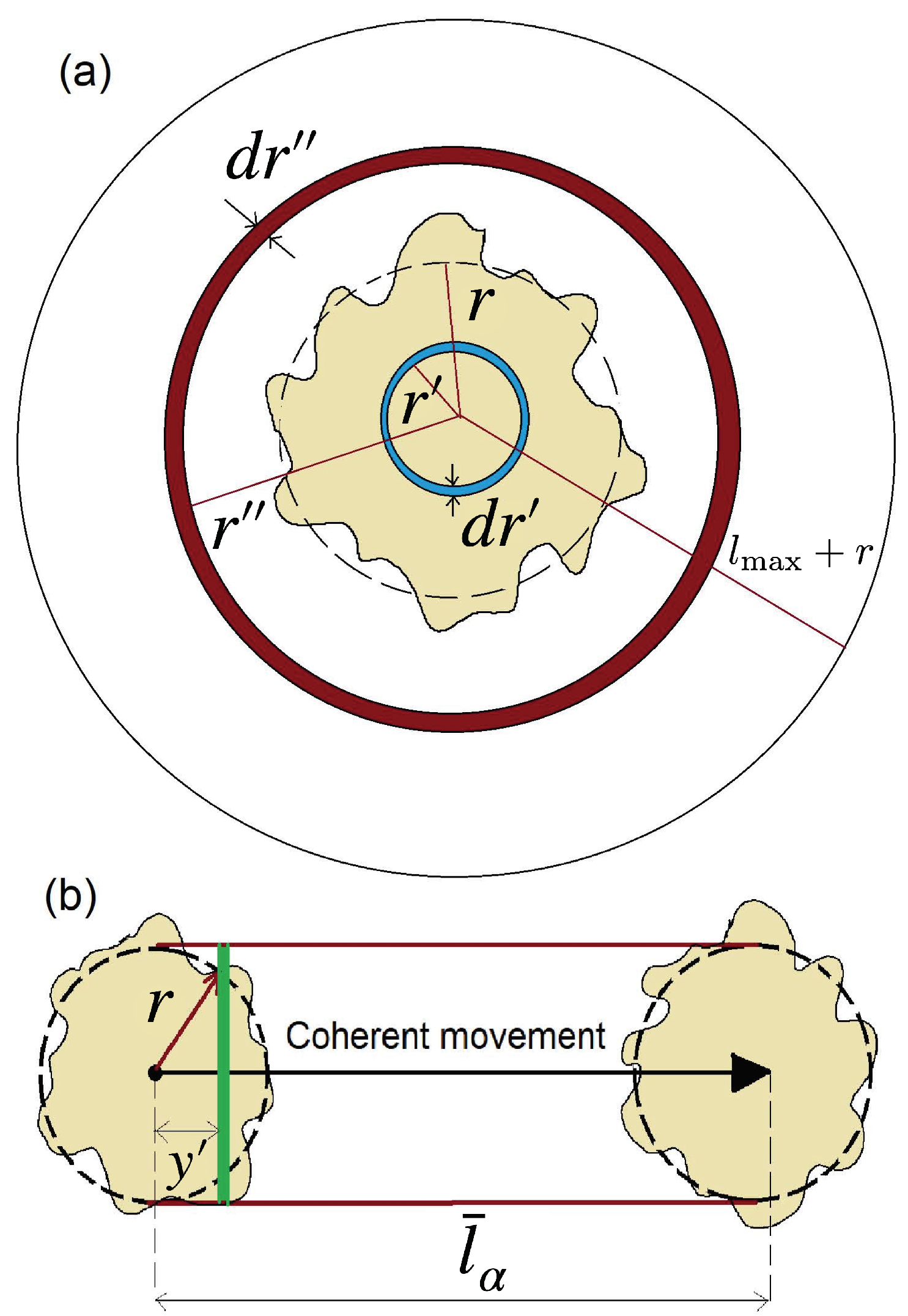
5. Geometrical Observables
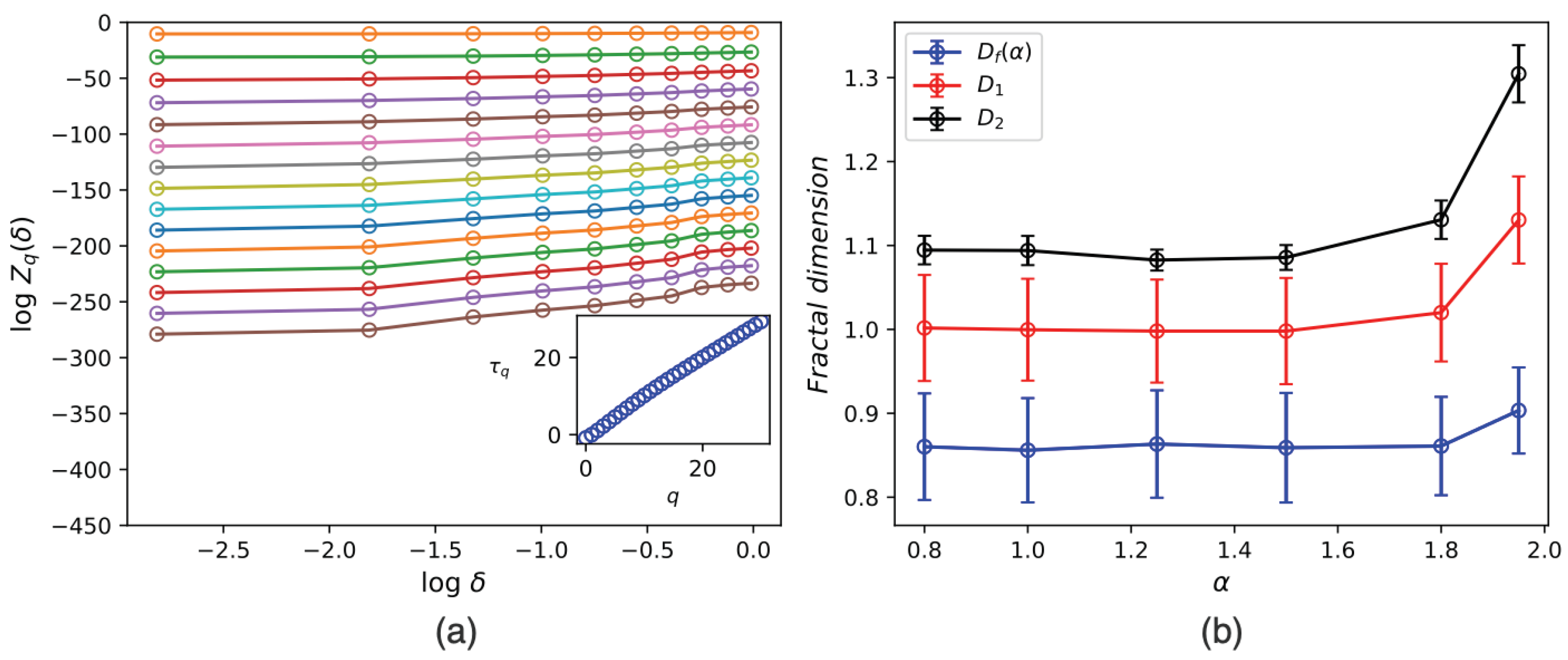
5.1. Density Fractal Analysis
5.2. Contour Line Analysis
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
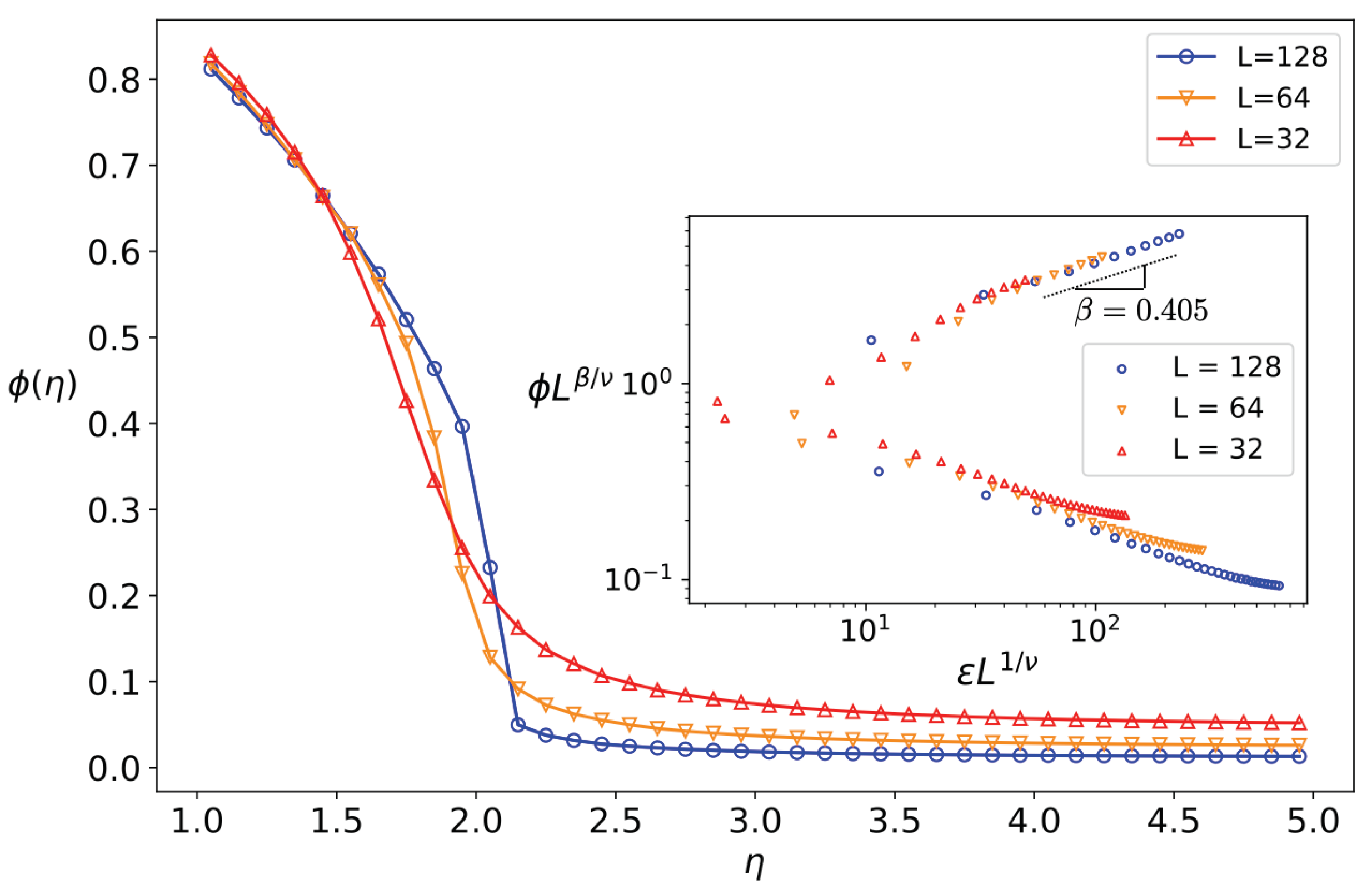
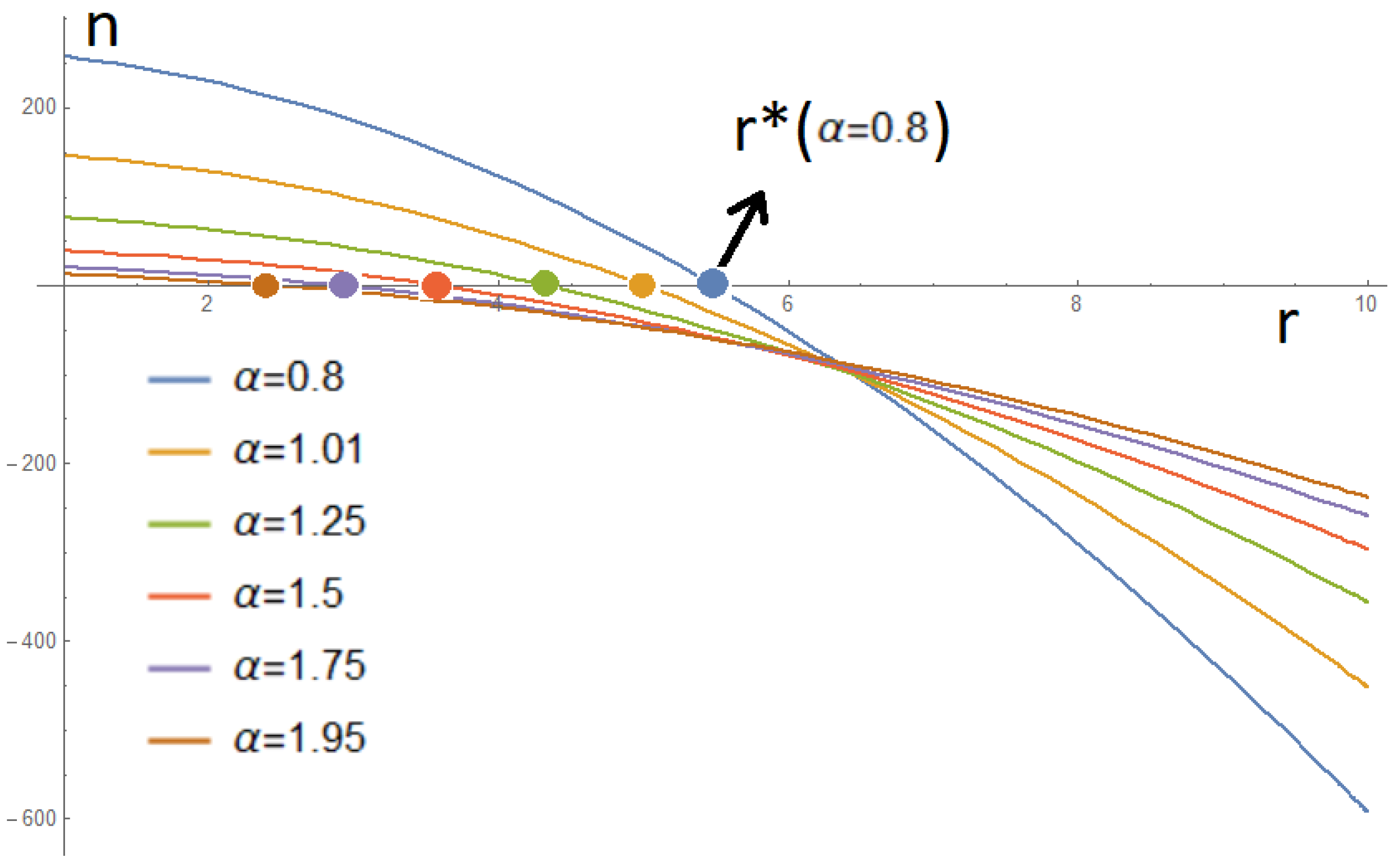
Appendix A. Crossover to Continuous Transition
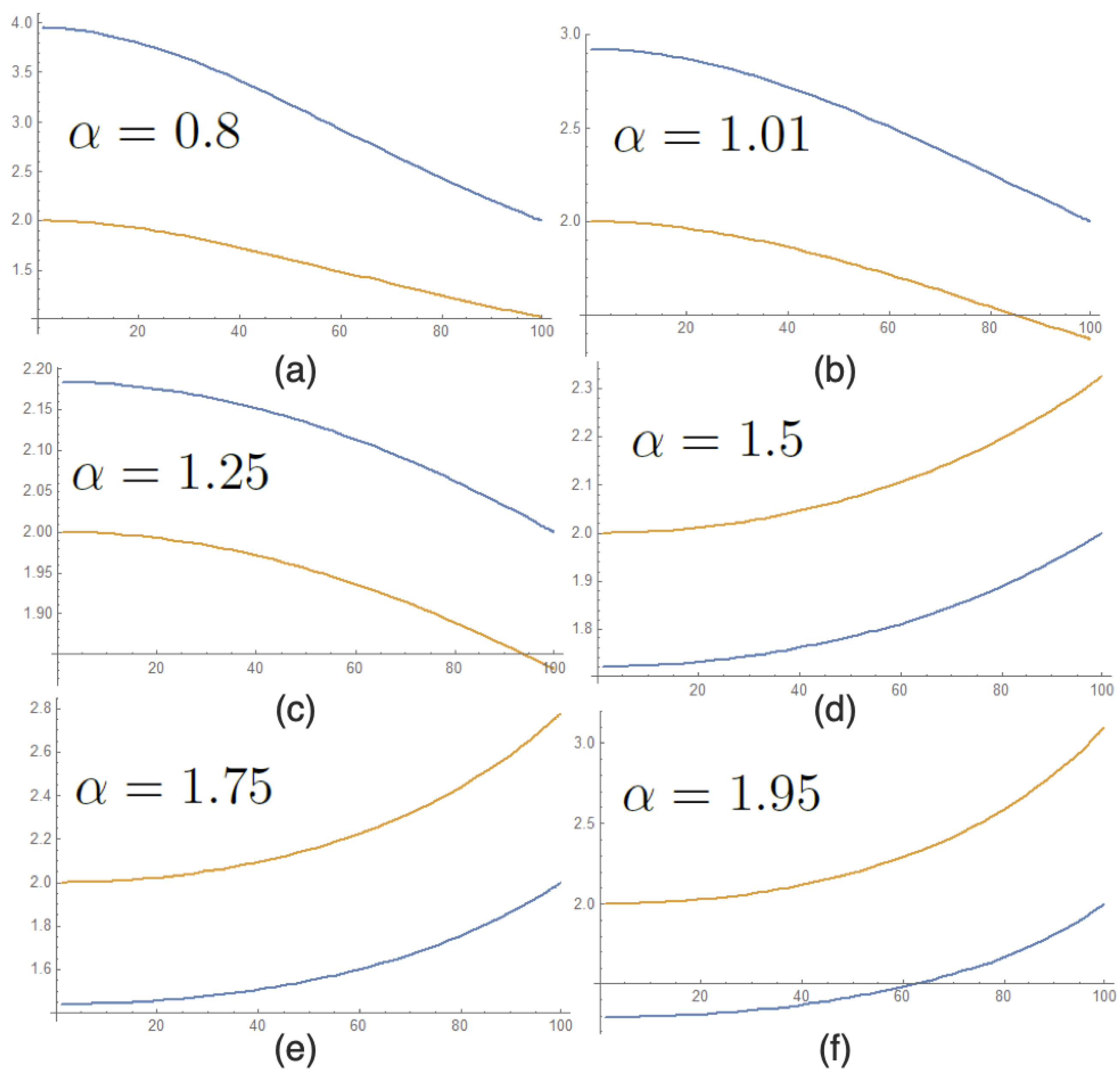
Appendix B. Mean Field Theory
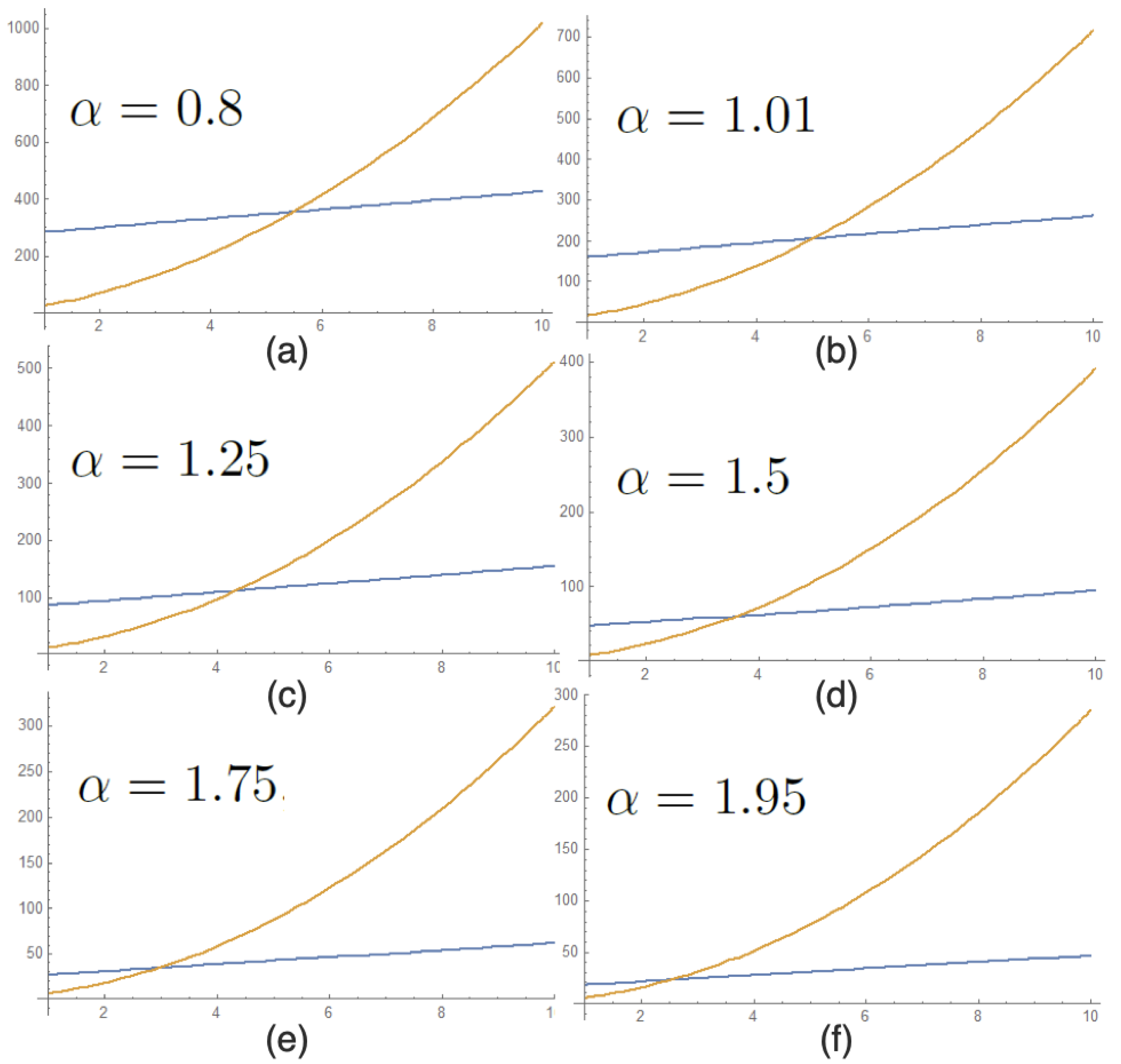
Appendix C. Similarities with Q-State Potts Model
| our model | − | 1.5–1.6 | − | − | ≈1.3 | ||||
| − | − | − | |||||||
| (Ising) | 0 | 1 | |||||||
| 1 |
References
- Gompper, G.; Winkler, R.G.; Speck, T.; Solon, A.; Nardini, C.; Peruani, F.; Löwen, H.; Golestanian, R.; Kaupp, U.B.; Alvarez, L.; et al. The 2020 motile active matter roadmap. J. Phys. Condens. Matter 2020, 32, 193001. [Google Scholar] [CrossRef] [PubMed]
- Calovi, D.S.; Lopez, U.; Ngo, S.; Sire, C.; Chaté, H.; Theraulaz, G. Swarming, schooling, milling: Phase diagram of a data-driven fish school model. New J. Phys. 2014, 16, 015026. [Google Scholar] [CrossRef]
- Kearns, D.B. A field guide to bacterial swarming motility. Nat. Rev. Microbiol. 2010, 8, 634–644. [Google Scholar] [CrossRef] [PubMed]
- Copeland, M.F.; Weibel, D.B. Bacterial swarming: A model system for studying dynamic self-assembly. Soft Matter 2009, 5, 1174–1187. [Google Scholar] [CrossRef]
- Darnton, N.C.; Turner, L.; Rojevsky, S.; Berg, H.C. Dynamics of bacterial swarming. Biophys. J. 2010, 98, 2082–2090. [Google Scholar] [CrossRef] [PubMed]
- Allison, C.; Hughes, C. Bacterial swarming: An example of prokaryotic differentiation and multicellular behaviour. Sci. Prog. 1991, 75, 403–422. [Google Scholar]
- Verstraeten, N.; Braeken, K.; Debkumari, B.; Fauvart, M.; Fransaer, J.; Vermant, J.; Michiels, J. Living on a surface: Swarming and biofilm formation. Trends Microbiol. 2008, 16, 496–506. [Google Scholar] [CrossRef]
- Buhl, J.; Sumpter, D.J.; Couzin, I.D.; Hale, J.J.; Despland, E.; Miller, E.R.; Simpson, S.J. From disorder to order in marching locusts. Science 2006, 312, 1402–1406. [Google Scholar] [CrossRef]
- Attanasi, A.; Cavagna, A.; Del Castello, L.; Giardina, I.; Melillo, S.; Parisi, L.; Pohl, O.; Rossaro, B.; Shen, E.; Silvestri, E.; et al. Finite-size scaling as a way to probe near-criticality in natural swarms. Phys. Rev. Lett. 2014, 113, 238102. [Google Scholar] [CrossRef]
- Shimoyama, N.; Sugawara, K.; Mizuguchi, T.; Hayakawa, Y.; Sano, M. Collective motion in a system of motile elements. Phys. Rev. Lett. 1996, 76, 3870. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef] [PubMed]
- Baglietto, G.; Albano, E.V.; Candia, J. Criticality and the onset of ordering in the standard Vicsek model. Interface Focus 2012, 2, 708–714. [Google Scholar] [CrossRef] [PubMed]
- Toner, J.; Tu, Y. Long-range order in a two-dimensional dynamical XY model: How birds fly together. Phys. Rev. Lett. 1995, 75, 4326. [Google Scholar] [CrossRef] [PubMed]
- Toner, J.; Tu, Y. Flocks, herds, and schools: A quantitative theory of flocking. Phys. Rev. E 1998, 58, 4828. [Google Scholar] [CrossRef]
- Toner, J. Reanalysis of the hydrodynamic theory of fluid, polar-ordered flocks. Phys. Rev. E 2012, 86, 031918. [Google Scholar] [CrossRef]
- Clusella, P.; Pastor-Satorras, R. Phase transitions on a class of generalized Vicsek-like models of collective motion. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 043116. [Google Scholar] [CrossRef]
- Xue, T.; Li, X.; Grassberger, P.; Chen, L. Swarming transitions in hierarchical societies. Phys. Rev. Res. 2020, 2, 042017. [Google Scholar] [CrossRef]
- Ginelli, F. The physics of the Vicsek model. Eur. Phys. J. Spec. Top. 2016, 225, 2099–2117. [Google Scholar] [CrossRef]
- Grégoire, G.; Chaté, H. Onset of collective and cohesive motion. Phys. Rev. Lett. 2004, 92, 025702. [Google Scholar] [CrossRef]
- Chaté, H.; Ginelli, F.; Grégoire, G.; Raynaud, F. Collective motion of self-propelled particles interacting without cohesion. Phys. Rev. E 2008, 77, 046113. [Google Scholar] [CrossRef]
- Aldana, M.; Dossetti, V.; Huepe, C.; Kenkre, V.; Larralde, H. Phase transitions in systems of self-propelled agents and related network models. Phys. Rev. Lett. 2007, 98, 095702. [Google Scholar] [CrossRef] [PubMed]
- Baglietto, G.; Albano, E.V. Nature of the order-disorder transition in the Vicsek model for the collective motion of self-propelled particles. Phys. Rev. E 2009, 80, 050103. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E.; Ma, S.K.; Nickel, B. Critical exponents for long-range interactions. Phys. Rev. Lett. 1972, 29, 917. [Google Scholar] [CrossRef]
- Aizenman, M.; Fernández, R. Critical exponents for long-range interactions. Lett. Math. Phys. 1988, 16, 39–49. [Google Scholar] [CrossRef]
- Defenu, N.; Codello, A.; Ruffo, S.; Trombettoni, A. Criticality of spin systems with weak long-range interactions. J. Phys. A Math. Theor. 2020, 53, 143001. [Google Scholar] [CrossRef]
- Jung, N.; Weon, B.M.; Kim, P. Effects of adaptive acceleration response of birds on collective behaviors. J. Phys. Complex. 2022, 3, 015014. [Google Scholar] [CrossRef]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef]
- Attanasi, A.; Cavagna, A.; Del Castello, L.; Giardina, I.; Grigera, T.S.; Jelić, A.; Melillo, S.; Parisi, L.; Pohl, O.; Shen, E.; et al. Information transfer and behavioural inertia in starling flocks. Nat. Phys. 2014, 10, 691–696. [Google Scholar] [CrossRef]
- Mora, T.; Bialek, W. Are biological systems poised at criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef]
- Hemelrijk, C.K.; Hildenbrandt, H. Scale-free correlations, influential neighbours and speed control in flocks of birds. J. Stat. Phys. 2015, 158, 563–578. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Peck, S.L. Quantitative Analysis of Movement: Measuring and Modeling Population Redistribution in Animals and Plants. Ecology 1999, 80, 1451–1453. [Google Scholar] [CrossRef]
- Caspi, A.; Granek, R.; Elbaum, M. Enhanced diffusion in active intracellular transport. Phys. Rev. Lett. 2000, 85, 5655. [Google Scholar] [CrossRef] [PubMed]
- Wong, I.; Gardel, M.; Reichman, D.; Weeks, E.R.; Valentine, M.; Bausch, A.; Weitz, D.A. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks. Phys. Rev. Lett. 2004, 92, 178101. [Google Scholar] [CrossRef]
- Caspi, A.; Granek, R.; Elbaum, M. Diffusion and directed motion in cellular transport. Phys. Rev. E 2002, 66, 011916. [Google Scholar] [CrossRef] [PubMed]
- Tolić-Nørrelykke, I.M.; Munteanu, E.L.; Thon, G.; Oddershede, L.; Berg-Sørensen, K. Anomalous diffusion in living yeast cells. Phys. Rev. Lett. 2004, 93, 078102. [Google Scholar] [CrossRef]
- Golding, I.; Cox, E.C. Physical nature of bacterial cytoplasm. Phys. Rev. Lett. 2006, 96, 098102. [Google Scholar] [CrossRef]
- Magdziarz, M.; Weron, A.; Burnecki, K.; Klafter, J. Fractional Brownian motion versus the continuous-time random walk: A simple test for subdiffusive dynamics. Phys. Rev. Lett. 2009, 103, 180602. [Google Scholar] [CrossRef]
- Bronstein, I.; Israel, Y.; Kepten, E.; Mai, S.; Shav-Tal, Y.; Barkai, E.; Garini, Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009, 103, 018102. [Google Scholar] [CrossRef]
- Basak, S.; Sengupta, S.; Chattopadhyay, K. Understanding biochemical processes in the presence of sub-diffusive behavior of biomolecules in solution and living cells. Biophys. Rev. 2019, 11, 851–872. [Google Scholar] [CrossRef]
- Seisenberger, G.; Ried, M.U.; Endress, T.; Buning, H.; Hallek, M.; Brauchle, C. Real-time single-molecule imaging of the infection pathway of an adeno-associated virus. Science 2001, 294, 1929–1932. [Google Scholar] [CrossRef] [PubMed]
- Souza Vilela Podestá, T.; Venzel Rosembach, T.; Aparecida dos Santos, A.; Lobato Martins, M. Anomalous diffusion and q-Weibull velocity distributions in epithelial cell migration. PLoS ONE 2017, 12, e0180777. [Google Scholar] [CrossRef] [PubMed]
- Shlesinger, M.F.; Zaslavsky, G.M.; Frisch, U. Lévy flights and related topics in physics. In Proceedings of the International Workshop Held, Nice, France, 27–30 June 1994. [Google Scholar]
- Umarov, S.; Tsallis, C.; Gell-Mann, M.; Steinberg, S. Symmetric (q,α)-Stable Distributions. Part I: First Representation. arXiv 2006, arXiv:cond-mat/0606038. [Google Scholar]
- Dubkov, A.A.; Spagnolo, B.; Uchaikin, V.V. Lévy flight superdiffusion: An introduction. Int. J. Bifurc. Chaos 2008, 18, 2649–2672. [Google Scholar] [CrossRef]
- Rahimi-Majd, M.; Restrepo, J.G.; Nattagh-Najafi, M. Stochastic and deterministic dynamics in networks with excitable nodes. arXiv 2021, arXiv:2112.04472. [Google Scholar] [CrossRef]
- Binder, K.; Landau, D. Finite-size scaling at first-order phase transitions. Phys. Rev. B 1984, 30, 1477. [Google Scholar] [CrossRef]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Binder, K. Finite size scaling analysis of Ising model block distribution functions. Z. Phys. Condens. Matter 1981, 43, 119–140. [Google Scholar] [CrossRef]
- Sampaio Filho, C.I.; Andrade, J.S., Jr.; Herrmann, H.J.; Moreira, A.A. Elastic backbone defines a new transition in the percolation model. Phys. Rev. Lett. 2018, 120, 175701. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kyriakopoulos, N.; Chaté, H.; Ginelli, F. Clustering and anisotropic correlated percolation in polar flocks. Phys. Rev. E 2019, 100, 022606. [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D Nonlinear Phenom. 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Martsepp, M.; Laas, T.; Laas, K.; Priimets, J.; Tõkke, S.; Mikli, V. Dependence of multifractal analysis parameters on the darkness of a processed image. Chaos Solitons Fractals 2022, 156, 111811. [Google Scholar] [CrossRef]
- Cheraghalizadeh, J.; Tizdast, S.; Doostdari, S.; Najafi, M. Statistical analysis of the drying pattern of coffee. arXiv 2022, arXiv:2211.12132. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1. [Google Scholar]
- Sheffield, S.; Werner, W. Conformal loop ensembles: The Markovian characterization and the loop-soup construction. Ann. Math. 2012, 176, 1827–1917. [Google Scholar] [CrossRef]
- Doyon, B. Conformal loop ensembles and the stress-energy tensor. I. Fundamental notions of CLE. arXiv 2009, arXiv:0903.0372. [Google Scholar]
- Lowner, K. Untersuchungen uber schlichte konforme Abbildungen des Einheitskreises. I. Math. Ann 1923, 89, 103. [Google Scholar] [CrossRef]
- Schramm, O. Scaling limits of loop-erased random walks and uniform spanning trees. In Selected Works of Oded Schramm; Springer: Berlin/Heidelberg, Germany, 2011; pp. 791–858. [Google Scholar]
- Cardy, J. SLE for theoretical physicists. Ann. Phys. 2005, 318, 81–118. [Google Scholar] [CrossRef]
- Janke, W.; Schakel, A.M. Geometrical vs. Fortuin–Kasteleyn clusters in the two-dimensional q-state Potts model. Nucl. Phys. B 2004, 700, 385–406. [Google Scholar] [CrossRef]
- Hoshen, J.; Berry, M.; Minser, K. Percolation and cluster structure parameters: The enhanced Hoshen-Kopelman algorithm. Phys. Rev. E 1997, 56, 1455. [Google Scholar] [CrossRef]
- Najafi, M.; Ghaedi, M. Geometrical clusters of Darcy’s reservoir model and Ising universality class. Phys. A Stat. Mech. Its Appl. 2015, 427, 82–91. [Google Scholar] [CrossRef]
- Den Nijs, M. Extended scaling relations for the magnetic critical exponents of the Potts model. Phys. Rev. B 1983, 27, 1674. [Google Scholar] [CrossRef]
- Di Francesco, P.; Saleur, H.; Zuber, J.B. Relations between the Coulomb gas picture and conformal invariance of two-dimensional critical models. J. Stat. Phys. 1987, 49, 57–79. [Google Scholar] [CrossRef]
- Den Nijs, M. A relation between the temperature exponents of the eight-vertex and q-state Potts model. J. Phys. Math. Gen. 1979, 12, 1857. [Google Scholar] [CrossRef]
- Zhang, L.R.; Ding, C.; Deng, Y.; Zhang, L. Surface criticality of the antiferromagnetic Potts model. Phys. Rev. B 2022, 105, 224415. [Google Scholar] [CrossRef]
- Nienhuis, B.; Berker, A.; Riedel, E.K.; Schick, M. First-and second-order phase transitions in Potts models: Renormalization-group solution. Phys. Rev. Lett. 1979, 43, 737. [Google Scholar] [CrossRef]
- Enting, I.; Wu, F. Triangular lattice Potts models. J. Stat. Phys. 1982, 28, 351–373. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nattagh Najafi, M.; Zayed, R.M.A.; Nabavizadeh, S.A. Swarming Transition in Super-Diffusive Self-Propelled Particles. Entropy 2023, 25, 817. https://doi.org/10.3390/e25050817
Nattagh Najafi M, Zayed RMA, Nabavizadeh SA. Swarming Transition in Super-Diffusive Self-Propelled Particles. Entropy. 2023; 25(5):817. https://doi.org/10.3390/e25050817
Chicago/Turabian StyleNattagh Najafi, Morteza, Rafe Md. Abu Zayed, and Seyed Amin Nabavizadeh. 2023. "Swarming Transition in Super-Diffusive Self-Propelled Particles" Entropy 25, no. 5: 817. https://doi.org/10.3390/e25050817
APA StyleNattagh Najafi, M., Zayed, R. M. A., & Nabavizadeh, S. A. (2023). Swarming Transition in Super-Diffusive Self-Propelled Particles. Entropy, 25(5), 817. https://doi.org/10.3390/e25050817






