Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory
Abstract
1. Introduction
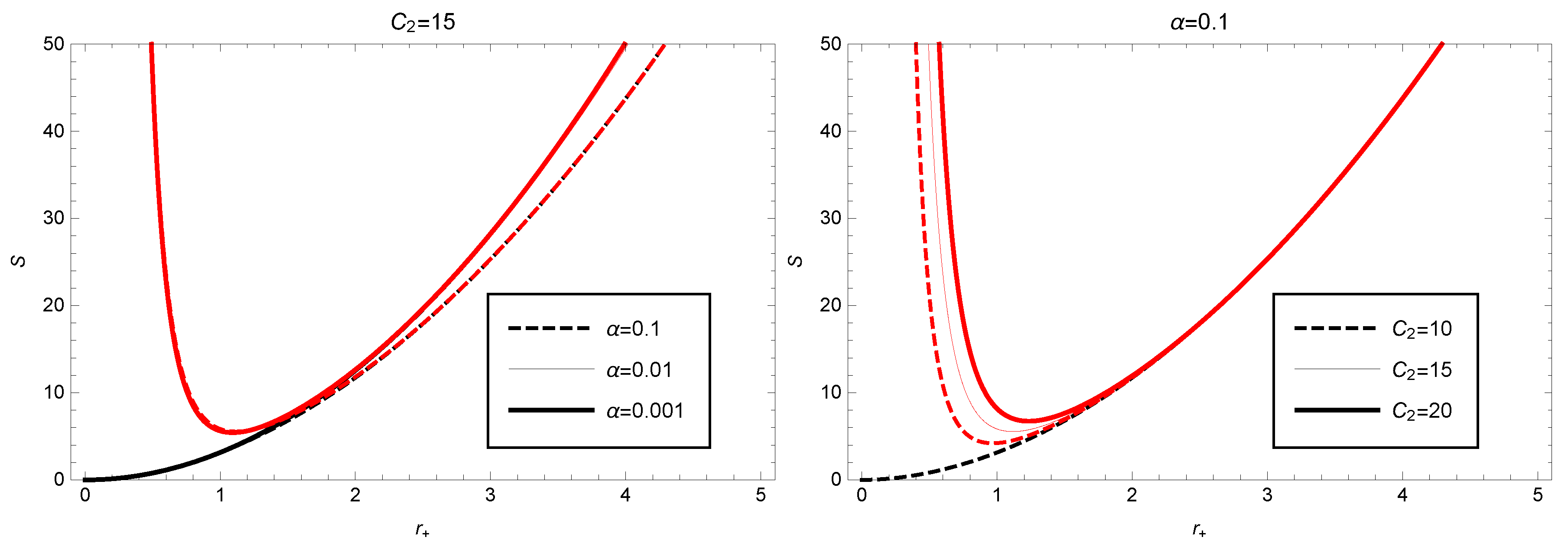
2. Entropy Correction of Black Hole Thermodynamics in GBD Modified Gravity Theory
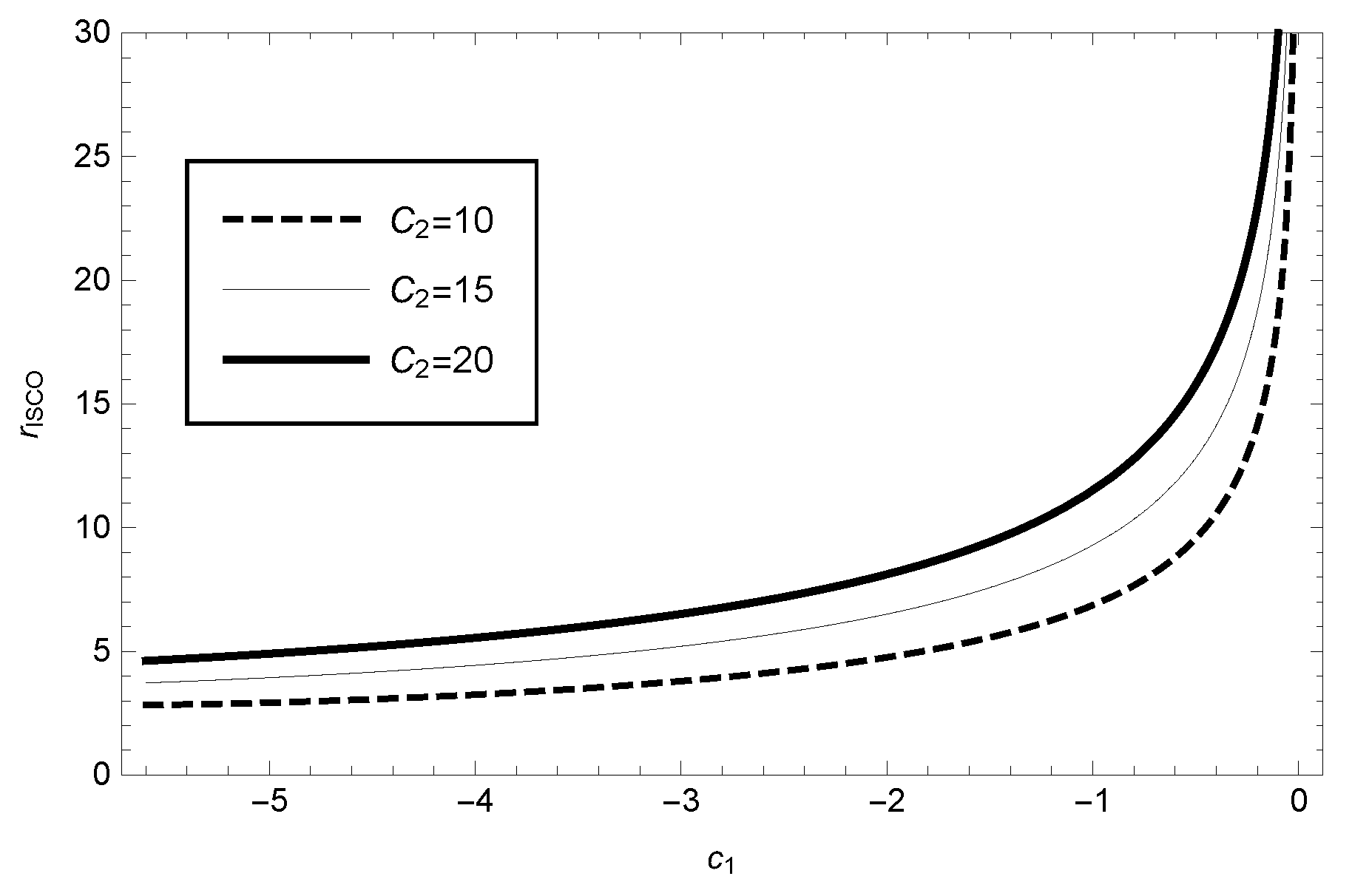
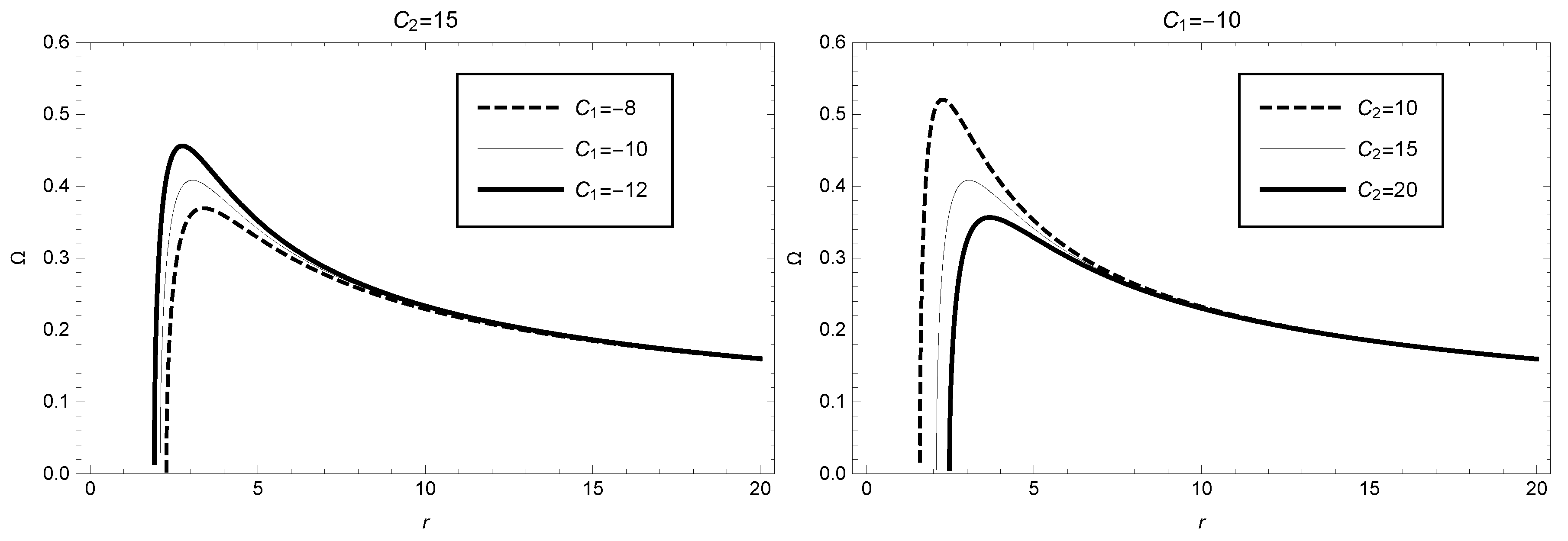
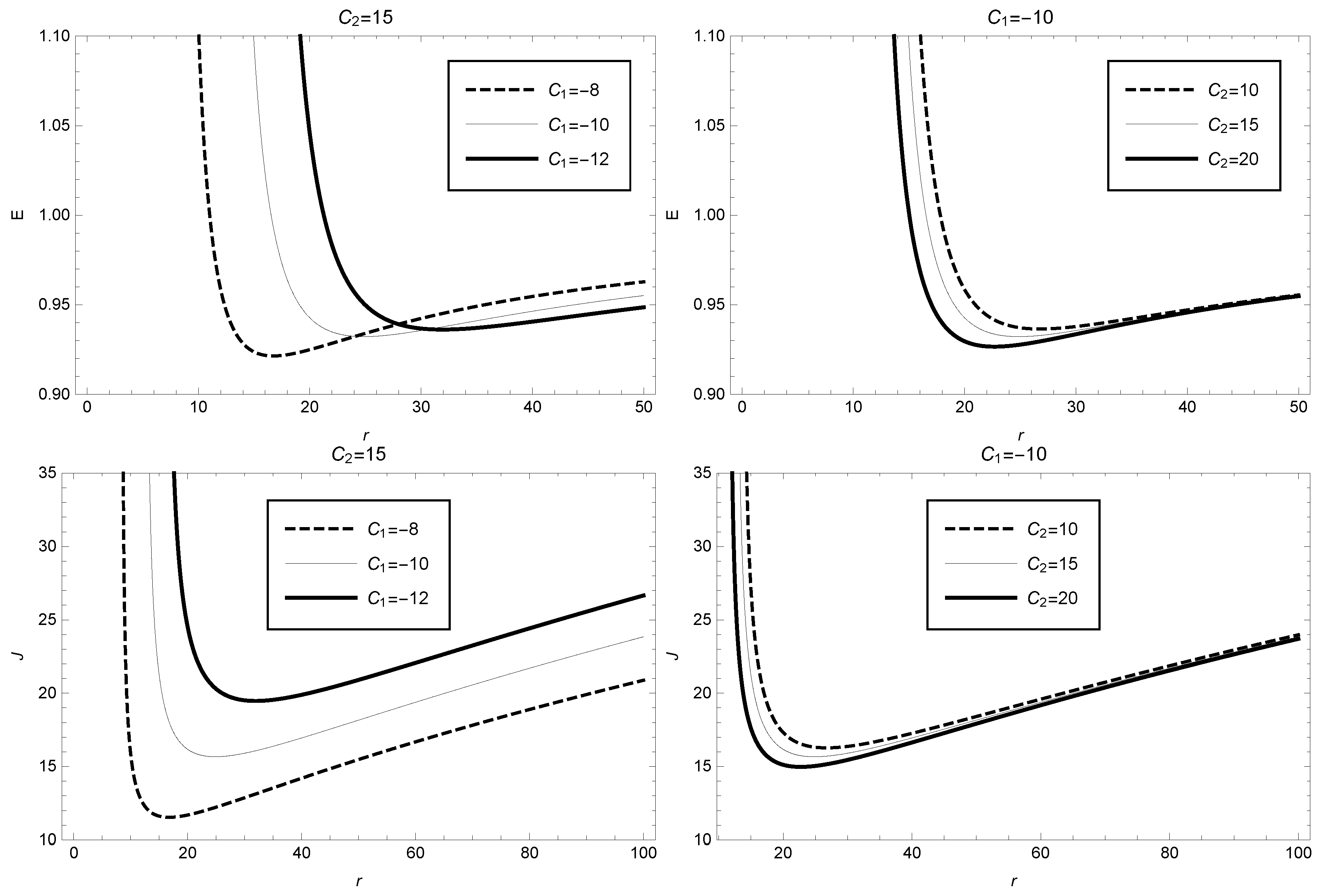
3. Stability Analysis of Particles’ Circular Orbits around a Black Hole under GBD Theory
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Kazunori, A.; Antxon, A.; Walter, A.; Kazunori, A.; Antxon, A.; Walter, A.; Keiichi, A.; Rebecca, A.; Anne-Kathrin, B.; David, B.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, 1. [Google Scholar]
- Felice, A.D.; Tsujikawa, S. f (R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. Rotating AdS black holes in Maxwell-f(T) gravity. Class. Quantum Gravity 2019, 36, 135005. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. Dark energy in modified Gauss-Bonnet gravity: Late-time acceleration and the hierarchy problem. Phys. Rev. D 2006, 73, 084007. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar-tensor theory. Int. J. Theor. Phys. 1968, 1, 25–36. [Google Scholar] [CrossRef]
- Deng, X.M. Constraints on a scalar-tensor theory with an intermediate-range force by binary pulsars. Sci. China Phys. Mech. Astron. 2011, 54, 2071–2077. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Two-post-Newtonian light propagation in the scalar-tensor theory: An N-point mass case. Phys. Rev. D 2012, 86, 044007. [Google Scholar] [CrossRef]
- Deng, X.M. Two-post-Newtonian approximation of the scalar-tensor theory with an intermediate-range force for general matter. Sci. China Phys. Mech. Astron. 2015, 58, 030002. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Solar System tests of a scalar-tensor gravity with a general potential: Insensitivity of light deflection and Cassini tracking. Phys. Rev. D 2016, 93, 044013. [Google Scholar] [CrossRef]
- Cheng, X.T.; Xie, Y. Probing a black-bounce, traversable wormhole with weak deflection gravitational lensing. Phys. Rev. D 2021, 103, 064040. [Google Scholar] [CrossRef]
- Moffat, J.W.J. Scalar–tensor–vector gravity theory. Cosmol. Astropart. Phys. 2006, 3, 4. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Modified scalar-tensor-vector gravity theory and the constraint on its parameters. Phys. Rev. D 2009, 79, 044014. [Google Scholar] [CrossRef]
- Lu, J.B.; Wang, Y.; Zhao, X. Linearized Modified Gravity Theories and Gravitational Waves Physics in the GBD Theory. Phys. Lett. B 2019, 795, 129–134. [Google Scholar] [CrossRef]
- Lu, J.B.; Wu, Y.B.; Yang, W.Q.; Liu, M.L.; Zhao, X. The Generalized Brans-Dicke Theory and its Cosmology. Eur. Phys. J. Plus 2019, 134, 138. [Google Scholar] [CrossRef]
- Lu, J.B.; Li, J.C.; Guo, H.; Zhuang, Z.T.; Zhao, X. Linearized Physics and Gravitational-waves Polarizations in the Palatini Formalism of GBD Theory. Phys. Lett. B 2020, 811, 135985. [Google Scholar] [CrossRef]
- Adler, S.L.; Virbhadra, K.S. Cosmological constant corrections to the photon sphere and black hole shadow radii. Gen. Relat. Grav. 2022, 54, 93. [Google Scholar] [CrossRef]
- Dimitrios, P.; Lia, M.; Pierre, C.; Feryal, O.; Kazunori, A.; Antxon, A.; Walter, A.; Keiichi, A.; Rebecca, A.; David, B.; et al. Gravitational Test Beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole. Phys. Rev. Lett. 2020, 125, 141104. [Google Scholar]
- Kumar, R.; Ghosh, S.G. Black Hole Parameter Estimation from Its Shadow. Astrophys. J. 2020, 892, 78. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Kumar, R.; Islam, S.U.I.J. Parameters estimation and strong gravitational lensing of nonsingular Kerr-Sen black holes. Cosmol. Astropart. Phys. 2021, 3, 56. [Google Scholar] [CrossRef]
- Afrin, M.; Kumar, R.; Ghosh, S.G. Parameter estimation of hairy Kerr black holes from its shadow and constraints from M87*. Mon. Not. R. Astron. Soc. 2021, 504, 5927–5940. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Afrin, M. Constraining Kerr-like black holes with Event Horizon Telescope results of Sgr A*. arXiv 2022, arXiv:2206.02488. [Google Scholar]
- Hu, S.Y.; Deng, C.; Li, D.; Wu, X.; Liang, E.W. Observational signatures of Schwarzschild-MOG black holes in scalar-tensor-vector gravity: Shadows and rings with different accretions. Eur. Phys. J. C 2022, 82, 885. [Google Scholar] [CrossRef]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Oliver, P.; Mariafelicia, D.L.; Hector, O.; Heino, F.; Michael, K.; Luciano, R. The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Psaltis, D. Testing general relativity with the Event Horizon Telescope. Gen. Relativ. Gravit. 2019, 51, 137. [Google Scholar] [CrossRef]
- Stepanian, A.; Khlghatyan, S.; Gurzadyan, V.G. Black hole shadow to probe modified gravity. Eur. Phys. J. Plus 2021, 136, 127. [Google Scholar] [CrossRef]
- Younsi, Z.; Psaltis, D.; Özel, F. Black Hole Images as Tests of General Relativity: Effects of Spacetime Geometry. arXiv 2021, arXiv:2111.01752. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y. Calculating black hole shadows: Review of analytical studies. Phys. Rep. 2022, 947, 1–39. [Google Scholar] [CrossRef]
- Walia, R.K.; Ghosh, S.G.; Maharaj, S.D. Testing Rotating Regular Spacetimes with EHT Results of Sgr A*. arXiv 2022, arXiv:2207.00078. [Google Scholar]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Luca, V. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Atamurotov, F.; Hussain, I.; Mustafa, G.; Jusufi, K. Shadow and quasinormal modes of the Kerr–Newman–Kiselev–Letelier black hole. Eur. Phys. J. C 2022, 82, 831. [Google Scholar] [CrossRef]
- Wu, M.H.; Guo, H.; Kuang, X.M. Shadow Cast of Rotating Charged Black Hole with Scalar Q-Hair. Symmetry 2022, 14, 2237. [Google Scholar] [CrossRef]
- Zhang, H.X.; Zhou, N.Y.; Liu, W.F.; Wu, X. Equivalence between two charged black holes in dynamics of orbits outside the event horizons. Gen. Relativ. Gravit. 2022, 54, 110. [Google Scholar] [CrossRef]
- Hu, S.Y.; Deng, C.; Guo, S.; Wu, X.; Liang, E.W. Observational signatures of Schwarzschild-MOG black holes in scalar–tensor–vector gravity: Images of the accretion disk. Eur. Phys. J. C 2023, 83, 264. [Google Scholar] [CrossRef]
- Nagy, C.; Keresztes, Z.; Laszlo, A.G. Spherically symmetric, static black holes with scalar hair, and naked singularities in nonminimally coupled k-essence. Phys. Rev. D 2011, 103, 124056. [Google Scholar] [CrossRef]
- Ghosh, R.; Rahman, M.; Mishra, A.K. Regularized stable Kerr black hole: Cosmic censorships, shadow and quasi-normal modes. Eur. Phys. J. C 2023, 83, 91. [Google Scholar] [CrossRef]
- Sharif, M.; Raza, A. Greybody factor for a static spherically symmetric black hole with non-linear electrodynamics. Ann. Phys. 2022, 442, 168920. [Google Scholar] [CrossRef]
- Hirotani, K.; Shang, H.; Krasnopolsky, R.; Nishikawa, K. Two-dimensional Particle-in-cell Simulations of Axisymmetric Black Hole Magnetospheres: Angular Dependence of the Blandford–Znajek Flux. Astrophys. J. 2023, 943, 164. [Google Scholar] [CrossRef]
- Hu, H.; Lan, C.; Miao, Y. A regular black hole as the final state of evolution of a singular black hole. arXiv 2023, arXiv:2303.03931. [Google Scholar]
- Fursaev, D.V.; Solodukhin, S.N. On one-loop renormalization of black-hole entropy. Phys. Lett. B 1996, 365, 51–55. [Google Scholar] [CrossRef]
- Kumar, S.G.; Sen, S. Further evidence for the conformal structure of a Schwarzschild black hole in an algebraic approach. Phys. Lett. B 2002, 526, 121. [Google Scholar]
- Sen, A. Logarithmic corrections to black hole entropy: An infrared window into the microstates. Gen. Relativ. Gravit. 2012, 44, 1207. [Google Scholar] [CrossRef]
- Sen, A. Logarithmic corrections to Schwarzschild and other non-extremal black hole entropy in different dimensions. J. High Energy Phys. 2013, 4, 156. [Google Scholar] [CrossRef]
- Nashed, G.G.; Emmanuel, N.S. Stability of motion and thermodynamics in charged black holes in f (T) gravity. J. Cosmol. Astropart. Phys. 2022, 5, 17. [Google Scholar] [CrossRef]
- Nashed, G.G.L. New rotating AdS/dS black holes in f (R) gravity. Phys. Lett. B 2012, 815, 136133. [Google Scholar] [CrossRef]
- Nashed, G.G.; Nojiri, S. Nontrivial black hole solutions ingravitational theory. Phys. Rev. D 2020, 102, 124022. [Google Scholar] [CrossRef]
- Elizalde, E.; Nashed, G.G.; Nojiri, S.; Odintsov, S.D. Spherically symmetric black holes with electric and magnetic charge in extended gravity: Physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames. Eur. Phys. J. C 2020, 80, 109. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Analytic charged BHs in f (R) gravity. Phys. Rev. D 2021, 104, 044043. [Google Scholar] [CrossRef]
- Ghosh, S.; Kar, S.; Nandan, H. Confinement of test particles in warped spacetimes. Phys. Rev. D 2010, 82, 024040. [Google Scholar] [CrossRef]
- Uniyal, R.; Nandan, H.; Purohit, K.D. Geodesic Motion in a Charged 2D Stringy Blackhole Spacetime. Mod. Phys. Lett. A 2014, 29, 1450157. [Google Scholar] [CrossRef]
- Tian, D.W. Supporting wormholes by spacetime parity and topology in Lovelock-Brans-Dicke gravity. arXiv 2015, arXiv:1508.02291. [Google Scholar]
- Capozziello, S. Matching torsion Lambda - term with observations. Int. J. Theor. Phys. 2002, 11, 483–492. [Google Scholar]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of explicit symplectic integrators in general relativity. II. Reissner-Nordstrom black holes. Astrophys. J. 2021, 909, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of explicit symplectic integrators in general relativity. III. Reissner–Nordström-(anti)-de Sitter black holes. Astrophys. J. Suppl. Ser. 2021, 254, 8. [Google Scholar] [CrossRef]
- Pourhassan, B.; Upadhyay, S.; Saadat, H.; Farahani, H. Quantum gravity effects on Hořava-Lifshitz black hole. Nucl. Phys. B 2018, 928, 415. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure (In 2 Volumes). Nucl. Struct. 1969, 1, 281–283. [Google Scholar]
- Bhaduri, R.K. Models of the nucleon: From quarks to soliton. Models of the Nucleon; Addison-Wesley: Boston, MA, USA, 1988; p. 116. [Google Scholar]
- Das, S.; Majumdar, P.; Bhaduri, R.K. General logarithmic corrections to black-hole entropy. Class. Quantum Gravity 2002, 19, 2355–2367. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, Y.; Zhang, J. Thermodynamic geometric analysis of Schwarzschild and RN black hole under f (R) gravity. arXiv 2021, arXiv:2112.06718. [Google Scholar]
- Edward, T. Spherical Photon Orbits Around a Kerr Black Hole. Gen. Relativ. Gravit. 2003, 35, 1909. [Google Scholar]
- Teo, E. Spherical orbits around a Kerr black hole. Gen. Relativ. Gravit. 2021, 53, 10. [Google Scholar] [CrossRef]
- Sun, X.; Wu, X.; Wang, Y.; Deng, C.; Liu, B.R.; Liang, E.W. Dynamics of charged particles moving around kerr black hole with inductive charge and external magnetic field. Universe 2021, 7, 410. [Google Scholar] [CrossRef]
- Cao, W.F.; Liu, W.F.; Wu, X. Integrability of Kerr-Newman spacetime with cloud strings, quintessence and electromagnetic field. Phys. Rev. D 2022, 105, 124039. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Precessing and periodic orbits around hairy black holes in Horndeski’s Theory. Eur. Phys. J. C 2023, 83, 311. [Google Scholar] [CrossRef]
- Zhang, H.X.; Zhou, N.Y.; Liu, W.F.; Wu, X. Charged particle motions near non-Schwarzschild black holes with external magnetic fields in modified theories of gravity. Universe 2021, 7, 488. [Google Scholar] [CrossRef]
- Yang, D.Q.; Cao, W.F.; Zhou, N.Y.; Zhang, H.X.; Liu, W.F.; Wu, X. Chaos in a magnetized modified gravity Schwarzschild spacetime. Universe 2022, 8, 320. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Y.; Sun, W.; Liu, F.Y.; Han, W.B. Explicit symplectic methods in black hole spacetimes. Astrophys. J. 2022, 940, 166. [Google Scholar] [CrossRef]
- Page, D.N.; Thorne, K.S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. Astrophys. J. 1974, 191, 499. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-accretion onto a black hole. II. Evolution of the hole. Astrophys. J. 1974, 191, 507. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Lu, J.; Yang, S.; Jiang, H. Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory. Entropy 2023, 25, 814. https://doi.org/10.3390/e25050814
Xu M, Lu J, Yang S, Jiang H. Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory. Entropy. 2023; 25(5):814. https://doi.org/10.3390/e25050814
Chicago/Turabian StyleXu, Mou, Jianbo Lu, Shining Yang, and Hongnan Jiang. 2023. "Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory" Entropy 25, no. 5: 814. https://doi.org/10.3390/e25050814
APA StyleXu, M., Lu, J., Yang, S., & Jiang, H. (2023). Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory. Entropy, 25(5), 814. https://doi.org/10.3390/e25050814



