Nontraditional Deterministic Remote State Preparation Using a Non-Maximally Entangled Channel without Additional Quantum Resources
Abstract
1. Introduction
2. Preliminaries
3. Deterministic RSP via a Generally Entangled Quantum Channel
3.1. Deterministic RSP of a 2-Dimensional Quantum State via a Generally Entangled Quantum Channel
3.2. Deterministic RSP of a d-Dimensional Quantum State via a Generally Entangled Quantum Channel
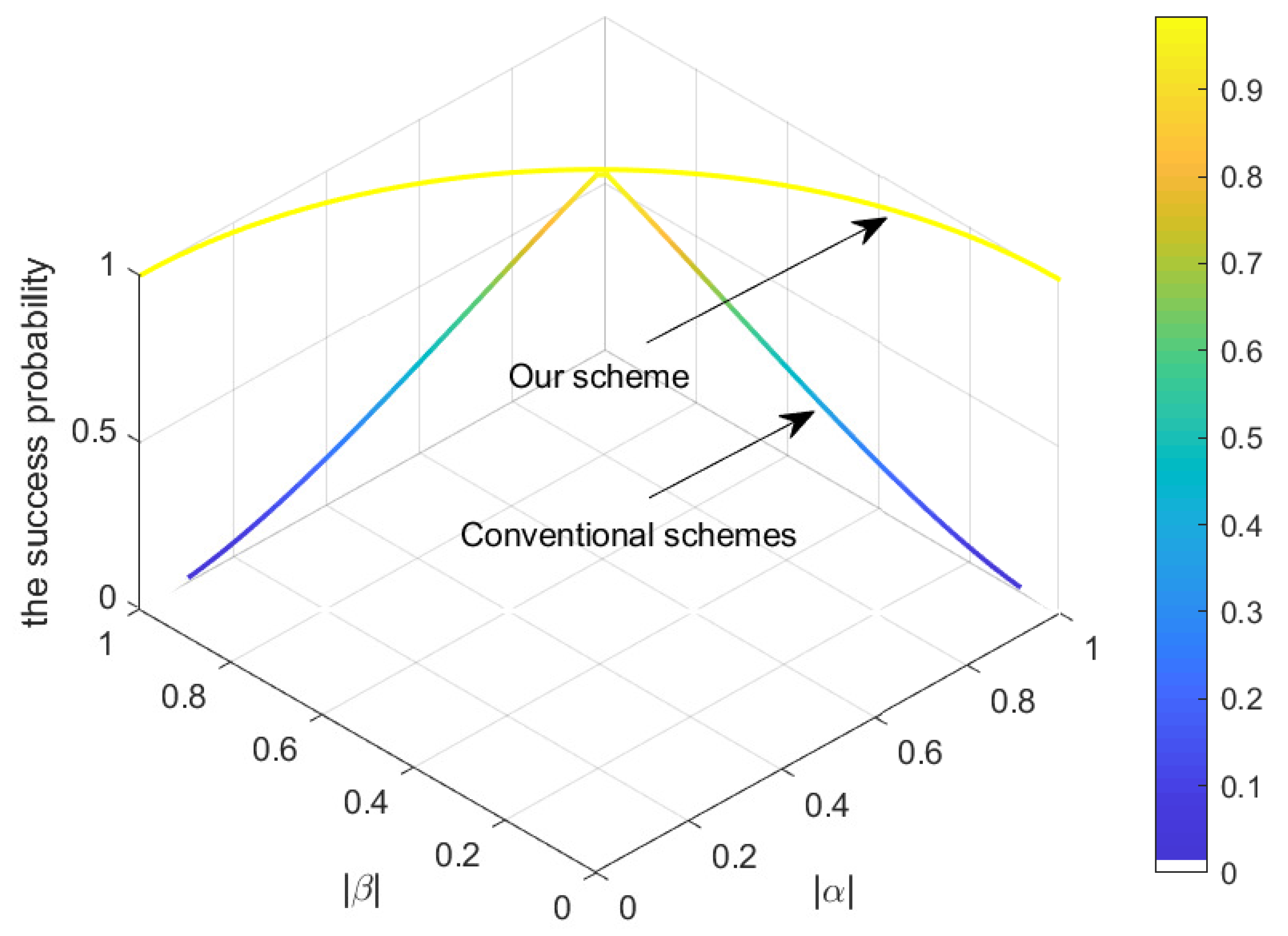
4. Realization
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QT | Quantum Teleportation |
| QKD | Quantum Key Distribution |
| QDC | Quantum Dense Coding |
| QSDC | Quantum Secure Direct Communication |
| RSP | Remote State Preparation |
References
- Yurke, B.; Denker, J.S. Quantum network theory. Phys. Rev. A 1984, 29, 1419–1437. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P.; Kimble, H.J.; Mabuchi, H. Quantum State Transfer and Entanglement Distribution among Distant Nodes in a Quantum Network. Phys. Rev. Lett. 1997, 78, 3221–3224. [Google Scholar] [CrossRef]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195–200. [Google Scholar] [CrossRef]
- Simon, C. Towards a global quantum network. Nat. Photonics 2017, 11, 678–680. [Google Scholar] [CrossRef]
- Liao, S.K.; Cai, W.Q.; Handsteiner, J.; Liu, B.; Yin, J.; Zhang, L.; Rauch, D.; Fink, M.; Ren, J.G.; Liu, W.Y.; et al. Satellite-Relayed Intercontinental Quantum Network. Phys. Rev. Lett. 2018, 120, 030501. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Chen, Y.; Zhou, Z.; Long, G. A quantum convolutional neural network on NISQ devices. AAPPS Bull. 2022, 32, 2. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Ruan, D.; Long, G. Quantum direct portation. Acta Phys. Sin. 2001, 70, 190301. [Google Scholar] [CrossRef]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.; Trojek, P.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481–486. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, A.; Bourennane, M. Quantum teleportation using three-particle entanglement. Phys. Rev. A 1998, 58, 4394–4400. [Google Scholar] [CrossRef]
- Stenholm, S.; Bardroff, P.J. Teleportation of N-dimensional states. Phys. Rev. A 1998, 58, 4373–4376. [Google Scholar] [CrossRef]
- Cabello, A. Quantum Key Distribution in the Holevo Limit. Phys. Rev. Lett. 2000, 85, 5635–5638. [Google Scholar] [CrossRef]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [PubMed]
- Barrett, J.; Hardy, L.; Kent, A. No Signaling and Quantum Key Distribution. Phys. Rev. Lett. 2005, 95, 010503. [Google Scholar] [CrossRef]
- Qi, R.; Zhang, H.; Gao, J.; Yin, L.; Long, G.L. Loophole-free plug-and-play quantum key distribution. N. J. Phys. 2021, 23, 063058. [Google Scholar] [CrossRef]
- Kwek, L.C.; Cao, L.; Luo, W.; Wang, Y.; Sun, S.; Wang, X.; Liu, A.Q. Chip-based quantum key distribution. AAPPS Bull. 2021, 31, 15. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
- Mattle, K.; Weinfurter, H.; Kwiat, P.G.; Zeilinger, A. Dense Coding in Experimental Quantum Communication. Phys. Rev. Lett. 1996, 76, 4656–4659. [Google Scholar] [CrossRef]
- Bruß, D.; D’Ariano, G.M.; Lewenstein, M.; Macchiavello, C.; Sen, A.; Sen, U. Distributed Quantum Dense Coding. Phys. Rev. Lett. 2004, 93, 210501. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Advances in Quantum Dense Coding. Adv. Quantum Technol. 2019, 2, 1900011. [Google Scholar] [CrossRef]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L. Secure direct communication with a quantum one-time pad. Phys. Rev. A 2004, 69, 052319. [Google Scholar] [CrossRef]
- Zhang, W.; Ding, D.S.; Sheng, Y.B.; Zhou, L.; Shi, B.S.; Guo, G.C. Quantum Secure Direct Communication with Quantum Memory. Phys. Rev. Lett. 2017, 118, 220501. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H.; Habib, S.; Paz, J.P. Coherent states via decoherence. Phys. Rev. Lett. 1993, 70, 1187–1190. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1998, 81, 2594–2597. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2005, 76, 1267–1305. [Google Scholar] [CrossRef]
- Xiang, G.Y.; Li, J.; Yu, B.; Guo, G.C. Remote preparation of mixed states via noisy entanglement. Phys. Rev. A 2005, 72, 012315. [Google Scholar] [CrossRef]
- Banaszek, K. Optimal quantum teleportation with an arbitrary pure state. Phys. Rev. A 2000, 62, 024301. [Google Scholar] [CrossRef]
- Li, W.L.; Li, C.F.; Guo, G.C. Probabilistic teleportation and entanglement matching. Phys. Rev. A 2000, 61, 034301. [Google Scholar] [CrossRef]
- Roa, L.; Delgado, A.; Fuentes-Guridi, I. Optimal conclusive teleportation of quantum states. Phys. Rev. A 2003, 68, 022310. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Hoehn, R.D.; Ye, L.; Kais, S. Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements. Entropy 2015, 17, 1755–1774. [Google Scholar] [CrossRef]
- Pirandola, S.; Braunstein, S.L. Physics: Unite to build a quantum Internet. Nat. News 2016, 532, 169. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362. [Google Scholar] [CrossRef]
- Yang, F.; Chen, X.; Zhao, D.; Wei, S.; Wen, J.; Wang, H.; Xin, T.; Long, G. Quantum Multi-Round Resonant Transition Algorithm. Entropy 2023, 25, 61. [Google Scholar] [CrossRef]
- Lu, B.; Liu, L.; Song, J.Y.; Wen, K.; Wang, C. Recent progress on coherent computation based on quantum squeezing. AAPPS Bull. 2023, 33, 7. [Google Scholar] [CrossRef]
- Xu, G.F.; Tong, D.M. Realizing multi-qubit controlled nonadiabatic holonomic gates with connecting systems. AAPPS Bull. 2022, 32, 13. [Google Scholar] [CrossRef]
- Dakić, B.; Lipp, Y.O.; Ma, X.; Ringbauer, M.; Kropatschek, S.; Barz, S.; Paterek, T.; Vedral, V.; Zeilinger, A.; Brukner, Č.; et al. Quantum discord as resource for remote state preparation. Nat. Phys. 2012, 8, 666–670. [Google Scholar] [CrossRef]
- Monz, T.; Schindler, P.; Barreiro, J.T.; Chwalla, M.; Nigg, D.; Coish, W.A.; Harlander, M.; Hänsel, W.; Hennrich, M.; Blatt, R. 14-Qubit Entanglement: Creation and Coherence. Phys. Rev. Lett. 2011, 106, 130506. [Google Scholar] [CrossRef]
- Yao, X.C.; Wang, T.X.; Xu, P.; Lu, H.; Pan, G.S.; Bao, X.H.; Peng, C.Z.; Lu, C.Y.; Chen, Y.A.; Pan, J.W. Observation of eight-photon entanglement. Nat. Photonics 2012, 6, 225–228. [Google Scholar] [CrossRef]
- Huang, Y.F.; Liu, B.H.; Peng, L.; Li, Y.H.; Li, L.; Li, C.F.; Guo, G.C. Experimental generation of an eight-photon Greenberger–Horne–Zeilinger state. Nat. Commun. 2011, 2, 1–6. [Google Scholar] [CrossRef]
- Zhang, F.; Xing, J.; Hu, X.; Pan, X.; Long, G. Coupling-selective quantum optimal control in weak-coupling NV-13 C system. AAPPS Bull. 2023, 33, 2. [Google Scholar] [CrossRef]
- Wagenknecht, C.; Li, C.M.; Reingruber, A.; Bao, X.H.; Goebel, A.; Chen, Y.A.; Zhang, Q.; Chen, K.; Pan, J.W. Experimental demonstration of a heralded entanglement source. Nat. Photonics 2010, 4, 549–552. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, X.M.; Yang, J.; Dai, H.N.; Yang, S.J.; Zhao, T.M.; Rui, J.; He, Y.; Jiang, X.; Yang, F.; et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nat. Photonics 2011, 5, 628–632. [Google Scholar] [CrossRef]
- Yin, J.; Li, Y.H.; Liao, S.K.; Yang, M.; Cao, Y.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, S.L.; et al. Entanglement-based secure quantum cryptography over 1,120 kilometres. Nature 2020, 582, 501–505. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Popescu, S.; Schumacher, B.; Smolin, J.A.; Wootters, W.K. Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels. Phys. Rev. Lett. 1996, 76, 722–725. [Google Scholar] [CrossRef]
- Deutsch, D.; Ekert, A.; Jozsa, R.; Macchiavello, C.; Popescu, S.; Sanpera, A. Quantum Privacy Amplification and the Security of Quantum Cryptography over Noisy Channels. Phys. Rev. Lett. 1996, 77, 2818–2821. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar] [CrossRef]
- Bombin, H.; Martin-Delgado, M.A. Topological Quantum Distillation. Phys. Rev. Lett. 2006, 97, 180501. [Google Scholar] [CrossRef]
- Zwerger, M.; Briegel, H.J.; Dür, W. Universal and Optimal Error Thresholds for Measurement-Based Entanglement Purification. Phys. Rev. Lett. 2013, 110, 260503. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.M.; Huang, C.X.; Sheng, Y.B.; Zhou, L.; Liu, B.H.; Guo, Y.; Zhang, C.; Xing, W.B.; Huang, Y.F.; Li, C.F.; et al. Long-Distance Entanglement Purification for Quantum Communication. Phys. Rev. Lett. 2021, 126, 010503. [Google Scholar] [CrossRef] [PubMed]
- Jonathan, D.; Plenio, M.B. Entanglement-assisted local manipulation of pure quantum states. Phys. Rev. Lett. 1999, 83, 3566. [Google Scholar] [CrossRef]
- Daftuar, S.; Klimesh, M. Mathematical structure of entanglement catalysis. Phys. Rev. A 2001, 64, 042314. [Google Scholar] [CrossRef]
- Van Dam, W.; Hayden, P. Universal entanglement transformations without communication. Phys. Rev. A 2003, 67, 060302. [Google Scholar] [CrossRef]
- Sanders, Y.R.; Gour, G. Necessary conditions for entanglement catalysts. Phys. Rev. A 2009, 79, 054302. [Google Scholar] [CrossRef]
- Popescu, S. Bell’s Inequalities and Density Matrices: Revealing “Hidden” Nonlocality. Phys. Rev. Lett. 1995, 74, 2619–2622. [Google Scholar] [CrossRef]
- Peres, A. Collective tests for quantum nonlocality. Phys. Rev. A 1996, 54, 2685–2689. [Google Scholar] [CrossRef]
- Masanes, L. All Bipartite Entangled States Are Useful for Information Processing. Phys. Rev. Lett. 2006, 96, 150501. [Google Scholar] [CrossRef]
- Masanes, L.; Liang, Y.C.; Doherty, A.C. All Bipartite Entangled States Display Some Hidden Nonlocality. Phys. Rev. Lett. 2008, 100, 090403. [Google Scholar] [CrossRef]
- Liang, Y.C.; Masanes, L.; Rosset, D. All entangled states display some hidden nonlocality. Phys. Rev. A 2012, 86, 052115. [Google Scholar] [CrossRef]
- Riera-Sàbat, F.; Sekatski, P.; Pirker, A.; Dür, W. Entanglement-Assisted Entanglement Purification. Phys. Rev. Lett. 2021, 127, 040502. [Google Scholar] [CrossRef]
- Lipka-Bartosik, P.; Skrzypczyk, P. Catalytic Quantum Teleportation. Phys. Rev. Lett. 2021, 127, 080502. [Google Scholar] [CrossRef]
- Li, J.Y.; Fang, X.X.; Zhang, T.; Tabia, G.N.M.; Lu, H.; Liang, Y.C. Activating hidden teleportation power: Theory and experiment. Phys. Rev. Res. 2021, 3, 023045. [Google Scholar] [CrossRef]
- Lo, H.K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Shor, P.W.; Smolin, J.A.; Terhal, B.M.; Wootters, W.K. Remote State Preparation. Phys. Rev. Lett. 2001, 87, 077902. [Google Scholar] [CrossRef] [PubMed]
- Pati, A.K. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A 2000, 63, 014302. [Google Scholar] [CrossRef]
- Nguyen, B.A.; Cao, T.B.; Nung, V.D.; Kim, J. Remote state preparation with unit success probability. Adv. Nat. Sci. 2011, 2, 035009. [Google Scholar] [CrossRef]
- Xu, G.; Chen, X.B.; Dou, Z.; Li, J.; Liu, X.; Li, Z. Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State. Entropy 2016, 18, 267. [Google Scholar] [CrossRef]
- An, N.B.; Dat, L.T.; Kim, J. Nonstandard protocols for joint remote preparation of a general quantum state and hybrid entanglement of any dimension. Phys. Rev. A 2018, 98, 042329. [Google Scholar] [CrossRef]
- Du, Z.; Li, X. Deterministic joint remote state preparation of four-qubit cluster type with tripartite involvement. Quantum Inf. Process. 2019, 19, 39. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. Two-bit gates are universal for quantum computation. Phys. Rev. A 1995, 51, 1015–1022. [Google Scholar] [CrossRef]
- Sleator, T.; Weinfurter, H. Realizable Universal Quantum Logic Gates. Phys. Rev. Lett. 1995, 74, 4087–4090. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef]
- Kim, Y.H. Single-photon two-qubit entangled states: Preparation and measurement. Phys. Rev. A 2003, 67, 040301. [Google Scholar] [CrossRef]
- U’Ren, A.B.; Silberhorn, C.; Banaszek, K.; Walmsley, I.A. Efficient Conditional Preparation of High-Fidelity Single Photon States for Fiber-Optic Quantum Networks. Phys. Rev. Lett. 2004, 93, 093601. [Google Scholar] [CrossRef]
- Mosley, P.J.; Lundeen, J.S.; Smith, B.J.; Wasylczyk, P.; U’Ren, A.B.; Silberhorn, C.; Walmsley, I.A. Heralded Generation of Ultrafast Single Photons in Pure Quantum States. Phys. Rev. Lett. 2008, 100, 133601. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Remote Preparation of Single-Photon “Hybrid” Entangled and Vector-Polarization States. Phys. Rev. Lett. 2010, 105, 030407. [Google Scholar] [CrossRef]
- Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Burnham, D.C.; Weinberg, D.L. Observation of Simultaneity in Parametric Production of Optical Photon Pairs. Phys. Rev. Lett. 1970, 25, 84–87. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Mattle, K.; Weinfurter, H.; Zeilinger, A.; Sergienko, A.V.; Shih, Y. New High-Intensity Source of Polarization-Entangled Photon Pairs. Phys. Rev. Lett. 1995, 75, 4337–4341. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Waks, E.; White, A.G.; Appelbaum, I.; Eberhard, P.H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 1999, 60, R773–R776. [Google Scholar] [CrossRef]
- De Caro, L.; Garuccio, A. Reliability of Bell-inequality measurements using polarization correlations in parametric-down-conversion photon sources. Phys. Rev. A 1994, 50, R2803–R2805. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Pan, J.W.; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. Experimental test of quantum nonlocality in three-photon Greenberger-Horne-Zeilinger entanglement. Nature 2000, 403, 515–519. [Google Scholar] [CrossRef]
- Yin, J.; Ren, J.G.; Lu, H.; Cao, Y.; Yong, H.L.; Wu, Y.P.; Liu, C.; Liao, S.K.; Zhou, F.; Jiang, Y.; et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature 2012, 488, 185–188. [Google Scholar] [CrossRef]
- Ren, J.G.; Xu, P.; Yong, H.L.; Zhang, L.; Liao, S.K.; Yin, J.; Liu, W.Y.; Cai, W.Q.; Yang, M.; Li, L.; et al. Ground-to-satellite quantum teleportation. Nature 2017, 549, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.M.; Chen, J.S.; Liu, B.H.; Guo, Y.; Huang, Y.F.; Zhou, Z.Q.; Han, Y.J.; Li, C.F.; Guo, G.C. Experimental Test of Compatibility-Loophole-Free Contextuality with Spatially Separated Entangled Qutrits. Phys. Rev. Lett. 2016, 117, 170403. [Google Scholar] [CrossRef]
- Hu, X.M.; Zhang, C.; Liu, B.H.; Cai, Y.; Ye, X.J.; Guo, Y.; Xing, W.B.; Huang, C.X.; Huang, Y.F.; Li, C.F.; et al. Experimental High-Dimensional Quantum Teleportation. Phys. Rev. Lett. 2020, 125, 230501. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Y.; Gong, S.; Wu, W.; Cai, W.; Ren, M.; Ren, X.; Zhang, S.; Guo, G.; Xu, J. All-optical modulation of quantum states by nonlinear metasurface. Light Sci. Appl. 2022, 11, 58. [Google Scholar] [CrossRef]
- Nemoto, K.; Munro, W.J. Nearly Deterministic Linear Optical Controlled-NOT Gate. Phys. Rev. Lett. 2004, 93, 250502. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, A.N.; Chen, Y.A.; Zhang, H.; Du, J.F.; Yang, T.; Pan, J.W. Experimental Demonstration of a Nondestructive Controlled-NOT Quantum Gate for Two Independent Photon Qubits. Phys. Rev. Lett. 2005, 94, 030501. [Google Scholar] [CrossRef]
- Yamamoto, T.; Pashkin, Y.A.; Astafiev, O.; Nakamura, Y.; Tsai, J.S. Demonstration of conditional gate operation using superconducting charge qubits. Nature 2003, 425, 941–944. [Google Scholar] [CrossRef]
- Tipsmark, A.; Dong, R.; Laghaout, A.; Marek, P.; Ježek, M.; Andersen, U.L. Experimental demonstration of a Hadamard gate for coherent state qubits. Phys. Rev. A 2011, 84, 050301. [Google Scholar] [CrossRef]
- Podoshvedov, S.A. Building of one-way Hadamard gate for squeezed coherent states. Phys. Rev. A 2013, 87, 012307. [Google Scholar] [CrossRef]
- Larsen, M.V.; Guo, X.; Breum, C.R.; Neergaard-Nielsen, J.S.; Andersen, U.L. Deterministic multi-mode gates on a scalable photonic quantum computing platform. Nat. Phys. 2021, 17, 1018–1023. [Google Scholar] [CrossRef]
- Rauschenbeutel, A.; Nogues, G.; Osnaghi, S.; Bertet, P.; Brune, M.; Raimond, J.M.; Haroche, S. Coherent Operation of a Tunable Quantum Phase Gate in Cavity QED. Phys. Rev. Lett. 1999, 83, 5166–5169. [Google Scholar] [CrossRef]
- Lemr, K.; Černoch, A.; Soubusta, J.; Kieling, K.; Eisert, J.; Dušek, M. Experimental Implementation of the Optimal Linear-Optical Controlled Phase Gate. Phys. Rev. Lett. 2011, 106, 013602. [Google Scholar] [CrossRef]
- Heuck, M.; Jacobs, K.; Englund, D.R. Controlled-Phase Gate Using Dynamically Coupled Cavities and Optical Nonlinearities. Phys. Rev. Lett. 2020, 124, 160501. [Google Scholar] [CrossRef]
- Leonhardt, U. Quantum-State Tomography and Discrete Wigner Function. Phys. Rev. Lett. 1995, 74, 4101–4105. [Google Scholar] [CrossRef]
- Gross, D.; Liu, Y.K.; Flammia, S.T.; Becker, S.; Eisert, J. Quantum State Tomography via Compressed Sensing. Phys. Rev. Lett. 2010, 105, 150401. [Google Scholar] [CrossRef]
- Rambach, M.; Qaryan, M.; Kewming, M.; Ferrie, C.; White, A.G.; Romero, J. Robust and Efficient High-Dimensional Quantum State Tomography. Phys. Rev. Lett. 2021, 126, 100402. [Google Scholar] [CrossRef] [PubMed]
- Roa, L.; Groiseau, C. Probabilistic teleportation without loss of information. Phys. Rev. A 2015, 91, 012344. [Google Scholar] [CrossRef]
- Yu, C.S.; Song, H.S.; Wang, Y.H. Remote preparation of a qudit using maximally entangled states of qubits. Phys. Rev. A 2006, 73, 022340. [Google Scholar] [CrossRef]
- Zeng, B.; Zhang, P. Remote-state preparation in higher dimension and the parallelizable manifold Sn−1. Phys. Rev. A 2002, 65, 022316. [Google Scholar] [CrossRef]
- Dada, A.C.; Leach, J.; Buller, G.S.; Padgett, M.J.; Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nat. Phys. 2011, 7, 677–680. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Erhard, M.; Krenn, M.; Zeilinger, A. Advances in high-dimensional quantum entanglement. Nat. Rev. Phys. 2020, 2, 365–381. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; He, S.; Li, Y.; Li, C. Nontraditional Deterministic Remote State Preparation Using a Non-Maximally Entangled Channel without Additional Quantum Resources. Entropy 2023, 25, 768. https://doi.org/10.3390/e25050768
Xin X, He S, Li Y, Li C. Nontraditional Deterministic Remote State Preparation Using a Non-Maximally Entangled Channel without Additional Quantum Resources. Entropy. 2023; 25(5):768. https://doi.org/10.3390/e25050768
Chicago/Turabian StyleXin, Xuanxuan, Shiwen He, Yongxing Li, and Chong Li. 2023. "Nontraditional Deterministic Remote State Preparation Using a Non-Maximally Entangled Channel without Additional Quantum Resources" Entropy 25, no. 5: 768. https://doi.org/10.3390/e25050768
APA StyleXin, X., He, S., Li, Y., & Li, C. (2023). Nontraditional Deterministic Remote State Preparation Using a Non-Maximally Entangled Channel without Additional Quantum Resources. Entropy, 25(5), 768. https://doi.org/10.3390/e25050768






