On Two Non-Ergodic Reversible Cellular Automata, One Classical, the Other Quantum †
Abstract
1. Introduction
2. Matter–Field Automaton
2.1. Definition of the Automaton
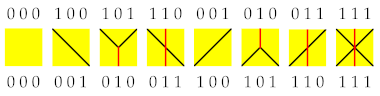
- “Charge” conjugation C, , i.e., if is a valid trajectory, then is a valid trajectory,
- Parity P, , i.e., if is a valid trajectory, then is a valid trajectory,
- Time reversal T, , i.e., if is a valid trajectory, then is a valid trajectory.
2.2. Time Evolution over Abelian Algebra of Local Observables
2.3. Conservation Laws
3. Deformed (Quantized) Hardpoint Lattice Gas
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casati, G.; Prosen, T. Mixing property of triangular billiards. Phys. Rev. Lett. 1999, 83, 4729–4732. [Google Scholar] [CrossRef]
- Casati, G.; Prosen, T. Triangle map: A model of quantum chaos. Phys. Rev. Lett. 2000, 85, 4261–4264. [Google Scholar] [CrossRef] [PubMed]
- Casati, G.; Prosen, T. Nonergodicity and localization of invariant measure for two colliding masses. Phys. Rev. E 2014, 89, 042918. [Google Scholar]
- Lozej, Č.; Casati, G.; Prosen, T. Quantum chaos in triangular billiards. Phys. Rev. Res. 2022, 4, 013138. [Google Scholar] [CrossRef]
- Cornfeld, I.P.; Fomin, S.V.; Sinai, Y.G. Ergodic Theory; Springer: New York, NY, USA, 1982. [Google Scholar]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Moudgalya, S.; Bernevig, B.A.; Regnault, N. Quantum many-body scars and Hilbert space fragmentation: A review of exact results. Rep. Prog. Phys. 2022, 85, 086501. [Google Scholar] [CrossRef]
- Spohn, H. Hydrodynamic scales of integrable many-particle systems. arXiv 2023, arXiv:2301.08504. [Google Scholar]
- Medenjak, M.; Klobas, K.; Prosen, T. Diffusion in Deterministic Interacting Lattice Systems. Phys. Rev. Lett. 2017, 119, 110603. [Google Scholar] [CrossRef]
- Medenjak, M.; Popkov, V.; Prosen, T.; Ragoucy, R.; Vanicat, M. Two-species hardcore reversible cellular automaton: Matrix ansatz for dynamics and nonequilibrium stationary state. SciPost Phys. 2019, 6, 074. [Google Scholar] [CrossRef]
- Krajnik, Ž.; Schmidt, J.; Pasquier, V.; Ilievski, I.; Prosen, T. Exact Anomalous Current Fluctuations in a Deterministic Interacting Model. Phys. Rev. Lett. 2022, 128, 160601. [Google Scholar] [CrossRef] [PubMed]
- Buča, B.; Klobas, K.; Prosen, T. Rule 54: Exactly solvable model of nonequilibrium statistical mechanics. J. Stat. Mech. 2021, 7, 074001. [Google Scholar] [CrossRef]
- Klobas, K.; Medenjak, M.; Prosen, T.; Vanicat, M. Time-Dependent Matrix Product Ansatz for Interacting Reversible Dynamics. Commun. Math. Phys. 2019, 371, 651–688. [Google Scholar] [CrossRef]
- Gombor, T.; Pozsgay, B. Integrable deformations of superintegrable quantum circuits. arXiv 2022, arXiv:2205.02038. [Google Scholar]
- Gombor, T.; Pozsgay, B. Superintegrable cellular automata and dual unitary gates from Yang-Baxter maps. SciPost Phys. 2022, 12, 102. [Google Scholar] [CrossRef]
- Maassarani, Z. The XXC models. Phys. Lett. A 1998, 244, 160–164. [Google Scholar] [CrossRef]
- Kormos, M.; Vörös, D.; Zaránd, G. Finite temperature dynamics in gapped 1D models in the sine-Gordon family. Phys. Rev. B 2022, 106, 205151. [Google Scholar] [CrossRef]
- Gütschow, J.; Uphoff, S.; Werner, R.F.; Zimborás, Z. Time Asymptotics and Entanglement Generation of Clifford Quantum Cellular Automata. J. Math. Phys. 2010, 51, 015203. [Google Scholar] [CrossRef]
- Vanicat, M.; Zadnik, L.; Prosen, T. Integrable Trotterization: Local Conservation Laws and Boundary Driving. Phys. Rev. Lett. 2018, 121, 030606. [Google Scholar] [CrossRef]
- Casati, G.; Ford, J.; Vivaldi, F.; Visscher, W.M. One-Dimensional Classical Many-Body System Having a Normal Thermal Conductivity. Phys. Rev. Lett. 1984, 52, 1861. [Google Scholar] [CrossRef]
- Prosen, T.; Robnik, M. Energy transport and detailed verification of Fourier heat law in a chain of colliding harmonic oscillators. J. Phys. A Math. Gen. 1992, 25, 3449. [Google Scholar] [CrossRef]
- Casati, G.; Prosen, T. Anomalous heat conduction in a one-dimensional ideal gas. Phys. Rev. E 2003, 67, 015203(R). [Google Scholar] [CrossRef] [PubMed]
- Gopalakrishnan, S.; Huse, D.A.; Khemani, V.; Vasseur, R. Hydrodynamics of operator spreading and quasiparticle diffusion in interacting integrable systems. Phys. Rev. B 2018, 98, 220303(R). [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prosen, T. On Two Non-Ergodic Reversible Cellular Automata, One Classical, the Other Quantum. Entropy 2023, 25, 739. https://doi.org/10.3390/e25050739
Prosen T. On Two Non-Ergodic Reversible Cellular Automata, One Classical, the Other Quantum. Entropy. 2023; 25(5):739. https://doi.org/10.3390/e25050739
Chicago/Turabian StyleProsen, Tomaž. 2023. "On Two Non-Ergodic Reversible Cellular Automata, One Classical, the Other Quantum" Entropy 25, no. 5: 739. https://doi.org/10.3390/e25050739
APA StyleProsen, T. (2023). On Two Non-Ergodic Reversible Cellular Automata, One Classical, the Other Quantum. Entropy, 25(5), 739. https://doi.org/10.3390/e25050739





