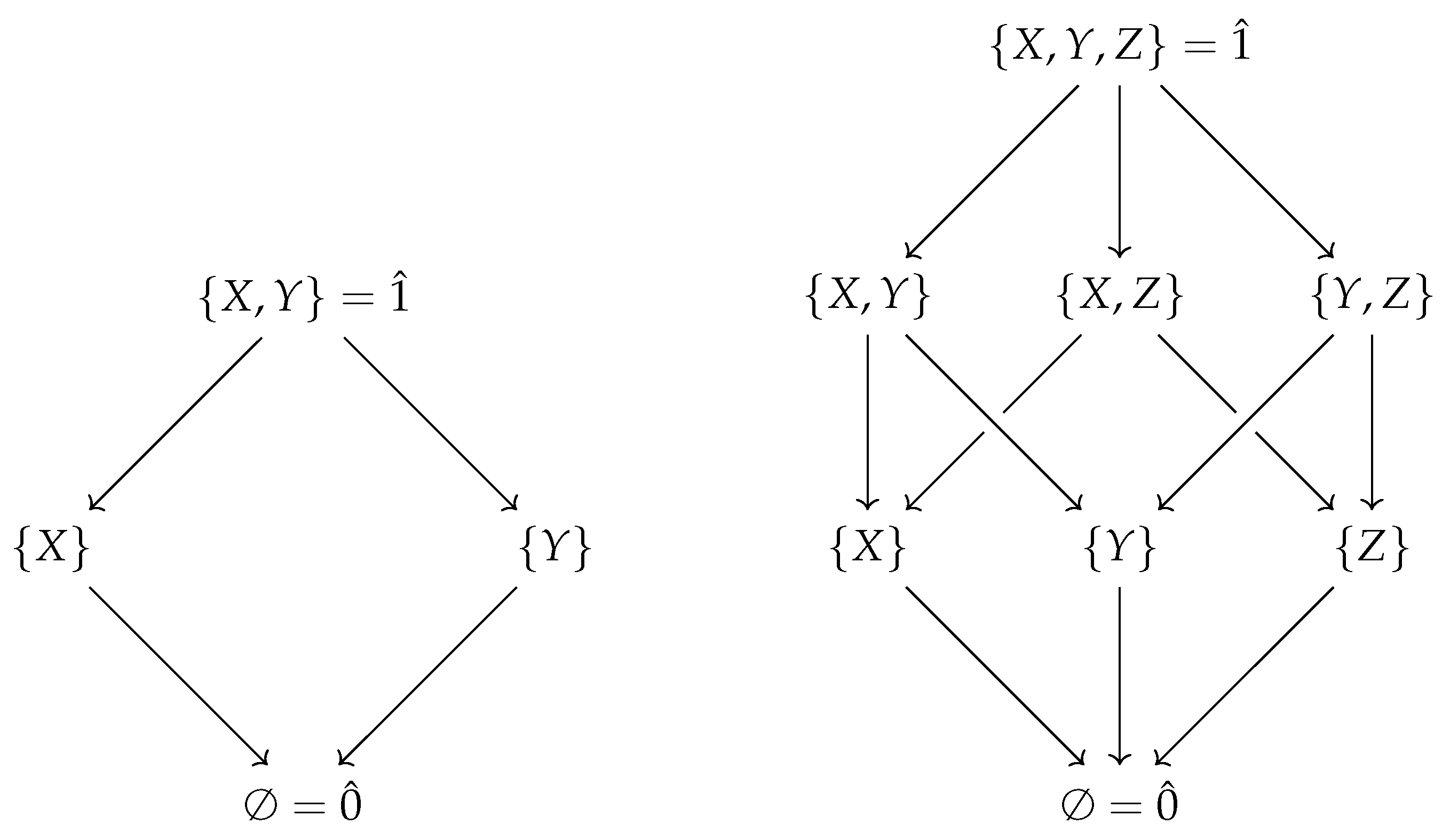3.1. MFIs as Möbius Inversions
With mutual information defined in terms of Möbius inversions, the same can be done for the model-free interactions. Again, we start with (negative) surprisal. However, on Boolean variables a state is just a partition of the variables into two sets: one in which the variables are set to 1, and another in which they are set to 0. That means that the surprisal of observing a particular state is completely specified by which variables
are set to 1 while keeping all other variables
at 0, which can be written as
Definition 5 (interactions as Möbius inversions)
. Let p be a probability distribution over a set T of random variables and let , the powerset of a set ordered by inclusion. Then, the interaction among variables τ is provided by For example, when
contains a single variable
, then
which coincides with the 1-point interaction in Equation (7). Similarly, when
contains two variables
, then
which coincides with the 2-point interaction in Equation (8). In fact, this pattern holds in general.
Theorem 1 (equivalence of interactions)
. The interaction from Definition 5 is the same as the model-free interaction from Definition 2, that is, for any set of variables it is the case that Proof. Both sides of this equation are sums of ±, where s is some binary string; thus, we have to show that the same strings appear with the same sign.
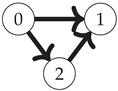
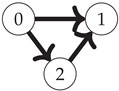
First, note that the Boolean algebra of sets ordered by inclusion (as in
Figure 1) is equivalent to the poset of binary strings where for any two strings
a and
b,
. The equivalence follows immediately upon setting each element
to the string where
and
. This map is one-to-one and monotonic with respect to the partial order, as
. This means that Definition 5 can be rewritten as a Möbius inversion on the lattice of Boolean strings
(shown for the three-variable case on the left side of
Figure 2):
Note that for any pair (
where
with respective string representations
, we have the following:
Thus, we can write
To see that this exactly coincides with Definition 2, we can define a map
where
is the set of functions from
n Boolean variables to
. This map is defined as
With this map, the Boolean derivative of a function
(see Definition 3) can be written as
In this way, the derivative with respect to a set
S of
m variables becomes function composition:
From this, it is clear that a term
appears with a minus sign iff
has been applied an odd number of times. Therefore, terms for which
s contains an odd number of 0s receive a minus sign. This can be summarised as
Therefore, we can write
The sums
and
contain exactly the same terms, meaning that Equations (
38) and (
45) are equal. This completes the proof. □
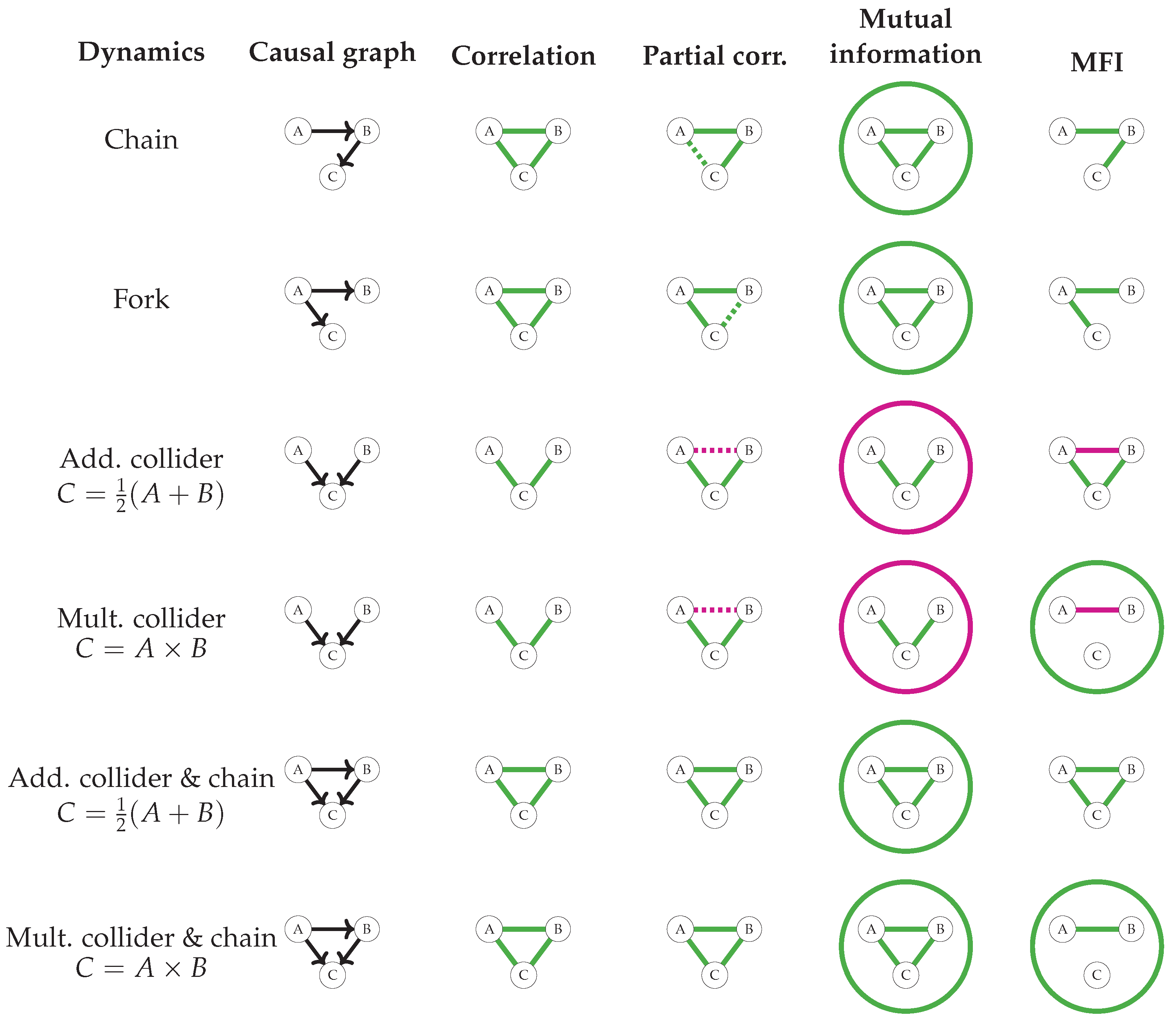
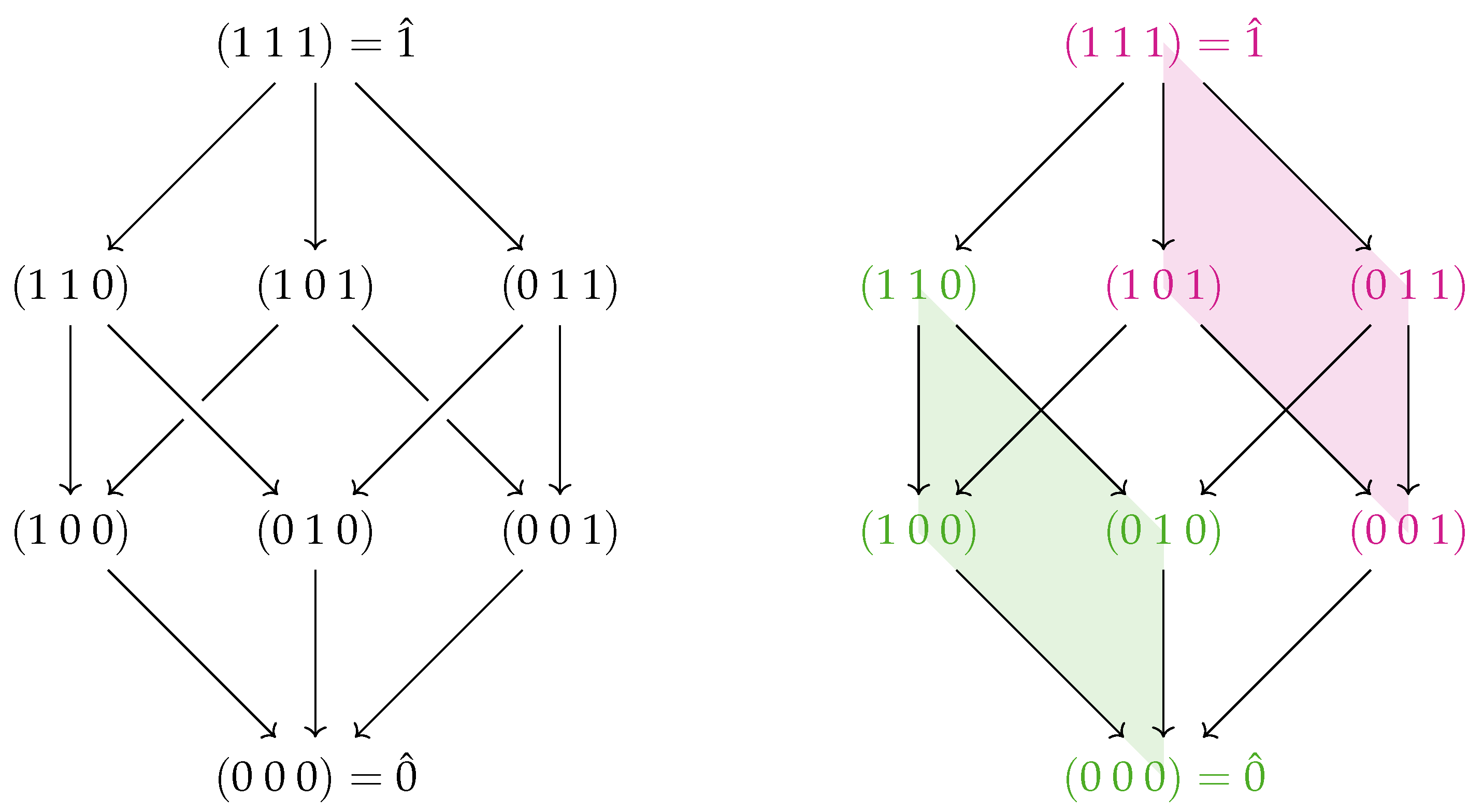
Note that the structure of the lattice reveals structure in the interactions, as previously noted in [
32]. On the right-hand side of
Figure 2, two faces of the three-variable lattice are shaded. The green region corresponds to the 2-point interaction between the first two variables. The red region contains a similar interaction between the first two variables, except this time in the context of the third variable fixed to 1 instead of 0. This illustrates the interpretation of a 3-point interaction as the difference in two 2-point interactions (
; note that
is usually written as just
). The symmetry of the cube reveals the three different (though equivalent) choices as to which variable to set to 1. Treating the Boolean algebra as a die, where the sides facing up are ⚀, ⚁, and ⚂, we have
As before, we can invert Definition 5 and express the surprise of observing a state with all ones in terms of interactions, as follows:
For example, in the case where
and
which illustrates that when
X and
Y tend to be off (
and
) and
X and
Y tend to be different (
), observing the state (1, 1, 0) is very surprising.
3.3. Information and Interactions on Dual Lattices
Lattices have the property that a set with the reverse order remains a lattice; that is, if is a lattice, then (where ) is a lattice. This raises the question of what corresponds to mutual information and interaction on such dual lattices. Recognising that a poset is a category with objects S and a morphism iff , these become definitions in the opposite category , meaning that they define dual objects.
Let us start with mutual information. We can calculate the dual mutual information, denoted
, by first noting that the dual to a Boolean algebra is another Boolean algebra, meaning that we have
. Simply replacing
P with
in Equation (15) yields
The dual mutual information of
is simply
, that is, the mutual information among all variables. However, the dual mutual information of a singleton set
X is
where
is known as the differential mutual information and describes the change in mutual information when leaving out
X [
40], i.e., when marginalising over the variable
X. Note that a similar construction was already anticipated in [
41] and that the differential mutual information has previously been used to describe information structures in genetics [
39]. On the Boolean algebra of three variables
, the dual mutual information of
X can be written out as follows:
Because
is the dual of mutual information, it should arguably be called the mutual co-information; however, the term co-information is unfortunately already in use to refer to normal higher-order mutual information.
To find the dual to the interactions, we start from Equation (
36) and construct
, the dual to the lattice of binary strings
. A dual interaction of variables
is denoted as
, and is defined as follows:
Again, when
, this is simply (
, while the dual interaction of a singleton set
X is
For example, on the three variable lattice in
Figure 2, the dual interaction of
X is
Writing
for
, it can be seen that this is equal to
which is similar to the 2-point interaction
defined in Equation (8), now conditioned on
instead of 0. Note the difference between dual mutual information and dual interactions here; the dual mutual information of
X describes the effect on the mutual information from
marginalising over
X, whereas the dual interaction of
X describes the effect on an interaction when
fixing. This reflects a fundamental difference between mutual information and the interactions, in that the former is an
averaged quantity and the latter a
pointwise quantity.
Dual interactions should probably be called co-interactions; however, to avoid confusion with the term co-information, we instead refer to them simply as dual interactions. Dual interactions are interactions that are conditioned on certain variables being 1 instead of 0. This makes them no longer equal to the Ising interactions between Boolean variables; however, there are situations in which an interaction is more interesting in the context of instead of , for example, if Z is always 1 in the data under consideration.
Summary
Mutual information is the Möbius inversion of marginal entropy on the lattice of subsets ordered by inclusion.
Differential (or conditional) mutual information is the Möbius inversion of marginal entropy on the dual lattice.
Model-free interactions are the Möbius inversion of surprisal on the lattice of subsets ordered by inclusion.
Model-free dual interactions are the Möbius inversion of surprisal on the dual lattice.
Dual interactions of a variable X are interactions between the other variables where X is set to 1 instead of 0.
To summarise these relationships diagrammatically, note that surprisals form a vector space as follows. Let
be the powerset of a set of variables
T and let
. This forms a lattice
ordered by inclusion, meaning that
can be assigned a topological ordering indexed by
i as
. Let
be the set of linear combinations of surprisals of subsets of T:
This set is assigned a vector space structure over
by the usual scalar multiplication and addition. Note that the set
forms a basis for this vector space, because
has no non-trivial solutions and a
. Only when two variables
a and
b are independent do we have linear dependencies in
, as it is then the case that
. To define a map from
, we only need to specify its action on
and extend the definition linearly. This means that we can fully define the map
by specifying
Similarly, we can define the expectation map
as
which outputs the expected surprise over all realisations
. Finally, note that the Möbius inversion over a poset
P is an endomorphism of the set
of functions over
P, defined as
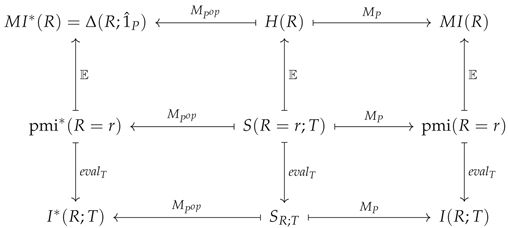
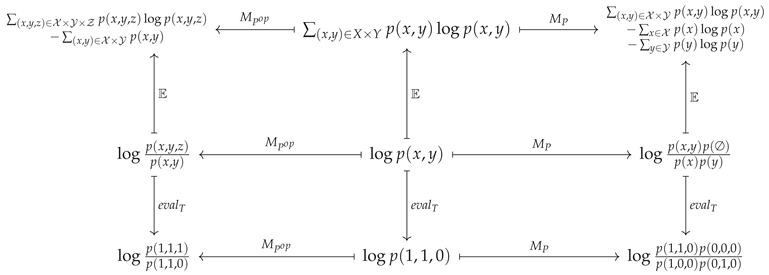
Together, these three maps ensure that the following diagram commutes:
![Entropy 25 00648 i001 Entropy 25 00648 i001]()
For the case where and , this explicitly amounts to