A Stable Large-Scale Multiobjective Optimization Algorithm with Two Alternative Optimization Methods
Abstract
1. Introduction
- (1)
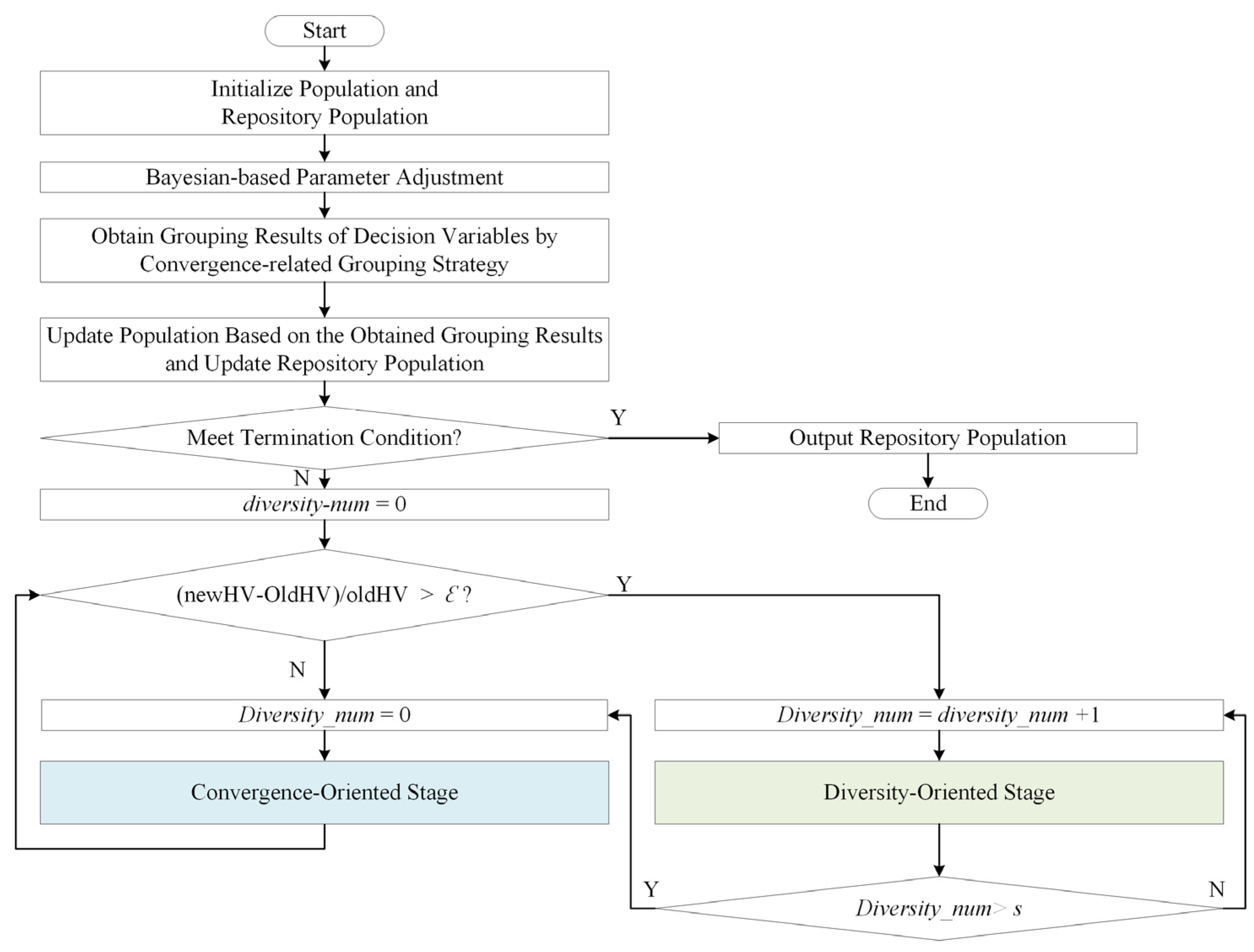
- In the proposed two alternative optimization methods, two group strategies, namely, the convergence-related grouping strategy and the diversity-related grouping strategy, are introduced to group the large-scale decision variables based on the evaluation of the population. Specifically, if there is a significant performance degradation in the current population, the diversity-oriented stage is implemented by adopting the diversity-related grouping strategy. Suppose the diversity-oriented stage has been carried out for a certain number of generations. In that case, LSMOEA-TM implements the convergence-oriented stage with the help of the convergence-related grouping strategy.
- (2)
- A Bayesian-based parameter adjustment strategy is proposed to modify the parameters in the convergence-related and diversity-related grouping strategies to reduce the computational cost of the proposed algorithm.
2. Background
2.1. Large-Scale Multiobjective Optimization Problems (LSMOPs)
2.2. Large-Scale Multiobjective Evolutionary Algorithms (LSMOEAs)
2.2.1. LSMOEAs Based on Fixed Grouping
2.2.2. LSMOEAs Based on Dynamic Grouping
2.2.3. Other LSMOEAs
3. Method
3.1. Initialization
3.2. Two Alternative Optimization Methods
3.2.1. Update of and
| Algorithm 1: Update of |
| Input: population ; convergence-related decision variables ; diversity-related decision variables |
| Output: updated population _POP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2.2. Bayesian-Based Parameter Adjustment Strategy
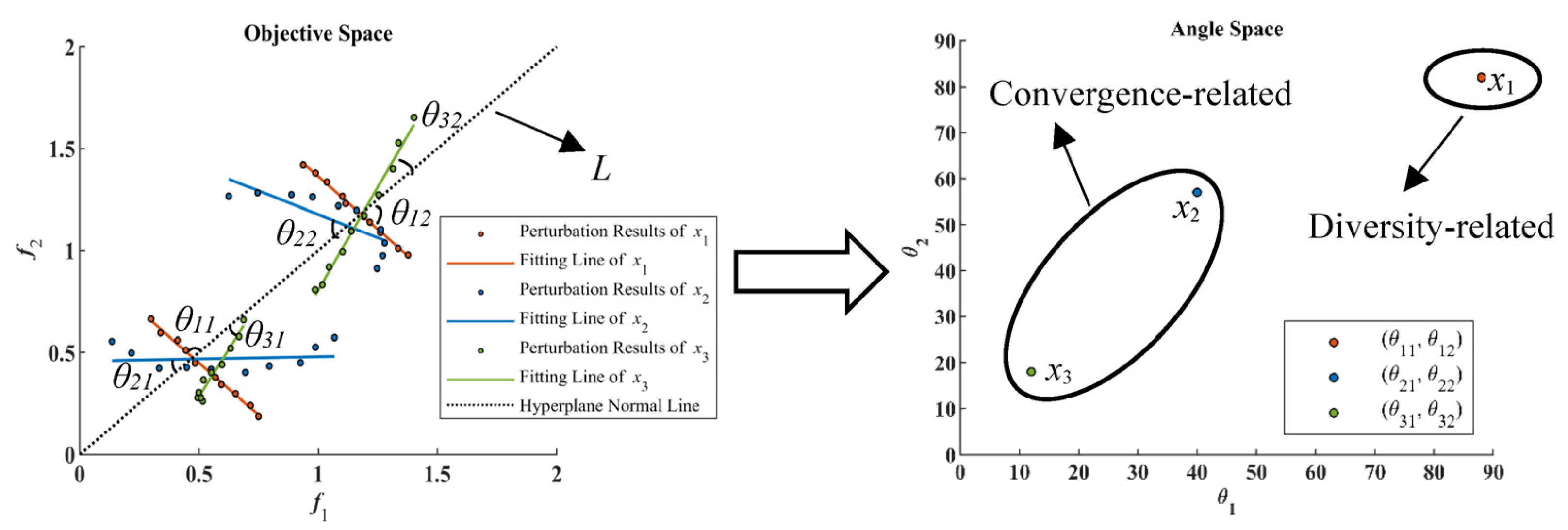
3.2.3. Convergence-Related and Diversity-Related Grouping Strategy
4. Results
4.1. Test Suites and Algorithms to Be Compared
- (1)
- MOEA/D2 [21], which is a representative algorithm based on the dynamic grouping strategy.
- (2)
- LMEA [16], which is a representative algorithm based on the fixed grouping strategy.
- (3)
- IM-MOEA/D [30], which uses a decomposition-based strategy to solve LSMOPs.
- (4)
- FDV [31], which utilizes a fuzzy search strategy to group decision variables when solving LSMOPs.
4.2. Experiment Setting and Measurement Methodology
4.3. Performance Comparison between LSMOEA-TM and Other Large-Scale MOEAs
5. Discussion
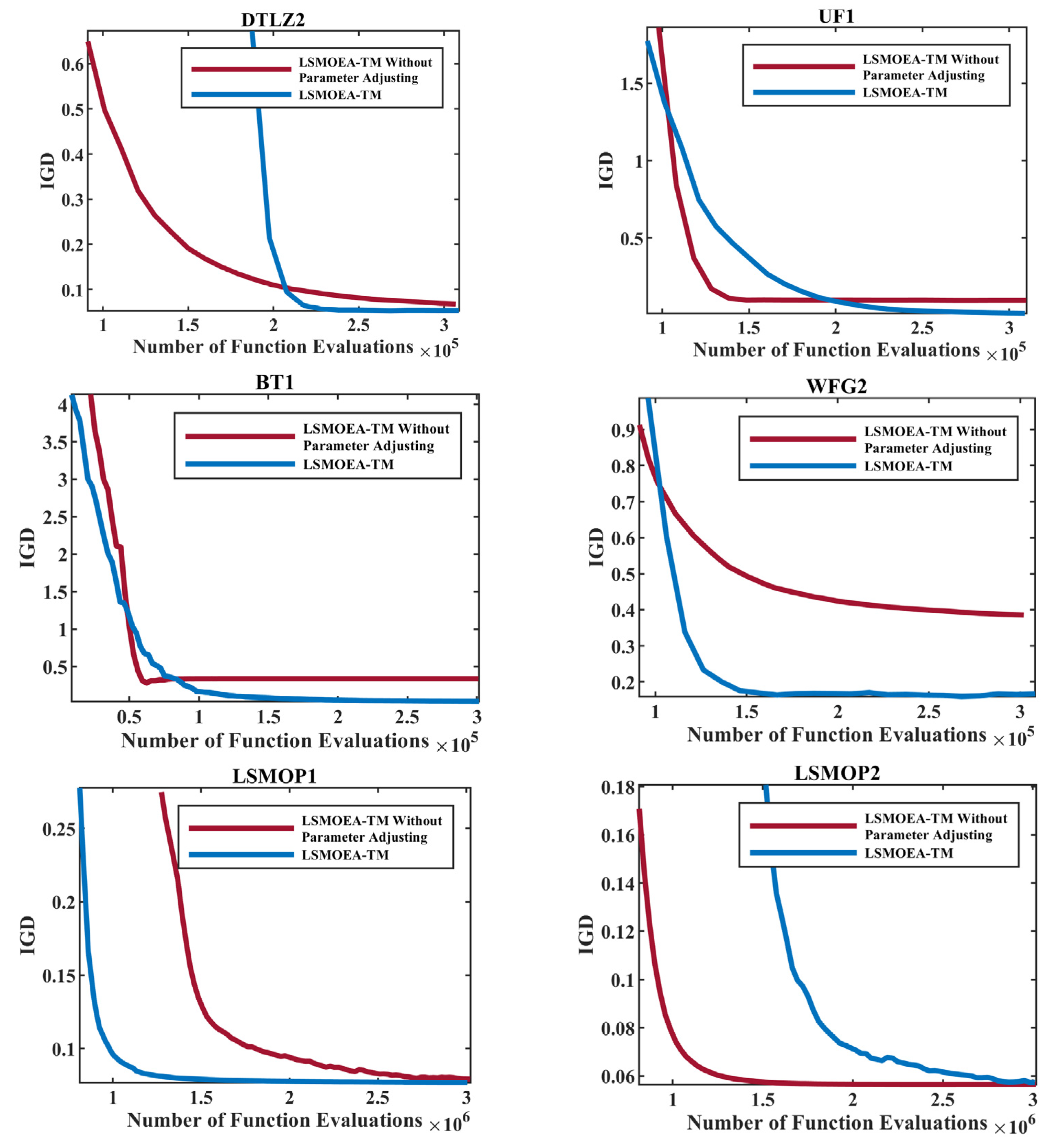
5.1. Investigation of the Bayesian-Based Parameter Adjusting Strategy
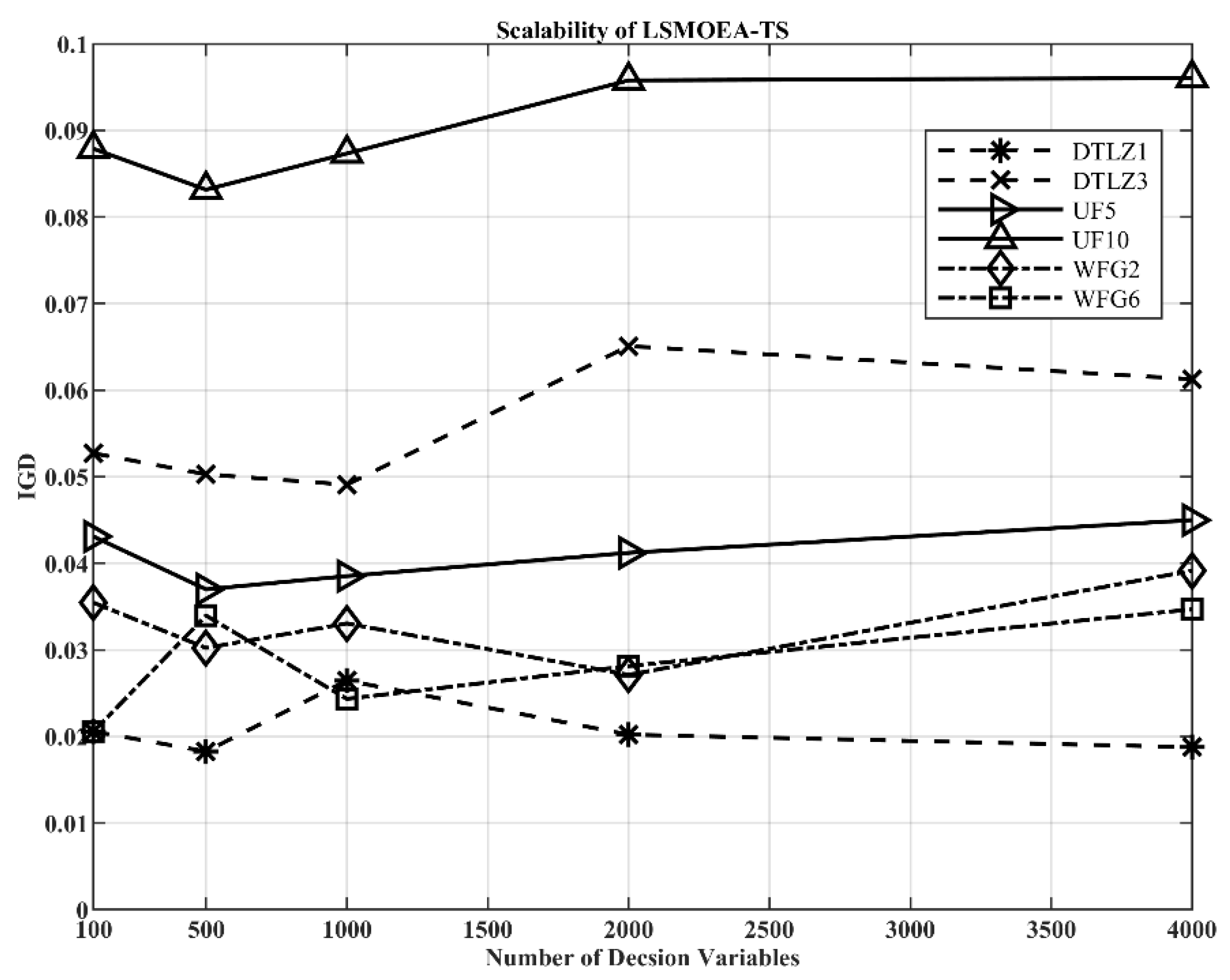
5.2. Investigation of the Scalability of LSMOEA-TM
5.3. Investigation of the Computational Efficiency of LSMOEA-TM
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Harada, T.; Kaidan, M.; Thawonmas, R. Comparison of synchronous and asynchronous parallelization of extreme surrogate-assisted multi-objective evolutionary algorithm. Nat. Comput. 2022, 21, 187–217. [Google Scholar] [CrossRef]
- Wu, Z.; Feng, H.; Chen, L.; Ge, Y. Performance Optimization of a Condenser in Ocean Thermal Energy Conversion (OTEC) System Based on Constructal Theory and a Multi-Objective Genetic Algorithm. Entropy 2020, 22, 641. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H. Multi-Objective Optimization and Performance Assessments of an Integrated Energy System Based on Fuel, Wind and Solar Energies. Entropy 2021, 23, 431. [Google Scholar] [CrossRef]
- Qiu, X.; Chen, L.; Ge, Y.; Shi, S. Efficient Power Characteristic Analysis and Multi-Objective Optimization for an Irreversible Simple Closed Gas Turbine Cycle. Entropy 2022, 24, 1531. [Google Scholar] [CrossRef]
- Zhou, Y.; Ruan, J.; Hong, G.; Miao, Z. Multi-Objective Optimization of the Basic and Regenerative ORC Integrated with Working Fluid Selection. Entropy 2022, 24, 902. [Google Scholar] [CrossRef]
- Cheng, R. Nature Inspired Optimization of Large Problems.; University of Surrey: Guildford, UK, 2016. [Google Scholar]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. Test Problems for Large-Scale Multiobjective and Many-Objective Optimization. IEEE Trans. Cybern. 2017, 47, 4108–4121. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Computat. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Ling, H.; Zhu, X.; Zhu, T.; Nie, M.; Liu, Z.-H.; Liu, H.-Y. A Parallel Multiobjective PSO Weighted Average Clustering Algorithm Based on Apache Spark. Entropy 2023, 25, 259. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, C.; Zhang, X.; Tan, K.C.; Jin, Y. Solving Large-Scale Multiobjective Optimization Problems with Sparse Optimal Solutions via Unsupervised Neural Networks. IEEE Trans. Cybern. 2021, 51, 3115–3128. [Google Scholar] [CrossRef]
- Tian, Y.; Si, L.; Zhang, X.; Cheng, R.; He, C.; Tan, K.C.; Jin, Y. Evolutionary Large-Scale Multi-Objective Optimization: A Survey. ACM Comput. Surv. 2022, 54, 1–34. [Google Scholar] [CrossRef]
- Li, X.; Yao, X. Cooperatively Coevolving Particle Swarms for Large Scale Optimization. IEEE Trans. Evol. Comput. 2012, 16, 210–224. [Google Scholar] [CrossRef]
- Ma, X.; Liu, F.; Qi, Y.; Wang, X.; Li, L.; Jiao, L.; Yin, M.; Gong, M. A Multiobjective Evolutionary Algorithm Based on Decision Variable Analyses for Multiobjective Optimization Problems With Large-Scale Variables. IEEE Trans. Evol. Comput. 2016, 20, 275–298. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, X.; Pedrycz, W.; Yin, S.; Wu, G.; Yan, H. PEA: Parallel Evolutionary Algorithm by Separating Convergence and Diversity for Large-Scale Multi-Objective Optimization. In Proceedings of the 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS), Vienna, Austria, 2–6 July 2018. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization. IEEE Trans. Evol. Comput. 2018, 22, 97–112. [Google Scholar] [CrossRef]
- Liu, H.-L.; Gu, F.; Zhang, Q. Decomposition of a Multiobjective Optimization Problem into a Number of Simple Multiobjective Subproblems. IEEE Trans. Evol. Comput. 2014, 18, 450–455. [Google Scholar] [CrossRef]
- Du, W.; Tong, L.; Tang, Y. A framework for high-dimensional robust evolutionary multi-objective optimization. In Proceedings of the 2018 Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018. [Google Scholar] [CrossRef]
- Du, W.; Zhong, W.; Tang, Y.; Du, W.; Jin, Y. High-Dimensional Robust Multi-Objective Optimization for Order Scheduling: A Decision Variable Classification Approach. IEEE Trans. Ind. Inf. 2019, 15, 293–304. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Gu, Y.; Ling, Y.; Ma, X. Applying graph-based differential grouping for multiobjective large-scale optimization. Swarm Evol. Comput. 2020, 53, 100626. [Google Scholar] [CrossRef]
- Antonio, L.M.; Coello, C.A.C. Use of cooperative coevolution for solving large scale multiobjective optimization problems. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013. [Google Scholar] [CrossRef]
- Miguel Antonio, L.; Coello Coello, C.A. Decomposition-Based Approach for Solving Large Scale Multi-objective Problems. In Proceedings of the Parallel Problem Solving from Nature–PPSN XIV: 14th International Conference, Edinburgh, UK, 17–21 September 2016. [Google Scholar] [CrossRef]
- Antonio, L.M.; Coello, C.A.C.; Brambila, S.G.; González, J.F.; Tapia, G.C. Operational decomposition for large scale multi-objective optimization problems. In Proceedings of the 2019 Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019. [Google Scholar] [CrossRef]
- Song, A.; Yang, Q.; Chen, W.-N.; Zhang, J. A random-based dynamic grouping strategy for large scale multi-objective optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Deng, J. Biased Multiobjective Optimization and Decomposition Algorithm. IEEE Trans. Cybern. 2017, 47, 52–66. [Google Scholar] [CrossRef]
- Zhu, W.; Tianyu, L. A Novel Multi-Objective Scheduling Method for Energy Based Unrelated Parallel Machines With Auxiliary Resource Constraints. IEEE Access 2019, 7, 168688–168699. [Google Scholar] [CrossRef]
- He, C.; Li, L.; Tian, Y.; Zhang, X.; Cheng, R.; Jin, Y.; Yao, X. Accelerating Large-Scale Multiobjective Optimization via Problem Reformulation. IEEE Trans. Evol. Comput. 2019, 23, 949–961. [Google Scholar] [CrossRef]
- He, C.; Cheng, R.; Yazdani, D. Adaptive Offspring Generation for Evolutionary Large-Scale Multiobjective Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 786–798. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, R.; Wen, J.; Li, H.; Weng, J. Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations. Inf. Sci. 2020, 509, 457–469. [Google Scholar] [CrossRef]
- Farias, L.R.C.; Araujo, A.F.R. IM-MOEA/D: An Inverse Modeling Multi-Objective Evolutionary Algorithm Based on Decomposition. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021. [Google Scholar] [CrossRef]
- Yang, X.; Zou, J.; Yang, S.; Zheng, J.; Liu, Y. A Fuzzy Decision Variables Framework for Large-scale Multiobjective Optimization. IEEE Trans. Evol. Comput. 2022, 23, 1. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M. Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. IEEE Trans. Inform. Theory 2012, 58, 3250–3265. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Test Problems for Evolutionary Multiobjective Optimization; Springer: London, UK, 2005; pp. 105–145. [Google Scholar] [CrossRef]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Zhao, S.; Suganthan, P.N.; Liu, W.; Tiwari, S. Multiobjective Optimization Test Instances for the CEC 2009 Special Session and Competition; special session on performance assessment of multi-objective optimization algorithms, technical report; University of Essex: Colchester, UK; Nanyang Technological University: Singapore, 2008; Volume 264, pp. 1–30. [Google Scholar]
- Coello, C.A.C.; Cortes, N.C. Solving Multiobjective Optimization Problems Using an Artificial Immune System. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Li, M.; Jin, Y. Diversity Assessment of Multi-Objective Evolutionary Algorithms: Performance Metric and Benchmark Problems. IEEE Comput. Intell. Mag. 2019, 14, 61–74. [Google Scholar] [CrossRef]



| Problem | D | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|---|
| DTLZ1 | 100 | 1.17 × 103 (2.45 × 102) − | 2.05 × 10−2 (1.42 × 10−6) + | 3.16 × 10−1 (1.05 × 10−1) − | 2.05 × 10−2 (8.72 × 10−6) + | 2.09 × 10−2 (2.53 × 10−4) |
| 500 | 3.03 × 103 (3.54 × 102) − | 2.05 × 10−2 (1.59 × 10−6) + | 5.34 × 100 (8.06 × 10−1) − | 2.12 × 10−2 (2.20 × 10−4) = | 2.11 × 10−2 (3.96 × 10−4) | |
| 1000 | 4.67 × 103 (6.89 × 102) − | 2.05 × 10−2 (1.84 × 10−6) + | 1.65 × 101 (1.57 × 100) − | 2.87 × 10−2 (1.65 × 10−3) − | 2.12 × 10−2 (3.01 × 10−4) | |
| DTLZ2 | 100 | 1.90 × 100 (6.12 × 10−1) − | 5.44 × 10−2 (3.85 × 10−6) − | 5.92 × 10−2 (1.17 × 10−9) − | 5.44 × 10−2 (1.82 × 10−6) − | 5.33 × 10−2 (4.29 × 10−4) |
| 500 | 4.42 × 100 (8.40 × 10−1) − | 5.44 × 10−2 (5.19 × 10−6) − | 5.92 × 10−2 (6.74 × 10−9) − | 5.44 × 10−2 (6.38 × 10−8) − | 5.38 × 10−2 (5.64 × 10−4) | |
| 1000 | 7.74 × 100 (1.71 × 100) − | 5.44 × 10−2 (4.25 × 10−6) − | 5.92 × 10−2 (3.75 × 10−8) − | 5.44 × 10−2 (2.73 × 10−8) − | 5.39 × 10−2 (4.68 × 10−4) | |
| DTLZ3 | 100 | 3.37 × 103 (7.76 × 102) − | 5.44 × 10−2 (3.69 × 10−6) − | 8.61 × 10−1 (3.98 × 10−1) − | 5.45 × 10−2 (1.86 × 10−5) − | 5.34 × 10−2 (5.10 × 10−4) |
| 500 | 7.88 × 103 (1.21 × 103) − | 5.44 × 10−2 (5.79 × 10−6) − | 1.41 × 101 (2.29 × 100) − | 5.66 × 10−2 (8.20 × 10−4) − | 5.40 × 10−2 (6.39 × 10−4) | |
| 1000 | 1.32 × 104 (2.19 × 103) − | 5.44 × 10−2 (4.94 × 10−6) = | 4.60 × 101 (6.83 × 100) − | 7.97 × 10−2 (5.60 × 10−3) − | 5.46 × 10−2 (7.88 × 10−4) | |
| DTLZ7 | 100 | 3.21 × 100 (3.66 × 10−1) − | 2.91 × 10−1 (1.81 × 10−1) − | 1.24 × 10−1 (1.05 × 10−16) − | 7.76 × 10−2 (3.20 × 10−3) − | 5.89 × 10−2 (1.33 × 10−3) |
| 500 | 3.72 × 100 (2.29 × 10−1) − | 2.85 × 10−1 (1.83 × 10−1) − | 1.24 × 10−1 (5.70 × 10−13) − | 7.89 × 10−2 (3.01 × 10−3) − | 5.90 × 10−2 (1.21 × 10−3) | |
| 1000 | 3.97 × 100 (1.91 × 10−1) − | 2.46 × 10−1 (1.85 × 10−1) − | 1.24 × 10−1 (1.89 × 10−7) − | 7.85 × 10−2 (3.62 × 10−3) − | 5.94 × 10−2 (1.21 × 10−3) | |
| UF1 | 100 | 5.92 × 10−1 (7.68 × 10−2) − | 5.92 × 10−1 (7.68 × 10−2) − | 8.30 × 10−2 (9.00 × 10−3) − | 8.06 × 10−3 (3.34 × 10−3) − | 3.73 × 10−3 (1.56 × 10−8) |
| 500 | 6.92 × 10−1 (7.72 × 10−2) − | 6.92 × 10−1 (7.72 × 10−2) − | 9.33 × 10−2 (1.02 × 10−2) − | 8.12 × 10−3 (2.78 × 10−3) − | 3.73 × 10−3 (4.78 × 10−8) | |
| 1000 | 7.55 × 10−1 (7.47 × 10−2) − | 7.55 × 10−1 (7.47 × 10−2) − | 1.01 × 10−1 (1.19 × 10−2) − | 8.22 × 10−3 (2.41 × 10−3) − | 3.73 × 10−3 (9.09 × 10−8) | |
| UF2 | 100 | 2.18 × 10−1 (3.94 × 10−2) − | 2.18 × 10−1 (3.94 × 10−2) − | 4.22 × 10−2 (2.09 × 10−2) − | 7.96 × 10−3 (1.07 × 10−3) − | 3.73 × 10−3 (1.17 × 10−9) |
| 500 | 2.88 × 10−1 (5.56 × 10−2) − | 2.88 × 10−1 (5.56 × 10−2) − | 5.06 × 10−2 (2.08 × 10−2) − | 8.37 × 10−3 (1.11 × 10−3) − | 3.73 × 10−3 (4.36 × 10−9) | |
| 1000 | 3.23 × 10−1 (5.93 × 10−2) − | 3.23 × 10−1 (5.93 × 10−2) − | 5.69 × 10−2 (1.75 × 10−2) − | 9.15 × 10−3 (9.22 × 10−4) − | 3.73 × 10−3 (1.09 × 10−8) | |
| UF4 | 100 | 1.07 × 10−1 (4.09 × 10−3) − | 5.59 × 10−2 (3.01 × 10−3) − | 4.21 × 10−2 (1.97 × 10−3) − | 1.09 × 10−2 (1.11 × 10−3) + | 2.07 × 10−2 (1.64 × 10−4) |
| 500 | 1.33 × 10−1 (5.55 × 10−3) − | 6.27 × 10−2 (5.02 × 10−3) − | 5.12 × 10−2 (2.23 × 10−3) − | 1.89 × 10−2 (1.16 × 10−3) + | 2.32 × 10−2 (1.05 × 10−4) | |
| 1000 | 1.45 × 10−1 (3.63 × 10−3) − | 6.78 × 10−2 (4.50 × 10−3) − | 5.63 × 10−2 (1.86 × 10−3) − | 2.59 × 10−2 (4.84 × 10−4) − | 2.43 × 10−2 (8.24 × 10−5) | |
| UF7 | 100 | 6.22 × 10−1 (1.14 × 10−1) − | 9.72 × 10−2 (2.08 × 10−1) − | 8.02 × 10−2 (1.03 × 10−1) − | 3.24 × 10−2 (3.94 × 10−2) + | 5.97 × 10−2 (5.79 × 10−7) |
| 500 | 8.01 × 10−1 (8.70 × 10−2) − | 2.23 × 10−1 (3.12 × 10−1) − | 8.48 × 10−2 (9.00 × 10−2) − | 4.77 × 10−2 (4.55 × 10−2) + | 5.97 × 10−2 (1.42 × 10−6) | |
| 1000 | 8.37 × 10−1 (9.75 × 10−2) − | 2.52 × 10−1 (3.22 × 10−1) = | 5.67 × 10−2 (1.34 × 10−2) + | 8.07 × 10−2 (6.75 × 10−2) = | 5.97 × 10−2 (2.55 × 10−6) | |
| WFG1 | 100 | 2.24 × 100 (7.82 × 10−2) − | 1.38 × 100 (1.34 × 10−1) − | 3.11 × 10−1 (2.42 × 10−2) + | 1.41 × 10−1 (4.28 × 10−4) + | 6.32 × 10−1 (8.79 × 10−2) |
| 500 | 2.25 × 100 (7.21 × 10−2) − | 1.50 × 100 (1.18 × 10−1) − | 2.74 × 10−1 (3.68 × 10−2) + | 1.41 × 10−1 (7.56 × 10−5) + | 8.13 × 10−1 (7.58 × 10−2) | |
| 1000 | 2.24 × 100 (7.73 × 10−2) − | 1.52 × 100 (9.55 × 10−2) − | 2.87 × 10−1 (1.96 × 10−1) + | 1.41 × 10−1 (2.15 × 10−5) + | 7.77 × 10−1 (9.23 × 10−2) | |
| WFG2 | 100 | 4.65 × 10−1 (5.75 × 10−4) − | 5.71 × 10−1 (4.84 × 10−2) − | 1.87 × 10−1 (4.60 × 10−3) − | 1.65 × 10−1 (1.01 × 10−3) − | 1.65 × 10−1 (5.24 × 10−3) |
| 500 | 4.65 × 10−1 (5.97 × 10−4) − | 5.68 × 10−1 (3.79 × 10−2) − | 2.14 × 10−1 (6.55 × 10−3) − | 1.74 × 10−1 (3.12 × 10−3) − | 1.74 × 10−1 (5.98 × 10−2) | |
| 1000 | 4.65 × 10−1 (4.53 × 10−4) − | 5.85 × 10−1 (3.50 × 10−2) − | 2.24 × 10−1 (6.22 × 10−3) − | 1.83 × 10−1 (4.43 × 10−3) − | 1.63 × 10−1 (3.33 × 10−3) | |
| WFG3 | 100 | 1.08 × 10−1 (2.65 × 10−2) − | 6.06 × 10−1 (4.08 × 10−2) − | 2.33 × 10−1 (1.72 × 10−2) − | 6.76 × 10−2 (6.12 × 10−3) − | 3.06 × 10−2 (4.74 × 10−3) |
| 500 | 1.15 × 10−1 (1.88 × 10−2) − | 6.62 × 10−1 (4.51 × 10−2) − | 2.60 × 10−1 (2.05 × 10−2) − | 9.22 × 10−2 (6.72 × 10−3) − | 3.14 × 10−2 (3.90 × 10−3) | |
| 1000 | 1.19 × 10−1 (1.62 × 10−2) − | 6.66 × 10−1 (4.51 × 10−2) − | 2.56 × 10−1 (2.02 × 10−2) − | 1.36 × 10−1 (2.37 × 10−2) − | 3.19 × 10−2 (4.13 × 10−3) | |
| BT1 | 100 | 1.09 × 101 (8.92 × 10−1) − | 9.25 × 100 (9.19 × 10−1) − | 1.74 × 100 (3.03 × 10−1) − | 1.83 × 100 (2.16 × 10−1) − | 3.77 × 10−2 (8.90 × 10−3) |
| 500 | 2.54 × 101 (3.08 × 100) − | 1.79 × 101 (1.53 × 100) − | 3.86 × 100 (5.68 × 10−1) − | 4.42 × 100 (3.39 × 10−1) − | 7.97 × 10−2 (1.28 × 10−2) | |
| 1000 | 3.96 × 101 (4.46 × 100) − | 2.85 × 101 (2.46 × 100) − | 8.49 × 100 (8.65 × 10−1) − | 9.39 × 100 (4.05 × 10−1) − | 1.33 × 10−1 (2.25 × 10−2) | |
| BT2 | 100 | 8.42 × 100 (6.39 × 10−1) − | 1.85 × 100 (9.82 × 10−2) − | 7.84 × 10−1 (4.69 × 10−2) − | 8.18 × 10−1 (1.96 × 10−2) − | 3.45 × 10−1 (4.32 × 10−2) |
| 500 | 1.91 × 101 (1.29 × 100) − | 3.95 × 100 (2.02 × 10−1) − | 1.65 × 100 (4.89 × 10−2) − | 1.77 × 100 (3.10 × 10−2) − | 7.39 × 10−1 (5.64 × 10−2) | |
| 1000 | 3.06 × 101 (1.58 × 100) − | 6.40 × 100 (2.18 × 10−1) − | 2.66 × 100 (7.64 × 10−2) − | 3.21 × 100 (4.68 × 10−2) − | 1.22 × 100 (8.36 × 10−2) | |
| BT3 | 100 | 1.12 × 101 (1.36 × 100) − | 3.23 × 100 (9.68 × 10−1) − | 2.33 × 10−1 (6.59 × 10−2) − | 8.81 × 10−1 (9.40 × 10−2) − | 1.05 × 10−2 (2.82 × 10−3) |
| 500 | 2.42 × 101 (3.08 × 100) − | 6.69 × 100 (1.30 × 100) − | 2.71 × 10−1 (8.65 × 10−2) − | 1.90 × 100 (1.77 × 10−1) − | 1.83 × 10−2 (4.97 × 10−3) | |
| 1000 | 3.86 × 101 (4.71 × 100) − | 1.23 × 101 (1.70 × 100) − | 5.06 × 10−1 (1.02 × 10−1) − | 3.85 × 100 (3.29 × 10−1) − | 3.05 × 10−2 (5.04 × 10−3) | |
| BT6 | 100 | 1.10 × 101 (1.05 × 100) − | 9.12 × 100 (8.70 × 10−1) − | 1.47 × 100 (3.43 × 10−1) − | 1.95 × 100 (1.92 × 10−1) − | 2.61 × 10−2 (1.01 × 10−2) |
| 500 | 2.52 × 101 (3.16 × 100) − | 1.80 × 101 (1.88 × 100) − | 3.77 × 100 (5.81 × 10−1) − | 4.65 × 100 (2.31 × 10−1) − | 5.29 × 10−2 (8.05 × 10−3) | |
| 1000 | 3.94 × 101 (4.66 × 100) − | 2.82 × 101 (3.08 × 100) − | 7.98 × 100 (6.22 × 10−1) − | 9.53 × 100 (4.77 × 10−1) − | 8.38 × 10−2 (1.36 × 10−2) | |
| +/−/= | 0/45/0 | 3/40/2 | 4/41/0 | 8/36/1 | ||
| Problem | D | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|---|
| DTLZ1 | 100 | 0.00 × 100 (0.00 × 100) − | 8.41 × 10−1 (3.51 × 10−5) + | 1.56 × 10−1 (1.39 × 10−1) − | 8.41 × 10−1 (1.06 × 10−4) + | 8.40 × 10−1 (5.22 × 10−4) |
| 500 | 0.00 × 100 (0.00 × 100) − | 8.41 × 10−1 (3.09 × 10−5) + | 0.00 × 100 (0.00 × 100) − | 8.36 × 10−1 (1.25 × 10−3) − | 8.39 × 10−1 (8.68 × 10−4) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 8.41 × 10−1 (2.27 × 10−5) + | 0.00 × 100 (0.00 × 100) − | 8.11 × 10−1 (4.36 × 10−3) − | 8.37 × 10−1 (8.24 × 10−4) | |
| DTLZ2 | 100 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (3.46 × 10−5) − | 5.39 × 10−1 (3.94 × 10−8) − | 5.59 × 10−1 (1.70 × 10−5) − | 5.61 × 10−1 (5.84 × 10−4) |
| 500 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (4.56 × 10−5) − | 5.39 × 10−1 (3.09 × 10−7) − | 5.59 × 10−1 (1.83 × 10−7) − | 5.61 × 10−1 (7.25 × 10−4) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (4.19 × 10−5) − | 5.39 × 10−1 (1.41 × 10−6) − | 5.59 × 10−1 (7.20 × 10−8) − | 5.60 × 10−1 (8.03 × 10−4) | |
| DTLZ3 | 100 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (5.74 × 10−5) − | 4.24 × 10−2 (4.42 × 10−2) − | 5.58 × 10−1 (4.27 × 10−4) − | 5.61 × 10−1 (9.12 × 10−4) |
| 500 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (5.04 × 10−5) − | 0.00 × 100 (0.00 × 100) − | 5.42 × 10−1 (3.66 × 10−3) − | 5.59 × 10−1 (6.82 × 10−4) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 5.59 × 10−1 (4.40 × 10−5) + | 0.00 × 100 (0.00 × 100) − | 4.84 × 10−1 (1.14 × 10−2) − | 5.54 × 10−1 (1.65 × 10−3) | |
| DTLZ7 | 100 | 0.00 × 100 (0.00 × 100) − | 2.42 × 10−1 (1.58 × 10−2) − | 2.60 × 10−1 (1.01 × 10−16) − | 2.67 × 10−1 (1.72 × 10−3) − | 2.79 × 10−1 (6.07 × 10−4) |
| 500 | 0.00 × 100 (0.00 × 100) − | 2.42 × 10−1 (1.62 × 10−2) − | 2.60 × 10−1 (1.03 × 10−14) − | 2.68 × 10−1 (1.73 × 10−3) − | 2.79 × 10−1 (6.12 × 10−4) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 2.46 × 10−1 (1.65 × 10−2) − | 2.60 × 10−1 (4.84 × 10−9) − | 2.69 × 10−1 (1.55 × 10−3) − | 2.79 × 10−1 (6.79 × 10−4) | |
| UF1 | 100 | 1.02 × 10−1 (4.38 × 10−2) − | 7.16 × 10−1 (9.80 × 10−3) − | 7.14 × 10−1 (3.98 × 10−3) − | 6.23 × 10−1 (1.60 × 10−2) − | 7.20 × 10−1 (6.99 × 10−7) |
| 500 | 5.78 × 10−2 (3.52 × 10−2) − | 7.14 × 10−1 (1.27 × 10−2) − | 7.14 × 10−1 (3.07 × 10−3) − | 6.12 × 10−1 (1.84 × 10−2) − | 7.20 × 10−1 (1.51 × 10−6) | |
| 1000 | 3.74 × 10−2 (2.01 × 10−2) − | 6.87 × 10−1 (9.42 × 10−2) − | 7.14 × 10−1 (2.42 × 10−3) − | 6.00 × 10−1 (1.70 × 10−2) − | 7.20 × 10−1 (1.80 × 10−6) | |
| UF2 | 100 | 4.48 × 10−1 (4.00 × 10−2) − | 7.17 × 10−1 (6.27 × 10−4) − | 7.14 × 10−1 (1.22 × 10−3) − | 6.86 × 10−1 (1.12 × 10−2) − | 7.20 × 10−1 (3.93 × 10−8) |
| 500 | 3.77 × 10−1 (5.18 × 10−2) − | 7.16 × 10−1 (6.13 × 10−4) − | 7.13 × 10−1 (1.47 × 10−3) − | 6.76 × 10−1 (1.17 × 10−2) − | 7.20 × 10−1 (1.07 × 10−7) | |
| 1000 | 3.44 × 10−1 (5.36 × 10−2) − | 7.15 × 10−1 (8.32 × 10−4) − | 7.11 × 10−1 (1.26 × 10−3) − | 6.68 × 10−1 (1.10 × 10−2) − | 7.20 × 10−1 (2.16 × 10−7) | |
| UF4 | 100 | 3.00 × 10−1 (5.28 × 10−3) − | 3.67 × 10−1 (4.10 × 10−3) − | 4.35 × 10−1 (1.50 × 10−3) + | 3.89 × 10−1 (2.12 × 10−3) − | 4.17 × 10−1 (2.61 × 10−4) |
| 500 | 2.66 × 10−1 (6.65 × 10−3) − | 3.58 × 10−1 (6.78 × 10−3) − | 4.21 × 10−1 (1.22 × 10−3) + | 3.77 × 10−1 (2.90 × 10−3) − | 4.13 × 10−1 (1.87 × 10−4) | |
| 1000 | 2.52 × 10−1 (3.97 × 10−3) − | 3.51 × 10−1 (6.02 × 10−3) − | 4.09 × 10−1 (1.47 × 10−3) − | 3.68 × 10−1 (2.61 × 10−3) − | 4.12 × 10−1 (1.44 × 10−4) | |
| UF7 | 100 | 3.85 × 10−2 (3.73 × 10−2) − | 5.08 × 10−1 (1.45 × 10−1) − | 5.51 × 10−1 (3.63 × 10−2) + | 5.05 × 10−1 (7.37 × 10−2) − | 5.16 × 10−1 (1.46 × 10−6) |
| 500 | 3.65 × 10−3 (6.82 × 10−3) − | 4.20 × 10−1 (2.14 × 10−1) − | 5.34 × 10−1 (3.96 × 10−2) + | 4.97 × 10−1 (6.72 × 10−2) − | 5.16 × 10−1 (2.45 × 10−6) | |
| 1000 | 1.82 × 10−3 (3.67 × 10−3) − | 3.98 × 10−1 (2.20 × 10−1) = | 5.51 × 10−1 (3.63 × 10−2) + | 5.15 × 10−1 (1.57 × 10−2) − | 5.16 × 10−1 (4.55 × 10−6) | |
| WFG1 | 100 | 3.09 × 10−4 (1.69 × 10−3) − | 3.62 × 10−1 (5.77 × 10−2) − | 5.34 × 10−1 (3.96 × 10−2) + | 9.44 × 10−1 (1.36 × 10−4) + | 8.34 × 10−1 (1.96 × 10−2) |
| 500 | 0.00 × 100 (0.00 × 100) − | 3.03 × 10−1 (3.93 × 10−2) − | 5.51 × 10−1 (3.63 × 10−2) + | 9.44 × 10−1 (4.67 × 10−5) + | 7.42 × 10−1 (2.91 × 10−2) | |
| 1000 | 4.83 × 10−4 (2.65 × 10−3) − | 2.94 × 10−1 (3.38 × 10−2) − | 5.34 × 10−1 (3.96 × 10−2) + | 9.44 × 10−1 (2.87 × 10−5) + | 7.67 × 10−1 (2.67 × 10−2) | |
| WFG2 | 100 | 8.64 × 10−1 (3.93 × 10−3) − | 6.77 × 10−1 (1.77 × 10−2) − | 5.51 × 10−1 (3.63 × 10−2) + | 9.23 × 10−1 (2.24 × 10−3) − | 9.26 × 10−1 (2.55 × 10−3) |
| 500 | 8.60 × 10−1 (2.81 × 10−3) − | 6.71 × 10−1 (1.27 × 10−2) − | 5.34 × 10−1 (3.96 × 10−2) + | 9.00 × 10−1 (5.24 × 10−3) − | 9.21 × 10−1 (2.62 × 10−2) | |
| 1000 | 8.60 × 10−1 (2.74 × 10−3) − | 6.61 × 10−1 (1.29 × 10−2) − | 5.51 × 10−1 (3.63 × 10−2) + | 8.87 × 10−1 (5.44 × 10−3) − | 9.24 × 10−1 (2.93 × 10−3) | |
| WFG3 | 100 | 3.66 × 10−1 (1.33 × 10−2) − | 1.73 × 10−1 (9.82 × 10−3) − | 5.34 × 10−1 (3.96 × 10−2) + | 3.96 × 10−1 (2.14 × 10−3) − | 4.13 × 10−1 (3.08 × 10−3) |
| 500 | 3.62 × 10−1 (9.48 × 10−3) − | 1.53 × 10−1 (1.35 × 10−2) − | 5.51 × 10−1 (3.63 × 10−2) + | 3.84 × 10−1 (2.91 × 10−3) − | 4.11 × 10−1 (2.50 × 10−3) | |
| 1000 | 3.60 × 10−1 (7.88 × 10−3) − | 1.51 × 10−1 (1.02 × 10−2) − | 5.34 × 10−1 (3.96 × 10−2) + | 3.62 × 10−1 (1.14 × 10−2) − | 4.10 × 10−1 (2.66 × 10−3) | |
| BT1 | 100 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 6.71 × 10−1 (1.14 × 10−2) |
| 500 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 6.18 × 10−1 (1.61 × 10−2) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 5.53 × 10−1 (2.72 × 10−2) | |
| BT2 | 100 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 1.34 × 10−2 (4.55 × 10−3) − | 3.24 × 10−1 (4.09 × 10−2) |
| 500 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 5.49 × 10−2 (2.24 × 10−2) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 3.72 × 10−1 (9.24 × 10−3) | |
| BT3 | 100 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 1.45 × 10−3 (3.99 × 10−3) − | 7.06 × 10−1 (4.61 × 10−3) |
| 500 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 6.96 × 10−1 (7.10 × 10−3) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 6.79 × 10−1 (6.91 × 10−3) | |
| BT6 | 100 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 6.24 × 10−1 (1.54 × 10−2) |
| 500 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.51 × 10−1 (3.63 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 5.85 × 10−1 (1.08 × 10−2) | |
| 1000 | 0.00 × 100 (0.00 × 100) − | 0.00 × 100 (0.00 × 100) − | 5.34 × 10−1 (3.96 × 10−2) + | 0.00 × 100 (0.00 × 100) − | 5.43 × 10−1 (1.90 × 10−2) | |
| +/−/= | 0/45/0 | 4/40/1 | 7/37/1 | 4/41/0 | ||
| Problem | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|
| LSMOP1 | 6.94 × 100 (8.21 × 10−1) − | 1.65 × 10−1 (1.82 × 10−1) − | 2.40 × 10−1 (8.69 × 10−2) − | 2.19 × 10−1 (2.59 × 10−3) − | 5.62 × 10−2 (3.52 × 10−3) |
| LSMOP2 | 1.08 × 10−1 (4.91 × 10−3) − | 9.69 × 10−2 (8.76 × 10−2) − | 6.03 × 10−2 (1.08 × 10−3) + | 7.28 × 10−2 (1.34 × 10−3) + | 8.63 × 10−2 (2.42 × 10−3) |
| LSMOP3 | 1.69 × 101 (2.32 × 100) − | 9.38 × 10−1 (1.21 × 100) = | 6.96 × 10−1 (1.65 × 10−1) − | 4.12 × 10−1 (6.30 × 10−2) + | 6.10 × 10−1 (7.95 × 10−2) |
| LSMOP4 | 3.03 × 10−1 (9.56 × 10−3) − | 1.37 × 10−1 (1.02 × 10−1) − | 9.90 × 10−2 (2.49 × 10−3) − | 1.24 × 10−1 (3.35 × 10−3) − | 8.87 × 10−2 (5.95 × 10−3) |
| LSMOP5 | 1.04 × 101 (2.98 × 100) − | 3.84 × 100 (2.98 × 100) − | 2.29 × 10−1 (8.94 × 10−2) − | 5.41 × 10−1 (2.16 × 10−4) − | 7.29 × 10−2 (3.62 × 10−3) |
| LSMOP6 | 1.59 × 101 (6.45 × 102) − | 3.08 × 101 (1.23 × 102) − | 1.04 × 10−2 (3.21 × 10−1) + | 1.18 × 10−1 (2.02 × 10−3) − | 5.26 × 10−2 (9.46 × 10−1) |
| LSMOP7 | 1.58 × 100 (6.60 × 10−2) − | 1.36 × 100 (1.90 × 10−1) − | 9.78 × 10−1 (7.00 × 10−2) − | 9.00 × 10−1 (1.22 × 10−2) + | 9.17 × 10−1 (2.27 × 10−1) |
| LSMOP8 | 9.26 × 10−1 (6.60 × 10−2) − | 1.08 × 10−1 (7.33 × 10−3) − | 3.51 × 10−1 (1.98 × 10−2) − | 3.60 × 10−1 (9.23 × 10−3) − | 8.29 × 10−2 (4.33 × 10−3) |
| LSMOP9 | 4.07 × 101 (9.28 × 100) − | 1.29 × 100 (1.16 × 100) − | 1.30 × 100 (2.48 × 10−1) − | 1.19 × 100 (4.06 × 10−1) − | 1.82 × 10−1 (9.94 × 10−3) |
| +/−/= | 0/9/0 | 0/8/1 | 2/7/0 | 3/6/0 |
| Problem | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|
| LSMOP1 | 0.00 × 100 (0.00 × 100) − | 6.71 × 10−1 (2.21 × 10−1) − | 6.12 × 10−1 (7.79 × 10−4) − | 6.03 × 10−1 (1.24 × 10−1) − | 8.03 × 10−1 (7.08 × 10−3) |
| LSMOP2 | 7.41 × 10−1 (6.55 × 10−3) − | 7.70 × 10−1 (6.06 × 10−2) + | 7.95 × 10−1 (1.38 × 10−3) + | 8.08 × 10−1 (1.35 × 10−3) + | 7.50 × 10−1 (7.16 × 10−3) |
| LSMOP3 | 0.00 × 100 (0.00 × 100) − | 1.46 × 10−1 (1.02 × 10−1) = | 4.27 × 10−1 (1.03 × 10−1) + | 1.26 × 10−1 (1.16 × 10−1) = | 1.11 × 10−1 (5.89 × 10−2) |
| LSMOP4 | 4.78 × 10−1 (1.06 × 10−2) − | 7.13 × 10−1 (9.47 × 10−2) − | 7.37 × 10−1 (3.49 × 10−3) − | 7.62 × 10−1 (2.75 × 10−3) + | 7.51 × 10−1 (1.08 × 10−2) |
| LSMOP5 | 0.00 × 100 (0.00 × 100) − | 1.08 × 10−1 (1.63 × 10−1) − | 3.35 × 10−1 (1.66 × 10−3) − | 4.19 × 10−1 (4.33 × 10−2) − | 5.05 × 10−1 (6.57 × 10−3) |
| LSMOP6 | 0.00 × 100 (0.00 × 100) − | 1.27 × 10−1 (1.57 × 10−2) − | 8.54 × 10−1 (4.85 × 10−2) + | 6.32 × 10−1 (4.24 × 10−3) − | 8.14 × 10−1 (2.67 × 10−2) |
| LSMOP7 | 0.00 × 100 (0.00 × 100) − | 1.57 × 10−1 (1.92 × 10−2) − | 6.78 × 10−1 (1.71 × 10−2) − | 8.49 × 10−1 (4.74 × 10−2) + | 8.18 × 10−1 (1.71 × 10−2) |
| LSMOP8 | 2.78 × 10−2 (1.20 × 10−3) − | 4.31 × 10−1 (1.22 × 10−2) − | 3.64 × 10−1 (1.80 × 10−3) − | 3.51 × 10−1 (9.96 × 10−3) − | 4.77 × 10−1 (6.62 × 10−3) |
| LSMOP9 | 0.00 × 100 (0.00 × 100) − | 8.55 × 10−2 (6.57 × 10−2) − | 1.28 × 10−1 (4.18 × 10−2) − | 1.14 × 10−1 (2.18 × 10−2) − | 2.04 × 10−1 (5.25 × 10−3) |
| +/−/= | 0/9/0 | 1/7/1 | 3/6/0 | 3/5/1 |
| Problem | D | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|---|
| DTLZ1 | 100 | 168.83 | 224.63 | 474.65 | 243.91 | 227.60 |
| 300 | 272.06 | 384.71 | 607.00 | 576.66 | 352.90 | |
| 500 | 380.38 | 551.08 | 615.88 | 786.35 | 481.02 | |
| DTLZ2 | 100 | 157.58 | 230.39 | 464.97 | 240.74 | 230.78 |
| 300 | 236.75 | 370.66 | 577.62 | 561.55 | 346.33 | |
| 500 | 319.52 | 521.12 | 562.91 | 739.27 | 470.82 | |
| UF1 | 100 | 165.81 | 234.19 | 498.66 | 251.45 | 244.10 |
| 300 | 261.72 | 407.26 | 632.01 | 598.13 | 379.70 | |
| 500 | 369.13 | 572.05 | 625.15 | 810.61 | 496.00 | |
| UF2 | 100 | 175.96 | 257.42 | 577.15 | 271.65 | 268.19 |
| 300 | 313.04 | 460.12 | 901.47 | 733.59 | 458.52 | |
| 500 | 450.95 | 652.48 | 808.19 | 940.94 | 618.54 | |
| WFG1 | 100 | 66.41 | 88.65 | 216.48 | 91.92 | 129.69 |
| 300 | 270.90 | 366.31 | 664.18 | 529.00 | 436.69 | |
| 500 | 702.05 | 918.97 | 1420.00 | 1380.80 | 1192.80 | |
| WFG2 | 100 | 61.70 | 85.43 | 199.48 | 79.09 | 101.67 |
| 300 | 236.76 | 344.46 | 564.17 | 440.87 | 566.61 | |
| 500 | 586.46 | 881.83 | 1113.90 | 1107.10 | 1211.00 | |
| BT1 | 100 | 50.26 | 70.73 | 147.84 | 801.63 | 119.52 |
| 300 | 206.88 | 356.95 | 559.30 | 499.84 | 493.77 | |
| 500 | 568.67 | 936.16 | 1245.70 | 1526.20 | 1038.00 | |
| BT2 | 100 | 67.98 | 91.76 | 185.13 | 101.60 | 151.59 |
| 300 | 335.92 | 449.34 | 619.96 | 541.92 | 526.43 | |
| 500 | 886.51 | 1193.81 | 1559.92 | 1732.30 | 1193.90 | |
| LSMOP1 | 300 | 196.34 | 292.76 | 475.78 | 418.54 | 289.54 |
| LSMOP2 | 300 | 194.60 | 307.84 | 578.82 | 429.64 | 296.92 |
| LSMOP3 | 300 | 205.80 | 299.76 | 571.12 | 457.34 | 310.92 |
| LSMOP4 | 300 | 205.80 | 299.76 | 571.12 | 457.34 | 310.92 |
| Problem | D | MOEA/D2 | LMEA | IM-MOEA/D | FDV | LSMOEA-TM |
|---|---|---|---|---|---|---|
| DTLZ | 100 | 163.47 | 232.56 | 468.09 | 237.06 | 255.88 |
| 300 | 255.47 | 387.12 | 581.66 | 553.52 | 379.97 | |
| 500 | 359.72 | 554.70 | 591.68 | 744.48 | 499.60 | |
| UF | 100 | 170.09 | 245.30 | 528.12 | 262.98 | 252.13 |
| 300 | 286.20 | 440.89 | 733.59 | 643.87 | 437.47 | |
| 500 | 412.96 | 612.12 | 693.62 | 869.50 | 587.71 | |
| WFG | 100 | 67.56 | 88.97 | 208.45 | 84.90 | 115.65 |
| 300 | 262.25 | 359.12 | 605.24 | 472.18 | 475.27 | |
| 500 | 651.99 | 911.01 | 1228.20 | 1203.77 | 1066.97 | |
| BT | 100 | 59.95 | 82.81 | 166.00 | 333.91 | 117.82 |
| 300 | 282.39 | 409.16 | 600.34 | 542.06 | 499.83 | |
| 500 | 812.32 | 957.18 | 1061.06 | 1717.90 | 1103.87 | |
| LSMOP | 300 | 194.35 | 303.05 | 570.10 | 440.48 | 303.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Zhu, J.; Cao, L. A Stable Large-Scale Multiobjective Optimization Algorithm with Two Alternative Optimization Methods. Entropy 2023, 25, 561. https://doi.org/10.3390/e25040561
Liu T, Zhu J, Cao L. A Stable Large-Scale Multiobjective Optimization Algorithm with Two Alternative Optimization Methods. Entropy. 2023; 25(4):561. https://doi.org/10.3390/e25040561
Chicago/Turabian StyleLiu, Tianyu, Junjie Zhu, and Lei Cao. 2023. "A Stable Large-Scale Multiobjective Optimization Algorithm with Two Alternative Optimization Methods" Entropy 25, no. 4: 561. https://doi.org/10.3390/e25040561
APA StyleLiu, T., Zhu, J., & Cao, L. (2023). A Stable Large-Scale Multiobjective Optimization Algorithm with Two Alternative Optimization Methods. Entropy, 25(4), 561. https://doi.org/10.3390/e25040561






