Estimating the Number of Communities in Weighted Networks
Abstract
1. Introduction
2. Methodology
2.1. The Degree-Corrected Distribution-Free Model
2.2. Estimation of the Number of Communities
- Let be the top-k eigendecomposition of A.
- Let the matrix be the row normalization of such that for .
- Apply k-means algorithm on all rows of with k clusters to obtain .
3. Experimental Results
3.1. Simulations
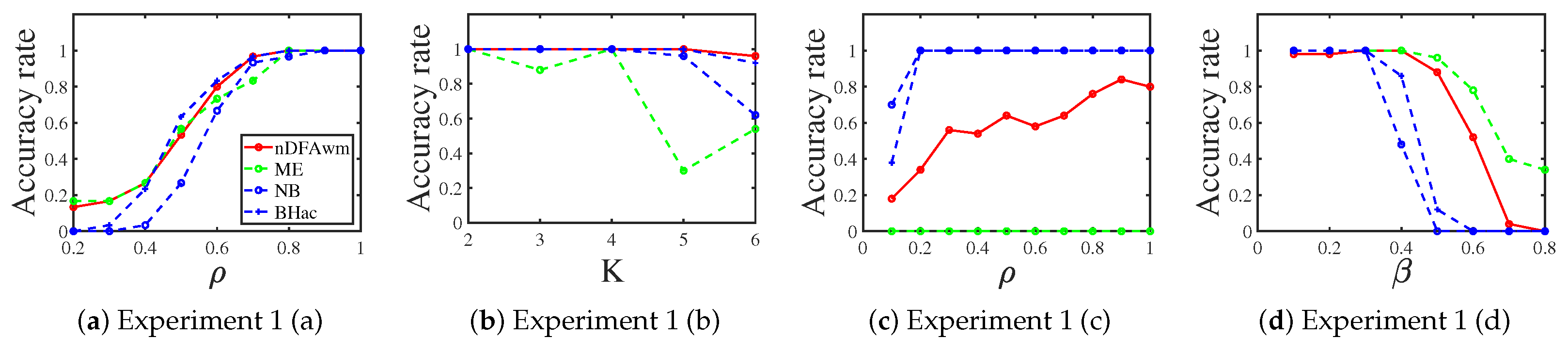
3.1.1. Bernoulli Distribution
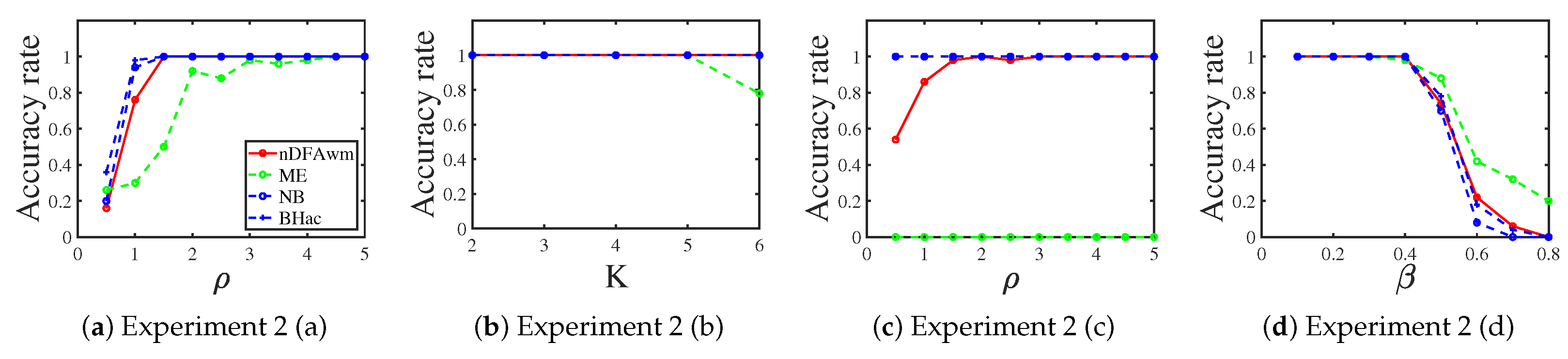
3.1.2. Binomial Distribution
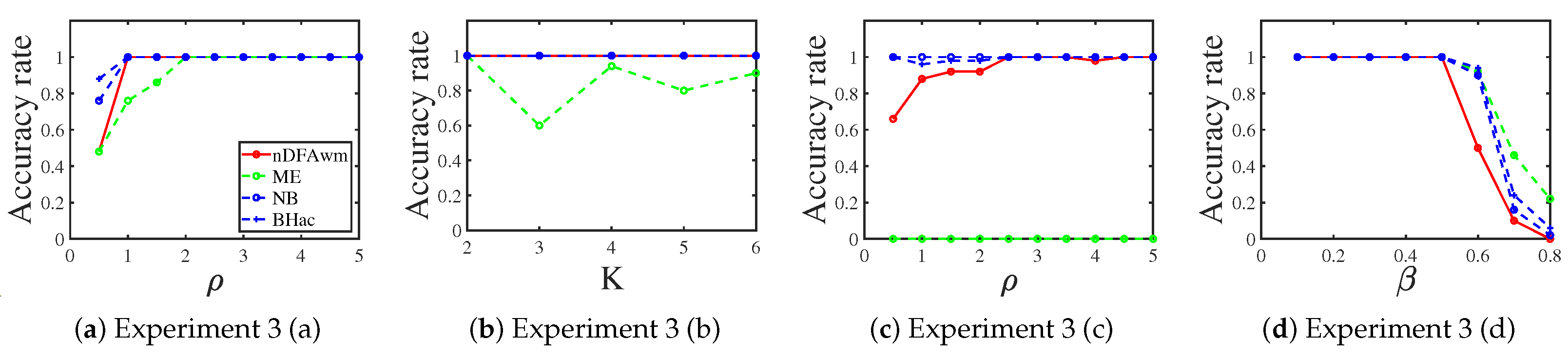
3.1.3. Poisson Distribution
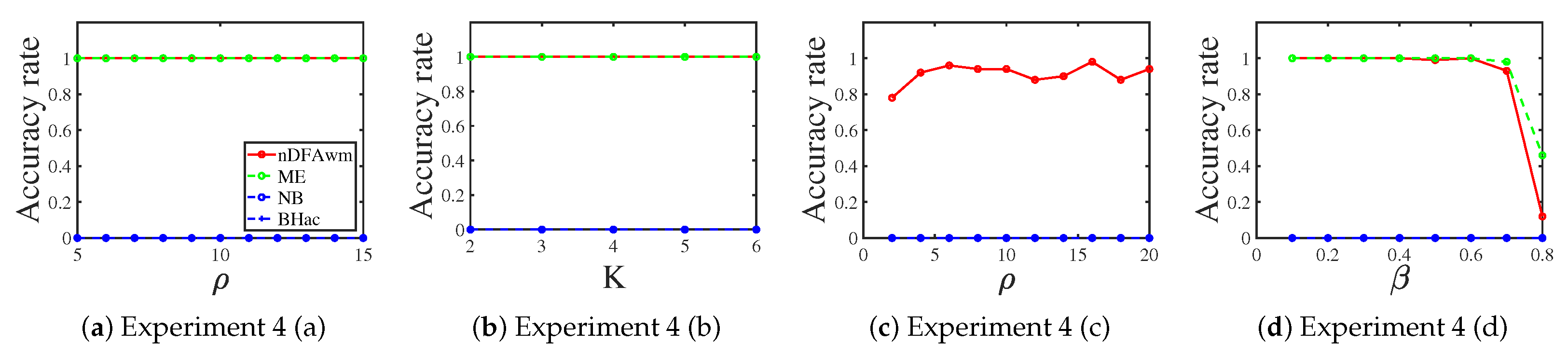
3.1.4. Geometric Distribution
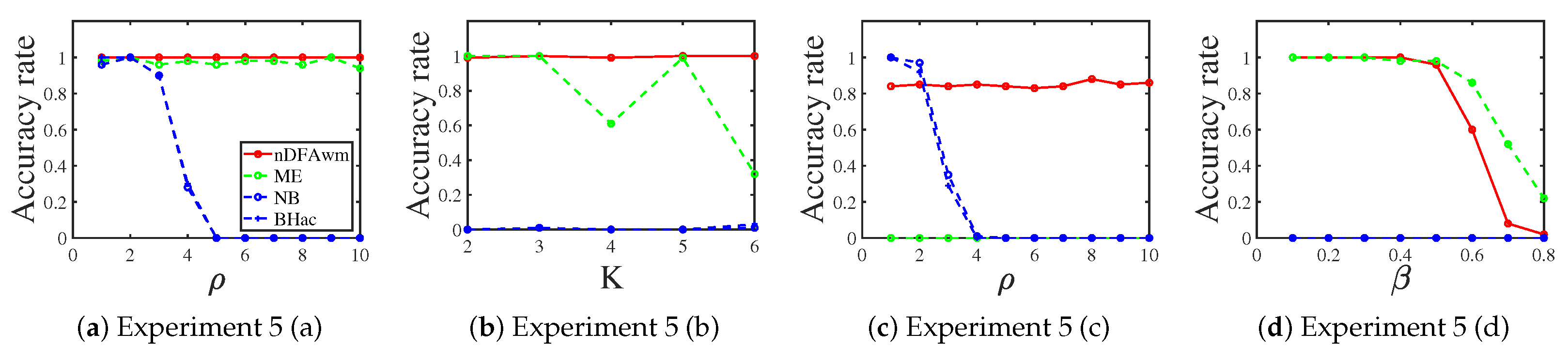
3.1.5. Exponential Distribution
3.1.6. Normal Distribution
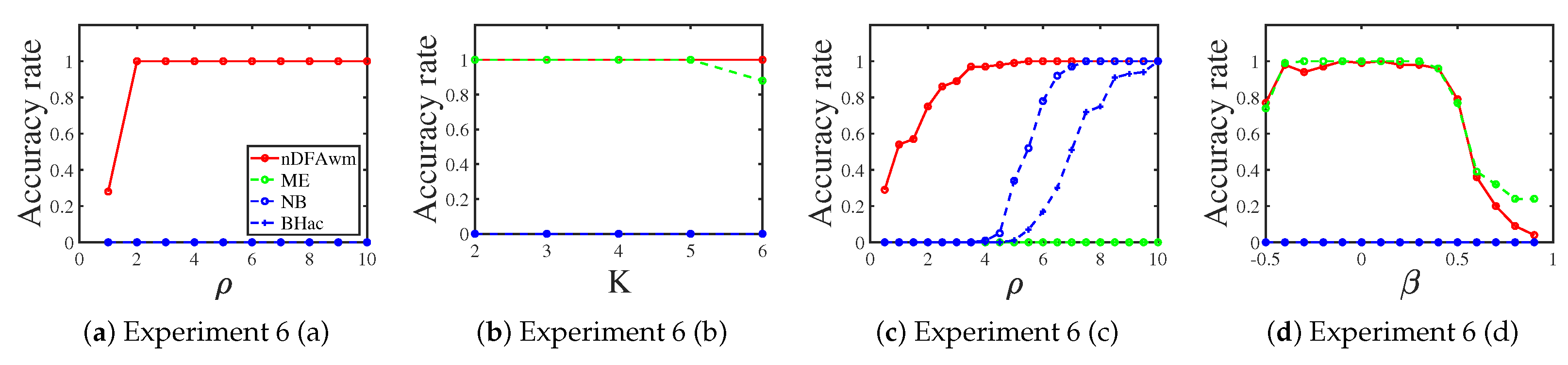
3.1.7. Laplace Distribution
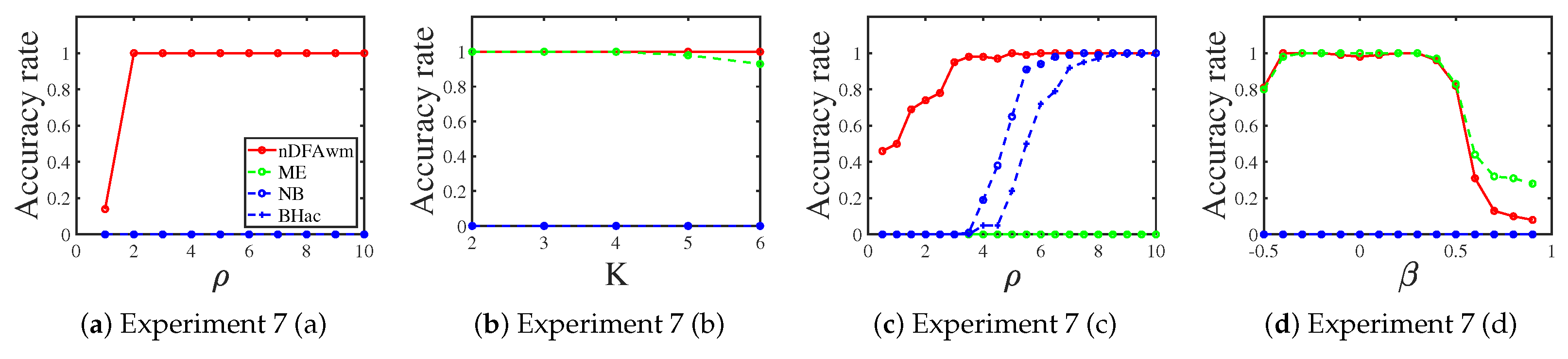
3.1.8. Uniform Distribution
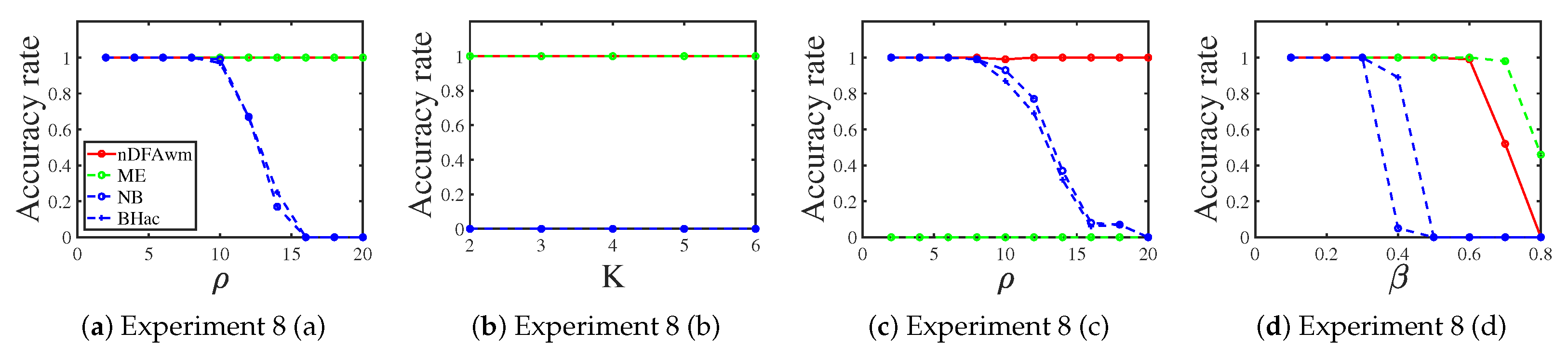
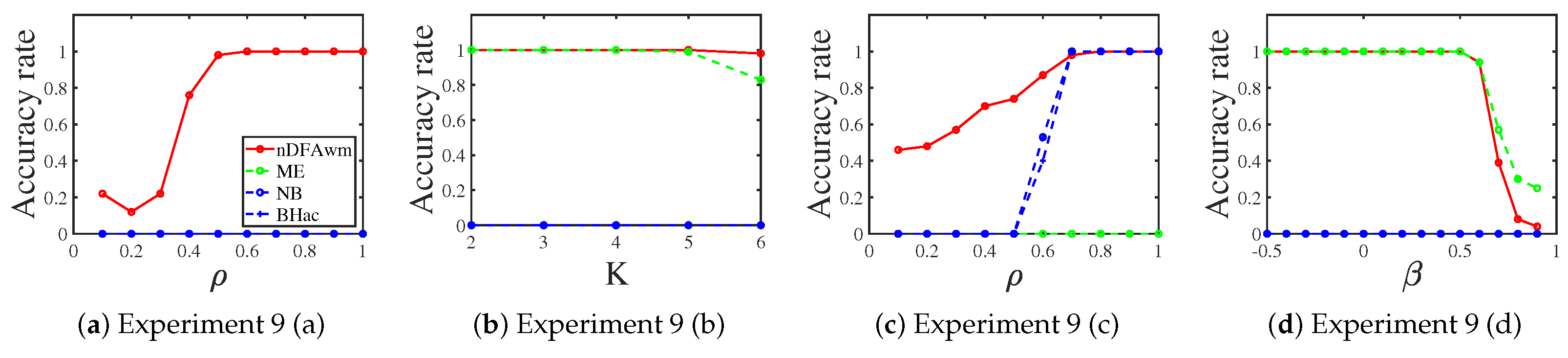
3.1.9. Signed Networks
3.2. Real-World Networks
4. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Lusseau, D.; Newman, M.E. Identifying the role that animals play in their social networks. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2004, 271, S477–S481. [Google Scholar] [CrossRef] [PubMed]
- Guimera, R.; Nunes Amaral, L.A. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef]
- Palla, G.; Barabási, A.L.; Vicsek, T. Quantifying social group evolution. Nature 2007, 446, 664–667. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Foster, J. From simplistic to complex systems in economics. Camb. J. Econ. 2005, 29, 873–892. [Google Scholar] [CrossRef]
- Schweitzer, F.; Fagiolo, G.; Sornette, D.; Vega-Redondo, F.; Vespignani, A.; White, D.R. Economic networks: The new challenges. Science 2009, 325, 422–425. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Chow, K.; Ay, A.; Elhesha, R.; Kahveci, T. ANCA: Alignment-based network construction algorithm. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, Washington, DC, USA, 29 August–1 September 2018; pp. 21–26. [Google Scholar]
- Elhesha, R.; Sarkar, A.; Cinaglia, P.; Boucher, C.; Kahveci, T. Co-evolving patterns in temporal networks of varying evolution. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, New York, NY, USA, 7–10 September 2019; pp. 494–503. [Google Scholar]
- Cinaglia, P.; Cannataro, M. Network alignment and motif discovery in dynamic networks. Netw. Model. Anal. Health Inform. Bioinform. 2022, 11, 38. [Google Scholar] [CrossRef]
- Newman, M.E. Analysis of weighted networks. Phys. Rev. E 2004, 70, 056131. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Newman, M.E. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. USA 2001, 98, 404–409. [Google Scholar] [CrossRef]
- Ji, P.; Jin, J. Coauthorship and citation networks for statisticians. Ann. Appl. Stat. 2016, 10, 1779–1812. [Google Scholar] [CrossRef]
- Ji, P.; Jin, J.; Ke, Z.T.; Li, W. Co-citation and Co-authorship Networks of Statisticians. J. Bus. Econ. Stat. 2022, 40, 469–485. [Google Scholar] [CrossRef]
- Schwikowski, B.; Uetz, P.; Fields, S. A network of protein–protein interactions in yeast. Nat. Biotechnol. 2000, 18, 1257–1261. [Google Scholar] [CrossRef]
- Ideker, T.; Sharan, R. Protein networks in disease. Genome Res. 2008, 18, 644–652. [Google Scholar] [CrossRef] [PubMed]
- Holland, P.W.; Laskey, K.B.; Leinhardt, S. Stochastic blockmodels: First steps. Soc. Netw. 1983, 5, 109–137. [Google Scholar] [CrossRef]
- Rohe, K.; Chatterjee, S.; Yu, B. Spectral clustering and the high-dimensional stochastic blockmodel. Ann. Stat. 2011, 39, 1878–1915. [Google Scholar] [CrossRef]
- Amini, A.A.; Chen, A.; Bickel, P.J.; Levina, E. Pseudo-likelihood methods for community detection in large sparse networks. Ann. Stat. 2013, 41, 2097–2122. [Google Scholar] [CrossRef]
- Lei, J.; Rinaldo, A. Consistency of spectral clustering in stochastic block models. Ann. Stat. 2015, 43, 215–237. [Google Scholar] [CrossRef]
- Jin, J. Fast community detection by SCORE. Ann. Stat. 2015, 43, 57–89. [Google Scholar] [CrossRef]
- Joseph, A.; Yu, B. Impact of regularization on spectral clustering. Ann. Stat. 2016, 44, 1765–1791. [Google Scholar] [CrossRef]
- Mao, X.; Sarkar, P.; Chakrabarti, D. On Mixed Memberships and Symmetric Nonnegative Matrix Factorizations. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2324–2333. [Google Scholar]
- Chen, Y.; Li, X.; Xu, J. Convexified modularity maximization for degree-corrected stochastic block models. Ann. Stat. 2018, 46, 1573–1602. [Google Scholar] [CrossRef]
- Zhang, Y.; Levina, E.; Zhu, J. Detecting overlapping communities in networks using spectral methods. SIAM J. Math. Data Sci. 2020, 2, 265–283. [Google Scholar] [CrossRef]
- Mao, X.; Sarkar, P.; Chakrabarti, D. Overlapping Clustering Models, and One (class) SVM to Bind Them All. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31, pp. 2126–2136. [Google Scholar]
- Mao, X.; Sarkar, P.; Chakrabarti, D. Estimating Mixed Memberships With Sharp Eigenvector Deviations. J. Am. Stat. Assoc. 2020, 116, 1928–1940. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Xu, J. Convex relaxation methods for community detection. Stat. Sci. 2021, 36, 2–15. [Google Scholar] [CrossRef]
- Jing, B.; Li, T.; Ying, N.; Yu, X. Community detection in sparse networks using the symmetrized laplacian inverse matrix (slim). Stat. Sin. 2022, 32, 1. [Google Scholar] [CrossRef]
- Newman, M.E.; Reinert, G. Estimating the number of communities in a network. Phys. Rev. Lett. 2016, 117, 078301. [Google Scholar] [CrossRef] [PubMed]
- Bickel, P.J.; Sarkar, P. Hypothesis testing for automated community detection in networks. J. R. Stat. Soc. Ser. B Stat. Methodol. 2016, 78, 253–273. [Google Scholar] [CrossRef]
- Lei, J. A goodness-of-fit test for stochastic block models. Ann. Stat. 2016, 44, 401–424. [Google Scholar] [CrossRef]
- Riolo, M.A.; Cantwell, G.T.; Reinert, G.; Newman, M.E. Efficient method for estimating the number of communities in a network. Phys. Rev. E 2017, 96, 032310. [Google Scholar] [CrossRef]
- Saldaña, D.F.; Yu, Y.; Feng, Y. How many communities are there. J. Comput. Graph. Stat. 2017, 26, 171–181. [Google Scholar] [CrossRef]
- Wang, Y.R.; Bickel, P.J. Likelihood-based model selection for stochastic block models. Ann. Stat. 2017, 45, 500–528. [Google Scholar] [CrossRef]
- Yan, B.; Sarkar, P.; Cheng, X. Provable estimation of the number of blocks in block models. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual Event, 28–30 March 2022; pp. 1185–1194. [Google Scholar]
- Chen, K.; Lei, J. Network cross-validation for determining the number of communities in network data. J. Am. Stat. Assoc. 2018, 113, 241–251. [Google Scholar] [CrossRef]
- Ma, S.; Su, L.; Zhang, Y. Determining the number of communities in degree-corrected stochastic block models. J. Mach. Learn. Res. 2021, 22. [Google Scholar]
- Le, C.M.; Levina, E. Estimating the number of communities by spectral methods. Electron. J. Stat. 2022, 16, 3315–3342. [Google Scholar] [CrossRef]
- Jin, J.; Ke, Z.T.; Luo, S.; Wang, M. Optimal estimation of the number of network communities. J. Am. Stat. Assoc. 2022. [Google Scholar] [CrossRef]
- Aicher, C.; Jacobs, A.Z.; Clauset, A. Learning latent block structure in weighted networks. J. Complex Netw. 2015, 3, 221–248. [Google Scholar] [CrossRef]
- Jog, V.; Loh, P.L. Recovering communities in weighted stochastic block models. In Proceedings of the 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–2 October 2015; pp. 1308–1315. [Google Scholar]
- Ahn, K.; Lee, K.; Suh, C. Hypergraph Spectral Clustering in the Weighted Stochastic Block Model. IEEE J. Sel. Top. Signal Process. 2018, 12, 959–974. [Google Scholar] [CrossRef]
- Palowitch, J.; Bhamidi, S.; Nobel, A.B. Significance-based community detection in weighted networks. J. Mach. Learn. Res. 2018, 18, 1–48. [Google Scholar]
- Peixoto, T.P. Nonparametric weighted stochastic block models. Phys. Rev. E 2018, 97, 12306. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Jog, V.; Loh, P.L. Optimal rates for community estimation in the weighted stochastic block model. Ann. Stat. 2020, 48, 183–204. [Google Scholar] [CrossRef]
- Ng, T.L.J.; Murphy, T.B. Weighted stochastic block model. Stat. Methods Appl. 2021, 30, 1365–1398. [Google Scholar] [CrossRef] [PubMed]
- Qing, H. Distribution-Free Model for Community Detection. Prog. Theor. Exp. Phys. 2023, 2023, 033A01. [Google Scholar] [CrossRef]
- Qing, H. Degree-corrected distribution-free model for community detection in weighted networks. Sci. Rep. 2022, 12, 15153. [Google Scholar] [CrossRef]
- Karrer, B.; Newman, M.E.J. Stochastic blockmodels and community structure in networks. Phys. Rev. E 2011, 83, 16107. [Google Scholar] [CrossRef] [PubMed]
- Gómez, S.; Jensen, P.; Arenas, A. Analysis of community structure in networks of correlated data. Phys. Rev. E 2009, 80, 016114. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Budel, G.; Van Mieghem, P. Detecting the number of clusters in a network. J. Complex Netw. 2020, 8, cnaa047. [Google Scholar] [CrossRef]
- Yang, B.; Cheung, W.; Liu, J. Community mining from signed social networks. IEEE Trans. Knowl. Data Eng. 2007, 19, 1333–1348. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, X.; Pellegrini, M.; Wang, X. Discovering communities in complex networks by edge label propagation. Sci. Rep. 2016, 6, 22470. [Google Scholar] [CrossRef]
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Read, K.E. Cultures of the central highlands, New Guinea. Southwest. J. Anthropol. 1954, 10, 1–43. [Google Scholar] [CrossRef]
- Ferligoj, A.; Kramberger, A. An analysis of the slovene parliamentary parties network. Dev. Stat. Methodol. 1996, 12, 209–216. [Google Scholar]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Adamic, L.A.; Glance, N. The political blogosphere and the 2004 US election: Divided they blog. In Proceedings of the 3rd International Workshop on Link Discovery, Chicago, IL, USA, 21–25 August 2005; pp. 36–43. [Google Scholar]
- Qing, H. Mixed membership distribution-free model. arXiv 2021, arXiv:2112.04389. [Google Scholar]
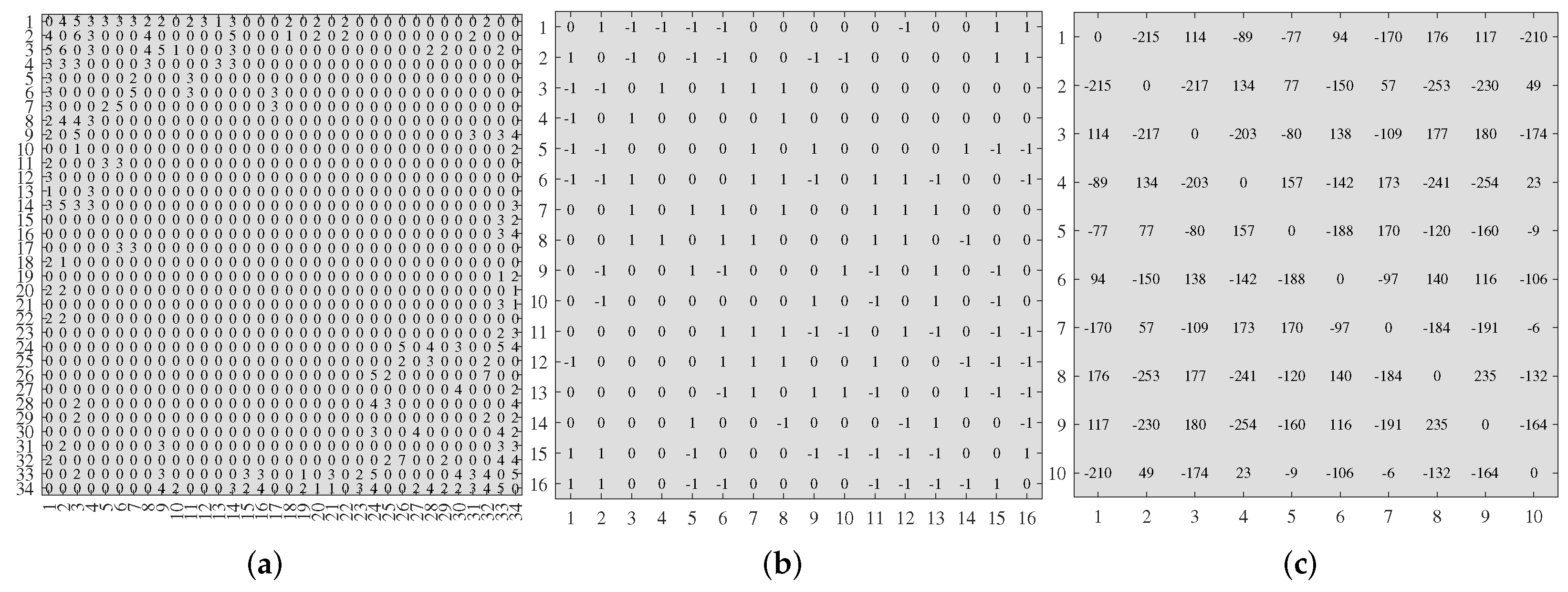

| Dataset | Source | n | K | Weighted? | nDFAwm | ME | NB | BHm | BHa | BHmc | BHac |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Karate club (weighted) | [63] | 34 | 2 | Yes | 2 | 2 | 4 | 4 | 4 | 4 | 4 |
| Gahuku-Gama subtribes | [64] | 16 | 3 | Yes | 3 | N/A | 1 | 1 | 12 | N/A | 13 |
| Slovene Parliamentary Party | [65] | 10 | 2 | Yes | 2 | 2 | N/A | N/A | N/A | N/A | N/A |
| Dolphins | [66] | 62 | 2, 4 | No | 4 | 2 | 2 | 2 | 2 | 2 | 2 |
| College football | [67] | 110 | 11 | No | 11 | 10 | 10 | 10 | 10 | 10 | 10 |
| Karate club | [63] | 34 | 2 | No | 2 | 34 | 2 | 2 | 2 | 2 | 2 |
| Political books | [68] | 105 | 3 | No | 4 | 2 | 3 | 3 | 4 | 4 | 4 |
| Political blogs | [69] | 1222 | 2 | No | 2 | 2 | 7 | 7 | 7 | 8 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qing, H. Estimating the Number of Communities in Weighted Networks. Entropy 2023, 25, 551. https://doi.org/10.3390/e25040551
Qing H. Estimating the Number of Communities in Weighted Networks. Entropy. 2023; 25(4):551. https://doi.org/10.3390/e25040551
Chicago/Turabian StyleQing, Huan. 2023. "Estimating the Number of Communities in Weighted Networks" Entropy 25, no. 4: 551. https://doi.org/10.3390/e25040551
APA StyleQing, H. (2023). Estimating the Number of Communities in Weighted Networks. Entropy, 25(4), 551. https://doi.org/10.3390/e25040551






