Piecewise Business Bubble System under Classical and Nonsingular Kernel of Mittag–Leffler Law
Abstract
1. Introduction


 and represent the Atangana—Baleanu and integer-order global derivative, respectively. from are defined in Equation (2).
and represent the Atangana—Baleanu and integer-order global derivative, respectively. from are defined in Equation (2).2. Basic Results

 by
by  in (4) to obtain the Caputo–Fabrizio operator.
in (4) to obtain the Caputo–Fabrizio operator.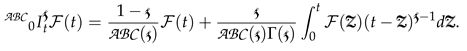


3. Theoretical Analysis


- (A1)
- ∃; ∀ we have
- (A2)
- ∃&;







4. Numerical Scheme






5. Numerical Simulation
 .
.6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shilnikov, L.P. A case of the existence of a denumerable set of periodic motion. Sov. Math. Dokl. 1965, 6, 163–166. [Google Scholar]
- Bella, G.; Mattana, P.; Venturi, B. Shilnikov chaos in the Lucas model of endogenous growth. J. Econ. Theory 2017, 172, 451–477. [Google Scholar] [CrossRef]
- Bernanke, B.; Mark, G. VAgency costs. Net Worth and Business Fluctuations. Am. Econ. Rev. 1989, 14, 14–31. [Google Scholar]
- Carlstrom, C.T.; Fuerst, T.S. Agency costs, net worth, and business fluctuations: A computable general equilibrium analysis. Am. Econ. Rev. 1997, 87, 893–910. [Google Scholar]
- Kiyotaki, N.; Moore, J. Credit cycles. J. Political Econ. 1997, 105, 211–248. [Google Scholar] [CrossRef]
- Bernanke, B.S.; Gertler, M.; Gilchrist, S. The financial accelerator in a quantitative business cycle framework. Handb. Macroecon. 1999, 1, 1341–1393. [Google Scholar]
- Blanchard, O.; Watson, M. Bubbles, Rational Expectations and Financial Markets; D.C. Heathand Company: Lexington, MA, USA, 1982. [Google Scholar]
- Kocherlakota, N. Bursting Bubbles: Consequences and Cures; Federal Reserve Bank of Minneapolis: Minneapolis, MN, USA, 2009; Volume 84, Unpublished manuscript. [Google Scholar]
- Miao, J.; Wang, P. Bubbles and total factor productivity. Am. Econ. Rev. 2012, 102, 82–87. [Google Scholar] [CrossRef]
- Weil, P. Confidence and the real value of money in an overlapping generations economy. Q. J. Econ. 1987, 102, 1–22. [Google Scholar] [CrossRef]
- Miao, J.; Wang, P.; Zhou, J. Housing Bubbles and Policy Analysis; Unpublished Working Paper; Boston University and HKUST: Boston, MA, USA, 2014. [Google Scholar]
- Bella, G.; Mattana, P. Chaos control in presence of financial bubbles. Econ. Lett. 2020, 193, 109314. [Google Scholar] [CrossRef]
- Miao, J.; Wang, P. Banking bubbles and financial crises. J. Econ. Theory 2015, 157, 763–792. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A 1995, 28, 6567–6584. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Hilfer, R. Threefold Introduction to Fractional Derivatives. In Anomalous Transport: Foundations and Applications; Wiley-VCH Verlag: Weinheim, Germany, 2008. [Google Scholar]
- Miller, K.S. Fractional differential equations. J. Fract. Calc. 1993, 3, 49–57. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Xuan, L.; Arfan, M.; Rahman, M.u.; Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Eng. 2022, 26, 98–112. [Google Scholar]
- Zhang, L.; Rahman, M.u.; Arfan, M.; Ali, A. Investigation of mathematical model of transmission co-infection TB in HIV community with a non-singular kernel. Results Phys. 2021, 28, 104559. [Google Scholar] [CrossRef]
- Liu, X.; ur Rahmamn, M.; Ahmad, S.; Baleanu, D.; Nadeem Anjam, Y. A new fractional infectious disease model under the non-singular Mittag–Leffler derivative. Waves Random Complex Media 2022, 1–27, Unpublished manuscript. [Google Scholar] [CrossRef]
- Mahmood, T.; Al-Duais, F.S.; Sun, M. Dynamics of Middle East Respiratory Syndrome Coronavirus (MERS-CoV) involving fractional derivative with Mittag-Leffler kernel. Phys. A Stat. Mech. Appl. 2022, 606, 128144. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Ghaziani, R.K.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2022; Unpublished manuscript. [Google Scholar]
- Li, B.; Zhang, Y.; Li, X.; Eskandari, Z.; He, Q. Bifurcation analysis and complex dynamics of a Kopel triopoly model. J. Comput. Appl. Math. 2023, 426, 115089. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New concept in calculus:Piecewise differential and integral operators. Chaos Soliton Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Sohail, A.; Yu, Z.; Arif, R.; Nutini, A.; Nofal, T.A. Piecewise differentiation of the fractional order CAR-T cells-SARS-2 virus model. Results Phys. 2022, 33, 105046. [Google Scholar] [CrossRef]
- Atangana, A.; Toufik, M. A piecewise heat equation with constant and variable order coefficients: A new approach to capture crossover behaviors in heat diffusion. AIMS Math. 2022, 7, 8374–8389. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M. A numerical approach for a class of nonlinear optimal control problems with piecewise fractional derivative. Chaos Solitons Fractals 2021, 152, 111465. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T.; Ali, A. Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative. Chaos Solitons Fractals 2022, 161, 112356. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Saifullah, S.; Inc, M. Oscillatory, crossover behavior and chaos analysis of HIV-1 infection model using piece-wise Atangana–Baleanu fractional operator: Real data approach. Chaos, Solitons Fractals 2022, 164, 112662. [Google Scholar] [CrossRef]
- Mahmood, T.; Rahman, M.u.; Arfan, M.; Kayani, S.I.; Sun, M. Mathematical study of Algae as a bio-fertilizer using fractal–fractional dynamic model. Math. Comput. Simul. 2023, 203, 207–222. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. Study of a mathematical model of COVID-19 outbreak using some advanced analysis. Waves Random Complex Media, 2022; 1–18, Unpublished manuscript. [Google Scholar]
- Shah, K.; Abdeljawad, T.; Abdalla, B.; Abualrub, M.S. Utilizing fixed point approach to investigate piecewise equations with non-singular type derivative. AIMS Math. 2022, 7, 14614–14630. [Google Scholar] [CrossRef]
- Shah, K.; Naz, H.; Abdeljawad, T.; Abdalla, B. Study of Fractional Order Dynamical System of Viral Infection Disease under Piecewise Derivative. Comput. Model. Eng. Sci. 2023, 136, 921–941. [Google Scholar]
 and the time durations on the subintervals.
and the time durations on the subintervals.
 and the time durations on the subintervals.
and the time durations on the subintervals.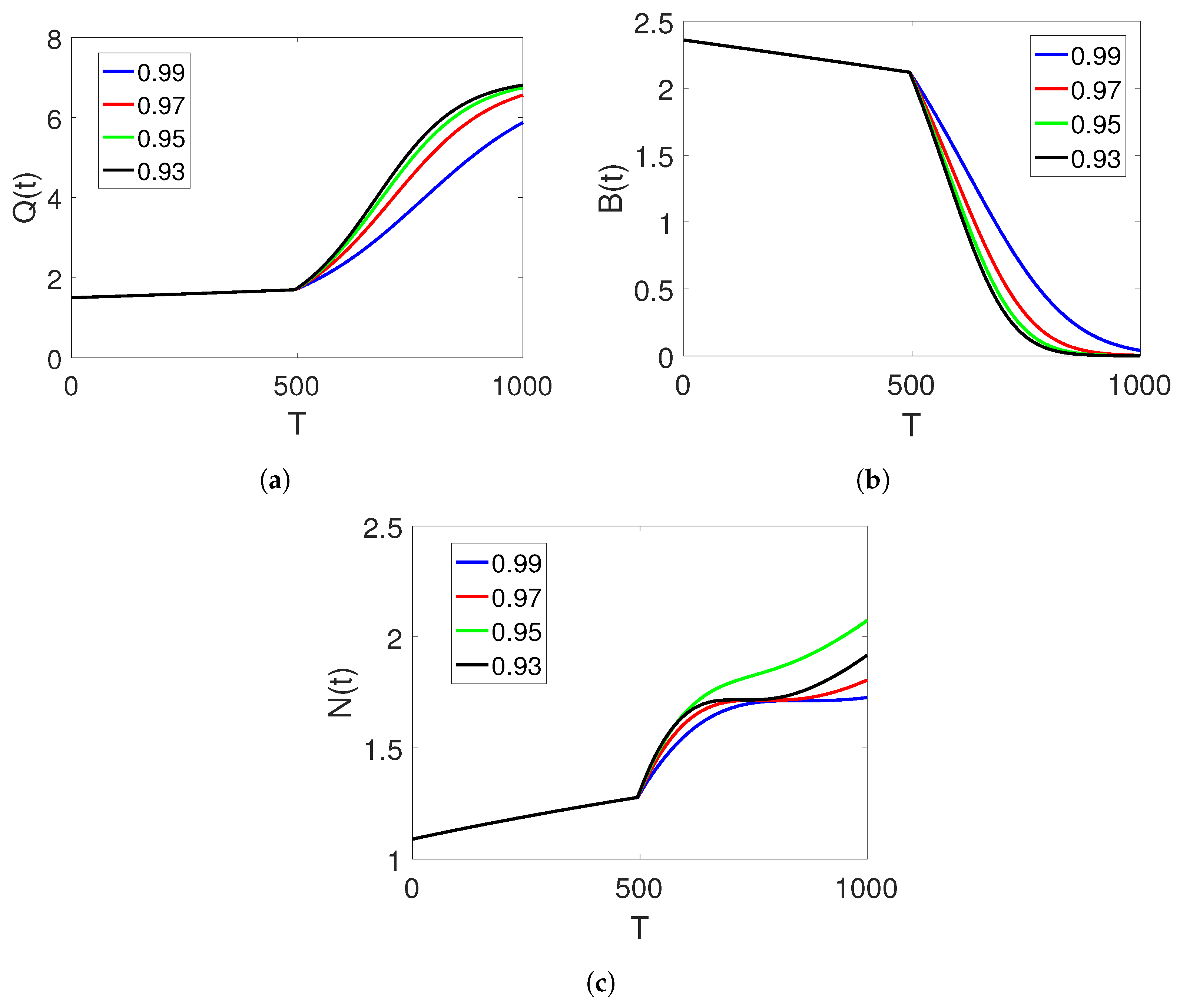
 , and the time durations on two sets of intervals.
, and the time durations on two sets of intervals.
 , and the time durations on two sets of intervals.
, and the time durations on two sets of intervals.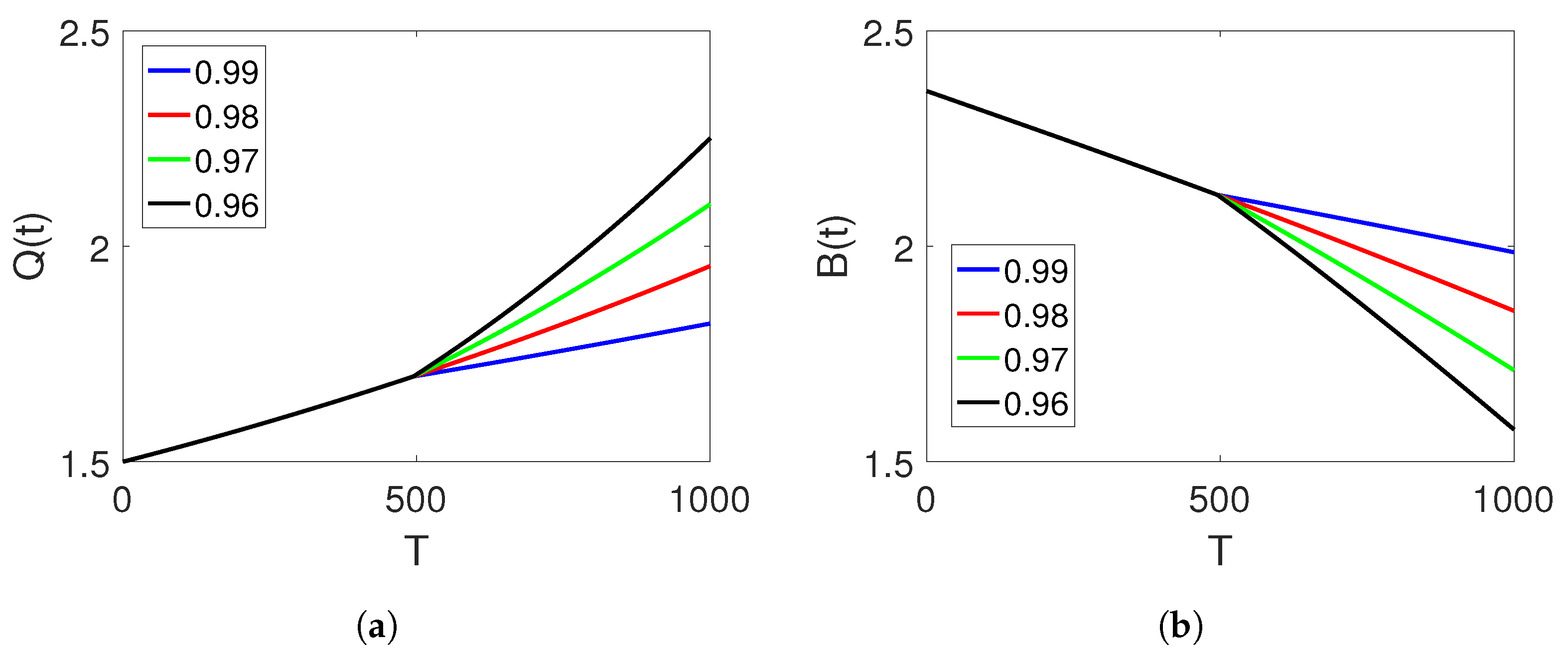
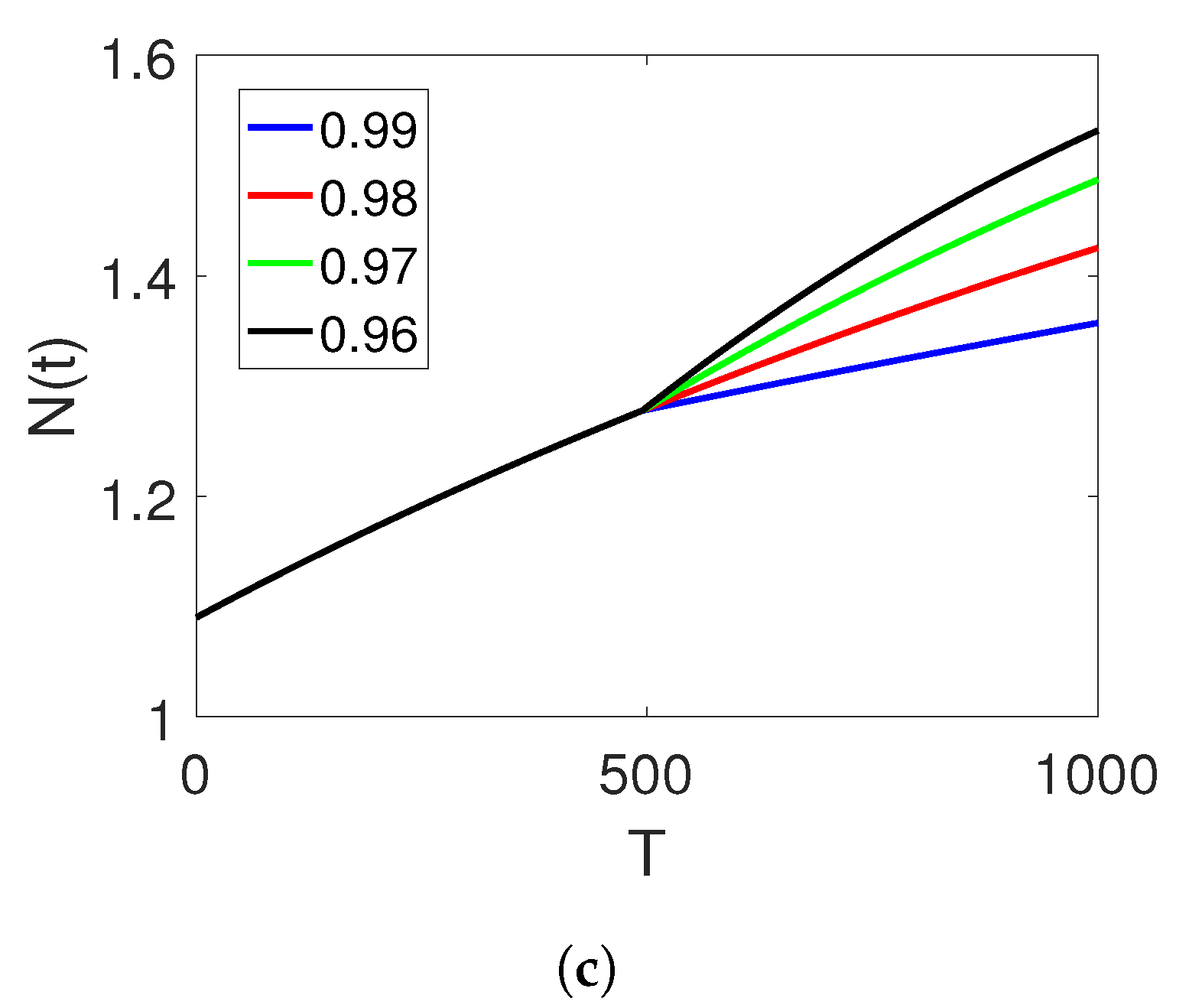
 and the time durations on the two sets of intervals.
and the time durations on the two sets of intervals.
 and the time durations on the two sets of intervals.
and the time durations on the two sets of intervals.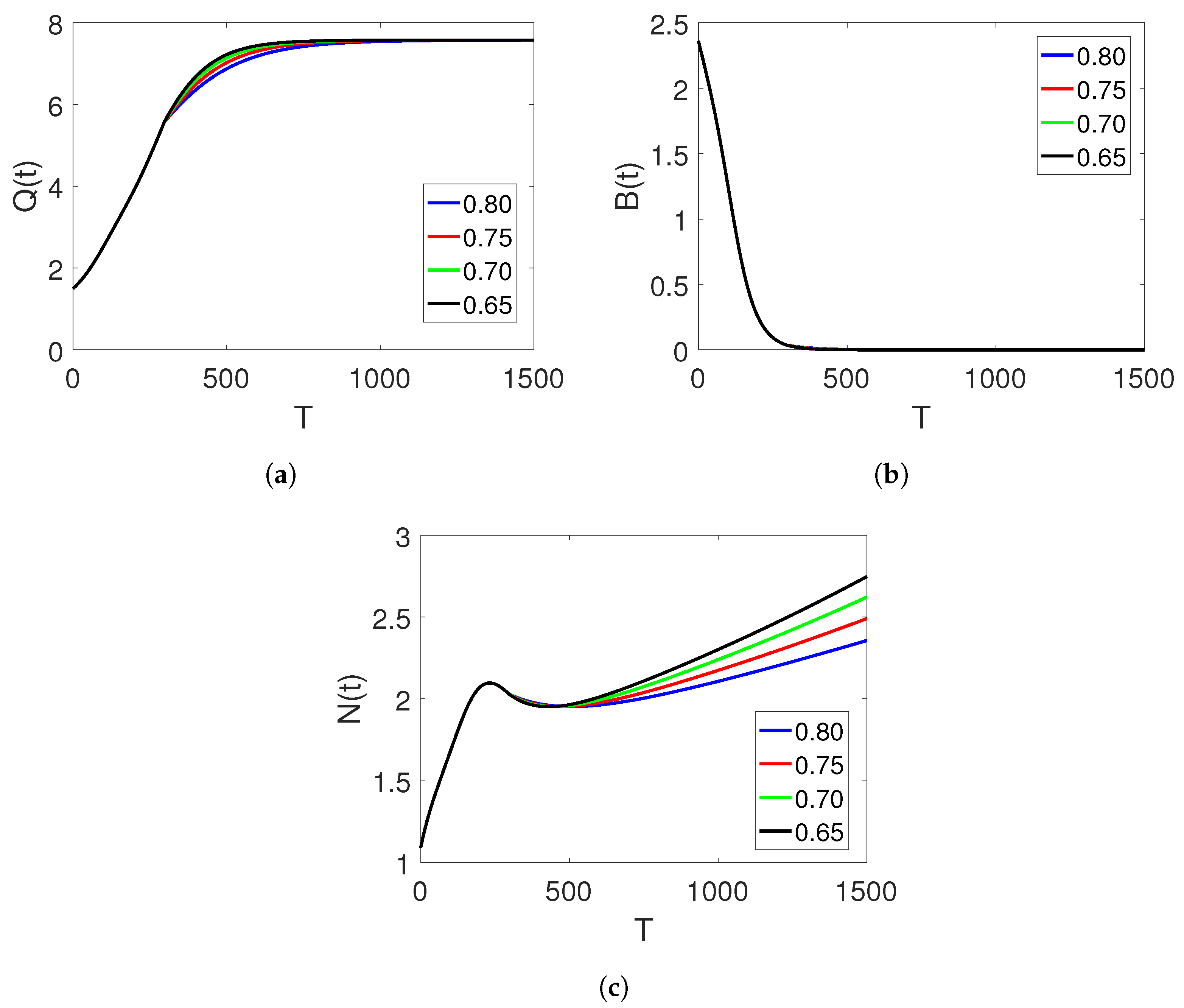
 , and the time durations on two set of intervals.
, and the time durations on two set of intervals.
 , and the time durations on two set of intervals.
, and the time durations on two set of intervals.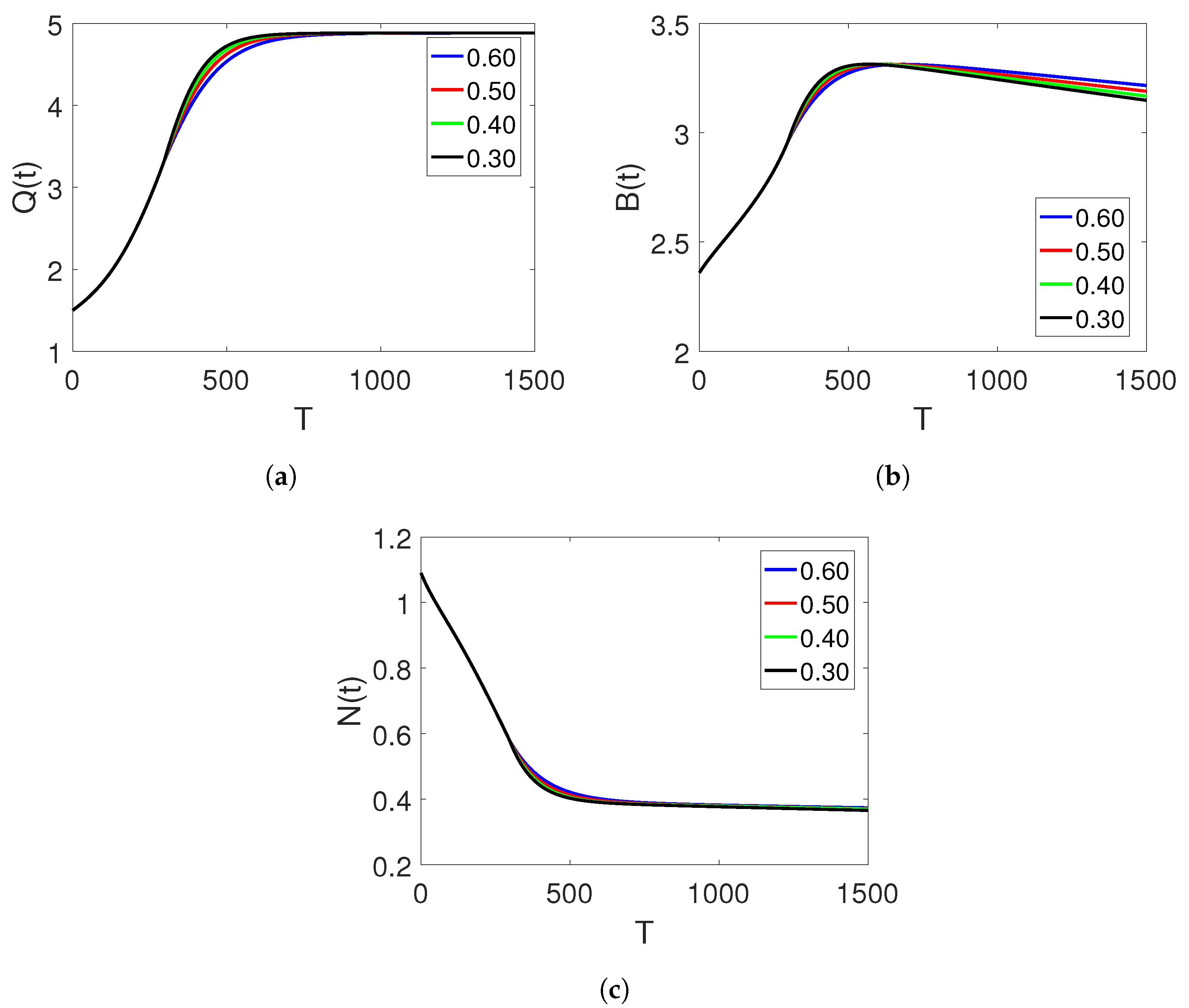
 , and the time durations on two sets of intervals.
, and the time durations on two sets of intervals.
 , and the time durations on two sets of intervals.
, and the time durations on two sets of intervals.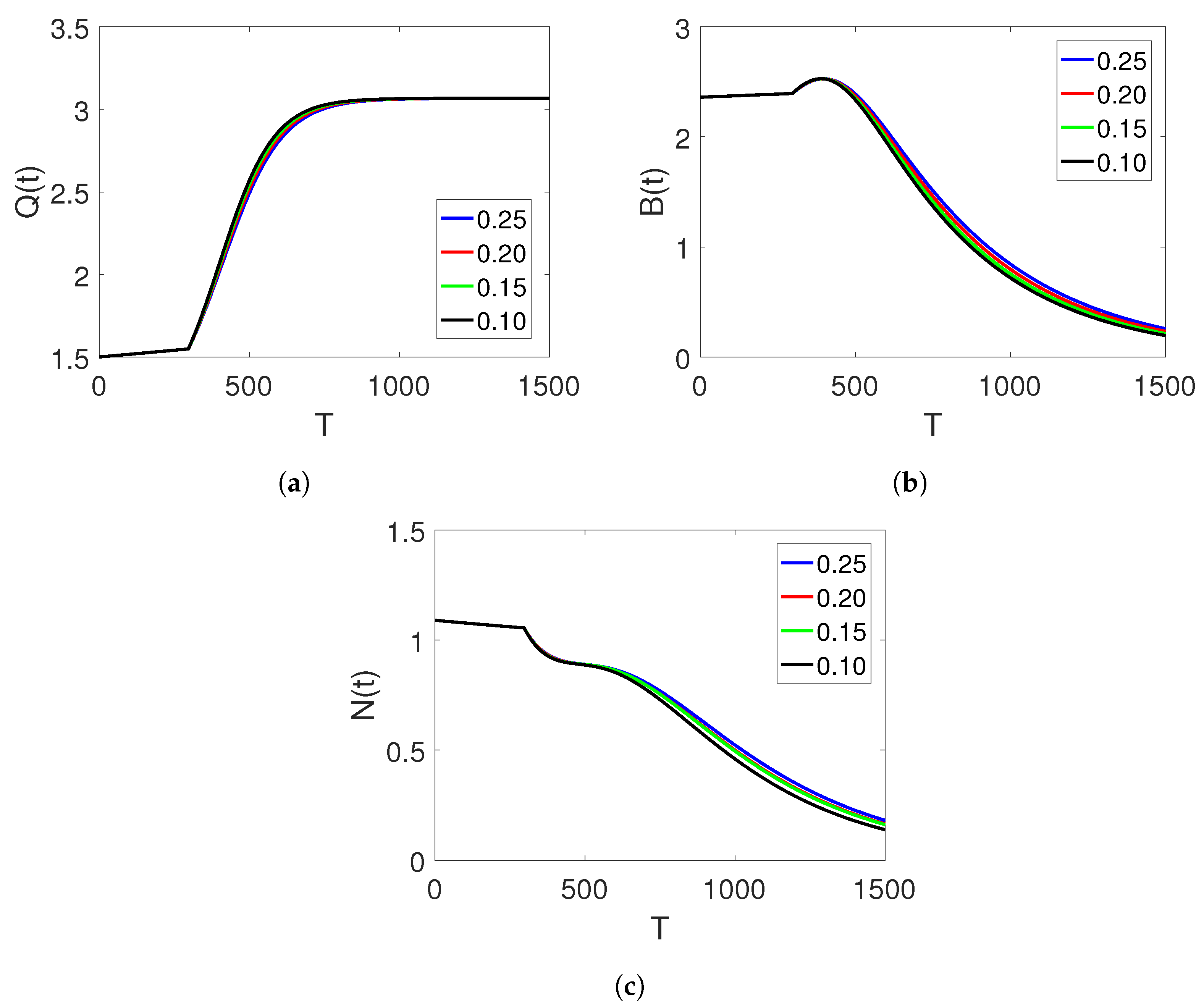
 and the time durations on the two set of intervals.
and the time durations on the two set of intervals.
 and the time durations on the two set of intervals.
and the time durations on the two set of intervals.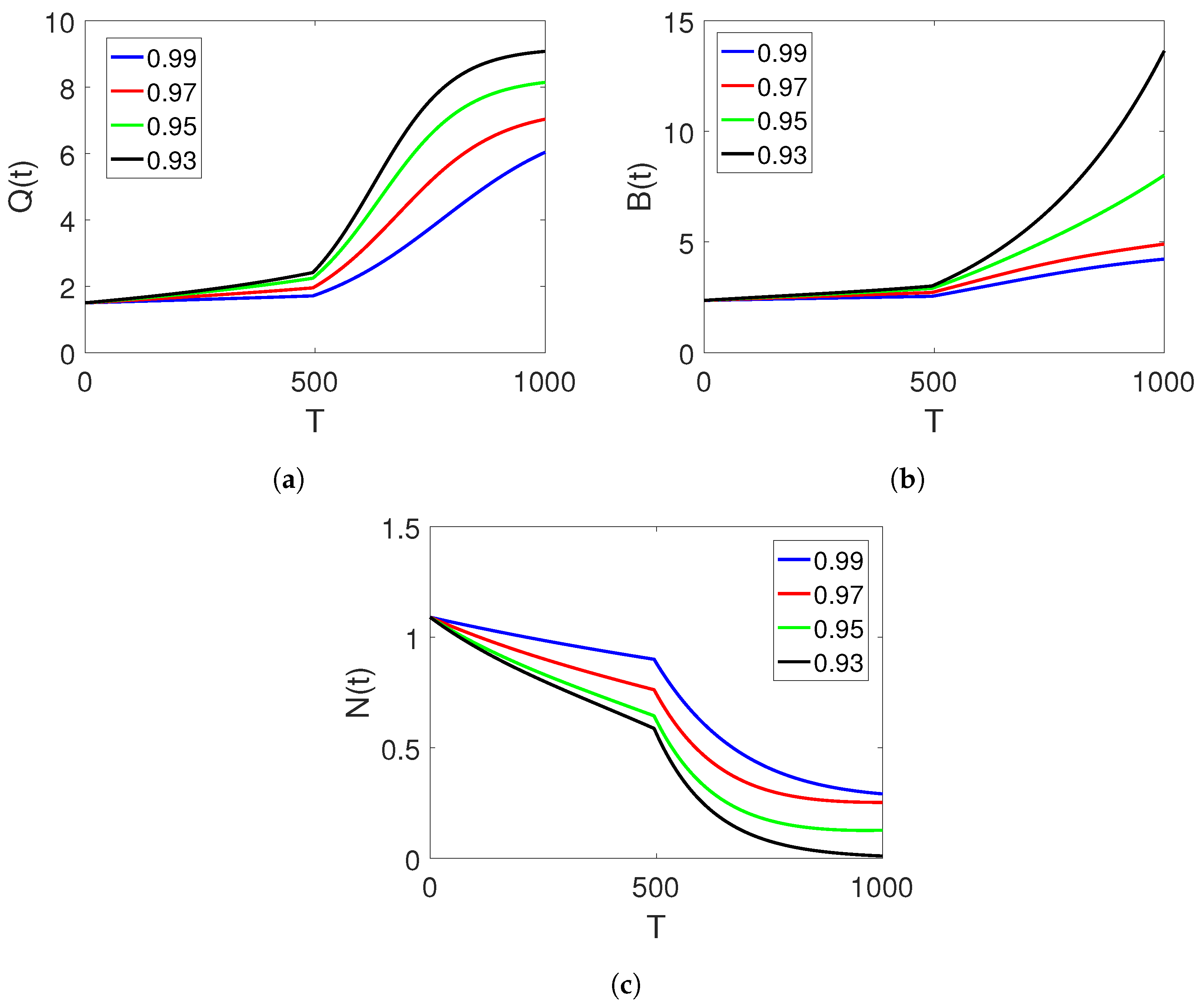
 , and the time durations on the two set of intervals.
, and the time durations on the two set of intervals.
 , and the time durations on the two set of intervals.
, and the time durations on the two set of intervals.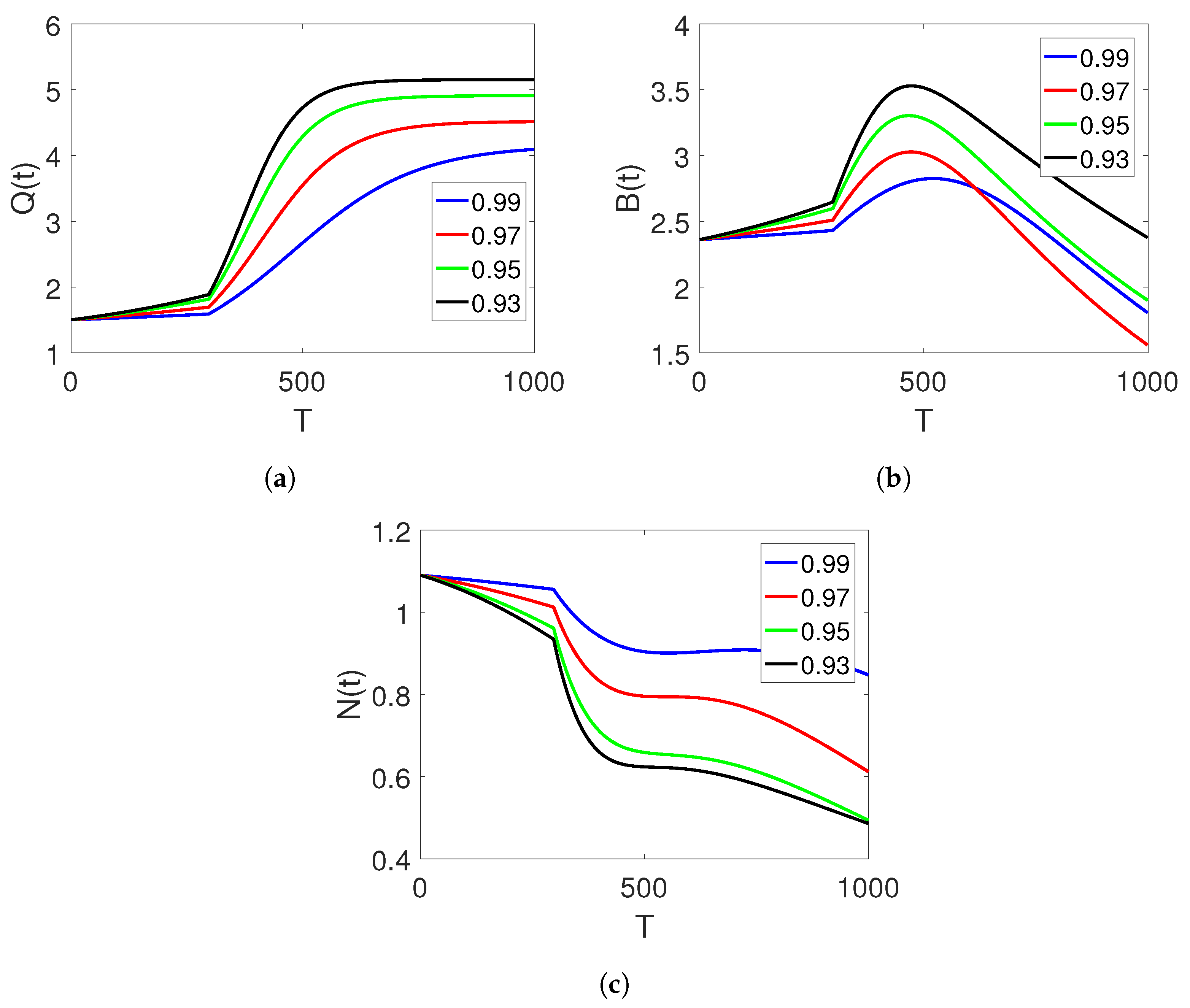
 and the time durations on the two set of intervals.
and the time durations on the two set of intervals.
 and the time durations on the two set of intervals.
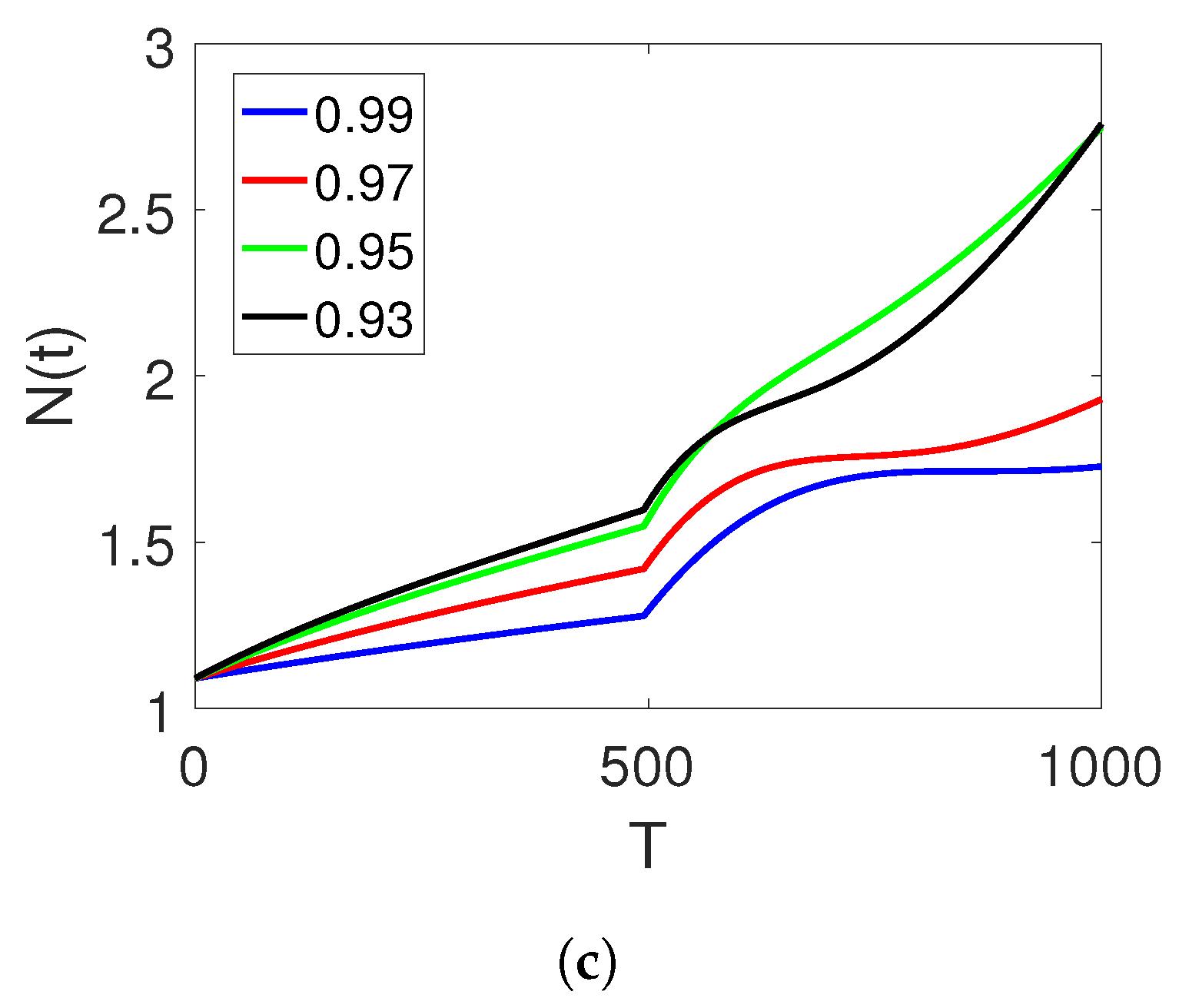
and the time durations on the two set of intervals.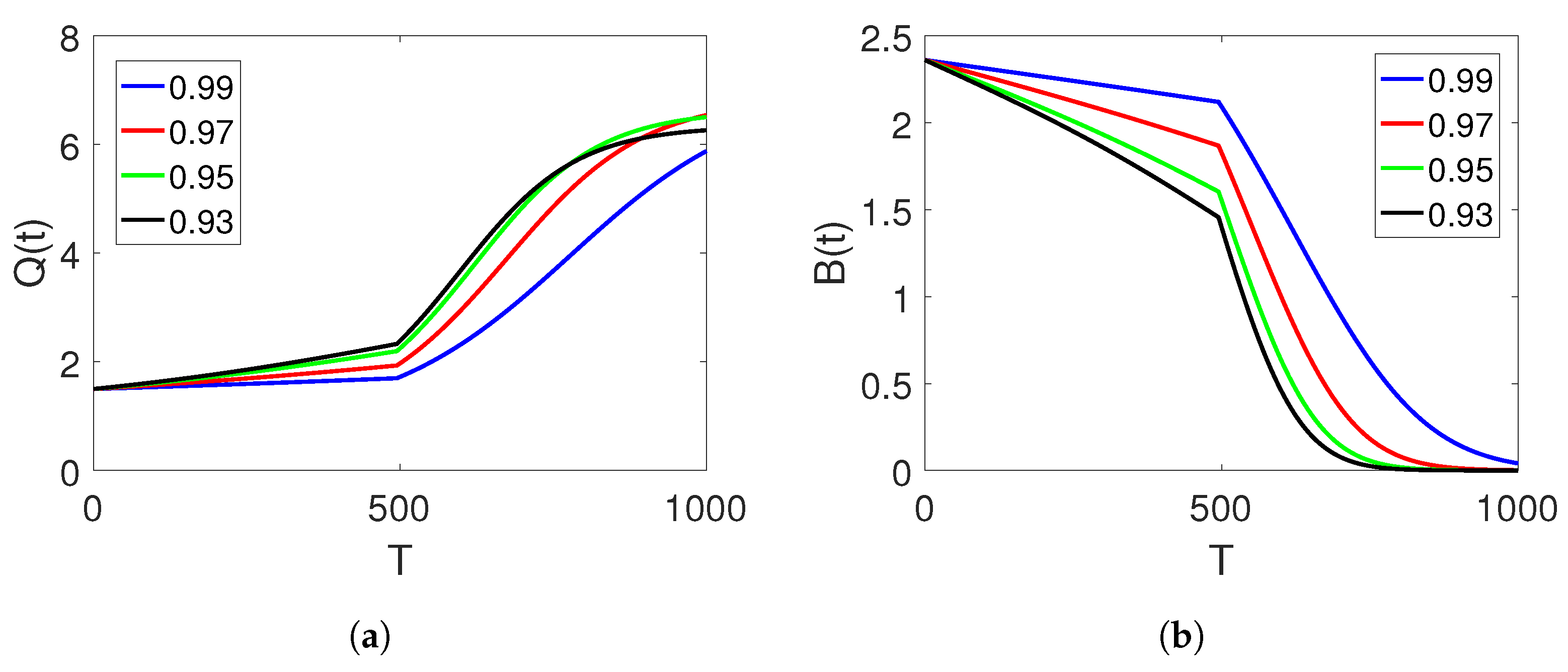
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, B. Piecewise Business Bubble System under Classical and Nonsingular Kernel of Mittag–Leffler Law. Entropy 2023, 25, 459. https://doi.org/10.3390/e25030459
Zhang C, Li B. Piecewise Business Bubble System under Classical and Nonsingular Kernel of Mittag–Leffler Law. Entropy. 2023; 25(3):459. https://doi.org/10.3390/e25030459
Chicago/Turabian StyleZhang, Chao, and Bo Li. 2023. "Piecewise Business Bubble System under Classical and Nonsingular Kernel of Mittag–Leffler Law" Entropy 25, no. 3: 459. https://doi.org/10.3390/e25030459
APA StyleZhang, C., & Li, B. (2023). Piecewise Business Bubble System under Classical and Nonsingular Kernel of Mittag–Leffler Law. Entropy, 25(3), 459. https://doi.org/10.3390/e25030459





